13.2.1 平面的基本性质 学案(2课时,含答案) 2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 13.2.1 平面的基本性质 学案(2课时,含答案) 2024-2025学年高一数学苏教版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 392.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 21:07:11 | ||
图片预览



文档简介
13.2.1 平面的基本性质(1)
1. 借助长方体,直观认识空间的点、直线、平面的位置关系.
2. 了解3个基本事实,并能解决一些简单的问题.
活动一 背景引入
背景1:生活中常见的如黑板、平整的操场、桌面、平静的湖面等等,都给我们以平面的形象;
背景2:椅子放不稳,是地面不平还是椅子本身有问题?
背景3:用两个合页和一把锁就可以将一扇门固定,将一把直尺置于桌面,通过是否漏光就能检查桌面是否平整,为什么?
活动二 平面的概念及表示方法
1. 几何画法:
一般用水平放置的__________作为平面的直观图
一个平面被另一个平面遮挡住,为了增强立体感,被遮挡部分用________画出来
2. 符号表示:
平面通常用希腊字母α,β,γ,…表示,如图中的平面α,也可以用平行四边形的两个相对顶点的字母表示,如平面AC等.
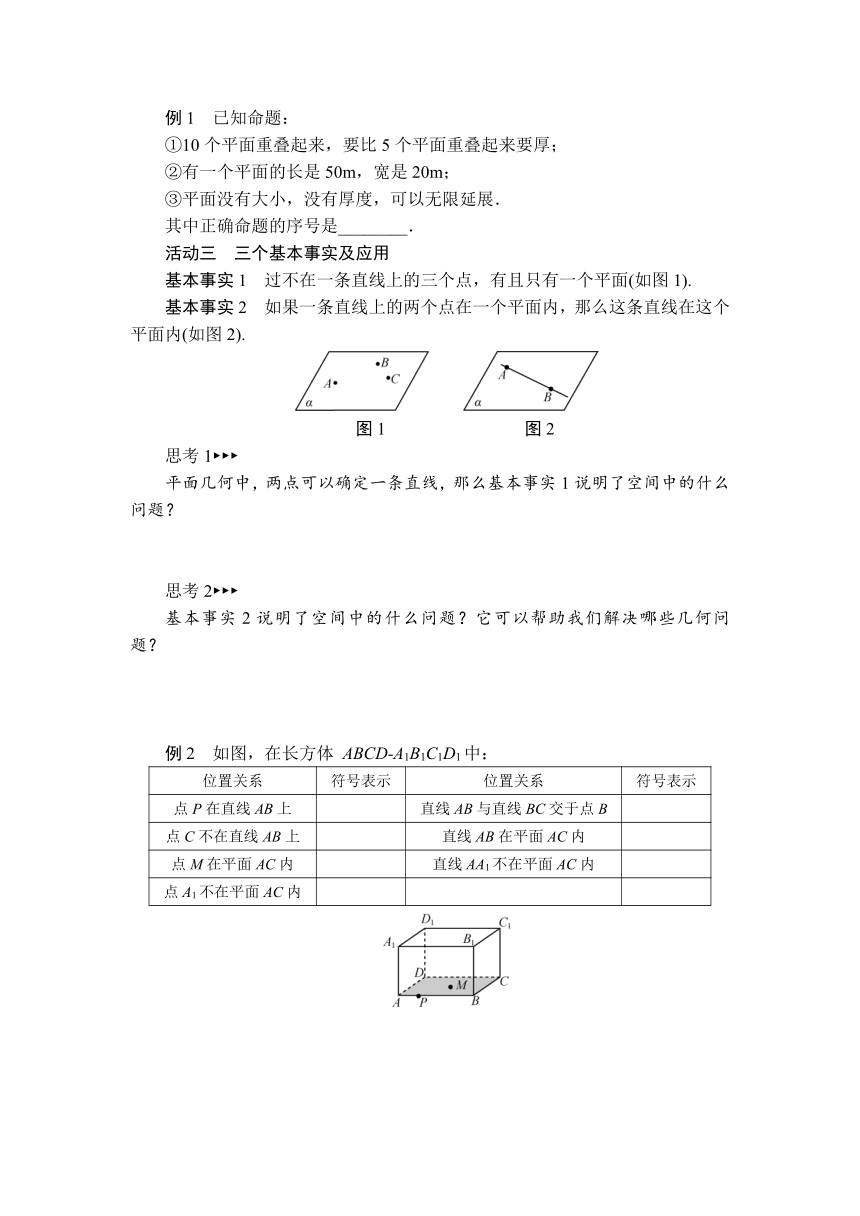
例1 已知命题:
①10个平面重叠起来,要比5个平面重叠起来要厚;
②有一个平面的长是50m,宽是20m;
③平面没有大小,没有厚度,可以无限延展.
其中正确命题的序号是________.
活动三 三个基本事实及应用
基本事实1 过不在一条直线上的三个点,有且只有一个平面(如图1).
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内(如图2).
图1 图2
思考1
平面几何中,两点可以确定一条直线,那么基本事实1说明了空间中的什么问题?
思考2
基本事实2说明了空间中的什么问题?它可以帮助我们解决哪些几何问题?
例2 如图,在长方体 ABCD-A1B1C1D1中:
位置关系 符号表示 位置关系 符号表示
点P在直线AB上 直线AB与直线BC交于点B
点C不在直线AB上 直线AB在平面AC内
点M在平面AC内 直线AA1不在平面AC内
点A1不在平面AC内
1. 点与直线的关系,是元素与集合的关系,只有∈, 两种关系.
2. 直线与平面都是由点构成的集合,它们之间的关系是集合与集合的关系,用 , 来表示.
3. 空间图形中用大写的英文字母表示点,小写的英文字母表示直线,这一点与集合中的表示不同.
用符号可以表示基本事实2:
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
基本事实3用图形表示为:
用符号表示为:
思考3
基本事实3说明了空间中的什么问题?它可以帮助我们解决哪些空间问题?
例3 根据下列符号语言画出相应图形.
α∩β=l,A∈l,AB α,AC β.
1. 借助集合中的符号,将空间的点看成元素,将直线与平面看成表示点的集合,但表示两直线或直线与平面的交点时,点的字母外不加集合的符号.
2. 对于空间中的符号语言和图形语言及文字语言要灵活转换.
用数学符号表示图中的点、直线、平面之间的位置关系.
例4 已知D,E分别是△ABC的边AC,BC上的点,平面α经过D,E 两点.
(1) 求作直线AB 与平面α的交点P;
(2) 求证:D,E,P三点共线.
依据基本事实3,要证明三点共线,只要说明这三个点是两个平面的公共点即可.
如图,在正方体ABCD-A1B1C1D1 中,点Q 在线段A1C上,且点Q在平面ABC1D1 内,求证:B,Q,D1 三点共线.
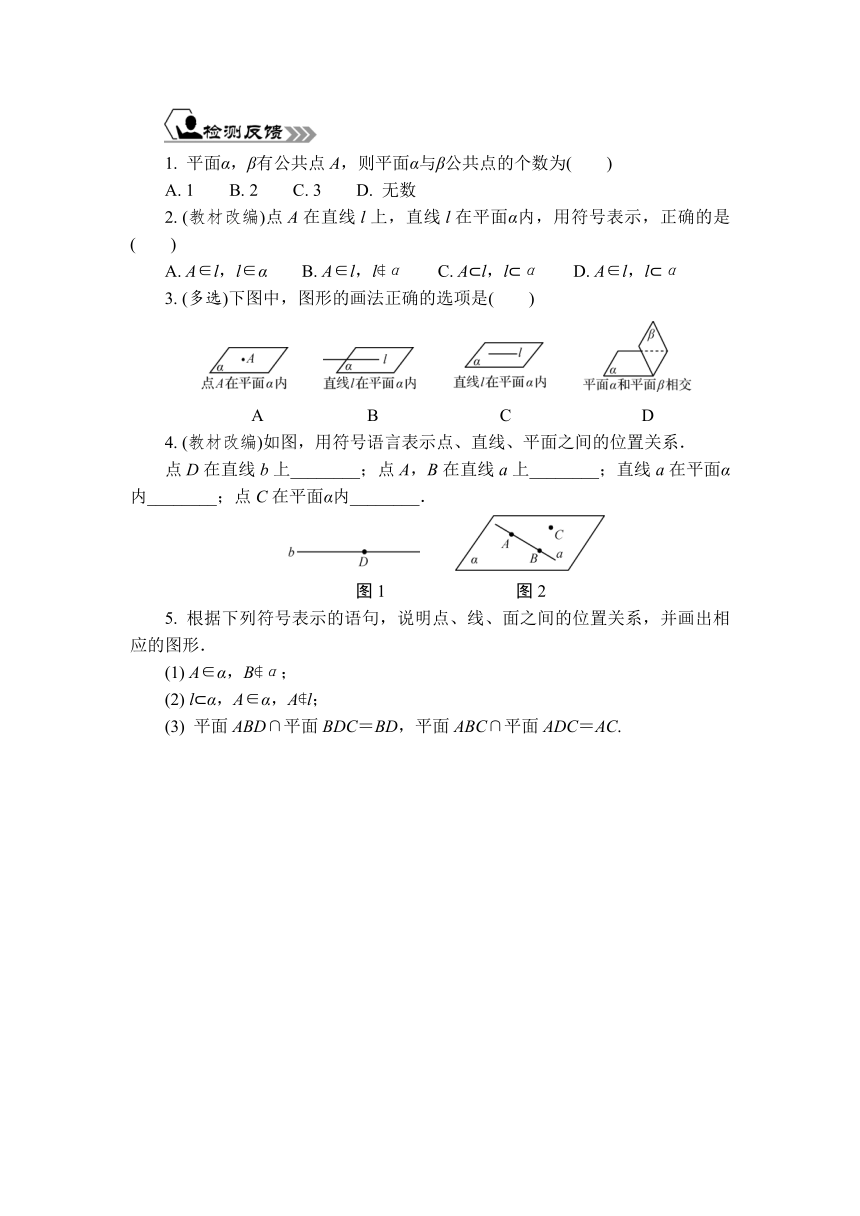
1. 平面α,β有公共点A,则平面α与β公共点的个数为( )
A. 1 B. 2 C. 3 D. 无数
2. (教材改编)点A在直线l上,直线l在平面α内,用符号表示,正确的是( )
A. A∈l,l∈α B. A∈l,l α C. A l,l α D. A∈l,l α
3. (多选)下图中,图形的画法正确的选项是( )
A B C D
4. (教材改编)如图,用符号语言表示点、直线、平面之间的位置关系.
点D在直线b上________;点A,B在直线a上________;直线a在平面α内________;点C在平面α内________.
图1 图2
5. 根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形.
(1) A∈α,B α;
(2) l α,A∈α,A l;
(3) 平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC.
13.2.1 平面的基本性质(2)
1. 了解由基本事实得到的三个推论.
2. 能运用3个基本事实及其推论解决一些简单的问题.
活动一 了解确定平面的依据
经过不在同一条直线上的三点,有且只有一个平面,即不共线的三点确定一个平面.
用图形表示为
过不共线的三点A,B,C的平面通常记作“平面ABC”.
思考1
自行车的撑脚一般安装在自行车的什么位置?能不能安装在前后轮一条直线的地方
思考2
照相机支架需要几条腿?两条行不行?
回顾基本事实1,体会确定一个平面的条件.
思考3
分别经过三点、四点能确定唯一的平面吗?为什么?
思考4
过一条直线l和直线l外一点A的平面有几个?
推论1:经过一条直线和这条直线外的一点,有且只有一个平面.
已知:直线l,点A l.
求证:过直线l和点A有且只有一个平面.
证明:
推论2:经过两条相交直线,有且只有一个平面.
已知:直线a,b相交.
求证:过直线a,b有且只有一个平面.
证明:
推论3:经过两条平行直线,有且只有一个平面.
已知:直线a∥b.
求证:过直线a,b有且只有一个平面.
证明:
思考5
下图是一张倒置的桌子,你能用所学的知识检查一下桌子的四条腿的底端是否在同一个平面内吗?
活动二 平面基本性质的简单应用
例1 已知A∈l,B∈l,C∈l,D l.求证:直线AD,BD,CD共面.
确定一个平面,只要根据基本事实1及 3个推论即可.
如图,已知l1∩l2=A,l2∩l3=B,l1∩l3=C.求证:直线l1,l2,l3在同一平面内.
例2 如图,已知直线a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:a,b,c,l共面.
在证明共面问题时,先根据条件确定平面,再证明其他的点或线也在这个平面内.
如图,在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别是边AB,BC上的点,且==.求证:
(1) E,F,G,H四点共面;
(2) 直线EH,BD,FG相交于同一点.
1. (2024广东月考)空间四个点中,“三点共线”是“这四个点共面”的( )
A. 充分且不必要条件
B. 必要且不充分条件
C. 充要条件
D. 既不充分又不必要条件
2. (教材改编)在空间中,下列命题中不正确的是( )
A. 若两个平面有一个公共点,则它们有无数个公共点,且在一条直线上
B. 若已知四个点不共面,则其中任意三点不共线
C. 梯形可确定一个平面
D. 任意三点能确定一个平面
3. (多选)(2024洛阳月考)如图,在正方体ABCD-A1B1C1D1中,P,Q分别是棱AA1,CC1的中点,平面D1PQ∩平面ABCD=l,则下列结论中正确的是( )
A. 直线l一定过点B
B. 直线l不一定过点B
C. D1P的延长线与DA的延长线的交点在直线l上
D. D1Q的延长线与DC的延长线的交点在直线l上
4. (教材改编)如图,A,B,C,D为不共面的四点,点E,F,G,H分别在线段AB,BC,CD,DA上.
(1) 如果EH∩FG=P,那么点P在直线________上;
(2) 如果EF∩GH=Q,那么点Q在直线________上.
5. (2023唐山开滦二中月考)如图,正方体ABCD-A1B1C1D1的棱长为6,M是A1B1的中点,点N在棱CC1上,且CN=2NC1.作出过点D,M,N的平面截正方体ABCD-A1B1C1D1所得的截面,并写出作法.
13.2.1 平面的基本性质(1)
【活动方案】
活动一 略
1. 正方形的直观图 虚线
例1 ③
思考1:不在同一条直线上的三点,可以确定一个平面.
思考2:基本事实2说明平面是平的.基本事实2可以帮助我们证明或判断直线在平面内.
例2 略
跟踪训练 AB α
基本事实3用符号表示为: α∩β=l且P∈l.
思考3:基本事实3说明了平面是“无限延展的”,两个相交平面只有一条交线.基本事实3可以帮助我们证明点共线问题.
例3 略
跟踪训练 α∩β=l,a β,a∩l=A,A∈l.
例4 (1) 如图,连接DE并延长,交AB的延长线于点P,则P为直线AB与平面α的交点.
(2) 因为D∈平面ABC,E∈平面ABC,
所以DE 平面ABC.
因为D∈α,E∈α,所以DE α,
所以平面α∩平面ABC=DE.
因为P∈AB,AB 平面ABC,
所以P∈平面ABC.
又P∈α,所以点P在平面α与平面ABC的交线DE上,
所以D,E,P三点共线.
跟踪训练 如图,连接A1B,CD1.
因为B∈平面A1BCD1,D1∈平面A1BCD1,
所以BD1 平面A1BCD1.
同理BD1 平面ABC1D1,
所以平面ABC1D1∩平面A1BCD1=BD1.
因为A1C 平面A1BCD1,Q∈A1C,
所以Q∈平面A1BCD1.
又因为Q∈平面ABC1D1,
所以Q∈BD1,即B,Q,D1三点共线.
【检测反馈】
1. D
2. D 点A在直线l上,则A∈l;l在平面α内,则l α.
3. ACD A,D显然正确;对于B,直线l应画在表示平面的平行四边形内,故B错误,C正确.故选ACD.
4. D∈b A∈a,B∈a a α C∈α
5. (1) 点A在平面α内,点B不在平面α内,如图1.
(2) 直线l在平面α内,点A不在直线l上,但在平面α内,如图2.
(3) 平面ABD与平面BDC相交于BD,平面ABC与平面ADC相交于AC,如图3.
图1 图2 图3
13.2.1 平面的基本性质(2)
【活动方案】
思考1:略
思考2:3条 不行
思考3:不能.因为如果这三点、四点在同一条直线上就不能确定一个平面.
思考4:一个
推论1证明:在直线l上任取两点B,C.因为点A不在直线l上,根据基本事实1,经过不共线三点A,B,C有一个平面α.
因为B∈α,C∈α,所以根据基本事实2,l α,即平面α 经过直线l和点A.
因为点B,C在直线l上,所以经过直线l和点A的平面一定经过点A,B,C.
于是再根据基本事实1,经过不共线的三点A,B,C的平面只有一个,所以经过直线l和点A的平面只有一个.
推论2证明:设直线a,b相交于点C,在直线a上取不同于点C的点A,点A在直线b外.由推论1,得过直线b和点A有一个平面α.因为直线a上有两点A,C在α内,所以a α,因此经过a,b有一个平面α.
经过a,b的平面一定经过点A和直线b,由推论1,这样的平面只有一个,所以经过两条相交直线a,b的平面有且只有一个.
推论3证明:根据平行线的定义(同一平面内没有公共点的两条直线)可知,直线a和直线b一定在同一个平面内.
在直线a上任取一点A,因为a∥b,所以点A不在直线b上,由推论1可知,经过点A和直线b的平面只有一个.
因为经过直线a和直线b的平面一定经过点A和直线b,故经过直线a和直线b的平面只有一个.
思考5:用两根细绳沿桌子四条腿的对角拉直,如果这两根细绳相交,说明桌子四条腿的底端在同一平面内,否则就不在同一平面内,依据是推论2.
例1 因为D l,所以直线l与点D可以确定平面α.
又因为A∈l,所以A∈α.
因为D∈α,所以AD α.同理BD α,CD α,
所以直线AD,BD,CD在同一平面α内,
即它们共面.
跟踪训练 因为l1∩l2=A,
所以l1和l2确定一个平面α.
因为l2∩l3=B,所以B∈l2.
又因为l2 α,所以B∈α.同理可证C∈α.
因为B∈l3,C∈l3,所以l3 α,
所以直线l1,l2,l3在同一平面内.
例2 因为a∥b,所以a,b确定一个平面α.
因为l∩a=A,l∩b=B,
所以A∈a,B∈b,所以A∈α,B∈α.
又因为A∈l,B∈l,所以l α.
因为b∥c,所以b,c确定一个平面β.
同理可证l β.
于是b α,l α,b β,l β,
即α∩β=b,α∩β=l.
又因为b与l不重合,所以α与β重合,
所以a,b,c,l共面.
跟踪训练 (1) 如图,连接EF,HG.
因为在空间四边形ABCD中,H,G分别是AD,CD的中点,
所以HG∥AC,且HG=AC.
又==,
所以EF∥AC,且EF=AC.
故EF∥HG,则E,F,G,H四点共面.
(2) 由(1)知EF∥HG,且EF≠HG,
所以设EH与FG相交于点P,如图,延长EH,FG相交于点P.
因为EH 平面ABD,
所以点P在平面ABD内,
同理点P在平面BCD内.
又平面ABD∩平面BCD=BD,
所以点P在直线BD上,
所以直线EH,BD,FG相交于同一点.
【检测反馈】
1. A 空间四个点中,有三个点共线,根据“经过一条直线和这条直线外的一点,有且只有一个平面”,得到这四个点共面,即充分性成立;反之,当四个点共面时,不一定有三点共线,即必要性不成立.综上,空间四个点中,“三点共线”是“这四个点共面”的充分且不必要条件.
2. D 对于A,若两个平面有一个公共点,则它们有经过该点的一条公共直线,即两平面有无数个公共点,故A正确;对于B,若已知四个点不共面,则其中任意三点不共线,否则,若存在三点共线,则问题转化为一条直线与直线外一点,则四点共面,故B正确;对于C,因为两条平行直线确定一个平面,所以梯形可确定一个平面,故C正确;对于D,共线的三点不能确定一个平面,故D错误.
3. ACD 如图,连接PB,QB.因为P,Q分别是棱AA1,CC1的中点,由勾股定理可得D1P=D1Q=QB=BP,所以四边形D1PBQ是菱形,所以D1,P,B,Q四点共面,即B∈平面D1PBQ.又B∈平面ABCD,所以B∈l,故A正确,B错误;如图,延长D1P与DA的延长线交于点F,延长D1Q与DC的延长线交于点E.因为D1F 平面D1PBQ,所以F∈平面D1PBQ.因为DF 平面ABCD,所以F∈平面ABCD,所以F∈l,同理E∈l,故C,D正确.故选ACD.
4. (1) BD 连接BD.若EH∩FG=P,则P∈平面ABD,且P∈平面BCD.因为平面ABD∩平面BCD=BD,所以P∈BD.
(2) AC 连接AC.若EF∩GH=Q,则Q∈平面ABC,且Q∈平面ACD.因为平面ABC∩平面ACD=AC,所以Q∈AC.
5. 如图所示,五边形DQMFN即为所求截面.
作法如下:连接DN并延长交D1C1的延长线于点E,连接ME交B1C1于点F,交D1A1的延长线于点H,连接DH交AA1于点Q,连接QM,FN,所以五边形DQMFN即为所求截面.
1. 借助长方体,直观认识空间的点、直线、平面的位置关系.
2. 了解3个基本事实,并能解决一些简单的问题.
活动一 背景引入
背景1:生活中常见的如黑板、平整的操场、桌面、平静的湖面等等,都给我们以平面的形象;
背景2:椅子放不稳,是地面不平还是椅子本身有问题?
背景3:用两个合页和一把锁就可以将一扇门固定,将一把直尺置于桌面,通过是否漏光就能检查桌面是否平整,为什么?
活动二 平面的概念及表示方法
1. 几何画法:
一般用水平放置的__________作为平面的直观图
一个平面被另一个平面遮挡住,为了增强立体感,被遮挡部分用________画出来
2. 符号表示:
平面通常用希腊字母α,β,γ,…表示,如图中的平面α,也可以用平行四边形的两个相对顶点的字母表示,如平面AC等.
例1 已知命题:
①10个平面重叠起来,要比5个平面重叠起来要厚;
②有一个平面的长是50m,宽是20m;
③平面没有大小,没有厚度,可以无限延展.
其中正确命题的序号是________.
活动三 三个基本事实及应用
基本事实1 过不在一条直线上的三个点,有且只有一个平面(如图1).
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内(如图2).
图1 图2
思考1
平面几何中,两点可以确定一条直线,那么基本事实1说明了空间中的什么问题?
思考2
基本事实2说明了空间中的什么问题?它可以帮助我们解决哪些几何问题?
例2 如图,在长方体 ABCD-A1B1C1D1中:
位置关系 符号表示 位置关系 符号表示
点P在直线AB上 直线AB与直线BC交于点B
点C不在直线AB上 直线AB在平面AC内
点M在平面AC内 直线AA1不在平面AC内
点A1不在平面AC内
1. 点与直线的关系,是元素与集合的关系,只有∈, 两种关系.
2. 直线与平面都是由点构成的集合,它们之间的关系是集合与集合的关系,用 , 来表示.
3. 空间图形中用大写的英文字母表示点,小写的英文字母表示直线,这一点与集合中的表示不同.
用符号可以表示基本事实2:
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
基本事实3用图形表示为:
用符号表示为:
思考3
基本事实3说明了空间中的什么问题?它可以帮助我们解决哪些空间问题?
例3 根据下列符号语言画出相应图形.
α∩β=l,A∈l,AB α,AC β.
1. 借助集合中的符号,将空间的点看成元素,将直线与平面看成表示点的集合,但表示两直线或直线与平面的交点时,点的字母外不加集合的符号.
2. 对于空间中的符号语言和图形语言及文字语言要灵活转换.
用数学符号表示图中的点、直线、平面之间的位置关系.
例4 已知D,E分别是△ABC的边AC,BC上的点,平面α经过D,E 两点.
(1) 求作直线AB 与平面α的交点P;
(2) 求证:D,E,P三点共线.
依据基本事实3,要证明三点共线,只要说明这三个点是两个平面的公共点即可.
如图,在正方体ABCD-A1B1C1D1 中,点Q 在线段A1C上,且点Q在平面ABC1D1 内,求证:B,Q,D1 三点共线.
1. 平面α,β有公共点A,则平面α与β公共点的个数为( )
A. 1 B. 2 C. 3 D. 无数
2. (教材改编)点A在直线l上,直线l在平面α内,用符号表示,正确的是( )
A. A∈l,l∈α B. A∈l,l α C. A l,l α D. A∈l,l α
3. (多选)下图中,图形的画法正确的选项是( )
A B C D
4. (教材改编)如图,用符号语言表示点、直线、平面之间的位置关系.
点D在直线b上________;点A,B在直线a上________;直线a在平面α内________;点C在平面α内________.
图1 图2
5. 根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形.
(1) A∈α,B α;
(2) l α,A∈α,A l;
(3) 平面ABD∩平面BDC=BD,平面ABC∩平面ADC=AC.
13.2.1 平面的基本性质(2)
1. 了解由基本事实得到的三个推论.
2. 能运用3个基本事实及其推论解决一些简单的问题.
活动一 了解确定平面的依据
经过不在同一条直线上的三点,有且只有一个平面,即不共线的三点确定一个平面.
用图形表示为
过不共线的三点A,B,C的平面通常记作“平面ABC”.
思考1
自行车的撑脚一般安装在自行车的什么位置?能不能安装在前后轮一条直线的地方
思考2
照相机支架需要几条腿?两条行不行?
回顾基本事实1,体会确定一个平面的条件.
思考3
分别经过三点、四点能确定唯一的平面吗?为什么?
思考4
过一条直线l和直线l外一点A的平面有几个?
推论1:经过一条直线和这条直线外的一点,有且只有一个平面.
已知:直线l,点A l.
求证:过直线l和点A有且只有一个平面.
证明:
推论2:经过两条相交直线,有且只有一个平面.
已知:直线a,b相交.
求证:过直线a,b有且只有一个平面.
证明:
推论3:经过两条平行直线,有且只有一个平面.
已知:直线a∥b.
求证:过直线a,b有且只有一个平面.
证明:
思考5
下图是一张倒置的桌子,你能用所学的知识检查一下桌子的四条腿的底端是否在同一个平面内吗?
活动二 平面基本性质的简单应用
例1 已知A∈l,B∈l,C∈l,D l.求证:直线AD,BD,CD共面.
确定一个平面,只要根据基本事实1及 3个推论即可.
如图,已知l1∩l2=A,l2∩l3=B,l1∩l3=C.求证:直线l1,l2,l3在同一平面内.
例2 如图,已知直线a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:a,b,c,l共面.
在证明共面问题时,先根据条件确定平面,再证明其他的点或线也在这个平面内.
如图,在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别是边AB,BC上的点,且==.求证:
(1) E,F,G,H四点共面;
(2) 直线EH,BD,FG相交于同一点.
1. (2024广东月考)空间四个点中,“三点共线”是“这四个点共面”的( )
A. 充分且不必要条件
B. 必要且不充分条件
C. 充要条件
D. 既不充分又不必要条件
2. (教材改编)在空间中,下列命题中不正确的是( )
A. 若两个平面有一个公共点,则它们有无数个公共点,且在一条直线上
B. 若已知四个点不共面,则其中任意三点不共线
C. 梯形可确定一个平面
D. 任意三点能确定一个平面
3. (多选)(2024洛阳月考)如图,在正方体ABCD-A1B1C1D1中,P,Q分别是棱AA1,CC1的中点,平面D1PQ∩平面ABCD=l,则下列结论中正确的是( )
A. 直线l一定过点B
B. 直线l不一定过点B
C. D1P的延长线与DA的延长线的交点在直线l上
D. D1Q的延长线与DC的延长线的交点在直线l上
4. (教材改编)如图,A,B,C,D为不共面的四点,点E,F,G,H分别在线段AB,BC,CD,DA上.
(1) 如果EH∩FG=P,那么点P在直线________上;
(2) 如果EF∩GH=Q,那么点Q在直线________上.
5. (2023唐山开滦二中月考)如图,正方体ABCD-A1B1C1D1的棱长为6,M是A1B1的中点,点N在棱CC1上,且CN=2NC1.作出过点D,M,N的平面截正方体ABCD-A1B1C1D1所得的截面,并写出作法.
13.2.1 平面的基本性质(1)
【活动方案】
活动一 略
1. 正方形的直观图 虚线
例1 ③
思考1:不在同一条直线上的三点,可以确定一个平面.
思考2:基本事实2说明平面是平的.基本事实2可以帮助我们证明或判断直线在平面内.
例2 略
跟踪训练 AB α
基本事实3用符号表示为: α∩β=l且P∈l.
思考3:基本事实3说明了平面是“无限延展的”,两个相交平面只有一条交线.基本事实3可以帮助我们证明点共线问题.
例3 略
跟踪训练 α∩β=l,a β,a∩l=A,A∈l.
例4 (1) 如图,连接DE并延长,交AB的延长线于点P,则P为直线AB与平面α的交点.
(2) 因为D∈平面ABC,E∈平面ABC,
所以DE 平面ABC.
因为D∈α,E∈α,所以DE α,
所以平面α∩平面ABC=DE.
因为P∈AB,AB 平面ABC,
所以P∈平面ABC.
又P∈α,所以点P在平面α与平面ABC的交线DE上,
所以D,E,P三点共线.
跟踪训练 如图,连接A1B,CD1.
因为B∈平面A1BCD1,D1∈平面A1BCD1,
所以BD1 平面A1BCD1.
同理BD1 平面ABC1D1,
所以平面ABC1D1∩平面A1BCD1=BD1.
因为A1C 平面A1BCD1,Q∈A1C,
所以Q∈平面A1BCD1.
又因为Q∈平面ABC1D1,
所以Q∈BD1,即B,Q,D1三点共线.
【检测反馈】
1. D
2. D 点A在直线l上,则A∈l;l在平面α内,则l α.
3. ACD A,D显然正确;对于B,直线l应画在表示平面的平行四边形内,故B错误,C正确.故选ACD.
4. D∈b A∈a,B∈a a α C∈α
5. (1) 点A在平面α内,点B不在平面α内,如图1.
(2) 直线l在平面α内,点A不在直线l上,但在平面α内,如图2.
(3) 平面ABD与平面BDC相交于BD,平面ABC与平面ADC相交于AC,如图3.
图1 图2 图3
13.2.1 平面的基本性质(2)
【活动方案】
思考1:略
思考2:3条 不行
思考3:不能.因为如果这三点、四点在同一条直线上就不能确定一个平面.
思考4:一个
推论1证明:在直线l上任取两点B,C.因为点A不在直线l上,根据基本事实1,经过不共线三点A,B,C有一个平面α.
因为B∈α,C∈α,所以根据基本事实2,l α,即平面α 经过直线l和点A.
因为点B,C在直线l上,所以经过直线l和点A的平面一定经过点A,B,C.
于是再根据基本事实1,经过不共线的三点A,B,C的平面只有一个,所以经过直线l和点A的平面只有一个.
推论2证明:设直线a,b相交于点C,在直线a上取不同于点C的点A,点A在直线b外.由推论1,得过直线b和点A有一个平面α.因为直线a上有两点A,C在α内,所以a α,因此经过a,b有一个平面α.
经过a,b的平面一定经过点A和直线b,由推论1,这样的平面只有一个,所以经过两条相交直线a,b的平面有且只有一个.
推论3证明:根据平行线的定义(同一平面内没有公共点的两条直线)可知,直线a和直线b一定在同一个平面内.
在直线a上任取一点A,因为a∥b,所以点A不在直线b上,由推论1可知,经过点A和直线b的平面只有一个.
因为经过直线a和直线b的平面一定经过点A和直线b,故经过直线a和直线b的平面只有一个.
思考5:用两根细绳沿桌子四条腿的对角拉直,如果这两根细绳相交,说明桌子四条腿的底端在同一平面内,否则就不在同一平面内,依据是推论2.
例1 因为D l,所以直线l与点D可以确定平面α.
又因为A∈l,所以A∈α.
因为D∈α,所以AD α.同理BD α,CD α,
所以直线AD,BD,CD在同一平面α内,
即它们共面.
跟踪训练 因为l1∩l2=A,
所以l1和l2确定一个平面α.
因为l2∩l3=B,所以B∈l2.
又因为l2 α,所以B∈α.同理可证C∈α.
因为B∈l3,C∈l3,所以l3 α,
所以直线l1,l2,l3在同一平面内.
例2 因为a∥b,所以a,b确定一个平面α.
因为l∩a=A,l∩b=B,
所以A∈a,B∈b,所以A∈α,B∈α.
又因为A∈l,B∈l,所以l α.
因为b∥c,所以b,c确定一个平面β.
同理可证l β.
于是b α,l α,b β,l β,
即α∩β=b,α∩β=l.
又因为b与l不重合,所以α与β重合,
所以a,b,c,l共面.
跟踪训练 (1) 如图,连接EF,HG.
因为在空间四边形ABCD中,H,G分别是AD,CD的中点,
所以HG∥AC,且HG=AC.
又==,
所以EF∥AC,且EF=AC.
故EF∥HG,则E,F,G,H四点共面.
(2) 由(1)知EF∥HG,且EF≠HG,
所以设EH与FG相交于点P,如图,延长EH,FG相交于点P.
因为EH 平面ABD,
所以点P在平面ABD内,
同理点P在平面BCD内.
又平面ABD∩平面BCD=BD,
所以点P在直线BD上,
所以直线EH,BD,FG相交于同一点.
【检测反馈】
1. A 空间四个点中,有三个点共线,根据“经过一条直线和这条直线外的一点,有且只有一个平面”,得到这四个点共面,即充分性成立;反之,当四个点共面时,不一定有三点共线,即必要性不成立.综上,空间四个点中,“三点共线”是“这四个点共面”的充分且不必要条件.
2. D 对于A,若两个平面有一个公共点,则它们有经过该点的一条公共直线,即两平面有无数个公共点,故A正确;对于B,若已知四个点不共面,则其中任意三点不共线,否则,若存在三点共线,则问题转化为一条直线与直线外一点,则四点共面,故B正确;对于C,因为两条平行直线确定一个平面,所以梯形可确定一个平面,故C正确;对于D,共线的三点不能确定一个平面,故D错误.
3. ACD 如图,连接PB,QB.因为P,Q分别是棱AA1,CC1的中点,由勾股定理可得D1P=D1Q=QB=BP,所以四边形D1PBQ是菱形,所以D1,P,B,Q四点共面,即B∈平面D1PBQ.又B∈平面ABCD,所以B∈l,故A正确,B错误;如图,延长D1P与DA的延长线交于点F,延长D1Q与DC的延长线交于点E.因为D1F 平面D1PBQ,所以F∈平面D1PBQ.因为DF 平面ABCD,所以F∈平面ABCD,所以F∈l,同理E∈l,故C,D正确.故选ACD.
4. (1) BD 连接BD.若EH∩FG=P,则P∈平面ABD,且P∈平面BCD.因为平面ABD∩平面BCD=BD,所以P∈BD.
(2) AC 连接AC.若EF∩GH=Q,则Q∈平面ABC,且Q∈平面ACD.因为平面ABC∩平面ACD=AC,所以Q∈AC.
5. 如图所示,五边形DQMFN即为所求截面.
作法如下:连接DN并延长交D1C1的延长线于点E,连接ME交B1C1于点F,交D1A1的延长线于点H,连接DH交AA1于点Q,连接QM,FN,所以五边形DQMFN即为所求截面.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
