13.2.2 空间两条直线的位置关系 学案(2课时,含答案)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 13.2.2 空间两条直线的位置关系 学案(2课时,含答案)2024-2025学年高一数学苏教版(2019)必修第二册 |
|
|
| 格式 | docx | ||
| 文件大小 | 447.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 21:10:12 | ||
图片预览



文档简介
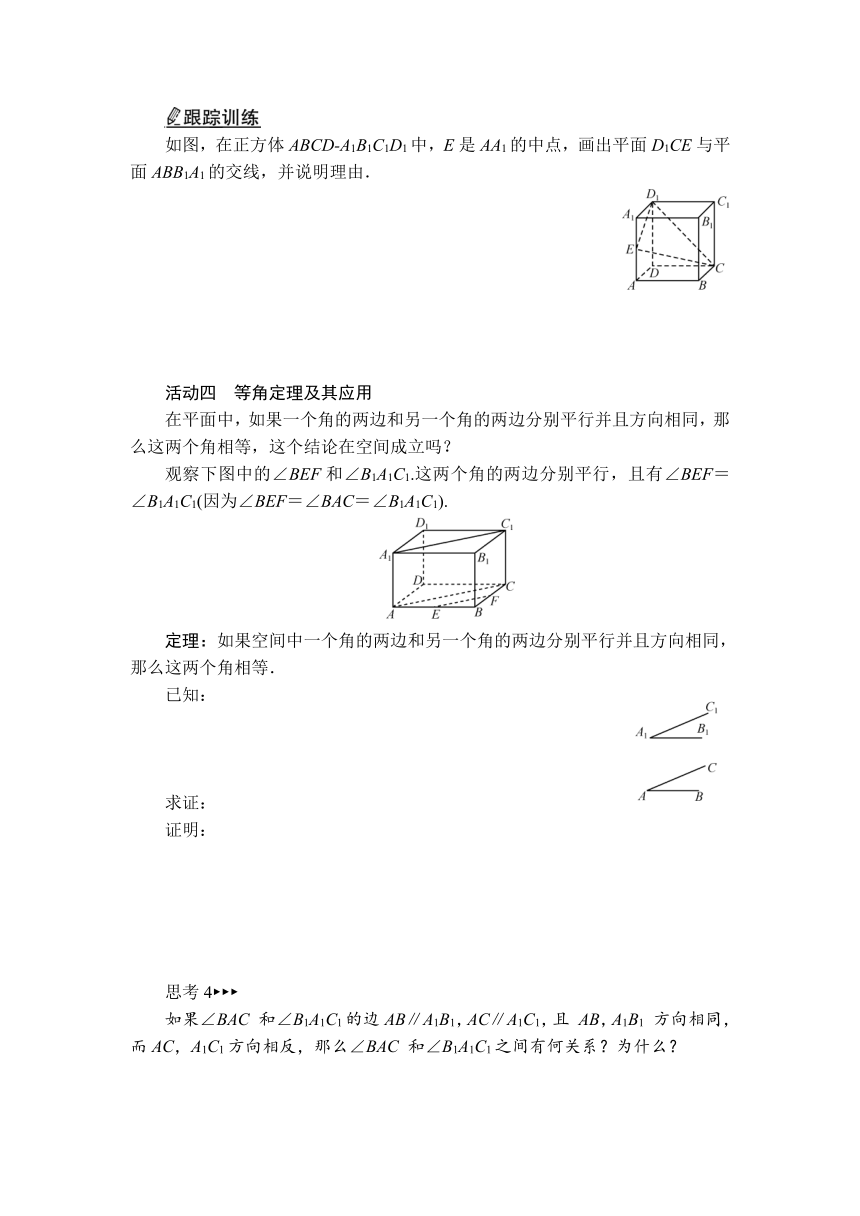
13.2.2 空间两条直线的位置关系(1)
1. 借助长方体,通过直观感知,了解空间两条直线的位置关系.
2. 掌握基本事实4及其应用.
3. 掌握等角定理,并能解决相关问题.
活动一 背景引入
平面内两条直线的位置关系只有平行和相交两种.
思考1
(1) 空间内两条直线的位置关系有哪些?
(2) 观察下面两张图片,你能找出每张图中既不平行又不相交的两条直线吗?
活动二 空间两条直线的位置关系
例1 如图,在长方体ABCD-A1B1C1D1中.
(1) 与AB平行的直线有哪些?
(2) 与AB相交的直线有哪些?
(3) 直线AA1和C1D1平行吗?相交吗?
定义:我们把不同在任何一个平面内的两条直线叫作异面直线.
空间两条直线的位置关系:
位置关系 共面情况 公共点个数
注:如无特殊说明,“两条直线”指不重合的两条直线,“两个平面”指不重合的两个平面.
活动三 基本事实4及其应用
在同一平面内,若a∥b,b∥c,则 a∥c.
思考2
那这个性质在空间中成立吗?你能在空间中找到三条平行直线吗?
基本事实4 平行于同一条直线的两条直线平行.
符号表示:
思考3
经过直线外一点,有几条直线和这条直线平行?
例2 如图,在长方体ABCD-A1B1C1D1中,已知E,F分别是AB,BC 的中点.求证:EF∥A1C1.
在空间中,直线的平行性具有传递性,同时说明了要证明两直线平行,应该把这两条直线放在同一平面内.
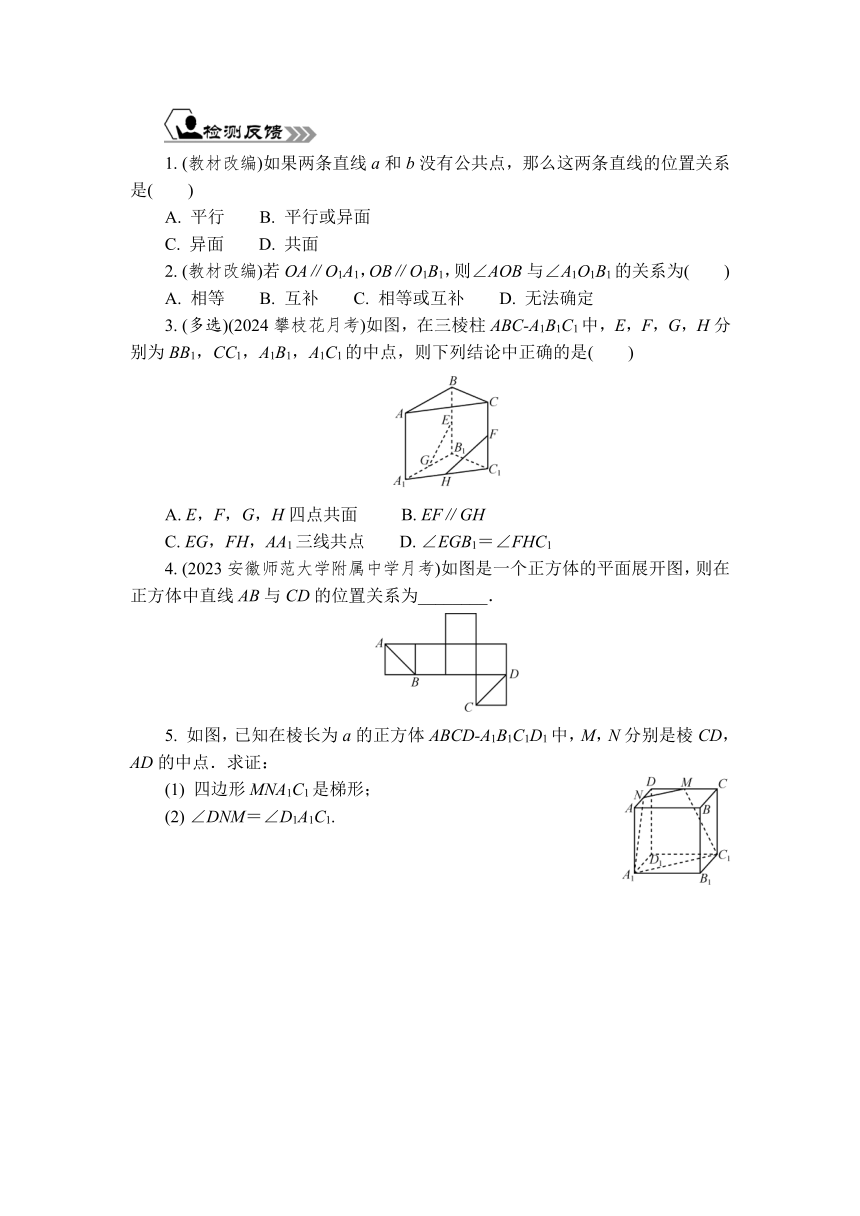
如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点,画出平面D1CE与平面ABB1A1的交线,并说明理由.
活动四 等角定理及其应用
在平面中,如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等,这个结论在空间成立吗?
观察下图中的∠BEF和∠B1A1C1.这两个角的两边分别平行,且有∠BEF=∠B1A1C1(因为∠BEF=∠BAC=∠B1A1C1).
定理:如果空间中一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.
已知:
求证:
证明:
思考4
如果∠BAC 和∠B1A1C1的边AB∥A1B1,AC∥A1C1,且 AB,A1B1 方向相同,而AC,A1C1方向相反,那么∠BAC 和∠B1A1C1之间有何关系?为什么?
例3 如图,已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD,A1D1的中点.求证:∠C1E1B1=∠CEB.
要说明空间中的两角相等,不仅要看它们的对应边是否平行,还要看它们的对应边的方向是否一致.若都同向或都反向,则这两个角相等;若一组同向一组反向,则这两个角互补.
如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且===.
(1) 求证:A′B′∥AB,A′C′∥AC,B′C′∥BC;
(2) 求的值.
1. (教材改编)如果两条直线a和b没有公共点,那么这两条直线的位置关系是( )
A. 平行 B. 平行或异面
C. 异面 D. 共面
2. (教材改编)若OA∥O1A1,OB∥O1B1,则∠AOB与∠A1O1B1的关系为( )
A. 相等 B. 互补 C. 相等或互补 D. 无法确定
3. (多选)(2024攀枝花月考)如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别为BB1,CC1,A1B1,A1C1的中点,则下列结论中正确的是( )
A. E,F,G,H四点共面 B. EF∥GH
C. EG,FH,AA1三线共点 D. ∠EGB1=∠FHC1
4. (2023安徽师范大学附属中学月考)如图是一个正方体的平面展开图,则在正方体中直线AB与CD的位置关系为________.
5. 如图,已知在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD,AD的中点.求证:
(1) 四边形MNA1C1是梯形;
(2) ∠DNM=∠D1A1C1.
13.2.2 空间两条直线的位置关系(2)
1. 理解两条异面直线所成角的定义及两条异面直线互相垂直的概念.
2. 掌握异面直线的判定方法.
3. 掌握异面直线所成角的计算方法.
活动一 巩固空间两条直线的位置关系
空间两条直线的位置关系:
位置关系 共面情况 公共点个数
思考1
分别在两个平面内的两条直线一定是异面直线吗?
练习 在两个相交平面内各画一条直线,使它们成为:
(1) 平行直线;(2) 相交直线;(3) 异面直线.
活动二 异面直线的定义及判定
问题:如图,在长方体ABCD-A1B1C1D1中,直线A1C和AD有什么位置关系?
思考2
如何判定两条直线是否异面?
异面直线的判定定理:
已知:
求证:
证明:
判断异面直线的方法:
方法 内容
定义法 不同在任何一个平面内的两条直线叫作异面直线
定理法 过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线
反证法 判定两条直线既不平行也不相交,那么这两条直线就是异面直线
练习 在三棱锥的所有棱中,互为异面直线的有________对.
例1 如图,在三棱锥A-BCD中,E,F是棱AD上异于点A,D的两点,G,H是棱BC上异于点B,C的两点,给出下列说法:
①AB与CD互为异面直线;
②FH分别与DC,DB互为异面直线;
③EG与FH互为异面直线;
④EG与AB互为异面直线.
其中正确的是____________.(填序号)
要判断两直线是异面直线,利用它的定义无法说明时,可以用它的定理,让其中的一条直线放一个平面内,另一条直线和这个平面相交,但交点不在第一条直线上即可.
若a和b是异面直线,b和c是异面直线,则a和c的位置关系是____________
_____________________________.
活动三 了解异面直线所成角的概念
异面直线所成的角:
定义 前提 两条异面直线a,b
作法 经过空间任意一点O,作直线a′∥a,b′∥b
结论 我们把直线a′和b′所成的锐角(或直角)叫作异面直线a,b所成的角或夹角
范围 记异面直线a与b所成的角为θ,则0°< θ ≤90°
特殊情况 当θ=90°时,异面直线a,b互相垂直,记作a⊥b
例2 如图,已知多面体ABCD-A1B1C1D1是棱长为a的正方体.
(1) 正方体中哪些棱所在的直线与直线BC1是异面直线?
(2) 求异面直线AA1与BC所成的角;
(3) 求异面直线BC1与AC所成的角.
1. 直线a与b所成角的大小只由a,b的位置关系来确定,与点O的选择无关,为了简便,点O一般取在两直线中的一条上.
2. 两条异面直线所成的角θ∈.
3. 当两条异面直线a,b所成的角是直角时,我们就说这两条异面直线互相垂直,记作a⊥b.
4. 两条直线互相垂直,有共面垂直与异面垂直两种情形.
5. 通常把两条异面直线所成的角转化为两条相交直线所成的角.
如图,在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面四边形ABCD是菱形,且AB=BC=2,∠ABC=120°,若异面直线A1B和AD1所成的角为90°,求AA1的长.
1. (教材改编)以P为顶点,圆O为底面的圆锥,轴截面三角形PAB为等边三角形,M为底面圆O上一点,∠AOM=60°,则异面直线OM与AP所成角的余弦值为( )
A. B. C. D.
2. (2023惠州期末)若空间中三条直线a,b,c满足a⊥b,b∥c,则直线a与c( )
A. 一定平行 B. 一定垂直
C. 一定是异面直线 D. 一定相交
3. (多选)(2024泉州期中)如图是正方体的平面展开图,则在这个正方体中,下列命题正确的是( )
A. AM∥BN B. △CEM是等边三角形
C. DB∥AE D. AM与DF是异面直线
(第3题) (第4题)
4. (2023深圳罗湖高级中学期中)如图,在三棱锥D-ABC中,AC=BD,且AC⊥BD,E,F分别是棱DC,AB的中点,则直线EF与AC所成的角等于________.
5. (教材改编)如图,在四面体ABCD中,E,F分别是线段AD,BC上的点,==.
(1) 求证:直线EF与BD是异面直线;
(2) 若AB=CD=3,EF=,求直线AB与CD所成角的大小.
13.2.2 空间两条直线的位置关系(1)
【活动方案】
思考1:(1) 平行、相交、既不平行又不相交
(2) 略
例1 (1) A1B1,CD,C1D1 (2) AD,AA1,BB1,BC
(3) 既不平行又不相交
填表略
思考2:略
符号表示: a∥c.
思考3:1条
例2 连接AC.
因为E,F分别为AB,BC的中点,
所以EF∥AC.
又因为AA1∥BB1,BB1∥CC1,
且AA1=BB1,BB1=CC1,
所以AA1∥CC1,且AA1=CC1,
所以四边形AA1C1C是平行四边形,
所以AC∥A1C1,所以EF∥A1C1.
跟踪训练 如图,取AB的中点F,连接EF,A1B,CF.
因为E是AA1的中点,
所以EF∥A1B.
在正方体ABCD-A1B1C1D1中,
A1D1∥BC,A1D1=BC,
所以四边形A1BCD1是平行四边形,
所以A1B∥CD1,
所以EF∥CD1,
所以E,F,C,D1四点共面.
因为E∈平面ABB1A1,E∈平面D1CE,
F∈平面ABB1A1,F∈平面D1CE,
所以平面ABB1A1∩平面D1CE=EF,
所以平面D1CE与平面ABB1A1的交线为EF.
已知:∠BAC和∠B1A1C1的边AB∥A1B1,AC∥A1C1,并且方向相同.
求证:∠BAC=∠B1A1C1.
证明:如图,分别在∠BAC和∠B1A1C1的两边上截取AD=A1D1,AE=A1E1,连接AA1,DD1,EE1,DE,D1E1.
因为AB∥A1B1,AD=A1D1,
所以四边形AA1D1D是平行四边形,
所以AA1∥DD1,且AA1=DD1.
同理AA1∥EE1,且AA1=EE1,
所以DD1∥EE1,且DD1=EE1,
所以四边形DD1E1E是平行四边形,
所以DE=D1E1.
在△ADE和△A1D1E1中,
所以△ADE≌△A1D1E1,
所以∠BAC=∠B1A1C1.
思考4:互补,理由略.
例3 连接EE1.
因为E1,E分别为A1D1,AD的中点,
所以A1E1∥AE,A1E1=AE,
所以四边形A1E1EA是平行四边形,
所以A1A∥E1E,A1A=E1E.
又因为A1A∥B1B,A1A=B1B,
所以E1E∥B1B,E1E=B1B,
所以四边形EE1B1B是平行四边形,
所以E1B1∥EB,同理可得E1C1∥EC.
又因为∠C1E1B1与∠CEB两边的方向相同,
所以∠C1E1B1=∠CEB.
跟踪训练 (1) 因为AA′∩BB′=O,且==,∠AOB=∠A′OB′,
所以△AOB∽△A′OB′,
所以∠ABO=∠A′B′O,
所以AB∥A′B′,
同理可得AC∥A′C′,BC∥B′C′.
(2) 因为A′B′∥AB,A′C′∥AC,且AB和A′B′,AC和A′C′方向均相反,
所以∠BAC=∠B′A′C′.
同理可得∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,
所以△ABC∽△A′B′C′.
又==,
所以==.
【检测反馈】
1. B 如果两条直线a和b没有公共点,那么这两条直线是同一平面内的平行直线或是异面直线.
2. C
3. ABC 对于A,B,如图,连接EF,GH.因为GH是△A1B1C1的中位线,所以GH∥B1C1.因为B1E∥C1F,且B1E=C1F,所以四边形B1EFC1是平行四边形,所以EF∥B1C1,可得EF∥GH,则E,F,G,H四点共面,故A,B正确;对于C,如图,延长EG,FH相交于点P.因为P∈EG,EG 平面ABB1A1,所以P∈平面ABB1A1.因为P∈FH,FH 平面ACC1A1,所以P∈平面ACC1A1.因为平面ABB1A1∩平面ACC1A1=AA1,所以P∈AA1,所以EG,FH,AA1三线共点,故C正确;对于D,因为EB1=FC1,当GB1≠HC1时,tan ∠EGB1≠tan ∠FHC1,所以∠EGB1≠∠FHC1,故D错误.故选ABC.
4. 异面 如图是正方体的直观图,则在正方体中直线AB与CD的位置关系为异面.
5. (1) 连接AC.
在△ACD中,因为M,N分别是CD,AD的中点,
所以MN是△ACD的中位线,
所以MN∥AC,MN=AC.
由正方体的性质,得AC∥A1C1,AC=A1C1,
所以MN∥A1C1,且MN=A1C1,
即MN≠A1C1,
所以四边形MNA1C1是梯形.
(2) 因为NM∥A1C1,ND∥A1D1,
且∠DNM与∠D1A1C1两边的方向相同,
所以∠DNM=∠D1A1C1.
13.2.2 空间两条直线的位置关系(2)
【活动方案】
活动一
位置关系 共面情况 公共点个数
相交 在同一平面内 有且只有1个
平行 在同一平面内 0个
异面 不同在任何一个平面内 0个
思考1:不一定,可能平行也可能相交.
练习:略
问题:A1C与AD是异面直线.
思考2:过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线.
已知:l α,A α,B∈α,B l.
求证:直线AB与l是异面直线.
证明:假设AB与l是共面直线,因为l α且 B∈α,所以 AB α与A α相矛盾,
所以直线AB与l是异面直线.
练习:3 在三棱锥A-BCD中,AB与CD异面,AD与BC异面,AC与BD异面,所以有3对异面直线.
例1 ①②③④ 因为直线DC 平面BCD,直线AB 平面BCD,点B 直线DC,所以由异面直线的判定定理可知,①正确;同理可得,②③④正确.
跟踪训练 相交、平行或异面 异面直线不具有传递性,可以以长方体为例加以说明,异面直线a,b,直线c的位置可如图所示,此时a和c异面.当c在c1处时,a和c相交;当c在c2处时,a和c平行.
例2 (1) 与直线BC1是异面直线的有AA1,A1B1,A1D1,DA,DC,DD1.
(2) 因为DA∥BC,所以∠A1AD即为异面直线AA1与BC所成的角,
所以异面直线AA1与BC所成的角为90°.
(3) 连接A1C1,A1B.
因为AA1∥BB1∥CC1,AA1=BB1=CC1,
所以四边形AA1C1C是平行四边形,
所以AC∥A1C1,
所以BC1与AC所成的角就是BC1与A1C1所成的角.
因为A1B=A1C1=BC1,
所以异面直线BC1与AC所成的角为60°.
跟踪训练 如图,连接CD1,AC.
由题意,得在四棱柱ABCD-A1B1C1D1中,
A1D1∥BC,A1D1=BC,
所以四边形A1BCD1是平行四边形,
所以A1B∥CD1,
所以∠AD1C(或其补角)为异面直线A1B和AD1所成的角.
因为异面直线A1B和AD1所成的角为90°,
所以∠AD1C=90°,
所以△ACD1是等腰直角三角形,
所以AD1=AC.
因为底面四边形ABCD是菱形,且AB=BC=2,∠ABC=120°,
所以AC=2×sin 60°×2=6,AD1=AC=3.
因为侧面都是矩形,
所以AA1===.
【检测反馈】
1. D 如图,过点A作AN∥OM,交圆O于点N,连接ON,PN,则∠PAN即异面直线OM与AP所成的角(或其补角).设 AO=ON=1,则∠OAN=∠ONA=60°,可得AN=1.因为轴截面三角形PAB为等边三角形,所以PA=PN=2.在△APN中,由余弦定理可得cos ∠PAN===,所以异面直线OM与AP所成角的余弦值为.
2. B 因为a⊥b,b∥c,所以a⊥c.
3. AB 如图,将正方体的平面展开图折起,复原为正方体.对于A,因为AB∥MN,AB=MN,所以四边形ABNM为平行四边形,则AM∥BN,故A正确;对于B,在正方体ABCDFENM中,CE,EM,CM为面对角线,则CE=EM=CM,所以△CEM是等边三角形,故B正确;对于C,因为DB 平面ABCD,AE∩平面ABCD=A,A BD,所以DB,AE为异面直线,故C错误;对于D,在正方体ABCD-FENM中,AM,DF均在平面ADMF内,且AM,DF相交,故D错误.故选AB.
4. 30° 如图,取BC的中点G,连接FG,EG.因为E,F分别是CD,AB的中点,所以FG∥AC,EG∥BD,且FG=AC,EG=BD,所以∠EFG为直线EF与AC所成的角(或其补角).又因为AC=BD,所以FG=EG.又因为AC⊥BD,所以FG⊥EG,所以∠FGE=90°,所以△EFG为直角三角形,所以tan ∠EFG==.又∠EFG为锐角,所以∠EFG=30°,即直线EF与AC所成的角为30°.
5. (1) 如图1,取DC上靠近点D的三等分点为G,连接FG,则==,可得FG∥BD,
所以F,G,B,D四点共面,显然F,B,D三点不共线,故平面FDB与平面FGDB为同一个平面,
又E 平面FDB,F∈平面FDB,所以EF∩平面FDB=F,BD 平面FDB,F BD,
故直线EF与BD是异面直线.
(2) 如图2,分别取AC,BD上靠近点A,B的三等分点为H,I,连接EI,FI,EH,FH,则====,
所以EI∥AB∥FH,FI∥DC∥HE,
故四边形IFHE为平行四边形,且直线AB与CD所成角为∠IFH或其补角.
又HE=CD=1,FH=AB=2,
所以cos ∠IFH=cos (π-∠EHF)=-cos ∠EHF=-=.
因为∠IFH∈(0,π),所以∠IFH=,
故直线AB与CD所成的角为.
图1 图2
1. 借助长方体,通过直观感知,了解空间两条直线的位置关系.
2. 掌握基本事实4及其应用.
3. 掌握等角定理,并能解决相关问题.
活动一 背景引入
平面内两条直线的位置关系只有平行和相交两种.
思考1
(1) 空间内两条直线的位置关系有哪些?
(2) 观察下面两张图片,你能找出每张图中既不平行又不相交的两条直线吗?
活动二 空间两条直线的位置关系
例1 如图,在长方体ABCD-A1B1C1D1中.
(1) 与AB平行的直线有哪些?
(2) 与AB相交的直线有哪些?
(3) 直线AA1和C1D1平行吗?相交吗?
定义:我们把不同在任何一个平面内的两条直线叫作异面直线.
空间两条直线的位置关系:
位置关系 共面情况 公共点个数
注:如无特殊说明,“两条直线”指不重合的两条直线,“两个平面”指不重合的两个平面.
活动三 基本事实4及其应用
在同一平面内,若a∥b,b∥c,则 a∥c.
思考2
那这个性质在空间中成立吗?你能在空间中找到三条平行直线吗?
基本事实4 平行于同一条直线的两条直线平行.
符号表示:
思考3
经过直线外一点,有几条直线和这条直线平行?
例2 如图,在长方体ABCD-A1B1C1D1中,已知E,F分别是AB,BC 的中点.求证:EF∥A1C1.
在空间中,直线的平行性具有传递性,同时说明了要证明两直线平行,应该把这两条直线放在同一平面内.
如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点,画出平面D1CE与平面ABB1A1的交线,并说明理由.
活动四 等角定理及其应用
在平面中,如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等,这个结论在空间成立吗?
观察下图中的∠BEF和∠B1A1C1.这两个角的两边分别平行,且有∠BEF=∠B1A1C1(因为∠BEF=∠BAC=∠B1A1C1).
定理:如果空间中一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.
已知:
求证:
证明:
思考4
如果∠BAC 和∠B1A1C1的边AB∥A1B1,AC∥A1C1,且 AB,A1B1 方向相同,而AC,A1C1方向相反,那么∠BAC 和∠B1A1C1之间有何关系?为什么?
例3 如图,已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD,A1D1的中点.求证:∠C1E1B1=∠CEB.
要说明空间中的两角相等,不仅要看它们的对应边是否平行,还要看它们的对应边的方向是否一致.若都同向或都反向,则这两个角相等;若一组同向一组反向,则这两个角互补.
如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且===.
(1) 求证:A′B′∥AB,A′C′∥AC,B′C′∥BC;
(2) 求的值.
1. (教材改编)如果两条直线a和b没有公共点,那么这两条直线的位置关系是( )
A. 平行 B. 平行或异面
C. 异面 D. 共面
2. (教材改编)若OA∥O1A1,OB∥O1B1,则∠AOB与∠A1O1B1的关系为( )
A. 相等 B. 互补 C. 相等或互补 D. 无法确定
3. (多选)(2024攀枝花月考)如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别为BB1,CC1,A1B1,A1C1的中点,则下列结论中正确的是( )
A. E,F,G,H四点共面 B. EF∥GH
C. EG,FH,AA1三线共点 D. ∠EGB1=∠FHC1
4. (2023安徽师范大学附属中学月考)如图是一个正方体的平面展开图,则在正方体中直线AB与CD的位置关系为________.
5. 如图,已知在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD,AD的中点.求证:
(1) 四边形MNA1C1是梯形;
(2) ∠DNM=∠D1A1C1.
13.2.2 空间两条直线的位置关系(2)
1. 理解两条异面直线所成角的定义及两条异面直线互相垂直的概念.
2. 掌握异面直线的判定方法.
3. 掌握异面直线所成角的计算方法.
活动一 巩固空间两条直线的位置关系
空间两条直线的位置关系:
位置关系 共面情况 公共点个数
思考1
分别在两个平面内的两条直线一定是异面直线吗?
练习 在两个相交平面内各画一条直线,使它们成为:
(1) 平行直线;(2) 相交直线;(3) 异面直线.
活动二 异面直线的定义及判定
问题:如图,在长方体ABCD-A1B1C1D1中,直线A1C和AD有什么位置关系?
思考2
如何判定两条直线是否异面?
异面直线的判定定理:
已知:
求证:
证明:
判断异面直线的方法:
方法 内容
定义法 不同在任何一个平面内的两条直线叫作异面直线
定理法 过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线
反证法 判定两条直线既不平行也不相交,那么这两条直线就是异面直线
练习 在三棱锥的所有棱中,互为异面直线的有________对.
例1 如图,在三棱锥A-BCD中,E,F是棱AD上异于点A,D的两点,G,H是棱BC上异于点B,C的两点,给出下列说法:
①AB与CD互为异面直线;
②FH分别与DC,DB互为异面直线;
③EG与FH互为异面直线;
④EG与AB互为异面直线.
其中正确的是____________.(填序号)
要判断两直线是异面直线,利用它的定义无法说明时,可以用它的定理,让其中的一条直线放一个平面内,另一条直线和这个平面相交,但交点不在第一条直线上即可.
若a和b是异面直线,b和c是异面直线,则a和c的位置关系是____________
_____________________________.
活动三 了解异面直线所成角的概念
异面直线所成的角:
定义 前提 两条异面直线a,b
作法 经过空间任意一点O,作直线a′∥a,b′∥b
结论 我们把直线a′和b′所成的锐角(或直角)叫作异面直线a,b所成的角或夹角
范围 记异面直线a与b所成的角为θ,则0°< θ ≤90°
特殊情况 当θ=90°时,异面直线a,b互相垂直,记作a⊥b
例2 如图,已知多面体ABCD-A1B1C1D1是棱长为a的正方体.
(1) 正方体中哪些棱所在的直线与直线BC1是异面直线?
(2) 求异面直线AA1与BC所成的角;
(3) 求异面直线BC1与AC所成的角.
1. 直线a与b所成角的大小只由a,b的位置关系来确定,与点O的选择无关,为了简便,点O一般取在两直线中的一条上.
2. 两条异面直线所成的角θ∈.
3. 当两条异面直线a,b所成的角是直角时,我们就说这两条异面直线互相垂直,记作a⊥b.
4. 两条直线互相垂直,有共面垂直与异面垂直两种情形.
5. 通常把两条异面直线所成的角转化为两条相交直线所成的角.
如图,在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面四边形ABCD是菱形,且AB=BC=2,∠ABC=120°,若异面直线A1B和AD1所成的角为90°,求AA1的长.
1. (教材改编)以P为顶点,圆O为底面的圆锥,轴截面三角形PAB为等边三角形,M为底面圆O上一点,∠AOM=60°,则异面直线OM与AP所成角的余弦值为( )
A. B. C. D.
2. (2023惠州期末)若空间中三条直线a,b,c满足a⊥b,b∥c,则直线a与c( )
A. 一定平行 B. 一定垂直
C. 一定是异面直线 D. 一定相交
3. (多选)(2024泉州期中)如图是正方体的平面展开图,则在这个正方体中,下列命题正确的是( )
A. AM∥BN B. △CEM是等边三角形
C. DB∥AE D. AM与DF是异面直线
(第3题) (第4题)
4. (2023深圳罗湖高级中学期中)如图,在三棱锥D-ABC中,AC=BD,且AC⊥BD,E,F分别是棱DC,AB的中点,则直线EF与AC所成的角等于________.
5. (教材改编)如图,在四面体ABCD中,E,F分别是线段AD,BC上的点,==.
(1) 求证:直线EF与BD是异面直线;
(2) 若AB=CD=3,EF=,求直线AB与CD所成角的大小.
13.2.2 空间两条直线的位置关系(1)
【活动方案】
思考1:(1) 平行、相交、既不平行又不相交
(2) 略
例1 (1) A1B1,CD,C1D1 (2) AD,AA1,BB1,BC
(3) 既不平行又不相交
填表略
思考2:略
符号表示: a∥c.
思考3:1条
例2 连接AC.
因为E,F分别为AB,BC的中点,
所以EF∥AC.
又因为AA1∥BB1,BB1∥CC1,
且AA1=BB1,BB1=CC1,
所以AA1∥CC1,且AA1=CC1,
所以四边形AA1C1C是平行四边形,
所以AC∥A1C1,所以EF∥A1C1.
跟踪训练 如图,取AB的中点F,连接EF,A1B,CF.
因为E是AA1的中点,
所以EF∥A1B.
在正方体ABCD-A1B1C1D1中,
A1D1∥BC,A1D1=BC,
所以四边形A1BCD1是平行四边形,
所以A1B∥CD1,
所以EF∥CD1,
所以E,F,C,D1四点共面.
因为E∈平面ABB1A1,E∈平面D1CE,
F∈平面ABB1A1,F∈平面D1CE,
所以平面ABB1A1∩平面D1CE=EF,
所以平面D1CE与平面ABB1A1的交线为EF.
已知:∠BAC和∠B1A1C1的边AB∥A1B1,AC∥A1C1,并且方向相同.
求证:∠BAC=∠B1A1C1.
证明:如图,分别在∠BAC和∠B1A1C1的两边上截取AD=A1D1,AE=A1E1,连接AA1,DD1,EE1,DE,D1E1.
因为AB∥A1B1,AD=A1D1,
所以四边形AA1D1D是平行四边形,
所以AA1∥DD1,且AA1=DD1.
同理AA1∥EE1,且AA1=EE1,
所以DD1∥EE1,且DD1=EE1,
所以四边形DD1E1E是平行四边形,
所以DE=D1E1.
在△ADE和△A1D1E1中,
所以△ADE≌△A1D1E1,
所以∠BAC=∠B1A1C1.
思考4:互补,理由略.
例3 连接EE1.
因为E1,E分别为A1D1,AD的中点,
所以A1E1∥AE,A1E1=AE,
所以四边形A1E1EA是平行四边形,
所以A1A∥E1E,A1A=E1E.
又因为A1A∥B1B,A1A=B1B,
所以E1E∥B1B,E1E=B1B,
所以四边形EE1B1B是平行四边形,
所以E1B1∥EB,同理可得E1C1∥EC.
又因为∠C1E1B1与∠CEB两边的方向相同,
所以∠C1E1B1=∠CEB.
跟踪训练 (1) 因为AA′∩BB′=O,且==,∠AOB=∠A′OB′,
所以△AOB∽△A′OB′,
所以∠ABO=∠A′B′O,
所以AB∥A′B′,
同理可得AC∥A′C′,BC∥B′C′.
(2) 因为A′B′∥AB,A′C′∥AC,且AB和A′B′,AC和A′C′方向均相反,
所以∠BAC=∠B′A′C′.
同理可得∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,
所以△ABC∽△A′B′C′.
又==,
所以==.
【检测反馈】
1. B 如果两条直线a和b没有公共点,那么这两条直线是同一平面内的平行直线或是异面直线.
2. C
3. ABC 对于A,B,如图,连接EF,GH.因为GH是△A1B1C1的中位线,所以GH∥B1C1.因为B1E∥C1F,且B1E=C1F,所以四边形B1EFC1是平行四边形,所以EF∥B1C1,可得EF∥GH,则E,F,G,H四点共面,故A,B正确;对于C,如图,延长EG,FH相交于点P.因为P∈EG,EG 平面ABB1A1,所以P∈平面ABB1A1.因为P∈FH,FH 平面ACC1A1,所以P∈平面ACC1A1.因为平面ABB1A1∩平面ACC1A1=AA1,所以P∈AA1,所以EG,FH,AA1三线共点,故C正确;对于D,因为EB1=FC1,当GB1≠HC1时,tan ∠EGB1≠tan ∠FHC1,所以∠EGB1≠∠FHC1,故D错误.故选ABC.
4. 异面 如图是正方体的直观图,则在正方体中直线AB与CD的位置关系为异面.
5. (1) 连接AC.
在△ACD中,因为M,N分别是CD,AD的中点,
所以MN是△ACD的中位线,
所以MN∥AC,MN=AC.
由正方体的性质,得AC∥A1C1,AC=A1C1,
所以MN∥A1C1,且MN=A1C1,
即MN≠A1C1,
所以四边形MNA1C1是梯形.
(2) 因为NM∥A1C1,ND∥A1D1,
且∠DNM与∠D1A1C1两边的方向相同,
所以∠DNM=∠D1A1C1.
13.2.2 空间两条直线的位置关系(2)
【活动方案】
活动一
位置关系 共面情况 公共点个数
相交 在同一平面内 有且只有1个
平行 在同一平面内 0个
异面 不同在任何一个平面内 0个
思考1:不一定,可能平行也可能相交.
练习:略
问题:A1C与AD是异面直线.
思考2:过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线.
已知:l α,A α,B∈α,B l.
求证:直线AB与l是异面直线.
证明:假设AB与l是共面直线,因为l α且 B∈α,所以 AB α与A α相矛盾,
所以直线AB与l是异面直线.
练习:3 在三棱锥A-BCD中,AB与CD异面,AD与BC异面,AC与BD异面,所以有3对异面直线.
例1 ①②③④ 因为直线DC 平面BCD,直线AB 平面BCD,点B 直线DC,所以由异面直线的判定定理可知,①正确;同理可得,②③④正确.
跟踪训练 相交、平行或异面 异面直线不具有传递性,可以以长方体为例加以说明,异面直线a,b,直线c的位置可如图所示,此时a和c异面.当c在c1处时,a和c相交;当c在c2处时,a和c平行.
例2 (1) 与直线BC1是异面直线的有AA1,A1B1,A1D1,DA,DC,DD1.
(2) 因为DA∥BC,所以∠A1AD即为异面直线AA1与BC所成的角,
所以异面直线AA1与BC所成的角为90°.
(3) 连接A1C1,A1B.
因为AA1∥BB1∥CC1,AA1=BB1=CC1,
所以四边形AA1C1C是平行四边形,
所以AC∥A1C1,
所以BC1与AC所成的角就是BC1与A1C1所成的角.
因为A1B=A1C1=BC1,
所以异面直线BC1与AC所成的角为60°.
跟踪训练 如图,连接CD1,AC.
由题意,得在四棱柱ABCD-A1B1C1D1中,
A1D1∥BC,A1D1=BC,
所以四边形A1BCD1是平行四边形,
所以A1B∥CD1,
所以∠AD1C(或其补角)为异面直线A1B和AD1所成的角.
因为异面直线A1B和AD1所成的角为90°,
所以∠AD1C=90°,
所以△ACD1是等腰直角三角形,
所以AD1=AC.
因为底面四边形ABCD是菱形,且AB=BC=2,∠ABC=120°,
所以AC=2×sin 60°×2=6,AD1=AC=3.
因为侧面都是矩形,
所以AA1===.
【检测反馈】
1. D 如图,过点A作AN∥OM,交圆O于点N,连接ON,PN,则∠PAN即异面直线OM与AP所成的角(或其补角).设 AO=ON=1,则∠OAN=∠ONA=60°,可得AN=1.因为轴截面三角形PAB为等边三角形,所以PA=PN=2.在△APN中,由余弦定理可得cos ∠PAN===,所以异面直线OM与AP所成角的余弦值为.
2. B 因为a⊥b,b∥c,所以a⊥c.
3. AB 如图,将正方体的平面展开图折起,复原为正方体.对于A,因为AB∥MN,AB=MN,所以四边形ABNM为平行四边形,则AM∥BN,故A正确;对于B,在正方体ABCDFENM中,CE,EM,CM为面对角线,则CE=EM=CM,所以△CEM是等边三角形,故B正确;对于C,因为DB 平面ABCD,AE∩平面ABCD=A,A BD,所以DB,AE为异面直线,故C错误;对于D,在正方体ABCD-FENM中,AM,DF均在平面ADMF内,且AM,DF相交,故D错误.故选AB.
4. 30° 如图,取BC的中点G,连接FG,EG.因为E,F分别是CD,AB的中点,所以FG∥AC,EG∥BD,且FG=AC,EG=BD,所以∠EFG为直线EF与AC所成的角(或其补角).又因为AC=BD,所以FG=EG.又因为AC⊥BD,所以FG⊥EG,所以∠FGE=90°,所以△EFG为直角三角形,所以tan ∠EFG==.又∠EFG为锐角,所以∠EFG=30°,即直线EF与AC所成的角为30°.
5. (1) 如图1,取DC上靠近点D的三等分点为G,连接FG,则==,可得FG∥BD,
所以F,G,B,D四点共面,显然F,B,D三点不共线,故平面FDB与平面FGDB为同一个平面,
又E 平面FDB,F∈平面FDB,所以EF∩平面FDB=F,BD 平面FDB,F BD,
故直线EF与BD是异面直线.
(2) 如图2,分别取AC,BD上靠近点A,B的三等分点为H,I,连接EI,FI,EH,FH,则====,
所以EI∥AB∥FH,FI∥DC∥HE,
故四边形IFHE为平行四边形,且直线AB与CD所成角为∠IFH或其补角.
又HE=CD=1,FH=AB=2,
所以cos ∠IFH=cos (π-∠EHF)=-cos ∠EHF=-=.
因为∠IFH∈(0,π),所以∠IFH=,
故直线AB与CD所成的角为.
图1 图2
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
