13.2.3 直线与平面的位置关系 —直线与平面平行 学案(2课时,含答案)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 13.2.3 直线与平面的位置关系 —直线与平面平行 学案(2课时,含答案)2024-2025学年高一数学苏教版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 469.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 21:12:06 | ||
图片预览




文档简介
13.2.3 直线与平面的位置关系
——直线与平面平行(1)
1. 借助长方体,通过直观感知,了解直线与平面的位置关系.
2. 掌握直线与平面平行的判定定理及其简单应用.
活动一 了解直线与平面的位置关系
问题:如图,在长方体ABCD-A1B1C1D1中,线段BC1所在的直线与长方体的六个面所在的平面分别有哪些位置关系?
直线与平面的位置关系:
位置 关系 直线a在 平面α内 直线a在平面α外
直线a与平面α相交 直线a与平面α平行
公共点 无数个 有且只有1个 0个
符号表示 a α a∩α=A a∥α
图形表示
注:直线a和平面α相交或平行的情况统称为直线在平面外,记作:a α.
活动二 直线与平面平行的判定定理
探究1:如图,一块矩形木板ABCD的一边AB在平面α内,把这块木板绕AB转动,在转动过程中,AB的对边CD(不落在α内)和平面α有何位置关系?
探究2:如图,平面α外的直线a平行于平面α内的直线b,那么这两条直线共面吗?直线a与平面α相交吗?
思考
如何判定一条直线与一个平面平行?
直线与平面平行的判定定理:
定理 表示
图形 文字 符号
直线与平面平 行的判定定理 如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行 若a α,b α,a∥b, 则a∥α
活动三 直线与平面平行的判定定理的应用
例 如图,已知E,F分别是三棱锥A-BCD的侧棱AB,AD的中点.求证:EF∥平面BCD.
要证明一条直线与一个平面平行,就是要在这个平面内找一条直线与已知直线平行,当然这两条直线应该同在另外一个平面内.
如图,已知E,F,G,H分别是空间四边形ABCD中AB,BC,CD,AD的中点.求证:
(1) E,F,G,H四点共面;
(2) BD∥平面EFGH,AC∥平面EFGH.
如图,已知M,N分别是底面为矩形的四棱锥PABCD的棱AB,PC的中点,求证:MN∥平面PAD.
1. (教材改编)若空间中的平面α及两条直线a,b满足a α且b α,则“a∩b= ”是 “a∥α”的( )
A. 充分且不必要条件 B. 必要且不充分条件
C. 充要条件 D. 既不充分又不必要条件
2. (教材改编)过四棱锥PABCD任意两条棱的中点作直线,其中与平面PBD平行的直线有( )
A. 4条 B. 5条 C. 6条 D. 7条
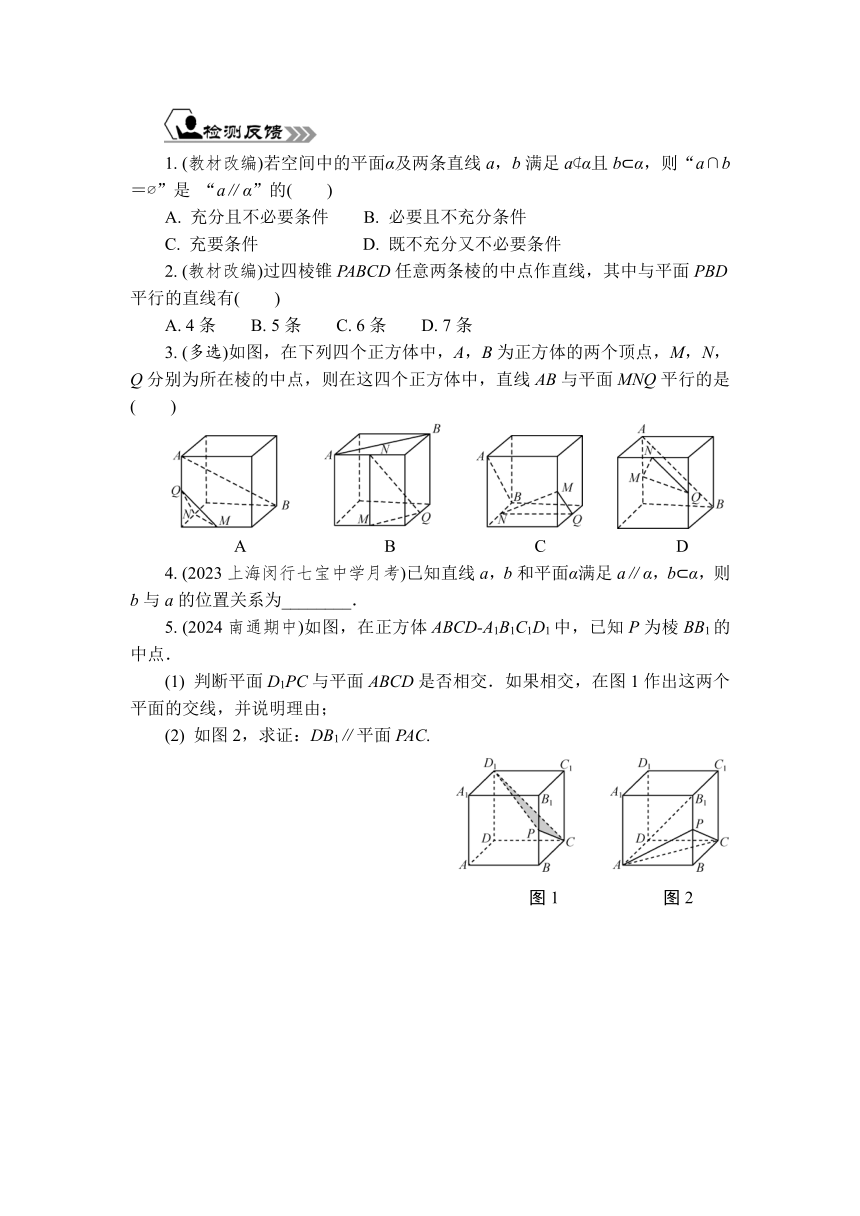
3. (多选)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q分别为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ平行的是( )
A B C D
4. (2023上海闵行七宝中学月考)已知直线a,b和平面α满足a∥α,b α,则b与a的位置关系为________.
5. (2024南通期中)如图,在正方体ABCD-A1B1C1D1中,已知P为棱BB1的中点.
(1) 判断平面D1PC与平面ABCD是否相交.如果相交,在图1作出这两个平面的交线,并说明理由;
(2) 如图2,求证:DB1∥平面PAC.
图1 图2
13.2.3 直线与平面的位置关系
——直线与平面平行(2)
1. 巩固直线与平面的位置关系及直线与平面平行的判定.
2. 掌握直线与平面平行的性质定理及其简单应用.
活动一 巩固直线与平面的位置关系及直线与平面平行的判定
1. 直线与平面的位置关系:
位置关系 直线a在平面α内 直线a在平面α外
直线a与平面α相交 直线a与平面α平行
公共点 无数个 有且只有1个 0个
符号表示 a α a∩α=A a∥α
图形表示
2. 直线与平面平行的判定定理:
定理 表示
图形 文字 符号
直线与平面平行的判定定理 如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行 若a α,b α,a∥b,则a∥α
活动二 探究直线与平面平行的性质及其推论
思考1
如图,l∥α,a α,直线l与直线a一定平行吗?为什么?
思考2
如图,a∥α,a β,α∩β=b,满足以上条件的平面β有多少个?直线a,b有什么位置关系?
思考3
如果一条直线与一个平面平行,那么这条直线是否与这个平面内的任意一条直线都平行? 如果不是,那么平面内怎样的直线才和已知直线平行呢?
直线与平面平行的性质定理:
一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.
已知:
求证:
证明:
直线与平面平行的性质定理:
定理 表示
图形 文字 符号
直线与平面平 行的性质定理 一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行 若l∥α,l β,α∩β=m,则l∥m
活动三 直线与平面平行的性质定理的应用
例 如图,E,H分别是三棱锥A-BCD的边AB,AD的中点,平面α过EH分别交BC,CD于点F,G.求证:EH∥FG.
要得到两直线平行,可以用基本事实4,也可以用线面平行的性质定理,在用线面平行的性质定理时,务必要注意过已知的那条直线作(或找)一个辅助平面,使得这个辅助平面与已知平面相交,所得的交线才和已知直线平行.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AC与BD交于点O,M是PC的中点,在DM上取一点G,过点G和AP作平面交平面BDM于GH,求证:AP∥GH.
如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.
1. (教材改编)若直线a∥平面α,P∈α,则过点P且平行于a的直线( )
A. 只有一条,不在平面α内 B. 有无数条,不一定在平面α内
C. 只有一条,且在平面α内 D. 有无数条,一定在平面α内
2. (教材改编)如图,直线a∥平面α,A α,且直线a与点A位于α的两侧,B,C∈a,AB,AC分别交平面α于点E,F,若BC=4,CF=5,AF=3,则EF的长为( )
A. 3 B.
C. D.
3. (多选)(2024衡阳期末)若三个不同的平面α,β,γ两两相交,且α∩β=l1,α∩γ=l2,β∩γ=l3,则交线l1,l2,l3的位置关系可能是( )
A. 重合 B. 相交于一点
C. 两两平行 D. 恰有两条交线平行
4. 如图,四棱锥S-ABCD的所有棱长都等于2,E为线段SA的中点,过C,D,E三点的平面与棱SB交于点F,则四边形DEFC的周长为________.
5. (2024福州期中)如图,在三棱柱ABC-A1B1C1中,点D在线段AC上.
(1) 若D是AC的中点,求证:AB1∥平面BC1D;
(2) 若M为BC的中点,直线AB1∥平面C1DM,求的值.
13.2.3 直线与平面的位置关系
——直线与平面平行(1)
【活动方案】
问题:直线BC1与平面ABCD、平面A1B1C1D1、平面ABB1A1、平面CDD1C1相交,直线BC1与平面ADD1A1平行,直线BC1在平面BCC1B1内.
探究1:CD∥α
探究2:直线a,b共面,直线 a和平面α不相交.
思考:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
例 因为E,F分别为AB,AD的中点,
所以EF∥BD.
因为EF 平面BCD,BD 平面BCD,
所以EF∥平面BCD.
跟踪训练1 (1) 因为E,F,G,H分别为AB,BC,CD,AD的中点,
所以EF∥AC,GH∥AC,所以EF∥GH,
所以E,F,G,H四点共面.
(2) 因为E,H分别为AB,AD的中点,
所以EH∥BD.
因为BD 平面EFGH,EH 平面EFGH,
所以BD∥平面EFGH.
同理可证AC∥平面EFGH.
跟踪训练2 取PD的中点E,连接AE,NE.
因为N是PC的中点,
所以EN∥CD,EN=CD.
因为在矩形ABCD中,M为AB的中点,
所以AM∥CD,AM=CD,
所以EN∥AM,EN=AM,
所以四边形AMNE是平行四边形,
所以MN∥AE.
又因为AE 平面PAD,MN 平面PAD,
所以MN∥平面PAD.
【检测反馈】
1. B 当a∩b= 时,因为a α且b α,所以a与α可能相交,故充分性不成立;当a∥α时,因为a α且b α,所以a∩b= ,故必要性成立,故“a∩b= ”是“a∥α”的必要且不充分条件.
2. C 如图,设E,F,G,H,I,J,M,N分别为相应棱的中点,则NE∥PB,且NE 平面PBD,PB 平面PBD,所以NE∥平面PBD.同理可得HE,NH,GF,MF,MG与平面PBD平行,由图可知,其他的任意两条棱的中点的连线与平面PBD相交或在平面PBD内,所以与平面PBD平行的直线有6条.
3. BCD 对于A,如图1,连接A1B,取A1B的中点O,连接OQ,因为Q为AA1的中点,所以OQ∥AB.又Q∈平面MNQ,O 平面MNQ,所以OQ与平面MNQ相交,所以AB与平面MNQ不平行,故A错误;对于B,如图2,连接CD,由正方体的性质可得AB∥CD.因为M,Q分别是所在棱的中点,所以MQ∥CD,所以AB∥MQ.又AB 平面MNQ,MQ 平面MNQ,所以AB∥平面MNQ.同理可证,C,D选项中均有AB∥平面MNQ.故选BCD.
图1 图2
4. 异面或平行 如图所示,a∥α,b α,则a与b没有公共点,所以a与b异面或平行.
5. (1) 平面D1PC与平面ABCD相交,理由如下:
因为DD1∥BP,DD1=2BP,
所以D,D1,B,P四点共面.
显然DB与D1P不平行,则DB与D1P必相交,
所以平面D1PC与平面ABCD相交.
如图1,连接DB,D1P并延长交于点Q,连接CQ,
则平面D1PC∩平面ABCD=CQ.
(2) 如图2,连接BD交AC于点O,连接OP.
在△BB1D中,因为O,P分别是BD,BB1的中点,
所以OP∥DB1.
又OP 平面PAC,DB1 平面PAC,
所以DB1∥平面PAC.
图1 图2
13.2.3 直线与平面的位置关系
——直线与平面平行(2)
【活动方案】
思考1:不一定,因为还可能是异面直线.
思考2:无数个,a∥b.
思考3:已知:a∥α,a β,α∩β=b.
求证:a∥b.
证明:因为a∥α,
所以直线a与平面α没有公共点.
因为b α,
所以直线a与直线b没有公共点.
因为直线a 平面β,b 平面β,所以a∥b.
例 因为E,H分别是AB,AD的中点,
所以EH∥BD.
又BD 平面BCD,EH 平面BCD,
所以EH∥平面BCD.
又EH 平面α,平面α∩平面BCD=FG,
所以EH∥FG.
跟踪训练1 连接OM.
因为四边形ABCD是平行四边形,
所以O是AC的中点.
因为M是PC的中点,
所以AP∥OM.
又因为AP 平面BDM,OM 平面BDM,
所以AP∥平面BDM.
因为AP 平面APGH,平面APGH∩平面BDM=GH,
所以AP∥GH.
跟踪训练2 因为EH∥A1D1,A1D1∥B1C1,
所以EH∥B1C1.
因为EH 平面BCC1B1,B1C1 平面BCC1B1,
所以EH∥平面BCC1B1.
因为EH 平面FGHE,平面FGHE∩平面BCC1B1=FG,
所以EH∥FG.
又EH∥A1D1,
所以FG∥A1D1.
因为FG 平面ADD1A1,A1D1 平面ADD1A1,
所以FG∥平面ADD1A1.
【检测反馈】
1. C 由线面平行的性质定理知,过点P平行于a的直线只有一条,且在平面α内.
2. B 因为BC∥α,BC 平面ABC,平面ABC∩α=EF,所以EF∥BC,所以=,即=,解得EF=.
3. ABC 如图,作出一个长方体ABCD-A1B1C1D1.对于A,可把平面DCC1D1,DCB1A1,BCDA依次取为平面α,β,γ,它们两两相交于共同的交线DC,故A正确;对于B,可把平面DCC1D1,ADD1A1,BCDA依次取为平面α,β,γ,此时α∩β=DD1,α∩γ=DC,β∩γ=AD,易得三条交线交于同一点D,故B正确;对于C,可把平面DCB1A1,ABB1A1,BCDA依次取为平面α,β,γ,此时α∩β=A1B1,α∩γ=DC,β∩γ=AB,易得三条交线两两平行,故C正确;对于D,若l1∥l2,则可证得l1∥γ,又l1 β,β∩γ=l3,所以l1∥l3,即交线l1,l2,l3的位置关系不可能是恰有两条交线平行,故D错误.故选ABC.
4. 3+2 由题意知,四边形ABCD为菱形,所以CD∥AB.因为CD 平面SAB,AB 平面SAB,所以CD∥平面SAB.因为CD 平面CDE,平面CDE∩平面SAB=EF,所以EF∥CD,则EF∥AB.又E为SA的中点,则F为SB的中点,所以EF=AB=1.因为△SAD是边长为2的等边三角形,所以DE⊥SA,且DE=2sin 60°=, 同理可得CF=,故四边形DEFC的周长为3+2.
5. (1) 如图,连接B1C交BC1于点O,连接OD.
由三棱柱ABC-A1B1C1的几何特征,
得四边形BCC1B1为平行四边形,
所以O为B1C的中点.
又因为D为AC的中点,
所以OD∥AB1.
因为AB1 平面BC1D,OD 平面BC1D,
所以AB1∥平面BC1D.
(2) 如图,设B1C交C1M于点E,连接DE.
因为AB1∥平面C1DM,AB1 平面AB1C,平面AB1C∩平面C1DM=DE,
所以AB1∥DE,所以=.
又因为四边形BCC1B1为平行四边形,
M为BC的中点,
所以==2,
所以=2.
——直线与平面平行(1)
1. 借助长方体,通过直观感知,了解直线与平面的位置关系.
2. 掌握直线与平面平行的判定定理及其简单应用.
活动一 了解直线与平面的位置关系
问题:如图,在长方体ABCD-A1B1C1D1中,线段BC1所在的直线与长方体的六个面所在的平面分别有哪些位置关系?
直线与平面的位置关系:
位置 关系 直线a在 平面α内 直线a在平面α外
直线a与平面α相交 直线a与平面α平行
公共点 无数个 有且只有1个 0个
符号表示 a α a∩α=A a∥α
图形表示
注:直线a和平面α相交或平行的情况统称为直线在平面外,记作:a α.
活动二 直线与平面平行的判定定理
探究1:如图,一块矩形木板ABCD的一边AB在平面α内,把这块木板绕AB转动,在转动过程中,AB的对边CD(不落在α内)和平面α有何位置关系?
探究2:如图,平面α外的直线a平行于平面α内的直线b,那么这两条直线共面吗?直线a与平面α相交吗?
思考
如何判定一条直线与一个平面平行?
直线与平面平行的判定定理:
定理 表示
图形 文字 符号
直线与平面平 行的判定定理 如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行 若a α,b α,a∥b, 则a∥α
活动三 直线与平面平行的判定定理的应用
例 如图,已知E,F分别是三棱锥A-BCD的侧棱AB,AD的中点.求证:EF∥平面BCD.
要证明一条直线与一个平面平行,就是要在这个平面内找一条直线与已知直线平行,当然这两条直线应该同在另外一个平面内.
如图,已知E,F,G,H分别是空间四边形ABCD中AB,BC,CD,AD的中点.求证:
(1) E,F,G,H四点共面;
(2) BD∥平面EFGH,AC∥平面EFGH.
如图,已知M,N分别是底面为矩形的四棱锥PABCD的棱AB,PC的中点,求证:MN∥平面PAD.
1. (教材改编)若空间中的平面α及两条直线a,b满足a α且b α,则“a∩b= ”是 “a∥α”的( )
A. 充分且不必要条件 B. 必要且不充分条件
C. 充要条件 D. 既不充分又不必要条件
2. (教材改编)过四棱锥PABCD任意两条棱的中点作直线,其中与平面PBD平行的直线有( )
A. 4条 B. 5条 C. 6条 D. 7条
3. (多选)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q分别为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ平行的是( )
A B C D
4. (2023上海闵行七宝中学月考)已知直线a,b和平面α满足a∥α,b α,则b与a的位置关系为________.
5. (2024南通期中)如图,在正方体ABCD-A1B1C1D1中,已知P为棱BB1的中点.
(1) 判断平面D1PC与平面ABCD是否相交.如果相交,在图1作出这两个平面的交线,并说明理由;
(2) 如图2,求证:DB1∥平面PAC.
图1 图2
13.2.3 直线与平面的位置关系
——直线与平面平行(2)
1. 巩固直线与平面的位置关系及直线与平面平行的判定.
2. 掌握直线与平面平行的性质定理及其简单应用.
活动一 巩固直线与平面的位置关系及直线与平面平行的判定
1. 直线与平面的位置关系:
位置关系 直线a在平面α内 直线a在平面α外
直线a与平面α相交 直线a与平面α平行
公共点 无数个 有且只有1个 0个
符号表示 a α a∩α=A a∥α
图形表示
2. 直线与平面平行的判定定理:
定理 表示
图形 文字 符号
直线与平面平行的判定定理 如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行 若a α,b α,a∥b,则a∥α
活动二 探究直线与平面平行的性质及其推论
思考1
如图,l∥α,a α,直线l与直线a一定平行吗?为什么?
思考2
如图,a∥α,a β,α∩β=b,满足以上条件的平面β有多少个?直线a,b有什么位置关系?
思考3
如果一条直线与一个平面平行,那么这条直线是否与这个平面内的任意一条直线都平行? 如果不是,那么平面内怎样的直线才和已知直线平行呢?
直线与平面平行的性质定理:
一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.
已知:
求证:
证明:
直线与平面平行的性质定理:
定理 表示
图形 文字 符号
直线与平面平 行的性质定理 一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行 若l∥α,l β,α∩β=m,则l∥m
活动三 直线与平面平行的性质定理的应用
例 如图,E,H分别是三棱锥A-BCD的边AB,AD的中点,平面α过EH分别交BC,CD于点F,G.求证:EH∥FG.
要得到两直线平行,可以用基本事实4,也可以用线面平行的性质定理,在用线面平行的性质定理时,务必要注意过已知的那条直线作(或找)一个辅助平面,使得这个辅助平面与已知平面相交,所得的交线才和已知直线平行.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AC与BD交于点O,M是PC的中点,在DM上取一点G,过点G和AP作平面交平面BDM于GH,求证:AP∥GH.
如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.
1. (教材改编)若直线a∥平面α,P∈α,则过点P且平行于a的直线( )
A. 只有一条,不在平面α内 B. 有无数条,不一定在平面α内
C. 只有一条,且在平面α内 D. 有无数条,一定在平面α内
2. (教材改编)如图,直线a∥平面α,A α,且直线a与点A位于α的两侧,B,C∈a,AB,AC分别交平面α于点E,F,若BC=4,CF=5,AF=3,则EF的长为( )
A. 3 B.
C. D.
3. (多选)(2024衡阳期末)若三个不同的平面α,β,γ两两相交,且α∩β=l1,α∩γ=l2,β∩γ=l3,则交线l1,l2,l3的位置关系可能是( )
A. 重合 B. 相交于一点
C. 两两平行 D. 恰有两条交线平行
4. 如图,四棱锥S-ABCD的所有棱长都等于2,E为线段SA的中点,过C,D,E三点的平面与棱SB交于点F,则四边形DEFC的周长为________.
5. (2024福州期中)如图,在三棱柱ABC-A1B1C1中,点D在线段AC上.
(1) 若D是AC的中点,求证:AB1∥平面BC1D;
(2) 若M为BC的中点,直线AB1∥平面C1DM,求的值.
13.2.3 直线与平面的位置关系
——直线与平面平行(1)
【活动方案】
问题:直线BC1与平面ABCD、平面A1B1C1D1、平面ABB1A1、平面CDD1C1相交,直线BC1与平面ADD1A1平行,直线BC1在平面BCC1B1内.
探究1:CD∥α
探究2:直线a,b共面,直线 a和平面α不相交.
思考:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
例 因为E,F分别为AB,AD的中点,
所以EF∥BD.
因为EF 平面BCD,BD 平面BCD,
所以EF∥平面BCD.
跟踪训练1 (1) 因为E,F,G,H分别为AB,BC,CD,AD的中点,
所以EF∥AC,GH∥AC,所以EF∥GH,
所以E,F,G,H四点共面.
(2) 因为E,H分别为AB,AD的中点,
所以EH∥BD.
因为BD 平面EFGH,EH 平面EFGH,
所以BD∥平面EFGH.
同理可证AC∥平面EFGH.
跟踪训练2 取PD的中点E,连接AE,NE.
因为N是PC的中点,
所以EN∥CD,EN=CD.
因为在矩形ABCD中,M为AB的中点,
所以AM∥CD,AM=CD,
所以EN∥AM,EN=AM,
所以四边形AMNE是平行四边形,
所以MN∥AE.
又因为AE 平面PAD,MN 平面PAD,
所以MN∥平面PAD.
【检测反馈】
1. B 当a∩b= 时,因为a α且b α,所以a与α可能相交,故充分性不成立;当a∥α时,因为a α且b α,所以a∩b= ,故必要性成立,故“a∩b= ”是“a∥α”的必要且不充分条件.
2. C 如图,设E,F,G,H,I,J,M,N分别为相应棱的中点,则NE∥PB,且NE 平面PBD,PB 平面PBD,所以NE∥平面PBD.同理可得HE,NH,GF,MF,MG与平面PBD平行,由图可知,其他的任意两条棱的中点的连线与平面PBD相交或在平面PBD内,所以与平面PBD平行的直线有6条.
3. BCD 对于A,如图1,连接A1B,取A1B的中点O,连接OQ,因为Q为AA1的中点,所以OQ∥AB.又Q∈平面MNQ,O 平面MNQ,所以OQ与平面MNQ相交,所以AB与平面MNQ不平行,故A错误;对于B,如图2,连接CD,由正方体的性质可得AB∥CD.因为M,Q分别是所在棱的中点,所以MQ∥CD,所以AB∥MQ.又AB 平面MNQ,MQ 平面MNQ,所以AB∥平面MNQ.同理可证,C,D选项中均有AB∥平面MNQ.故选BCD.
图1 图2
4. 异面或平行 如图所示,a∥α,b α,则a与b没有公共点,所以a与b异面或平行.
5. (1) 平面D1PC与平面ABCD相交,理由如下:
因为DD1∥BP,DD1=2BP,
所以D,D1,B,P四点共面.
显然DB与D1P不平行,则DB与D1P必相交,
所以平面D1PC与平面ABCD相交.
如图1,连接DB,D1P并延长交于点Q,连接CQ,
则平面D1PC∩平面ABCD=CQ.
(2) 如图2,连接BD交AC于点O,连接OP.
在△BB1D中,因为O,P分别是BD,BB1的中点,
所以OP∥DB1.
又OP 平面PAC,DB1 平面PAC,
所以DB1∥平面PAC.
图1 图2
13.2.3 直线与平面的位置关系
——直线与平面平行(2)
【活动方案】
思考1:不一定,因为还可能是异面直线.
思考2:无数个,a∥b.
思考3:已知:a∥α,a β,α∩β=b.
求证:a∥b.
证明:因为a∥α,
所以直线a与平面α没有公共点.
因为b α,
所以直线a与直线b没有公共点.
因为直线a 平面β,b 平面β,所以a∥b.
例 因为E,H分别是AB,AD的中点,
所以EH∥BD.
又BD 平面BCD,EH 平面BCD,
所以EH∥平面BCD.
又EH 平面α,平面α∩平面BCD=FG,
所以EH∥FG.
跟踪训练1 连接OM.
因为四边形ABCD是平行四边形,
所以O是AC的中点.
因为M是PC的中点,
所以AP∥OM.
又因为AP 平面BDM,OM 平面BDM,
所以AP∥平面BDM.
因为AP 平面APGH,平面APGH∩平面BDM=GH,
所以AP∥GH.
跟踪训练2 因为EH∥A1D1,A1D1∥B1C1,
所以EH∥B1C1.
因为EH 平面BCC1B1,B1C1 平面BCC1B1,
所以EH∥平面BCC1B1.
因为EH 平面FGHE,平面FGHE∩平面BCC1B1=FG,
所以EH∥FG.
又EH∥A1D1,
所以FG∥A1D1.
因为FG 平面ADD1A1,A1D1 平面ADD1A1,
所以FG∥平面ADD1A1.
【检测反馈】
1. C 由线面平行的性质定理知,过点P平行于a的直线只有一条,且在平面α内.
2. B 因为BC∥α,BC 平面ABC,平面ABC∩α=EF,所以EF∥BC,所以=,即=,解得EF=.
3. ABC 如图,作出一个长方体ABCD-A1B1C1D1.对于A,可把平面DCC1D1,DCB1A1,BCDA依次取为平面α,β,γ,它们两两相交于共同的交线DC,故A正确;对于B,可把平面DCC1D1,ADD1A1,BCDA依次取为平面α,β,γ,此时α∩β=DD1,α∩γ=DC,β∩γ=AD,易得三条交线交于同一点D,故B正确;对于C,可把平面DCB1A1,ABB1A1,BCDA依次取为平面α,β,γ,此时α∩β=A1B1,α∩γ=DC,β∩γ=AB,易得三条交线两两平行,故C正确;对于D,若l1∥l2,则可证得l1∥γ,又l1 β,β∩γ=l3,所以l1∥l3,即交线l1,l2,l3的位置关系不可能是恰有两条交线平行,故D错误.故选ABC.
4. 3+2 由题意知,四边形ABCD为菱形,所以CD∥AB.因为CD 平面SAB,AB 平面SAB,所以CD∥平面SAB.因为CD 平面CDE,平面CDE∩平面SAB=EF,所以EF∥CD,则EF∥AB.又E为SA的中点,则F为SB的中点,所以EF=AB=1.因为△SAD是边长为2的等边三角形,所以DE⊥SA,且DE=2sin 60°=, 同理可得CF=,故四边形DEFC的周长为3+2.
5. (1) 如图,连接B1C交BC1于点O,连接OD.
由三棱柱ABC-A1B1C1的几何特征,
得四边形BCC1B1为平行四边形,
所以O为B1C的中点.
又因为D为AC的中点,
所以OD∥AB1.
因为AB1 平面BC1D,OD 平面BC1D,
所以AB1∥平面BC1D.
(2) 如图,设B1C交C1M于点E,连接DE.
因为AB1∥平面C1DM,AB1 平面AB1C,平面AB1C∩平面C1DM=DE,
所以AB1∥DE,所以=.
又因为四边形BCC1B1为平行四边形,
M为BC的中点,
所以==2,
所以=2.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
