13.2.4 平面与平面的位置关系—两平面平行 学案(含答案)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 13.2.4 平面与平面的位置关系—两平面平行 学案(含答案)2024-2025学年高一数学苏教版(2019)必修第二册 |
|
|
| 格式 | docx | ||
| 文件大小 | 288.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 00:00:00 | ||
图片预览




文档简介
13.2.4 平面与平面的位置关系—两平面平行
1. 借助长方体,通过直观感知,了解两个平面的位置关系.
2. 理解并掌握两个平面平行与两个平面相交的定义.
3. 掌握两个平面平行的判定定理和性质定理,并能运用其解决一些具体问题.
4. 了解两个平行平面间的距离的概念.
活动一 了解空间两个平面的位置关系
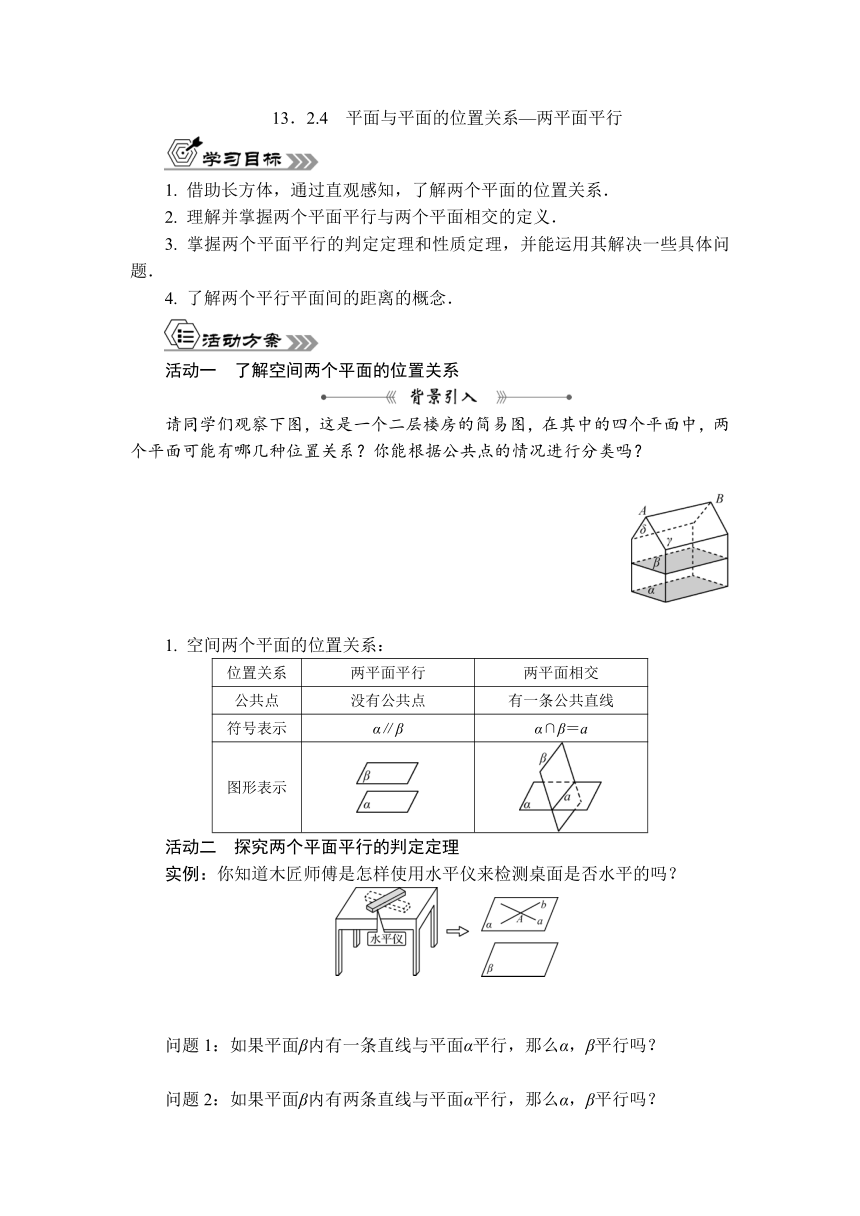
请同学们观察下图,这是一个二层楼房的简易图,在其中的四个平面中,两个平面可能有哪几种位置关系?你能根据公共点的情况进行分类吗?
1. 空间两个平面的位置关系:
位置关系 两平面平行 两平面相交
公共点 没有公共点 有一条公共直线
符号表示 α∥β α∩β=a
图形表示
活动二 探究两个平面平行的判定定理
实例:你知道木匠师傅是怎样使用水平仪来检测桌面是否水平的吗?
问题1:如果平面β内有一条直线与平面α平行,那么α,β平行吗?
问题2:如果平面β内有两条直线与平面α平行,那么α,β平行吗?
2. 两个平面平行的判定定理:
图形 文字 符号
两个平面平 行的判定定理
例1 如图,在正方体ABCD-A1B1C1D1中,求证:平面C1DB∥平面AB1D1.
要得到两个平面平行,只能根据面面平行的判定定理,先证明一个平面内的两条相交直线与另一个平面平行,坚决不能由线线平行得到面面平行.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上(不与端点重合),且PM∶MA=BN∶ND=PQ∶QD.求证:平面MNQ∥平面PBC.
活动三 探究两个平面平行的性质定理
3. 观察长方体ABCD-A1B1C1D1中的两个平面:平面ABCD及平面A1B1C1D1.
思考1
平面A1B1C1D1中的所有直线都平行于平面ABCD吗?
思考2
若m 平面ABCD,n 平面A1B1C1D1,则m∥n吗?
思考3
过BC的平面交平面A1B1C1D1于B2C2,B2C2与BC是什么关系?
思考4
如果两个平面平行,那么
(1) 一个平面内的直线是否平行于另一个平面?
(2) 分别在两个平面内的两条直线是否平行?
(3) 如果第三个平面与这两个平面相交,那么所得的交线平行吗?
探究:两个平面平行的性质定理:
已知:
求证:
证明:
例2 求证:如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.
这是得到线面垂直的另一条途径,虽然结论正确,但不能作为定理使用.
求证:如果一条直线垂直于两个平面,那么这两个平面平行.
1. 与两个平行平面都垂直的直线叫作两个平行平面的公垂线.
2. 公垂线夹在两个平行平面间的线段叫作两个平行平面的公垂线段.
3. 公垂线段的长度叫作两个平行平面间的距离.
1. (教材改编)设有两条不同的直线m,n和两个不同的平面α,β,则下列命题中正确的是( )
A. 若m∥α,n∥α,则m∥n B. 若m∥α,m∥β,则α∥β
C. 若m∥n,m∥α,则n∥α D. 若α∥β,m α,则m∥β
2. (教材改编)(2024哈尔滨期中)如图,平面α∥平面β,△PAB所在的平面与α,β分别交于CD,AB.若PC=2,CA=3,CD=1,则线段AB的长为( )
A.
B. 2
C.
D. 3
3. (多选)如图,在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,则下列四个推断中正确的是( )
A. FG∥平面AA1D1D
B. EF∥平面BC1D1
C. FG∥平面BC1D1
D. 平面EFG∥平面BC1D1
4. 若平面外的一条直线上有两点到这个平面的距离相等,则这条直线与该平面的位置关系是________.
5. (2024佛山月考)如图,在六面体ABCDEF中,DE∥CF,四边形ABCD是平行四边形,DE=2CF.
(1) 证明:平面ADE∥平面BCF;
(2) 若G是棱BC的中点,证明:AE∥FG.
13.2.4 平面与平面的位置关系—两平面平行
【活动方案】
背景引入:两个平面有两种位置关系:相交、平行.
如果两个平面没有公共点,那么称这两个平面互相平行.
如果两个平面有一个公共点,那么由基本事实3可知,它们相交于经过这个点的一条直线,此时称这两个平面相交.
实例:木匠师傅将水平仪在桌面上交叉放置两次,如果水平仪的气泡两次都在中央,那么就能判断桌面是水平的.
问题1:如果平面β内有一条直线与平面α平行,那么α,β不一定平行.
问题2:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行;
如果一个平面内有两条平行直线都平行于另一个平面,那么这两个平面不一定平行.
2. 图形:
文字:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行.
符号:若a α,b α,a∩b=A,且a∥β,b∥β,则α∥β.
例1 易知AB∥C1D1,AB=C1D1,
所以四边形ABC1D1是平行四边形,
所以AD1∥BC1.
因为BC1 平面C1DB,AD1 平面C1DB,
所以AD1∥平面C1DB.
因为AD∥B1C1,AD=B1C1,
所以四边形ADC1B1是平行四边形,
所以AB1∥C1D.
因为C1D 平面C1DB,AB1 平面C1DB,
所以AB1∥平面C1DB.
因为AD1∩AB1=A,AD1 平面AB1D1,AB1 平面AB1D1,
所以平面C1DB∥平面AB1D1.
跟踪训练 因为PM∶MA=BN∶ND=PQ∶QD,
所以MQ∥AD,NQ∥BP.
因为BP 平面PBC,NQ 平面PBC,
所以NQ∥平面PBC.
因为底面ABCD为平行四边形,
所以BC∥AD,所以MQ∥BC.
因为BC 平面PBC,MQ 平面PBC,
所以MQ∥平面PBC.
又MQ∩NQ=Q,MQ 平面MNQ,NQ 平面MNQ,
所以平面MNQ∥平面PBC.
思考1:平面A1B1C1D1中的所有直线都平行于平面ABCD.
思考2:不一定,m与n平行或异面.
思考3:BC∥B2C2
思考4:(1) 根据两个平面平行及直线和平面平行的定义可知,两个平面平行,其中一个平面内的直线必定平行于另一个平面.
(2) 分别在两个平行平面内的两条直线必定没有公共点,所以只能判定它们平行或异面.
(3) 如果第三个平面都与两个平行平面相交,那么所得的两条交线平行.
探究:已知:α∥β,α∩γ=a,β∩γ=b.
求证:a∥b.
证明:因为α∥β,所以α与β没有公共点,
所以交线a,b也没有公共点.
又因为a,b都在平面γ内,所以a∥b.
例2 已知α∥β,l⊥α.求证:l⊥β.
证明:设l∩α=A,在平面β内任取一条直线b.
因为点A不在β内,
所以点A与直线b可确定平面γ.
设γ∩α=a.
因为α∥β,α∩γ=a,β∩γ=b,所以a∥b.
因为l⊥α,a α,
所以l⊥a,所以l⊥b.
因为直线b是平面β内的任意一条直线,
所以l⊥β.
跟踪训练 已知l⊥α,l⊥β,求证:α∥β.
证明:如图,令平面γ与平面α,β分别相交于直线a,c.
由l⊥β,l⊥α,可得l⊥a,l⊥c.
又a γ,c γ,故a∥c.
因为c β,a β,所以a∥β.
再取与γ相交的另一个平面 λ与平面α,β分别相交于直线b,d,同理可得b∥d.
因为d β,b β,所以b∥β.
又因为a∩b=A,所以α∥β.
【检测反馈】
1. D 若m∥α,n∥α,则m,n平行、相交或异面,故A错误;若m∥α,m∥β,则α∥β或α,β相交,故B错误;若m∥n,m∥α,则n∥α或n α,故C错误;若α∥β,m α,则m∥β,故D正确.
2. C 因为平面α∥平面β,且平面PAB∩平面α=CD,平面PAB∩平面β=AB,所以CD∥AB,所以△PCD∽△PAB,可得=,所以AB===.
3. AC 对于A,如图,连接AD1,因为在正方体ABCD-A1B1C1D1中,F,G分别是B1C1,BB1的中点,所以FG∥BC1.因为BC1∥AD1,所以FG∥AD1.因为FG 平面AA1D1D,AD1 平面AA1D1D,所以FG∥平面AA1D1D,故A正确;对于B,因为EF∥A1C1,A1C1与平面BC1D1相交,所以EF与平面BC1D1相交,故B错误;对于C,因为F,G分别是B1C1,BB1的中点,所以FG∥BC1.因为FG 平面BC1D1,BC1 平面BC1D1,所以FG∥平面BC1D1,故C正确;对于D,因为EF与平面BC1D1相交,所以平面EFG与平面BC1D1相交,故D错误.故选AC.
4. 平行或相交
5. (1) 因为四边形ABCD是平行四边形,
所以BC∥AD.
又AD 平面ADE,BC 平面ADE,
所以BC∥平面ADE.
因为DE∥CF,CF 平面ADE,DE 平面ADE,
所以CF∥平面ADE.
又BC∩CF=C,BC 平面BCF,CF 平面BCF,
所以平面ADE∥平面BCF.
(2) 如图,延长EF,AG与DC的延长线分别交DC于点O1,O2.
由DE∥CF,DE=2CF,
得CO1=CD.
由BC∥AD,G是棱BC的中点,
得CO2=CD,
因此点O1,O2重合,记为点O.
显然平面AOE∩平面ADE=AE,
平面AOE∩平面BCF=FG,
又平面ADE∥平面BCF,
所以AE∥FG.
1. 借助长方体,通过直观感知,了解两个平面的位置关系.
2. 理解并掌握两个平面平行与两个平面相交的定义.
3. 掌握两个平面平行的判定定理和性质定理,并能运用其解决一些具体问题.
4. 了解两个平行平面间的距离的概念.
活动一 了解空间两个平面的位置关系
请同学们观察下图,这是一个二层楼房的简易图,在其中的四个平面中,两个平面可能有哪几种位置关系?你能根据公共点的情况进行分类吗?
1. 空间两个平面的位置关系:
位置关系 两平面平行 两平面相交
公共点 没有公共点 有一条公共直线
符号表示 α∥β α∩β=a
图形表示
活动二 探究两个平面平行的判定定理
实例:你知道木匠师傅是怎样使用水平仪来检测桌面是否水平的吗?
问题1:如果平面β内有一条直线与平面α平行,那么α,β平行吗?
问题2:如果平面β内有两条直线与平面α平行,那么α,β平行吗?
2. 两个平面平行的判定定理:
图形 文字 符号
两个平面平 行的判定定理
例1 如图,在正方体ABCD-A1B1C1D1中,求证:平面C1DB∥平面AB1D1.
要得到两个平面平行,只能根据面面平行的判定定理,先证明一个平面内的两条相交直线与另一个平面平行,坚决不能由线线平行得到面面平行.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上(不与端点重合),且PM∶MA=BN∶ND=PQ∶QD.求证:平面MNQ∥平面PBC.
活动三 探究两个平面平行的性质定理
3. 观察长方体ABCD-A1B1C1D1中的两个平面:平面ABCD及平面A1B1C1D1.
思考1
平面A1B1C1D1中的所有直线都平行于平面ABCD吗?
思考2
若m 平面ABCD,n 平面A1B1C1D1,则m∥n吗?
思考3
过BC的平面交平面A1B1C1D1于B2C2,B2C2与BC是什么关系?
思考4
如果两个平面平行,那么
(1) 一个平面内的直线是否平行于另一个平面?
(2) 分别在两个平面内的两条直线是否平行?
(3) 如果第三个平面与这两个平面相交,那么所得的交线平行吗?
探究:两个平面平行的性质定理:
已知:
求证:
证明:
例2 求证:如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.
这是得到线面垂直的另一条途径,虽然结论正确,但不能作为定理使用.
求证:如果一条直线垂直于两个平面,那么这两个平面平行.
1. 与两个平行平面都垂直的直线叫作两个平行平面的公垂线.
2. 公垂线夹在两个平行平面间的线段叫作两个平行平面的公垂线段.
3. 公垂线段的长度叫作两个平行平面间的距离.
1. (教材改编)设有两条不同的直线m,n和两个不同的平面α,β,则下列命题中正确的是( )
A. 若m∥α,n∥α,则m∥n B. 若m∥α,m∥β,则α∥β
C. 若m∥n,m∥α,则n∥α D. 若α∥β,m α,则m∥β
2. (教材改编)(2024哈尔滨期中)如图,平面α∥平面β,△PAB所在的平面与α,β分别交于CD,AB.若PC=2,CA=3,CD=1,则线段AB的长为( )
A.
B. 2
C.
D. 3
3. (多选)如图,在正方体ABCD-A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,则下列四个推断中正确的是( )
A. FG∥平面AA1D1D
B. EF∥平面BC1D1
C. FG∥平面BC1D1
D. 平面EFG∥平面BC1D1
4. 若平面外的一条直线上有两点到这个平面的距离相等,则这条直线与该平面的位置关系是________.
5. (2024佛山月考)如图,在六面体ABCDEF中,DE∥CF,四边形ABCD是平行四边形,DE=2CF.
(1) 证明:平面ADE∥平面BCF;
(2) 若G是棱BC的中点,证明:AE∥FG.
13.2.4 平面与平面的位置关系—两平面平行
【活动方案】
背景引入:两个平面有两种位置关系:相交、平行.
如果两个平面没有公共点,那么称这两个平面互相平行.
如果两个平面有一个公共点,那么由基本事实3可知,它们相交于经过这个点的一条直线,此时称这两个平面相交.
实例:木匠师傅将水平仪在桌面上交叉放置两次,如果水平仪的气泡两次都在中央,那么就能判断桌面是水平的.
问题1:如果平面β内有一条直线与平面α平行,那么α,β不一定平行.
问题2:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行;
如果一个平面内有两条平行直线都平行于另一个平面,那么这两个平面不一定平行.
2. 图形:
文字:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行.
符号:若a α,b α,a∩b=A,且a∥β,b∥β,则α∥β.
例1 易知AB∥C1D1,AB=C1D1,
所以四边形ABC1D1是平行四边形,
所以AD1∥BC1.
因为BC1 平面C1DB,AD1 平面C1DB,
所以AD1∥平面C1DB.
因为AD∥B1C1,AD=B1C1,
所以四边形ADC1B1是平行四边形,
所以AB1∥C1D.
因为C1D 平面C1DB,AB1 平面C1DB,
所以AB1∥平面C1DB.
因为AD1∩AB1=A,AD1 平面AB1D1,AB1 平面AB1D1,
所以平面C1DB∥平面AB1D1.
跟踪训练 因为PM∶MA=BN∶ND=PQ∶QD,
所以MQ∥AD,NQ∥BP.
因为BP 平面PBC,NQ 平面PBC,
所以NQ∥平面PBC.
因为底面ABCD为平行四边形,
所以BC∥AD,所以MQ∥BC.
因为BC 平面PBC,MQ 平面PBC,
所以MQ∥平面PBC.
又MQ∩NQ=Q,MQ 平面MNQ,NQ 平面MNQ,
所以平面MNQ∥平面PBC.
思考1:平面A1B1C1D1中的所有直线都平行于平面ABCD.
思考2:不一定,m与n平行或异面.
思考3:BC∥B2C2
思考4:(1) 根据两个平面平行及直线和平面平行的定义可知,两个平面平行,其中一个平面内的直线必定平行于另一个平面.
(2) 分别在两个平行平面内的两条直线必定没有公共点,所以只能判定它们平行或异面.
(3) 如果第三个平面都与两个平行平面相交,那么所得的两条交线平行.
探究:已知:α∥β,α∩γ=a,β∩γ=b.
求证:a∥b.
证明:因为α∥β,所以α与β没有公共点,
所以交线a,b也没有公共点.
又因为a,b都在平面γ内,所以a∥b.
例2 已知α∥β,l⊥α.求证:l⊥β.
证明:设l∩α=A,在平面β内任取一条直线b.
因为点A不在β内,
所以点A与直线b可确定平面γ.
设γ∩α=a.
因为α∥β,α∩γ=a,β∩γ=b,所以a∥b.
因为l⊥α,a α,
所以l⊥a,所以l⊥b.
因为直线b是平面β内的任意一条直线,
所以l⊥β.
跟踪训练 已知l⊥α,l⊥β,求证:α∥β.
证明:如图,令平面γ与平面α,β分别相交于直线a,c.
由l⊥β,l⊥α,可得l⊥a,l⊥c.
又a γ,c γ,故a∥c.
因为c β,a β,所以a∥β.
再取与γ相交的另一个平面 λ与平面α,β分别相交于直线b,d,同理可得b∥d.
因为d β,b β,所以b∥β.
又因为a∩b=A,所以α∥β.
【检测反馈】
1. D 若m∥α,n∥α,则m,n平行、相交或异面,故A错误;若m∥α,m∥β,则α∥β或α,β相交,故B错误;若m∥n,m∥α,则n∥α或n α,故C错误;若α∥β,m α,则m∥β,故D正确.
2. C 因为平面α∥平面β,且平面PAB∩平面α=CD,平面PAB∩平面β=AB,所以CD∥AB,所以△PCD∽△PAB,可得=,所以AB===.
3. AC 对于A,如图,连接AD1,因为在正方体ABCD-A1B1C1D1中,F,G分别是B1C1,BB1的中点,所以FG∥BC1.因为BC1∥AD1,所以FG∥AD1.因为FG 平面AA1D1D,AD1 平面AA1D1D,所以FG∥平面AA1D1D,故A正确;对于B,因为EF∥A1C1,A1C1与平面BC1D1相交,所以EF与平面BC1D1相交,故B错误;对于C,因为F,G分别是B1C1,BB1的中点,所以FG∥BC1.因为FG 平面BC1D1,BC1 平面BC1D1,所以FG∥平面BC1D1,故C正确;对于D,因为EF与平面BC1D1相交,所以平面EFG与平面BC1D1相交,故D错误.故选AC.
4. 平行或相交
5. (1) 因为四边形ABCD是平行四边形,
所以BC∥AD.
又AD 平面ADE,BC 平面ADE,
所以BC∥平面ADE.
因为DE∥CF,CF 平面ADE,DE 平面ADE,
所以CF∥平面ADE.
又BC∩CF=C,BC 平面BCF,CF 平面BCF,
所以平面ADE∥平面BCF.
(2) 如图,延长EF,AG与DC的延长线分别交DC于点O1,O2.
由DE∥CF,DE=2CF,
得CO1=CD.
由BC∥AD,G是棱BC的中点,
得CO2=CD,
因此点O1,O2重合,记为点O.
显然平面AOE∩平面ADE=AE,
平面AOE∩平面BCF=FG,
又平面ADE∥平面BCF,
所以AE∥FG.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
