13.3.2 空间图形的体积 学案(含答案)2024-2025学年高一数学苏教版(2019)必修第二册
文档属性
| 名称 | 13.3.2 空间图形的体积 学案(含答案)2024-2025学年高一数学苏教版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 514.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 00:00:00 | ||
图片预览



文档简介
13.3.2 空间图形的体积(1)
知道柱、锥、台的体积的计算公式,能用此公式解决简单的实际问题.
活动一 了解柱、锥、台的体积的计算公式
1. 如果一个长方体的长、宽、高分别为a,b,c,那么它的体积V长方体=abc或V长方体=Sh(S表示长方体的底面积,h表示高).
2. 如何求柱、锥、台的体积?
祖暅原理:
两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.
棱柱(圆柱)可由多边形(圆)沿某一方向平移得到,因此,两个底面积相等、高也相等的棱柱(圆柱)应该具有相等的体积.
柱体(棱柱、圆柱)的体积等于它的底面积S和高h的积,即V柱体=Sh.
类似地,底面积相等、高也相等的两个锥体,它们的体积也相等,由圆锥体积公式可知,V锥体=Sh.
台体(棱台、圆台)的体积可以转化为锥体的体积来计算.如果台体的上、下底面面积分别为S′,S,高是h,那么可以推得它的体积V台体=h(S++S′).
思考
上一节中,我们知道正棱柱、正棱锥、正棱台的侧面积之间有一定的关系,那么柱体、锥体、台体的体积公式之间有没有类似的关系?
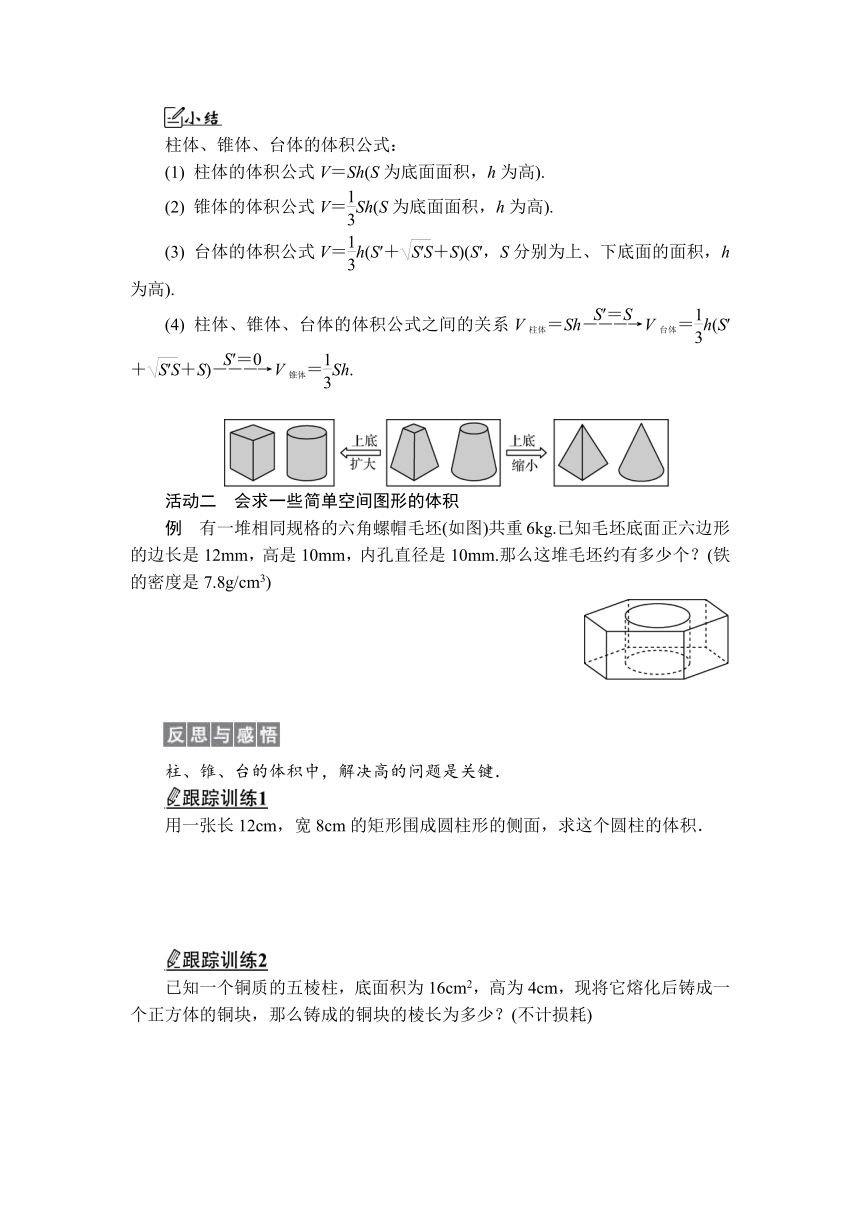
柱体、锥体、台体的体积公式:
(1) 柱体的体积公式V=Sh(S为底面面积,h为高).
(2) 锥体的体积公式V=Sh(S为底面面积,h为高).
(3) 台体的体积公式V=h(S′++S)(S′,S分别为上、下底面的面积,h为高).
(4) 柱体、锥体、台体的体积公式之间的关系V柱体=ShV台体=h(S′++S)V锥体=Sh.
活动二 会求一些简单空间图形的体积
例 有一堆相同规格的六角螺帽毛坯(如图)共重6kg.已知毛坯底面正六边形的边长是12mm,高是10mm,内孔直径是10mm.那么这堆毛坯约有多少个?(铁的密度是7.8g/cm3)
柱、锥、台的体积中,解决高的问题是关键.
用一张长12cm,宽8cm的矩形围成圆柱形的侧面,求这个圆柱的体积.
已知一个铜质的五棱柱,底面积为16cm2,高为4cm,现将它熔化后铸成一个正方体的铜块,那么铸成的铜块的棱长为多少?(不计损耗)
1. 艳阳高照的夏天,冰淇淋是孩子们喜爱的食品之一.一个冰淇淋近似为一个圆锥,若该圆锥的侧面展开的扇形面积是底面圆面积的2倍,圆锥的母线长为12 cm,则该圆锥的体积为( )
A. 96π cm3 B. 124π cm3 C. 72π cm3 D. 168π cm3
2. (教材改编)如图,已知直三棱柱ABC-A1B1C1的体积为6,△A1BC的面积为 2,则点A到平面A1BC的距离为( )
A.
B.
C. 2
D.
3. (多选)(2023枣庄期中)已知在正四棱台ABCD-A1B1C1D1中,AB=4,A1B1=2,AA1=2,则下列关于该正四棱台的说法中正确的是( )
A. ∠A1AB= B. 高为
C. 体积为 D. 表面积为12
4. (2024天津河西区期中)已知正三棱柱ABC-A1B1C1的所有棱长均为a,且其体积为16,则a=________.
5. (2023平湖当湖高级中学期中)龙洗是我国著名的文物之一,因盆内有龙纹故称龙洗(如图),为古代皇宫盥洗用具,其盆体可以近似看作一个圆台. 现有一龙洗盆高15cm,盆口直径36cm,盆底直径18cm.现往盆内倒入水,当水深5cm时,盆内水的体积大约为多少?
13.3.2 空间图形的体积(2)
1. 知道球的体积与表面积的计算公式.
2. 会求一些球的组合体中表面积与体积的问题.
3. 体会积分思想在计算球的表面积和体积中的应用.
活动一 探究球的体积与表面积的计算公式
思考1
球既没有底面,也无法像柱体、锥体和台体那样展开成平面图形,那么怎样来求球的表面积与体积呢?
1. 阅读课本,了解球的体积与表面积公式的推导过程.
思考2
球的大小与球的半径有关,如何用球的半径来表示球的体积和表面积?
2. 球的表面积和体积公式:
(1) 球的表面积公式S=4πR2;
(2) 球的体积公式V=πR3.
3. 球体截面的特点:
球既是中心对称的空间图形,又是轴对称的空间图形,它的任何截面均为圆.
活动二 掌握球的体积、表面积的求解方法
例1 设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,求该球的表面积.
拓展:
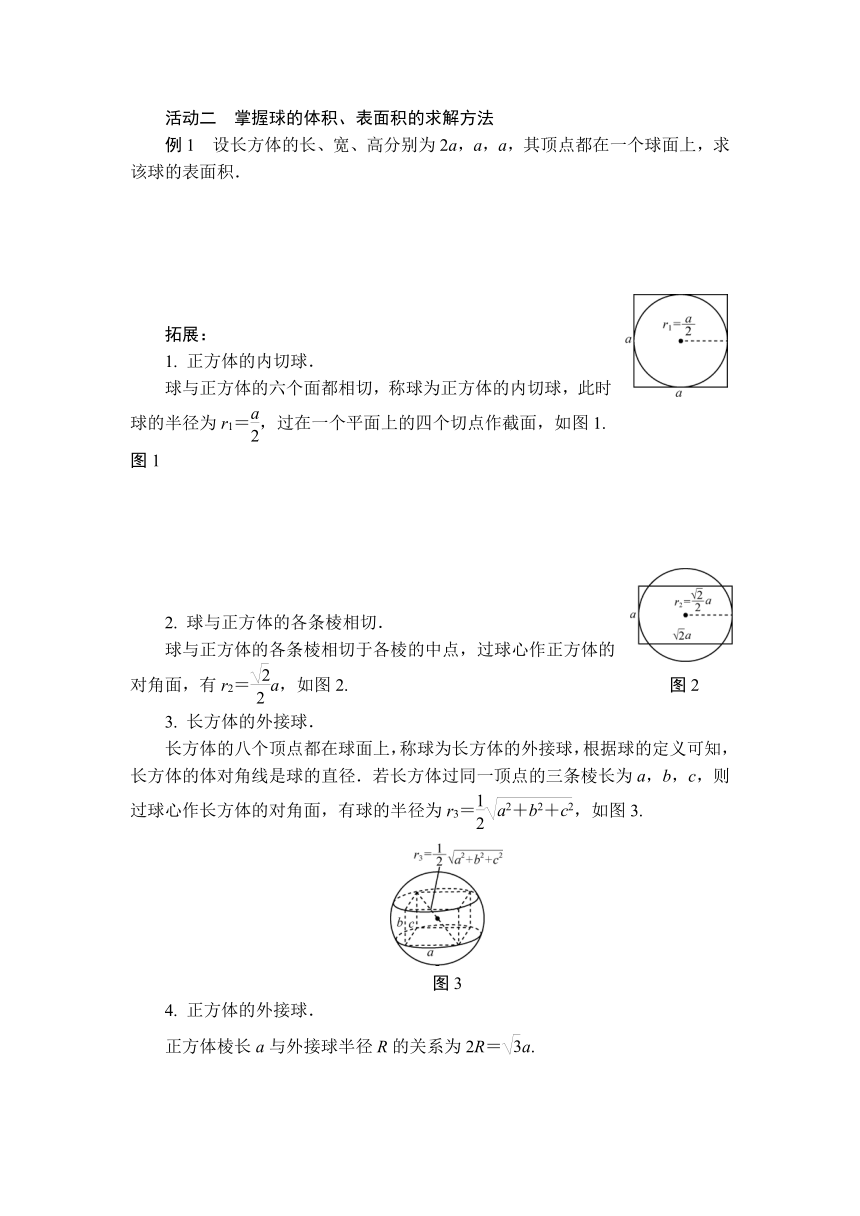
1. 正方体的内切球.
球与正方体的六个面都相切,称球为正方体的内切球,此时球的半径为r1=,过在一个平面上的四个切点作截面,如图1. 图1
2. 球与正方体的各条棱相切.
球与正方体的各条棱相切于各棱的中点,过球心作正方体的对角面,有r2=a,如图2. 图2
3. 长方体的外接球.
长方体的八个顶点都在球面上,称球为长方体的外接球,根据球的定义可知,长方体的体对角线是球的直径.若长方体过同一顶点的三条棱长为a,b,c,则过球心作长方体的对角面,有球的半径为r3=,如图3.
图3
4. 正方体的外接球.
正方体棱长a与外接球半径R的关系为2R=a.
已知三棱锥D-ABC的所有顶点都在球O的球面上,AB=BC=2,AC=2,若三棱锥D ABC体积的最大值为2,求球O的表面积.
当多面体与球组成组合体后,一定要分清是内切还是外接,然后可以画出空间图形的截面图,有利于一些长度的计算.
例2 已知圆柱的底面直径与高都等于球的直径.求证:
(1) 球的表面积等于圆柱的侧面积;
(2) 球的表面积等于圆柱全面积的.
已知一圆锥的母线长为10 cm,底面圆半径为 6 cm.
(1) 求圆锥的高;
(2) 若圆锥内有一球,球与圆锥的底面及圆锥的所有母线都相切,求球的表面积.
球和前面所学的圆柱、圆锥、圆台都是旋转体,只要画出它们的轴截面,都可以解决问题.
1. (教材改编)若平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则球O的体积为( )
A. π B. 4π C. 4π D. 6π
2. (2023深圳罗湖高级中学期中)把一个铁制的底面半径为4,侧面积为 的实心圆柱熔化后铸成一个球,则这个铁球的表面积为( )
A. 16π B. 12π C. 24π D. 9π
3. (多选)(2024湖南月考)已知三棱锥P-ABC的所有棱长都是6,D,E分别是三棱锥P-ABC外接球和内切球上的点,则下列结论中正确的是( )
A. 三棱锥P-ABC的体积是18
B. 三棱锥P-ABC内切球的半径是
C. DE长度的取值范围是[,2]
D. 三棱锥P-ABC外接球的体积是27π
4. (2024杭州月考)在一个如图所示的直角梯形ABCD内挖去一个扇形,E恰好是梯形的下底边的中点,将所得平面图形绕直线DE旋转一圈,则所得几何体的体积为________.
5. 已知圆锥的侧面展开图为一个半圆,求该圆锥内半径最大的球的表面积与圆锥外接球的表面积之比.
13.3.2 空间图形的体积(1)
【活动方案】
思考:略
例 因为V六棱柱=×122×6×10≈3 741(mm3),
V圆柱=π××10≈785(mm3),
所以V螺帽=3 741-785=2 956(mm3)=2.956(cm3),
则≈260(个),
故这堆毛坯约有260个.
跟踪训练1 设圆柱的底面半径为R.
当圆柱的高为8cm时,则2πR=12,
所以R=,
所以V=π××8= (cm3);
当圆柱的高为12cm时,则2πR=8,
所以R=,
所以V=π××12= (cm3),
故圆柱的体积为 cm3或 cm3.
跟踪训练2 由题意,得V=16×4=64(cm3).
设正方体铜块的棱长为a cm,则a3=64,
解得a=4,即铸成的铜块的棱长为4cm.
【检测反馈】
1. C 设圆锥的底面圆的半径为r,则底面圆的面积为S1=πr2,侧面面积为S2=×2πr×12=12πr.由题意知2S1=S2,所以12πr=2πr2,解得r=6,则该圆锥的高h==6,故该圆锥的体积V=×π×62×6=72π(cm3).
2. B 由直三棱柱ABC-A1B1C1的体积为6,可得VA1-ABC=VA1B1C1-ABC=2.设点A到平面A1BC的距离为d.因为VA1-ABC=VA-A1BC,所以S△A1BC·d=2,所以×2d=2,解得d=,即点A到平面A1BC的距离为.
3. BC 如图,过点A1分别作底面ABCD,AB的垂线,垂足分别为M,N,则AM=AC=,AN=AB=1,可得A1M==,A1N==.对于A,在Rt△AA1N中,可得sin ∠A1AN==,且∠A1AN为锐角,则∠A1AB=,故A错误;对于B,正四棱台的高即为A1M=,故B正确;对于C,正四棱台的体积V=(4×4+2×2+)×=,故C正确;对于D,正四棱台的表面积S=4×4+2×2+4×=20+12,故D错误.故选BC.
4. 4 因为正三棱柱ABC-A1B1C1的所有棱长均为a,且其体积为16,则S△ABC=a2sin 60°=a2,所以VABC-A1B1C1=S△ABC·AA1=a3=16,解得a=4.
5. 如图1,画出圆台的立体图形和轴截面平面图形,并延长EC,FD,交于点G,如图2.
根据题意知,AB=18cm,CD=9cm,AC=15cm,EC=5cm.
设CG=xcm,EF=ycm,
所以=,=,
解得x=15,y=12,
所以V=(π×122+π×92+π×12×9)×5=555π(cm3).
图1 图2
13.3.2 空间图形的体积(2)
【活动方案】
思考1:略
思考2:略
例1 由题意,得该球为长方体的外接球,则长方体的体对角线是其外接球的直径.
由长方体的体对角线为=a,得球的半径为,
所以球的表面积为4π×=6πa2.
跟踪训练 因为AB=BC=2,AC=2,
所以AB⊥BC.
如图,过AC的中点M作平面ABC的垂线MN,
则球心O在直线MN上.
设OM=h,球的半径为R,
则棱锥高的最大值为R+h.
因为VD -ABC=××2×2×(R+h)=2,
所以R+h=3,由勾股定理,得R2=(3-R)2+2,
解得R=,
所以球的表面积为S=4π×=.
例2 设球的直径为d,则圆柱的底面半径为,高为d.
(1) S球=4π·=πd2,S圆柱侧=2π··d=πd2=S球,
所以球的表面积等于圆柱的侧面积.
(2) S圆柱底=2π·=d2,S圆柱全=d2+πd2=d2,
所以S球=πd2=d2×=S圆柱全,
所以球的表面积等于圆柱全面积的.
跟踪训练 (1) 根据题意知,圆锥的高h==8(cm).
(2) 由(1)知,圆锥的高为8 cm.
设圆锥内切球的半径为r cm,
则(10-6)2+r2=(8-r)2,解得r=3,
所以所求球的表面积S=4πr2=4π×32=36π(cm2).
【检测反馈】
1. B 由题意,得球O的半径r==,所以球O的体积为×()3=4π.
2. A 设实心圆柱的高为h.因为实心圆柱的底面半径为4,所以侧面积为2π×4×h=,解得h=,则圆柱的体积为V=π×42×=.设球的半径为R,则πR3=,解得R=2,所以该铁球的表面积为4πR2=4π×22=16π.
3. ACD 如图,取BC的中点M,连接AM,PM,作PH⊥平面ABC.易证点H在AM上,且AH=2HM=2,则PH==2,从而三棱锥P-ABC的体积V=Sh=××62×2=18,故A正确;设三棱锥P-ABC内切球的半径为r,则VPABC=SP-ABC·r,所以r===,故B错误;设三棱锥P-ABC外接球的半径为R,球心为O,则R2=AH2+OH2=(PH-OH)2,即R2=12+OH2=(2-OH)2,解得OH=,所以R=,则三棱锥P-ABC外接球的体积是27π,显然DE长度的取值范围是[,2],故C,D正确.故选ACD.
4. 由题意,将所得平面图形绕直线DE旋转一圈后,所得几何体是上部是圆锥,下部是圆柱挖去一个半球体的组合体,则该组合体的体积为V组合体=V圆锥+V圆柱-V半球=×π×42×4+π×42×4-××π×43=.
5. 设圆锥的母线长为l,底面圆半径为r.
因为圆锥的侧面展开图为一个半圆,
所以2πr=×2πl,解得l=2r.
圆锥内半径最大的球即圆锥的内切球,设内切球半径为R1,设圆锥的一个轴截面为△PAB,如图所示,则△PAB内切圆的半径为圆锥内切球的半径.
因为在△PAB中,PA=PB=l,C为AB的中点,AB=2r=l,
所以△PAB为等边三角形,
则·PA·PB·sin 60°=R1(PA+PB+AB),
即×l×l×=R1(l+l+2r),
解得R1=l,
所以圆锥内半径最大的球的表面积为
S1=4πR=4π×=πl2.
又△PAB外接圆的直径为2R2==l,
所以圆锥的外接球的半径R2=l,
所以圆锥外接球的表面积为
S2=4πR=4π×=πl2,
所以==.
故所求的表面积之比为1∶4.
知道柱、锥、台的体积的计算公式,能用此公式解决简单的实际问题.
活动一 了解柱、锥、台的体积的计算公式
1. 如果一个长方体的长、宽、高分别为a,b,c,那么它的体积V长方体=abc或V长方体=Sh(S表示长方体的底面积,h表示高).
2. 如何求柱、锥、台的体积?
祖暅原理:
两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.
棱柱(圆柱)可由多边形(圆)沿某一方向平移得到,因此,两个底面积相等、高也相等的棱柱(圆柱)应该具有相等的体积.
柱体(棱柱、圆柱)的体积等于它的底面积S和高h的积,即V柱体=Sh.
类似地,底面积相等、高也相等的两个锥体,它们的体积也相等,由圆锥体积公式可知,V锥体=Sh.
台体(棱台、圆台)的体积可以转化为锥体的体积来计算.如果台体的上、下底面面积分别为S′,S,高是h,那么可以推得它的体积V台体=h(S++S′).
思考
上一节中,我们知道正棱柱、正棱锥、正棱台的侧面积之间有一定的关系,那么柱体、锥体、台体的体积公式之间有没有类似的关系?
柱体、锥体、台体的体积公式:
(1) 柱体的体积公式V=Sh(S为底面面积,h为高).
(2) 锥体的体积公式V=Sh(S为底面面积,h为高).
(3) 台体的体积公式V=h(S′++S)(S′,S分别为上、下底面的面积,h为高).
(4) 柱体、锥体、台体的体积公式之间的关系V柱体=ShV台体=h(S′++S)V锥体=Sh.
活动二 会求一些简单空间图形的体积
例 有一堆相同规格的六角螺帽毛坯(如图)共重6kg.已知毛坯底面正六边形的边长是12mm,高是10mm,内孔直径是10mm.那么这堆毛坯约有多少个?(铁的密度是7.8g/cm3)
柱、锥、台的体积中,解决高的问题是关键.
用一张长12cm,宽8cm的矩形围成圆柱形的侧面,求这个圆柱的体积.
已知一个铜质的五棱柱,底面积为16cm2,高为4cm,现将它熔化后铸成一个正方体的铜块,那么铸成的铜块的棱长为多少?(不计损耗)
1. 艳阳高照的夏天,冰淇淋是孩子们喜爱的食品之一.一个冰淇淋近似为一个圆锥,若该圆锥的侧面展开的扇形面积是底面圆面积的2倍,圆锥的母线长为12 cm,则该圆锥的体积为( )
A. 96π cm3 B. 124π cm3 C. 72π cm3 D. 168π cm3
2. (教材改编)如图,已知直三棱柱ABC-A1B1C1的体积为6,△A1BC的面积为 2,则点A到平面A1BC的距离为( )
A.
B.
C. 2
D.
3. (多选)(2023枣庄期中)已知在正四棱台ABCD-A1B1C1D1中,AB=4,A1B1=2,AA1=2,则下列关于该正四棱台的说法中正确的是( )
A. ∠A1AB= B. 高为
C. 体积为 D. 表面积为12
4. (2024天津河西区期中)已知正三棱柱ABC-A1B1C1的所有棱长均为a,且其体积为16,则a=________.
5. (2023平湖当湖高级中学期中)龙洗是我国著名的文物之一,因盆内有龙纹故称龙洗(如图),为古代皇宫盥洗用具,其盆体可以近似看作一个圆台. 现有一龙洗盆高15cm,盆口直径36cm,盆底直径18cm.现往盆内倒入水,当水深5cm时,盆内水的体积大约为多少?
13.3.2 空间图形的体积(2)
1. 知道球的体积与表面积的计算公式.
2. 会求一些球的组合体中表面积与体积的问题.
3. 体会积分思想在计算球的表面积和体积中的应用.
活动一 探究球的体积与表面积的计算公式
思考1
球既没有底面,也无法像柱体、锥体和台体那样展开成平面图形,那么怎样来求球的表面积与体积呢?
1. 阅读课本,了解球的体积与表面积公式的推导过程.
思考2
球的大小与球的半径有关,如何用球的半径来表示球的体积和表面积?
2. 球的表面积和体积公式:
(1) 球的表面积公式S=4πR2;
(2) 球的体积公式V=πR3.
3. 球体截面的特点:
球既是中心对称的空间图形,又是轴对称的空间图形,它的任何截面均为圆.
活动二 掌握球的体积、表面积的求解方法
例1 设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,求该球的表面积.
拓展:
1. 正方体的内切球.
球与正方体的六个面都相切,称球为正方体的内切球,此时球的半径为r1=,过在一个平面上的四个切点作截面,如图1. 图1
2. 球与正方体的各条棱相切.
球与正方体的各条棱相切于各棱的中点,过球心作正方体的对角面,有r2=a,如图2. 图2
3. 长方体的外接球.
长方体的八个顶点都在球面上,称球为长方体的外接球,根据球的定义可知,长方体的体对角线是球的直径.若长方体过同一顶点的三条棱长为a,b,c,则过球心作长方体的对角面,有球的半径为r3=,如图3.
图3
4. 正方体的外接球.
正方体棱长a与外接球半径R的关系为2R=a.
已知三棱锥D-ABC的所有顶点都在球O的球面上,AB=BC=2,AC=2,若三棱锥D ABC体积的最大值为2,求球O的表面积.
当多面体与球组成组合体后,一定要分清是内切还是外接,然后可以画出空间图形的截面图,有利于一些长度的计算.
例2 已知圆柱的底面直径与高都等于球的直径.求证:
(1) 球的表面积等于圆柱的侧面积;
(2) 球的表面积等于圆柱全面积的.
已知一圆锥的母线长为10 cm,底面圆半径为 6 cm.
(1) 求圆锥的高;
(2) 若圆锥内有一球,球与圆锥的底面及圆锥的所有母线都相切,求球的表面积.
球和前面所学的圆柱、圆锥、圆台都是旋转体,只要画出它们的轴截面,都可以解决问题.
1. (教材改编)若平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则球O的体积为( )
A. π B. 4π C. 4π D. 6π
2. (2023深圳罗湖高级中学期中)把一个铁制的底面半径为4,侧面积为 的实心圆柱熔化后铸成一个球,则这个铁球的表面积为( )
A. 16π B. 12π C. 24π D. 9π
3. (多选)(2024湖南月考)已知三棱锥P-ABC的所有棱长都是6,D,E分别是三棱锥P-ABC外接球和内切球上的点,则下列结论中正确的是( )
A. 三棱锥P-ABC的体积是18
B. 三棱锥P-ABC内切球的半径是
C. DE长度的取值范围是[,2]
D. 三棱锥P-ABC外接球的体积是27π
4. (2024杭州月考)在一个如图所示的直角梯形ABCD内挖去一个扇形,E恰好是梯形的下底边的中点,将所得平面图形绕直线DE旋转一圈,则所得几何体的体积为________.
5. 已知圆锥的侧面展开图为一个半圆,求该圆锥内半径最大的球的表面积与圆锥外接球的表面积之比.
13.3.2 空间图形的体积(1)
【活动方案】
思考:略
例 因为V六棱柱=×122×6×10≈3 741(mm3),
V圆柱=π××10≈785(mm3),
所以V螺帽=3 741-785=2 956(mm3)=2.956(cm3),
则≈260(个),
故这堆毛坯约有260个.
跟踪训练1 设圆柱的底面半径为R.
当圆柱的高为8cm时,则2πR=12,
所以R=,
所以V=π××8= (cm3);
当圆柱的高为12cm时,则2πR=8,
所以R=,
所以V=π××12= (cm3),
故圆柱的体积为 cm3或 cm3.
跟踪训练2 由题意,得V=16×4=64(cm3).
设正方体铜块的棱长为a cm,则a3=64,
解得a=4,即铸成的铜块的棱长为4cm.
【检测反馈】
1. C 设圆锥的底面圆的半径为r,则底面圆的面积为S1=πr2,侧面面积为S2=×2πr×12=12πr.由题意知2S1=S2,所以12πr=2πr2,解得r=6,则该圆锥的高h==6,故该圆锥的体积V=×π×62×6=72π(cm3).
2. B 由直三棱柱ABC-A1B1C1的体积为6,可得VA1-ABC=VA1B1C1-ABC=2.设点A到平面A1BC的距离为d.因为VA1-ABC=VA-A1BC,所以S△A1BC·d=2,所以×2d=2,解得d=,即点A到平面A1BC的距离为.
3. BC 如图,过点A1分别作底面ABCD,AB的垂线,垂足分别为M,N,则AM=AC=,AN=AB=1,可得A1M==,A1N==.对于A,在Rt△AA1N中,可得sin ∠A1AN==,且∠A1AN为锐角,则∠A1AB=,故A错误;对于B,正四棱台的高即为A1M=,故B正确;对于C,正四棱台的体积V=(4×4+2×2+)×=,故C正确;对于D,正四棱台的表面积S=4×4+2×2+4×=20+12,故D错误.故选BC.
4. 4 因为正三棱柱ABC-A1B1C1的所有棱长均为a,且其体积为16,则S△ABC=a2sin 60°=a2,所以VABC-A1B1C1=S△ABC·AA1=a3=16,解得a=4.
5. 如图1,画出圆台的立体图形和轴截面平面图形,并延长EC,FD,交于点G,如图2.
根据题意知,AB=18cm,CD=9cm,AC=15cm,EC=5cm.
设CG=xcm,EF=ycm,
所以=,=,
解得x=15,y=12,
所以V=(π×122+π×92+π×12×9)×5=555π(cm3).
图1 图2
13.3.2 空间图形的体积(2)
【活动方案】
思考1:略
思考2:略
例1 由题意,得该球为长方体的外接球,则长方体的体对角线是其外接球的直径.
由长方体的体对角线为=a,得球的半径为,
所以球的表面积为4π×=6πa2.
跟踪训练 因为AB=BC=2,AC=2,
所以AB⊥BC.
如图,过AC的中点M作平面ABC的垂线MN,
则球心O在直线MN上.
设OM=h,球的半径为R,
则棱锥高的最大值为R+h.
因为VD -ABC=××2×2×(R+h)=2,
所以R+h=3,由勾股定理,得R2=(3-R)2+2,
解得R=,
所以球的表面积为S=4π×=.
例2 设球的直径为d,则圆柱的底面半径为,高为d.
(1) S球=4π·=πd2,S圆柱侧=2π··d=πd2=S球,
所以球的表面积等于圆柱的侧面积.
(2) S圆柱底=2π·=d2,S圆柱全=d2+πd2=d2,
所以S球=πd2=d2×=S圆柱全,
所以球的表面积等于圆柱全面积的.
跟踪训练 (1) 根据题意知,圆锥的高h==8(cm).
(2) 由(1)知,圆锥的高为8 cm.
设圆锥内切球的半径为r cm,
则(10-6)2+r2=(8-r)2,解得r=3,
所以所求球的表面积S=4πr2=4π×32=36π(cm2).
【检测反馈】
1. B 由题意,得球O的半径r==,所以球O的体积为×()3=4π.
2. A 设实心圆柱的高为h.因为实心圆柱的底面半径为4,所以侧面积为2π×4×h=,解得h=,则圆柱的体积为V=π×42×=.设球的半径为R,则πR3=,解得R=2,所以该铁球的表面积为4πR2=4π×22=16π.
3. ACD 如图,取BC的中点M,连接AM,PM,作PH⊥平面ABC.易证点H在AM上,且AH=2HM=2,则PH==2,从而三棱锥P-ABC的体积V=Sh=××62×2=18,故A正确;设三棱锥P-ABC内切球的半径为r,则VPABC=SP-ABC·r,所以r===,故B错误;设三棱锥P-ABC外接球的半径为R,球心为O,则R2=AH2+OH2=(PH-OH)2,即R2=12+OH2=(2-OH)2,解得OH=,所以R=,则三棱锥P-ABC外接球的体积是27π,显然DE长度的取值范围是[,2],故C,D正确.故选ACD.
4. 由题意,将所得平面图形绕直线DE旋转一圈后,所得几何体是上部是圆锥,下部是圆柱挖去一个半球体的组合体,则该组合体的体积为V组合体=V圆锥+V圆柱-V半球=×π×42×4+π×42×4-××π×43=.
5. 设圆锥的母线长为l,底面圆半径为r.
因为圆锥的侧面展开图为一个半圆,
所以2πr=×2πl,解得l=2r.
圆锥内半径最大的球即圆锥的内切球,设内切球半径为R1,设圆锥的一个轴截面为△PAB,如图所示,则△PAB内切圆的半径为圆锥内切球的半径.
因为在△PAB中,PA=PB=l,C为AB的中点,AB=2r=l,
所以△PAB为等边三角形,
则·PA·PB·sin 60°=R1(PA+PB+AB),
即×l×l×=R1(l+l+2r),
解得R1=l,
所以圆锥内半径最大的球的表面积为
S1=4πR=4π×=πl2.
又△PAB外接圆的直径为2R2==l,
所以圆锥的外接球的半径R2=l,
所以圆锥外接球的表面积为
S2=4πR=4π×=πl2,
所以==.
故所求的表面积之比为1∶4.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
