【中考押题卷】2025年中考数学高频易错考前冲刺:投影与视图(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:投影与视图(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 00:00:00 | ||
图片预览

文档简介
2025年中考数学高频易错考前冲刺:投影与视图
一.选择题(共10小题)
1.(2024秋 凉州区校级期末)如图,小树AB在路灯O的照射下形成投影BC.若这棵树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m,则路灯的高度OP为( )
A.3m B.5m C.6m D.7.5m
2.(2024秋 白银期末)某积木配件如图所示,它的主视图是( )
A. B.
C. D.
3.(2024秋 白银期末)一块三角形纸板ABC如图所示,BC=15cm,AC=12cm,测得BC边的中心投影B1C1的长为20cm,则AC边的中心投影A1C1的长为( )
A.24cm B.20cm C.16cm D.8cm
4.(2024秋 海门区期末)如图是从不同方向看一个立体图形得到的平面图形,那么这个立体图形是( )
A. B. C. D.
5.(2024秋 长沙期末)黑陶是继彩陶之后中国新石器时代制陶工艺的又一个高峰,被誉为“土与火的艺术,力与美的结晶”.如图是山东博物馆收藏的蛋壳黑陶高柄杯.从三个不同方向观察,下列说法正确的是( )
A.从正面、左面看到的形状图相同
B.从正面、上面看到的形状图相同
C.从左面、上面看到的形状图相同
D.从正面、左面、上面看到的形状图都相同
6.(2024秋 贵阳期末)在一间黑屋子里用一盏白炽灯照射如图所示的球.当球向下移动时,这个球在地面上的影子大小的变化情况是( )
A.保持不变 B.越来越大 C.越来越小 D.不能确定
7.(2024秋 太原期末)中国古代的数学研究成果辉煌,产生的一些数学名词,颠有趣味,如《九章算术》中的“刍童”,原指上、下底面都是长方形的草垛.如图是一个“刍童”形状的几何体,它的主视图和左视图如图所示,则其俯视图是( )
A.
B.
C.
D.
8.(2024秋 北京期末)如图①是由方尊缶(中间小正方形,冷藏食物)和方鉴(外围大正方形,放置冰块)组成的套器青铜冰鉴,古人用于冷藏保存食物,其从上面看到的图形如图②所示,若大正方形的边长为2a+b,小正方形的边长为2a﹣b,则放置冰块部分的面积为( )
A.2ab B.4ab C.6ab D.8ab
9.(2024秋 法库县期末)由6个大小相同的正方体搭成的几何体如图所示,其左视图为( )
A. B.
C. D.
10.(2024秋 洛阳期末)如图是由若干个相同的小正方体组成的几何体,将其中一个小正方体移动位置后,下列说法正确的是( )
A.从正面看没有变化 B.从上面看没有变化
C.从左面看没有变化 D.从各个方向看都变化
二.填空题(共5小题)
11.(2024秋 莱阳市期末)如图所示是某一天不同时刻同一棵树的影子,则它们按时间先后顺序排列序号应为 .
12.(2024秋 白银期末)已知某几何体的三视图如图所示,则该几何体可能是 .
13.(2024秋 榕城区期末)一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,那么搭成该几何体至少需用小立方块 个.
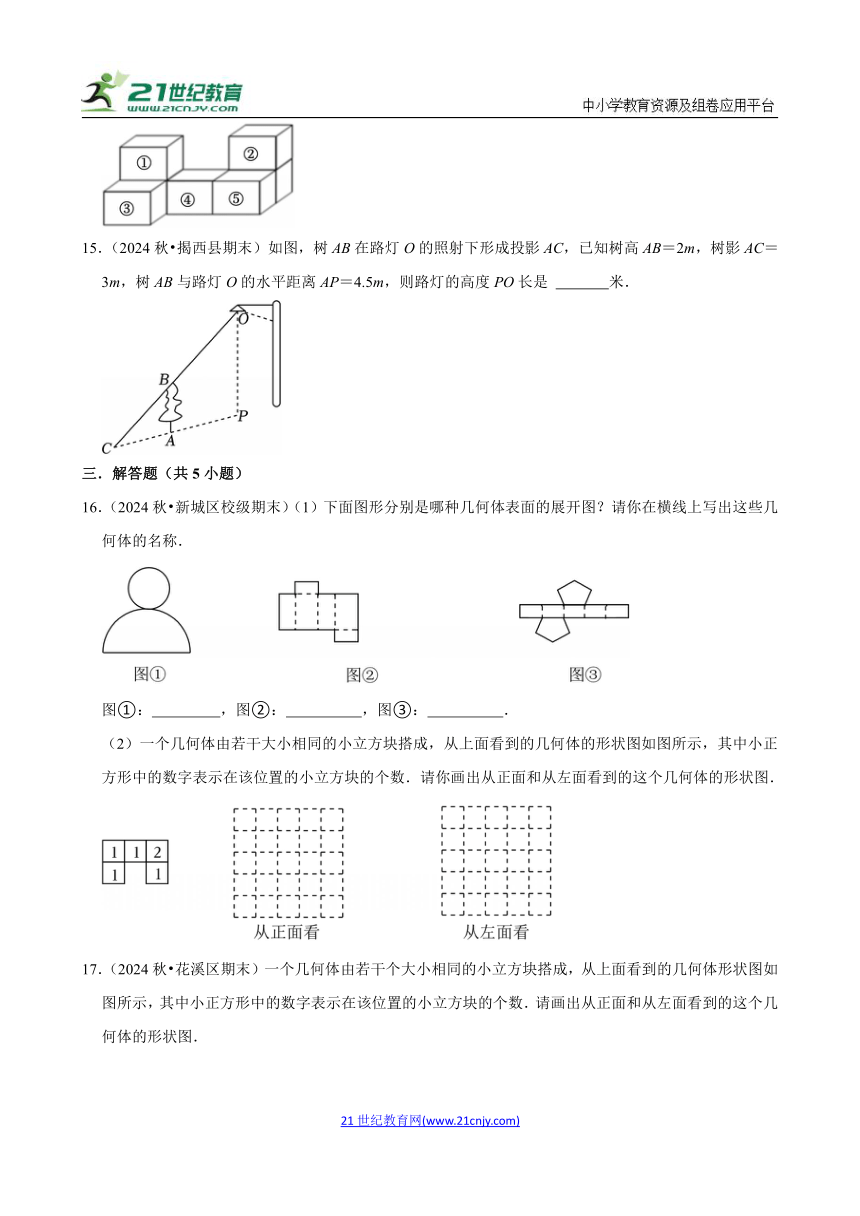
14.(2024秋 连平县期末)用7块相同的小正方体搭成的几何体如图所示.若拿走一块小正方体后,从正面和从左面看到的该几何体的形状图都没改变,则这块小长方体的序号是 .
15.(2024秋 揭西县期末)如图,树AB在路灯O的照射下形成投影AC,已知树高AB=2m,树影AC=3m,树AB与路灯O的水平距离AP=4.5m,则路灯的高度PO长是 米.
三.解答题(共5小题)
16.(2024秋 新城区校级期末)(1)下面图形分别是哪种几何体表面的展开图?请你在横线上写出这些几何体的名称.
图①: ,图②: ,图③: .
(2)一个几何体由若干大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请你画出从正面和从左面看到的这个几何体的形状图.
17.(2024秋 花溪区期末)一个几何体由若干个大小相同的小立方块搭成,从上面看到的几何体形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.
18.(2024秋 贵阳期末)如图①是一个几何体,图②是小星所画的这个几何体的三视图,但左视图和俯视图不完整.
(1)请帮小星补全三视图;
(2)按图中所标出的数据,求出该几何体的底面积.
19.(2024秋 高陵区期末)如图是由7个完全相同的小正方体堆叠成的几何体.
(1)请在指定位置画出从正面、左面、上面看这个几何体得到的形状图;
(2)若在标有①、②、③、④的其中一个小正方体上放置一个小正方体,从正面看该几何体的形状图不会发生变化,则该正方体的标号是 .
20.(2024秋 沈丘县期末)如图①,由9个相同的小立方块搭成一个几何体,请画出这个几何体从三个方向看到的形状图.
2025年中考数学高频易错考前冲刺:投影与视图
参考答案与试题解析
一.选择题(共10小题)
1.(2024秋 凉州区校级期末)如图,小树AB在路灯O的照射下形成投影BC.若这棵树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m,则路灯的高度OP为( )
A.3m B.5m C.6m D.7.5m
【考点】中心投影.
【专题】投影与视图;推理能力.
【答案】B
【分析】先求解CP=7.5m,再根据相似三角形的判定证出△ABC∽△OPC,然后利用相似三角形的性质求解即可得.
【解答】解:∵BC=3m,BP=4.5m,
∴CP=BC+BP=7.5m,
由题意得:AB⊥CP,OP⊥CP,
∴AB∥OP,
∴△ABC∽△OPC,而AB=2m,
∴,即,
解得OP=5(m),
答:路灯的高度OP为5m.
故选:B.
【点评】本题考查了中心投影,熟练掌握相似三角形的判定与性质是解题关键.
2.(2024秋 白银期末)某积木配件如图所示,它的主视图是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据主视图是从正面看到的图形解答即可.
【解答】解:从正面看,可得选项C的图形,即主视图为C.
故选:C.
【点评】本题考查了简单组合体的三视图,掌握三视图的定义是解答本题的关键.
3.(2024秋 白银期末)一块三角形纸板ABC如图所示,BC=15cm,AC=12cm,测得BC边的中心投影B1C1的长为20cm,则AC边的中心投影A1C1的长为( )
A.24cm B.20cm C.16cm D.8cm
【考点】中心投影.
【专题】投影与视图;运算能力.
【答案】C
【分析】利用中心投影的性质求解.
【解答】解:由中心投影的性质可知△ABC∽△A1B1C1,
∴,
∴,
∴A1C1=16(cm).
故选:C.
【点评】本题考查中心投影,解题的关键是掌握中心投影的性质.
4.(2024秋 海门区期末)如图是从不同方向看一个立体图形得到的平面图形,那么这个立体图形是( )
A. B. C. D.
【考点】由三视图判断几何体.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据三棱柱的三视图的特征进行解答即可.
【解答】解:由从不同方向看一个立体图形得到的平面图形,可得这个立体图形是三棱柱,
故选:C.
【点评】本题考查简单几何体的三视图,理解视图的定义,掌握简单组合体三视图的画法和形状是正确解答的关键.
5.(2024秋 长沙期末)黑陶是继彩陶之后中国新石器时代制陶工艺的又一个高峰,被誉为“土与火的艺术,力与美的结晶”.如图是山东博物馆收藏的蛋壳黑陶高柄杯.从三个不同方向观察,下列说法正确的是( )
A.从正面、左面看到的形状图相同
B.从正面、上面看到的形状图相同
C.从左面、上面看到的形状图相同
D.从正面、左面、上面看到的形状图都相同
【考点】简单组合体的三视图.
【专题】投影与视图;几何直观.
【答案】A
【分析】根据从前往后,从左到右,从上到下看到的图形,进行判断即可.
【解答】解:从正面看和从左面看,看到的图形相同.
故选:A.
【点评】本题考查了简单组合体的三视图,掌握几何体的空间结构是关键.
6.(2024秋 贵阳期末)在一间黑屋子里用一盏白炽灯照射如图所示的球.当球向下移动时,这个球在地面上的影子大小的变化情况是( )
A.保持不变 B.越来越大 C.越来越小 D.不能确定
【考点】中心投影.
【专题】投影与视图;几何直观.
【答案】C
【分析】根据中心投影的特点,灯光下影子与物体离灯源的距离有关,此距离越大,影子越小.
【解答】解:当把球向下平移时,圆形阴影的大小的变化情况是:越来越小,
故选:C.
【点评】本题考查了中心投影,熟练掌握中心投影的特点是解题的关键.
7.(2024秋 太原期末)中国古代的数学研究成果辉煌,产生的一些数学名词,颠有趣味,如《九章算术》中的“刍童”,原指上、下底面都是长方形的草垛.如图是一个“刍童”形状的几何体,它的主视图和左视图如图所示,则其俯视图是( )
A.
B.
C.
D.
【考点】由三视图判断几何体;简单几何体的三视图.
【专题】投影与视图;几何直观.
【答案】D
【分析】根据立体图形的特点,结合三视图分析即可,能看到的线用实线,不能看到的,但存在的线用虚线表示.
【解答】解:由“刍童”形状的几何体的主视图和左视图可知,其俯视图是
,
故选:D.
【点评】本题考查了由三视图判断几何体,简单几何体的三视图,掌握立体图形三视图的特点,数形结合分析是解题的关键.
8.(2024秋 北京期末)如图①是由方尊缶(中间小正方形,冷藏食物)和方鉴(外围大正方形,放置冰块)组成的套器青铜冰鉴,古人用于冷藏保存食物,其从上面看到的图形如图②所示,若大正方形的边长为2a+b,小正方形的边长为2a﹣b,则放置冰块部分的面积为( )
A.2ab B.4ab C.6ab D.8ab
【考点】由三视图判断几何体;完全平方公式的几何背景.
【专题】投影与视图;空间观念.
【答案】D
【分析】根据俯视图这两个正方体的面积差即可.
【解答】解:由题意得,放置冰块部分的面积可以看作两个正方形的面积差,即(2a+b)2﹣(2a﹣b)2=8ab,
故选:D.
【点评】本题考查完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的关键.
9.(2024秋 法库县期末)由6个大小相同的正方体搭成的几何体如图所示,其左视图为( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】D
【分析】根据简单组合体三视图的画法画出它的左视图即可.
【解答】解:这个组合体的左视图为:
故选:D.
【点评】本题考查简单组合体的三视图,理解视图的定义,掌握简单组合体三视图的画法是正确解答的关键.
10.(2024秋 洛阳期末)如图是由若干个相同的小正方体组成的几何体,将其中一个小正方体移动位置后,下列说法正确的是( )
A.从正面看没有变化 B.从上面看没有变化
C.从左面看没有变化 D.从各个方向看都变化
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据三视图的变化解答即可.
【解答】解:这两个几何体的主视图改变,左视图不变,俯视图变化,
故选:C.
【点评】本题考查了简单组合体的三视图,利用三视图的意义是解题关键.
二.填空题(共5小题)
11.(2024秋 莱阳市期末)如图所示是某一天不同时刻同一棵树的影子,则它们按时间先后顺序排列序号应为 ④②①③ .
【考点】平行投影.
【专题】投影与视图;几何直观.
【答案】④②①③.
【分析】根据不同时刻物体在太阳光下的影子的大小、方向的改变规律:就北半球而言,从早晨到傍晚物体的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长.
【解答】解:西为④,西北为②,东北为①,东为③,
故其按时间的先后顺序为:④②①③.
故答案为:④②①③.
【点评】本题考查平行投影,在不同时刻物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚物体的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长.
12.(2024秋 白银期末)已知某几何体的三视图如图所示,则该几何体可能是 圆柱 .
【考点】由三视图判断几何体.
【专题】投影与视图;空间观念.
【答案】圆柱.
【分析】根据两个视图是三角形得出该几何体是柱体,再根据俯视图是圆,得出几何体是柱.
【解答】解:∵主视图和左视图是长方形,
∴几何体是柱体,
∵俯视图的大致轮廓是圆,
∴该几何体是圆柱.
故答案为:圆柱.
【点评】此题考查由三视图判断几何体,三视图里有两个相同可确定该几何体是柱体,锥体还是球体,由另一个视图确定其具体形状.
13.(2024秋 榕城区期末)一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,那么搭成该几何体至少需用小立方块 6 个.
【考点】由三视图判断几何体;简单组合体的三视图.
【专题】投影与视图;空间观念;几何直观;推理能力.
【答案】6.
【分析】根据题意可以得到该几何体从正面和上面看至少有多少个小立方体,综合考虑即可解答本题.
【解答】解:根据主视图可得,俯视图中第一列中至少一处有2层;
所以该几何体至少是用6个小立方块搭成的.
故答案为:6.
【点评】本题考查了由三视图判断几何体,由三视图想象几何体的形状,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
14.(2024秋 连平县期末)用7块相同的小正方体搭成的几何体如图所示.若拿走一块小正方体后,从正面和从左面看到的该几何体的形状图都没改变,则这块小长方体的序号是 ⑤ .
【考点】简单组合体的三视图.
【专题】投影与视图;几何直观.
【答案】⑤.
【分析】根据题意把分别使正面和左面看到的图形不变的情况找到,再选择共同都有的即可.
【解答】解:由图可知,拿走一块小正方体后,要使得该几何体正面看到的图形没改变,可以是:③、⑤,
拿走一块小正方体后,要使得左面看到的图形没改变,可以是:④、⑤,
综上所述,从正面和从左面看到的该几何体的形状图都没改变只有:⑤,
故答案为:⑤.
【点评】本题考查了简单组合体的三视图,解题的关键是看出从正面、左面、上面看出的图形.
15.(2024秋 揭西县期末)如图,树AB在路灯O的照射下形成投影AC,已知树高AB=2m,树影AC=3m,树AB与路灯O的水平距离AP=4.5m,则路灯的高度PO长是 5 米.
【考点】中心投影.
【专题】投影与视图;应用意识.
【答案】见试题解答内容
【分析】利用中心投影的性质得到AB∥OP,则可判断△CAB∽△CPO,然后利用相似三角形的性质求OP的长即可.
【解答】解:∵AB在路灯O的照射下形成投影AC,
∴AB∥OP,
∴△CAB∽△CPO,
∴,
∵AB=2m,AC=3m,AP=4.5m,
∴,
解得OP=5,
即路灯的高度PO长是5米.
故答案为:5.
【点评】本题考查了中心投影:中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.
三.解答题(共5小题)
16.(2024秋 新城区校级期末)(1)下面图形分别是哪种几何体表面的展开图?请你在横线上写出这些几何体的名称.
图①: 圆锥 ,图②: 长方体 ,图③: 五棱柱 .
(2)一个几何体由若干大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请你画出从正面和从左面看到的这个几何体的形状图.
【考点】由三视图判断几何体;几何体的展开图.
【专题】几何图形;投影与视图;几何直观.
【答案】(1)圆锥,长方体,五棱柱;
(2)见解析.
【分析】(1)根据几何体的展开图特征即可得出答案;
(2)由题意可得,这个几何体从正面看有3列,每列小正方形的数目为1、1、2,从左面看有2列,每列小正方形的数目是2、1,据此可画出图形.
【解答】解:(1)由立体图形的展开图可知,图①:圆锥,图②:长方体,图③:五棱柱;
故答案为:圆锥,长方体,五棱柱;
(2)如图所示:
【点评】本题考查了由三视图判断几何体,几何体的展开图,熟练掌握几何体的画法是解题的关键.
17.(2024秋 花溪区期末)一个几何体由若干个大小相同的小立方块搭成,从上面看到的几何体形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.
【考点】由三视图判断几何体;作图﹣三视图;简单组合体的三视图.
【专题】投影与视图;几何直观.
【答案】见解析.
【分析】主视图有2列,每列小正方形数目分别为2,3,左视图有2列,每列小正方数形数目分别为1,3,据此可画出图形.
【解答】解:图形如图所示:
【点评】本题考查由三视图判断几何体和作图﹣三视图,熟练掌握几何体的画法是解题的关键.
18.(2024秋 贵阳期末)如图①是一个几何体,图②是小星所画的这个几何体的三视图,但左视图和俯视图不完整.
(1)请帮小星补全三视图;
(2)按图中所标出的数据,求出该几何体的底面积.
【考点】作图﹣三视图;由三视图判断几何体.
【专题】投影与视图;几何直观.
【答案】(1)见解析;
(2)28.
【分析】(1)根据三视图的定义作出图形;
(2)判断出底面矩形的长宽,再利用矩形面积公式求解.
【解答】解:(1)三视图如图所示:
(2)这个几何体的底面积=4(2+3+2)=28.
【点评】本题考查作图﹣三视图,由三视图判定几何体,解题的关键是理解三视图的定义.
19.(2024秋 高陵区期末)如图是由7个完全相同的小正方体堆叠成的几何体.
(1)请在指定位置画出从正面、左面、上面看这个几何体得到的形状图;
(2)若在标有①、②、③、④的其中一个小正方体上放置一个小正方体,从正面看该几何体的形状图不会发生变化,则该正方体的标号是 ④ .
【考点】作图﹣三视图.
【专题】投影与视图;空间观念.
【答案】(1)见解答;(2)④.
【分析】(1)从正面看:共有3列,从左往右分别有3,2,1个小正方形;从左面看:共有2列,从左往右分别有3,1个小正方形;从上面看:共分3列,从左往右分别有1,2,1个小正方形.据此可画出图形.
(2)根据三视图的定义解答即可.
【解答】解:(1)如图所示:
(2)若在标有①、②、③、④的其中一个小正方体上放置一个小正方体,从正面看该几何体的形状图不会发生变化,则该正方体的标号是④.
故答案为:④.
【点评】本题考查作图﹣三视图,解题的关键是理解三视图的定义,灵活运用所学知识解决问题.
20.(2024秋 沈丘县期末)如图①,由9个相同的小立方块搭成一个几何体,请画出这个几何体从三个方向看到的形状图.
【考点】作图﹣三视图.
【专题】几何直观.
【答案】见详解.
【分析】从正面看,得到从左往右3列正方形的个数依次为1,3,1,1;从左面看得到从左往右2列正方形的个数依次为3,2;从上面看得到从左往右4列正方形的个数依次为1,2,1,2,依此画出图形即可.
【解答】解:这个几何体从三个方向看到的形状图如图所示:
【点评】此题主要考查了从不同方向看几何体,弄清题意是解本题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 凉州区校级期末)如图,小树AB在路灯O的照射下形成投影BC.若这棵树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m,则路灯的高度OP为( )
A.3m B.5m C.6m D.7.5m
2.(2024秋 白银期末)某积木配件如图所示,它的主视图是( )
A. B.
C. D.
3.(2024秋 白银期末)一块三角形纸板ABC如图所示,BC=15cm,AC=12cm,测得BC边的中心投影B1C1的长为20cm,则AC边的中心投影A1C1的长为( )
A.24cm B.20cm C.16cm D.8cm
4.(2024秋 海门区期末)如图是从不同方向看一个立体图形得到的平面图形,那么这个立体图形是( )
A. B. C. D.
5.(2024秋 长沙期末)黑陶是继彩陶之后中国新石器时代制陶工艺的又一个高峰,被誉为“土与火的艺术,力与美的结晶”.如图是山东博物馆收藏的蛋壳黑陶高柄杯.从三个不同方向观察,下列说法正确的是( )
A.从正面、左面看到的形状图相同
B.从正面、上面看到的形状图相同
C.从左面、上面看到的形状图相同
D.从正面、左面、上面看到的形状图都相同
6.(2024秋 贵阳期末)在一间黑屋子里用一盏白炽灯照射如图所示的球.当球向下移动时,这个球在地面上的影子大小的变化情况是( )
A.保持不变 B.越来越大 C.越来越小 D.不能确定
7.(2024秋 太原期末)中国古代的数学研究成果辉煌,产生的一些数学名词,颠有趣味,如《九章算术》中的“刍童”,原指上、下底面都是长方形的草垛.如图是一个“刍童”形状的几何体,它的主视图和左视图如图所示,则其俯视图是( )
A.
B.
C.
D.
8.(2024秋 北京期末)如图①是由方尊缶(中间小正方形,冷藏食物)和方鉴(外围大正方形,放置冰块)组成的套器青铜冰鉴,古人用于冷藏保存食物,其从上面看到的图形如图②所示,若大正方形的边长为2a+b,小正方形的边长为2a﹣b,则放置冰块部分的面积为( )
A.2ab B.4ab C.6ab D.8ab
9.(2024秋 法库县期末)由6个大小相同的正方体搭成的几何体如图所示,其左视图为( )
A. B.
C. D.
10.(2024秋 洛阳期末)如图是由若干个相同的小正方体组成的几何体,将其中一个小正方体移动位置后,下列说法正确的是( )
A.从正面看没有变化 B.从上面看没有变化
C.从左面看没有变化 D.从各个方向看都变化
二.填空题(共5小题)
11.(2024秋 莱阳市期末)如图所示是某一天不同时刻同一棵树的影子,则它们按时间先后顺序排列序号应为 .
12.(2024秋 白银期末)已知某几何体的三视图如图所示,则该几何体可能是 .
13.(2024秋 榕城区期末)一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,那么搭成该几何体至少需用小立方块 个.
14.(2024秋 连平县期末)用7块相同的小正方体搭成的几何体如图所示.若拿走一块小正方体后,从正面和从左面看到的该几何体的形状图都没改变,则这块小长方体的序号是 .
15.(2024秋 揭西县期末)如图,树AB在路灯O的照射下形成投影AC,已知树高AB=2m,树影AC=3m,树AB与路灯O的水平距离AP=4.5m,则路灯的高度PO长是 米.
三.解答题(共5小题)
16.(2024秋 新城区校级期末)(1)下面图形分别是哪种几何体表面的展开图?请你在横线上写出这些几何体的名称.
图①: ,图②: ,图③: .
(2)一个几何体由若干大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请你画出从正面和从左面看到的这个几何体的形状图.
17.(2024秋 花溪区期末)一个几何体由若干个大小相同的小立方块搭成,从上面看到的几何体形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.
18.(2024秋 贵阳期末)如图①是一个几何体,图②是小星所画的这个几何体的三视图,但左视图和俯视图不完整.
(1)请帮小星补全三视图;
(2)按图中所标出的数据,求出该几何体的底面积.
19.(2024秋 高陵区期末)如图是由7个完全相同的小正方体堆叠成的几何体.
(1)请在指定位置画出从正面、左面、上面看这个几何体得到的形状图;
(2)若在标有①、②、③、④的其中一个小正方体上放置一个小正方体,从正面看该几何体的形状图不会发生变化,则该正方体的标号是 .
20.(2024秋 沈丘县期末)如图①,由9个相同的小立方块搭成一个几何体,请画出这个几何体从三个方向看到的形状图.
2025年中考数学高频易错考前冲刺:投影与视图
参考答案与试题解析
一.选择题(共10小题)
1.(2024秋 凉州区校级期末)如图,小树AB在路灯O的照射下形成投影BC.若这棵树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m,则路灯的高度OP为( )
A.3m B.5m C.6m D.7.5m
【考点】中心投影.
【专题】投影与视图;推理能力.
【答案】B
【分析】先求解CP=7.5m,再根据相似三角形的判定证出△ABC∽△OPC,然后利用相似三角形的性质求解即可得.
【解答】解:∵BC=3m,BP=4.5m,
∴CP=BC+BP=7.5m,
由题意得:AB⊥CP,OP⊥CP,
∴AB∥OP,
∴△ABC∽△OPC,而AB=2m,
∴,即,
解得OP=5(m),
答:路灯的高度OP为5m.
故选:B.
【点评】本题考查了中心投影,熟练掌握相似三角形的判定与性质是解题关键.
2.(2024秋 白银期末)某积木配件如图所示,它的主视图是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据主视图是从正面看到的图形解答即可.
【解答】解:从正面看,可得选项C的图形,即主视图为C.
故选:C.
【点评】本题考查了简单组合体的三视图,掌握三视图的定义是解答本题的关键.
3.(2024秋 白银期末)一块三角形纸板ABC如图所示,BC=15cm,AC=12cm,测得BC边的中心投影B1C1的长为20cm,则AC边的中心投影A1C1的长为( )
A.24cm B.20cm C.16cm D.8cm
【考点】中心投影.
【专题】投影与视图;运算能力.
【答案】C
【分析】利用中心投影的性质求解.
【解答】解:由中心投影的性质可知△ABC∽△A1B1C1,
∴,
∴,
∴A1C1=16(cm).
故选:C.
【点评】本题考查中心投影,解题的关键是掌握中心投影的性质.
4.(2024秋 海门区期末)如图是从不同方向看一个立体图形得到的平面图形,那么这个立体图形是( )
A. B. C. D.
【考点】由三视图判断几何体.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据三棱柱的三视图的特征进行解答即可.
【解答】解:由从不同方向看一个立体图形得到的平面图形,可得这个立体图形是三棱柱,
故选:C.
【点评】本题考查简单几何体的三视图,理解视图的定义,掌握简单组合体三视图的画法和形状是正确解答的关键.
5.(2024秋 长沙期末)黑陶是继彩陶之后中国新石器时代制陶工艺的又一个高峰,被誉为“土与火的艺术,力与美的结晶”.如图是山东博物馆收藏的蛋壳黑陶高柄杯.从三个不同方向观察,下列说法正确的是( )
A.从正面、左面看到的形状图相同
B.从正面、上面看到的形状图相同
C.从左面、上面看到的形状图相同
D.从正面、左面、上面看到的形状图都相同
【考点】简单组合体的三视图.
【专题】投影与视图;几何直观.
【答案】A
【分析】根据从前往后,从左到右,从上到下看到的图形,进行判断即可.
【解答】解:从正面看和从左面看,看到的图形相同.
故选:A.
【点评】本题考查了简单组合体的三视图,掌握几何体的空间结构是关键.
6.(2024秋 贵阳期末)在一间黑屋子里用一盏白炽灯照射如图所示的球.当球向下移动时,这个球在地面上的影子大小的变化情况是( )
A.保持不变 B.越来越大 C.越来越小 D.不能确定
【考点】中心投影.
【专题】投影与视图;几何直观.
【答案】C
【分析】根据中心投影的特点,灯光下影子与物体离灯源的距离有关,此距离越大,影子越小.
【解答】解:当把球向下平移时,圆形阴影的大小的变化情况是:越来越小,
故选:C.
【点评】本题考查了中心投影,熟练掌握中心投影的特点是解题的关键.
7.(2024秋 太原期末)中国古代的数学研究成果辉煌,产生的一些数学名词,颠有趣味,如《九章算术》中的“刍童”,原指上、下底面都是长方形的草垛.如图是一个“刍童”形状的几何体,它的主视图和左视图如图所示,则其俯视图是( )
A.
B.
C.
D.
【考点】由三视图判断几何体;简单几何体的三视图.
【专题】投影与视图;几何直观.
【答案】D
【分析】根据立体图形的特点,结合三视图分析即可,能看到的线用实线,不能看到的,但存在的线用虚线表示.
【解答】解:由“刍童”形状的几何体的主视图和左视图可知,其俯视图是
,
故选:D.
【点评】本题考查了由三视图判断几何体,简单几何体的三视图,掌握立体图形三视图的特点,数形结合分析是解题的关键.
8.(2024秋 北京期末)如图①是由方尊缶(中间小正方形,冷藏食物)和方鉴(外围大正方形,放置冰块)组成的套器青铜冰鉴,古人用于冷藏保存食物,其从上面看到的图形如图②所示,若大正方形的边长为2a+b,小正方形的边长为2a﹣b,则放置冰块部分的面积为( )
A.2ab B.4ab C.6ab D.8ab
【考点】由三视图判断几何体;完全平方公式的几何背景.
【专题】投影与视图;空间观念.
【答案】D
【分析】根据俯视图这两个正方体的面积差即可.
【解答】解:由题意得,放置冰块部分的面积可以看作两个正方形的面积差,即(2a+b)2﹣(2a﹣b)2=8ab,
故选:D.
【点评】本题考查完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的关键.
9.(2024秋 法库县期末)由6个大小相同的正方体搭成的几何体如图所示,其左视图为( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】D
【分析】根据简单组合体三视图的画法画出它的左视图即可.
【解答】解:这个组合体的左视图为:
故选:D.
【点评】本题考查简单组合体的三视图,理解视图的定义,掌握简单组合体三视图的画法是正确解答的关键.
10.(2024秋 洛阳期末)如图是由若干个相同的小正方体组成的几何体,将其中一个小正方体移动位置后,下列说法正确的是( )
A.从正面看没有变化 B.从上面看没有变化
C.从左面看没有变化 D.从各个方向看都变化
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据三视图的变化解答即可.
【解答】解:这两个几何体的主视图改变,左视图不变,俯视图变化,
故选:C.
【点评】本题考查了简单组合体的三视图,利用三视图的意义是解题关键.
二.填空题(共5小题)
11.(2024秋 莱阳市期末)如图所示是某一天不同时刻同一棵树的影子,则它们按时间先后顺序排列序号应为 ④②①③ .
【考点】平行投影.
【专题】投影与视图;几何直观.
【答案】④②①③.
【分析】根据不同时刻物体在太阳光下的影子的大小、方向的改变规律:就北半球而言,从早晨到傍晚物体的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长.
【解答】解:西为④,西北为②,东北为①,东为③,
故其按时间的先后顺序为:④②①③.
故答案为:④②①③.
【点评】本题考查平行投影,在不同时刻物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚物体的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长.
12.(2024秋 白银期末)已知某几何体的三视图如图所示,则该几何体可能是 圆柱 .
【考点】由三视图判断几何体.
【专题】投影与视图;空间观念.
【答案】圆柱.
【分析】根据两个视图是三角形得出该几何体是柱体,再根据俯视图是圆,得出几何体是柱.
【解答】解:∵主视图和左视图是长方形,
∴几何体是柱体,
∵俯视图的大致轮廓是圆,
∴该几何体是圆柱.
故答案为:圆柱.
【点评】此题考查由三视图判断几何体,三视图里有两个相同可确定该几何体是柱体,锥体还是球体,由另一个视图确定其具体形状.
13.(2024秋 榕城区期末)一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,那么搭成该几何体至少需用小立方块 6 个.
【考点】由三视图判断几何体;简单组合体的三视图.
【专题】投影与视图;空间观念;几何直观;推理能力.
【答案】6.
【分析】根据题意可以得到该几何体从正面和上面看至少有多少个小立方体,综合考虑即可解答本题.
【解答】解:根据主视图可得,俯视图中第一列中至少一处有2层;
所以该几何体至少是用6个小立方块搭成的.
故答案为:6.
【点评】本题考查了由三视图判断几何体,由三视图想象几何体的形状,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
14.(2024秋 连平县期末)用7块相同的小正方体搭成的几何体如图所示.若拿走一块小正方体后,从正面和从左面看到的该几何体的形状图都没改变,则这块小长方体的序号是 ⑤ .
【考点】简单组合体的三视图.
【专题】投影与视图;几何直观.
【答案】⑤.
【分析】根据题意把分别使正面和左面看到的图形不变的情况找到,再选择共同都有的即可.
【解答】解:由图可知,拿走一块小正方体后,要使得该几何体正面看到的图形没改变,可以是:③、⑤,
拿走一块小正方体后,要使得左面看到的图形没改变,可以是:④、⑤,
综上所述,从正面和从左面看到的该几何体的形状图都没改变只有:⑤,
故答案为:⑤.
【点评】本题考查了简单组合体的三视图,解题的关键是看出从正面、左面、上面看出的图形.
15.(2024秋 揭西县期末)如图,树AB在路灯O的照射下形成投影AC,已知树高AB=2m,树影AC=3m,树AB与路灯O的水平距离AP=4.5m,则路灯的高度PO长是 5 米.
【考点】中心投影.
【专题】投影与视图;应用意识.
【答案】见试题解答内容
【分析】利用中心投影的性质得到AB∥OP,则可判断△CAB∽△CPO,然后利用相似三角形的性质求OP的长即可.
【解答】解:∵AB在路灯O的照射下形成投影AC,
∴AB∥OP,
∴△CAB∽△CPO,
∴,
∵AB=2m,AC=3m,AP=4.5m,
∴,
解得OP=5,
即路灯的高度PO长是5米.
故答案为:5.
【点评】本题考查了中心投影:中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.
三.解答题(共5小题)
16.(2024秋 新城区校级期末)(1)下面图形分别是哪种几何体表面的展开图?请你在横线上写出这些几何体的名称.
图①: 圆锥 ,图②: 长方体 ,图③: 五棱柱 .
(2)一个几何体由若干大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请你画出从正面和从左面看到的这个几何体的形状图.
【考点】由三视图判断几何体;几何体的展开图.
【专题】几何图形;投影与视图;几何直观.
【答案】(1)圆锥,长方体,五棱柱;
(2)见解析.
【分析】(1)根据几何体的展开图特征即可得出答案;
(2)由题意可得,这个几何体从正面看有3列,每列小正方形的数目为1、1、2,从左面看有2列,每列小正方形的数目是2、1,据此可画出图形.
【解答】解:(1)由立体图形的展开图可知,图①:圆锥,图②:长方体,图③:五棱柱;
故答案为:圆锥,长方体,五棱柱;
(2)如图所示:
【点评】本题考查了由三视图判断几何体,几何体的展开图,熟练掌握几何体的画法是解题的关键.
17.(2024秋 花溪区期末)一个几何体由若干个大小相同的小立方块搭成,从上面看到的几何体形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.
【考点】由三视图判断几何体;作图﹣三视图;简单组合体的三视图.
【专题】投影与视图;几何直观.
【答案】见解析.
【分析】主视图有2列,每列小正方形数目分别为2,3,左视图有2列,每列小正方数形数目分别为1,3,据此可画出图形.
【解答】解:图形如图所示:
【点评】本题考查由三视图判断几何体和作图﹣三视图,熟练掌握几何体的画法是解题的关键.
18.(2024秋 贵阳期末)如图①是一个几何体,图②是小星所画的这个几何体的三视图,但左视图和俯视图不完整.
(1)请帮小星补全三视图;
(2)按图中所标出的数据,求出该几何体的底面积.
【考点】作图﹣三视图;由三视图判断几何体.
【专题】投影与视图;几何直观.
【答案】(1)见解析;
(2)28.
【分析】(1)根据三视图的定义作出图形;
(2)判断出底面矩形的长宽,再利用矩形面积公式求解.
【解答】解:(1)三视图如图所示:
(2)这个几何体的底面积=4(2+3+2)=28.
【点评】本题考查作图﹣三视图,由三视图判定几何体,解题的关键是理解三视图的定义.
19.(2024秋 高陵区期末)如图是由7个完全相同的小正方体堆叠成的几何体.
(1)请在指定位置画出从正面、左面、上面看这个几何体得到的形状图;
(2)若在标有①、②、③、④的其中一个小正方体上放置一个小正方体,从正面看该几何体的形状图不会发生变化,则该正方体的标号是 ④ .
【考点】作图﹣三视图.
【专题】投影与视图;空间观念.
【答案】(1)见解答;(2)④.
【分析】(1)从正面看:共有3列,从左往右分别有3,2,1个小正方形;从左面看:共有2列,从左往右分别有3,1个小正方形;从上面看:共分3列,从左往右分别有1,2,1个小正方形.据此可画出图形.
(2)根据三视图的定义解答即可.
【解答】解:(1)如图所示:
(2)若在标有①、②、③、④的其中一个小正方体上放置一个小正方体,从正面看该几何体的形状图不会发生变化,则该正方体的标号是④.
故答案为:④.
【点评】本题考查作图﹣三视图,解题的关键是理解三视图的定义,灵活运用所学知识解决问题.
20.(2024秋 沈丘县期末)如图①,由9个相同的小立方块搭成一个几何体,请画出这个几何体从三个方向看到的形状图.
【考点】作图﹣三视图.
【专题】几何直观.
【答案】见详解.
【分析】从正面看,得到从左往右3列正方形的个数依次为1,3,1,1;从左面看得到从左往右2列正方形的个数依次为3,2;从上面看得到从左往右4列正方形的个数依次为1,2,1,2,依此画出图形即可.
【解答】解:这个几何体从三个方向看到的形状图如图所示:
【点评】此题主要考查了从不同方向看几何体,弄清题意是解本题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
