【中考押题卷】2025年中考数学高频易错考前冲刺:图形的旋转(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:图形的旋转(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 07:39:06 | ||
图片预览

文档简介
2025年中考数学高频易错考前冲刺:图形的旋转
一.选择题(共10小题)
1.(2024秋 本溪期末)2024年7月27日,第33届夏季奥运会在法国巴黎举行,如图所示巴黎奥运会项目图标中,是中心对称图形的是( )
A. B.
C. D.
2.(2024秋 泰兴市期末)如图,△ABC绕点B旋转得到△EBD,A,B,D三点在同一条直线上,且AD=5,BE=2,则BC的长为( )
A.1 B.2 C.3 D.4
3.(2024秋 天津期末)如图,若点D是等边三角形ABC的边BC上任意一点,将△ADC绕点A顺时针旋转得到△AEB,连接ED,则下列结论一定正确的是( )
A.AB⊥ED B.∠BDE=30° C.ED=AD D.BE∥AD
4.(2024秋 河西区期末)如图,在△ABC中,∠BAC=90°,AB=AC.点D在BC上,连接AD,将线段AD绕点A顺时针旋转90°得到线段AE,连接BE,DE,则下列结论一定正确的是( )
A.∠EBC=∠BAC B.AD=AC C.∠AEB=∠ABE D.BA=BE
5.(2024秋 丰都县期末)如图,△ABC中,∠ABC=45°,将△ABC绕点B逆时针旋转60°得到△DBE,点A、C的对应点分别为D、E,延长CA交DE于点F,下列结论错误的是( )
A.∠BED=30° B.∠DBE=45° C.∠ABD=60° D.∠CBE=60°
6.(2024秋 江汉区期末)如图,在△ABC中,AB=AC,∠BAC=40°,AD⊥BC于D.△ABC绕点B逆时针旋转得到△FBE,点C的对应点E落在AD上,则∠CBF的度数是( )
A.140° B.130° C.120° D.110°
7.(2024秋 澄海区期末)如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A'是对称点 B.BO=B'O
C.AB=A'B' D.∠ACB=∠C'A'B'
8.(2024秋 肇庆期末)在直角坐标系中,点(﹣2,3)关于原点的对称点的坐标是( )
A.(2,﹣3) B.(﹣2,3) C.(0,﹣3) D.(0,3)
9.(2024秋 秦皇岛校级期末)如图,在小正方形网格中,将△ABC绕某一点旋转变换得到△DEF,则旋转中心为( )
A.点M B.点N C.点O D.点P
10.(2024秋 澄海区期末)如图,在平面直角坐标系中有一等边△ABC,其坐标分别为A(0,0),B(2,0),将△ABC绕点B顺时针方向旋转60°,则旋转后C点的坐标为( )
A.(3,1) B. C. D.
二.填空题(共5小题)
11.(2024秋 泉港区期末)如图,利用两个含30°的全等直角三角板做旋转运动,绕着直角顶点O将其中一块三角板逆时针旋转,使得点C恰好在BD上.若OB=1,则OA= .
12.(2024秋 东莞市期末)如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是 度.
13.(2024秋 澄海区期末)如图,将矩形ABCD绕点A旋转至矩形AB'C'D'的位置,此时AC'的中点恰好与D点重合.若,则AB'的长为 .
14.(2024秋 延边州期末)点(1,2)关于原点的对称点坐标是 .
15.(2024秋 天津期末)若点P(x,﹣3)与点Q(4,y)关于原点对称,则x+y= .
三.解答题(共5小题)
16.(2024秋 岳麓区校级期末)在平面直角坐标系中,A(a,0),B(0,b),a,b满足,点C与点A关于y轴对称.
(1)请直接写出B,C两点的坐标;
(2)如图1,分别以AB,BC 为直角边向右侧作等腰Rt△BAD 和等腰Rt△BCE,连接DE交x轴于点M,连接BM,求证:BM⊥DE;
(3)如图2,点F为y轴上一动点,点G(m,﹣3m+6)在直线 BC上,若连接E,F,G三点(按逆时针顺序排列)恰好围成一个等腰直角三角形,求符合要求的m的值.
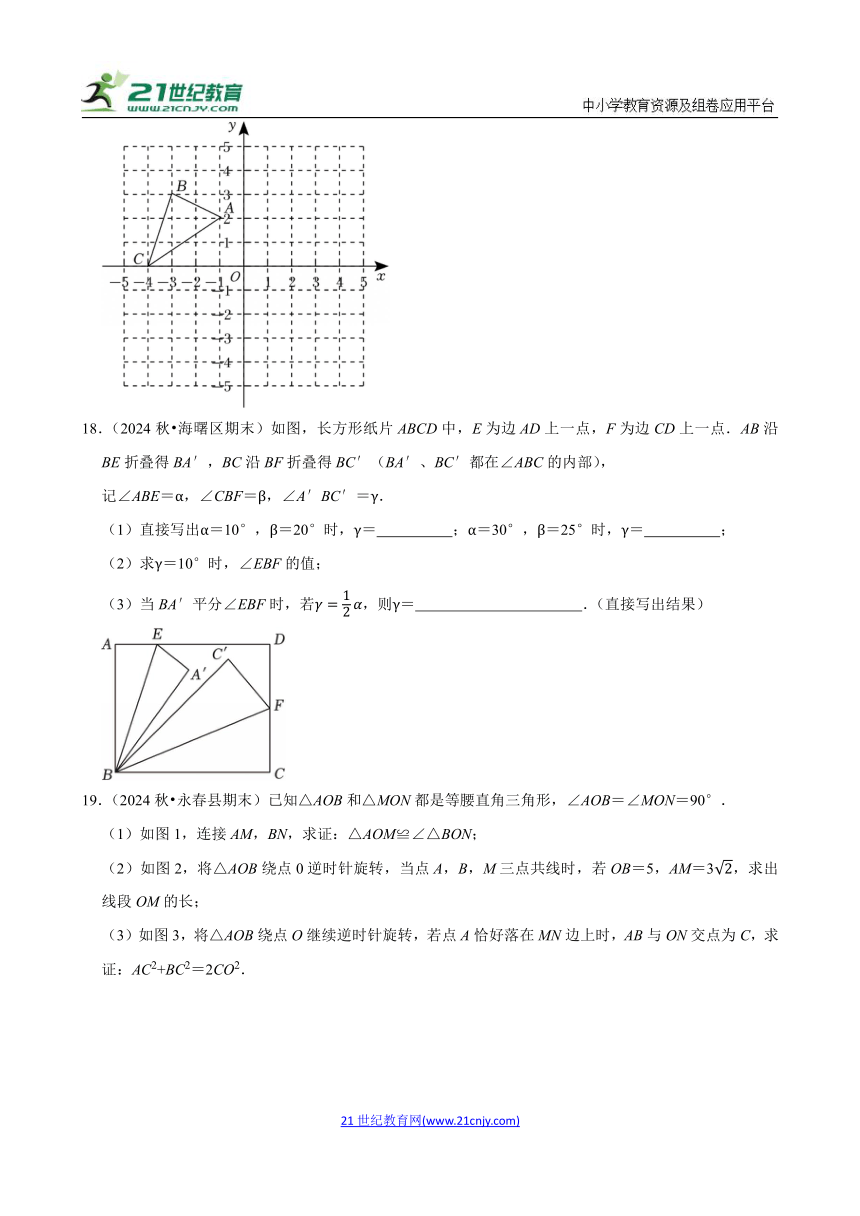
17.(2024秋 凉州区期末)△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点A逆时针旋转90°得到△A2B2C2;
③△A1B1C1中顶点A1坐标为 .
18.(2024秋 海曙区期末)如图,长方形纸片ABCD中,E为边AD上一点,F为边CD上一点.AB沿BE折叠得BA′,BC沿BF折叠得BC′(BA′、BC′都在∠ABC的内部),
记∠ABE=α,∠CBF=β,∠A′BC′=γ.
(1)直接写出α=10°,β=20°时,γ= ;α=30°,β=25°时,γ= ;
(2)求γ=10°时,∠EBF的值;
(3)当BA′平分∠EBF时,若,则γ= .(直接写出结果)
19.(2024秋 永春县期末)已知△AOB和△MON都是等腰直角三角形,∠AOB=∠MON=90°.
(1)如图1,连接AM,BN,求证:△AOM≌∠△BON;
(2)如图2,将△AOB绕点0逆时针旋转,当点A,B,M三点共线时,若OB=5,AM=3,求出线段OM的长;
(3)如图3,将△AOB绕点O继续逆时针旋转,若点A恰好落在MN边上时,AB与ON交点为C,求证:AC2+BC2=2CO2.
20.(2024秋 哈尔滨期末)【探究发现】
如图1,EF∥BC,点A在EF,BC之间,连接AE,AB.求证:∠A+∠AEF+∠ABC=360°.
【学以致用】
哈尔滨某商场地下车库出口处安装了“两段式栏杆”,如图2所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF升起到如图3所示的位置,其示意图如图4所示(AB⊥BC,EF∥BC,栏杆宽度忽略不计),已知∠AEE=150°,填空:∠BAE= 度.
【拓展应用】
如图5,已知GF∥BC,点E在GF上,点A在GF,BC之间,AD⊥AE交BC于点D,过点A作AB⊥CD于点B,AH平分∠BAD,AC平分∠EAB,若∠AEC+∠GEC=180°,∠ACE=3∠BAH,求∠GEA的度数.
2025年中考数学高频易错考前冲刺:图形的旋转
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C A A B D A B B
一.选择题(共10小题)
1.(2024秋 本溪期末)2024年7月27日,第33届夏季奥运会在法国巴黎举行,如图所示巴黎奥运会项目图标中,是中心对称图形的是( )
A.
B.
C.
D.
【考点】中心对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】根据中心对称图形的定义逐项判断即可.
【解答】解:A、图形是中心对称图形,符合题意;
B、图形不是中心对称图形,不符合题意;
C、图形不是中心对称图形,不符合题意;
D、图形不是中心对称图形,不符合题意,
故选:A.
【点评】本题主要考查了中心对称图形的定义,熟知将一个图形绕某点旋转180°,能与本身重合的图形,这样的图形称为中心对称图形是解题的关键.
2.(2024秋 泰兴市期末)如图,△ABC绕点B旋转得到△EBD,A,B,D三点在同一条直线上,且AD=5,BE=2,则BC的长为( )
A.1 B.2 C.3 D.4
【考点】旋转的性质.
【专题】平移、旋转与对称;运算能力.
【答案】C
【分析】由旋转的性质可得AB=BE=2,BC=BD,再根据线段的和差即可解答.
【解答】解:由题意可得:AB=BE=2,BC=BD,
∵AD=5,BE=2,
∴BD=AD﹣AB=AD﹣BE=5﹣2=3,
∴BC=BD=3.
故选:C.
【点评】本题主要考查了旋转的性质、线段的和差等知识点,熟练掌握旋转的性质是解题的关键.
3.(2024秋 天津期末)如图,若点D是等边三角形ABC的边BC上任意一点,将△ADC绕点A顺时针旋转得到△AEB,连接ED,则下列结论一定正确的是( )
A.AB⊥ED B.∠BDE=30° C.ED=AD D.BE∥AD
【考点】旋转的性质;全等三角形的判定与性质;等边三角形的性质.
【专题】平移、旋转与对称;推理能力.
【答案】C
【分析】根据旋转的性质得出AD=AE,∠CAD=∠BAE,证明三角形ADE是等边三角形即可得出结论.
【解答】解:∵将△ADC绕点A顺时针旋转得到△AEB,△ABC是等边三角形,
∴AD=AE,∠CAD=∠BAE,
∴∠DAE=∠CAB=60°,
∴△DAE是等边三角形,
∴ED=AD,
故选项C正确;
由已知条件无法证明A、B、D正确,
故选:C.
【点评】本题主要考查了旋转的性质,熟记旋转的性质是解题的关键.
4.(2024秋 河西区期末)如图,在△ABC中,∠BAC=90°,AB=AC.点D在BC上,连接AD,将线段AD绕点A顺时针旋转90°得到线段AE,连接BE,DE,则下列结论一定正确的是( )
A.∠EBC=∠BAC B.AD=AC C.∠AEB=∠ABE D.BA=BE
【考点】旋转的性质;全等三角形的判定与性质;等腰直角三角形.
【专题】图形的全等;平移、旋转与对称;推理能力.
【答案】A
【分析】证明△AEB≌△ADC(SAS),得出∠ABE=∠C,可得出结论.
【解答】解:∵将线段AD绕点A顺时针旋转90°得到线段AE,
∴AD=AE,∠DAE=90°,
又∵∠BAC=90°,
∴∠EAB+∠BAD=∠BAD+∠DAC,
∴∠EAB=∠DAC,
又∵AB=AC,
∴△AEB≌△ADC(SAS),
∴∠ABE=∠C,
∵∠BAC=90°,AB=AC,
∴∠ABE=∠ABC=∠C=45°,
∴∠EBC=∠BAC=90°,
故选项A一定正确,
由已知条件无法一定得出B、C、D正确,
故选:A.
【点评】本题考查了旋转的性质,全等三角形的判定与性质,熟记旋转的性质,全等三角形的判定与性质是解题的关键.
5.(2024秋 丰都县期末)如图,△ABC中,∠ABC=45°,将△ABC绕点B逆时针旋转60°得到△DBE,点A、C的对应点分别为D、E,延长CA交DE于点F,下列结论错误的是( )
A.∠BED=30° B.∠DBE=45° C.∠ABD=60° D.∠CBE=60°
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】直接根据旋转的性质逐一判断即可.
【解答】解:∵△ABC中,∠ABC=45°,将△ABC绕点B逆时针旋转60°得到△DBE,
∴∠DBE=∠ABC=45°,∠ABD=∠CBE=60°,
故选项B、C、D正确,
由已知条件无法得出∠BED=30°,
故选项A错误,
故选:A.
【点评】本题考查了旋转的性质,熟记旋转前后对应角相等是解题的关键.
6.(2024秋 江汉区期末)如图,在△ABC中,AB=AC,∠BAC=40°,AD⊥BC于D.△ABC绕点B逆时针旋转得到△FBE,点C的对应点E落在AD上,则∠CBF的度数是( )
A.140° B.130° C.120° D.110°
【考点】旋转的性质;等腰三角形的性质.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】连接CE,如图,根据等腰三角形的性质得到AD垂直平分BC,根据等腰三角形的性质和三角形内角和定理可计算出∠ABC=∠ACB=70°,再根据旋转的性质得到BE=BC,∠FBE=∠ABC=70°,则可判断△BCE为等边三角形,所以∠CBE=60°,然后计算∠CBE+∠FBE即可.
【解答】解:连接CE,如图,
∵AB=AC,
∴∠ABC=∠ACB(180°﹣∠BAC)(180°﹣40°)=70°,
∵AD⊥BC,
∴BD=CD,
即AD垂直平分BC,
∴BE=CE,
∵△ABC绕点B逆时针旋转得到△FBE,点C的对应点E落在AD上,
∴BE=BC,∠FBE=∠ABC=70°,
∵BE=CE=BC,
∴△BCE为等边三角形,
∴∠CBE=60°,
∴∠CBF=∠CBE+∠FBE=60°+70°=130°.
故选:B.
【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质.
7.(2024秋 澄海区期末)如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A'是对称点 B.BO=B'O
C.AB=A'B' D.∠ACB=∠C'A'B'
【考点】中心对称.
【专题】平移、旋转与对称;应用意识.
【答案】D
【分析】利用中心对称的性质一一判断即可.
【解答】解:∵△ABC与△A'B'C'关于点O成中心对称,
∴点A与点A'是对称点,BO=B'O,AB=A'B',
∴A,B,C正确,
故选:D.
【点评】本题考查中心对称,解题的关键是理解中心对称的性质,属于中考常考题型.
8.(2024秋 肇庆期末)在直角坐标系中,点(﹣2,3)关于原点的对称点的坐标是( )
A.(2,﹣3) B.(﹣2,3) C.(0,﹣3) D.(0,3)
【考点】关于原点对称的点的坐标.
【专题】平面直角坐标系;推理能力.
【答案】A
【分析】根据关于原点对称的点横、纵坐标互为相反数,进行求解即可.
【解答】解:点(﹣2,3)关于原点的对称点得到的点的坐标(2,﹣3).
故选:A.
【点评】本题主要考查了关于原点对称的点的坐标,关键是掌握关于原点对称点的特点.
9.(2024秋 秦皇岛校级期末)如图,在小正方形网格中,将△ABC绕某一点旋转变换得到△DEF,则旋转中心为( )
A.点M B.点N C.点O D.点P
【考点】旋转的性质.
【专题】作图题;几何直观.
【答案】B
【分析】求出CF的垂直平分线与BE的垂直平分线的交点即可.
【解答】解:CF的垂直平分线ME与BE的垂直平分线CN的交点N即为所求.
故选:B.
【点评】本题主要考查了旋转的性质,解题关键是正确应用旋转的性质.
10.(2024秋 澄海区期末)如图,在平面直角坐标系中有一等边△ABC,其坐标分别为A(0,0),B(2,0),将△ABC绕点B顺时针方向旋转60°,则旋转后C点的坐标为( )
A.(3,1) B. C. D.
【考点】坐标与图形变化﹣旋转;等边三角形的性质.
【专题】平面直角坐标系;平移、旋转与对称;运算能力.
【答案】B
【分析】先过点C作x轴的垂线,求出垂线段的长,进而得出点C的坐标,再结合旋转得出∠ABM=120°,进一步得出CM∥AB,再由CM=2即可解决问题.
【解答】解:令旋转后点C的对应点为M,过点C作x轴的垂线,垂足为N,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∴∠ACN∠ACB=30°.
∵点B的坐标为(2,0),
∴AC=AB=2,
∴AN.
在Rt△ACN中,
CN,
∴点C的坐标为(1,).
由旋转可知,
∠CBM=∠M=60°,CM=AC=2,
∴∠ABM=60°+60°=120°,
∴∠ABM+∠M=180°,
∴CM∥AB,
∴点M的坐标为().
故选:B.
【点评】本题主要考查了坐标与图形变化﹣旋转及等边三角形的性质,熟知等边三角形的性质及图形旋转的性质是解题的关键.
二.填空题(共5小题)
11.(2024秋 泉港区期末)如图,利用两个含30°的全等直角三角板做旋转运动,绕着直角顶点O将其中一块三角板逆时针旋转,使得点C恰好在BD上.若OB=1,则OA= .
【考点】旋转的性质;等边三角形的判定与性质;含30度角的直角三角形;勾股定理.
【专题】平移、旋转与对称;推理能力.
【答案】.
【分析】根据旋转的性质得出OB=OC=1,再根据含30°角的直角三角形的性质得出AC的长,再根据勾股定理即可求解.
【解答】解:∵利用两个含30°的全等直角三角板做旋转运动,绕着直角顶点O将其中一块三角板逆时针旋转,使得点C恰好在BD上,OB=1,
∴OB=OC=1,
∴AC=2OC=2,
∴OA,
故答案为:.
【点评】本题考查了旋转的性质,含30°角的直角三角形的性质,熟记旋转的性质,含30°角的直角三角形的性质是解题的关键.
12.(2024秋 东莞市期末)如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是 60 度.
【考点】旋转的性质;等边三角形的性质.
【专题】平移、旋转与对称;应用意识.
【答案】60.
【分析】根据旋转得到旋转角为∠BAC,根据等边三角形的性质,得到∠BAC=60°,即可.
【解答】解:由题意可得:△ABC是等边三角形,
∴∠BAC=60°;
故答案为:60.
【点评】本题考查旋转的性质,等边三角形的性质,正确记忆相关知识点是解题关键.
13.(2024秋 澄海区期末)如图,将矩形ABCD绕点A旋转至矩形AB'C'D'的位置,此时AC'的中点恰好与D点重合.若,则AB'的长为 6 .
【考点】旋转的性质;矩形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;运算能力;推理能力.
【答案】6.
【分析】由矩形的性质得AD=BC,∠B=90°,由旋转得AD=BC=B′C′=2,∠B′=∠B=90°,因为AC'的中点恰好与D点重合,所以C′D=AD=2,则AC′=2AD=4,求得AB′6,于是得到问题的答案.
【解答】解:∵四边形ABCD是矩形,
∴AD=BC,∠B=90°,
∵将矩形ABCD绕点A旋转得到矩形AB'C'D',B′C′=2,
∴AD=BC=B′C′=2,∠B′=∠B=90°,
∵AC'的中点恰好与D点重合,
∴C′D=AD=2,
∴AC′=2AD=4,
∴AB′6,
故答案为:6.
【点评】此题重点考查矩形的性质、旋转的性质、勾股定理等知识,求得AC′=2AD=4是解题的关键.
14.(2024秋 延边州期末)点(1,2)关于原点的对称点坐标是 (﹣1,﹣2) .
【考点】关于原点对称的点的坐标.
【专题】平移、旋转与对称;运算能力.
【答案】(﹣1,﹣2).
【分析】根据平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),可得答案.
【解答】解:点(1,2)关于原点的对称点坐标是(﹣1,﹣2).
故答案为:(﹣1,﹣2).
【点评】本题考查了关于原点对称的点的坐标,关于原点的对称点,横纵坐标都变成相反数.
15.(2024秋 天津期末)若点P(x,﹣3)与点Q(4,y)关于原点对称,则x+y= ﹣1 .
【考点】关于原点对称的点的坐标.
【专题】常规题型.
【答案】见试题解答内容
【分析】根据关于原点对称的点的坐标特点:两个点关于原点对称时,它们的坐标符号相反可得到x、y的值,再算出x+y即可.
【解答】解:∵点P(x,﹣3)与点Q(4,y) 关于原点对称,
∴x=﹣4,y=3,
故x+y=﹣4+3=﹣1.
故答案为:﹣1.
【点评】此题主要考查了关于原点对称的点的坐标,关键是掌握点的坐标的变化规律.
三.解答题(共5小题)
16.(2024秋 岳麓区校级期末)在平面直角坐标系中,A(a,0),B(0,b),a,b满足,点C与点A关于y轴对称.
(1)请直接写出B,C两点的坐标;
(2)如图1,分别以AB,BC 为直角边向右侧作等腰Rt△BAD 和等腰Rt△BCE,连接DE交x轴于点M,连接BM,求证:BM⊥DE;
(3)如图2,点F为y轴上一动点,点G(m,﹣3m+6)在直线 BC上,若连接E,F,G三点(按逆时针顺序排列)恰好围成一个等腰直角三角形,求符合要求的m的值.
【考点】几何变换综合题.
【专题】三角形.
【答案】(1)B(0,6),C(2,0);(2)见解析;(3)2或4或6.
【分析】(1)根据非负数的性质求出a,b的值,然后轴对称的性质写出点C的坐标即可;
(2)作DN∥CE,交x轴于点N,先证明Rt△BCE≌Rt△BAD,再证明△CME≌△NMD,即可证明DM=ME,再结合BD=BE即可证明BM⊥DE;
(3)作EL⊥x轴于点L,证明△BOC≌△CLE(AAS),证明BO=CL=6,OC=LE=2,得出OL=OC+CL=2+6=8,得出L(8,0),E(8,2);分三种情况:①当∠EGF=90°时,②当∠FEG=90°时,③当∠EFG=90°时,分别求出m的值即可.
【解答】(1)解:∵,
∴a+2=0,b﹣6=0,
∴a=﹣2,b=6,
∴A(﹣2,0),B(0,6),
又∵点C与点A关于y轴对称,
∴C(2,0);
(2)证明:如图1,作DN∥CE,交x轴于点N,则∠ECM=∠DNM,
∵点A、C关于y轴对称,
∴y轴是线段AC的垂直平分线,
∴CB=AB,
∵△BAD与△BCE是等腰直角三角形,
∴CB=CE,AB=AD,∠BCE=∠BAD=90°,
∴△BCE≌△BAD(SAS),
∴CE=AD,BD=BE,
∵∠ECM+∠BCA=90°,∠DAC+∠BAC=90°,且∠BCA=∠BAC,
∴∠ECM=∠DAC,
∴∠DNM=∠DAC,
∴AD=ND,
又∵CE=AD,
∴CE=ND,
∵∠CME=∠NMD,
又∵∠ECM=∠DNM,
∴△CME≌△NMD(AAS),
∴DM=ME,
∵BD=BE,
∴BM⊥DE;
(3)解:∵△BCE是等腰直角三角形,
∴BC=CE,∠CBE=∠CEB=45°,
如图2,作EL⊥x轴于点L,则∠BOC=∠CLE=90°,
∵∠CBO=90°﹣∠OCB=∠ECL,BC=CE,
∴△BOC≌△CLE(AAS),
∴BO=CL=6,OC=LE=2,
∴OL=OC+CL=2+6=8,
∴L(8,0),E(8,2);
①当∠EGF=90°时,如图2,
∵△BCE为等腰直角三角形,点F为y轴上一动点,点G(m,﹣3m+6)在直线BC上,
∴此时点F与点B重合,点G与点C重合,
∴m=2;
②当∠FEG=90°时,点F与点B重合,如图所示:
∵∠CEB=45°,
∴∠CEG=90°﹣45°=45°,
∴∠CEF=∠CEG,
∵EF=GE,
∴BC=CG,
∴点C为B、G的中点,
∴,
解得:m=4;
③当∠EFG=90°时,过点E作EM⊥y轴于点M,过点G作GN⊥y轴于点N,如图所示:
则∠EMF=∠GNF=90°,
∵∠MEF+∠MFE=∠MFE+∠NFG=90°,
∴∠MEF=∠NFG,
∵EF=FG,
∴△EMF≌△FNG(AAS),
∴NF=ME,MF=NG=m,
∵E(8,2),
∴NF=ME=8,OM=2,
∵G(m,﹣3m+6),
∴ON=3m﹣6,
∵ON+OM﹣MF=NF,
∴3m﹣6+2﹣m=8,
解得:m=6;
综上所述,m的值为2或4或6.
【点评】本题属于三角形综合题,考查非负数的性质、全等三角形的判定与性质、等腰三角形的判定与性质、平面直角坐标系、轴对称的性质等知识,解题的关键是正确地作出所需要的辅助线,构造全等三角形,解第(3)题时应注意分类讨论.
17.(2024秋 凉州区期末)△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点A逆时针旋转90°得到△A2B2C2;
③△A1B1C1中顶点A1坐标为 (1,﹣2) .
【考点】作图﹣旋转变换;中心对称.
【专题】几何直观.
【答案】①见解析;
②见解析;
③(1,﹣2).
【分析】①分别找出A、B、C关于原点O的中心对称的对应点A1、B1、C1,再顺次连接对应点A1、B1、C1即可;
②按照旋转角度、旋转方向、旋转中心进行旋转作图即可;
③根据①中图形写出顶点A1坐标即可.
【解答】解:①如图,△A1B1C1即为所求作;
②如图△A2B2C2即为所求作;
③由图知△A1B1C1中顶点A1坐标为(1,﹣2),
故答案为:(1,﹣2).
【点评】本题考查作中心对称图形,旋转作图,写出平面直角坐标系中点的坐标,解题的关键在于熟练掌握相关作图步骤.
18.(2024秋 海曙区期末)如图,长方形纸片ABCD中,E为边AD上一点,F为边CD上一点.AB沿BE折叠得BA′,BC沿BF折叠得BC′(BA′、BC′都在∠ABC的内部),
记∠ABE=α,∠CBF=β,∠A′BC′=γ.
(1)直接写出α=10°,β=20°时,γ= 30° ;α=30°,β=25°时,γ= 20° ;
(2)求γ=10°时,∠EBF的值;
(3)当BA′平分∠EBF时,若,则γ= 或10° .(直接写出结果)
【考点】几何变换综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)30°;20°;
(2)∠EBF=50°或40°;
(3)或10°.
【分析】(1)由折叠可得:∠A′BE=∠ABE=α,∠C′BF=∠CBF=β,则∠ABA′=2∠ABE=2α,∠CBC′=2∠CBF=2β,当α=10°,β=20°时,根据∠A′BC′=∠ABC﹣∠ABA′﹣∠CBC′,即可求解;α=30°,β=25°时,根据∠A′BC′=∠ABA′+∠CBC′﹣∠ABC,即可求解;
(2)分两种情况:当点A′在C′的左侧时,当点A′在C′的右侧时,根据折叠的性质和角的和差求解即可;
(3)由BA′平分∠EBF,可得∠EBF=2∠A′BE=2α,分两种情况:当点A′在C′的左侧时,当点A′在C′的右侧时,根据折叠的性质和角的和差列方程求解即可.
【解答】解:(1)30°;20°;理由如下:
∵长方形纸片ABCD中,E为边AD上一点,F为边CD上一点.AB沿BE折叠得BA′,BC沿BF折叠得BC′(BA′、BC′都在∠ABC的内部),∠ABE=α,∠CBF=β,∠A′BC′=γ,
∴∠A′BE=∠ABE=α,∠C′BF=∠CBF=β,
∴∠ABA′=2∠ABE=2α,∠CBC′=2∠CBF=2β,
当α=10°,β=20°时,
∠A′BC′=∠ABC﹣∠ABA′﹣∠CBC′=90°﹣2α﹣2β=90°﹣2×10°﹣2×20°=30°,
即γ=30°;
当α=30°,β=25°时,
∠A′BC′=∠ABA′+∠CBC′﹣∠ABC=2α+2β﹣90°=2×30°+2×25°﹣90°=20°,
即γ=20°;
故答案为:30°;20°;
(2)当点A′在C′的左侧时,
∠ABA′+∠CBC′=∠ABC﹣∠A′BC′=90°﹣10°=80°,
∵,,
∴2(∠A′BE+∠C′BF)=∠ABA′+∠CBC′=80°,
∴∠A′BE+∠C′BF=40°,
∴∠EBF=∠A′BE+∠C′BF+∠A′BC′=40°+10°=50°;
当点A′在C′的右侧时,
∠ABA′+∠CBC′=∠ABC+∠A′BC′=90°+10°=100°,
∵,,
∴2(∠A′BE+∠C′BF)=∠ABA′+∠CBC′=100°,
∴∠A′BE+∠C′BF=50°,
∴∠EBF=∠A′BE+∠C′BF﹣∠A′BC′=50°﹣10°=40°,
∴∠EBF=50°或40°;
(3)γ或10°;理由如下:
∵BA′平分∠EBF,,
∴∠EBF=2∠A′BE=2α,
当点A′在C′的左侧时,由(2)得:,
∴,
∴,
∴,
解得:;
当点A′在C′的右侧时,由(2)得:,
∴,
∴
∴,
解得:γ=10°;
综上所述,或γ=10°,
故答案为:或10°.
【点评】本题属于几何变换综合题,主要考查了几何图形中的角度计算问题,角平分线的定义,解题的关键是分情况讨论.
19.(2024秋 永春县期末)已知△AOB和△MON都是等腰直角三角形,∠AOB=∠MON=90°.
(1)如图1,连接AM,BN,求证:△AOM≌∠△BON;
(2)如图2,将△AOB绕点0逆时针旋转,当点A,B,M三点共线时,若OB=5,AM=3,求出线段OM的长;
(3)如图3,将△AOB绕点O继续逆时针旋转,若点A恰好落在MN边上时,AB与ON交点为C,求证:AC2+BC2=2CO2.
【考点】几何变换综合题.
【专题】几何综合题;三角形;图形的全等;等腰三角形与直角三角形;几何直观;运算能力;推理能力.
【答案】(1)证明见解答;
(2);
(3)证明见解答.
【分析】(1)根等腰直角三角形的性质即可得证;
(2)证明△AOM≌△BON(SAS),利用勾股定理即可解答;
(3)在OM上取点E,使得OE=OC,连接AE、CE,证明△AOE≌△BOC(SAS),利用勾股定理即可得证.
【解答】(1)证明:∵△AOB,△MON都是等腰直角三角形,∠AOB=∠MON=90°,
∴AO=OB,OM=ON,
∴△AOM≌△BON(SAS);
(2)解:如图,
∵∠MON=∠1+∠2=90°,∠AOB=∠2+∠3=90°,
∴∠1=∠3,
又∵OA=OB,OM=ON,
∴△AOM≌△BON(SAS),
∴,
在Rt△OAB中,∠AOB=90°,OA=OB=5,
∴,
∴,∠NBO=∠MAO=180°﹣∠4=135°,
∴∠NBM=∠NBO﹣∠ABO=135°﹣45°=90°,
∴,
在Rt△MON中,∠MON=90°,OM=ON,
∴OM2+ON2=MN2,
∴OM2=146,
∴;
(3)证明:如图,在OM上取点E,使得OE=OC,连接AE、CE,
∵AO=OB,∠AOB=∠MON=90°,
∴∠OAB=∠B=45°,
∵∠AOB=∠MON=90°,
∴∠AOE=∠BOC,
又∵AO=OB,OE=OC,
∴△AOE≌△BOC(SAS),
∴∠EAO=∠B=45°,
∴∠EAB=∠EAO+∠OAB=90°,
∴AC2+BC2=AC2+AE2=CE2,
又∵CE2=OE2+OC2=2OC2,
∴AC2+BC2=2CO2.
【点评】本题考查几何变换的综合应用,主要考查旋转的性质,等腰直角三角形的性质,全等三角形的性质与判定,掌握旋转的性质,等腰直角三角形的性质,全等三角形的性质与判定是解题的关键.
20.(2024秋 哈尔滨期末)【探究发现】
如图1,EF∥BC,点A在EF,BC之间,连接AE,AB.求证:∠A+∠AEF+∠ABC=360°.
【学以致用】
哈尔滨某商场地下车库出口处安装了“两段式栏杆”,如图2所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF升起到如图3所示的位置,其示意图如图4所示(AB⊥BC,EF∥BC,栏杆宽度忽略不计),已知∠AEE=150°,填空:∠BAE= 120 度.
【拓展应用】
如图5,已知GF∥BC,点E在GF上,点A在GF,BC之间,AD⊥AE交BC于点D,过点A作AB⊥CD于点B,AH平分∠BAD,AC平分∠EAB,若∠AEC+∠GEC=180°,∠ACE=3∠BAH,求∠GEA的度数.
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】【探究发现】证明见解析;
【学以致用】120;
【拓展应用】30°.
【分析】【探究发现】过点A作AK∥EF,根据两直线平行,同旁内角互补解答即可;
【学以致用】根据【探究发现】的结论解答即可;
【拓展应用】过点A作AM∥BC,根据平行线的判定与性质解答即可.
【解答】【探究发现】证明:如图1,过点A作AK∥EF,
∵AK∥EF,
∴∠AEF+∠EAK=180°,
∵EF∥BC,AK∥EF,
∴AK∥BC.
∴∠ABC+∠KAB=180°,
∴∠AEF+∠EAK+∠ABC+∠KAB=360°,
即∠A+∠AEF+∠ABC=360°;
【学以致用】解:由∠A+∠AEF+∠ABC=360°;
∴∠BAE=360°﹣90°﹣150°=120°,
故答案为:120;
【拓展应用】解:∵AD⊥AE,
∴∠DAE=90°.
∵AH平分∠BAD,
∴∠BAH=∠HAD∠ACE=3∠BAH=3α,
∴∠BAC=2α+β,
∵AC平分∠BAE,
∴∠EAC=∠BAC=2α+β,
∴∠DAE=∠DAC+∠CAE=2α+2β=90°,
∴∠HAC=α+β=45°,
∵AB⊥BC,
∴∠ABC=90°,
过点A作AM∥BC,如图5,
∴∠ABC+∠BAM=180°,
∴∠BAM=90°,
∴∠MAC=∠BAM﹣∠BAC=90°﹣(2α+β)=45°﹣α,∠MAD=∠MAB﹣∠BAD=90°﹣2α,
∴∠EAM=∠EAD=∠MAD=2α,
∵GF∥BC,AM∥BC,
∴AM∥GF,
∴∠GEA=∠EAM=2α,
∴∠AEF=180°﹣2a,
∵∠AEC+∠GEC=180°,∠GEC+∠CEF=180°,
∴,
∵AM∥BC,
∴∠ACB=∠MAC=45°﹣α,
∴∠ECB=∠ECA+∠ACB=3α+45°﹣α=2α+45°,
∵GF∥BC,
∴∠FEC=∠ECB,
∴2α+45°=90°﹣a.
∴∠a=15°,
∴∠GEA=2a=30°.
【点评】本题是几何变换综合题,考查了平行线的判定与选择,难度适中.关键是通过作辅助线,构造平行线,把实际问题转化为数学问题加以计算.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 本溪期末)2024年7月27日,第33届夏季奥运会在法国巴黎举行,如图所示巴黎奥运会项目图标中,是中心对称图形的是( )
A. B.
C. D.
2.(2024秋 泰兴市期末)如图,△ABC绕点B旋转得到△EBD,A,B,D三点在同一条直线上,且AD=5,BE=2,则BC的长为( )
A.1 B.2 C.3 D.4
3.(2024秋 天津期末)如图,若点D是等边三角形ABC的边BC上任意一点,将△ADC绕点A顺时针旋转得到△AEB,连接ED,则下列结论一定正确的是( )
A.AB⊥ED B.∠BDE=30° C.ED=AD D.BE∥AD
4.(2024秋 河西区期末)如图,在△ABC中,∠BAC=90°,AB=AC.点D在BC上,连接AD,将线段AD绕点A顺时针旋转90°得到线段AE,连接BE,DE,则下列结论一定正确的是( )
A.∠EBC=∠BAC B.AD=AC C.∠AEB=∠ABE D.BA=BE
5.(2024秋 丰都县期末)如图,△ABC中,∠ABC=45°,将△ABC绕点B逆时针旋转60°得到△DBE,点A、C的对应点分别为D、E,延长CA交DE于点F,下列结论错误的是( )
A.∠BED=30° B.∠DBE=45° C.∠ABD=60° D.∠CBE=60°
6.(2024秋 江汉区期末)如图,在△ABC中,AB=AC,∠BAC=40°,AD⊥BC于D.△ABC绕点B逆时针旋转得到△FBE,点C的对应点E落在AD上,则∠CBF的度数是( )
A.140° B.130° C.120° D.110°
7.(2024秋 澄海区期末)如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A'是对称点 B.BO=B'O
C.AB=A'B' D.∠ACB=∠C'A'B'
8.(2024秋 肇庆期末)在直角坐标系中,点(﹣2,3)关于原点的对称点的坐标是( )
A.(2,﹣3) B.(﹣2,3) C.(0,﹣3) D.(0,3)
9.(2024秋 秦皇岛校级期末)如图,在小正方形网格中,将△ABC绕某一点旋转变换得到△DEF,则旋转中心为( )
A.点M B.点N C.点O D.点P
10.(2024秋 澄海区期末)如图,在平面直角坐标系中有一等边△ABC,其坐标分别为A(0,0),B(2,0),将△ABC绕点B顺时针方向旋转60°,则旋转后C点的坐标为( )
A.(3,1) B. C. D.
二.填空题(共5小题)
11.(2024秋 泉港区期末)如图,利用两个含30°的全等直角三角板做旋转运动,绕着直角顶点O将其中一块三角板逆时针旋转,使得点C恰好在BD上.若OB=1,则OA= .
12.(2024秋 东莞市期末)如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是 度.
13.(2024秋 澄海区期末)如图,将矩形ABCD绕点A旋转至矩形AB'C'D'的位置,此时AC'的中点恰好与D点重合.若,则AB'的长为 .
14.(2024秋 延边州期末)点(1,2)关于原点的对称点坐标是 .
15.(2024秋 天津期末)若点P(x,﹣3)与点Q(4,y)关于原点对称,则x+y= .
三.解答题(共5小题)
16.(2024秋 岳麓区校级期末)在平面直角坐标系中,A(a,0),B(0,b),a,b满足,点C与点A关于y轴对称.
(1)请直接写出B,C两点的坐标;
(2)如图1,分别以AB,BC 为直角边向右侧作等腰Rt△BAD 和等腰Rt△BCE,连接DE交x轴于点M,连接BM,求证:BM⊥DE;
(3)如图2,点F为y轴上一动点,点G(m,﹣3m+6)在直线 BC上,若连接E,F,G三点(按逆时针顺序排列)恰好围成一个等腰直角三角形,求符合要求的m的值.
17.(2024秋 凉州区期末)△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点A逆时针旋转90°得到△A2B2C2;
③△A1B1C1中顶点A1坐标为 .
18.(2024秋 海曙区期末)如图,长方形纸片ABCD中,E为边AD上一点,F为边CD上一点.AB沿BE折叠得BA′,BC沿BF折叠得BC′(BA′、BC′都在∠ABC的内部),
记∠ABE=α,∠CBF=β,∠A′BC′=γ.
(1)直接写出α=10°,β=20°时,γ= ;α=30°,β=25°时,γ= ;
(2)求γ=10°时,∠EBF的值;
(3)当BA′平分∠EBF时,若,则γ= .(直接写出结果)
19.(2024秋 永春县期末)已知△AOB和△MON都是等腰直角三角形,∠AOB=∠MON=90°.
(1)如图1,连接AM,BN,求证:△AOM≌∠△BON;
(2)如图2,将△AOB绕点0逆时针旋转,当点A,B,M三点共线时,若OB=5,AM=3,求出线段OM的长;
(3)如图3,将△AOB绕点O继续逆时针旋转,若点A恰好落在MN边上时,AB与ON交点为C,求证:AC2+BC2=2CO2.
20.(2024秋 哈尔滨期末)【探究发现】
如图1,EF∥BC,点A在EF,BC之间,连接AE,AB.求证:∠A+∠AEF+∠ABC=360°.
【学以致用】
哈尔滨某商场地下车库出口处安装了“两段式栏杆”,如图2所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF升起到如图3所示的位置,其示意图如图4所示(AB⊥BC,EF∥BC,栏杆宽度忽略不计),已知∠AEE=150°,填空:∠BAE= 度.
【拓展应用】
如图5,已知GF∥BC,点E在GF上,点A在GF,BC之间,AD⊥AE交BC于点D,过点A作AB⊥CD于点B,AH平分∠BAD,AC平分∠EAB,若∠AEC+∠GEC=180°,∠ACE=3∠BAH,求∠GEA的度数.
2025年中考数学高频易错考前冲刺:图形的旋转
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C A A B D A B B
一.选择题(共10小题)
1.(2024秋 本溪期末)2024年7月27日,第33届夏季奥运会在法国巴黎举行,如图所示巴黎奥运会项目图标中,是中心对称图形的是( )
A.
B.
C.
D.
【考点】中心对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】根据中心对称图形的定义逐项判断即可.
【解答】解:A、图形是中心对称图形,符合题意;
B、图形不是中心对称图形,不符合题意;
C、图形不是中心对称图形,不符合题意;
D、图形不是中心对称图形,不符合题意,
故选:A.
【点评】本题主要考查了中心对称图形的定义,熟知将一个图形绕某点旋转180°,能与本身重合的图形,这样的图形称为中心对称图形是解题的关键.
2.(2024秋 泰兴市期末)如图,△ABC绕点B旋转得到△EBD,A,B,D三点在同一条直线上,且AD=5,BE=2,则BC的长为( )
A.1 B.2 C.3 D.4
【考点】旋转的性质.
【专题】平移、旋转与对称;运算能力.
【答案】C
【分析】由旋转的性质可得AB=BE=2,BC=BD,再根据线段的和差即可解答.
【解答】解:由题意可得:AB=BE=2,BC=BD,
∵AD=5,BE=2,
∴BD=AD﹣AB=AD﹣BE=5﹣2=3,
∴BC=BD=3.
故选:C.
【点评】本题主要考查了旋转的性质、线段的和差等知识点,熟练掌握旋转的性质是解题的关键.
3.(2024秋 天津期末)如图,若点D是等边三角形ABC的边BC上任意一点,将△ADC绕点A顺时针旋转得到△AEB,连接ED,则下列结论一定正确的是( )
A.AB⊥ED B.∠BDE=30° C.ED=AD D.BE∥AD
【考点】旋转的性质;全等三角形的判定与性质;等边三角形的性质.
【专题】平移、旋转与对称;推理能力.
【答案】C
【分析】根据旋转的性质得出AD=AE,∠CAD=∠BAE,证明三角形ADE是等边三角形即可得出结论.
【解答】解:∵将△ADC绕点A顺时针旋转得到△AEB,△ABC是等边三角形,
∴AD=AE,∠CAD=∠BAE,
∴∠DAE=∠CAB=60°,
∴△DAE是等边三角形,
∴ED=AD,
故选项C正确;
由已知条件无法证明A、B、D正确,
故选:C.
【点评】本题主要考查了旋转的性质,熟记旋转的性质是解题的关键.
4.(2024秋 河西区期末)如图,在△ABC中,∠BAC=90°,AB=AC.点D在BC上,连接AD,将线段AD绕点A顺时针旋转90°得到线段AE,连接BE,DE,则下列结论一定正确的是( )
A.∠EBC=∠BAC B.AD=AC C.∠AEB=∠ABE D.BA=BE
【考点】旋转的性质;全等三角形的判定与性质;等腰直角三角形.
【专题】图形的全等;平移、旋转与对称;推理能力.
【答案】A
【分析】证明△AEB≌△ADC(SAS),得出∠ABE=∠C,可得出结论.
【解答】解:∵将线段AD绕点A顺时针旋转90°得到线段AE,
∴AD=AE,∠DAE=90°,
又∵∠BAC=90°,
∴∠EAB+∠BAD=∠BAD+∠DAC,
∴∠EAB=∠DAC,
又∵AB=AC,
∴△AEB≌△ADC(SAS),
∴∠ABE=∠C,
∵∠BAC=90°,AB=AC,
∴∠ABE=∠ABC=∠C=45°,
∴∠EBC=∠BAC=90°,
故选项A一定正确,
由已知条件无法一定得出B、C、D正确,
故选:A.
【点评】本题考查了旋转的性质,全等三角形的判定与性质,熟记旋转的性质,全等三角形的判定与性质是解题的关键.
5.(2024秋 丰都县期末)如图,△ABC中,∠ABC=45°,将△ABC绕点B逆时针旋转60°得到△DBE,点A、C的对应点分别为D、E,延长CA交DE于点F,下列结论错误的是( )
A.∠BED=30° B.∠DBE=45° C.∠ABD=60° D.∠CBE=60°
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】直接根据旋转的性质逐一判断即可.
【解答】解:∵△ABC中,∠ABC=45°,将△ABC绕点B逆时针旋转60°得到△DBE,
∴∠DBE=∠ABC=45°,∠ABD=∠CBE=60°,
故选项B、C、D正确,
由已知条件无法得出∠BED=30°,
故选项A错误,
故选:A.
【点评】本题考查了旋转的性质,熟记旋转前后对应角相等是解题的关键.
6.(2024秋 江汉区期末)如图,在△ABC中,AB=AC,∠BAC=40°,AD⊥BC于D.△ABC绕点B逆时针旋转得到△FBE,点C的对应点E落在AD上,则∠CBF的度数是( )
A.140° B.130° C.120° D.110°
【考点】旋转的性质;等腰三角形的性质.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】连接CE,如图,根据等腰三角形的性质得到AD垂直平分BC,根据等腰三角形的性质和三角形内角和定理可计算出∠ABC=∠ACB=70°,再根据旋转的性质得到BE=BC,∠FBE=∠ABC=70°,则可判断△BCE为等边三角形,所以∠CBE=60°,然后计算∠CBE+∠FBE即可.
【解答】解:连接CE,如图,
∵AB=AC,
∴∠ABC=∠ACB(180°﹣∠BAC)(180°﹣40°)=70°,
∵AD⊥BC,
∴BD=CD,
即AD垂直平分BC,
∴BE=CE,
∵△ABC绕点B逆时针旋转得到△FBE,点C的对应点E落在AD上,
∴BE=BC,∠FBE=∠ABC=70°,
∵BE=CE=BC,
∴△BCE为等边三角形,
∴∠CBE=60°,
∴∠CBF=∠CBE+∠FBE=60°+70°=130°.
故选:B.
【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质.
7.(2024秋 澄海区期末)如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A'是对称点 B.BO=B'O
C.AB=A'B' D.∠ACB=∠C'A'B'
【考点】中心对称.
【专题】平移、旋转与对称;应用意识.
【答案】D
【分析】利用中心对称的性质一一判断即可.
【解答】解:∵△ABC与△A'B'C'关于点O成中心对称,
∴点A与点A'是对称点,BO=B'O,AB=A'B',
∴A,B,C正确,
故选:D.
【点评】本题考查中心对称,解题的关键是理解中心对称的性质,属于中考常考题型.
8.(2024秋 肇庆期末)在直角坐标系中,点(﹣2,3)关于原点的对称点的坐标是( )
A.(2,﹣3) B.(﹣2,3) C.(0,﹣3) D.(0,3)
【考点】关于原点对称的点的坐标.
【专题】平面直角坐标系;推理能力.
【答案】A
【分析】根据关于原点对称的点横、纵坐标互为相反数,进行求解即可.
【解答】解:点(﹣2,3)关于原点的对称点得到的点的坐标(2,﹣3).
故选:A.
【点评】本题主要考查了关于原点对称的点的坐标,关键是掌握关于原点对称点的特点.
9.(2024秋 秦皇岛校级期末)如图,在小正方形网格中,将△ABC绕某一点旋转变换得到△DEF,则旋转中心为( )
A.点M B.点N C.点O D.点P
【考点】旋转的性质.
【专题】作图题;几何直观.
【答案】B
【分析】求出CF的垂直平分线与BE的垂直平分线的交点即可.
【解答】解:CF的垂直平分线ME与BE的垂直平分线CN的交点N即为所求.
故选:B.
【点评】本题主要考查了旋转的性质,解题关键是正确应用旋转的性质.
10.(2024秋 澄海区期末)如图,在平面直角坐标系中有一等边△ABC,其坐标分别为A(0,0),B(2,0),将△ABC绕点B顺时针方向旋转60°,则旋转后C点的坐标为( )
A.(3,1) B. C. D.
【考点】坐标与图形变化﹣旋转;等边三角形的性质.
【专题】平面直角坐标系;平移、旋转与对称;运算能力.
【答案】B
【分析】先过点C作x轴的垂线,求出垂线段的长,进而得出点C的坐标,再结合旋转得出∠ABM=120°,进一步得出CM∥AB,再由CM=2即可解决问题.
【解答】解:令旋转后点C的对应点为M,过点C作x轴的垂线,垂足为N,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∴∠ACN∠ACB=30°.
∵点B的坐标为(2,0),
∴AC=AB=2,
∴AN.
在Rt△ACN中,
CN,
∴点C的坐标为(1,).
由旋转可知,
∠CBM=∠M=60°,CM=AC=2,
∴∠ABM=60°+60°=120°,
∴∠ABM+∠M=180°,
∴CM∥AB,
∴点M的坐标为().
故选:B.
【点评】本题主要考查了坐标与图形变化﹣旋转及等边三角形的性质,熟知等边三角形的性质及图形旋转的性质是解题的关键.
二.填空题(共5小题)
11.(2024秋 泉港区期末)如图,利用两个含30°的全等直角三角板做旋转运动,绕着直角顶点O将其中一块三角板逆时针旋转,使得点C恰好在BD上.若OB=1,则OA= .
【考点】旋转的性质;等边三角形的判定与性质;含30度角的直角三角形;勾股定理.
【专题】平移、旋转与对称;推理能力.
【答案】.
【分析】根据旋转的性质得出OB=OC=1,再根据含30°角的直角三角形的性质得出AC的长,再根据勾股定理即可求解.
【解答】解:∵利用两个含30°的全等直角三角板做旋转运动,绕着直角顶点O将其中一块三角板逆时针旋转,使得点C恰好在BD上,OB=1,
∴OB=OC=1,
∴AC=2OC=2,
∴OA,
故答案为:.
【点评】本题考查了旋转的性质,含30°角的直角三角形的性质,熟记旋转的性质,含30°角的直角三角形的性质是解题的关键.
12.(2024秋 东莞市期末)如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是 60 度.
【考点】旋转的性质;等边三角形的性质.
【专题】平移、旋转与对称;应用意识.
【答案】60.
【分析】根据旋转得到旋转角为∠BAC,根据等边三角形的性质,得到∠BAC=60°,即可.
【解答】解:由题意可得:△ABC是等边三角形,
∴∠BAC=60°;
故答案为:60.
【点评】本题考查旋转的性质,等边三角形的性质,正确记忆相关知识点是解题关键.
13.(2024秋 澄海区期末)如图,将矩形ABCD绕点A旋转至矩形AB'C'D'的位置,此时AC'的中点恰好与D点重合.若,则AB'的长为 6 .
【考点】旋转的性质;矩形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;运算能力;推理能力.
【答案】6.
【分析】由矩形的性质得AD=BC,∠B=90°,由旋转得AD=BC=B′C′=2,∠B′=∠B=90°,因为AC'的中点恰好与D点重合,所以C′D=AD=2,则AC′=2AD=4,求得AB′6,于是得到问题的答案.
【解答】解:∵四边形ABCD是矩形,
∴AD=BC,∠B=90°,
∵将矩形ABCD绕点A旋转得到矩形AB'C'D',B′C′=2,
∴AD=BC=B′C′=2,∠B′=∠B=90°,
∵AC'的中点恰好与D点重合,
∴C′D=AD=2,
∴AC′=2AD=4,
∴AB′6,
故答案为:6.
【点评】此题重点考查矩形的性质、旋转的性质、勾股定理等知识,求得AC′=2AD=4是解题的关键.
14.(2024秋 延边州期末)点(1,2)关于原点的对称点坐标是 (﹣1,﹣2) .
【考点】关于原点对称的点的坐标.
【专题】平移、旋转与对称;运算能力.
【答案】(﹣1,﹣2).
【分析】根据平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),可得答案.
【解答】解:点(1,2)关于原点的对称点坐标是(﹣1,﹣2).
故答案为:(﹣1,﹣2).
【点评】本题考查了关于原点对称的点的坐标,关于原点的对称点,横纵坐标都变成相反数.
15.(2024秋 天津期末)若点P(x,﹣3)与点Q(4,y)关于原点对称,则x+y= ﹣1 .
【考点】关于原点对称的点的坐标.
【专题】常规题型.
【答案】见试题解答内容
【分析】根据关于原点对称的点的坐标特点:两个点关于原点对称时,它们的坐标符号相反可得到x、y的值,再算出x+y即可.
【解答】解:∵点P(x,﹣3)与点Q(4,y) 关于原点对称,
∴x=﹣4,y=3,
故x+y=﹣4+3=﹣1.
故答案为:﹣1.
【点评】此题主要考查了关于原点对称的点的坐标,关键是掌握点的坐标的变化规律.
三.解答题(共5小题)
16.(2024秋 岳麓区校级期末)在平面直角坐标系中,A(a,0),B(0,b),a,b满足,点C与点A关于y轴对称.
(1)请直接写出B,C两点的坐标;
(2)如图1,分别以AB,BC 为直角边向右侧作等腰Rt△BAD 和等腰Rt△BCE,连接DE交x轴于点M,连接BM,求证:BM⊥DE;
(3)如图2,点F为y轴上一动点,点G(m,﹣3m+6)在直线 BC上,若连接E,F,G三点(按逆时针顺序排列)恰好围成一个等腰直角三角形,求符合要求的m的值.
【考点】几何变换综合题.
【专题】三角形.
【答案】(1)B(0,6),C(2,0);(2)见解析;(3)2或4或6.
【分析】(1)根据非负数的性质求出a,b的值,然后轴对称的性质写出点C的坐标即可;
(2)作DN∥CE,交x轴于点N,先证明Rt△BCE≌Rt△BAD,再证明△CME≌△NMD,即可证明DM=ME,再结合BD=BE即可证明BM⊥DE;
(3)作EL⊥x轴于点L,证明△BOC≌△CLE(AAS),证明BO=CL=6,OC=LE=2,得出OL=OC+CL=2+6=8,得出L(8,0),E(8,2);分三种情况:①当∠EGF=90°时,②当∠FEG=90°时,③当∠EFG=90°时,分别求出m的值即可.
【解答】(1)解:∵,
∴a+2=0,b﹣6=0,
∴a=﹣2,b=6,
∴A(﹣2,0),B(0,6),
又∵点C与点A关于y轴对称,
∴C(2,0);
(2)证明:如图1,作DN∥CE,交x轴于点N,则∠ECM=∠DNM,
∵点A、C关于y轴对称,
∴y轴是线段AC的垂直平分线,
∴CB=AB,
∵△BAD与△BCE是等腰直角三角形,
∴CB=CE,AB=AD,∠BCE=∠BAD=90°,
∴△BCE≌△BAD(SAS),
∴CE=AD,BD=BE,
∵∠ECM+∠BCA=90°,∠DAC+∠BAC=90°,且∠BCA=∠BAC,
∴∠ECM=∠DAC,
∴∠DNM=∠DAC,
∴AD=ND,
又∵CE=AD,
∴CE=ND,
∵∠CME=∠NMD,
又∵∠ECM=∠DNM,
∴△CME≌△NMD(AAS),
∴DM=ME,
∵BD=BE,
∴BM⊥DE;
(3)解:∵△BCE是等腰直角三角形,
∴BC=CE,∠CBE=∠CEB=45°,
如图2,作EL⊥x轴于点L,则∠BOC=∠CLE=90°,
∵∠CBO=90°﹣∠OCB=∠ECL,BC=CE,
∴△BOC≌△CLE(AAS),
∴BO=CL=6,OC=LE=2,
∴OL=OC+CL=2+6=8,
∴L(8,0),E(8,2);
①当∠EGF=90°时,如图2,
∵△BCE为等腰直角三角形,点F为y轴上一动点,点G(m,﹣3m+6)在直线BC上,
∴此时点F与点B重合,点G与点C重合,
∴m=2;
②当∠FEG=90°时,点F与点B重合,如图所示:
∵∠CEB=45°,
∴∠CEG=90°﹣45°=45°,
∴∠CEF=∠CEG,
∵EF=GE,
∴BC=CG,
∴点C为B、G的中点,
∴,
解得:m=4;
③当∠EFG=90°时,过点E作EM⊥y轴于点M,过点G作GN⊥y轴于点N,如图所示:
则∠EMF=∠GNF=90°,
∵∠MEF+∠MFE=∠MFE+∠NFG=90°,
∴∠MEF=∠NFG,
∵EF=FG,
∴△EMF≌△FNG(AAS),
∴NF=ME,MF=NG=m,
∵E(8,2),
∴NF=ME=8,OM=2,
∵G(m,﹣3m+6),
∴ON=3m﹣6,
∵ON+OM﹣MF=NF,
∴3m﹣6+2﹣m=8,
解得:m=6;
综上所述,m的值为2或4或6.
【点评】本题属于三角形综合题,考查非负数的性质、全等三角形的判定与性质、等腰三角形的判定与性质、平面直角坐标系、轴对称的性质等知识,解题的关键是正确地作出所需要的辅助线,构造全等三角形,解第(3)题时应注意分类讨论.
17.(2024秋 凉州区期末)△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点A逆时针旋转90°得到△A2B2C2;
③△A1B1C1中顶点A1坐标为 (1,﹣2) .
【考点】作图﹣旋转变换;中心对称.
【专题】几何直观.
【答案】①见解析;
②见解析;
③(1,﹣2).
【分析】①分别找出A、B、C关于原点O的中心对称的对应点A1、B1、C1,再顺次连接对应点A1、B1、C1即可;
②按照旋转角度、旋转方向、旋转中心进行旋转作图即可;
③根据①中图形写出顶点A1坐标即可.
【解答】解:①如图,△A1B1C1即为所求作;
②如图△A2B2C2即为所求作;
③由图知△A1B1C1中顶点A1坐标为(1,﹣2),
故答案为:(1,﹣2).
【点评】本题考查作中心对称图形,旋转作图,写出平面直角坐标系中点的坐标,解题的关键在于熟练掌握相关作图步骤.
18.(2024秋 海曙区期末)如图,长方形纸片ABCD中,E为边AD上一点,F为边CD上一点.AB沿BE折叠得BA′,BC沿BF折叠得BC′(BA′、BC′都在∠ABC的内部),
记∠ABE=α,∠CBF=β,∠A′BC′=γ.
(1)直接写出α=10°,β=20°时,γ= 30° ;α=30°,β=25°时,γ= 20° ;
(2)求γ=10°时,∠EBF的值;
(3)当BA′平分∠EBF时,若,则γ= 或10° .(直接写出结果)
【考点】几何变换综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)30°;20°;
(2)∠EBF=50°或40°;
(3)或10°.
【分析】(1)由折叠可得:∠A′BE=∠ABE=α,∠C′BF=∠CBF=β,则∠ABA′=2∠ABE=2α,∠CBC′=2∠CBF=2β,当α=10°,β=20°时,根据∠A′BC′=∠ABC﹣∠ABA′﹣∠CBC′,即可求解;α=30°,β=25°时,根据∠A′BC′=∠ABA′+∠CBC′﹣∠ABC,即可求解;
(2)分两种情况:当点A′在C′的左侧时,当点A′在C′的右侧时,根据折叠的性质和角的和差求解即可;
(3)由BA′平分∠EBF,可得∠EBF=2∠A′BE=2α,分两种情况:当点A′在C′的左侧时,当点A′在C′的右侧时,根据折叠的性质和角的和差列方程求解即可.
【解答】解:(1)30°;20°;理由如下:
∵长方形纸片ABCD中,E为边AD上一点,F为边CD上一点.AB沿BE折叠得BA′,BC沿BF折叠得BC′(BA′、BC′都在∠ABC的内部),∠ABE=α,∠CBF=β,∠A′BC′=γ,
∴∠A′BE=∠ABE=α,∠C′BF=∠CBF=β,
∴∠ABA′=2∠ABE=2α,∠CBC′=2∠CBF=2β,
当α=10°,β=20°时,
∠A′BC′=∠ABC﹣∠ABA′﹣∠CBC′=90°﹣2α﹣2β=90°﹣2×10°﹣2×20°=30°,
即γ=30°;
当α=30°,β=25°时,
∠A′BC′=∠ABA′+∠CBC′﹣∠ABC=2α+2β﹣90°=2×30°+2×25°﹣90°=20°,
即γ=20°;
故答案为:30°;20°;
(2)当点A′在C′的左侧时,
∠ABA′+∠CBC′=∠ABC﹣∠A′BC′=90°﹣10°=80°,
∵,,
∴2(∠A′BE+∠C′BF)=∠ABA′+∠CBC′=80°,
∴∠A′BE+∠C′BF=40°,
∴∠EBF=∠A′BE+∠C′BF+∠A′BC′=40°+10°=50°;
当点A′在C′的右侧时,
∠ABA′+∠CBC′=∠ABC+∠A′BC′=90°+10°=100°,
∵,,
∴2(∠A′BE+∠C′BF)=∠ABA′+∠CBC′=100°,
∴∠A′BE+∠C′BF=50°,
∴∠EBF=∠A′BE+∠C′BF﹣∠A′BC′=50°﹣10°=40°,
∴∠EBF=50°或40°;
(3)γ或10°;理由如下:
∵BA′平分∠EBF,,
∴∠EBF=2∠A′BE=2α,
当点A′在C′的左侧时,由(2)得:,
∴,
∴,
∴,
解得:;
当点A′在C′的右侧时,由(2)得:,
∴,
∴
∴,
解得:γ=10°;
综上所述,或γ=10°,
故答案为:或10°.
【点评】本题属于几何变换综合题,主要考查了几何图形中的角度计算问题,角平分线的定义,解题的关键是分情况讨论.
19.(2024秋 永春县期末)已知△AOB和△MON都是等腰直角三角形,∠AOB=∠MON=90°.
(1)如图1,连接AM,BN,求证:△AOM≌∠△BON;
(2)如图2,将△AOB绕点0逆时针旋转,当点A,B,M三点共线时,若OB=5,AM=3,求出线段OM的长;
(3)如图3,将△AOB绕点O继续逆时针旋转,若点A恰好落在MN边上时,AB与ON交点为C,求证:AC2+BC2=2CO2.
【考点】几何变换综合题.
【专题】几何综合题;三角形;图形的全等;等腰三角形与直角三角形;几何直观;运算能力;推理能力.
【答案】(1)证明见解答;
(2);
(3)证明见解答.
【分析】(1)根等腰直角三角形的性质即可得证;
(2)证明△AOM≌△BON(SAS),利用勾股定理即可解答;
(3)在OM上取点E,使得OE=OC,连接AE、CE,证明△AOE≌△BOC(SAS),利用勾股定理即可得证.
【解答】(1)证明:∵△AOB,△MON都是等腰直角三角形,∠AOB=∠MON=90°,
∴AO=OB,OM=ON,
∴△AOM≌△BON(SAS);
(2)解:如图,
∵∠MON=∠1+∠2=90°,∠AOB=∠2+∠3=90°,
∴∠1=∠3,
又∵OA=OB,OM=ON,
∴△AOM≌△BON(SAS),
∴,
在Rt△OAB中,∠AOB=90°,OA=OB=5,
∴,
∴,∠NBO=∠MAO=180°﹣∠4=135°,
∴∠NBM=∠NBO﹣∠ABO=135°﹣45°=90°,
∴,
在Rt△MON中,∠MON=90°,OM=ON,
∴OM2+ON2=MN2,
∴OM2=146,
∴;
(3)证明:如图,在OM上取点E,使得OE=OC,连接AE、CE,
∵AO=OB,∠AOB=∠MON=90°,
∴∠OAB=∠B=45°,
∵∠AOB=∠MON=90°,
∴∠AOE=∠BOC,
又∵AO=OB,OE=OC,
∴△AOE≌△BOC(SAS),
∴∠EAO=∠B=45°,
∴∠EAB=∠EAO+∠OAB=90°,
∴AC2+BC2=AC2+AE2=CE2,
又∵CE2=OE2+OC2=2OC2,
∴AC2+BC2=2CO2.
【点评】本题考查几何变换的综合应用,主要考查旋转的性质,等腰直角三角形的性质,全等三角形的性质与判定,掌握旋转的性质,等腰直角三角形的性质,全等三角形的性质与判定是解题的关键.
20.(2024秋 哈尔滨期末)【探究发现】
如图1,EF∥BC,点A在EF,BC之间,连接AE,AB.求证:∠A+∠AEF+∠ABC=360°.
【学以致用】
哈尔滨某商场地下车库出口处安装了“两段式栏杆”,如图2所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF升起到如图3所示的位置,其示意图如图4所示(AB⊥BC,EF∥BC,栏杆宽度忽略不计),已知∠AEE=150°,填空:∠BAE= 120 度.
【拓展应用】
如图5,已知GF∥BC,点E在GF上,点A在GF,BC之间,AD⊥AE交BC于点D,过点A作AB⊥CD于点B,AH平分∠BAD,AC平分∠EAB,若∠AEC+∠GEC=180°,∠ACE=3∠BAH,求∠GEA的度数.
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】【探究发现】证明见解析;
【学以致用】120;
【拓展应用】30°.
【分析】【探究发现】过点A作AK∥EF,根据两直线平行,同旁内角互补解答即可;
【学以致用】根据【探究发现】的结论解答即可;
【拓展应用】过点A作AM∥BC,根据平行线的判定与性质解答即可.
【解答】【探究发现】证明:如图1,过点A作AK∥EF,
∵AK∥EF,
∴∠AEF+∠EAK=180°,
∵EF∥BC,AK∥EF,
∴AK∥BC.
∴∠ABC+∠KAB=180°,
∴∠AEF+∠EAK+∠ABC+∠KAB=360°,
即∠A+∠AEF+∠ABC=360°;
【学以致用】解:由∠A+∠AEF+∠ABC=360°;
∴∠BAE=360°﹣90°﹣150°=120°,
故答案为:120;
【拓展应用】解:∵AD⊥AE,
∴∠DAE=90°.
∵AH平分∠BAD,
∴∠BAH=∠HAD∠ACE=3∠BAH=3α,
∴∠BAC=2α+β,
∵AC平分∠BAE,
∴∠EAC=∠BAC=2α+β,
∴∠DAE=∠DAC+∠CAE=2α+2β=90°,
∴∠HAC=α+β=45°,
∵AB⊥BC,
∴∠ABC=90°,
过点A作AM∥BC,如图5,
∴∠ABC+∠BAM=180°,
∴∠BAM=90°,
∴∠MAC=∠BAM﹣∠BAC=90°﹣(2α+β)=45°﹣α,∠MAD=∠MAB﹣∠BAD=90°﹣2α,
∴∠EAM=∠EAD=∠MAD=2α,
∵GF∥BC,AM∥BC,
∴AM∥GF,
∴∠GEA=∠EAM=2α,
∴∠AEF=180°﹣2a,
∵∠AEC+∠GEC=180°,∠GEC+∠CEF=180°,
∴,
∵AM∥BC,
∴∠ACB=∠MAC=45°﹣α,
∴∠ECB=∠ECA+∠ACB=3α+45°﹣α=2α+45°,
∵GF∥BC,
∴∠FEC=∠ECB,
∴2α+45°=90°﹣a.
∴∠a=15°,
∴∠GEA=2a=30°.
【点评】本题是几何变换综合题,考查了平行线的判定与选择,难度适中.关键是通过作辅助线,构造平行线,把实际问题转化为数学问题加以计算.
21世纪教育网(www.21cnjy.com)
同课章节目录
