【中考押题卷】2025年中考数学高频易错考前冲刺:相交线与平行线(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:相交线与平行线(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 07:38:24 | ||
图片预览

文档简介
2025年中考数学高频易错考前冲刺:相交线与平行线
一.选择题(共10小题)
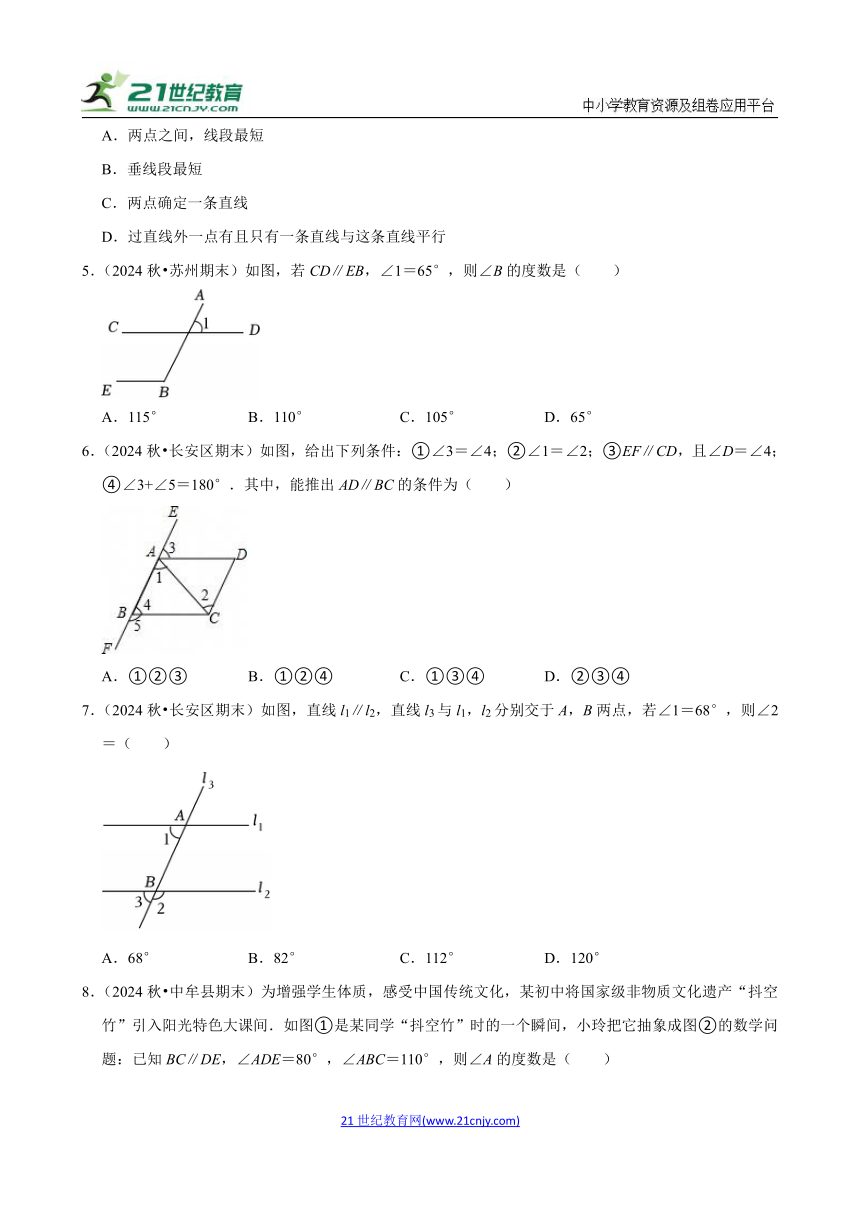
1.(2024秋 苏州期末)如图,我们利用直尺和三角板画平行线或者验证两条直线是否平行,这样做的依据是( )
A.内错角相等,两直线平行
B.同位角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
2.(2024秋 三亚期末)已知AB∥CD,现将一个含30°角的直角三角尺EFG按如图方式放置,其中顶点F、G分别落在直线AB,CD上,GE交AB于点H,若∠EHB=45°,则∠AFG的度数为( )
A.120° B.115° C.110° D.105°
3.(2024秋 中原区期末)如图是一副初中专用三角尺拼成的图案,∠A=∠E=90°,∠B=30°,∠D=45°,AB∥CD,则∠BCE的度数为( )
A.60° B.75° C.90° D.105°
4.(2024秋 长沙期末)在一次植树活动中,小明说“只要定出两棵树的位置,就能确定同一行树所在的直线”,其数学依据是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.过直线外一点有且只有一条直线与这条直线平行
5.(2024秋 苏州期末)如图,若CD∥EB,∠1=65°,则∠B的度数是( )
A.115° B.110° C.105° D.65°
6.(2024秋 长安区期末)如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为( )
A.①②③ B.①②④ C.①③④ D.②③④
7.(2024秋 长安区期末)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=68°,则∠2=( )
A.68° B.82° C.112° D.120°
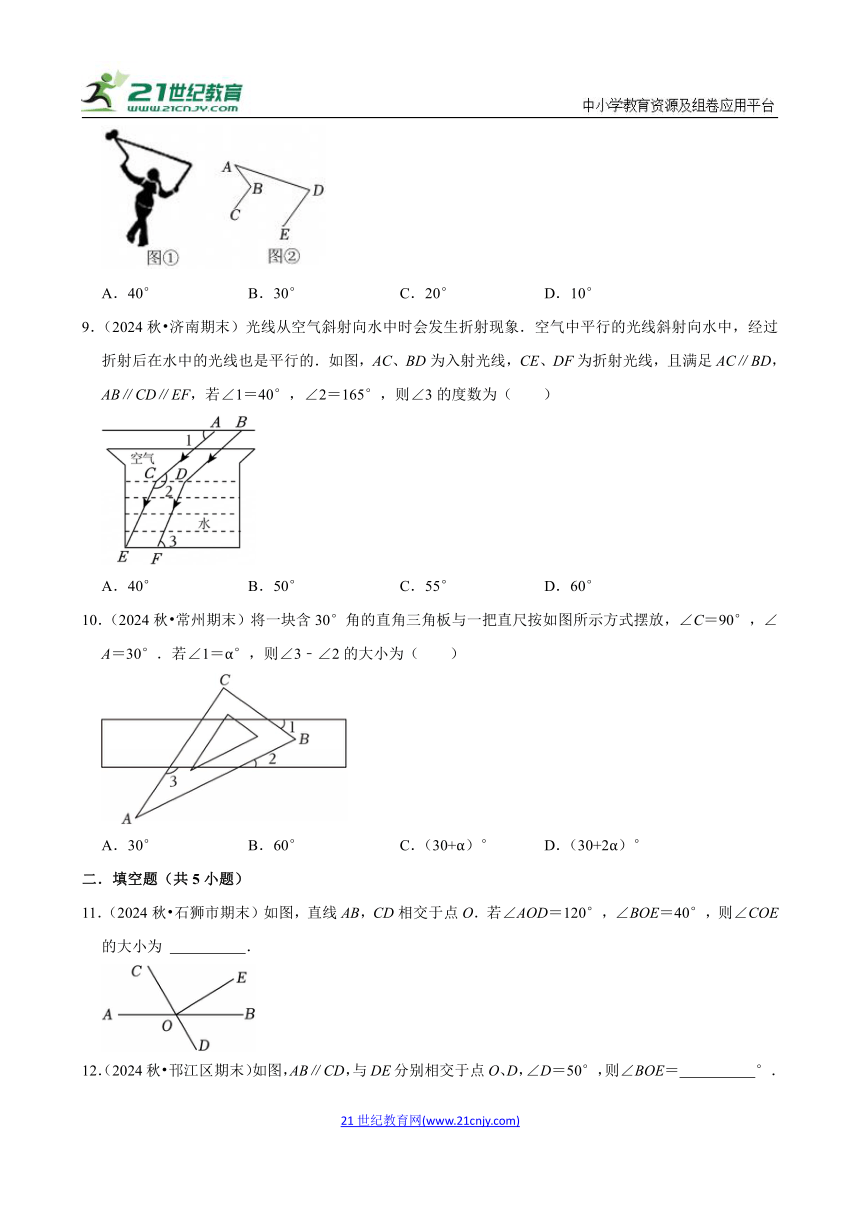
8.(2024秋 中牟县期末)为增强学生体质,感受中国传统文化,某初中将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图①是某同学“抖空竹”时的一个瞬间,小玲把它抽象成图②的数学问题:已知BC∥DE,∠ADE=80°,∠ABC=110°,则∠A的度数是( )
A.40° B.30° C.20° D.10°
9.(2024秋 济南期末)光线从空气斜射向水中时会发生折射现象.空气中平行的光线斜射向水中,经过折射后在水中的光线也是平行的.如图,AC、BD为入射光线,CE、DF为折射光线,且满足AC∥BD,AB∥CD∥EF,若∠1=40°,∠2=165°,则∠3的度数为( )
A.40° B.50° C.55° D.60°
10.(2024秋 常州期末)将一块含30°角的直角三角板与一把直尺按如图所示方式摆放,∠C=90°,∠A=30°.若∠1=α°,则∠3﹣∠2的大小为( )
A.30° B.60° C.(30+α)° D.(30+2α)°
二.填空题(共5小题)
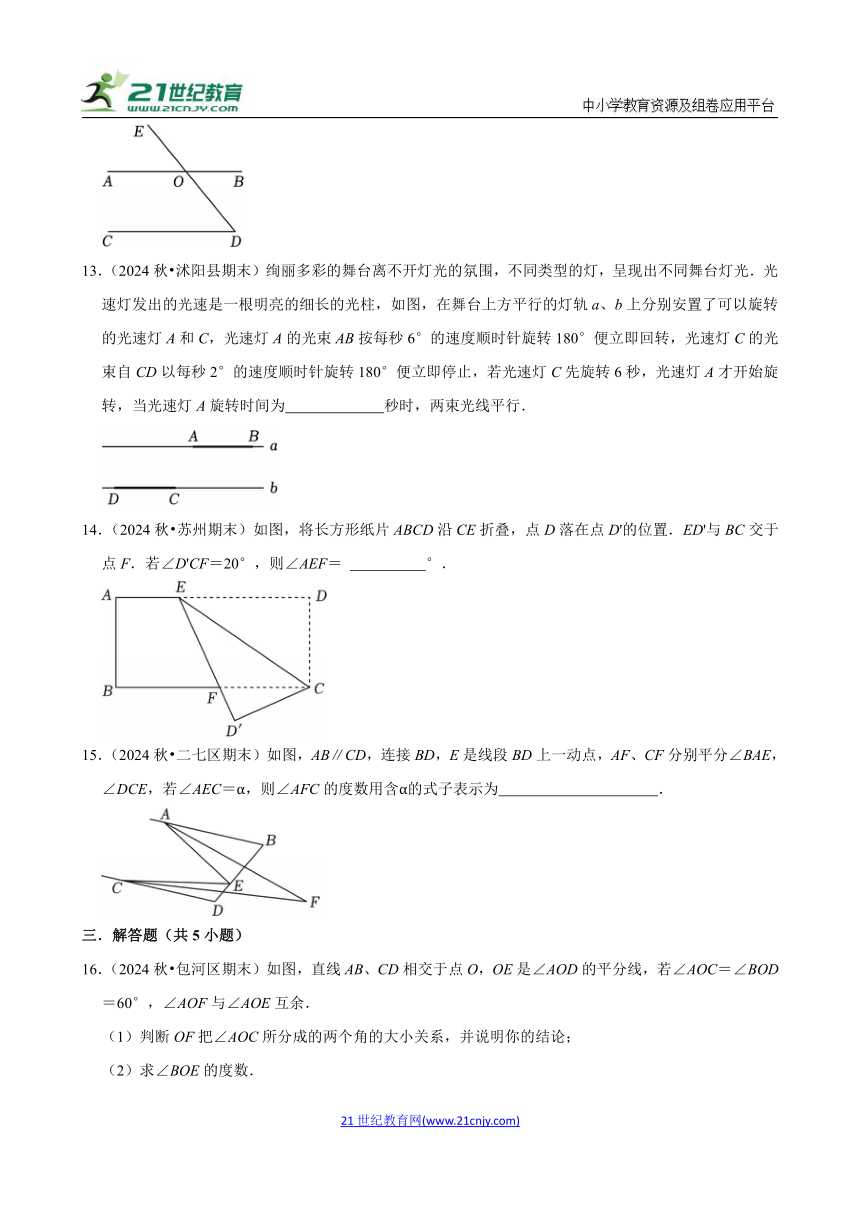
11.(2024秋 石狮市期末)如图,直线AB,CD相交于点O.若∠AOD=120°,∠BOE=40°,则∠COE的大小为 .
12.(2024秋 邗江区期末)如图,AB∥CD,与DE分别相交于点O、D,∠D=50°,则∠BOE= °.
13.(2024秋 沭阳县期末)绚丽多彩的舞台离不开灯光的氛围,不同类型的灯,呈现出不同舞台灯光.光速灯发出的光速是一根明亮的细长的光柱,如图,在舞台上方平行的灯轨a、b上分别安置了可以旋转的光速灯A和C,光速灯A的光束AB按每秒6°的速度顺时针旋转180°便立即回转,光速灯C的光束自CD以每秒2°的速度顺时针旋转180°便立即停止,若光速灯C先旋转6秒,光速灯A才开始旋转,当光速灯A旋转时间为 秒时,两束光线平行.
14.(2024秋 苏州期末)如图,将长方形纸片ABCD沿CE折叠,点D落在点D'的位置.ED'与BC交于点F.若∠D'CF=20°,则∠AEF= °.
15.(2024秋 二七区期末)如图,AB∥CD,连接BD,E是线段BD上一动点,AF、CF分别平分∠BAE,∠DCE,若∠AEC=α,则∠AFC的度数用含α的式子表示为 .
三.解答题(共5小题)
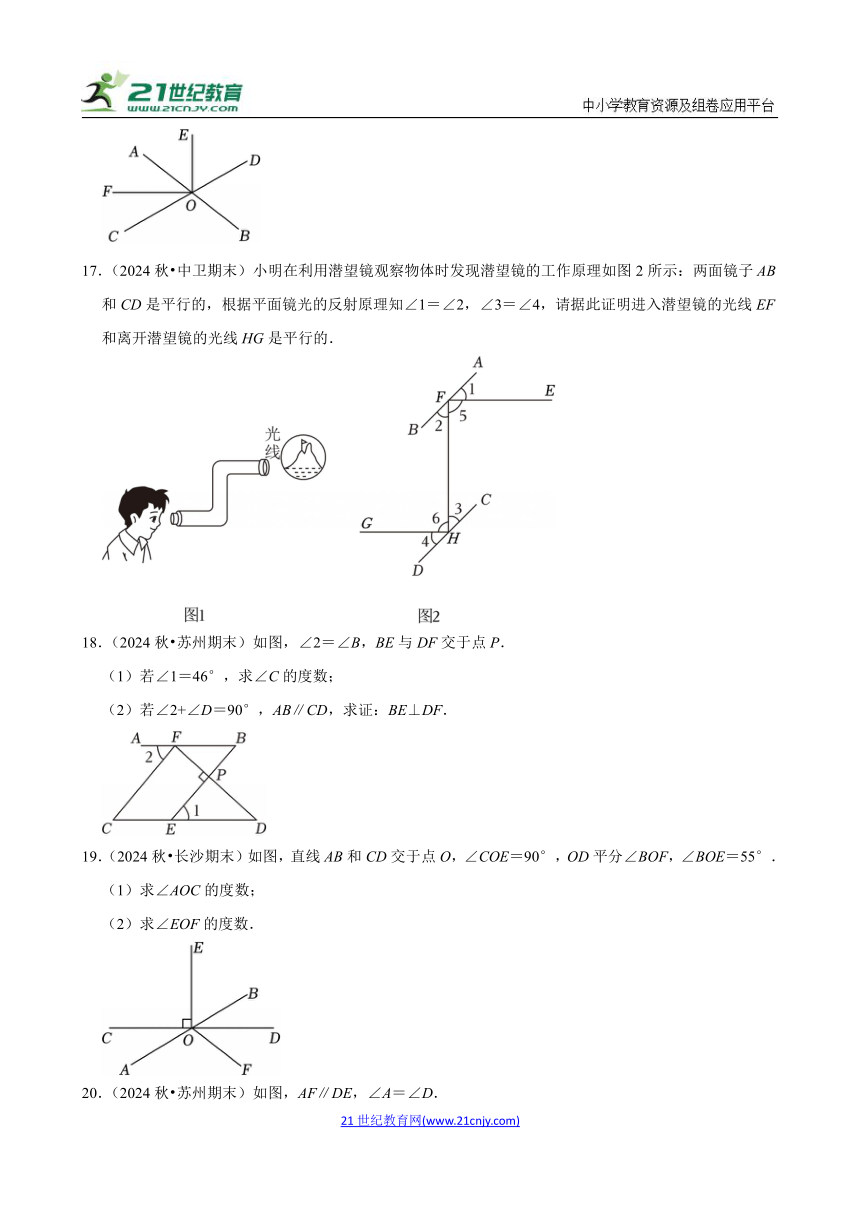
16.(2024秋 包河区期末)如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=∠BOD=60°,∠AOF与∠AOE互余.
(1)判断OF把∠AOC所分成的两个角的大小关系,并说明你的结论;
(2)求∠BOE的度数.
17.(2024秋 中卫期末)小明在利用潜望镜观察物体时发现潜望镜的工作原理如图2所示:两面镜子AB和CD是平行的,根据平面镜光的反射原理知∠1=∠2,∠3=∠4,请据此证明进入潜望镜的光线EF和离开潜望镜的光线HG是平行的.
18.(2024秋 苏州期末)如图,∠2=∠B,BE与DF交于点P.
(1)若∠1=46°,求∠C的度数;
(2)若∠2+∠D=90°,AB∥CD,求证:BE⊥DF.
19.(2024秋 长沙期末)如图,直线AB和CD交于点O,∠COE=90°,OD平分∠BOF,∠BOE=55°.
(1)求∠AOC的度数;
(2)求∠EOF的度数.
20.(2024秋 苏州期末)如图,AF∥DE,∠A=∠D.
(1)填空:
因为AF∥DE,
所以∠A=∠BED( ).
因为∠A=∠D,
所以∠D= (等量代换).
所以AB∥CD( ).
(2)若∠BED=75°,求∠AFD的度数.
2025年中考数学高频易错考前冲刺:相交线与平行线
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B C A C C B C D
一.选择题(共10小题)
1.(2024秋 苏州期末)如图,我们利用直尺和三角板画平行线或者验证两条直线是否平行,这样做的依据是( )
A.内错角相等,两直线平行
B.同位角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
【考点】平行线的判定;作图—复杂作图.
【专题】推理能力.
【答案】B
【分析】根据平行线的判定方法,进行判断即可.
【解答】解:由题意,这样做的依据是同位角相等,两直线平行;
故选:B.
【点评】本题考查平行线的判定,掌握平行线的判定是解题的关键.
2.(2024秋 三亚期末)已知AB∥CD,现将一个含30°角的直角三角尺EFG按如图方式放置,其中顶点F、G分别落在直线AB,CD上,GE交AB于点H,若∠EHB=45°,则∠AFG的度数为( )
A.120° B.115° C.110° D.105°
【考点】平行线的性质.
【专题】运算能力.
【答案】D
【分析】由AB∥CD可得∠EGD=∠EHB=45°,结合∠FGE=60°可得出∠FGD的度数,再由AB∥CD得出∠AFG=∠FGD,即可得出结论.
【解答】解:∵AB∥CD,∠EHB=45°,
∴∠EGD=∠EHB=45°,
∵∠E=30°,∠FGE=60°,
∴∠FGD=∠FGE+∠EGD=60°+45°=105°,
∵AB∥CD,
∴∠AFG=∠FGD=105°.
故选:D.
【点评】本题主要考查平行线的性质,熟练掌握平行线的性质:①两直线平行,同位角相等;②两直线平行,内错角相等是解题的关键.
3.(2024秋 中原区期末)如图是一副初中专用三角尺拼成的图案,∠A=∠E=90°,∠B=30°,∠D=45°,AB∥CD,则∠BCE的度数为( )
A.60° B.75° C.90° D.105°
【考点】平行线的性质;角的计算.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】由平行线的性质推出∠BCD=∠B=30°,求出∠DCE=90°﹣45°=45°,即可得到∠BCE的度数.
【解答】解:∵AB∥CD,
∴∠BCD=∠B=30°,
∵∠E=90°,∠D=45°,
∴∠DCE=90°﹣45°=45°,
∴∠BCE=∠BCD+∠DCE=75°.
故选:B.
【点评】本题考查平行线的性质,关键是由平行线的性质推出∠BCD=∠B.
4.(2024秋 长沙期末)在一次植树活动中,小明说“只要定出两棵树的位置,就能确定同一行树所在的直线”,其数学依据是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.过直线外一点有且只有一条直线与这条直线平行
【考点】平行公理及推论;直线的性质:两点确定一条直线;线段的性质:两点之间线段最短;垂线段最短.
【专题】线段、角、相交线与平行线;应用意识.
【答案】C
【分析】两棵树的位置相当于两个点,要确定同一行树所在的直线,即两点确定一条直线.
【解答】解:由题意得:
两点确定一条直线,
故选:C.
【点评】本题考查了数学在实际生活中应用,培养了学生学以致用的意识.
5.(2024秋 苏州期末)如图,若CD∥EB,∠1=65°,则∠B的度数是( )
A.115° B.110° C.105° D.65°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】由平行线的性质推出∠B+∠2=180°,由对顶角的性质得到∠2=∠1=65°,即可求出∠B的度数.
【解答】解:∵CD∥EB,
∴∠B+∠2=180°,
∵∠2=∠1=65°,
∴∠B=115°.
故选:A.
【点评】本题考查平行线的性质,关键是由平行线的性质推出∠B+∠2=180°.
6.(2024秋 长安区期末)如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为( )
A.①②③ B.①②④ C.①③④ D.②③④
【考点】平行线的判定.
【答案】C
【分析】根据平行线的判定方法结合题目所给的条件进行推理即可.
【解答】解:①∠3=∠4可以根据同位角相等,两直线平行判定AD∥BC,故此选项正确;
②∠1=∠2可以根据内错角相等,两直线平行判定AB∥DC,故此选项错误,
③因为EF∥CD得∠1=∠2又因为∠D=∠4,根据三角形内角和是180°得∠DAC=∠BCA得AD∥BC,
故此选项正确;
④∠3+∠5=180°,可得到∠5=∠DAB,再根据同位角相等,两直线平行判定AD∥BC,故此选项正确;
故选:C.
【点评】此题主要考查了平行线的判定,关键是掌握:
(1)定理1:同位角相等,两直线平行.
(2)定理2:内错角相等,两直线平行.
(3 )定理3:同旁内角互补,两直线平行.
(4)定理4:两条直线都和第三条直线平行,那么这两条直线平行.
(5)定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.
7.(2024秋 长安区期末)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=68°,则∠2=( )
A.68° B.82° C.112° D.120°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】C
【分析】先利用平行线的性质可得:∠1=∠3=68°,然后利用平角定义进行计算即可解答.
【解答】解:∵直线l1∥l2,
∴∠1=∠3=68°,
∴∠2=180°﹣∠3=112°,
故选:C.
【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.
8.(2024秋 中牟县期末)为增强学生体质,感受中国传统文化,某初中将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图①是某同学“抖空竹”时的一个瞬间,小玲把它抽象成图②的数学问题:已知BC∥DE,∠ADE=80°,∠ABC=110°,则∠A的度数是( )
A.40° B.30° C.20° D.10°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】过A作AF∥BC,得到AF∥DE,由平行线的性质推出∠FAD=∠ADE=80°,∠FAB=∠ABC=110°,即可求出∠BAD的度数.
【解答】解:过A作AF∥BC,
∵BC∥DE,
∴AF∥DE,
∴∠FAD=∠ADE=80°,∠FAB=∠ABC=110°,
∴∠BAD=∠FAB﹣∠FAD=30°.
故选:B.
【点评】本题考查平行线的性质,关键是由平行线的性质推出∠FAD=∠ADE,∠FAB=∠ABC.
9.(2024秋 济南期末)光线从空气斜射向水中时会发生折射现象.空气中平行的光线斜射向水中,经过折射后在水中的光线也是平行的.如图,AC、BD为入射光线,CE、DF为折射光线,且满足AC∥BD,AB∥CD∥EF,若∠1=40°,∠2=165°,则∠3的度数为( )
A.40° B.50° C.55° D.60°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】根据平行线的性质求出∠ACD=40°,根据∠2=165°求出∠ECD=125°,进而求出∠CEF的度数,进而求出∠3即可.
【解答】解:∵AB∥CD,
∴∠ACD=∠1=40°,
∵∠2=165°,
∴∠DCE=165°﹣40°=125°,
∵CD∥EF,
∴∠DCE+∠CEF=180°,
∴∠CEF=55°,
∵CE、DF为折射光线,
∴CE∥DF,
∴∠3=∠CEF=55°.
故选:C.
【点评】本题考查了平行线的性质,解题的关键是熟练掌握平行线的性质.
10.(2024秋 常州期末)将一块含30°角的直角三角板与一把直尺按如图所示方式摆放,∠C=90°,∠A=30°.若∠1=α°,则∠3﹣∠2的大小为( )
A.30° B.60° C.(30+α)° D.(30+2α)°
【考点】平行线的性质;余角和补角.
【专题】线段、角、相交线与平行线;运算能力;推理能力.
【答案】D
【分析】过B作BK∥MN,得到BK∥PQ,推出∠5=∠1=α°,∠6=∠2,得到∠2+α°=60°,因此2∠2+2α°=120°,由三角形内角和定理得到∠3+∠2=150°,即可求出∠3﹣∠2=(30+2α)°.
【解答】解:过B作BK∥MN,
∵MN∥PQ,
∴BK∥PQ,
∴∠5=∠1=α°,∠6=∠2,
∴∠2+α°=∠5+∠6=∠ABC=60°,
∴2∠2+2α°=120°,
∵∠3+∠4=180°﹣∠A=150°,∠4=∠2,
∴∠3+∠2=150°,
∴∠3+∠2﹣(2∠2+2α°)=150°﹣120°,
∴∠3﹣∠2=(30+2α)°.
故选:D.
【点评】本题考查平行线的性质,关键是由平行线的性质推出∠2+∠1=∠ABC.
二.填空题(共5小题)
11.(2024秋 石狮市期末)如图,直线AB,CD相交于点O.若∠AOD=120°,∠BOE=40°,则∠COE的大小为 80° .
【考点】对顶角、邻补角.
【专题】运算能力.
【答案】80°.
【分析】先根据对顶角相等可得∠AOD=∠BOC=120°,再根据∠BOE=40°,然后利用角的和差关系进行计算,即可解答.
【解答】解:∵直线AB,CD相交于点O,∠AOD=120°,
∴∠BOC=∠AOD=120°,
∵∠BOE=40°,
∴∠COE=∠BOC﹣∠BOE=80°,
故答案为:80°.
【点评】本题考查了对顶角,根据题目的已知条件并结合图形进行分析是解题的关键.
12.(2024秋 邗江区期末)如图,AB∥CD,与DE分别相交于点O、D,∠D=50°,则∠BOE= 130 °.
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】130.
【分析】先根据平行线的性质求出∠AOE=∠D=50°,然后根据邻补角的定义求解即可.
【解答】解:根据题意可知,AB∥CD,与DE分别相交于点O、D,∠D=50°,
∴∠AOE=∠D=50°,
∴∠BOE=180°﹣∠AOE=180°﹣50°=130°.
故答案为:130.
【点评】本题考查了平行线的性质,关键是平行线性质的熟练掌握.
13.(2024秋 沭阳县期末)绚丽多彩的舞台离不开灯光的氛围,不同类型的灯,呈现出不同舞台灯光.光速灯发出的光速是一根明亮的细长的光柱,如图,在舞台上方平行的灯轨a、b上分别安置了可以旋转的光速灯A和C,光速灯A的光束AB按每秒6°的速度顺时针旋转180°便立即回转,光速灯C的光束自CD以每秒2°的速度顺时针旋转180°便立即停止,若光速灯C先旋转6秒,光速灯A才开始旋转,当光速灯A旋转时间为 3或43.5 秒时,两束光线平行.
【考点】平行线的性质;一元一次方程的应用;平行线的判定.
【专题】运算能力.
【答案】3或43.5.
【分析】分旋转小于180°时和大于180°两种情况,根据平行线的性质表示出数据,列出一元一次方程,求解即可.
【解答】解:设光速灯A旋转时间为t秒,则C旋转的时间为(t+6)秒,
当AB旋转小于180°时,如图所示:
∵AB∥CD,
∴∠1=∠2(两直线平行,同位角相等),
∵a∥b,
∴∠2=∠3(两直线平行,内错角相等),
∴∠1=∠3,
∵AB按每秒6°的速度顺时针旋转,CD以每秒2°的速度顺时针旋转,
∴∠1=(6t)°,∠3=(12+2t)°,
∴6t=12+2t,
∴t=3;
当AB旋转大于180°回转时,如图所示:
∵a∥b,AB∥CD,
∴∠1=∠2,∠2=∠3,
∴∠1=∠3,
∵∠1=[180﹣(6t﹣180)]°=(360﹣6t)°,∠3=(12+2t)°,
∴360﹣6t=12+2t,
∴t=43.5;
综上:旋转时间为3秒或43.5秒,
故答案为:3或43.5.
【点评】本题考查了平行线的性质,一元一次方程,正确计算相应的旋转角度数是解题的关键.
14.(2024秋 苏州期末)如图,将长方形纸片ABCD沿CE折叠,点D落在点D'的位置.ED'与BC交于点F.若∠D'CF=20°,则∠AEF= 110 °.
【考点】平行线的性质;翻折变换(折叠问题).
【专题】线段、角、相交线与平行线;平移、旋转与对称;推理能力.
【答案】110.
【分析】由长方形的性质得到∠D=90°,AD∥BC,由折叠的性质得到∠D′=∠D=90°,求出∠CFD′=90°﹣20°=70°,由对顶角的性质得到∠EFB=∠CFD′=70°,由平行线的性质推出∠AEF+∠EFB=180°,即可求出∠AEF的度数.
【解答】解:∵四边形ABCD是长方形,
∴∠D=90°,AD∥BC,
由折叠的性质得到:∠D′=∠D=90°,
∵∠D′CF=20°,
∴∠CFD′=90°﹣20°=70°,
∴∠EFB=∠CFD′=70°,
∵AD∥BC,
∴∠AEF+∠EFB=180°,
∴∠AEF=110°.
故答案为:110.
【点评】本题考查平行线的性质,折叠问题,关键是由平行线的性质推出∠AEF+∠EFB=180°,由折叠的性质得到∠D′=∠D=90°.
15.(2024秋 二七区期末)如图,AB∥CD,连接BD,E是线段BD上一动点,AF、CF分别平分∠BAE,∠DCE,若∠AEC=α,则∠AFC的度数用含α的式子表示为 α .
【考点】平行线的性质;列代数式.
【专题】线段、角、相交线与平行线;运算能力.
【答案】α.
【分析】通过作辅助线,得到∠BAE+∠ECD=∠AEC=α,同理可得∠BAF+∠DCF=∠AFC,结合角平分线,得到结果.
【解答】解:过E点作EM∥AB,过F点作FN∥AB,
∵AB∥CD,
∴AB∥CD∥EM∥FN,
∴∠BAE=∠AEM,∠ECD=∠MEC,
∵∠AEC=α,
∴∠BAE+∠ECD=∠AEC=α,
同理,∠BAF=∠AFN,∠DCF=∠CFN,
∴∠BAF+∠DCF=∠AFC,
∵AF、CF分别平分∠BAE,∠DCE,
∴∠BAF∠BAE,∠DCF∠ECD,
∴∠BAF+∠DCF(∠BAE+∠ECD),
∴∠AFCα.
故答案为:α.
【点评】本题考查了平行线性质的应用,熟练掌握平行线的性质是解题的关键.
三.解答题(共5小题)
16.(2024秋 包河区期末)如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=∠BOD=60°,∠AOF与∠AOE互余.
(1)判断OF把∠AOC所分成的两个角的大小关系,并说明你的结论;
(2)求∠BOE的度数.
【考点】对顶角、邻补角;角的概念;角平分线的定义;余角和补角;角的大小比较.
【专题】线段、角、相交线与平行线;几何直观;运算能力.
【答案】(1)∠AOF=∠COF;
(2)∠BOE=120°.
【分析】(1)根据对顶角、邻补角以及角平分线的定义进行解答即可;
(2)由对顶角、角平分线的定义进行计算即可.
【解答】解:(1)∠AOF=∠COF,理由:
∵∠AOC=∠BOD=60°,
∴∠AOD=180°﹣60°=120°,
∵OE平分∠AOD,
∴∠AOE=∠DOE60°,
∵∠AOF与∠AOE互余,即∠AOF+∠AOE=90°,
∴∠AOF=90°﹣60°=30°,∠COF=60°﹣30°=30°,
∴∠AOF=∠COF;
(2)∠BOE=∠BOD+∠DOE=60°+60°=120°.
【点评】本题考查对顶角、邻补角,角平分线以及余角和补角,掌握角平分线的定义以及对顶角、邻补角的定义是正确解答的关键.
17.(2024秋 中卫期末)小明在利用潜望镜观察物体时发现潜望镜的工作原理如图2所示:两面镜子AB和CD是平行的,根据平面镜光的反射原理知∠1=∠2,∠3=∠4,请据此证明进入潜望镜的光线EF和离开潜望镜的光线HG是平行的.
【考点】平行线的判定.
【专题】推理能力.
【答案】见解析.
【分析】根据∠2和∠3是内错角,且两面镜子是平行放置的,得到∠2=∠3;再结合∠1=∠2,∠3=∠4,可得∠5=∠6,根据平行线的判定定理即可解答.
【解答】解:∵AB∥CD,
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4.
∵∠5=180°﹣∠1﹣∠2,∠6=180°﹣∠3﹣∠4,
∴∠5=∠6.
∴FE∥GH(内错角相等,两直线平行).
【点评】本题主要考查了平行线的判定和性质,熟记平行线的判定定理和性质定理是解答本题的关键.
18.(2024秋 苏州期末)如图,∠2=∠B,BE与DF交于点P.
(1)若∠1=46°,求∠C的度数;
(2)若∠2+∠D=90°,AB∥CD,求证:BE⊥DF.
【考点】平行线的性质;垂线.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)∠C=46°;
(2)见解析.
【分析】(1)根据平行线的判定得出CF∥EB,再根据平行线的性质得出∠C=∠1,即可得出答案;
(2)根据平行线的性质得出∠BFD=∠D,根据∠2+∠D=90°,得出∠BFD+∠2=90°,求出∠CFD=90°,根据平行线的性质得出∠EPD=∠CFD=90°,即可证明结论.
【解答】(1)解:∵∠2=∠B,
∴CF∥BE,
∴∠C=∠1,
∵∠1=46°,
∴∠C=46°,
所以∠C的度数为46°;
(2)证明:∵AB∥CD,
∴∠BFD=∠D,
∵∠2+∠D=90°,
∴∠BFD+∠2=∠D+∠2=90°,
∴∠CFD=90°,
由(1)可知,CF∥BE,
∴∠EPD=∠CFD=90°,
∴BE⊥DF.
【点评】本题主要考查了平行线的判定和性质,解题的关键是熟练掌握平行线的判定和性质.
19.(2024秋 长沙期末)如图,直线AB和CD交于点O,∠COE=90°,OD平分∠BOF,∠BOE=55°.
(1)求∠AOC的度数;
(2)求∠EOF的度数.
【考点】对顶角、邻补角;角平分线的定义.
【专题】线段、角、相交线与平行线;几何直观;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)根据平角的定义进行计算即可;
(2)根据角平分线的定义以及图形中线段之间的和差关系进行计算即可.
【解答】解:(1)∵∠BOE=55°,∠COE=90°,而∠AOC+∠COE+∠BOE=180°,
∴∠AOC=180°﹣55°﹣90°=35°,
(2)∵∠DOE=∠COE=90°,
∴∠BOD=90°﹣55°=35°,
又∵DO平分∠BOF,
∴∠BOD=∠DOF=35°,
∴∠EOF=55°+35°+35°
=125°.
【点评】本题考查角平分线的定义,对顶角、邻补角,理解对顶角、邻补角以及角平分线的定义是正确解答的关键.
20.(2024秋 苏州期末)如图,AF∥DE,∠A=∠D.
(1)填空:
因为AF∥DE,
所以∠A=∠BED( 两直线平行,同位角相等 ).
因为∠A=∠D,
所以∠D= ∠BED (等量代换).
所以AB∥CD( 内错角相等,两直线平行 ).
(2)若∠BED=75°,求∠AFD的度数.
【考点】平行线的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)两直线平行,同位角相等;∠BED;内错角相等,两直线平行;
(2)105°.
【分析】(1)根据平行线的判定与性质求解即可;
(2)根据平行线的性质求解即可.
【解答】解:(1)因为AF∥DE,
所以∠A=∠BED(两直线平行,同位角相等).
因为∠A=∠D,
所以∠D=∠BED(等量代换).
所以AB∥CD(内错角相等,两直线平行).
故答案为:两直线平行,同位角相等;∠BED;内错角相等,两直线平行;
(2)∵AF∥DE,
∴∠AFD+∠D=180°,
∵∠D=∠BED=75°,
∴∠AFD=105°.
【点评】此题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 苏州期末)如图,我们利用直尺和三角板画平行线或者验证两条直线是否平行,这样做的依据是( )
A.内错角相等,两直线平行
B.同位角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
2.(2024秋 三亚期末)已知AB∥CD,现将一个含30°角的直角三角尺EFG按如图方式放置,其中顶点F、G分别落在直线AB,CD上,GE交AB于点H,若∠EHB=45°,则∠AFG的度数为( )
A.120° B.115° C.110° D.105°
3.(2024秋 中原区期末)如图是一副初中专用三角尺拼成的图案,∠A=∠E=90°,∠B=30°,∠D=45°,AB∥CD,则∠BCE的度数为( )
A.60° B.75° C.90° D.105°
4.(2024秋 长沙期末)在一次植树活动中,小明说“只要定出两棵树的位置,就能确定同一行树所在的直线”,其数学依据是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.过直线外一点有且只有一条直线与这条直线平行
5.(2024秋 苏州期末)如图,若CD∥EB,∠1=65°,则∠B的度数是( )
A.115° B.110° C.105° D.65°
6.(2024秋 长安区期末)如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为( )
A.①②③ B.①②④ C.①③④ D.②③④
7.(2024秋 长安区期末)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=68°,则∠2=( )
A.68° B.82° C.112° D.120°
8.(2024秋 中牟县期末)为增强学生体质,感受中国传统文化,某初中将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图①是某同学“抖空竹”时的一个瞬间,小玲把它抽象成图②的数学问题:已知BC∥DE,∠ADE=80°,∠ABC=110°,则∠A的度数是( )
A.40° B.30° C.20° D.10°
9.(2024秋 济南期末)光线从空气斜射向水中时会发生折射现象.空气中平行的光线斜射向水中,经过折射后在水中的光线也是平行的.如图,AC、BD为入射光线,CE、DF为折射光线,且满足AC∥BD,AB∥CD∥EF,若∠1=40°,∠2=165°,则∠3的度数为( )
A.40° B.50° C.55° D.60°
10.(2024秋 常州期末)将一块含30°角的直角三角板与一把直尺按如图所示方式摆放,∠C=90°,∠A=30°.若∠1=α°,则∠3﹣∠2的大小为( )
A.30° B.60° C.(30+α)° D.(30+2α)°
二.填空题(共5小题)
11.(2024秋 石狮市期末)如图,直线AB,CD相交于点O.若∠AOD=120°,∠BOE=40°,则∠COE的大小为 .
12.(2024秋 邗江区期末)如图,AB∥CD,与DE分别相交于点O、D,∠D=50°,则∠BOE= °.
13.(2024秋 沭阳县期末)绚丽多彩的舞台离不开灯光的氛围,不同类型的灯,呈现出不同舞台灯光.光速灯发出的光速是一根明亮的细长的光柱,如图,在舞台上方平行的灯轨a、b上分别安置了可以旋转的光速灯A和C,光速灯A的光束AB按每秒6°的速度顺时针旋转180°便立即回转,光速灯C的光束自CD以每秒2°的速度顺时针旋转180°便立即停止,若光速灯C先旋转6秒,光速灯A才开始旋转,当光速灯A旋转时间为 秒时,两束光线平行.
14.(2024秋 苏州期末)如图,将长方形纸片ABCD沿CE折叠,点D落在点D'的位置.ED'与BC交于点F.若∠D'CF=20°,则∠AEF= °.
15.(2024秋 二七区期末)如图,AB∥CD,连接BD,E是线段BD上一动点,AF、CF分别平分∠BAE,∠DCE,若∠AEC=α,则∠AFC的度数用含α的式子表示为 .
三.解答题(共5小题)
16.(2024秋 包河区期末)如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=∠BOD=60°,∠AOF与∠AOE互余.
(1)判断OF把∠AOC所分成的两个角的大小关系,并说明你的结论;
(2)求∠BOE的度数.
17.(2024秋 中卫期末)小明在利用潜望镜观察物体时发现潜望镜的工作原理如图2所示:两面镜子AB和CD是平行的,根据平面镜光的反射原理知∠1=∠2,∠3=∠4,请据此证明进入潜望镜的光线EF和离开潜望镜的光线HG是平行的.
18.(2024秋 苏州期末)如图,∠2=∠B,BE与DF交于点P.
(1)若∠1=46°,求∠C的度数;
(2)若∠2+∠D=90°,AB∥CD,求证:BE⊥DF.
19.(2024秋 长沙期末)如图,直线AB和CD交于点O,∠COE=90°,OD平分∠BOF,∠BOE=55°.
(1)求∠AOC的度数;
(2)求∠EOF的度数.
20.(2024秋 苏州期末)如图,AF∥DE,∠A=∠D.
(1)填空:
因为AF∥DE,
所以∠A=∠BED( ).
因为∠A=∠D,
所以∠D= (等量代换).
所以AB∥CD( ).
(2)若∠BED=75°,求∠AFD的度数.
2025年中考数学高频易错考前冲刺:相交线与平行线
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B C A C C B C D
一.选择题(共10小题)
1.(2024秋 苏州期末)如图,我们利用直尺和三角板画平行线或者验证两条直线是否平行,这样做的依据是( )
A.内错角相等,两直线平行
B.同位角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
【考点】平行线的判定;作图—复杂作图.
【专题】推理能力.
【答案】B
【分析】根据平行线的判定方法,进行判断即可.
【解答】解:由题意,这样做的依据是同位角相等,两直线平行;
故选:B.
【点评】本题考查平行线的判定,掌握平行线的判定是解题的关键.
2.(2024秋 三亚期末)已知AB∥CD,现将一个含30°角的直角三角尺EFG按如图方式放置,其中顶点F、G分别落在直线AB,CD上,GE交AB于点H,若∠EHB=45°,则∠AFG的度数为( )
A.120° B.115° C.110° D.105°
【考点】平行线的性质.
【专题】运算能力.
【答案】D
【分析】由AB∥CD可得∠EGD=∠EHB=45°,结合∠FGE=60°可得出∠FGD的度数,再由AB∥CD得出∠AFG=∠FGD,即可得出结论.
【解答】解:∵AB∥CD,∠EHB=45°,
∴∠EGD=∠EHB=45°,
∵∠E=30°,∠FGE=60°,
∴∠FGD=∠FGE+∠EGD=60°+45°=105°,
∵AB∥CD,
∴∠AFG=∠FGD=105°.
故选:D.
【点评】本题主要考查平行线的性质,熟练掌握平行线的性质:①两直线平行,同位角相等;②两直线平行,内错角相等是解题的关键.
3.(2024秋 中原区期末)如图是一副初中专用三角尺拼成的图案,∠A=∠E=90°,∠B=30°,∠D=45°,AB∥CD,则∠BCE的度数为( )
A.60° B.75° C.90° D.105°
【考点】平行线的性质;角的计算.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】由平行线的性质推出∠BCD=∠B=30°,求出∠DCE=90°﹣45°=45°,即可得到∠BCE的度数.
【解答】解:∵AB∥CD,
∴∠BCD=∠B=30°,
∵∠E=90°,∠D=45°,
∴∠DCE=90°﹣45°=45°,
∴∠BCE=∠BCD+∠DCE=75°.
故选:B.
【点评】本题考查平行线的性质,关键是由平行线的性质推出∠BCD=∠B.
4.(2024秋 长沙期末)在一次植树活动中,小明说“只要定出两棵树的位置,就能确定同一行树所在的直线”,其数学依据是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.过直线外一点有且只有一条直线与这条直线平行
【考点】平行公理及推论;直线的性质:两点确定一条直线;线段的性质:两点之间线段最短;垂线段最短.
【专题】线段、角、相交线与平行线;应用意识.
【答案】C
【分析】两棵树的位置相当于两个点,要确定同一行树所在的直线,即两点确定一条直线.
【解答】解:由题意得:
两点确定一条直线,
故选:C.
【点评】本题考查了数学在实际生活中应用,培养了学生学以致用的意识.
5.(2024秋 苏州期末)如图,若CD∥EB,∠1=65°,则∠B的度数是( )
A.115° B.110° C.105° D.65°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】由平行线的性质推出∠B+∠2=180°,由对顶角的性质得到∠2=∠1=65°,即可求出∠B的度数.
【解答】解:∵CD∥EB,
∴∠B+∠2=180°,
∵∠2=∠1=65°,
∴∠B=115°.
故选:A.
【点评】本题考查平行线的性质,关键是由平行线的性质推出∠B+∠2=180°.
6.(2024秋 长安区期末)如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为( )
A.①②③ B.①②④ C.①③④ D.②③④
【考点】平行线的判定.
【答案】C
【分析】根据平行线的判定方法结合题目所给的条件进行推理即可.
【解答】解:①∠3=∠4可以根据同位角相等,两直线平行判定AD∥BC,故此选项正确;
②∠1=∠2可以根据内错角相等,两直线平行判定AB∥DC,故此选项错误,
③因为EF∥CD得∠1=∠2又因为∠D=∠4,根据三角形内角和是180°得∠DAC=∠BCA得AD∥BC,
故此选项正确;
④∠3+∠5=180°,可得到∠5=∠DAB,再根据同位角相等,两直线平行判定AD∥BC,故此选项正确;
故选:C.
【点评】此题主要考查了平行线的判定,关键是掌握:
(1)定理1:同位角相等,两直线平行.
(2)定理2:内错角相等,两直线平行.
(3 )定理3:同旁内角互补,两直线平行.
(4)定理4:两条直线都和第三条直线平行,那么这两条直线平行.
(5)定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.
7.(2024秋 长安区期末)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=68°,则∠2=( )
A.68° B.82° C.112° D.120°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】C
【分析】先利用平行线的性质可得:∠1=∠3=68°,然后利用平角定义进行计算即可解答.
【解答】解:∵直线l1∥l2,
∴∠1=∠3=68°,
∴∠2=180°﹣∠3=112°,
故选:C.
【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.
8.(2024秋 中牟县期末)为增强学生体质,感受中国传统文化,某初中将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图①是某同学“抖空竹”时的一个瞬间,小玲把它抽象成图②的数学问题:已知BC∥DE,∠ADE=80°,∠ABC=110°,则∠A的度数是( )
A.40° B.30° C.20° D.10°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】过A作AF∥BC,得到AF∥DE,由平行线的性质推出∠FAD=∠ADE=80°,∠FAB=∠ABC=110°,即可求出∠BAD的度数.
【解答】解:过A作AF∥BC,
∵BC∥DE,
∴AF∥DE,
∴∠FAD=∠ADE=80°,∠FAB=∠ABC=110°,
∴∠BAD=∠FAB﹣∠FAD=30°.
故选:B.
【点评】本题考查平行线的性质,关键是由平行线的性质推出∠FAD=∠ADE,∠FAB=∠ABC.
9.(2024秋 济南期末)光线从空气斜射向水中时会发生折射现象.空气中平行的光线斜射向水中,经过折射后在水中的光线也是平行的.如图,AC、BD为入射光线,CE、DF为折射光线,且满足AC∥BD,AB∥CD∥EF,若∠1=40°,∠2=165°,则∠3的度数为( )
A.40° B.50° C.55° D.60°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】根据平行线的性质求出∠ACD=40°,根据∠2=165°求出∠ECD=125°,进而求出∠CEF的度数,进而求出∠3即可.
【解答】解:∵AB∥CD,
∴∠ACD=∠1=40°,
∵∠2=165°,
∴∠DCE=165°﹣40°=125°,
∵CD∥EF,
∴∠DCE+∠CEF=180°,
∴∠CEF=55°,
∵CE、DF为折射光线,
∴CE∥DF,
∴∠3=∠CEF=55°.
故选:C.
【点评】本题考查了平行线的性质,解题的关键是熟练掌握平行线的性质.
10.(2024秋 常州期末)将一块含30°角的直角三角板与一把直尺按如图所示方式摆放,∠C=90°,∠A=30°.若∠1=α°,则∠3﹣∠2的大小为( )
A.30° B.60° C.(30+α)° D.(30+2α)°
【考点】平行线的性质;余角和补角.
【专题】线段、角、相交线与平行线;运算能力;推理能力.
【答案】D
【分析】过B作BK∥MN,得到BK∥PQ,推出∠5=∠1=α°,∠6=∠2,得到∠2+α°=60°,因此2∠2+2α°=120°,由三角形内角和定理得到∠3+∠2=150°,即可求出∠3﹣∠2=(30+2α)°.
【解答】解:过B作BK∥MN,
∵MN∥PQ,
∴BK∥PQ,
∴∠5=∠1=α°,∠6=∠2,
∴∠2+α°=∠5+∠6=∠ABC=60°,
∴2∠2+2α°=120°,
∵∠3+∠4=180°﹣∠A=150°,∠4=∠2,
∴∠3+∠2=150°,
∴∠3+∠2﹣(2∠2+2α°)=150°﹣120°,
∴∠3﹣∠2=(30+2α)°.
故选:D.
【点评】本题考查平行线的性质,关键是由平行线的性质推出∠2+∠1=∠ABC.
二.填空题(共5小题)
11.(2024秋 石狮市期末)如图,直线AB,CD相交于点O.若∠AOD=120°,∠BOE=40°,则∠COE的大小为 80° .
【考点】对顶角、邻补角.
【专题】运算能力.
【答案】80°.
【分析】先根据对顶角相等可得∠AOD=∠BOC=120°,再根据∠BOE=40°,然后利用角的和差关系进行计算,即可解答.
【解答】解:∵直线AB,CD相交于点O,∠AOD=120°,
∴∠BOC=∠AOD=120°,
∵∠BOE=40°,
∴∠COE=∠BOC﹣∠BOE=80°,
故答案为:80°.
【点评】本题考查了对顶角,根据题目的已知条件并结合图形进行分析是解题的关键.
12.(2024秋 邗江区期末)如图,AB∥CD,与DE分别相交于点O、D,∠D=50°,则∠BOE= 130 °.
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】130.
【分析】先根据平行线的性质求出∠AOE=∠D=50°,然后根据邻补角的定义求解即可.
【解答】解:根据题意可知,AB∥CD,与DE分别相交于点O、D,∠D=50°,
∴∠AOE=∠D=50°,
∴∠BOE=180°﹣∠AOE=180°﹣50°=130°.
故答案为:130.
【点评】本题考查了平行线的性质,关键是平行线性质的熟练掌握.
13.(2024秋 沭阳县期末)绚丽多彩的舞台离不开灯光的氛围,不同类型的灯,呈现出不同舞台灯光.光速灯发出的光速是一根明亮的细长的光柱,如图,在舞台上方平行的灯轨a、b上分别安置了可以旋转的光速灯A和C,光速灯A的光束AB按每秒6°的速度顺时针旋转180°便立即回转,光速灯C的光束自CD以每秒2°的速度顺时针旋转180°便立即停止,若光速灯C先旋转6秒,光速灯A才开始旋转,当光速灯A旋转时间为 3或43.5 秒时,两束光线平行.
【考点】平行线的性质;一元一次方程的应用;平行线的判定.
【专题】运算能力.
【答案】3或43.5.
【分析】分旋转小于180°时和大于180°两种情况,根据平行线的性质表示出数据,列出一元一次方程,求解即可.
【解答】解:设光速灯A旋转时间为t秒,则C旋转的时间为(t+6)秒,
当AB旋转小于180°时,如图所示:
∵AB∥CD,
∴∠1=∠2(两直线平行,同位角相等),
∵a∥b,
∴∠2=∠3(两直线平行,内错角相等),
∴∠1=∠3,
∵AB按每秒6°的速度顺时针旋转,CD以每秒2°的速度顺时针旋转,
∴∠1=(6t)°,∠3=(12+2t)°,
∴6t=12+2t,
∴t=3;
当AB旋转大于180°回转时,如图所示:
∵a∥b,AB∥CD,
∴∠1=∠2,∠2=∠3,
∴∠1=∠3,
∵∠1=[180﹣(6t﹣180)]°=(360﹣6t)°,∠3=(12+2t)°,
∴360﹣6t=12+2t,
∴t=43.5;
综上:旋转时间为3秒或43.5秒,
故答案为:3或43.5.
【点评】本题考查了平行线的性质,一元一次方程,正确计算相应的旋转角度数是解题的关键.
14.(2024秋 苏州期末)如图,将长方形纸片ABCD沿CE折叠,点D落在点D'的位置.ED'与BC交于点F.若∠D'CF=20°,则∠AEF= 110 °.
【考点】平行线的性质;翻折变换(折叠问题).
【专题】线段、角、相交线与平行线;平移、旋转与对称;推理能力.
【答案】110.
【分析】由长方形的性质得到∠D=90°,AD∥BC,由折叠的性质得到∠D′=∠D=90°,求出∠CFD′=90°﹣20°=70°,由对顶角的性质得到∠EFB=∠CFD′=70°,由平行线的性质推出∠AEF+∠EFB=180°,即可求出∠AEF的度数.
【解答】解:∵四边形ABCD是长方形,
∴∠D=90°,AD∥BC,
由折叠的性质得到:∠D′=∠D=90°,
∵∠D′CF=20°,
∴∠CFD′=90°﹣20°=70°,
∴∠EFB=∠CFD′=70°,
∵AD∥BC,
∴∠AEF+∠EFB=180°,
∴∠AEF=110°.
故答案为:110.
【点评】本题考查平行线的性质,折叠问题,关键是由平行线的性质推出∠AEF+∠EFB=180°,由折叠的性质得到∠D′=∠D=90°.
15.(2024秋 二七区期末)如图,AB∥CD,连接BD,E是线段BD上一动点,AF、CF分别平分∠BAE,∠DCE,若∠AEC=α,则∠AFC的度数用含α的式子表示为 α .
【考点】平行线的性质;列代数式.
【专题】线段、角、相交线与平行线;运算能力.
【答案】α.
【分析】通过作辅助线,得到∠BAE+∠ECD=∠AEC=α,同理可得∠BAF+∠DCF=∠AFC,结合角平分线,得到结果.
【解答】解:过E点作EM∥AB,过F点作FN∥AB,
∵AB∥CD,
∴AB∥CD∥EM∥FN,
∴∠BAE=∠AEM,∠ECD=∠MEC,
∵∠AEC=α,
∴∠BAE+∠ECD=∠AEC=α,
同理,∠BAF=∠AFN,∠DCF=∠CFN,
∴∠BAF+∠DCF=∠AFC,
∵AF、CF分别平分∠BAE,∠DCE,
∴∠BAF∠BAE,∠DCF∠ECD,
∴∠BAF+∠DCF(∠BAE+∠ECD),
∴∠AFCα.
故答案为:α.
【点评】本题考查了平行线性质的应用,熟练掌握平行线的性质是解题的关键.
三.解答题(共5小题)
16.(2024秋 包河区期末)如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=∠BOD=60°,∠AOF与∠AOE互余.
(1)判断OF把∠AOC所分成的两个角的大小关系,并说明你的结论;
(2)求∠BOE的度数.
【考点】对顶角、邻补角;角的概念;角平分线的定义;余角和补角;角的大小比较.
【专题】线段、角、相交线与平行线;几何直观;运算能力.
【答案】(1)∠AOF=∠COF;
(2)∠BOE=120°.
【分析】(1)根据对顶角、邻补角以及角平分线的定义进行解答即可;
(2)由对顶角、角平分线的定义进行计算即可.
【解答】解:(1)∠AOF=∠COF,理由:
∵∠AOC=∠BOD=60°,
∴∠AOD=180°﹣60°=120°,
∵OE平分∠AOD,
∴∠AOE=∠DOE60°,
∵∠AOF与∠AOE互余,即∠AOF+∠AOE=90°,
∴∠AOF=90°﹣60°=30°,∠COF=60°﹣30°=30°,
∴∠AOF=∠COF;
(2)∠BOE=∠BOD+∠DOE=60°+60°=120°.
【点评】本题考查对顶角、邻补角,角平分线以及余角和补角,掌握角平分线的定义以及对顶角、邻补角的定义是正确解答的关键.
17.(2024秋 中卫期末)小明在利用潜望镜观察物体时发现潜望镜的工作原理如图2所示:两面镜子AB和CD是平行的,根据平面镜光的反射原理知∠1=∠2,∠3=∠4,请据此证明进入潜望镜的光线EF和离开潜望镜的光线HG是平行的.
【考点】平行线的判定.
【专题】推理能力.
【答案】见解析.
【分析】根据∠2和∠3是内错角,且两面镜子是平行放置的,得到∠2=∠3;再结合∠1=∠2,∠3=∠4,可得∠5=∠6,根据平行线的判定定理即可解答.
【解答】解:∵AB∥CD,
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4.
∵∠5=180°﹣∠1﹣∠2,∠6=180°﹣∠3﹣∠4,
∴∠5=∠6.
∴FE∥GH(内错角相等,两直线平行).
【点评】本题主要考查了平行线的判定和性质,熟记平行线的判定定理和性质定理是解答本题的关键.
18.(2024秋 苏州期末)如图,∠2=∠B,BE与DF交于点P.
(1)若∠1=46°,求∠C的度数;
(2)若∠2+∠D=90°,AB∥CD,求证:BE⊥DF.
【考点】平行线的性质;垂线.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)∠C=46°;
(2)见解析.
【分析】(1)根据平行线的判定得出CF∥EB,再根据平行线的性质得出∠C=∠1,即可得出答案;
(2)根据平行线的性质得出∠BFD=∠D,根据∠2+∠D=90°,得出∠BFD+∠2=90°,求出∠CFD=90°,根据平行线的性质得出∠EPD=∠CFD=90°,即可证明结论.
【解答】(1)解:∵∠2=∠B,
∴CF∥BE,
∴∠C=∠1,
∵∠1=46°,
∴∠C=46°,
所以∠C的度数为46°;
(2)证明:∵AB∥CD,
∴∠BFD=∠D,
∵∠2+∠D=90°,
∴∠BFD+∠2=∠D+∠2=90°,
∴∠CFD=90°,
由(1)可知,CF∥BE,
∴∠EPD=∠CFD=90°,
∴BE⊥DF.
【点评】本题主要考查了平行线的判定和性质,解题的关键是熟练掌握平行线的判定和性质.
19.(2024秋 长沙期末)如图,直线AB和CD交于点O,∠COE=90°,OD平分∠BOF,∠BOE=55°.
(1)求∠AOC的度数;
(2)求∠EOF的度数.
【考点】对顶角、邻补角;角平分线的定义.
【专题】线段、角、相交线与平行线;几何直观;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)根据平角的定义进行计算即可;
(2)根据角平分线的定义以及图形中线段之间的和差关系进行计算即可.
【解答】解:(1)∵∠BOE=55°,∠COE=90°,而∠AOC+∠COE+∠BOE=180°,
∴∠AOC=180°﹣55°﹣90°=35°,
(2)∵∠DOE=∠COE=90°,
∴∠BOD=90°﹣55°=35°,
又∵DO平分∠BOF,
∴∠BOD=∠DOF=35°,
∴∠EOF=55°+35°+35°
=125°.
【点评】本题考查角平分线的定义,对顶角、邻补角,理解对顶角、邻补角以及角平分线的定义是正确解答的关键.
20.(2024秋 苏州期末)如图,AF∥DE,∠A=∠D.
(1)填空:
因为AF∥DE,
所以∠A=∠BED( 两直线平行,同位角相等 ).
因为∠A=∠D,
所以∠D= ∠BED (等量代换).
所以AB∥CD( 内错角相等,两直线平行 ).
(2)若∠BED=75°,求∠AFD的度数.
【考点】平行线的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)两直线平行,同位角相等;∠BED;内错角相等,两直线平行;
(2)105°.
【分析】(1)根据平行线的判定与性质求解即可;
(2)根据平行线的性质求解即可.
【解答】解:(1)因为AF∥DE,
所以∠A=∠BED(两直线平行,同位角相等).
因为∠A=∠D,
所以∠D=∠BED(等量代换).
所以AB∥CD(内错角相等,两直线平行).
故答案为:两直线平行,同位角相等;∠BED;内错角相等,两直线平行;
(2)∵AF∥DE,
∴∠AFD+∠D=180°,
∵∠D=∠BED=75°,
∴∠AFD=105°.
【点评】此题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
