【中考押题卷】2025年中考数学高频易错考前冲刺:有理数(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:有理数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 379.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 08:10:54 | ||
图片预览




文档简介
2025年中考数学高频易错考前冲刺:有理数
一.选择题(共10小题)
1.(2024秋 诸暨市期末)截至2024年12月6日,全国家电以旧换新数据平台显示,八大类家电产品带动销售约2020亿元.数“2020亿”用科学记数法表示为( )
A.2.020×1011 B.20.20×1011
C.0.2020×1012 D.0.2020×1013
2.(2024秋 大足区期末)按下列图示的程序计算,若开始输入的值为x=2,则最后输出的结果是( )
A.6 B.21 C.115 D.231
3.(2024秋 泸县校级期末)下列有理数中,是负数的是( )
A. B.2 C.0 D.﹣1
4.(2024秋 丰台区期末)中国是最早使用正负数表示具有相反意义的量的国家,早在我国秦汉时期的《九章算术》中就引入了负数.若在粮谷计算中,益实一斗(增加1斗)记为+1斗,那么损实七斗(减少7斗)记为( )
A.﹣1斗 B.+1斗 C.﹣7斗 D.+7斗
5.(2024秋 松江区期末)下列各数互为相反数的是( )
A.|﹣2|和﹣2 B.|﹣2|和2 C.﹣(﹣2)和2 D.|﹣2|和﹣(﹣2)
6.(2024秋 昆明期末)﹣2025的相反数是( )
A.2025 B. C.﹣2025 D.
7.(2024秋 包头期末)已知a的相反数是﹣2024,则a的倒数是( )
A.﹣2024 B.2024 C. D.
8.(2024秋 海曙区期末)算式﹣3﹣(﹣5)+(﹣2)写成省略加号的和式,正确的是( )
A.﹣3+5﹣2 B.﹣3+5+2 C.﹣3﹣5﹣2 D.3+5﹣2
9.(2024秋 长沙期末)我们在生活中经常使用的数是十进制数,如2639=2×103+6×102+3×101+9,表示十进制的数要用到10个数码(也叫数字):0,1,2,3,4,5,6,7,8,9.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制 0 1 2 3 4 5 6 7 8 9
A
B
C
D
E
F
十进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
例如,十六进制数71B=7×162+1×161+11=1819,即十六进制数71B相当于十进制数1819.那么十六进制数1D9相当于十进制数( )
A.473 B.117 C.1139 D.250
10.(2024秋 贵阳期末)中国是最早认识正数和负数的国家,魏晋时期的数学家刘徽就提出了负数的概念,如果零下3℃记作﹣3℃,那么+5℃表示( )
A.零上5℃ B.零下5℃ C.零上2℃ D.零下8℃
二.填空题(共5小题)
11.(2024秋 淮北期末)近似数5.08×103精确到 位.
12.(2024秋 常州期末)按图中程序计算,若输入﹣14,则输出的数为a;若输入正数b,则输出的数也为b,则ba+2的值为 .
13.(2024秋 泰兴市期末)﹣(﹣2025)= .
14.(2024秋 泸县校级期末)赤道半径为6378200米,用科学记数法表示为 米.
15.(2024秋 苏州期末)苏州地铁7号线于2024年12月1日正式开通运营,全长40500米,途径相城区、工业园区、吴中区,是古城东侧重要的客流通道.数据40500用科学记数法可表示为 .
三.解答题(共5小题)
16.(2024秋 大足区期末)2024年11月12日,第十五届中国航展在广东珠海举行,中国空军“八一”飞行表演队在航展上表演特技飞行,表演从空中某一位置开始,上升的高度记作正数,下降的高度记作负数,五次特技飞行高度记录如下:+2.5,﹣1.2,+1.2,﹣1.5,+0.8.(单位:千米)
(1)求飞机最后所在的位置比开始位置高还是低?高了或低了多少千米?
(2)若飞机平均上升1千米需消耗6升燃油,平均下降1千米需消耗4升燃油,则飞机在这5次特技飞行中,一共消耗多少升燃油?
17.(2024秋 海曙区期末)如图,数轴上每一小段的长度为1,点A、B、C、D在数轴上对应的数分别为a、b、c、d,
(1)若a与d互为相反数,则c= ;
(2)若|b|>|d|,则c 0(填“大于”或“小于”);a、b、c、d中,可能互为相反数的是 .
18.(2024秋 云岩区期末)贵阳地铁3号线自运营以来,为市民和游客带来了前所未有的便捷体验.如图是3号线部分站点示意图,小红作为地铁志愿者,从茶店站开始乘坐地铁做引导服务,最后她在A站结束服务活动.
若规定向花果园站方向为正,则小红当天乘地铁的站数按先后顺序依次记录如下(单位:站):﹣3,+4,+5,+1,﹣5,+2.
(1)请通过计算说明A站是哪一站?
(2)假设相邻两站之间的平均距离为1.5km,求这次小红志愿服务期间乘坐地铁的总路程为多少千米?
19.(2024秋 海门区期末)计算:
(1);
(2)(﹣10)3+[(﹣4)2﹣(1﹣32)×2].
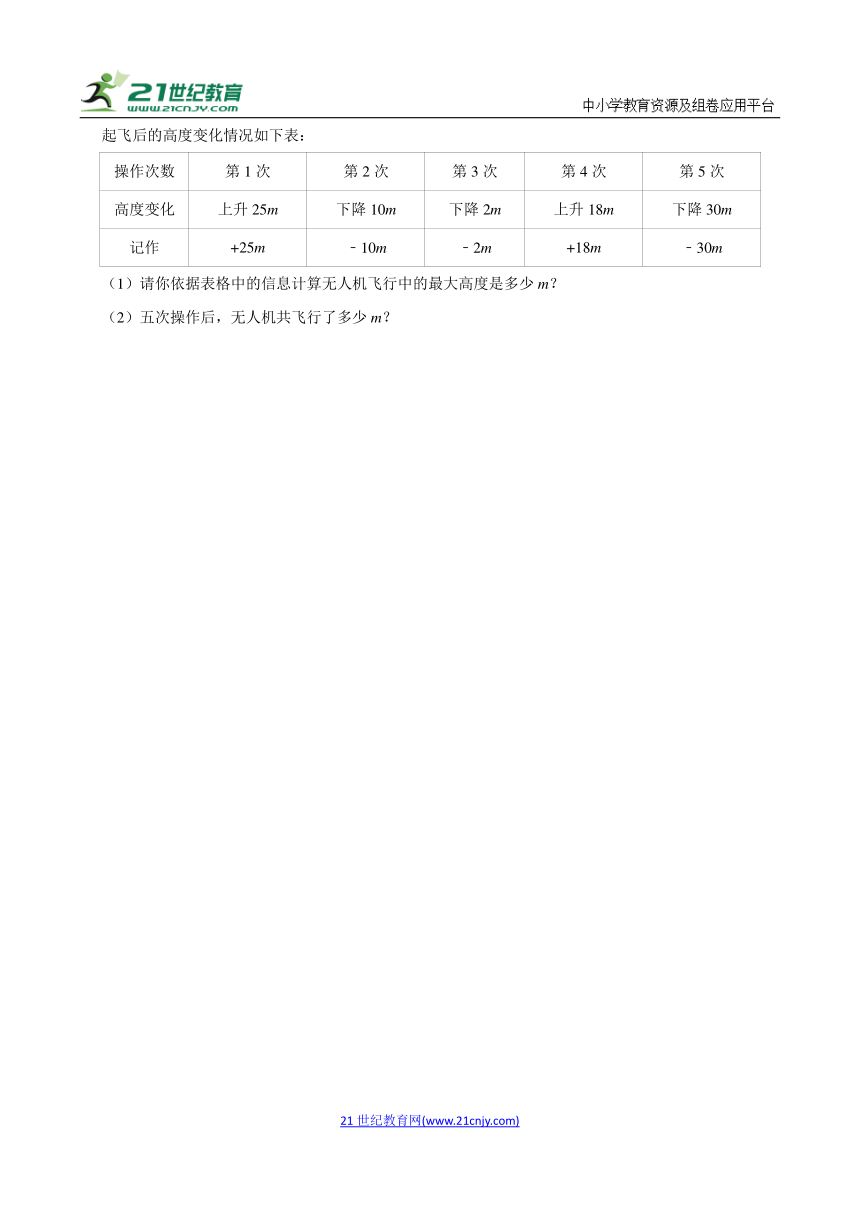
20.(2024秋 金水区期末)无人机社团课上,悠悠同学在操纵一架无人机进行功能测试,无压人机从地面起飞后的高度变化情况如下表:
操作次数 第1次 第2次 第3次 第4次 第5次
高度变化 上升25m 下降10m 下降2m 上升18m 下降30m
记作 +25m ﹣10m ﹣2m +18m ﹣30m
(1)请你依据表格中的信息计算无人机飞行中的最大高度是多少m?
(2)五次操作后,无人机共飞行了多少m?
2025年中考数学高频易错考前冲刺:有理数
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 A D D. C A A D A A A
一.选择题(共10小题)
1.(2024秋 诸暨市期末)截至2024年12月6日,全国家电以旧换新数据平台显示,八大类家电产品带动销售约2020亿元.数“2020亿”用科学记数法表示为( )
A.2.020×1011 B.20.20×1011
C.0.2020×1012 D.0.2020×1013
【考点】科学记数法—表示较大的数.
【专题】实数;符号意识.
【答案】A
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:2020亿=202000000000=2.020×1011.
故选:A.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.(2024秋 大足区期末)按下列图示的程序计算,若开始输入的值为x=2,则最后输出的结果是( )
A.6 B.21 C.115 D.231
【考点】有理数的混合运算;代数式求值.
【专题】实数;运算能力.
【答案】D
【分析】根据题意列式计算,直至结果大于100即可.
【解答】解:若开始输入的值为x=2,
则3<100,返回继续运算,
6<100,返回继续运算,
21<100,返回继续运算,
231>100,输出结果,
故选:D.
【点评】本题考查有理数的混合运算,代数式求值,结合已知条件列得正确的算式是解题的关键.
3.(2024秋 泸县校级期末)下列有理数中,是负数的是( )
A. B.2 C.0 D.﹣1
【考点】正数和负数.
【专题】实数;符号意识.
【答案】D.
【分析】根据正数和负数的定义判断即可,注意:0既不是负数也不是正数.
【解答】解:A.0,是正数,故A选项错误;
B.2>0,是正数,故B选项错误;
C.0既不是正数,也不是负数,故C选项错误;
D.﹣1<0,是负数,故D选项正确;
故选:D.
【点评】本题考查了对正数和负数定义的理解,难度不大,注意0既不是正数也不是负数.
4.(2024秋 丰台区期末)中国是最早使用正负数表示具有相反意义的量的国家,早在我国秦汉时期的《九章算术》中就引入了负数.若在粮谷计算中,益实一斗(增加1斗)记为+1斗,那么损实七斗(减少7斗)记为( )
A.﹣1斗 B.+1斗 C.﹣7斗 D.+7斗
【考点】正数和负数.
【专题】实数;符号意识.
【答案】C
【分析】根据正数和负数是一组具有相反意义的量,据此即可求得答案.
【解答】解:中国是最早使用正负数表示具有相反意义的量的国家,早在我国秦汉时期的《九章算术》中就引入了负数.若在粮谷计算中,益实一斗(增加1斗)记为+1斗,那么损实七斗(减少7斗)记为﹣7斗,
故选:C.
【点评】本题考查正数和负数,掌握正数和负数是一组具有相反意义的量是解答本题的关键.
5.(2024秋 松江区期末)下列各数互为相反数的是( )
A.|﹣2|和﹣2 B.|﹣2|和2 C.﹣(﹣2)和2 D.|﹣2|和﹣(﹣2)
【考点】相反数.
【专题】实数;数感.
【答案】A
【分析】根据互为相反数的定义,只有符号不同的两个数叫做相反数,逐一判断各个选项即可.
【解答】解:A、|﹣2|=2,2和﹣2互为相反数,故该选项正确;
B、|﹣2|=2,2和2不互为相反数,故该选项错误;
C、﹣(﹣2)=2,2和2不互为相反数,故该选项错误;
D、|﹣2|=2,﹣(﹣2)=2,2和2不互为相反数,故该选项错误;
故选:A.
【点评】本题主要考查相反数的定义,掌握只有符号不同的两个数叫做相反数是关键.
6.(2024秋 昆明期末)﹣2025的相反数是( )
A.2025 B. C.﹣2025 D.
【考点】相反数.
【专题】实数;符号意识.
【答案】A
【分析】根据符号不同,绝对值相同的两个数互为相反数即可求得答案.
【解答】解:﹣2025的相反数是2025.
故选:A.
【点评】本题考查了相反数的概念,掌握只有符号不同的两个数叫做互为相反数是解答此题的关键.
7.(2024秋 包头期末)已知a的相反数是﹣2024,则a的倒数是( )
A.﹣2024 B.2024 C. D.
【考点】倒数;相反数.
【专题】实数;符号意识.
【答案】D
【分析】根据相反数、倒数的定义解答即可求得答案.
【解答】解:∵a和﹣2024互为相反数,
∴a+(﹣2024)=0,
∴a=2024,
2024的倒数是.
故选:D.
【点评】本题考查了相反数、倒数,掌握相反数、倒数的定义是解答此题的关键.
8.(2024秋 海曙区期末)算式﹣3﹣(﹣5)+(﹣2)写成省略加号的和式,正确的是( )
A.﹣3+5﹣2 B.﹣3+5+2 C.﹣3﹣5﹣2 D.3+5﹣2
【考点】有理数的加减混合运算.
【答案】A
【分析】利用去括号法则省略括号后直接选取答案.
【解答】解:﹣3﹣(﹣5)+(﹣2)=﹣3+5﹣2.
故选:A.
【点评】本题主要考查有理数的加法省略的书写,要学好有理数的加减运算须熟练掌握方法.
9.(2024秋 长沙期末)我们在生活中经常使用的数是十进制数,如2639=2×103+6×102+3×101+9,表示十进制的数要用到10个数码(也叫数字):0,1,2,3,4,5,6,7,8,9.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制 0 1 2 3 4 5 6 7 8 9
A
B
C
D
E
F
十进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
例如,十六进制数71B=7×162+1×161+11=1819,即十六进制数71B相当于十进制数1819.那么十六进制数1D9相当于十进制数( )
A.473 B.117 C.1139 D.250
【考点】有理数的混合运算.
【答案】A
【分析】由十六进制转化为十进制的方法,我们将各数位上的数字乘以其权重累加后,即可得到答案.
【解答】解:1D9=1×162+13×16+9
=256+208+9
=473.
故选:A.
【点评】本题考查的知识点是进制之间的转换,有理数的混合运算,解本题的关键是从表格中找出十六进制与十进制间的转换关系.
10.(2024秋 贵阳期末)中国是最早认识正数和负数的国家,魏晋时期的数学家刘徽就提出了负数的概念,如果零下3℃记作﹣3℃,那么+5℃表示( )
A.零上5℃ B.零下5℃ C.零上2℃ D.零下8℃
【考点】正数和负数;数学常识.
【专题】符号意识.
【答案】A
【分析】根据正负数表示意义相反的量即可求解.
【解答】解:∵零下3℃记作﹣3℃,
∴+5℃表示零上5℃,
故选:A.
【点评】本题考查了正负数的意义,了解正负数是表示意义相反的量是解题的关键.
二.填空题(共5小题)
11.(2024秋 淮北期末)近似数5.08×103精确到 十 位.
【考点】科学记数法与有效数字.
【专题】实数;数感.
【答案】十.
【分析】将科学记数法还原,确定数字8所在的数位即可.
【解答】解:将科学记数法还原得5.08×103=5080,8是十位数字,
故答案为:十.
【点评】本题考查判断近似数的精确数位,熟练掌握该知识点是关键.
12.(2024秋 常州期末)按图中程序计算,若输入﹣14,则输出的数为a;若输入正数b,则输出的数也为b,则ba+2的值为 8 .
【考点】有理数的混合运算;代数式求值.
【专题】实数;整式;运算能力.
【答案】8.
【分析】根据题意列式计算后求得a,b的值,然后代入ba+2中计算即可.
【解答】解:若输入﹣14,
则(﹣14+6)÷(﹣2)2=﹣8÷4=﹣2<0,返回继续运算,
(﹣2+6)÷(﹣2)2=4÷4=1>0,输出结果,
则a=1,
∵输入正数b,则输出的数也为b,
∴(b+6)÷(﹣2)2=b,
解得:b=2,
则ba+2=21+2=8,
故答案为:8.
【点评】本题考查有理数的混合运算,代数式求值,结合已知条件列得正确的算式是解题的关键.
13.(2024秋 泰兴市期末)﹣(﹣2025)= 2025 .
【考点】相反数.
【专题】实数;运算能力.
【答案】2025.
【分析】利用相反数的含义化简双重符号即可.
【解答】解:根据题意可知,﹣(﹣2025)=2025.
故答案为:2025.
【点评】本题考查的是相反数的含义,掌握相反数的含义是关键.
14.(2024秋 泸县校级期末)赤道半径为6378200米,用科学记数法表示为 6.3782×106 米.
【考点】科学记数法—表示较大的数.
【专题】实数;符号意识.
【答案】6.3782×106.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:6378200=6.3782×106.
故答案为:6.3782×106.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
15.(2024秋 苏州期末)苏州地铁7号线于2024年12月1日正式开通运营,全长40500米,途径相城区、工业园区、吴中区,是古城东侧重要的客流通道.数据40500用科学记数法可表示为 4.05×104 .
【考点】科学记数法—表示较大的数.
【专题】实数;符号意识.
【答案】4.05×104.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:40500=4.05×104.
故答案为:4.05×104.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
三.解答题(共5小题)
16.(2024秋 大足区期末)2024年11月12日,第十五届中国航展在广东珠海举行,中国空军“八一”飞行表演队在航展上表演特技飞行,表演从空中某一位置开始,上升的高度记作正数,下降的高度记作负数,五次特技飞行高度记录如下:+2.5,﹣1.2,+1.2,﹣1.5,+0.8.(单位:千米)
(1)求飞机最后所在的位置比开始位置高还是低?高了或低了多少千米?
(2)若飞机平均上升1千米需消耗6升燃油,平均下降1千米需消耗4升燃油,则飞机在这5次特技飞行中,一共消耗多少升燃油?
【考点】有理数的混合运算;正数和负数.
【专题】实数;运算能力.
【答案】(1)飞机最后所在的位置比开始位置高了,高了1.8千米;
(2)37.8升燃油.
【分析】(1)根据正数和负数的实际意义列式计算即可;
(2)根据正数和负数的实际意义求得上升的总高度,将其乘以6,下降的总高度,将其乘以4,然后再相加即可.
【解答】解:(1)2.5﹣1.2+1.2﹣1.5+0.8=1.8(千米),
即飞机最后所在的位置比开始位置高了,高了1.8千米;
(2)(2.5+1.2+0.8)×6+(1.2+1.5)×4
=27+10.8
=37.8(升),
即飞机在这5次特技飞行中,一共消耗37.8升燃油.
【点评】本题考查有理数的混合运算,正数和负数,结合已知条件列得正确的算式是解题的关键.
17.(2024秋 海曙区期末)如图,数轴上每一小段的长度为1,点A、B、C、D在数轴上对应的数分别为a、b、c、d,
(1)若a与d互为相反数,则c= ﹣1 ;
(2)若|b|>|d|,则c 小于 0(填“大于”或“小于”);a、b、c、d中,可能互为相反数的是 c与d .
【考点】数轴;相反数;绝对值.
【专题】实数;数感.
【答案】(1)﹣1;
(2)小于;c与d.
【分析】(1)根据相反数的定义以及观察数轴即可求解;
(2)根据绝对值、相反数的定义,即可求解.
【解答】解:(1)由题意可得:
∴a在数轴上表示﹣4,d在数轴上表示4,
∴c=﹣1,
故答案为:﹣1;
(2)∵|b|>|d|,
∴c小于0,
∴a、b、c、d中,可能互为相反数的是c与d,
故答案为:小于;c与d.
【点评】本题考查了数轴,相反数、绝对值的定义,解题的关键是掌握相关知识并数形结合.
18.(2024秋 云岩区期末)贵阳地铁3号线自运营以来,为市民和游客带来了前所未有的便捷体验.如图是3号线部分站点示意图,小红作为地铁志愿者,从茶店站开始乘坐地铁做引导服务,最后她在A站结束服务活动.
若规定向花果园站方向为正,则小红当天乘地铁的站数按先后顺序依次记录如下(单位:站):﹣3,+4,+5,+1,﹣5,+2.
(1)请通过计算说明A站是哪一站?
(2)假设相邻两站之间的平均距离为1.5km,求这次小红志愿服务期间乘坐地铁的总路程为多少千米?
【考点】有理数的混合运算;正数和负数.
【专题】实数;运算能力.
【答案】(1)黔灵山公园站;
(2)30千米.
【分析】(1)根据正数和负数的实际意义列式计算即可;
(2)根据正数和负数的实际意义先求得总站数,再与1.5相乘并计算即可.
【解答】解:(1)﹣3+4+5+1﹣5+2=4(站),
则A站是黔灵山公园站;
(2)(3+4+5+1+5+2)×1.5
=20×1.5
=30(千米),
即这次小红志愿服务期间乘坐地铁的总路程为30千米.
【点评】本题考查有理数的混合运算,正数和负数,结合已知条件列得正确的算式是解题的关键.
19.(2024秋 海门区期末)计算:
(1);
(2)(﹣10)3+[(﹣4)2﹣(1﹣32)×2].
【考点】有理数的混合运算.
【专题】实数;运算能力.
【答案】(1)﹣8;
(2)﹣968.
【分析】(1)先算乘方,再算乘除即可;
(2)先算乘方,小括号里面的,中括号里面的,再算加法即可.
【解答】解:(1)原式=(﹣8)
=(﹣18)
=﹣8;
(2)原式=(﹣1000)+[16﹣(1﹣9)×2]
=﹣1000+(16+8×2)
=﹣1000+(16+16)
=﹣1000+32
=﹣968.
【点评】本题考查的是有理数的混合运算,熟知有理数混合运算的法则是解题的关键.
20.(2024秋 金水区期末)无人机社团课上,悠悠同学在操纵一架无人机进行功能测试,无压人机从地面起飞后的高度变化情况如下表:
操作次数 第1次 第2次 第3次 第4次 第5次
高度变化 上升25m 下降10m 下降2m 上升18m 下降30m
记作 +25m ﹣10m ﹣2m +18m ﹣30m
(1)请你依据表格中的信息计算无人机飞行中的最大高度是多少m?
(2)五次操作后,无人机共飞行了多少m?
【考点】有理数的混合运算;正数和负数.
【专题】实数;运算能力.
【答案】(1)31m;
(2)85m.
【分析】(1)根据正数和负数的实际意义求得每次变化后距地面的高度后即可求得答案;
(2)根据正数和负数的实际意义列式计算即可.
【解答】解:(1)第1次距地面的高度:25m,
第2次距地面的高度:25﹣10=15(m),
第3次距地面的高度:15﹣2=13(m),
第4次距地面的高度:13+18=31(m),
第5次距地面的高度:31﹣30=1(m),
则无人机飞行中的最大高度是31m;
(2)25+10+2+18+30=85(m),
即五次操作后,无人机共飞行了85m.
【点评】本题考查有理数的混合运算,正数和负数,结合已知条件列得正确的算式是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 诸暨市期末)截至2024年12月6日,全国家电以旧换新数据平台显示,八大类家电产品带动销售约2020亿元.数“2020亿”用科学记数法表示为( )
A.2.020×1011 B.20.20×1011
C.0.2020×1012 D.0.2020×1013
2.(2024秋 大足区期末)按下列图示的程序计算,若开始输入的值为x=2,则最后输出的结果是( )
A.6 B.21 C.115 D.231
3.(2024秋 泸县校级期末)下列有理数中,是负数的是( )
A. B.2 C.0 D.﹣1
4.(2024秋 丰台区期末)中国是最早使用正负数表示具有相反意义的量的国家,早在我国秦汉时期的《九章算术》中就引入了负数.若在粮谷计算中,益实一斗(增加1斗)记为+1斗,那么损实七斗(减少7斗)记为( )
A.﹣1斗 B.+1斗 C.﹣7斗 D.+7斗
5.(2024秋 松江区期末)下列各数互为相反数的是( )
A.|﹣2|和﹣2 B.|﹣2|和2 C.﹣(﹣2)和2 D.|﹣2|和﹣(﹣2)
6.(2024秋 昆明期末)﹣2025的相反数是( )
A.2025 B. C.﹣2025 D.
7.(2024秋 包头期末)已知a的相反数是﹣2024,则a的倒数是( )
A.﹣2024 B.2024 C. D.
8.(2024秋 海曙区期末)算式﹣3﹣(﹣5)+(﹣2)写成省略加号的和式,正确的是( )
A.﹣3+5﹣2 B.﹣3+5+2 C.﹣3﹣5﹣2 D.3+5﹣2
9.(2024秋 长沙期末)我们在生活中经常使用的数是十进制数,如2639=2×103+6×102+3×101+9,表示十进制的数要用到10个数码(也叫数字):0,1,2,3,4,5,6,7,8,9.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制 0 1 2 3 4 5 6 7 8 9
A
B
C
D
E
F
十进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
例如,十六进制数71B=7×162+1×161+11=1819,即十六进制数71B相当于十进制数1819.那么十六进制数1D9相当于十进制数( )
A.473 B.117 C.1139 D.250
10.(2024秋 贵阳期末)中国是最早认识正数和负数的国家,魏晋时期的数学家刘徽就提出了负数的概念,如果零下3℃记作﹣3℃,那么+5℃表示( )
A.零上5℃ B.零下5℃ C.零上2℃ D.零下8℃
二.填空题(共5小题)
11.(2024秋 淮北期末)近似数5.08×103精确到 位.
12.(2024秋 常州期末)按图中程序计算,若输入﹣14,则输出的数为a;若输入正数b,则输出的数也为b,则ba+2的值为 .
13.(2024秋 泰兴市期末)﹣(﹣2025)= .
14.(2024秋 泸县校级期末)赤道半径为6378200米,用科学记数法表示为 米.
15.(2024秋 苏州期末)苏州地铁7号线于2024年12月1日正式开通运营,全长40500米,途径相城区、工业园区、吴中区,是古城东侧重要的客流通道.数据40500用科学记数法可表示为 .
三.解答题(共5小题)
16.(2024秋 大足区期末)2024年11月12日,第十五届中国航展在广东珠海举行,中国空军“八一”飞行表演队在航展上表演特技飞行,表演从空中某一位置开始,上升的高度记作正数,下降的高度记作负数,五次特技飞行高度记录如下:+2.5,﹣1.2,+1.2,﹣1.5,+0.8.(单位:千米)
(1)求飞机最后所在的位置比开始位置高还是低?高了或低了多少千米?
(2)若飞机平均上升1千米需消耗6升燃油,平均下降1千米需消耗4升燃油,则飞机在这5次特技飞行中,一共消耗多少升燃油?
17.(2024秋 海曙区期末)如图,数轴上每一小段的长度为1,点A、B、C、D在数轴上对应的数分别为a、b、c、d,
(1)若a与d互为相反数,则c= ;
(2)若|b|>|d|,则c 0(填“大于”或“小于”);a、b、c、d中,可能互为相反数的是 .
18.(2024秋 云岩区期末)贵阳地铁3号线自运营以来,为市民和游客带来了前所未有的便捷体验.如图是3号线部分站点示意图,小红作为地铁志愿者,从茶店站开始乘坐地铁做引导服务,最后她在A站结束服务活动.
若规定向花果园站方向为正,则小红当天乘地铁的站数按先后顺序依次记录如下(单位:站):﹣3,+4,+5,+1,﹣5,+2.
(1)请通过计算说明A站是哪一站?
(2)假设相邻两站之间的平均距离为1.5km,求这次小红志愿服务期间乘坐地铁的总路程为多少千米?
19.(2024秋 海门区期末)计算:
(1);
(2)(﹣10)3+[(﹣4)2﹣(1﹣32)×2].
20.(2024秋 金水区期末)无人机社团课上,悠悠同学在操纵一架无人机进行功能测试,无压人机从地面起飞后的高度变化情况如下表:
操作次数 第1次 第2次 第3次 第4次 第5次
高度变化 上升25m 下降10m 下降2m 上升18m 下降30m
记作 +25m ﹣10m ﹣2m +18m ﹣30m
(1)请你依据表格中的信息计算无人机飞行中的最大高度是多少m?
(2)五次操作后,无人机共飞行了多少m?
2025年中考数学高频易错考前冲刺:有理数
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 A D D. C A A D A A A
一.选择题(共10小题)
1.(2024秋 诸暨市期末)截至2024年12月6日,全国家电以旧换新数据平台显示,八大类家电产品带动销售约2020亿元.数“2020亿”用科学记数法表示为( )
A.2.020×1011 B.20.20×1011
C.0.2020×1012 D.0.2020×1013
【考点】科学记数法—表示较大的数.
【专题】实数;符号意识.
【答案】A
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:2020亿=202000000000=2.020×1011.
故选:A.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.(2024秋 大足区期末)按下列图示的程序计算,若开始输入的值为x=2,则最后输出的结果是( )
A.6 B.21 C.115 D.231
【考点】有理数的混合运算;代数式求值.
【专题】实数;运算能力.
【答案】D
【分析】根据题意列式计算,直至结果大于100即可.
【解答】解:若开始输入的值为x=2,
则3<100,返回继续运算,
6<100,返回继续运算,
21<100,返回继续运算,
231>100,输出结果,
故选:D.
【点评】本题考查有理数的混合运算,代数式求值,结合已知条件列得正确的算式是解题的关键.
3.(2024秋 泸县校级期末)下列有理数中,是负数的是( )
A. B.2 C.0 D.﹣1
【考点】正数和负数.
【专题】实数;符号意识.
【答案】D.
【分析】根据正数和负数的定义判断即可,注意:0既不是负数也不是正数.
【解答】解:A.0,是正数,故A选项错误;
B.2>0,是正数,故B选项错误;
C.0既不是正数,也不是负数,故C选项错误;
D.﹣1<0,是负数,故D选项正确;
故选:D.
【点评】本题考查了对正数和负数定义的理解,难度不大,注意0既不是正数也不是负数.
4.(2024秋 丰台区期末)中国是最早使用正负数表示具有相反意义的量的国家,早在我国秦汉时期的《九章算术》中就引入了负数.若在粮谷计算中,益实一斗(增加1斗)记为+1斗,那么损实七斗(减少7斗)记为( )
A.﹣1斗 B.+1斗 C.﹣7斗 D.+7斗
【考点】正数和负数.
【专题】实数;符号意识.
【答案】C
【分析】根据正数和负数是一组具有相反意义的量,据此即可求得答案.
【解答】解:中国是最早使用正负数表示具有相反意义的量的国家,早在我国秦汉时期的《九章算术》中就引入了负数.若在粮谷计算中,益实一斗(增加1斗)记为+1斗,那么损实七斗(减少7斗)记为﹣7斗,
故选:C.
【点评】本题考查正数和负数,掌握正数和负数是一组具有相反意义的量是解答本题的关键.
5.(2024秋 松江区期末)下列各数互为相反数的是( )
A.|﹣2|和﹣2 B.|﹣2|和2 C.﹣(﹣2)和2 D.|﹣2|和﹣(﹣2)
【考点】相反数.
【专题】实数;数感.
【答案】A
【分析】根据互为相反数的定义,只有符号不同的两个数叫做相反数,逐一判断各个选项即可.
【解答】解:A、|﹣2|=2,2和﹣2互为相反数,故该选项正确;
B、|﹣2|=2,2和2不互为相反数,故该选项错误;
C、﹣(﹣2)=2,2和2不互为相反数,故该选项错误;
D、|﹣2|=2,﹣(﹣2)=2,2和2不互为相反数,故该选项错误;
故选:A.
【点评】本题主要考查相反数的定义,掌握只有符号不同的两个数叫做相反数是关键.
6.(2024秋 昆明期末)﹣2025的相反数是( )
A.2025 B. C.﹣2025 D.
【考点】相反数.
【专题】实数;符号意识.
【答案】A
【分析】根据符号不同,绝对值相同的两个数互为相反数即可求得答案.
【解答】解:﹣2025的相反数是2025.
故选:A.
【点评】本题考查了相反数的概念,掌握只有符号不同的两个数叫做互为相反数是解答此题的关键.
7.(2024秋 包头期末)已知a的相反数是﹣2024,则a的倒数是( )
A.﹣2024 B.2024 C. D.
【考点】倒数;相反数.
【专题】实数;符号意识.
【答案】D
【分析】根据相反数、倒数的定义解答即可求得答案.
【解答】解:∵a和﹣2024互为相反数,
∴a+(﹣2024)=0,
∴a=2024,
2024的倒数是.
故选:D.
【点评】本题考查了相反数、倒数,掌握相反数、倒数的定义是解答此题的关键.
8.(2024秋 海曙区期末)算式﹣3﹣(﹣5)+(﹣2)写成省略加号的和式,正确的是( )
A.﹣3+5﹣2 B.﹣3+5+2 C.﹣3﹣5﹣2 D.3+5﹣2
【考点】有理数的加减混合运算.
【答案】A
【分析】利用去括号法则省略括号后直接选取答案.
【解答】解:﹣3﹣(﹣5)+(﹣2)=﹣3+5﹣2.
故选:A.
【点评】本题主要考查有理数的加法省略的书写,要学好有理数的加减运算须熟练掌握方法.
9.(2024秋 长沙期末)我们在生活中经常使用的数是十进制数,如2639=2×103+6×102+3×101+9,表示十进制的数要用到10个数码(也叫数字):0,1,2,3,4,5,6,7,8,9.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制 0 1 2 3 4 5 6 7 8 9
A
B
C
D
E
F
十进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
例如,十六进制数71B=7×162+1×161+11=1819,即十六进制数71B相当于十进制数1819.那么十六进制数1D9相当于十进制数( )
A.473 B.117 C.1139 D.250
【考点】有理数的混合运算.
【答案】A
【分析】由十六进制转化为十进制的方法,我们将各数位上的数字乘以其权重累加后,即可得到答案.
【解答】解:1D9=1×162+13×16+9
=256+208+9
=473.
故选:A.
【点评】本题考查的知识点是进制之间的转换,有理数的混合运算,解本题的关键是从表格中找出十六进制与十进制间的转换关系.
10.(2024秋 贵阳期末)中国是最早认识正数和负数的国家,魏晋时期的数学家刘徽就提出了负数的概念,如果零下3℃记作﹣3℃,那么+5℃表示( )
A.零上5℃ B.零下5℃ C.零上2℃ D.零下8℃
【考点】正数和负数;数学常识.
【专题】符号意识.
【答案】A
【分析】根据正负数表示意义相反的量即可求解.
【解答】解:∵零下3℃记作﹣3℃,
∴+5℃表示零上5℃,
故选:A.
【点评】本题考查了正负数的意义,了解正负数是表示意义相反的量是解题的关键.
二.填空题(共5小题)
11.(2024秋 淮北期末)近似数5.08×103精确到 十 位.
【考点】科学记数法与有效数字.
【专题】实数;数感.
【答案】十.
【分析】将科学记数法还原,确定数字8所在的数位即可.
【解答】解:将科学记数法还原得5.08×103=5080,8是十位数字,
故答案为:十.
【点评】本题考查判断近似数的精确数位,熟练掌握该知识点是关键.
12.(2024秋 常州期末)按图中程序计算,若输入﹣14,则输出的数为a;若输入正数b,则输出的数也为b,则ba+2的值为 8 .
【考点】有理数的混合运算;代数式求值.
【专题】实数;整式;运算能力.
【答案】8.
【分析】根据题意列式计算后求得a,b的值,然后代入ba+2中计算即可.
【解答】解:若输入﹣14,
则(﹣14+6)÷(﹣2)2=﹣8÷4=﹣2<0,返回继续运算,
(﹣2+6)÷(﹣2)2=4÷4=1>0,输出结果,
则a=1,
∵输入正数b,则输出的数也为b,
∴(b+6)÷(﹣2)2=b,
解得:b=2,
则ba+2=21+2=8,
故答案为:8.
【点评】本题考查有理数的混合运算,代数式求值,结合已知条件列得正确的算式是解题的关键.
13.(2024秋 泰兴市期末)﹣(﹣2025)= 2025 .
【考点】相反数.
【专题】实数;运算能力.
【答案】2025.
【分析】利用相反数的含义化简双重符号即可.
【解答】解:根据题意可知,﹣(﹣2025)=2025.
故答案为:2025.
【点评】本题考查的是相反数的含义,掌握相反数的含义是关键.
14.(2024秋 泸县校级期末)赤道半径为6378200米,用科学记数法表示为 6.3782×106 米.
【考点】科学记数法—表示较大的数.
【专题】实数;符号意识.
【答案】6.3782×106.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:6378200=6.3782×106.
故答案为:6.3782×106.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
15.(2024秋 苏州期末)苏州地铁7号线于2024年12月1日正式开通运营,全长40500米,途径相城区、工业园区、吴中区,是古城东侧重要的客流通道.数据40500用科学记数法可表示为 4.05×104 .
【考点】科学记数法—表示较大的数.
【专题】实数;符号意识.
【答案】4.05×104.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:40500=4.05×104.
故答案为:4.05×104.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
三.解答题(共5小题)
16.(2024秋 大足区期末)2024年11月12日,第十五届中国航展在广东珠海举行,中国空军“八一”飞行表演队在航展上表演特技飞行,表演从空中某一位置开始,上升的高度记作正数,下降的高度记作负数,五次特技飞行高度记录如下:+2.5,﹣1.2,+1.2,﹣1.5,+0.8.(单位:千米)
(1)求飞机最后所在的位置比开始位置高还是低?高了或低了多少千米?
(2)若飞机平均上升1千米需消耗6升燃油,平均下降1千米需消耗4升燃油,则飞机在这5次特技飞行中,一共消耗多少升燃油?
【考点】有理数的混合运算;正数和负数.
【专题】实数;运算能力.
【答案】(1)飞机最后所在的位置比开始位置高了,高了1.8千米;
(2)37.8升燃油.
【分析】(1)根据正数和负数的实际意义列式计算即可;
(2)根据正数和负数的实际意义求得上升的总高度,将其乘以6,下降的总高度,将其乘以4,然后再相加即可.
【解答】解:(1)2.5﹣1.2+1.2﹣1.5+0.8=1.8(千米),
即飞机最后所在的位置比开始位置高了,高了1.8千米;
(2)(2.5+1.2+0.8)×6+(1.2+1.5)×4
=27+10.8
=37.8(升),
即飞机在这5次特技飞行中,一共消耗37.8升燃油.
【点评】本题考查有理数的混合运算,正数和负数,结合已知条件列得正确的算式是解题的关键.
17.(2024秋 海曙区期末)如图,数轴上每一小段的长度为1,点A、B、C、D在数轴上对应的数分别为a、b、c、d,
(1)若a与d互为相反数,则c= ﹣1 ;
(2)若|b|>|d|,则c 小于 0(填“大于”或“小于”);a、b、c、d中,可能互为相反数的是 c与d .
【考点】数轴;相反数;绝对值.
【专题】实数;数感.
【答案】(1)﹣1;
(2)小于;c与d.
【分析】(1)根据相反数的定义以及观察数轴即可求解;
(2)根据绝对值、相反数的定义,即可求解.
【解答】解:(1)由题意可得:
∴a在数轴上表示﹣4,d在数轴上表示4,
∴c=﹣1,
故答案为:﹣1;
(2)∵|b|>|d|,
∴c小于0,
∴a、b、c、d中,可能互为相反数的是c与d,
故答案为:小于;c与d.
【点评】本题考查了数轴,相反数、绝对值的定义,解题的关键是掌握相关知识并数形结合.
18.(2024秋 云岩区期末)贵阳地铁3号线自运营以来,为市民和游客带来了前所未有的便捷体验.如图是3号线部分站点示意图,小红作为地铁志愿者,从茶店站开始乘坐地铁做引导服务,最后她在A站结束服务活动.
若规定向花果园站方向为正,则小红当天乘地铁的站数按先后顺序依次记录如下(单位:站):﹣3,+4,+5,+1,﹣5,+2.
(1)请通过计算说明A站是哪一站?
(2)假设相邻两站之间的平均距离为1.5km,求这次小红志愿服务期间乘坐地铁的总路程为多少千米?
【考点】有理数的混合运算;正数和负数.
【专题】实数;运算能力.
【答案】(1)黔灵山公园站;
(2)30千米.
【分析】(1)根据正数和负数的实际意义列式计算即可;
(2)根据正数和负数的实际意义先求得总站数,再与1.5相乘并计算即可.
【解答】解:(1)﹣3+4+5+1﹣5+2=4(站),
则A站是黔灵山公园站;
(2)(3+4+5+1+5+2)×1.5
=20×1.5
=30(千米),
即这次小红志愿服务期间乘坐地铁的总路程为30千米.
【点评】本题考查有理数的混合运算,正数和负数,结合已知条件列得正确的算式是解题的关键.
19.(2024秋 海门区期末)计算:
(1);
(2)(﹣10)3+[(﹣4)2﹣(1﹣32)×2].
【考点】有理数的混合运算.
【专题】实数;运算能力.
【答案】(1)﹣8;
(2)﹣968.
【分析】(1)先算乘方,再算乘除即可;
(2)先算乘方,小括号里面的,中括号里面的,再算加法即可.
【解答】解:(1)原式=(﹣8)
=(﹣18)
=﹣8;
(2)原式=(﹣1000)+[16﹣(1﹣9)×2]
=﹣1000+(16+8×2)
=﹣1000+(16+16)
=﹣1000+32
=﹣968.
【点评】本题考查的是有理数的混合运算,熟知有理数混合运算的法则是解题的关键.
20.(2024秋 金水区期末)无人机社团课上,悠悠同学在操纵一架无人机进行功能测试,无压人机从地面起飞后的高度变化情况如下表:
操作次数 第1次 第2次 第3次 第4次 第5次
高度变化 上升25m 下降10m 下降2m 上升18m 下降30m
记作 +25m ﹣10m ﹣2m +18m ﹣30m
(1)请你依据表格中的信息计算无人机飞行中的最大高度是多少m?
(2)五次操作后,无人机共飞行了多少m?
【考点】有理数的混合运算;正数和负数.
【专题】实数;运算能力.
【答案】(1)31m;
(2)85m.
【分析】(1)根据正数和负数的实际意义求得每次变化后距地面的高度后即可求得答案;
(2)根据正数和负数的实际意义列式计算即可.
【解答】解:(1)第1次距地面的高度:25m,
第2次距地面的高度:25﹣10=15(m),
第3次距地面的高度:15﹣2=13(m),
第4次距地面的高度:13+18=31(m),
第5次距地面的高度:31﹣30=1(m),
则无人机飞行中的最大高度是31m;
(2)25+10+2+18+30=85(m),
即五次操作后,无人机共飞行了85m.
【点评】本题考查有理数的混合运算,正数和负数,结合已知条件列得正确的算式是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
