【中考押题卷】2025年中考数学高频易错考前冲刺:代数式(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:代数式(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 772.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 08:18:12 | ||
图片预览




文档简介
2025年中考数学高频易错考前冲刺:代数式
一.选择题(共10小题)
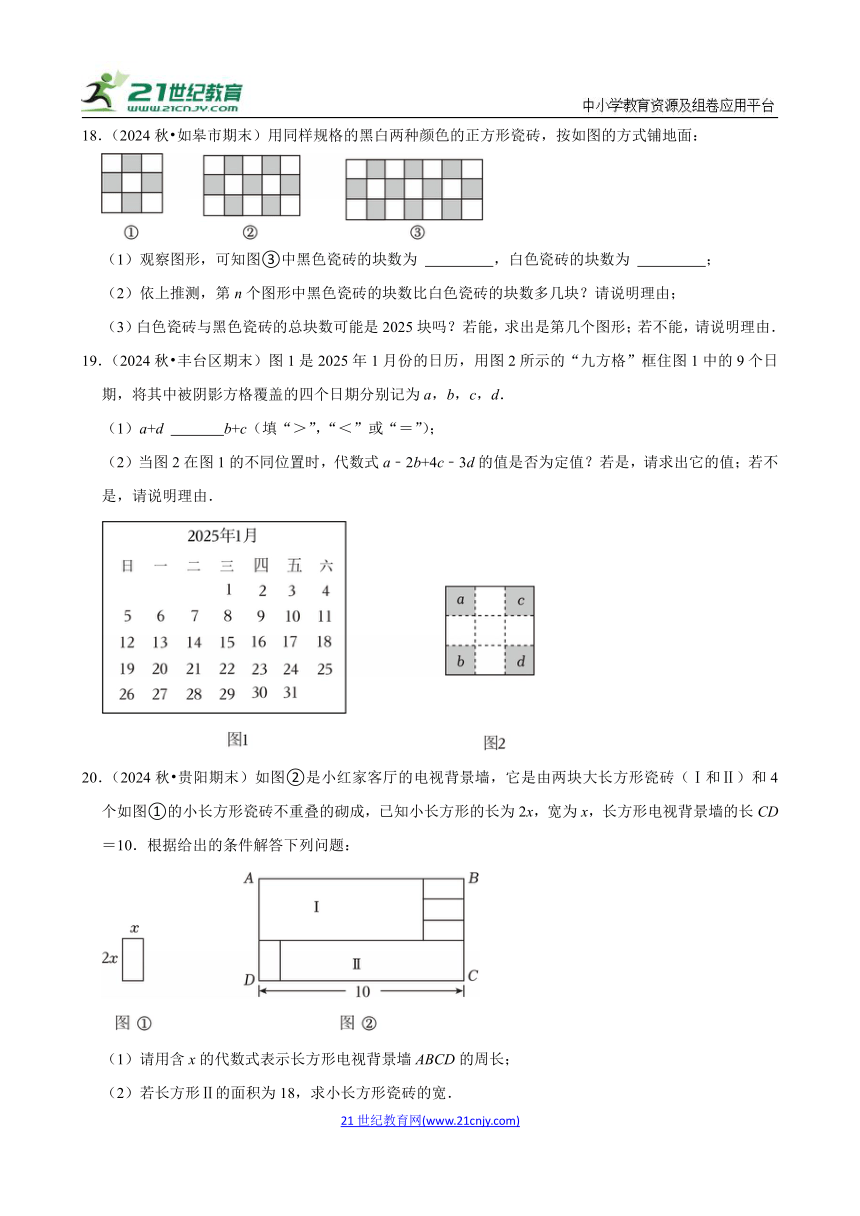
1.(2024秋 海沧区期末)下列单项式中,能与2a合并成一项的是( )
A.2 B.﹣3a C.2ab D.d2
2.(2024秋 郑州期末)在数学实践课上,小郑将五边形区域分割成若干个三角形,他在五边形内取一定数量的点,连同五边形的5个顶点,逐步连接这些点,保证所有连线不再相交产生新的点,直到五边形内所有区域都变成三角形.如当五边形内有1个点时,可分得5个三角形;当五边形内有2个点时,可分得7个三角形(不计被分割的三角形).则当五边形内有2025个点时,可分得三角形的个数为( )
A.22025 B.20252 C.4053 D.4050
3.(2024秋 越城区校级期末)如图,一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3.2米的正方形框.已知铺这个框恰好用了144块边长为0.8米的正方形花岗石.则这一标志性建筑的底面边长x是( )米.
A.3.8 B.4 C.4.2 D.5
4.(2024秋 包头期末)下列说法中正确的是( )
A.πx3的系数是
B.y﹣x2y+5xy2的次数是7
C.4不是单项式
D.﹣2xy与4yx是同类项
5.(2024秋 泸县校级期末)下列各组单项式中,不是同类项的是( )
A.ab2和 B.3x和4x
C.3ab和﹣ba D.2和3
6.(2024秋 松江区期末)下列各式中,不是代数式的是( )
A. B.3a+1=0
C.x D.0
7.(2024秋 苏州期末)下列运算中,正确的是( )
A.2a+a=2a2 B.2a+3b=5ab
C.5y2﹣3y2=2 D.3ab2﹣2ab2=ab2
8.(2024秋 海曙区期末)下列计算正确的是( )
A.3a﹣2a=1 B.3a+2a=5a2
C. D.3ab2﹣2a2b=ab
9.(2024秋 丰台区期末)下面计算正确的是( )
A.﹣2x﹣2x=0 B.x4﹣x2=x2
C.x2+x2=2x4 D.xy﹣2xy=﹣xy
10.(2024秋 泸县校级期末)近年来,重庆作为网红城市,旅游业市场发展迅速.据调查,今年重庆5月份旅游旺季全市旅游业收入为x亿元,6月份比5月份减少了25%,暑期如约而至,7月份比6月份增加了78%,则7月份重庆全市的旅游业收入是( )亿元.
A.(1﹣25%+78%)x B.(1﹣25%)(1+78%)x
C.(1﹣25%)x+(1+78%)x D.[1﹣25%(1+78%)]x
二.填空题(共5小题)
11.(2024秋 南通期末)若单项式﹣xmy3与单项式2x4y3是同类项,则m的值为 .
12.(2024秋 黄浦区期末)合并同类项: .
13.(2024秋 海曙区期末)若单项式5x﹣m+1y3与单项式﹣x3yn+1的和仍是一个单项式,则|mn|的值是 .
14.(2024秋 苏州期末)若x﹣2y﹣3=0,则代数式1﹣2x+4y的值为 .
15.(2024秋 长沙期末)单项式3am﹣5b3与﹣8a2b1﹣2n是同类项,则nm= .
三.解答题(共5小题)
16.(2024秋 临平区期末)在体育课中,我们经常根据“立正,向右转,向左转、向后转”这些口令进行相应的运动,这些运动是可以连续进行的,现规定:把连续执行2个口令的结果,叫作这2个口令相加所得到的和,并用“ ”表示相加.例如:向右转 向左转=立正,向左转 向左转=向后转,等等.分别用数字符号0,1,﹣1,2表示立正,向右转,向左转,向后转,可以建立如下的体育口令加法运算表.
0(立正) 1(向右转) ﹣1(向左转) 2(向后转)
0(立正) 0 1 ﹣1 2
1(向右转) 1 2 0 n
﹣1(向左转) ﹣1 0 2 1
2(向后转) 2 x y m
请完成下面问题:
(1)上述表格中,x= ,y= ,m= .
(2)若用字母a表示任何一种体育口令,则a 0= .
(3)判断这种体育口令的加法运算是否满足交换律和结合律?请举例验证(各举一个例子即可).
17.(2024秋 太仓市期末)已知线段AC,以AC为斜边作Rt△ABC和Rt△ADC,连接BD,M、N分别是线段AC、BD的中点,连接MN、MB.
(1)如图1,Rt△ABC和Rt△ADC在线段AC的两侧.
①求证:MN⊥BD;
②若∠BAC=45°,∠DAC=28°;请求出∠BMN的度数;
(2)如图2,Rt△ABC和Rt△ADC在线段AC的同侧,若∠BAC=α,∠DAC=β(α>β),则∠BMN的度数为 (用含α、β的代数式表示)
18.(2024秋 如皋市期末)用同样规格的黑白两种颜色的正方形瓷砖,按如图的方式铺地面:
(1)观察图形,可知图③中黑色瓷砖的块数为 ,白色瓷砖的块数为 ;
(2)依上推测,第n个图形中黑色瓷砖的块数比白色瓷砖的块数多几块?请说明理由;
(3)白色瓷砖与黑色瓷砖的总块数可能是2025块吗?若能,求出是第几个图形;若不能,请说明理由.
19.(2024秋 丰台区期末)图1是2025年1月份的日历,用图2所示的“九方格”框住图1中的9个日期,将其中被阴影方格覆盖的四个日期分别记为a,b,c,d.
(1)a+d b+c(填“>”,“<”或“=”);
(2)当图2在图1的不同位置时,代数式a﹣2b+4c﹣3d的值是否为定值?若是,请求出它的值;若不是,请说明理由.
20.(2024秋 贵阳期末)如图②是小红家客厅的电视背景墙,它是由两块大长方形瓷砖(Ⅰ和Ⅱ)和4个如图①的小长方形瓷砖不重叠的砌成,已知小长方形的长为2x,宽为x,长方形电视背景墙的长CD=10.根据给出的条件解答下列问题:
(1)请用含x的代数式表示长方形电视背景墙ABCD的周长;
(2)若长方形Ⅱ的面积为18,求小长方形瓷砖的宽.
2025年中考数学高频易错考前冲刺:代数式
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B D A. B. D. C. D. B
一.选择题(共10小题)
1.(2024秋 海沧区期末)下列单项式中,能与2a合并成一项的是( )
A.2 B.﹣3a C.2ab D.d2
【考点】合并同类项;单项式.
【专题】整式;运算能力.
【答案】B
【分析】所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
【解答】解:A、所含字母不相同,不是同类项;
B、符合同类项的定义,是同类项;
C、所含字母不相同,不是同类项;
D、所含字母不相同,不是同类项;
故选:B.
【点评】本题考查同类项的定义,解题的关键是正确理解同类项的定义,本题属于基础题型.
2.(2024秋 郑州期末)在数学实践课上,小郑将五边形区域分割成若干个三角形,他在五边形内取一定数量的点,连同五边形的5个顶点,逐步连接这些点,保证所有连线不再相交产生新的点,直到五边形内所有区域都变成三角形.如当五边形内有1个点时,可分得5个三角形;当五边形内有2个点时,可分得7个三角形(不计被分割的三角形).则当五边形内有2025个点时,可分得三角形的个数为( )
A.22025 B.20252 C.4053 D.4050
【考点】规律型:数字的变化类.
【专题】规律型;运算能力.
【答案】C
【分析】先找出规律,再计算即可.
【解答】解:根据题意结合图形,
当五边形内有1个点时,可分成的三角形个数为:5=1×2+3;
当五边形内有2个点时,可分成的三角形个数为:7=2×2+3;
当五边形内有3个点时,可分成的三角形个数为:9=3×2+3;
......;
当五边形内有n个点时,可分成的三角形个数为:(2n+3)个;
所以当五边形内有2025个点时,可分成的三角形个数为2×2025+3=4053个.
故选:C.
【点评】本题考查了图形的变化类问题,解题的关键是仔细观察图形并找到其中的规律.
3.(2024秋 越城区校级期末)如图,一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3.2米的正方形框.已知铺这个框恰好用了144块边长为0.8米的正方形花岗石.则这一标志性建筑的底面边长x是( )米.
A.3.8 B.4 C.4.2 D.5
【考点】列代数式.
【专题】整式;运算能力.
【答案】B
【分析】设标志性建筑底面的边长是x米,则外面的边长是(x+6.4)米,利用两个正方形的面积差等于144块边长为0.8米的正方形花岗石的面积列出方程解答即可.
【解答】解:∵标志性建筑底面正方形的边长是x米,
∴外面的边长是(x+3.2+3.2)米,
已知铺这个框恰好用了144块边长为0.8米的正方形花岗石,
∴(x+3.2+3.2)2﹣x2=0.8×0.8×144,
整理得:12x+36=108,
解得:x=4,
答:标志性建筑底面的边长是4米,
故选:B.
【点评】本题考查列代数式,掌握正方形的面积是解决问题的关键.
4.(2024秋 包头期末)下列说法中正确的是( )
A.πx3的系数是
B.y﹣x2y+5xy2的次数是7
C.4不是单项式
D.﹣2xy与4yx是同类项
【考点】同类项;单项式;多项式.
【答案】D
【分析】根据单项式的定义,同类项的定义,多项式的次数,可得答案.
【解答】解:A、πx3的系数是π,故A不符合题意;
B、y﹣x2y+5xy2的次数是3,故B不符合题意;
C、4是单项式,故C不符合题意;
D、﹣2xy与4yx是同类项,故D符合题意;
故选:D.
【点评】本题考查了同类项、单项式、多项式,熟记单项式的定义,同类项的定义,多项式的次数是解题关键.
5.(2024秋 泸县校级期末)下列各组单项式中,不是同类项的是( )
A.ab2和 B.3x和4x
C.3ab和﹣ba D.2和3
【考点】同类项;单项式.
【专题】整式;运算能力.
【答案】A.
【分析】所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
【解答】解:A、相同字母的指数不相同,不是同类项;
B、符合同类项的定义,是同类项;
C、符合同类项的定义,是同类项;
D、符合同类项的定义,是同类项;
故选:A.
【点评】本题考查同类项的定义,解题的关键是正确理解同类项的定义,本题属于基础题型.
6.(2024秋 松江区期末)下列各式中,不是代数式的是( )
A. B.3a+1=0
C.x D.0
【考点】代数式.
【专题】整式;符号意识.
【答案】B.
【分析】根据代数式的概念,用运算符号把数字与字母连接而成的式子叫做代数式.单独的一个数或一个字母也是代数式.
【解答】解:A.,是代数式;
B.3a+1=0,是等式,不是代数式;
C.x,是代数式;
D.0,是代数式.
故选:B.
【点评】本题主要考查了代数式,解题关键是熟练掌握代数式的定义.
7.(2024秋 苏州期末)下列运算中,正确的是( )
A.2a+a=2a2 B.2a+3b=5ab
C.5y2﹣3y2=2 D.3ab2﹣2ab2=ab2
【考点】合并同类项.
【专题】计算题;整式;运算能力.
【答案】D.
【分析】根据整式的加减运算法则即可求出答案.
【解答】解:A、2a+a=3a≠2a2,故A错误;
B、2a+3b≠5ab,故B错误;
C、5y2﹣3y2=2y2≠2,故C错误;
D、3ab2﹣2ab2=ab2,故D正确.
故选:D.
【点评】本题考查整式的运算法则,解题的关键是熟练运用整式的运算,本题属于基础题型.
8.(2024秋 海曙区期末)下列计算正确的是( )
A.3a﹣2a=1 B.3a+2a=5a2
C. D.3ab2﹣2a2b=ab
【考点】合并同类项.
【专题】计算题;整式;运算能力.
【答案】C.
【分析】根据整式的加减运算法则即可求出答案.
【解答】解:A、3a﹣2a=a≠1,故A错误;
B、3a+2a=5a≠5a2,故B错误;
C、0,故C正确;
D、3ab2﹣2a2b≠ab,故D错误.
故选:C.
【点评】本题考查整式的运算法则,解题的关键是熟练运用整式的运算,本题属于基础题型.
9.(2024秋 丰台区期末)下面计算正确的是( )
A.﹣2x﹣2x=0 B.x4﹣x2=x2
C.x2+x2=2x4 D.xy﹣2xy=﹣xy
【考点】合并同类项.
【专题】计算题;整式;运算能力.
【答案】D.
【分析】根据整式的加减运算法则即可求出答案.
【解答】解:A、﹣2x﹣2x=﹣4x≠0,故A错误;
B、x4﹣x2≠x2,故B错误;
C、x2+x2=2x2≠2x4,故C错误;
D、xy﹣2xy=﹣xy,故D正确.
故选:D.
【点评】本题考查整式的运算法则,解题的关键是熟练运用整式的运算,本题属于基础题型.
10.(2024秋 泸县校级期末)近年来,重庆作为网红城市,旅游业市场发展迅速.据调查,今年重庆5月份旅游旺季全市旅游业收入为x亿元,6月份比5月份减少了25%,暑期如约而至,7月份比6月份增加了78%,则7月份重庆全市的旅游业收入是( )亿元.
A.(1﹣25%+78%)x B.(1﹣25%)(1+78%)x
C.(1﹣25%)x+(1+78%)x D.[1﹣25%(1+78%)]x
【考点】列代数式.
【专题】整式;应用意识.
【答案】B
【分析】根据5月份的旅游业收入是x亿元,用x把6月份的旅游业收入表示出来为(1﹣25%)x亿元,进而得出7月份旅游业收入列出式子(1﹣25%)x×(1+78%)亿元,即可得出选项.
【解答】解:∵5月份的旅游业收入是x亿元,
则6月份的旅游业收入是(1﹣25%)x亿元,
7月份重庆全市的旅游业收入(1﹣25%)(1+78%)x亿元,
故选:B.
【点评】此题主要考查了列代数式,解此题的关键是能用x把6、7月份的旅游业收入表示出来.
二.填空题(共5小题)
11.(2024秋 南通期末)若单项式﹣xmy3与单项式2x4y3是同类项,则m的值为 4 .
【考点】同类项.
【专题】计算题;整式;运算能力.
【答案】4.
【分析】根据同类项的定义直接得出m的值.
【解答】解:由同类项的定义可知m=4.
故答案为:4.
【点评】本题考查了同类项的定义,掌握同类项的定义:所含字母相同,相同字母的指数也相同的项叫同类项.
12.(2024秋 黄浦区期末)合并同类项: .
【考点】合并同类项.
【专题】计算题;整式;运算能力.
【答案】.
【分析】合并同类项的法则是系数和系数相加作为系数,字母和字母的指数不变.
【解答】解:.
故答案为:.
【点评】本题主要考查了合并同类项的法则,熟练掌握运算法则是解题的关键.
13.(2024秋 海曙区期末)若单项式5x﹣m+1y3与单项式﹣x3yn+1的和仍是一个单项式,则|mn|的值是 4 .
【考点】合并同类项;单项式;绝对值.
【专题】计算题;方程思想;整式;运算能力.
【答案】4.
【分析】根据同类项的定义列出方程,再求解即可.
【解答】解:由同类项的定义可知﹣m+1=3,n+1=3,
解得m=﹣2,n=2,
∴|mn|=|(﹣2)×2|=4.
故答案为:4.
【点评】本题考查了同类项的定义,掌握同类项的定义:所含字母相同,相同字母的指数也相同的项叫同类项.
14.(2024秋 苏州期末)若x﹣2y﹣3=0,则代数式1﹣2x+4y的值为 ﹣5 .
【考点】代数式求值.
【专题】计算题;整体思想;整式;运算能力.
【答案】﹣5.
【分析】根据已知条件将要求代数式变形,然后整体代入求值即可.
【解答】解:∵1﹣2x+4y=﹣2x+4y+1,
∵x﹣2y﹣3=0,
∴x﹣2y=3,
∴当x﹣2y=3时,原式=﹣2x+4y+1=﹣2(x﹣2y)+1=﹣2×3+1=﹣5.
故答案为:﹣5.
【点评】本题考查代数式求值,按照代数式规定的运算,计算的结果就是代数式的值.
15.(2024秋 长沙期末)单项式3am﹣5b3与﹣8a2b1﹣2n是同类项,则nm= ﹣1 .
【考点】同类项.
【专题】计算题;方程思想;整式;运算能力.
【答案】见试题解答内容
【分析】根据同类项的定义列出方程,再求解即可.
【解答】解:由同类项的定义可知m﹣5=2,1﹣2n=3,
解得m=7,n=﹣1,
∴nm=(﹣1)7=﹣1.
故答案为:﹣1.
【点评】本题考查了同类项的定义,掌握同类项的定义:所含字母相同,相同字母的指数也相同的项叫同类项.
三.解答题(共5小题)
16.(2024秋 临平区期末)在体育课中,我们经常根据“立正,向右转,向左转、向后转”这些口令进行相应的运动,这些运动是可以连续进行的,现规定:把连续执行2个口令的结果,叫作这2个口令相加所得到的和,并用“ ”表示相加.例如:向右转 向左转=立正,向左转 向左转=向后转,等等.分别用数字符号0,1,﹣1,2表示立正,向右转,向左转,向后转,可以建立如下的体育口令加法运算表.
0(立正) 1(向右转) ﹣1(向左转) 2(向后转)
0(立正) 0 1 ﹣1 2
1(向右转) 1 2 0 n
﹣1(向左转) ﹣1 0 2 1
2(向后转) 2 x y m
请完成下面问题:
(1)上述表格中,x= ﹣1 ,y= 1 ,m= 0 .
(2)若用字母a表示任何一种体育口令,则a 0= a .
(3)判断这种体育口令的加法运算是否满足交换律和结合律?请举例验证(各举一个例子即可).
【考点】列代数式;正数和负数;有理数的混合运算.
【专题】实数;整式;运算能力.
【答案】(1)﹣1;1;0;
(2)a;
(3)都符合,举例见解析.
【分析】(1)根据新定义分别求出向后转 向右转,向后转 向左转,向后转 向后转的结果即可得到答案;
(2)根据任意口令 立正=该任意口令即可得到答案;
(3)只需要证明向右转 向左转=立正,向左转 向右转=立正,向右转 向左转+向后转=向右转 (向左转+向后转)即可.
【解答】解:(1)由向后转 向右转=向左转,可得x=﹣1;
由向后转 向左转=向右转,可得y=1,
∵向后转 向后转=立正,
∴m=0;
(2)由任意口令 立正=该任意口令可得a 0=a;
(3)由表可知向右转 向左转=立正,向左转 向右转=立正,
∴符合加法的交换律;
由条件可知向右转 向左转+向后转=向右转,
由条件可知向右转 向左转+向后转=向右转 (向左转+向后转),
∴符合加法交换律.
【点评】本题主要考查了新定义,熟练掌握有理数混合运算法则是关键.
17.(2024秋 太仓市期末)已知线段AC,以AC为斜边作Rt△ABC和Rt△ADC,连接BD,M、N分别是线段AC、BD的中点,连接MN、MB.
(1)如图1,Rt△ABC和Rt△ADC在线段AC的两侧.
①求证:MN⊥BD;
②若∠BAC=45°,∠DAC=28°;请求出∠BMN的度数;
(2)如图2,Rt△ABC和Rt△ADC在线段AC的同侧,若∠BAC=α,∠DAC=β(α>β),则∠BMN的度数为 α﹣β (用含α、β的代数式表示)
【考点】列代数式.
【专题】整式;线段、角、相交线与平行线;运算能力.
【答案】(1)①见解析;②73°;
(2)α﹣β.
【分析】(1)①根据直角三角形的性质得到,,根据等腰三角形的三线合一证明即可;②根据直角三角形的性质得到BM=AM=MC=DM,根据等腰三角形的性质、三角形内角和定理计算,得到答案.
(2)根据直角三角形的性质得到AM=BM=MD,根据等腰三角形的性质、三角形内角和定理计算,得到答案.
【解答】(1)①证明:连接MD,
由条件可知,,
∴BM=DM,
又∵N是BD的中点,
∴MN⊥BD;
②解:有条件可知BM=AM=MC=DM,
又∵∠BAC=45°,∠DAC=28°,
∴∠MBC=∠MCB=90°﹣45°=45°,∠MCD=∠CDM=90°﹣28°=62°,
∴∠BMD=360°﹣45°×2﹣62°×2=146°,
∵BM=DM,MN⊥BD,
∴,
∴.
(2)解:连接MD,
由条件可知AM=BM=MD,
∴∠MBA=∠BAC=α,∠MDA=∠DAC=β,
∴∠AMB=180°﹣2α,∠CMD=2β,
∴∠BMD=180°﹣∠AMB﹣∠CMD=2α﹣2β,
∵BM=MD,N是BD的中点,
∴.
【点评】本题考查的是直角三角形的性质、等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.
18.(2024秋 如皋市期末)用同样规格的黑白两种颜色的正方形瓷砖,按如图的方式铺地面:
(1)观察图形,可知图③中黑色瓷砖的块数为 11 ,白色瓷砖的块数为 10 ;
(2)依上推测,第n个图形中黑色瓷砖的块数比白色瓷砖的块数多几块?请说明理由;
(3)白色瓷砖与黑色瓷砖的总块数可能是2025块吗?若能,求出是第几个图形;若不能,请说明理由.
【考点】规律型:图形的变化类.
【专题】规律型;运算能力.
【答案】(1)11,10;
(2)1,理由见解析;
(3)能,第337个图形.
【分析】(1)直接由图形解答即可;
(2)根据每一个图形的黑色瓷砖块数比前一个图形多3,每一个图形的白色瓷砖块数比前一个图形多3,得出规律,由此求得答案即可;
(3)利用(2)的规律根据“白色瓷砖与黑色瓷砖的总块数是2025块”这个假设成立,列方程,求得整数解就能,否则不能.
【解答】解:(1)由图形可知图③中黑色瓷砖的块数为11,白色瓷砖的块数为10,
故答案为:11;10;
(2)第一个图形:黑色瓷砖的块数为5,白两种瓷砖的总块数为4;
第二个图形:黑色瓷砖的块数为8,白两种瓷砖的总块数为7;
第三个图形:黑色瓷砖的块数为11,白两种瓷砖的总块数为10;
……,
第n个图形中黑色瓷砖的块数为3n+2;白两种瓷砖的总块数为3n+1,
3n+2﹣(3n+1)=3n+2﹣3n﹣1=1;
(3)能,理由如下:
假设白色瓷砖与黑色瓷砖的总块数是2025块,
则可得:3n+2+(3n+1)=2025,
即6n=2022,
∴n=337,是整数
所以假设成立.
【点评】此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.
19.(2024秋 丰台区期末)图1是2025年1月份的日历,用图2所示的“九方格”框住图1中的9个日期,将其中被阴影方格覆盖的四个日期分别记为a,b,c,d.
(1)a+d = b+c(填“>”,“<”或“=”);
(2)当图2在图1的不同位置时,代数式a﹣2b+4c﹣3d的值是否为定值?若是,请求出它的值;若不是,请说明理由.
【考点】列代数式;代数式求值.
【专题】整式;几何直观;运算能力.
【答案】(1)=;(2)代数式a﹣2b+4c﹣3d的值是定值,这个定值是﹣68.
【分析】(1)根据图形,可以得到b、c、d和a的关系,然后计算即可;
(2)化简代数式a﹣2b+4c﹣3d,然后观察结果即可解答本题.
【解答】解:(1)由图可得,
b=a+14,c=a+2,d=a+16,
∴a+d=a+a+16=2a+16,b+c=a+14+a+2=2a+16,
∴a+d=b+c,
故答案为:=;
(2)由图可得,
b=a+14,c=a+2,d=a+16,
a﹣2b+4c﹣3d
=a﹣2(a+14)+4(a+2)﹣3(a+16)
=a﹣2a﹣28+4a+8﹣3a﹣48
=﹣68,
即代数式a﹣2b+4c﹣3d的值是定值,这个定值是﹣68.
【点评】本题考查整式的加减、列代数式,熟练掌握运算法则是解答本题的关键.
20.(2024秋 贵阳期末)如图②是小红家客厅的电视背景墙,它是由两块大长方形瓷砖(Ⅰ和Ⅱ)和4个如图①的小长方形瓷砖不重叠的砌成,已知小长方形的长为2x,宽为x,长方形电视背景墙的长CD=10.根据给出的条件解答下列问题:
(1)请用含x的代数式表示长方形电视背景墙ABCD的周长;
(2)若长方形Ⅱ的面积为18,求小长方形瓷砖的宽.
【考点】列代数式.
【专题】整式;运算能力.
【答案】(1)10x+20;
(2)小长方形瓷砖的宽为1.
【分析】(1)根据所给图形,得出长方形ABCD的宽可表示为5x,据此可解决问题.
(2)根据长方形Ⅱ的面积为18,建立关于x的方程,据此可解决问题.
【解答】解:(1)由题知,
长方形ABCD的宽可表示为5x,
又因为CD=10,
所以长方形电视背景墙ABCD的周长可表示为:2(5x+10)=10x+20.
(2)长方形Ⅱ的长为10﹣x,宽为2x,
因为长方形Ⅱ的面积为18,
所以2x(10﹣x)=18,
解得x1=1,x2=9.
当x=9时,BC=5×9=45>10,
故x=0舍去,
所以小长方形瓷砖的宽为1.
【点评】本题主要考查了列代数式,能根据题意分别表示出长方形ABCD及长方形Ⅱ的面积是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 海沧区期末)下列单项式中,能与2a合并成一项的是( )
A.2 B.﹣3a C.2ab D.d2
2.(2024秋 郑州期末)在数学实践课上,小郑将五边形区域分割成若干个三角形,他在五边形内取一定数量的点,连同五边形的5个顶点,逐步连接这些点,保证所有连线不再相交产生新的点,直到五边形内所有区域都变成三角形.如当五边形内有1个点时,可分得5个三角形;当五边形内有2个点时,可分得7个三角形(不计被分割的三角形).则当五边形内有2025个点时,可分得三角形的个数为( )
A.22025 B.20252 C.4053 D.4050
3.(2024秋 越城区校级期末)如图,一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3.2米的正方形框.已知铺这个框恰好用了144块边长为0.8米的正方形花岗石.则这一标志性建筑的底面边长x是( )米.
A.3.8 B.4 C.4.2 D.5
4.(2024秋 包头期末)下列说法中正确的是( )
A.πx3的系数是
B.y﹣x2y+5xy2的次数是7
C.4不是单项式
D.﹣2xy与4yx是同类项
5.(2024秋 泸县校级期末)下列各组单项式中,不是同类项的是( )
A.ab2和 B.3x和4x
C.3ab和﹣ba D.2和3
6.(2024秋 松江区期末)下列各式中,不是代数式的是( )
A. B.3a+1=0
C.x D.0
7.(2024秋 苏州期末)下列运算中,正确的是( )
A.2a+a=2a2 B.2a+3b=5ab
C.5y2﹣3y2=2 D.3ab2﹣2ab2=ab2
8.(2024秋 海曙区期末)下列计算正确的是( )
A.3a﹣2a=1 B.3a+2a=5a2
C. D.3ab2﹣2a2b=ab
9.(2024秋 丰台区期末)下面计算正确的是( )
A.﹣2x﹣2x=0 B.x4﹣x2=x2
C.x2+x2=2x4 D.xy﹣2xy=﹣xy
10.(2024秋 泸县校级期末)近年来,重庆作为网红城市,旅游业市场发展迅速.据调查,今年重庆5月份旅游旺季全市旅游业收入为x亿元,6月份比5月份减少了25%,暑期如约而至,7月份比6月份增加了78%,则7月份重庆全市的旅游业收入是( )亿元.
A.(1﹣25%+78%)x B.(1﹣25%)(1+78%)x
C.(1﹣25%)x+(1+78%)x D.[1﹣25%(1+78%)]x
二.填空题(共5小题)
11.(2024秋 南通期末)若单项式﹣xmy3与单项式2x4y3是同类项,则m的值为 .
12.(2024秋 黄浦区期末)合并同类项: .
13.(2024秋 海曙区期末)若单项式5x﹣m+1y3与单项式﹣x3yn+1的和仍是一个单项式,则|mn|的值是 .
14.(2024秋 苏州期末)若x﹣2y﹣3=0,则代数式1﹣2x+4y的值为 .
15.(2024秋 长沙期末)单项式3am﹣5b3与﹣8a2b1﹣2n是同类项,则nm= .
三.解答题(共5小题)
16.(2024秋 临平区期末)在体育课中,我们经常根据“立正,向右转,向左转、向后转”这些口令进行相应的运动,这些运动是可以连续进行的,现规定:把连续执行2个口令的结果,叫作这2个口令相加所得到的和,并用“ ”表示相加.例如:向右转 向左转=立正,向左转 向左转=向后转,等等.分别用数字符号0,1,﹣1,2表示立正,向右转,向左转,向后转,可以建立如下的体育口令加法运算表.
0(立正) 1(向右转) ﹣1(向左转) 2(向后转)
0(立正) 0 1 ﹣1 2
1(向右转) 1 2 0 n
﹣1(向左转) ﹣1 0 2 1
2(向后转) 2 x y m
请完成下面问题:
(1)上述表格中,x= ,y= ,m= .
(2)若用字母a表示任何一种体育口令,则a 0= .
(3)判断这种体育口令的加法运算是否满足交换律和结合律?请举例验证(各举一个例子即可).
17.(2024秋 太仓市期末)已知线段AC,以AC为斜边作Rt△ABC和Rt△ADC,连接BD,M、N分别是线段AC、BD的中点,连接MN、MB.
(1)如图1,Rt△ABC和Rt△ADC在线段AC的两侧.
①求证:MN⊥BD;
②若∠BAC=45°,∠DAC=28°;请求出∠BMN的度数;
(2)如图2,Rt△ABC和Rt△ADC在线段AC的同侧,若∠BAC=α,∠DAC=β(α>β),则∠BMN的度数为 (用含α、β的代数式表示)
18.(2024秋 如皋市期末)用同样规格的黑白两种颜色的正方形瓷砖,按如图的方式铺地面:
(1)观察图形,可知图③中黑色瓷砖的块数为 ,白色瓷砖的块数为 ;
(2)依上推测,第n个图形中黑色瓷砖的块数比白色瓷砖的块数多几块?请说明理由;
(3)白色瓷砖与黑色瓷砖的总块数可能是2025块吗?若能,求出是第几个图形;若不能,请说明理由.
19.(2024秋 丰台区期末)图1是2025年1月份的日历,用图2所示的“九方格”框住图1中的9个日期,将其中被阴影方格覆盖的四个日期分别记为a,b,c,d.
(1)a+d b+c(填“>”,“<”或“=”);
(2)当图2在图1的不同位置时,代数式a﹣2b+4c﹣3d的值是否为定值?若是,请求出它的值;若不是,请说明理由.
20.(2024秋 贵阳期末)如图②是小红家客厅的电视背景墙,它是由两块大长方形瓷砖(Ⅰ和Ⅱ)和4个如图①的小长方形瓷砖不重叠的砌成,已知小长方形的长为2x,宽为x,长方形电视背景墙的长CD=10.根据给出的条件解答下列问题:
(1)请用含x的代数式表示长方形电视背景墙ABCD的周长;
(2)若长方形Ⅱ的面积为18,求小长方形瓷砖的宽.
2025年中考数学高频易错考前冲刺:代数式
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B D A. B. D. C. D. B
一.选择题(共10小题)
1.(2024秋 海沧区期末)下列单项式中,能与2a合并成一项的是( )
A.2 B.﹣3a C.2ab D.d2
【考点】合并同类项;单项式.
【专题】整式;运算能力.
【答案】B
【分析】所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
【解答】解:A、所含字母不相同,不是同类项;
B、符合同类项的定义,是同类项;
C、所含字母不相同,不是同类项;
D、所含字母不相同,不是同类项;
故选:B.
【点评】本题考查同类项的定义,解题的关键是正确理解同类项的定义,本题属于基础题型.
2.(2024秋 郑州期末)在数学实践课上,小郑将五边形区域分割成若干个三角形,他在五边形内取一定数量的点,连同五边形的5个顶点,逐步连接这些点,保证所有连线不再相交产生新的点,直到五边形内所有区域都变成三角形.如当五边形内有1个点时,可分得5个三角形;当五边形内有2个点时,可分得7个三角形(不计被分割的三角形).则当五边形内有2025个点时,可分得三角形的个数为( )
A.22025 B.20252 C.4053 D.4050
【考点】规律型:数字的变化类.
【专题】规律型;运算能力.
【答案】C
【分析】先找出规律,再计算即可.
【解答】解:根据题意结合图形,
当五边形内有1个点时,可分成的三角形个数为:5=1×2+3;
当五边形内有2个点时,可分成的三角形个数为:7=2×2+3;
当五边形内有3个点时,可分成的三角形个数为:9=3×2+3;
......;
当五边形内有n个点时,可分成的三角形个数为:(2n+3)个;
所以当五边形内有2025个点时,可分成的三角形个数为2×2025+3=4053个.
故选:C.
【点评】本题考查了图形的变化类问题,解题的关键是仔细观察图形并找到其中的规律.
3.(2024秋 越城区校级期末)如图,一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3.2米的正方形框.已知铺这个框恰好用了144块边长为0.8米的正方形花岗石.则这一标志性建筑的底面边长x是( )米.
A.3.8 B.4 C.4.2 D.5
【考点】列代数式.
【专题】整式;运算能力.
【答案】B
【分析】设标志性建筑底面的边长是x米,则外面的边长是(x+6.4)米,利用两个正方形的面积差等于144块边长为0.8米的正方形花岗石的面积列出方程解答即可.
【解答】解:∵标志性建筑底面正方形的边长是x米,
∴外面的边长是(x+3.2+3.2)米,
已知铺这个框恰好用了144块边长为0.8米的正方形花岗石,
∴(x+3.2+3.2)2﹣x2=0.8×0.8×144,
整理得:12x+36=108,
解得:x=4,
答:标志性建筑底面的边长是4米,
故选:B.
【点评】本题考查列代数式,掌握正方形的面积是解决问题的关键.
4.(2024秋 包头期末)下列说法中正确的是( )
A.πx3的系数是
B.y﹣x2y+5xy2的次数是7
C.4不是单项式
D.﹣2xy与4yx是同类项
【考点】同类项;单项式;多项式.
【答案】D
【分析】根据单项式的定义,同类项的定义,多项式的次数,可得答案.
【解答】解:A、πx3的系数是π,故A不符合题意;
B、y﹣x2y+5xy2的次数是3,故B不符合题意;
C、4是单项式,故C不符合题意;
D、﹣2xy与4yx是同类项,故D符合题意;
故选:D.
【点评】本题考查了同类项、单项式、多项式,熟记单项式的定义,同类项的定义,多项式的次数是解题关键.
5.(2024秋 泸县校级期末)下列各组单项式中,不是同类项的是( )
A.ab2和 B.3x和4x
C.3ab和﹣ba D.2和3
【考点】同类项;单项式.
【专题】整式;运算能力.
【答案】A.
【分析】所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.
【解答】解:A、相同字母的指数不相同,不是同类项;
B、符合同类项的定义,是同类项;
C、符合同类项的定义,是同类项;
D、符合同类项的定义,是同类项;
故选:A.
【点评】本题考查同类项的定义,解题的关键是正确理解同类项的定义,本题属于基础题型.
6.(2024秋 松江区期末)下列各式中,不是代数式的是( )
A. B.3a+1=0
C.x D.0
【考点】代数式.
【专题】整式;符号意识.
【答案】B.
【分析】根据代数式的概念,用运算符号把数字与字母连接而成的式子叫做代数式.单独的一个数或一个字母也是代数式.
【解答】解:A.,是代数式;
B.3a+1=0,是等式,不是代数式;
C.x,是代数式;
D.0,是代数式.
故选:B.
【点评】本题主要考查了代数式,解题关键是熟练掌握代数式的定义.
7.(2024秋 苏州期末)下列运算中,正确的是( )
A.2a+a=2a2 B.2a+3b=5ab
C.5y2﹣3y2=2 D.3ab2﹣2ab2=ab2
【考点】合并同类项.
【专题】计算题;整式;运算能力.
【答案】D.
【分析】根据整式的加减运算法则即可求出答案.
【解答】解:A、2a+a=3a≠2a2,故A错误;
B、2a+3b≠5ab,故B错误;
C、5y2﹣3y2=2y2≠2,故C错误;
D、3ab2﹣2ab2=ab2,故D正确.
故选:D.
【点评】本题考查整式的运算法则,解题的关键是熟练运用整式的运算,本题属于基础题型.
8.(2024秋 海曙区期末)下列计算正确的是( )
A.3a﹣2a=1 B.3a+2a=5a2
C. D.3ab2﹣2a2b=ab
【考点】合并同类项.
【专题】计算题;整式;运算能力.
【答案】C.
【分析】根据整式的加减运算法则即可求出答案.
【解答】解:A、3a﹣2a=a≠1,故A错误;
B、3a+2a=5a≠5a2,故B错误;
C、0,故C正确;
D、3ab2﹣2a2b≠ab,故D错误.
故选:C.
【点评】本题考查整式的运算法则,解题的关键是熟练运用整式的运算,本题属于基础题型.
9.(2024秋 丰台区期末)下面计算正确的是( )
A.﹣2x﹣2x=0 B.x4﹣x2=x2
C.x2+x2=2x4 D.xy﹣2xy=﹣xy
【考点】合并同类项.
【专题】计算题;整式;运算能力.
【答案】D.
【分析】根据整式的加减运算法则即可求出答案.
【解答】解:A、﹣2x﹣2x=﹣4x≠0,故A错误;
B、x4﹣x2≠x2,故B错误;
C、x2+x2=2x2≠2x4,故C错误;
D、xy﹣2xy=﹣xy,故D正确.
故选:D.
【点评】本题考查整式的运算法则,解题的关键是熟练运用整式的运算,本题属于基础题型.
10.(2024秋 泸县校级期末)近年来,重庆作为网红城市,旅游业市场发展迅速.据调查,今年重庆5月份旅游旺季全市旅游业收入为x亿元,6月份比5月份减少了25%,暑期如约而至,7月份比6月份增加了78%,则7月份重庆全市的旅游业收入是( )亿元.
A.(1﹣25%+78%)x B.(1﹣25%)(1+78%)x
C.(1﹣25%)x+(1+78%)x D.[1﹣25%(1+78%)]x
【考点】列代数式.
【专题】整式;应用意识.
【答案】B
【分析】根据5月份的旅游业收入是x亿元,用x把6月份的旅游业收入表示出来为(1﹣25%)x亿元,进而得出7月份旅游业收入列出式子(1﹣25%)x×(1+78%)亿元,即可得出选项.
【解答】解:∵5月份的旅游业收入是x亿元,
则6月份的旅游业收入是(1﹣25%)x亿元,
7月份重庆全市的旅游业收入(1﹣25%)(1+78%)x亿元,
故选:B.
【点评】此题主要考查了列代数式,解此题的关键是能用x把6、7月份的旅游业收入表示出来.
二.填空题(共5小题)
11.(2024秋 南通期末)若单项式﹣xmy3与单项式2x4y3是同类项,则m的值为 4 .
【考点】同类项.
【专题】计算题;整式;运算能力.
【答案】4.
【分析】根据同类项的定义直接得出m的值.
【解答】解:由同类项的定义可知m=4.
故答案为:4.
【点评】本题考查了同类项的定义,掌握同类项的定义:所含字母相同,相同字母的指数也相同的项叫同类项.
12.(2024秋 黄浦区期末)合并同类项: .
【考点】合并同类项.
【专题】计算题;整式;运算能力.
【答案】.
【分析】合并同类项的法则是系数和系数相加作为系数,字母和字母的指数不变.
【解答】解:.
故答案为:.
【点评】本题主要考查了合并同类项的法则,熟练掌握运算法则是解题的关键.
13.(2024秋 海曙区期末)若单项式5x﹣m+1y3与单项式﹣x3yn+1的和仍是一个单项式,则|mn|的值是 4 .
【考点】合并同类项;单项式;绝对值.
【专题】计算题;方程思想;整式;运算能力.
【答案】4.
【分析】根据同类项的定义列出方程,再求解即可.
【解答】解:由同类项的定义可知﹣m+1=3,n+1=3,
解得m=﹣2,n=2,
∴|mn|=|(﹣2)×2|=4.
故答案为:4.
【点评】本题考查了同类项的定义,掌握同类项的定义:所含字母相同,相同字母的指数也相同的项叫同类项.
14.(2024秋 苏州期末)若x﹣2y﹣3=0,则代数式1﹣2x+4y的值为 ﹣5 .
【考点】代数式求值.
【专题】计算题;整体思想;整式;运算能力.
【答案】﹣5.
【分析】根据已知条件将要求代数式变形,然后整体代入求值即可.
【解答】解:∵1﹣2x+4y=﹣2x+4y+1,
∵x﹣2y﹣3=0,
∴x﹣2y=3,
∴当x﹣2y=3时,原式=﹣2x+4y+1=﹣2(x﹣2y)+1=﹣2×3+1=﹣5.
故答案为:﹣5.
【点评】本题考查代数式求值,按照代数式规定的运算,计算的结果就是代数式的值.
15.(2024秋 长沙期末)单项式3am﹣5b3与﹣8a2b1﹣2n是同类项,则nm= ﹣1 .
【考点】同类项.
【专题】计算题;方程思想;整式;运算能力.
【答案】见试题解答内容
【分析】根据同类项的定义列出方程,再求解即可.
【解答】解:由同类项的定义可知m﹣5=2,1﹣2n=3,
解得m=7,n=﹣1,
∴nm=(﹣1)7=﹣1.
故答案为:﹣1.
【点评】本题考查了同类项的定义,掌握同类项的定义:所含字母相同,相同字母的指数也相同的项叫同类项.
三.解答题(共5小题)
16.(2024秋 临平区期末)在体育课中,我们经常根据“立正,向右转,向左转、向后转”这些口令进行相应的运动,这些运动是可以连续进行的,现规定:把连续执行2个口令的结果,叫作这2个口令相加所得到的和,并用“ ”表示相加.例如:向右转 向左转=立正,向左转 向左转=向后转,等等.分别用数字符号0,1,﹣1,2表示立正,向右转,向左转,向后转,可以建立如下的体育口令加法运算表.
0(立正) 1(向右转) ﹣1(向左转) 2(向后转)
0(立正) 0 1 ﹣1 2
1(向右转) 1 2 0 n
﹣1(向左转) ﹣1 0 2 1
2(向后转) 2 x y m
请完成下面问题:
(1)上述表格中,x= ﹣1 ,y= 1 ,m= 0 .
(2)若用字母a表示任何一种体育口令,则a 0= a .
(3)判断这种体育口令的加法运算是否满足交换律和结合律?请举例验证(各举一个例子即可).
【考点】列代数式;正数和负数;有理数的混合运算.
【专题】实数;整式;运算能力.
【答案】(1)﹣1;1;0;
(2)a;
(3)都符合,举例见解析.
【分析】(1)根据新定义分别求出向后转 向右转,向后转 向左转,向后转 向后转的结果即可得到答案;
(2)根据任意口令 立正=该任意口令即可得到答案;
(3)只需要证明向右转 向左转=立正,向左转 向右转=立正,向右转 向左转+向后转=向右转 (向左转+向后转)即可.
【解答】解:(1)由向后转 向右转=向左转,可得x=﹣1;
由向后转 向左转=向右转,可得y=1,
∵向后转 向后转=立正,
∴m=0;
(2)由任意口令 立正=该任意口令可得a 0=a;
(3)由表可知向右转 向左转=立正,向左转 向右转=立正,
∴符合加法的交换律;
由条件可知向右转 向左转+向后转=向右转,
由条件可知向右转 向左转+向后转=向右转 (向左转+向后转),
∴符合加法交换律.
【点评】本题主要考查了新定义,熟练掌握有理数混合运算法则是关键.
17.(2024秋 太仓市期末)已知线段AC,以AC为斜边作Rt△ABC和Rt△ADC,连接BD,M、N分别是线段AC、BD的中点,连接MN、MB.
(1)如图1,Rt△ABC和Rt△ADC在线段AC的两侧.
①求证:MN⊥BD;
②若∠BAC=45°,∠DAC=28°;请求出∠BMN的度数;
(2)如图2,Rt△ABC和Rt△ADC在线段AC的同侧,若∠BAC=α,∠DAC=β(α>β),则∠BMN的度数为 α﹣β (用含α、β的代数式表示)
【考点】列代数式.
【专题】整式;线段、角、相交线与平行线;运算能力.
【答案】(1)①见解析;②73°;
(2)α﹣β.
【分析】(1)①根据直角三角形的性质得到,,根据等腰三角形的三线合一证明即可;②根据直角三角形的性质得到BM=AM=MC=DM,根据等腰三角形的性质、三角形内角和定理计算,得到答案.
(2)根据直角三角形的性质得到AM=BM=MD,根据等腰三角形的性质、三角形内角和定理计算,得到答案.
【解答】(1)①证明:连接MD,
由条件可知,,
∴BM=DM,
又∵N是BD的中点,
∴MN⊥BD;
②解:有条件可知BM=AM=MC=DM,
又∵∠BAC=45°,∠DAC=28°,
∴∠MBC=∠MCB=90°﹣45°=45°,∠MCD=∠CDM=90°﹣28°=62°,
∴∠BMD=360°﹣45°×2﹣62°×2=146°,
∵BM=DM,MN⊥BD,
∴,
∴.
(2)解:连接MD,
由条件可知AM=BM=MD,
∴∠MBA=∠BAC=α,∠MDA=∠DAC=β,
∴∠AMB=180°﹣2α,∠CMD=2β,
∴∠BMD=180°﹣∠AMB﹣∠CMD=2α﹣2β,
∵BM=MD,N是BD的中点,
∴.
【点评】本题考查的是直角三角形的性质、等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.
18.(2024秋 如皋市期末)用同样规格的黑白两种颜色的正方形瓷砖,按如图的方式铺地面:
(1)观察图形,可知图③中黑色瓷砖的块数为 11 ,白色瓷砖的块数为 10 ;
(2)依上推测,第n个图形中黑色瓷砖的块数比白色瓷砖的块数多几块?请说明理由;
(3)白色瓷砖与黑色瓷砖的总块数可能是2025块吗?若能,求出是第几个图形;若不能,请说明理由.
【考点】规律型:图形的变化类.
【专题】规律型;运算能力.
【答案】(1)11,10;
(2)1,理由见解析;
(3)能,第337个图形.
【分析】(1)直接由图形解答即可;
(2)根据每一个图形的黑色瓷砖块数比前一个图形多3,每一个图形的白色瓷砖块数比前一个图形多3,得出规律,由此求得答案即可;
(3)利用(2)的规律根据“白色瓷砖与黑色瓷砖的总块数是2025块”这个假设成立,列方程,求得整数解就能,否则不能.
【解答】解:(1)由图形可知图③中黑色瓷砖的块数为11,白色瓷砖的块数为10,
故答案为:11;10;
(2)第一个图形:黑色瓷砖的块数为5,白两种瓷砖的总块数为4;
第二个图形:黑色瓷砖的块数为8,白两种瓷砖的总块数为7;
第三个图形:黑色瓷砖的块数为11,白两种瓷砖的总块数为10;
……,
第n个图形中黑色瓷砖的块数为3n+2;白两种瓷砖的总块数为3n+1,
3n+2﹣(3n+1)=3n+2﹣3n﹣1=1;
(3)能,理由如下:
假设白色瓷砖与黑色瓷砖的总块数是2025块,
则可得:3n+2+(3n+1)=2025,
即6n=2022,
∴n=337,是整数
所以假设成立.
【点评】此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.
19.(2024秋 丰台区期末)图1是2025年1月份的日历,用图2所示的“九方格”框住图1中的9个日期,将其中被阴影方格覆盖的四个日期分别记为a,b,c,d.
(1)a+d = b+c(填“>”,“<”或“=”);
(2)当图2在图1的不同位置时,代数式a﹣2b+4c﹣3d的值是否为定值?若是,请求出它的值;若不是,请说明理由.
【考点】列代数式;代数式求值.
【专题】整式;几何直观;运算能力.
【答案】(1)=;(2)代数式a﹣2b+4c﹣3d的值是定值,这个定值是﹣68.
【分析】(1)根据图形,可以得到b、c、d和a的关系,然后计算即可;
(2)化简代数式a﹣2b+4c﹣3d,然后观察结果即可解答本题.
【解答】解:(1)由图可得,
b=a+14,c=a+2,d=a+16,
∴a+d=a+a+16=2a+16,b+c=a+14+a+2=2a+16,
∴a+d=b+c,
故答案为:=;
(2)由图可得,
b=a+14,c=a+2,d=a+16,
a﹣2b+4c﹣3d
=a﹣2(a+14)+4(a+2)﹣3(a+16)
=a﹣2a﹣28+4a+8﹣3a﹣48
=﹣68,
即代数式a﹣2b+4c﹣3d的值是定值,这个定值是﹣68.
【点评】本题考查整式的加减、列代数式,熟练掌握运算法则是解答本题的关键.
20.(2024秋 贵阳期末)如图②是小红家客厅的电视背景墙,它是由两块大长方形瓷砖(Ⅰ和Ⅱ)和4个如图①的小长方形瓷砖不重叠的砌成,已知小长方形的长为2x,宽为x,长方形电视背景墙的长CD=10.根据给出的条件解答下列问题:
(1)请用含x的代数式表示长方形电视背景墙ABCD的周长;
(2)若长方形Ⅱ的面积为18,求小长方形瓷砖的宽.
【考点】列代数式.
【专题】整式;运算能力.
【答案】(1)10x+20;
(2)小长方形瓷砖的宽为1.
【分析】(1)根据所给图形,得出长方形ABCD的宽可表示为5x,据此可解决问题.
(2)根据长方形Ⅱ的面积为18,建立关于x的方程,据此可解决问题.
【解答】解:(1)由题知,
长方形ABCD的宽可表示为5x,
又因为CD=10,
所以长方形电视背景墙ABCD的周长可表示为:2(5x+10)=10x+20.
(2)长方形Ⅱ的长为10﹣x,宽为2x,
因为长方形Ⅱ的面积为18,
所以2x(10﹣x)=18,
解得x1=1,x2=9.
当x=9时,BC=5×9=45>10,
故x=0舍去,
所以小长方形瓷砖的宽为1.
【点评】本题主要考查了列代数式,能根据题意分别表示出长方形ABCD及长方形Ⅱ的面积是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
