【中考押题卷】2025年中考数学高频易错考前冲刺:反比例函数(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:反比例函数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 07:36:11 | ||
图片预览

文档简介
2025年中考数学高频易错考前冲刺:反比例函数
一.选择题(共10小题)
1.(2024秋 滨海新区校级期末)已知函数的图象上有三点,则y1,y2,y3的大小关系( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y1<y2 D.y3<y2<y1
2.(2024秋 琼中县期末)在物理学中,导体中的电流Ⅰ跟导体两端的电压U,导体的电阻R之间有以下关系:去分母得IR=U,那么其变形的依据是( )
A.等式两边加(或减)同一个数(或式子),结果仍相等
B.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等
C.等式两边可以交换
D.相等关系可以传递
3.(2024秋 礼县期末)下列函数中,y是x的反比例函数的是( )
A. B. C.y=5x2 D.
4.(2025 浦东新区一模)下列四个函数中,图象经过原点的是( )
A. B. C.y=x2+2x D.y=(x+1)2
5.(2024秋 长沙期末)下列关系式中的两个量成反比例的是( )
A.圆的面积与它的半径
B.正方形的周长与它的边长
C.路程一定时,速度与时间
D.长方形一条边确定时,周长与另一边
6.(2024秋 河西区期末)下列函数中,当x>0时,y随着x的增大而增大的是( )
A.y=﹣x﹣3 B. C.y=x2﹣3 D.y=﹣x2﹣3
7.(2024秋 普陀区期末)下列关于反比例函数的说法中,正确的是( )
A.图象在第一、三象限
B.比例系数为﹣10
C.当自变量x的值逐渐增大时,y的值随着逐渐增大
D.如果点A(﹣3,y1)和点B(﹣5,y2)在该函数的图象上,那么y1>y2
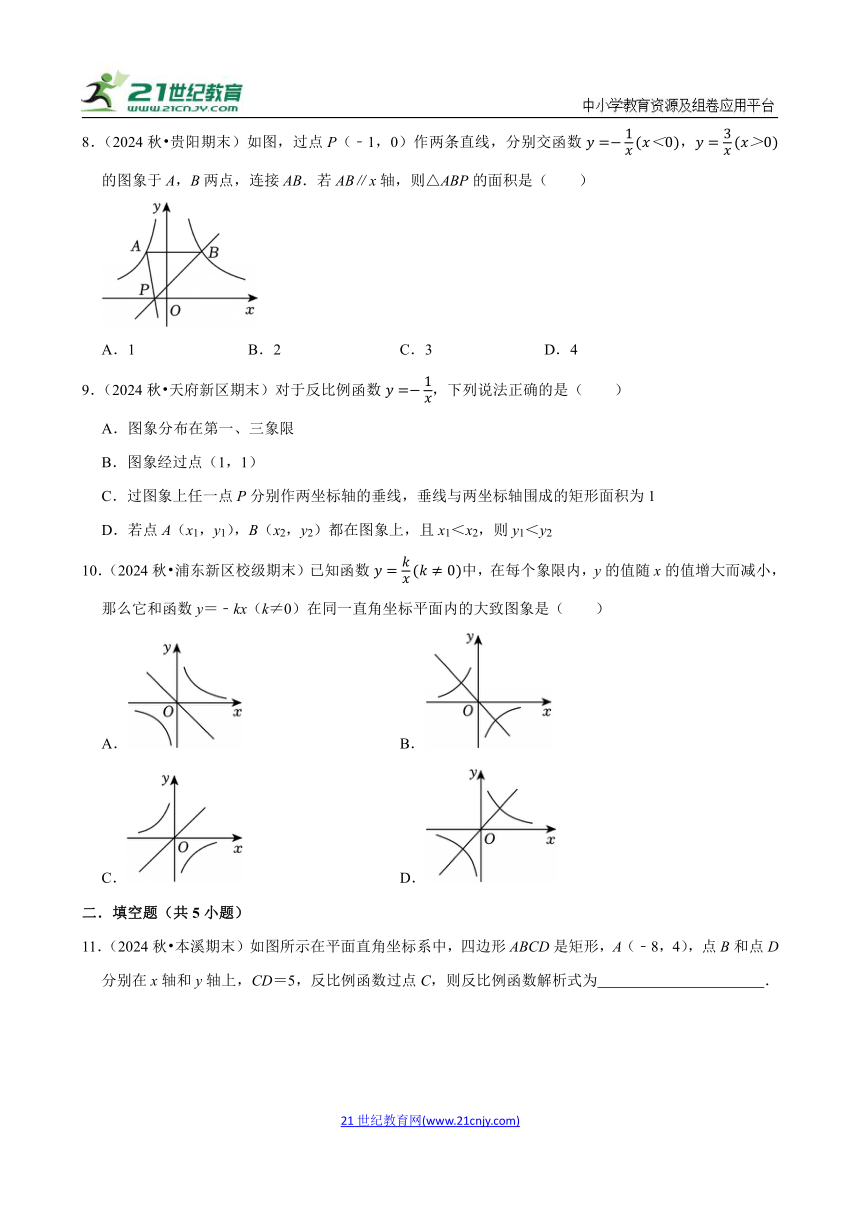
8.(2024秋 贵阳期末)如图,过点P(﹣1,0)作两条直线,分别交函数,的图象于A,B两点,连接AB.若AB∥x轴,则△ABP的面积是( )
A.1 B.2 C.3 D.4
9.(2024秋 天府新区期末)对于反比例函数,下列说法正确的是( )
A.图象分布在第一、三象限
B.图象经过点(1,1)
C.过图象上任一点P分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为1
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
10.(2024秋 浦东新区校级期末)已知函数中,在每个象限内,y的值随x的值增大而减小,那么它和函数y=﹣kx(k≠0)在同一直角坐标平面内的大致图象是( )
A. B.
C. D.
二.填空题(共5小题)
11.(2024秋 本溪期末)如图所示在平面直角坐标系中,四边形ABCD是矩形,A(﹣8,4),点B和点D分别在x轴和y轴上,CD=5,反比例函数过点C,则反比例函数解析式为 .
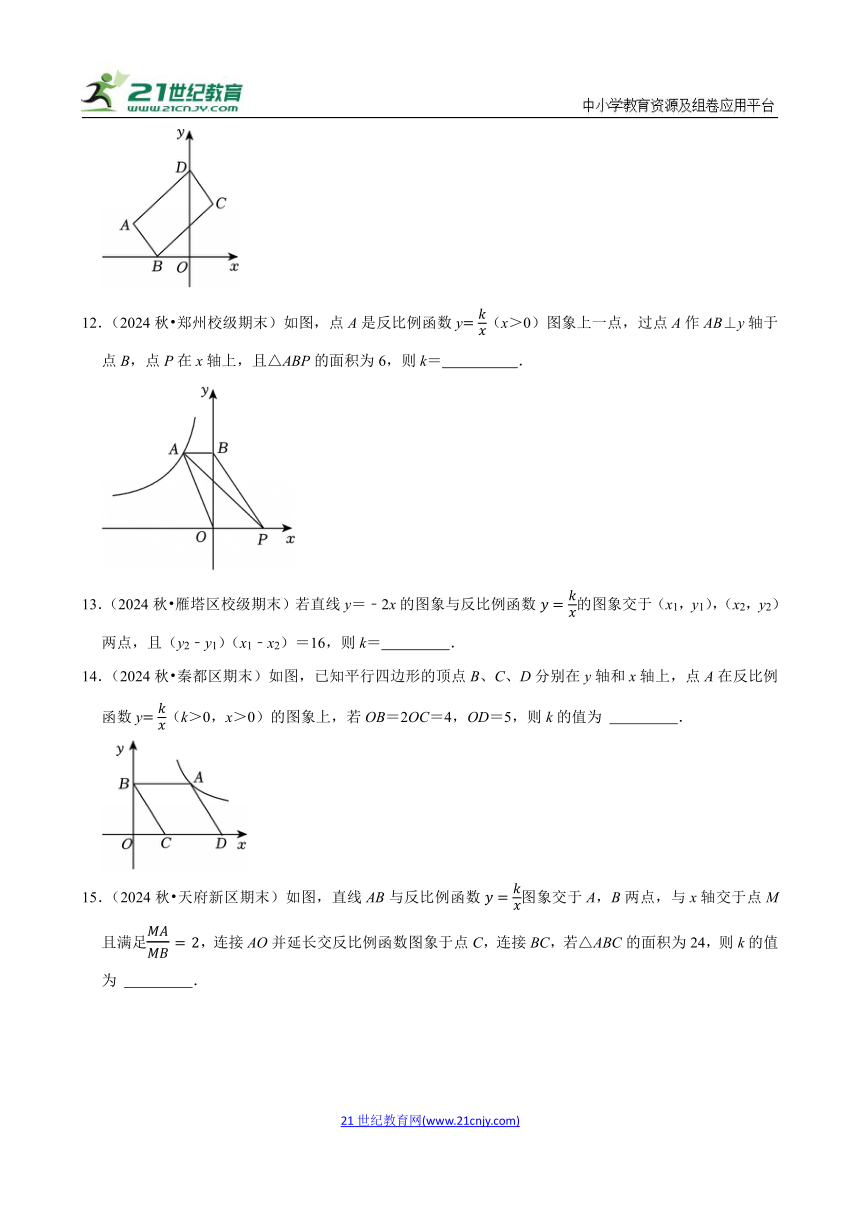
12.(2024秋 郑州校级期末)如图,点A是反比例函数y(x>0)图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,且△ABP的面积为6,则k= .
13.(2024秋 雁塔区校级期末)若直线y=﹣2x的图象与反比例函数的图象交于(x1,y1),(x2,y2)两点,且(y2﹣y1)(x1﹣x2)=16,则k= .
14.(2024秋 秦都区期末)如图,已知平行四边形的顶点B、C、D分别在y轴和x轴上,点A在反比例函数y(k>0,x>0)的图象上,若OB=2OC=4,OD=5,则k的值为 .
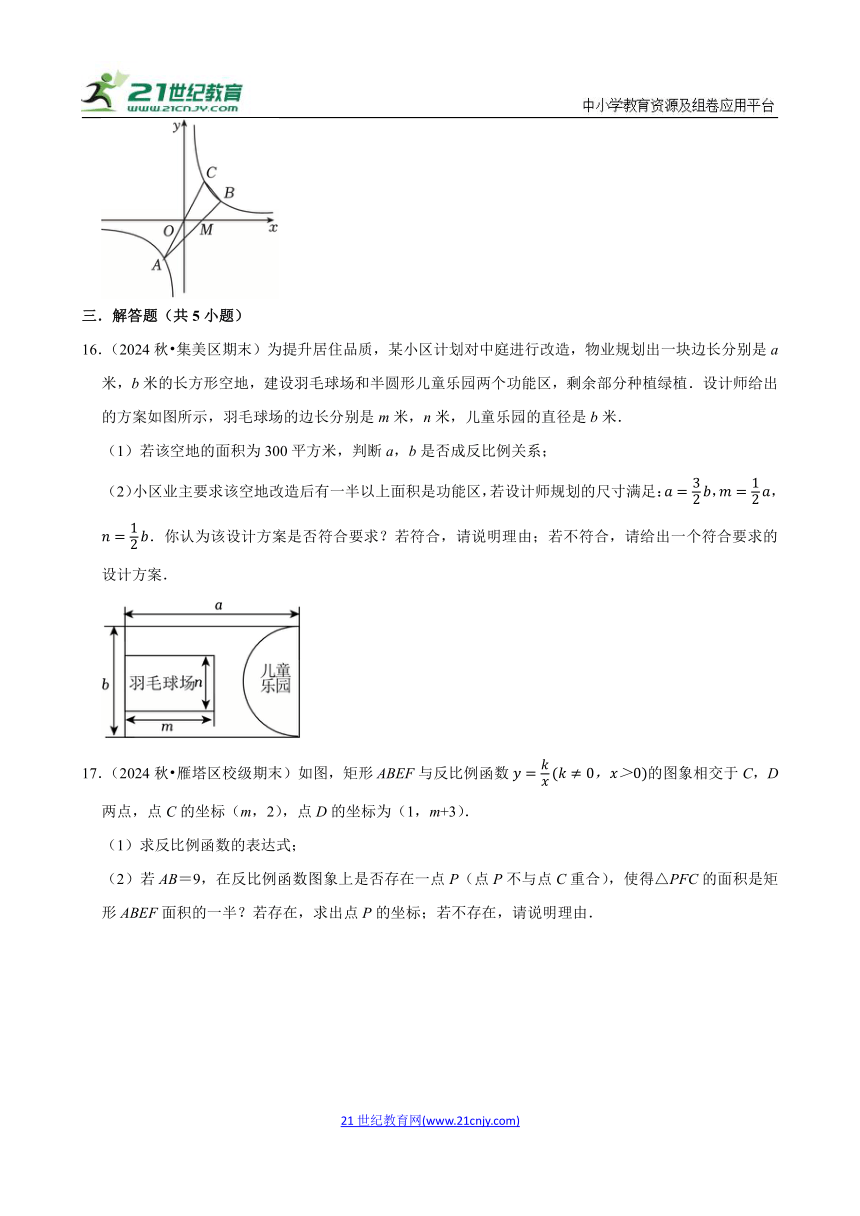
15.(2024秋 天府新区期末)如图,直线AB与反比例函数图象交于A,B两点,与x轴交于点M且满足,连接AO并延长交反比例函数图象于点C,连接BC,若△ABC的面积为24,则k的值为 .
三.解答题(共5小题)
16.(2024秋 集美区期末)为提升居住品质,某小区计划对中庭进行改造,物业规划出一块边长分别是a米,b米的长方形空地,建设羽毛球场和半圆形儿童乐园两个功能区,剩余部分种植绿植.设计师给出的方案如图所示,羽毛球场的边长分别是m米,n米,儿童乐园的直径是b米.
(1)若该空地的面积为300平方米,判断a,b是否成反比例关系;
(2)小区业主要求该空地改造后有一半以上面积是功能区,若设计师规划的尺寸满足:,,.你认为该设计方案是否符合要求?若符合,请说明理由;若不符合,请给出一个符合要求的设计方案.
17.(2024秋 雁塔区校级期末)如图,矩形ABEF与反比例函数的图象相交于C,D两点,点C的坐标(m,2),点D的坐标为(1,m+3).
(1)求反比例函数的表达式;
(2)若AB=9,在反比例函数图象上是否存在一点P(点P不与点C重合),使得△PFC的面积是矩形ABEF面积的一半?若存在,求出点P的坐标;若不存在,请说明理由.
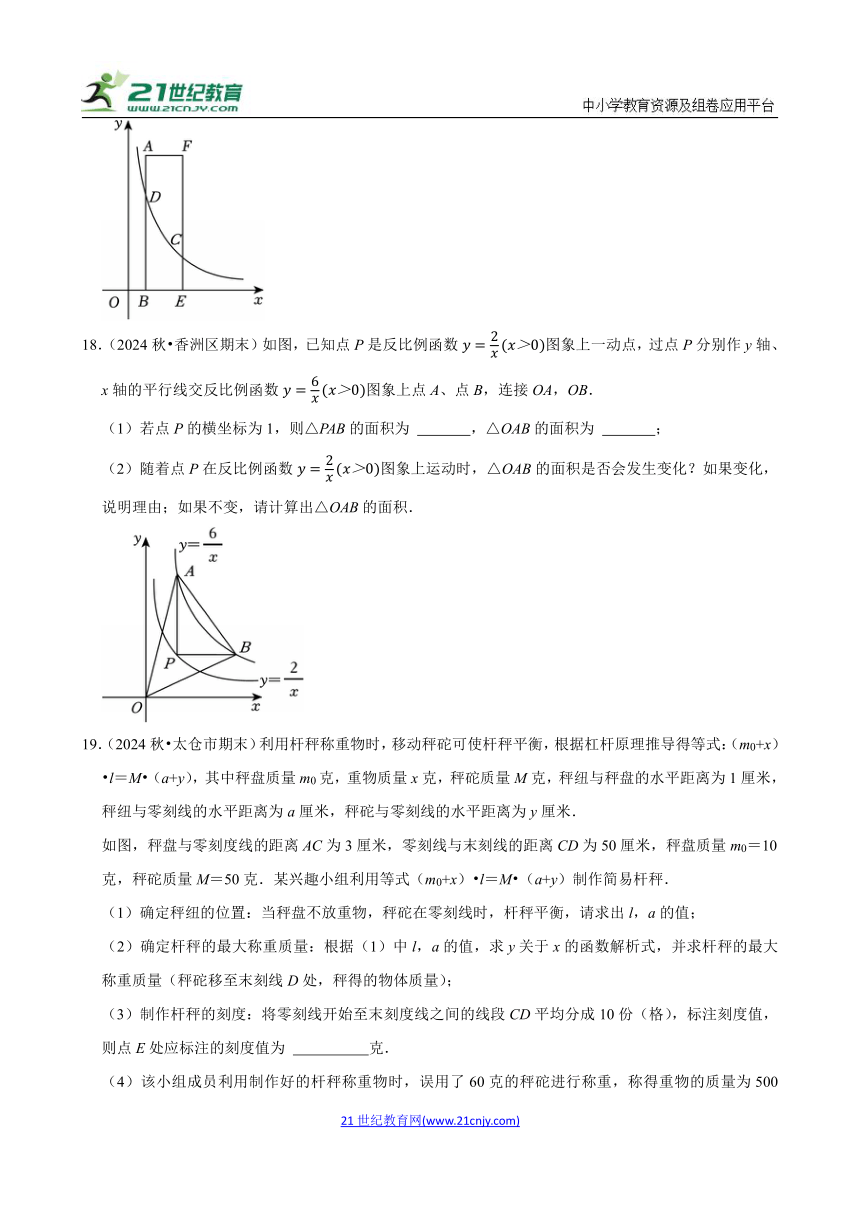
18.(2024秋 香洲区期末)如图,已知点P是反比例函数图象上一动点,过点P分别作y轴、x轴的平行线交反比例函数图象上点A、点B,连接OA,OB.
(1)若点P的横坐标为1,则△PAB的面积为 ,△OAB的面积为 ;
(2)随着点P在反比例函数图象上运动时,△OAB的面积是否会发生变化?如果变化,说明理由;如果不变,请计算出△OAB的面积.
19.(2024秋 太仓市期末)利用杆秤称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得等式:(m0+x) l=M (a+y),其中秤盘质量m0克,重物质量x克,秤砣质量M克,秤纽与秤盘的水平距离为1厘米,秤纽与零刻线的水平距离为a厘米,秤砣与零刻线的水平距离为y厘米.
如图,秤盘与零刻度线的距离AC为3厘米,零刻线与末刻线的距离CD为50厘米,秤盘质量m0=10克,秤砣质量M=50克.某兴趣小组利用等式(m0+x) l=M (a+y)制作简易杆秤.
(1)确定秤纽的位置:当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请求出l,a的值;
(2)确定杆秤的最大称重质量:根据(1)中l,a的值,求y关于x的函数解析式,并求杆秤的最大称重质量(秤砣移至末刻线D处,秤得的物体质量);
(3)制作杆秤的刻度:将零刻线开始至末刻度线之间的线段CD平均分成10份(格),标注刻度值,则点E处应标注的刻度值为 克.
(4)该小组成员利用制作好的杆秤称重物时,误用了60克的秤砣进行称重,称得重物的质量为500克,则该重物的实际质量为 克.
20.(2024秋 温州期末)【项目】小车沿斜面运动中路程s与时间t的关系.
图1是小车从斜面上静止滑下的实验装置,斜面刻度值单位为分米.小温和小州共同填写了如下实验记录表.
t(秒) 0 2 3 ……
s(分米) 0 4 9 ……
(1)小温发现,路程s与时间t可采用一次函数、反比例函数、二次函数中的一种进行刻画,请通过实验数据在图2中描点画图,判断可以采用的函数模型,并求出s关于t的函数表达式.
(2)若斜面足够长,请通过计算说明小车在斜面上第一个5秒和第二个5秒通过的路程之差.
(3)小州说:把单位时间设为1秒,还可以研究第t秒内通过的路程s′(分米)与第t秒之间的函数关系.
请写出一个路程s′(分米)与第t秒之间的结论,并通过计算说明理由.
2025年中考数学高频易错考前冲刺:反比例函数
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 B B A C C C D B C A
一.选择题(共10小题)
1.(2024秋 滨海新区校级期末)已知函数的图象上有三点,则y1,y2,y3的大小关系( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y1<y2 D.y3<y2<y1
【考点】反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力.
【答案】B
【分析】先根据反比例函数的性质判断出函数图象所在的象限,再根据反比例函数的性质即可作出判断.
【解答】解:∵k2+1>0,
∴函数的图象在一、三象限,且在每一象限内y随x的增大而减小,
∴点在第三象限,B(1,y2),C(4,y3)在第一象限,
∴y1<0<y3<y2.
故选:B.
【点评】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象的增减性是解答此题的关键.
2.(2024秋 琼中县期末)在物理学中,导体中的电流Ⅰ跟导体两端的电压U,导体的电阻R之间有以下关系:去分母得IR=U,那么其变形的依据是( )
A.等式两边加(或减)同一个数(或式子),结果仍相等
B.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等
C.等式两边可以交换
D.相等关系可以传递
【考点】反比例函数的应用;有理数的除法.
【专题】反比例函数及其应用;运算能力.
【答案】B
【分析】根据题目中的变形,可知依据是等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
【解答】解:去分母得IR=U,那么其变形的依据是等式两边乘同一个数,或除以同一个不为0的数,结果仍相等,
故选:B.
【点评】本题考查反比例函数的应用、等式的性质,解答本题的关键是明确等式的性质二,等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
3.(2024秋 礼县期末)下列函数中,y是x的反比例函数的是( )
A. B. C.y=5x2 D.
【考点】反比例函数的定义.
【专题】反比例函数及其应用;运算能力.
【答案】A
【分析】根据反比例函数的定义逐项判断即可.
【解答】解:A.符合反比例函数的定义,符合题意;
B.不符合反比例函数的定义,不符合题意;
C.该函数属于二次函数,不符合题意;
D.该函数不属于反比例函数,不符合题意.
故选:A.
【点评】本题主要考查了反比例函数的定义,熟知“一般地,如果两个变量x,y之间的关系可以表示成(k为常数,k≠0)的形式,那么称y是x的反比例函数”是解题关键.
4.(2025 浦东新区一模)下列四个函数中,图象经过原点的是( )
A. B. C.y=x2+2x D.y=(x+1)2
【考点】反比例函数图象上点的坐标特征;二次函数的性质;二次函数图象上点的坐标特征;一次函数的性质;一次函数图象上点的坐标特征;反比例函数的性质.
【专题】一次函数及其应用;反比例函数及其应用;二次函数图象及其性质;运算能力.
【答案】C
【分析】令x=0,函数值也等于0,则图象经过原点.
【解答】解:A、令x=0,则y,故不符合题意;
B、x=0无意义,故不符合题意;
C、x=0,则y=0,故符合题意;
D、x=0,则y=1,故不符合题意.
故选:C.
【点评】本题考查函数图象上的点,掌握函数图象上的点的坐标适合函数解析式是解题的关键.
5.(2024秋 长沙期末)下列关系式中的两个量成反比例的是( )
A.圆的面积与它的半径
B.正方形的周长与它的边长
C.路程一定时,速度与时间
D.长方形一条边确定时,周长与另一边
【考点】反比例函数的定义.
【专题】反比例函数及其应用;符号意识;应用意识.
【答案】C
【分析】根据反比例函数的定义解答即可.
【解答】解:A、圆的面积=π×半径2,不是反比例函数,故本选项不符合题意;
B、正方形的周长=边长×4,不是反比例函数,故本选项不符合题意;
C、路程s一定时,速度v和时间t的关系s=vt,是反比例函数,故本选项符合题意;
D、长方形一条a边确定时,周长s与另一边b的关系s=2×(a+b),不是反比例关系,故本选项不符合题意.
故选:C.
【点评】本题考查了反比例函数,熟练掌握反比例函数的定义是解题的关键.要注意:反比例函数的判断:判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系,然后根据反比例函数的意义去判断,其形式为y(k为常数,k≠0)或y=kx﹣1(k为常数,k≠0).
6.(2024秋 河西区期末)下列函数中,当x>0时,y随着x的增大而增大的是( )
A.y=﹣x﹣3 B. C.y=x2﹣3 D.y=﹣x2﹣3
【考点】反比例函数的性质;二次函数的性质;一次函数的性质.
【专题】反比例函数及其应用;推理能力.
【答案】C
【分析】分别根据反比例函数的性质,一次函数的性质及二次函数的性质对各选项进行逐一判断即可.
【解答】解:A、一次函数y=﹣x﹣3中,
∵k=﹣1<0,
∴y随着x的增大而减小,不符合题意;
B、反比例函数y中,
∵k=3>0,
∴此函数图象的两个分支分别位于第一、三象限,在每一项象限内y随x的增大而减小,不符合题意;
C、二次函数y=x2﹣3中,
∵a=1>0,
∴抛物线开口向上,顶点坐标为(0,﹣3),
∴当x>0时,y随着x的增大而增大,符合题意;
D、二次函数y=﹣x2﹣3中,
∵a=﹣1<0,
∴抛物线开口向下,顶点坐标为(0,﹣3),
∴当x>0时,y随着x的增大而减小,不符合题意,
故选:C.
【点评】本题考查的是反比例函数的性质,一次函数的性质及二次函数的性质,熟知以上知识是解题的关键.
7.(2024秋 普陀区期末)下列关于反比例函数的说法中,正确的是( )
A.图象在第一、三象限
B.比例系数为﹣10
C.当自变量x的值逐渐增大时,y的值随着逐渐增大
D.如果点A(﹣3,y1)和点B(﹣5,y2)在该函数的图象上,那么y1>y2
【考点】反比例函数的性质;反比例函数的定义.
【专题】反比例函数及其应用;应用意识.
【答案】D
【分析】根据k<0,利用反比例函数的性质一一判断即可.
【解答】解:∵y,
∴k0,
∴函数图象在二,四象限,在每个象限y随x的增大而增大,故选项A,B,C错误,选项D正确.
故选:D.
【点评】本题考查反比例函数的性质,反比例函数的定义,解题的关键是掌握反比例函数的性质.
8.(2024秋 贵阳期末)如图,过点P(﹣1,0)作两条直线,分别交函数,的图象于A,B两点,连接AB.若AB∥x轴,则△ABP的面积是( )
A.1 B.2 C.3 D.4
【考点】反比例函数系数k的几何意义;反比例函数的图象;反比例函数的性质.
【专题】反比例函数及其应用;运算能力.
【答案】B
【分析】根据反比例函数k值的几何意义解答即可.
【解答】解:如图,连接OA、OB,
∵AB∥x轴,
∴S△AOB=S△PAB2.
故选:B.
【点评】本题考查了反比例函数k值的几何意义,熟练掌握该知识点是关键.
9.(2024秋 天府新区期末)对于反比例函数,下列说法正确的是( )
A.图象分布在第一、三象限
B.图象经过点(1,1)
C.过图象上任一点P分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为1
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
【考点】反比例函数系数k的几何意义;反比例函数的性质.
【专题】反比例函数及其应用;运算能力.
【答案】C
【分析】根据反比例函数的图象与性质逐项分析判断即可.
【解答】解:A、反比例函数k=﹣1,图象分布在第二、四象限,选项说法错误,不符合题意;
B、当x=1时,y=﹣1≠1,故选项说法错误,不符合题意;
C、过图象上任一点P分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为1,选项说法正确,符合题意;
D、当x1<0<x2时,y1>y2,选项说法错误,不符合题意;
故选:C.
【点评】本题考查了反比例函数k值的几何意义,熟练掌握反比例函数k值的几何意义是关键.
10.(2024秋 浦东新区校级期末)已知函数中,在每个象限内,y的值随x的值增大而减小,那么它和函数y=﹣kx(k≠0)在同一直角坐标平面内的大致图象是( )
A. B.
C. D.
【考点】反比例函数的性质;正比例函数的图象;正比例函数的性质.
【专题】一次函数及其应用;反比例函数及其应用;推理能力.
【答案】A
【分析】首先根据反比例函数图象的性质判断出k的范围,在确定其所在象限,进而确定正比例函数图象所在象限,即可得到答案.
【解答】解:∵函数中,在每个象限内,y的值随x的值增大而减小,
∴k>0,
∴双曲线在第一、三象限,
∴函数y=﹣kx的图象经过第二、四象限,
故选:A.
【点评】此题主要考查了反比例函数图象的性质与正比例函数图象的性质,图象所在象限受k的影响.
二.填空题(共5小题)
11.(2024秋 本溪期末)如图所示在平面直角坐标系中,四边形ABCD是矩形,A(﹣8,4),点B和点D分别在x轴和y轴上,CD=5,反比例函数过点C,则反比例函数解析式为 y .
【考点】待定系数法求反比例函数解析式;矩形的性质;反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力.
【答案】.
【分析】如图,过A作AE⊥x轴于E,过C作CF⊥y轴于F,过C作CH⊥x轴于H,设BC与y轴交于G,得到AE=4,OE=8,根据矩形的性质得到CD=AB=5,∠ABC=∠DCB=90°,根据勾股定理得到,求得OB=5,根据全等三角形的性质得到CF=BE=3,根据矩形的性质得到OH=CF=3,求得BH=8,根据相似三角形的性质得到C(3,6),设反比例函数解析式为,将C(3,6)代入即可得解.
【解答】解:如图,过A作AE⊥x轴于E,过C作CF⊥y轴于F,过C作CH⊥x轴于H,设BC与y轴交于G,
由条件可知AE=4,OE=8,
由条件可知CD=AB=5,∠ABC=∠DCB=90°,
∴,
∴OB=OE﹣BE=5,
∵∠BOG=∠GCD=90°,∠CGD=∠BGO,
∴∠OBG=∠CDG,
∴∠BAE=∠OBG=∠CDF,
∵∠AEB=∠DFC=90°,
∴△CDF≌△BAE(AAS),
∴CF=BE=3,
∵∠CHO=∠HOF=∠CFO=90°,
∴四边形CHOF是矩形,
∴OH=CF=3,
∴BH=8,
∵∠CHB=∠AEB=90°,∠CBH=∠BAE,
∴△BCH∽△ABE,
∴,
∴,
∴CH=6,
∴C(3,6),
设反比例函数解析式为,
∴k=18,
∴反比例函数解析式为,
故答案为:.
【点评】本题主要考查了待定系数法求反比例函数的解析式,全等三角形的判定和性质,相似三角形的判定和性质,矩形的判定和性质等知识点,熟练掌握其性质并能正确地作出辅助线是解决此题的关键.
12.(2024秋 郑州校级期末)如图,点A是反比例函数y(x>0)图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,且△ABP的面积为6,则k= ﹣12 .
【考点】反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力.
【答案】﹣12.
【分析】由AB⊥y轴,则AB∥OP,故S△ABO=S△ABP,然后根据比例系数的几何意义即可求解.
【解答】解:由条件可知AB∥OP,
∴S△ABO=S△ABP|k|=6,
∵反比例函数图象在第二象限,
∴k=﹣12,
故答案为:﹣12.
【点评】本题考查了反比例函数比例系数的几何意义,掌握反比例函数比例系数的几何意义是解题的关键.
13.(2024秋 雁塔区校级期末)若直线y=﹣2x的图象与反比例函数的图象交于(x1,y1),(x2,y2)两点,且(y2﹣y1)(x1﹣x2)=16,则k= ﹣4 .
【考点】反比例函数与一次函数的交点问题.
【专题】一次函数及其应用;反比例函数及其应用;运算能力.
【答案】﹣4.
【分析】由直线y=﹣2x与反比例函数的图象都关于原点对称,可得(x1,y1),(x2,y2)两点也关于原点对称,则有x2=﹣x1,y2=﹣y1,再代入(y2﹣y1)(x1﹣x2)=16整理得x1y1=﹣4,再利用反比例函数的解析式即可求解.
【解答】解:∵直线y=﹣2x的图象与反比例函数的图象都关于原点对称,且交于(x1,y1),(x2,y2)两点,
∴x2=﹣x1,y2=﹣y1,
由条件可知(﹣y1﹣y1)(x1+x1)=16,
整理得:x1y1=﹣4,
∵(x1,y1)在反比例函数的图象上,
∴k=x1y1=﹣4.
故答案为:﹣4.
【点评】本题考查了一次函数与反比例函数的交点问题,熟练掌握一次函数与反比例函数的图象与性质是解题的关键.
14.(2024秋 秦都区期末)如图,已知平行四边形的顶点B、C、D分别在y轴和x轴上,点A在反比例函数y(k>0,x>0)的图象上,若OB=2OC=4,OD=5,则k的值为 12 .
【考点】反比例函数图象上点的坐标特征;平行四边形的性质.
【专题】反比例函数及其应用;运算能力.
【答案】12.
【分析】由平行四边形的性质可得AB=CD=OD﹣OC=3,进而可得A(3,4),将其代入即可求出k的值.
【解答】解:由条件可知OC=2,CD=OD﹣OC=3,
∵平行四边形的顶点B、C、D分别在y轴和x轴上,
∴AB=CD=OD﹣OC=3,∠ABO=∠BOC=90°,
∴A(3,4),
把A(3,4)代入,得:
,
解得:k=12,
故答案为:12.
【点评】本题主要考查了反比例函数与几何综合,平行四边形的性质,两直线平行同旁内角互补,求反比例函数解析式,线段的和与差,解一元一次方程等知识点,熟练掌握反比例函数与几何综合是解题的关键.
15.(2024秋 天府新区期末)如图,直线AB与反比例函数图象交于A,B两点,与x轴交于点M且满足,连接AO并延长交反比例函数图象于点C,连接BC,若△ABC的面积为24,则k的值为 16 .
【考点】反比例函数与一次函数的交点问题.
【专题】一次函数及其应用;反比例函数及其应用;运算能力.
【答案】16.
【分析】分别过A,B两点作x轴的垂线,垂足分别为E,F,利用相似三角形的性质得出AE=2BF,据此表示出点A和点B的坐标,进而表示出点C的坐标,最后利用△ABC的面积得出△BCO的面积,并据此列出等式即可解决问题.
【解答】解:分别过A,B两点作x轴的垂线,垂足分别为E,F,
则△AEM∽△BFM.
又因为,
所以,
即AE=2BF.
令点B的坐标为(),
则点A的坐标为().
因为A,C关于原点对称,
所以点C坐标为().
连接OB,
因为△ABC的面积为24,
所以△BCO面积为12.
过点C作x轴的垂线,垂足为P,
由S△COP+S梯形CBFP=S△BCO+S△BOF,且S△COP=S△BOF得,
S梯形CBFP=S△BCO=12,
所以,
解得k=16.
故答案为:16.
【点评】本题主要考查了反比例函数与一次函数的交点问题,熟知反比例函数及一次函数的图象与性质是解题的关键.
三.解答题(共5小题)
16.(2024秋 集美区期末)为提升居住品质,某小区计划对中庭进行改造,物业规划出一块边长分别是a米,b米的长方形空地,建设羽毛球场和半圆形儿童乐园两个功能区,剩余部分种植绿植.设计师给出的方案如图所示,羽毛球场的边长分别是m米,n米,儿童乐园的直径是b米.
(1)若该空地的面积为300平方米,判断a,b是否成反比例关系;
(2)小区业主要求该空地改造后有一半以上面积是功能区,若设计师规划的尺寸满足:,,.你认为该设计方案是否符合要求?若符合,请说明理由;若不符合,请给出一个符合要求的设计方案.
【考点】反比例函数的应用;一元二次方程的应用.
【专题】反比例函数及其应用;运算能力.
【答案】(1)是成反比例关系,理由见详解;
(2)改设计方案符合要求,理由见详解.
【分析】(1)根据长方形的面积公式可得ab=300,然后根据反比例关系的定义可进行求解;
(2)分别得出羽毛球场和儿童乐园的面积,然后用长方形的面积减去羽毛球场和儿童乐园的面积之和,进而问题可求解.
【解答】解:(1)根据长方形的面积公式可得ab=300,
因为a、b乘积一定,所以它们成反比例关系;
(2)长方形面积为,
羽毛球场的面积为,
儿童乐园的面积为,
∴功能区的面积为,
∵,
∴该设计方案符合要求.
【点评】本题考查列代数式,整式加减的应用,解题的关键是理解题意列出代数式.
17.(2024秋 雁塔区校级期末)如图,矩形ABEF与反比例函数的图象相交于C,D两点,点C的坐标(m,2),点D的坐标为(1,m+3).
(1)求反比例函数的表达式;
(2)若AB=9,在反比例函数图象上是否存在一点P(点P不与点C重合),使得△PFC的面积是矩形ABEF面积的一半?若存在,求出点P的坐标;若不存在,请说明理由.
【考点】待定系数法求反比例函数解析式;矩形的判定与性质;反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力.
【答案】(1);
(2)存在,或.
【分析】(1)根据反比例函数图象上点的坐标特征列出方程求出m,可得点C、D坐标,继而求出反比例函数解析式;
(2)先求出矩形的面积,进一步求得△PFC的面积,再设,则根据三角形面积公式得到,解方程求出m值可得点P坐标.
【解答】解:(1)由条件可知k=2m=m+3,
∴m=3,
∴C(3,2)、D(1,6),
∴k=3×2=6,
∴反比例函数解析式为;
(2)存在,
∵C(3,2)、D(1,6),
∴BE=2,
∵AB=9,
∴S矩形ABEF=2×9=18,FC=7,
∴S△PFC=9,
设,则,
即,
解得或,
∴或.
【点评】本题考查了反比例函数图象上点的坐标特征、待定系数法求反比例函数,熟练掌握待定系数法求函数解析式是关键.
18.(2024秋 香洲区期末)如图,已知点P是反比例函数图象上一动点,过点P分别作y轴、x轴的平行线交反比例函数图象上点A、点B,连接OA,OB.
(1)若点P的横坐标为1,则△PAB的面积为 4 ,△OAB的面积为 8 ;
(2)随着点P在反比例函数图象上运动时,△OAB的面积是否会发生变化?如果变化,说明理由;如果不变,请计算出△OAB的面积.
【考点】反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;几何直观;运算能力.
【答案】(1)4;8;
(2)△OAB的面积不发生变化,始终等于8,理由见解答过程.
【分析】(1)延长AP交x轴于点C,过点B作BD⊥x轴于点D,依题意得点P(1,2),四边形CDBP是矩形,四边形ABDC是梯形,点A(1,6),点B(3,2),则AC=6,OC=1,BD=PC=2,OD=3,BP=CD=2,PA=4,由此可得△PAB的面积,根据反比例函数比例系数k的几何意义得S△AOC=S△BOD=3,S梯形ABDC=8,由此得S△OAB=S梯形ABDC=8;
(2)延长AP交x轴于点C,过点B作BD⊥x轴于点D,设点P,则点A,点B,同理可证明四边形CDBP是矩形,四边形ABDC是梯形,则OC=a,AC,BD=PC,OD=3a,CD=BP=2a,S梯形ABDC(AC+BD) CD=8,由(1)可知S△OAB=S梯形ABDC=8.
【解答】解:(1)延长AP交x轴于点C,过点B作BD⊥x轴于点D,如图所示:
∵点P的横坐标为1,且点P在反比例函数的图象上,
∴点P(1,2),
∵PA平行y轴,PB平行y轴,
∴PA⊥PB,AC⊥x轴,点A的横坐标为1,点B的纵坐标为2,
∴四边形CDBP是矩形,四边形ABDC是梯形,
又∵点A,B在反比例函数的图象上,
∴点A(1,6),点B(3,2),
∴AC=6,OC=1,BD=PC=2,OD=3,
∴BP=CD=OD﹣OC=2,PA=AC﹣PC=4,
∴S△PABPA PB4,
根据反比例函数比例系数k的几何意义得:S△AOC=S△BOD3,
S梯形ABDC(AC+BD) CD8,
∴S△OAB=S△AOC+S梯形ABDC﹣S△BOD=S梯形ABDC=8,
故答案为:4;8;
(2)△OAB的面积不发生变化,始终等于8,理由如下:
设点P的坐标为,
则点A的横坐标为a,点B的纵坐标为,
∵点A,B在反比例函数的图象上,
∴点,点B,
同理可证明:四边形CDBP是矩形,四边形ABDC是梯形,
则OC=a,AC,BD=PC,OD=3a,
∴CD=BP=OD﹣OC=2a,
∴S梯形ABDC(AC+BD) CD8,
由(1)可知:S△OAB=S梯形ABDC=8.
【点评】此题主要考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标,理解反比例函数图象上点的坐标满足反比例函数的表达式,熟练掌握反比例函数系数k的几何意义是解决问题的关键.
19.(2024秋 太仓市期末)利用杆秤称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得等式:(m0+x) l=M (a+y),其中秤盘质量m0克,重物质量x克,秤砣质量M克,秤纽与秤盘的水平距离为1厘米,秤纽与零刻线的水平距离为a厘米,秤砣与零刻线的水平距离为y厘米.
如图,秤盘与零刻度线的距离AC为3厘米,零刻线与末刻线的距离CD为50厘米,秤盘质量m0=10克,秤砣质量M=50克.某兴趣小组利用等式(m0+x) l=M (a+y)制作简易杆秤.
(1)确定秤纽的位置:当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请求出l,a的值;
(2)确定杆秤的最大称重质量:根据(1)中l,a的值,求y关于x的函数解析式,并求杆秤的最大称重质量(秤砣移至末刻线D处,秤得的物体质量);
(3)制作杆秤的刻度:将零刻线开始至末刻度线之间的线段CD平均分成10份(格),标注刻度值,则点E处应标注的刻度值为 600 克.
(4)该小组成员利用制作好的杆秤称重物时,误用了60克的秤砣进行称重,称得重物的质量为500克,则该重物的实际质量为 602 克.
【考点】反比例函数的应用;单项式乘多项式.
【专题】反比例函数及其应用;运算能力.
【答案】(1);
(2),最大称重质量为1000克;
(3)600;
(4)602.
【分析】(1)由l+a=3知,l=3﹣a,再把m0=10,x=0,M=50,l=3﹣a,y=0代入(m0+x) l=M (a+y),求出a=0.5,l=2.5;
(2)将m0=10,M=50,a=0.5,l=2.5代入(m0+x) l=M (a+y),求得,当y=50时可求出杆秤的最大称重质量;
(3)求出每一刻度的称重,再乘以6即可;
(4)先计算出称重时y值的长度为25cm,再代入公式求解即可.
【解答】解:(1)∵l+a=3,
∴l=3﹣a,
把m0=10,x=0,M=50,l=3﹣a,y=0代入(m0+x) l=M (a+y):
(10+0)×(3﹣a)=50(a+0),
∴a=0.5,
∴l=3﹣0.5=2.5;
(2)将m0=10,M=50,a=0.5,l=2.5代入(m0+x) l=M (a+y),
(10+x)×2.5=50(0.5+y),
∴;
当y=50时,即,
∴x=1000,
(3)1000÷10×6=600克,
故答案为:600;
(4)由(1)知,l=2.5cm,a=0.5cm,
当重物质量为500克时,
(10+500)×2.5=50(0.5+y),
∴y=25cm,
而小组成员错误称量时,y值的长度为25cm,用了60克的秤砣进行称重,
所以有:(10+m)×2.5=60(0.5+25),
解得,m=602,
故答案为:602.
【点评】本题主要考查一次函数的应用、解一元一次方程,读懂题意,根据题干的描述正确列出等式是解题关键.
20.(2024秋 温州期末)【项目】小车沿斜面运动中路程s与时间t的关系.
图1是小车从斜面上静止滑下的实验装置,斜面刻度值单位为分米.小温和小州共同填写了如下实验记录表.
t(秒) 0 2 3 ……
s(分米) 0 4 9 ……
(1)小温发现,路程s与时间t可采用一次函数、反比例函数、二次函数中的一种进行刻画,请通过实验数据在图2中描点画图,判断可以采用的函数模型,并求出s关于t的函数表达式.
(2)若斜面足够长,请通过计算说明小车在斜面上第一个5秒和第二个5秒通过的路程之差.
(3)小州说:把单位时间设为1秒,还可以研究第t秒内通过的路程s′(分米)与第t秒之间的函数关系.
请写出一个路程s′(分米)与第t秒之间的结论,并通过计算说明理由.
【考点】反比例函数的图象;二次函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】(1)二次函数,s=t2(t≥0);
(2)50分米;
(3)s′=2t﹣1.
【分析】(1)在图2中描点画图,即可判断采用的函数模型,再利用待定系数法求出s关于t的函数表达式即可;
(2)先求出小车在斜面上第一个5秒通过的路程,再算出小车在斜面上第二个5秒通过的路程,作差即可解答;
(3)根据第t秒通过的路程等于前t秒通过的路程减去前(t﹣1)秒通过的路程列式化简即可解答.
【解答】解:(1)将题中给出的实验数据在图中描点,依次连接各点,如图所示:
可以采用的函数模型是二次函数,
设路程s与时间t的函数关系式为:y=at2+bt+c(a≠0),
将(0,0),(2,4),(3,9)代入,得:,
解得,
∴路程s与时间t的函数关系式为:s=t2(t≥0);
(2)当t=5时,s=52=25(分米),
当t=10时,s=102=100(分米),
∴第2个5秒小车通过的路程为:100﹣25=75(分米),
∴路程差为:75﹣25=50(分米);
(3)第1秒通过的路程=12=1(分米),
第2秒通过的路程=22﹣12=3(分米),
第3秒通过的路程=32﹣22=5(分米),
……,
第t秒通过的路程=t2﹣(t﹣1)2=2t﹣1(分米),
∴第t秒内通过的路程s′(分米)与第t秒之间的函数关系为s′=2t﹣1.
【点评】本题考查了画二次函数图象、用待定系数法求二次函数解析式、根据自变量求函数值,求一次函数解析式等知识点,熟练掌握以上知识点是解答本题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 滨海新区校级期末)已知函数的图象上有三点,则y1,y2,y3的大小关系( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y1<y2 D.y3<y2<y1
2.(2024秋 琼中县期末)在物理学中,导体中的电流Ⅰ跟导体两端的电压U,导体的电阻R之间有以下关系:去分母得IR=U,那么其变形的依据是( )
A.等式两边加(或减)同一个数(或式子),结果仍相等
B.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等
C.等式两边可以交换
D.相等关系可以传递
3.(2024秋 礼县期末)下列函数中,y是x的反比例函数的是( )
A. B. C.y=5x2 D.
4.(2025 浦东新区一模)下列四个函数中,图象经过原点的是( )
A. B. C.y=x2+2x D.y=(x+1)2
5.(2024秋 长沙期末)下列关系式中的两个量成反比例的是( )
A.圆的面积与它的半径
B.正方形的周长与它的边长
C.路程一定时,速度与时间
D.长方形一条边确定时,周长与另一边
6.(2024秋 河西区期末)下列函数中,当x>0时,y随着x的增大而增大的是( )
A.y=﹣x﹣3 B. C.y=x2﹣3 D.y=﹣x2﹣3
7.(2024秋 普陀区期末)下列关于反比例函数的说法中,正确的是( )
A.图象在第一、三象限
B.比例系数为﹣10
C.当自变量x的值逐渐增大时,y的值随着逐渐增大
D.如果点A(﹣3,y1)和点B(﹣5,y2)在该函数的图象上,那么y1>y2
8.(2024秋 贵阳期末)如图,过点P(﹣1,0)作两条直线,分别交函数,的图象于A,B两点,连接AB.若AB∥x轴,则△ABP的面积是( )
A.1 B.2 C.3 D.4
9.(2024秋 天府新区期末)对于反比例函数,下列说法正确的是( )
A.图象分布在第一、三象限
B.图象经过点(1,1)
C.过图象上任一点P分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为1
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
10.(2024秋 浦东新区校级期末)已知函数中,在每个象限内,y的值随x的值增大而减小,那么它和函数y=﹣kx(k≠0)在同一直角坐标平面内的大致图象是( )
A. B.
C. D.
二.填空题(共5小题)
11.(2024秋 本溪期末)如图所示在平面直角坐标系中,四边形ABCD是矩形,A(﹣8,4),点B和点D分别在x轴和y轴上,CD=5,反比例函数过点C,则反比例函数解析式为 .
12.(2024秋 郑州校级期末)如图,点A是反比例函数y(x>0)图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,且△ABP的面积为6,则k= .
13.(2024秋 雁塔区校级期末)若直线y=﹣2x的图象与反比例函数的图象交于(x1,y1),(x2,y2)两点,且(y2﹣y1)(x1﹣x2)=16,则k= .
14.(2024秋 秦都区期末)如图,已知平行四边形的顶点B、C、D分别在y轴和x轴上,点A在反比例函数y(k>0,x>0)的图象上,若OB=2OC=4,OD=5,则k的值为 .
15.(2024秋 天府新区期末)如图,直线AB与反比例函数图象交于A,B两点,与x轴交于点M且满足,连接AO并延长交反比例函数图象于点C,连接BC,若△ABC的面积为24,则k的值为 .
三.解答题(共5小题)
16.(2024秋 集美区期末)为提升居住品质,某小区计划对中庭进行改造,物业规划出一块边长分别是a米,b米的长方形空地,建设羽毛球场和半圆形儿童乐园两个功能区,剩余部分种植绿植.设计师给出的方案如图所示,羽毛球场的边长分别是m米,n米,儿童乐园的直径是b米.
(1)若该空地的面积为300平方米,判断a,b是否成反比例关系;
(2)小区业主要求该空地改造后有一半以上面积是功能区,若设计师规划的尺寸满足:,,.你认为该设计方案是否符合要求?若符合,请说明理由;若不符合,请给出一个符合要求的设计方案.
17.(2024秋 雁塔区校级期末)如图,矩形ABEF与反比例函数的图象相交于C,D两点,点C的坐标(m,2),点D的坐标为(1,m+3).
(1)求反比例函数的表达式;
(2)若AB=9,在反比例函数图象上是否存在一点P(点P不与点C重合),使得△PFC的面积是矩形ABEF面积的一半?若存在,求出点P的坐标;若不存在,请说明理由.
18.(2024秋 香洲区期末)如图,已知点P是反比例函数图象上一动点,过点P分别作y轴、x轴的平行线交反比例函数图象上点A、点B,连接OA,OB.
(1)若点P的横坐标为1,则△PAB的面积为 ,△OAB的面积为 ;
(2)随着点P在反比例函数图象上运动时,△OAB的面积是否会发生变化?如果变化,说明理由;如果不变,请计算出△OAB的面积.
19.(2024秋 太仓市期末)利用杆秤称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得等式:(m0+x) l=M (a+y),其中秤盘质量m0克,重物质量x克,秤砣质量M克,秤纽与秤盘的水平距离为1厘米,秤纽与零刻线的水平距离为a厘米,秤砣与零刻线的水平距离为y厘米.
如图,秤盘与零刻度线的距离AC为3厘米,零刻线与末刻线的距离CD为50厘米,秤盘质量m0=10克,秤砣质量M=50克.某兴趣小组利用等式(m0+x) l=M (a+y)制作简易杆秤.
(1)确定秤纽的位置:当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请求出l,a的值;
(2)确定杆秤的最大称重质量:根据(1)中l,a的值,求y关于x的函数解析式,并求杆秤的最大称重质量(秤砣移至末刻线D处,秤得的物体质量);
(3)制作杆秤的刻度:将零刻线开始至末刻度线之间的线段CD平均分成10份(格),标注刻度值,则点E处应标注的刻度值为 克.
(4)该小组成员利用制作好的杆秤称重物时,误用了60克的秤砣进行称重,称得重物的质量为500克,则该重物的实际质量为 克.
20.(2024秋 温州期末)【项目】小车沿斜面运动中路程s与时间t的关系.
图1是小车从斜面上静止滑下的实验装置,斜面刻度值单位为分米.小温和小州共同填写了如下实验记录表.
t(秒) 0 2 3 ……
s(分米) 0 4 9 ……
(1)小温发现,路程s与时间t可采用一次函数、反比例函数、二次函数中的一种进行刻画,请通过实验数据在图2中描点画图,判断可以采用的函数模型,并求出s关于t的函数表达式.
(2)若斜面足够长,请通过计算说明小车在斜面上第一个5秒和第二个5秒通过的路程之差.
(3)小州说:把单位时间设为1秒,还可以研究第t秒内通过的路程s′(分米)与第t秒之间的函数关系.
请写出一个路程s′(分米)与第t秒之间的结论,并通过计算说明理由.
2025年中考数学高频易错考前冲刺:反比例函数
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 B B A C C C D B C A
一.选择题(共10小题)
1.(2024秋 滨海新区校级期末)已知函数的图象上有三点,则y1,y2,y3的大小关系( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y1<y2 D.y3<y2<y1
【考点】反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力.
【答案】B
【分析】先根据反比例函数的性质判断出函数图象所在的象限,再根据反比例函数的性质即可作出判断.
【解答】解:∵k2+1>0,
∴函数的图象在一、三象限,且在每一象限内y随x的增大而减小,
∴点在第三象限,B(1,y2),C(4,y3)在第一象限,
∴y1<0<y3<y2.
故选:B.
【点评】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象的增减性是解答此题的关键.
2.(2024秋 琼中县期末)在物理学中,导体中的电流Ⅰ跟导体两端的电压U,导体的电阻R之间有以下关系:去分母得IR=U,那么其变形的依据是( )
A.等式两边加(或减)同一个数(或式子),结果仍相等
B.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等
C.等式两边可以交换
D.相等关系可以传递
【考点】反比例函数的应用;有理数的除法.
【专题】反比例函数及其应用;运算能力.
【答案】B
【分析】根据题目中的变形,可知依据是等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
【解答】解:去分母得IR=U,那么其变形的依据是等式两边乘同一个数,或除以同一个不为0的数,结果仍相等,
故选:B.
【点评】本题考查反比例函数的应用、等式的性质,解答本题的关键是明确等式的性质二,等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
3.(2024秋 礼县期末)下列函数中,y是x的反比例函数的是( )
A. B. C.y=5x2 D.
【考点】反比例函数的定义.
【专题】反比例函数及其应用;运算能力.
【答案】A
【分析】根据反比例函数的定义逐项判断即可.
【解答】解:A.符合反比例函数的定义,符合题意;
B.不符合反比例函数的定义,不符合题意;
C.该函数属于二次函数,不符合题意;
D.该函数不属于反比例函数,不符合题意.
故选:A.
【点评】本题主要考查了反比例函数的定义,熟知“一般地,如果两个变量x,y之间的关系可以表示成(k为常数,k≠0)的形式,那么称y是x的反比例函数”是解题关键.
4.(2025 浦东新区一模)下列四个函数中,图象经过原点的是( )
A. B. C.y=x2+2x D.y=(x+1)2
【考点】反比例函数图象上点的坐标特征;二次函数的性质;二次函数图象上点的坐标特征;一次函数的性质;一次函数图象上点的坐标特征;反比例函数的性质.
【专题】一次函数及其应用;反比例函数及其应用;二次函数图象及其性质;运算能力.
【答案】C
【分析】令x=0,函数值也等于0,则图象经过原点.
【解答】解:A、令x=0,则y,故不符合题意;
B、x=0无意义,故不符合题意;
C、x=0,则y=0,故符合题意;
D、x=0,则y=1,故不符合题意.
故选:C.
【点评】本题考查函数图象上的点,掌握函数图象上的点的坐标适合函数解析式是解题的关键.
5.(2024秋 长沙期末)下列关系式中的两个量成反比例的是( )
A.圆的面积与它的半径
B.正方形的周长与它的边长
C.路程一定时,速度与时间
D.长方形一条边确定时,周长与另一边
【考点】反比例函数的定义.
【专题】反比例函数及其应用;符号意识;应用意识.
【答案】C
【分析】根据反比例函数的定义解答即可.
【解答】解:A、圆的面积=π×半径2,不是反比例函数,故本选项不符合题意;
B、正方形的周长=边长×4,不是反比例函数,故本选项不符合题意;
C、路程s一定时,速度v和时间t的关系s=vt,是反比例函数,故本选项符合题意;
D、长方形一条a边确定时,周长s与另一边b的关系s=2×(a+b),不是反比例关系,故本选项不符合题意.
故选:C.
【点评】本题考查了反比例函数,熟练掌握反比例函数的定义是解题的关键.要注意:反比例函数的判断:判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系,然后根据反比例函数的意义去判断,其形式为y(k为常数,k≠0)或y=kx﹣1(k为常数,k≠0).
6.(2024秋 河西区期末)下列函数中,当x>0时,y随着x的增大而增大的是( )
A.y=﹣x﹣3 B. C.y=x2﹣3 D.y=﹣x2﹣3
【考点】反比例函数的性质;二次函数的性质;一次函数的性质.
【专题】反比例函数及其应用;推理能力.
【答案】C
【分析】分别根据反比例函数的性质,一次函数的性质及二次函数的性质对各选项进行逐一判断即可.
【解答】解:A、一次函数y=﹣x﹣3中,
∵k=﹣1<0,
∴y随着x的增大而减小,不符合题意;
B、反比例函数y中,
∵k=3>0,
∴此函数图象的两个分支分别位于第一、三象限,在每一项象限内y随x的增大而减小,不符合题意;
C、二次函数y=x2﹣3中,
∵a=1>0,
∴抛物线开口向上,顶点坐标为(0,﹣3),
∴当x>0时,y随着x的增大而增大,符合题意;
D、二次函数y=﹣x2﹣3中,
∵a=﹣1<0,
∴抛物线开口向下,顶点坐标为(0,﹣3),
∴当x>0时,y随着x的增大而减小,不符合题意,
故选:C.
【点评】本题考查的是反比例函数的性质,一次函数的性质及二次函数的性质,熟知以上知识是解题的关键.
7.(2024秋 普陀区期末)下列关于反比例函数的说法中,正确的是( )
A.图象在第一、三象限
B.比例系数为﹣10
C.当自变量x的值逐渐增大时,y的值随着逐渐增大
D.如果点A(﹣3,y1)和点B(﹣5,y2)在该函数的图象上,那么y1>y2
【考点】反比例函数的性质;反比例函数的定义.
【专题】反比例函数及其应用;应用意识.
【答案】D
【分析】根据k<0,利用反比例函数的性质一一判断即可.
【解答】解:∵y,
∴k0,
∴函数图象在二,四象限,在每个象限y随x的增大而增大,故选项A,B,C错误,选项D正确.
故选:D.
【点评】本题考查反比例函数的性质,反比例函数的定义,解题的关键是掌握反比例函数的性质.
8.(2024秋 贵阳期末)如图,过点P(﹣1,0)作两条直线,分别交函数,的图象于A,B两点,连接AB.若AB∥x轴,则△ABP的面积是( )
A.1 B.2 C.3 D.4
【考点】反比例函数系数k的几何意义;反比例函数的图象;反比例函数的性质.
【专题】反比例函数及其应用;运算能力.
【答案】B
【分析】根据反比例函数k值的几何意义解答即可.
【解答】解:如图,连接OA、OB,
∵AB∥x轴,
∴S△AOB=S△PAB2.
故选:B.
【点评】本题考查了反比例函数k值的几何意义,熟练掌握该知识点是关键.
9.(2024秋 天府新区期末)对于反比例函数,下列说法正确的是( )
A.图象分布在第一、三象限
B.图象经过点(1,1)
C.过图象上任一点P分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为1
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
【考点】反比例函数系数k的几何意义;反比例函数的性质.
【专题】反比例函数及其应用;运算能力.
【答案】C
【分析】根据反比例函数的图象与性质逐项分析判断即可.
【解答】解:A、反比例函数k=﹣1,图象分布在第二、四象限,选项说法错误,不符合题意;
B、当x=1时,y=﹣1≠1,故选项说法错误,不符合题意;
C、过图象上任一点P分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为1,选项说法正确,符合题意;
D、当x1<0<x2时,y1>y2,选项说法错误,不符合题意;
故选:C.
【点评】本题考查了反比例函数k值的几何意义,熟练掌握反比例函数k值的几何意义是关键.
10.(2024秋 浦东新区校级期末)已知函数中,在每个象限内,y的值随x的值增大而减小,那么它和函数y=﹣kx(k≠0)在同一直角坐标平面内的大致图象是( )
A. B.
C. D.
【考点】反比例函数的性质;正比例函数的图象;正比例函数的性质.
【专题】一次函数及其应用;反比例函数及其应用;推理能力.
【答案】A
【分析】首先根据反比例函数图象的性质判断出k的范围,在确定其所在象限,进而确定正比例函数图象所在象限,即可得到答案.
【解答】解:∵函数中,在每个象限内,y的值随x的值增大而减小,
∴k>0,
∴双曲线在第一、三象限,
∴函数y=﹣kx的图象经过第二、四象限,
故选:A.
【点评】此题主要考查了反比例函数图象的性质与正比例函数图象的性质,图象所在象限受k的影响.
二.填空题(共5小题)
11.(2024秋 本溪期末)如图所示在平面直角坐标系中,四边形ABCD是矩形,A(﹣8,4),点B和点D分别在x轴和y轴上,CD=5,反比例函数过点C,则反比例函数解析式为 y .
【考点】待定系数法求反比例函数解析式;矩形的性质;反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力.
【答案】.
【分析】如图,过A作AE⊥x轴于E,过C作CF⊥y轴于F,过C作CH⊥x轴于H,设BC与y轴交于G,得到AE=4,OE=8,根据矩形的性质得到CD=AB=5,∠ABC=∠DCB=90°,根据勾股定理得到,求得OB=5,根据全等三角形的性质得到CF=BE=3,根据矩形的性质得到OH=CF=3,求得BH=8,根据相似三角形的性质得到C(3,6),设反比例函数解析式为,将C(3,6)代入即可得解.
【解答】解:如图,过A作AE⊥x轴于E,过C作CF⊥y轴于F,过C作CH⊥x轴于H,设BC与y轴交于G,
由条件可知AE=4,OE=8,
由条件可知CD=AB=5,∠ABC=∠DCB=90°,
∴,
∴OB=OE﹣BE=5,
∵∠BOG=∠GCD=90°,∠CGD=∠BGO,
∴∠OBG=∠CDG,
∴∠BAE=∠OBG=∠CDF,
∵∠AEB=∠DFC=90°,
∴△CDF≌△BAE(AAS),
∴CF=BE=3,
∵∠CHO=∠HOF=∠CFO=90°,
∴四边形CHOF是矩形,
∴OH=CF=3,
∴BH=8,
∵∠CHB=∠AEB=90°,∠CBH=∠BAE,
∴△BCH∽△ABE,
∴,
∴,
∴CH=6,
∴C(3,6),
设反比例函数解析式为,
∴k=18,
∴反比例函数解析式为,
故答案为:.
【点评】本题主要考查了待定系数法求反比例函数的解析式,全等三角形的判定和性质,相似三角形的判定和性质,矩形的判定和性质等知识点,熟练掌握其性质并能正确地作出辅助线是解决此题的关键.
12.(2024秋 郑州校级期末)如图,点A是反比例函数y(x>0)图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,且△ABP的面积为6,则k= ﹣12 .
【考点】反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力.
【答案】﹣12.
【分析】由AB⊥y轴,则AB∥OP,故S△ABO=S△ABP,然后根据比例系数的几何意义即可求解.
【解答】解:由条件可知AB∥OP,
∴S△ABO=S△ABP|k|=6,
∵反比例函数图象在第二象限,
∴k=﹣12,
故答案为:﹣12.
【点评】本题考查了反比例函数比例系数的几何意义,掌握反比例函数比例系数的几何意义是解题的关键.
13.(2024秋 雁塔区校级期末)若直线y=﹣2x的图象与反比例函数的图象交于(x1,y1),(x2,y2)两点,且(y2﹣y1)(x1﹣x2)=16,则k= ﹣4 .
【考点】反比例函数与一次函数的交点问题.
【专题】一次函数及其应用;反比例函数及其应用;运算能力.
【答案】﹣4.
【分析】由直线y=﹣2x与反比例函数的图象都关于原点对称,可得(x1,y1),(x2,y2)两点也关于原点对称,则有x2=﹣x1,y2=﹣y1,再代入(y2﹣y1)(x1﹣x2)=16整理得x1y1=﹣4,再利用反比例函数的解析式即可求解.
【解答】解:∵直线y=﹣2x的图象与反比例函数的图象都关于原点对称,且交于(x1,y1),(x2,y2)两点,
∴x2=﹣x1,y2=﹣y1,
由条件可知(﹣y1﹣y1)(x1+x1)=16,
整理得:x1y1=﹣4,
∵(x1,y1)在反比例函数的图象上,
∴k=x1y1=﹣4.
故答案为:﹣4.
【点评】本题考查了一次函数与反比例函数的交点问题,熟练掌握一次函数与反比例函数的图象与性质是解题的关键.
14.(2024秋 秦都区期末)如图,已知平行四边形的顶点B、C、D分别在y轴和x轴上,点A在反比例函数y(k>0,x>0)的图象上,若OB=2OC=4,OD=5,则k的值为 12 .
【考点】反比例函数图象上点的坐标特征;平行四边形的性质.
【专题】反比例函数及其应用;运算能力.
【答案】12.
【分析】由平行四边形的性质可得AB=CD=OD﹣OC=3,进而可得A(3,4),将其代入即可求出k的值.
【解答】解:由条件可知OC=2,CD=OD﹣OC=3,
∵平行四边形的顶点B、C、D分别在y轴和x轴上,
∴AB=CD=OD﹣OC=3,∠ABO=∠BOC=90°,
∴A(3,4),
把A(3,4)代入,得:
,
解得:k=12,
故答案为:12.
【点评】本题主要考查了反比例函数与几何综合,平行四边形的性质,两直线平行同旁内角互补,求反比例函数解析式,线段的和与差,解一元一次方程等知识点,熟练掌握反比例函数与几何综合是解题的关键.
15.(2024秋 天府新区期末)如图,直线AB与反比例函数图象交于A,B两点,与x轴交于点M且满足,连接AO并延长交反比例函数图象于点C,连接BC,若△ABC的面积为24,则k的值为 16 .
【考点】反比例函数与一次函数的交点问题.
【专题】一次函数及其应用;反比例函数及其应用;运算能力.
【答案】16.
【分析】分别过A,B两点作x轴的垂线,垂足分别为E,F,利用相似三角形的性质得出AE=2BF,据此表示出点A和点B的坐标,进而表示出点C的坐标,最后利用△ABC的面积得出△BCO的面积,并据此列出等式即可解决问题.
【解答】解:分别过A,B两点作x轴的垂线,垂足分别为E,F,
则△AEM∽△BFM.
又因为,
所以,
即AE=2BF.
令点B的坐标为(),
则点A的坐标为().
因为A,C关于原点对称,
所以点C坐标为().
连接OB,
因为△ABC的面积为24,
所以△BCO面积为12.
过点C作x轴的垂线,垂足为P,
由S△COP+S梯形CBFP=S△BCO+S△BOF,且S△COP=S△BOF得,
S梯形CBFP=S△BCO=12,
所以,
解得k=16.
故答案为:16.
【点评】本题主要考查了反比例函数与一次函数的交点问题,熟知反比例函数及一次函数的图象与性质是解题的关键.
三.解答题(共5小题)
16.(2024秋 集美区期末)为提升居住品质,某小区计划对中庭进行改造,物业规划出一块边长分别是a米,b米的长方形空地,建设羽毛球场和半圆形儿童乐园两个功能区,剩余部分种植绿植.设计师给出的方案如图所示,羽毛球场的边长分别是m米,n米,儿童乐园的直径是b米.
(1)若该空地的面积为300平方米,判断a,b是否成反比例关系;
(2)小区业主要求该空地改造后有一半以上面积是功能区,若设计师规划的尺寸满足:,,.你认为该设计方案是否符合要求?若符合,请说明理由;若不符合,请给出一个符合要求的设计方案.
【考点】反比例函数的应用;一元二次方程的应用.
【专题】反比例函数及其应用;运算能力.
【答案】(1)是成反比例关系,理由见详解;
(2)改设计方案符合要求,理由见详解.
【分析】(1)根据长方形的面积公式可得ab=300,然后根据反比例关系的定义可进行求解;
(2)分别得出羽毛球场和儿童乐园的面积,然后用长方形的面积减去羽毛球场和儿童乐园的面积之和,进而问题可求解.
【解答】解:(1)根据长方形的面积公式可得ab=300,
因为a、b乘积一定,所以它们成反比例关系;
(2)长方形面积为,
羽毛球场的面积为,
儿童乐园的面积为,
∴功能区的面积为,
∵,
∴该设计方案符合要求.
【点评】本题考查列代数式,整式加减的应用,解题的关键是理解题意列出代数式.
17.(2024秋 雁塔区校级期末)如图,矩形ABEF与反比例函数的图象相交于C,D两点,点C的坐标(m,2),点D的坐标为(1,m+3).
(1)求反比例函数的表达式;
(2)若AB=9,在反比例函数图象上是否存在一点P(点P不与点C重合),使得△PFC的面积是矩形ABEF面积的一半?若存在,求出点P的坐标;若不存在,请说明理由.
【考点】待定系数法求反比例函数解析式;矩形的判定与性质;反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力.
【答案】(1);
(2)存在,或.
【分析】(1)根据反比例函数图象上点的坐标特征列出方程求出m,可得点C、D坐标,继而求出反比例函数解析式;
(2)先求出矩形的面积,进一步求得△PFC的面积,再设,则根据三角形面积公式得到,解方程求出m值可得点P坐标.
【解答】解:(1)由条件可知k=2m=m+3,
∴m=3,
∴C(3,2)、D(1,6),
∴k=3×2=6,
∴反比例函数解析式为;
(2)存在,
∵C(3,2)、D(1,6),
∴BE=2,
∵AB=9,
∴S矩形ABEF=2×9=18,FC=7,
∴S△PFC=9,
设,则,
即,
解得或,
∴或.
【点评】本题考查了反比例函数图象上点的坐标特征、待定系数法求反比例函数,熟练掌握待定系数法求函数解析式是关键.
18.(2024秋 香洲区期末)如图,已知点P是反比例函数图象上一动点,过点P分别作y轴、x轴的平行线交反比例函数图象上点A、点B,连接OA,OB.
(1)若点P的横坐标为1,则△PAB的面积为 4 ,△OAB的面积为 8 ;
(2)随着点P在反比例函数图象上运动时,△OAB的面积是否会发生变化?如果变化,说明理由;如果不变,请计算出△OAB的面积.
【考点】反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;几何直观;运算能力.
【答案】(1)4;8;
(2)△OAB的面积不发生变化,始终等于8,理由见解答过程.
【分析】(1)延长AP交x轴于点C,过点B作BD⊥x轴于点D,依题意得点P(1,2),四边形CDBP是矩形,四边形ABDC是梯形,点A(1,6),点B(3,2),则AC=6,OC=1,BD=PC=2,OD=3,BP=CD=2,PA=4,由此可得△PAB的面积,根据反比例函数比例系数k的几何意义得S△AOC=S△BOD=3,S梯形ABDC=8,由此得S△OAB=S梯形ABDC=8;
(2)延长AP交x轴于点C,过点B作BD⊥x轴于点D,设点P,则点A,点B,同理可证明四边形CDBP是矩形,四边形ABDC是梯形,则OC=a,AC,BD=PC,OD=3a,CD=BP=2a,S梯形ABDC(AC+BD) CD=8,由(1)可知S△OAB=S梯形ABDC=8.
【解答】解:(1)延长AP交x轴于点C,过点B作BD⊥x轴于点D,如图所示:
∵点P的横坐标为1,且点P在反比例函数的图象上,
∴点P(1,2),
∵PA平行y轴,PB平行y轴,
∴PA⊥PB,AC⊥x轴,点A的横坐标为1,点B的纵坐标为2,
∴四边形CDBP是矩形,四边形ABDC是梯形,
又∵点A,B在反比例函数的图象上,
∴点A(1,6),点B(3,2),
∴AC=6,OC=1,BD=PC=2,OD=3,
∴BP=CD=OD﹣OC=2,PA=AC﹣PC=4,
∴S△PABPA PB4,
根据反比例函数比例系数k的几何意义得:S△AOC=S△BOD3,
S梯形ABDC(AC+BD) CD8,
∴S△OAB=S△AOC+S梯形ABDC﹣S△BOD=S梯形ABDC=8,
故答案为:4;8;
(2)△OAB的面积不发生变化,始终等于8,理由如下:
设点P的坐标为,
则点A的横坐标为a,点B的纵坐标为,
∵点A,B在反比例函数的图象上,
∴点,点B,
同理可证明:四边形CDBP是矩形,四边形ABDC是梯形,
则OC=a,AC,BD=PC,OD=3a,
∴CD=BP=OD﹣OC=2a,
∴S梯形ABDC(AC+BD) CD8,
由(1)可知:S△OAB=S梯形ABDC=8.
【点评】此题主要考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标,理解反比例函数图象上点的坐标满足反比例函数的表达式,熟练掌握反比例函数系数k的几何意义是解决问题的关键.
19.(2024秋 太仓市期末)利用杆秤称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得等式:(m0+x) l=M (a+y),其中秤盘质量m0克,重物质量x克,秤砣质量M克,秤纽与秤盘的水平距离为1厘米,秤纽与零刻线的水平距离为a厘米,秤砣与零刻线的水平距离为y厘米.
如图,秤盘与零刻度线的距离AC为3厘米,零刻线与末刻线的距离CD为50厘米,秤盘质量m0=10克,秤砣质量M=50克.某兴趣小组利用等式(m0+x) l=M (a+y)制作简易杆秤.
(1)确定秤纽的位置:当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请求出l,a的值;
(2)确定杆秤的最大称重质量:根据(1)中l,a的值,求y关于x的函数解析式,并求杆秤的最大称重质量(秤砣移至末刻线D处,秤得的物体质量);
(3)制作杆秤的刻度:将零刻线开始至末刻度线之间的线段CD平均分成10份(格),标注刻度值,则点E处应标注的刻度值为 600 克.
(4)该小组成员利用制作好的杆秤称重物时,误用了60克的秤砣进行称重,称得重物的质量为500克,则该重物的实际质量为 602 克.
【考点】反比例函数的应用;单项式乘多项式.
【专题】反比例函数及其应用;运算能力.
【答案】(1);
(2),最大称重质量为1000克;
(3)600;
(4)602.
【分析】(1)由l+a=3知,l=3﹣a,再把m0=10,x=0,M=50,l=3﹣a,y=0代入(m0+x) l=M (a+y),求出a=0.5,l=2.5;
(2)将m0=10,M=50,a=0.5,l=2.5代入(m0+x) l=M (a+y),求得,当y=50时可求出杆秤的最大称重质量;
(3)求出每一刻度的称重,再乘以6即可;
(4)先计算出称重时y值的长度为25cm,再代入公式求解即可.
【解答】解:(1)∵l+a=3,
∴l=3﹣a,
把m0=10,x=0,M=50,l=3﹣a,y=0代入(m0+x) l=M (a+y):
(10+0)×(3﹣a)=50(a+0),
∴a=0.5,
∴l=3﹣0.5=2.5;
(2)将m0=10,M=50,a=0.5,l=2.5代入(m0+x) l=M (a+y),
(10+x)×2.5=50(0.5+y),
∴;
当y=50时,即,
∴x=1000,
(3)1000÷10×6=600克,
故答案为:600;
(4)由(1)知,l=2.5cm,a=0.5cm,
当重物质量为500克时,
(10+500)×2.5=50(0.5+y),
∴y=25cm,
而小组成员错误称量时,y值的长度为25cm,用了60克的秤砣进行称重,
所以有:(10+m)×2.5=60(0.5+25),
解得,m=602,
故答案为:602.
【点评】本题主要考查一次函数的应用、解一元一次方程,读懂题意,根据题干的描述正确列出等式是解题关键.
20.(2024秋 温州期末)【项目】小车沿斜面运动中路程s与时间t的关系.
图1是小车从斜面上静止滑下的实验装置,斜面刻度值单位为分米.小温和小州共同填写了如下实验记录表.
t(秒) 0 2 3 ……
s(分米) 0 4 9 ……
(1)小温发现,路程s与时间t可采用一次函数、反比例函数、二次函数中的一种进行刻画,请通过实验数据在图2中描点画图,判断可以采用的函数模型,并求出s关于t的函数表达式.
(2)若斜面足够长,请通过计算说明小车在斜面上第一个5秒和第二个5秒通过的路程之差.
(3)小州说:把单位时间设为1秒,还可以研究第t秒内通过的路程s′(分米)与第t秒之间的函数关系.
请写出一个路程s′(分米)与第t秒之间的结论,并通过计算说明理由.
【考点】反比例函数的图象;二次函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】(1)二次函数,s=t2(t≥0);
(2)50分米;
(3)s′=2t﹣1.
【分析】(1)在图2中描点画图,即可判断采用的函数模型,再利用待定系数法求出s关于t的函数表达式即可;
(2)先求出小车在斜面上第一个5秒通过的路程,再算出小车在斜面上第二个5秒通过的路程,作差即可解答;
(3)根据第t秒通过的路程等于前t秒通过的路程减去前(t﹣1)秒通过的路程列式化简即可解答.
【解答】解:(1)将题中给出的实验数据在图中描点,依次连接各点,如图所示:
可以采用的函数模型是二次函数,
设路程s与时间t的函数关系式为:y=at2+bt+c(a≠0),
将(0,0),(2,4),(3,9)代入,得:,
解得,
∴路程s与时间t的函数关系式为:s=t2(t≥0);
(2)当t=5时,s=52=25(分米),
当t=10时,s=102=100(分米),
∴第2个5秒小车通过的路程为:100﹣25=75(分米),
∴路程差为:75﹣25=50(分米);
(3)第1秒通过的路程=12=1(分米),
第2秒通过的路程=22﹣12=3(分米),
第3秒通过的路程=32﹣22=5(分米),
……,
第t秒通过的路程=t2﹣(t﹣1)2=2t﹣1(分米),
∴第t秒内通过的路程s′(分米)与第t秒之间的函数关系为s′=2t﹣1.
【点评】本题考查了画二次函数图象、用待定系数法求二次函数解析式、根据自变量求函数值,求一次函数解析式等知识点,熟练掌握以上知识点是解答本题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
