【中考押题卷】2025年中考数学高频易错考前冲刺:函数基础知识(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:函数基础知识(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 00:00:00 | ||
图片预览




文档简介
2025年中考数学高频易错考前冲刺:函数基础知识
一.选择题(共10小题)
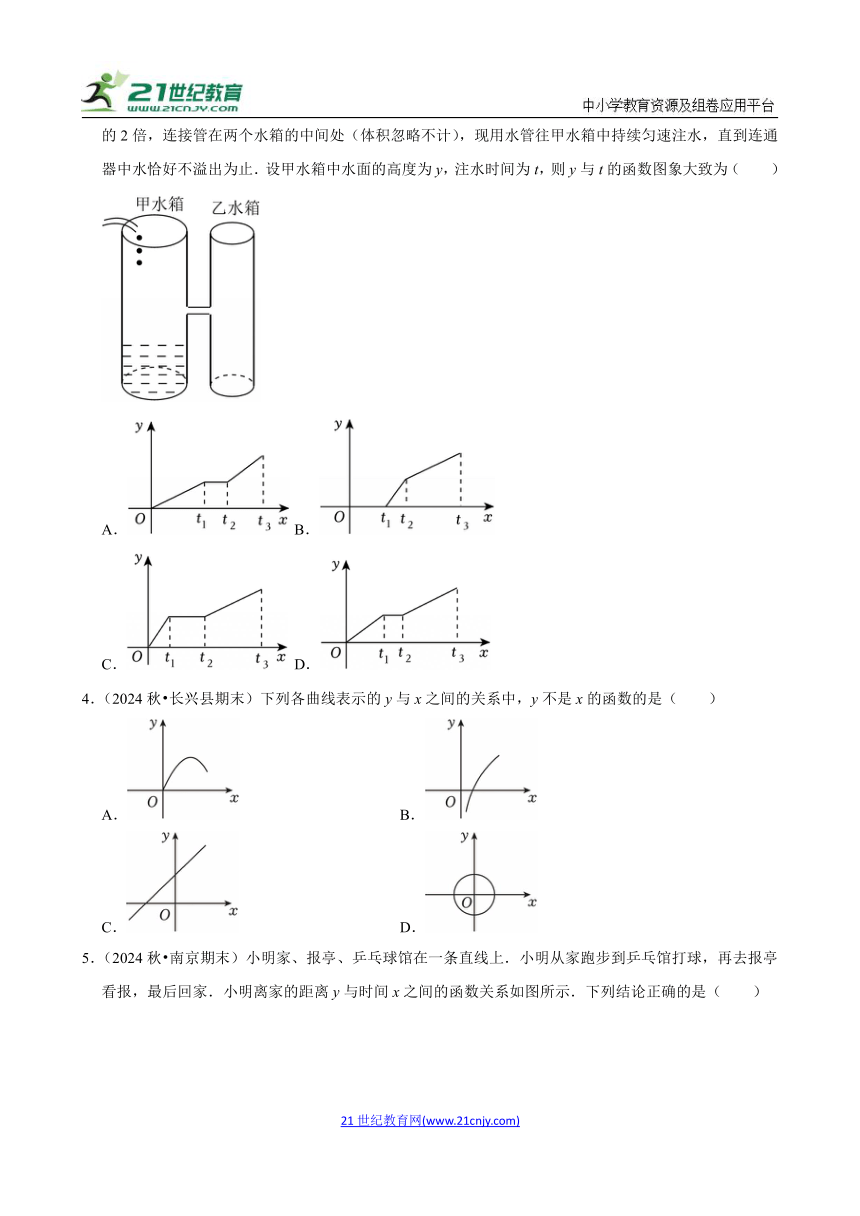
1.(2024秋 福田区期末)作为“新质生产力”和“低空经济主角”的无人机在快递配送领域,悄然改变了我们获取快递的方式.现在一条笔直的公路旁依次有A,C,B三个快递驿站(如图1),甲、乙两架无人机分别从A,B两个快递驿站同时出发,沿公路匀速飞行,运输冷链包裹至快递驿站C.已知甲、乙两架无人机到驿站C的距离S1,S2(km)与飞行时间t(min)之间的函数关系如图2所示.若甲、乙两架无人机同时到达驿站C,则驿站B离驿站C的距离是( )
A.13km B.14km C.15km D.16km
2.(2024秋 二七区期末)在测浮力的实验中,将一长方体铁块由玻璃器皿的上方,向下缓慢移动浸入水里的过程中,弹簧测力计的示数F(N)与铁块下降的高度h(cm)之间的关系如图所示.则以下说法正确的是( )
A.当铁块下降3cm时,此时铁块在水里
B.当5≤h≤10时,F(N)与h(cm)之间的函数表达式为
C.当弹簧测力计的示数为8N时,此时铁块底面距离水底8.5cm
D.当铁块下降高度为6cm时,此时弹簧测力计的示数是11.5N
3.(2024秋 济南期末)坎儿井是新疆吐鲁番盆地的一种特殊灌溉系统,主要是利用了连通器原理.如图是一个H型连通器模型,甲水箱、乙水箱是两个等高的圆柱体,甲水箱的底面面积是乙水箱底面面积的2倍,连接管在两个水箱的中间处(体积忽略不计),现用水管往甲水箱中持续匀速注水,直到连通器中水恰好不溢出为止.设甲水箱中水面的高度为y,注水时间为t,则y与t的函数图象大致为( )
A. B.
C. D.
4.(2024秋 长兴县期末)下列各曲线表示的y与x之间的关系中,y不是x的函数的是( )
A. B.
C. D.
5.(2024秋 南京期末)小明家、报亭、乒乓球馆在一条直线上.小明从家跑步到乒乓馆打球,再去报亭看报,最后回家.小明离家的距离y与时间x之间的函数关系如图所示.下列结论正确的是( )
A.小明从家到乒乓球馆的速度是250m/min
B.小明在报亭停留时间为10min
C.乒乓球馆在小明家与报亭之间
D.小明回家的速度是先慢后快
6.(2024秋 高陵区期末)下列属于定性数据的是( )
A.某市每年参加中考的人数
B.顾客对某超市服务的满意情况
C.高陵区12月1日的室外气温
D.高陵区居民月平均用电量
7.(2024秋 钱塘区期末)数学课上,李老师让同学们利用学习函数获得的经验去研究函数的图象特征.甲同学认为:该函数图象一定不经过第二象限.乙同学认为:该函数图象关于直线x=﹣1对称.以下对两位同学的看法判断正确的是( )
A.甲乙都正确 B.甲乙都错误
C.甲正确,乙错误 D.甲错误,乙正确
8.(2024秋 越城区校级期末)图1是变量y与变量x的函数关系图象,图2是变量z与变量y的函数关系图象,则变量z与变量x的函数关系图象可能是( )
A. B.
C. D.
9.(2024秋 柯桥区期末)如图,在等腰三角形ABC中,AB=AC,点D为BC中点,连结AD,若∠BAD=y,∠B=2x,则y与x之间的函数关系式是( )
A. B.
C. D.
10.(2024秋 嘉兴期末)材料:甲开汽车,乙骑自行车从A地沿一条笔直的公路匀速前往B地,乙比甲先出发.设乙行驶的时间为t(h),甲、乙两人之间的距离y(km)关于时间t(h)的函数图象如图所示.根据材料,获得正确的信息是( )
A.甲行驶的速度是20km/h
B.在甲出发后追上乙
C.A,B两地之间的距离为90km
D.甲比乙少行驶2小时
二.填空题(共5小题)
11.(2024秋 德化县期末)在实际情况中,我们都希望走的路程越短越好,如图,从A地到B地有三条路径,当然选择笔直的路线AB.若用数学知识解释,则其理由是 .
12.(2024秋 浦东新区期末)函数,则 .
13.(2024秋 浦东新区校级期末)已知函数,则f(﹣2)= .
14.(2024秋 普陀区期末)函数的定义域是 .
15.(2024秋 兴宁市期末)如图是1个纸杯和6个叠放在一起的相同纸杯的示意图.若设杯沿高为a(常量),杯子底部到杯沿底边高为b,写出杯子总高度h随着杯子数量n(自变量)的变化规律 .
三.解答题(共5小题)
16.(2024秋 苏州期末)某学校科技社团成员组装了一艘舰艇模型,并在一条笔直河道内进行往返航行测试,中途设置一个观测点P.他们根据测试结果绘制了如图所示的函数图象,其中t(min)表示航行时间,s(m)表示舰艇模型离出发点的距离.已知水流的速度为30m/min.
(1)根据图象回答:在OA段,舰艇模型是 水航行(填“顺”或“逆”);该舰艇模型在静水中的航行速度为 m/min;
(2)该舰艇模型先后两次经过观测点P的时间差为1.6min,求观察点P离出发点的距离.
17.(2024秋 高新区期末)为节省空间,工作人员常将购物车叠放在一起形成购物车列.如图1,表示一辆购物车的尺寸,如图2,表示3辆购物车叠放所形成的购物车列,长度为1.6米.购物车可以通过扶手电梯或直立电梯转运,直立电梯一次性最多能转运12辆购物车;如图3,扶手电梯一次性最多转运购物车时,需要在斜坡AC上预留CD=0.5m的安全距离.
(1)当x辆购物车按图2的方式叠放时,形成购物车列的长度为y米,则y与x的关系式是 ;
(2)若该超市扶手电梯水平距离BC为4m,高AB为3m,考虑安全距离,求扶手电梯一次性最多能转运的购物车数量,并比较哪种方式一次性转运的购物车数量多.
18.(2024秋 舟山期末)渔船常利用超声波来探测远处鱼群的方位,超声波的振幅h(m)与传输时间t(s)之间的关系如图所示.
(1)根据函数的定义,请判断变量h是否为关于t的函数?
(2)结合图象回答:
①当t=4s时,h的值是多少?
②在0≤t≤4内,当h随t的增大而增大,求t的取值范围.
19.(2024秋 浦东新区校级期末)某校科技节启用无人机航拍活动,在操控无人机时可调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是 ;
(2)无人机在75米高的上空停留的时间是 分钟;
(3)在上升或下降过程中,无人机的速度为 米/分;
(4)图中a表示的数是 ;b表示的数是 ;
(5)图中点A表示的实际意义是 .
20.(2024秋 云岩区期末)请用直观分析策略解答下面问题.
如图所示,一辆汽车以20m/s的速度匀速驶向正前方的山崖,驾驶员在鸣笛若干秒后听到从山崖反射回来的回声,已知声音在空气中的传播速度为340m/s,汽车鸣笛时与山崖的距离为540m.请想象一下汽车发出鸣笛声到反射传回驾驶员耳中的过程,用示意图直观地表示这一过程,并列出方程.
2025年中考数学高频易错考前冲刺:函数基础知识
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D D B B C B D C
一.选择题(共10小题)
1.(2024秋 福田区期末)作为“新质生产力”和“低空经济主角”的无人机在快递配送领域,悄然改变了我们获取快递的方式.现在一条笔直的公路旁依次有A,C,B三个快递驿站(如图1),甲、乙两架无人机分别从A,B两个快递驿站同时出发,沿公路匀速飞行,运输冷链包裹至快递驿站C.已知甲、乙两架无人机到驿站C的距离S1,S2(km)与飞行时间t(min)之间的函数关系如图2所示.若甲、乙两架无人机同时到达驿站C,则驿站B离驿站C的距离是( )
A.13km B.14km C.15km D.16km
【考点】函数的图象.
【专题】函数及其图象;应用意识.
【答案】C
【分析】根据A到C的距离大于B到C的距离,得到A到C的距离为20千米,甲2小时行了12千米,乙2小时行了9千米.再根据两架无人机用的时间相同,即可解答.
【解答】解:根据图中信息,得到A到C的距离为20千米,甲2小时行了12千米,乙2小时行了9千米.
甲从A到C用的时间:(小时),
乙从B到C的距离:915(千米),
故选:C.
【点评】本题考查了函数的图象,解题的关键是从图中获取信息来解答.
2.(2024秋 二七区期末)在测浮力的实验中,将一长方体铁块由玻璃器皿的上方,向下缓慢移动浸入水里的过程中,弹簧测力计的示数F(N)与铁块下降的高度h(cm)之间的关系如图所示.则以下说法正确的是( )
A.当铁块下降3cm时,此时铁块在水里
B.当5≤h≤10时,F(N)与h(cm)之间的函数表达式为
C.当弹簧测力计的示数为8N时,此时铁块底面距离水底8.5cm
D.当铁块下降高度为6cm时,此时弹簧测力计的示数是11.5N
【考点】动点问题的函数图象.
【专题】动点型;应用意识.
【答案】C
【分析】根据函数图象待定系数法求得线段AB的解析式,进而逐项分析判断即可求解.
【解答】解:A、由题图可知,石块下降到5cm时,石块正好接触水面,故选项A错误;
B、当5≤x≤10时,设AB所在直线的函数表达式为:F=kh+b(k≠0),
则,
解得,
∴Fh+20,故选项B错误;
C、当F=8N时,h+20=8,
解得h=7.5,
∴16﹣7.5=8.5(cm),
∴当弹簧测力计的示数为8N时,铁块底面距离水底8.5cm,故C正确;
D、当石块下降的高度为6cm时,即h=6时,
F6+20=10.4(N),
∴当铁块下降高度为6cm时,此时弹簧测力计的示数是10.4N,故D错误.
故选:C.
【点评】本题考查了动点问题的函数图象和一次函数的应用,求得函数解析式,数形结合是解题的关键.
3.(2024秋 济南期末)坎儿井是新疆吐鲁番盆地的一种特殊灌溉系统,主要是利用了连通器原理.如图是一个H型连通器模型,甲水箱、乙水箱是两个等高的圆柱体,甲水箱的底面面积是乙水箱底面面积的2倍,连接管在两个水箱的中间处(体积忽略不计),现用水管往甲水箱中持续匀速注水,直到连通器中水恰好不溢出为止.设甲水箱中水面的高度为y,注水时间为t,则y与t的函数图象大致为( )
A.
B.
C.
D.
【考点】函数的图象.
【专题】函数及其图象.
【答案】D
【分析】由连通器的原理可知,整个过程分为三个阶段:甲水面上升,乙水面上升,甲、乙水面一起上升,再根据甲、乙底面积的关系求出2的关系即可得到结论.
【解答】解:由连通器的原理可知,整个过程分为三个阶段,第一阶段为甲水箱中的水面随着时间的推移逐渐上升,直至到达连通器的入口,第二阶段为甲水箱中的水面不上升,注入的水通过连通器流入乙中,使乙水箱中的水面上升,直至到达连通器的入口,第三阶段为甲、乙两个水箱中的水以相同的速度上升(上升速度比第一阶段慢),
设单位时间内注水体积为V,甲水箱的底面积为2S,则乙水箱的底面积为S,
则连通器的高度为,
∴,
∴;
四个选项中,只有D选项中的函数图象符合题意,
故选:D.
【点评】本题考查了函数的图象,解题的关键是根据题意,结合图象来解答.
4.(2024秋 长兴县期末)下列各曲线表示的y与x之间的关系中,y不是x的函数的是( )
A. B.
C. D.
【考点】函数的概念.
【专题】函数及其图象;运算能力.
【答案】D
【分析】根据函数的概念:对于自变量x的每一个值,因变量y都有唯一的值与它对应,逐一判断即可解答.
【解答】解:A、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故A不符合题意;
B、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故B不符合题意;
C、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故C不符合题意;
D、对于自变量x的每一个值,因变量y不是都有唯一的值与它对应,所以y不是x的函数,故D符合题意;
故选:D.
【点评】本题考查了函数的概念,熟练掌握对于自变量x的每一个值,因变量y都有唯一的值与它对应是解题的关键.
5.(2024秋 南京期末)小明家、报亭、乒乓球馆在一条直线上.小明从家跑步到乒乓馆打球,再去报亭看报,最后回家.小明离家的距离y与时间x之间的函数关系如图所示.下列结论正确的是( )
A.小明从家到乒乓球馆的速度是250m/min
B.小明在报亭停留时间为10min
C.乒乓球馆在小明家与报亭之间
D.小明回家的速度是先慢后快
【考点】函数的图象.
【专题】函数及其图象;推理能力.
【答案】B
【分析】根据函数图象中每一段所表示关系,对各选项进行判断,即可得到结果.
【解答】解:∵根据函数图象,小明家到乒乓球馆的距离是1200m,用时为5 min,
∴小明从家到乒乓球馆的速度是1200÷5=240m/min,
故选项A错误,不符合题意;
∵图象中第二段与x轴平行的图象,表示在报亭停留时间,
∴对应的x轴上用时从39到49,用时为10min,
故选项B正确,符合题意;
根据函数图象,小明先到乒乓球馆,再往回走到报亭,再回到家,
∴乒乓球馆不在小明家与报亭之间,
故选项C错误,不符合题意;
∵小明从球馆出来到报亭用时4min,走了360m,速度为90m/min,
从报亭回到家用时14min,走了840m,速度为60m/min,
∴小明回家的速度是先快后慢,
故选项D错误,不符合题意,
故选:B.
【点评】本题考查了函数图象的应用,熟练看懂函数图象是解题的关键.
6.(2024秋 高陵区期末)下列属于定性数据的是( )
A.某市每年参加中考的人数
B.顾客对某超市服务的满意情况
C.高陵区12月1日的室外气温
D.高陵区居民月平均用电量
【考点】常量与变量.
【专题】数与式;应用意识.
【答案】B
【分析】根据定量数据与定性数据的定义解答即可.
【解答】解:A、某市每年参加中考的人数是定量数据,不符合题意;
B、顾客对某超市服务的满意情况是定性数据,符合题意;
C、高陵区12月1日的室外气温是定量数据,符合题意;
D、高陵区居民月平均用电量是定量数据,不符合题意;
故选:B.
【点评】本题考查了定量数据与定性数据,熟练掌握定量数据与定性数据的定义是解题的关键.
7.(2024秋 钱塘区期末)数学课上,李老师让同学们利用学习函数获得的经验去研究函数的图象特征.甲同学认为:该函数图象一定不经过第二象限.乙同学认为:该函数图象关于直线x=﹣1对称.以下对两位同学的看法判断正确的是( )
A.甲乙都正确 B.甲乙都错误
C.甲正确,乙错误 D.甲错误,乙正确
【考点】函数的图象.
【专题】推理能力.
【答案】C
【分析】根据所给函数解析式,分别对甲、乙两位同学的结论作出判断即可.
【解答】解:由题知,
因为函数解析式为,
所以当x<0(x≠﹣1)时,y一定小于零,
所以该函数图象一定不经过第二象限.
故甲正确.
当x=0时,y=0,
即该函数图象经过点(0,0).
点(0,0)关于直线x=﹣1的对称点坐标为(﹣2,0).
当x=﹣2时,y=﹣4≠0,
所以(﹣2,0)不在此函数图象上,
所以该函数图象不关于直线x=﹣1对称.
故乙错误.
故选:C.
【点评】本题主要考查了函数的图象,能对所给函数解析式进行正确的分析是解题的关键.
8.(2024秋 越城区校级期末)图1是变量y与变量x的函数关系图象,图2是变量z与变量y的函数关系图象,则变量z与变量x的函数关系图象可能是( )
A. B.
C. D.
【考点】函数的图象;函数自变量的取值范围.
【专题】函数及其图象;几何直观.
【答案】B
【分析】根据所给函数图象,分别设出一次函数及正比例函数的解析式,得出各系数的正负,最后得出z与x之间的关系式即可解决问题.
【解答】解:由题知,
令图1中直线的函数解析式为y=kx+b,
则k>0,b<0.
令图2中的直线的函数解析式为z=my,
则m<0,
所以z=m(kx+b)=mkx+mb.
因为mk<0,mb>0,
所以只有B选项符合题意.
故选:B.
【点评】本题主要考查了函数的图象及函数自变量的取值范围,能根据题意得出一次函数及正比例函数解析式中各系数的正负是解题的关键.
9.(2024秋 柯桥区期末)如图,在等腰三角形ABC中,AB=AC,点D为BC中点,连结AD,若∠BAD=y,∠B=2x,则y与x之间的函数关系式是( )
A. B.
C. D.
【考点】函数的图象;等腰三角形的性质;直角三角形的性质.
【专题】函数及其图象;几何直观.
【答案】D
【分析】根据题意,先得出y与x的函数关系式,再结合x的取值范围进行判断即可.
【解答】解:由题知,
因为AD⊥BC,
所以∠BAD+∠B=90°,
即y+2x=90°,
所以y=﹣2x+90°.
因为0°<﹣2x+90°<90°,
所以0°<x<45°,
显然D选项符合题意.
故选:D.
【点评】本题主要考查了函数的图象、等腰三角形的性质及直角三角形的性质,熟知等腰三角形的性质及直角三角形的性质是解题的关键.
10.(2024秋 嘉兴期末)材料:甲开汽车,乙骑自行车从A地沿一条笔直的公路匀速前往B地,乙比甲先出发.设乙行驶的时间为t(h),甲、乙两人之间的距离y(km)关于时间t(h)的函数图象如图所示.根据材料,获得正确的信息是( )
A.甲行驶的速度是20km/h
B.在甲出发后追上乙
C.A,B两地之间的距离为90km
D.甲比乙少行驶2小时
【考点】函数的图象.
【专题】函数及其图象;应用意识.
【答案】C
【分析】根据函数图象结合速度,时间,路程之间的关系逐项判断即可.
【解答】解:由图象可知,乙行驶的速度为20÷1=20(km/h),
∴甲行驶的速度为60(km/h),
故A错误;
由图象可知,当乙出发后追上甲,
故B错误;
A,B两地之间的距离为2090(km),
故C正确;
甲行驶的时间为1(h),乙行驶的时间为小时,
∴甲比乙少行驶3(h),
故D错误;
故选:C.
【点评】本题考查了函数图象,根据函数图象得出相关信息是解题关键.
二.填空题(共5小题)
11.(2024秋 德化县期末)在实际情况中,我们都希望走的路程越短越好,如图,从A地到B地有三条路径,当然选择笔直的路线AB.若用数学知识解释,则其理由是 两点之间,线段最短 .
【考点】函数的图象;线段的性质:两点之间线段最短.
【专题】线段、角、相交线与平行线;应用意识.
【答案】两点之间,线段最短.
【分析】根据两点之间线段最短解答.
【解答】解:如图,从A地到B地有三条路径,当然选择笔直的路线AB.若用数学知识解释,则其理由是两点之间,线段最短.
故答案为:两点之间,线段最短.
【点评】本题考查了线段的性质,熟记两点之间,线段最短是解题的关键.
12.(2024秋 浦东新区期末)函数,则 22 .
【考点】函数值.
【专题】函数及其图象;运算能力.
【答案】22.
【分析】先代入再化简,即可得出答案.
【解答】解:原式22.
故答案为:22.
【点评】本题主要考查函数值,熟练掌握分母有理化是解题的关键.
13.(2024秋 浦东新区校级期末)已知函数,则f(﹣2)= .
【考点】函数值.
【专题】函数及其图象;运算能力.
【答案】.
【分析】把x=﹣2代入函数关系式即可求解.
【解答】解:当x=﹣2时,f(﹣2)
故答案为:.
【点评】本题考查了函数求值,分式求值,熟练掌握知识点的应用是解题的关键.
14.(2024秋 普陀区期末)函数的定义域是 且x≠2 .
【考点】函数自变量的取值范围.
【专题】函数及其图象;数感.
【答案】见试题解答内容
【分析】根据二次根式的被开方数为非负数以及分式的分母不能为0,列不等式组求解即可.
【解答】解:由可得,
解得且x≠2,
故答案为:且x≠2.
【点评】此题考查了函数的定义域,使函数解析式有意义的自变量的取值范围为定义域,解题的关键是列出不等式组,并正确求解.
15.(2024秋 兴宁市期末)如图是1个纸杯和6个叠放在一起的相同纸杯的示意图.若设杯沿高为a(常量),杯子底部到杯沿底边高为b,写出杯子总高度h随着杯子数量n(自变量)的变化规律 h=an+b .
【考点】常量与变量.
【专题】整式;函数及其图象;运算能力.
【答案】h=an+b.
【分析】根据总高度与杯沿高a,杯子底部到杯沿底边高b与杯子的数量n之间的关系进行计算即可.
【解答】解:由题意可知,h=an+b,
故答案为:h=an+b.
【点评】本题考查常量与变量,掌握“总高度与杯沿高a,杯子底部到杯沿底边高b与杯子的数量n之间的关系”是正确解答的关键.
三.解答题(共5小题)
16.(2024秋 苏州期末)某学校科技社团成员组装了一艘舰艇模型,并在一条笔直河道内进行往返航行测试,中途设置一个观测点P.他们根据测试结果绘制了如图所示的函数图象,其中t(min)表示航行时间,s(m)表示舰艇模型离出发点的距离.已知水流的速度为30m/min.
(1)根据图象回答:在OA段,舰艇模型是 顺 水航行(填“顺”或“逆”);该舰艇模型在静水中的航行速度为 120 m/min;
(2)该舰艇模型先后两次经过观测点P的时间差为1.6min,求观察点P离出发点的距离.
【考点】函数的图象.
【专题】函数及其图象;推理能力.
【答案】(1)顺,120;
(2)观察点P离出发点的距离为360米.
【分析】(1)设顺水速度为v顺,逆水速度为v逆,v顺=v静+v水,v逆=v静﹣v水,列方程即可求解;
(2)设从P点去程到终点用时t1min,从终点返程到P点用时t2min,根据题意列方程即可求解;
【解答】解:(1)设顺水速度为v顺,则逆水速度为v逆,v顺=v静+v水,v逆=v静﹣v水,
∴v顺>v逆,
根据图像可知,从起点到终点,即OA,用时3min,
从终点到起点,即AB,用时8﹣3=5min,
路程相同,时间越短,速度越大,
可知,在OA段,舰艇模型是顺水航行,
设v静=x m/min,v水=30m/min,
∴3(x+30)=5(x﹣30),
解得:x=120;
故该舰艇模型在静水中的航行速度为120m/min;
故答案为:顺,120;
(2)设P点距离出发点的距离为y m,
由(1)可知v120m/min,v水=30m/min,
去程用时3min,可以计算出起点与终点的距离为:3×(120+30)=3×150=450(m),
∴P点距离终点的路程为(450﹣y)m,
设从P点去程到终点用时t1min,从终点返程到P点用时t2min,
∴t1+t2=1.6,
∵t1,
t2,
∴1.6,
解得:y=360,
∴观察点P离出发点的距离为360米.
【点评】本题考查一元一次方程与实际问题,函数图象和性质,根据题意列方程是解题的关键.
17.(2024秋 高新区期末)为节省空间,工作人员常将购物车叠放在一起形成购物车列.如图1,表示一辆购物车的尺寸,如图2,表示3辆购物车叠放所形成的购物车列,长度为1.6米.购物车可以通过扶手电梯或直立电梯转运,直立电梯一次性最多能转运12辆购物车;如图3,扶手电梯一次性最多转运购物车时,需要在斜坡AC上预留CD=0.5m的安全距离.
(1)当x辆购物车按图2的方式叠放时,形成购物车列的长度为y米,则y与x的关系式是 y=0.2x+1 ;
(2)若该超市扶手电梯水平距离BC为4m,高AB为3m,考虑安全距离,求扶手电梯一次性最多能转运的购物车数量,并比较哪种方式一次性转运的购物车数量多.
【考点】函数关系式.
【专题】函数及其图象;运算能力.
【答案】(1)y=0.2x+1;
(2)17辆,扶手电梯.
【分析】(1)1辆购物车时长度为1.2m,每增加一辆长度增加0.2m,据此写出y与x的关系式即可;
(2)在Rt△ABC中利用勾股定理求出AC,根据题意列关于x的一元一次不等式并求解,比较x的最大值与12的大小关系即可得出结论.
【解答】解:(1)y=0.2(x﹣1)+1.2=0.2x+1,
∴y与x的关系式是y=0.2x+1.
故答案为:y=0.2x+1.
(2)在Rt△ABC中利用勾股定理,得AC5(m),
根据题意,得5﹣(0.2x+1)≥0.5,
解得x≤17.5,
∴扶手电梯一次性最多能转运17辆购物车,
∵17>12,
∴扶手电梯一次性转运的购物车数量多.
【点评】本题考查函数关系式,根据题意写出函数关系式、掌握一元一次不等式的解法是解题的关键.
18.(2024秋 舟山期末)渔船常利用超声波来探测远处鱼群的方位,超声波的振幅h(m)与传输时间t(s)之间的关系如图所示.
(1)根据函数的定义,请判断变量h是否为关于t的函数?
(2)结合图象回答:
①当t=4s时,h的值是多少?
②在0≤t≤4内,当h随t的增大而增大,求t的取值范围.
【考点】函数的图象;函数的概念;函数值.
【专题】函数及其图象;几何直观.
【答案】(1)变量h是关于t的函数;
(2)①h的值为4;②2≤t≤4.
【分析】(1)根据所给函数图象,结合函数的定义进行判断即可.
(2)利用所给函数图象即可解决问题.
【解答】解:(1)由所给函数图象可知,
对于t的每一个值,总有唯一的h与之对应,
所以变量h是关于t的函数.
(2)①由函数图象可知,
当t=4s时,h的值为4.
②由函数图象可知,
在0≤t≤4内,当h随t的增大而增大时,
t的取值范围是:2≤t≤4.
【点评】本题主要考查了函数的图象、函数的概念及函数值,熟知函数的定义及正确识别所给函数图象是解题的关键.
19.(2024秋 浦东新区校级期末)某校科技节启用无人机航拍活动,在操控无人机时可调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是 时间(或t) ;
(2)无人机在75米高的上空停留的时间是 5 分钟;
(3)在上升或下降过程中,无人机的速度为 25 米/分;
(4)图中a表示的数是 2 ;b表示的数是 15 ;
(5)图中点A表示的实际意义是 在第6分钟时,无人机的飞行高度为50米 .
【考点】函数的图象;常量与变量.
【专题】函数及其图象;应用意识.
【答案】(1)时间(或t); (2)5; (3)25; (4)2,15;(5)第6分钟时,无人机飞行的高度是50米.
【分析】(1)根据图象信息得出自变量;
(2)根据图象信息得出无人机在75米高的上空停留的时间12﹣7=5分钟即可;
(3)根据“速度=路程÷时间”计算即可;
(4)根据速度、时间与路程的关系列式计算解得即可;
(5)根据点的实际意义解答即可.
【解答】解:(1)横轴是时间,纵轴是高度,所以自变量是时间(或t),因变量是高度(或h);
故答案为:时间(或t);
(2)无人机在75米高的上空停留的时间是12﹣7=5(分钟);
故答案为:5;
(3)在上升或下降过程中,无人机的速度=25(米/分);
故答案为:25;
(4)图中a表示的数是(分钟);b表示的数是(分钟);
故答案为:2,15;
(5)图中点A表示在第6分钟时,无人机的飞行高度为50米;
故答案为:在第6分钟时,无人机的飞行高度为50米.
【点评】此题考查函数图象问题,从图象中获取信息是学习函数的基本功,要结合题意熟练掌握.
20.(2024秋 云岩区期末)请用直观分析策略解答下面问题.
如图所示,一辆汽车以20m/s的速度匀速驶向正前方的山崖,驾驶员在鸣笛若干秒后听到从山崖反射回来的回声,已知声音在空气中的传播速度为340m/s,汽车鸣笛时与山崖的距离为540m.请想象一下汽车发出鸣笛声到反射传回驾驶员耳中的过程,用示意图直观地表示这一过程,并列出方程.
【考点】函数的图象;由实际问题抽象出一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】设驾驶员鸣笛x秒后听到从山崖反射回来的回声,方程为20x+340×20=2×540;图形示意图见解析过程.
【分析】设驾驶员鸣笛x秒后听到从山崖反射回来的回声,根据题意得出汽车x秒所走路程加上声音x秒传播的路程之和为2倍的540m,据此可解决问题.
【解答】解:设驾驶员鸣笛x秒后听到从山崖反射回来的回声,
如图所示,
根据汽车x秒所走路程加上声音x秒传播的路程之和为2倍的540m得,
20x+340×20=2×540.
【点评】本题主要考查了函数的图象及由实际问题抽象出一元一次方程,能根据题意得出汽车x秒所走路程加上声音x秒传播的路程之和为2倍的540m是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 福田区期末)作为“新质生产力”和“低空经济主角”的无人机在快递配送领域,悄然改变了我们获取快递的方式.现在一条笔直的公路旁依次有A,C,B三个快递驿站(如图1),甲、乙两架无人机分别从A,B两个快递驿站同时出发,沿公路匀速飞行,运输冷链包裹至快递驿站C.已知甲、乙两架无人机到驿站C的距离S1,S2(km)与飞行时间t(min)之间的函数关系如图2所示.若甲、乙两架无人机同时到达驿站C,则驿站B离驿站C的距离是( )
A.13km B.14km C.15km D.16km
2.(2024秋 二七区期末)在测浮力的实验中,将一长方体铁块由玻璃器皿的上方,向下缓慢移动浸入水里的过程中,弹簧测力计的示数F(N)与铁块下降的高度h(cm)之间的关系如图所示.则以下说法正确的是( )
A.当铁块下降3cm时,此时铁块在水里
B.当5≤h≤10时,F(N)与h(cm)之间的函数表达式为
C.当弹簧测力计的示数为8N时,此时铁块底面距离水底8.5cm
D.当铁块下降高度为6cm时,此时弹簧测力计的示数是11.5N
3.(2024秋 济南期末)坎儿井是新疆吐鲁番盆地的一种特殊灌溉系统,主要是利用了连通器原理.如图是一个H型连通器模型,甲水箱、乙水箱是两个等高的圆柱体,甲水箱的底面面积是乙水箱底面面积的2倍,连接管在两个水箱的中间处(体积忽略不计),现用水管往甲水箱中持续匀速注水,直到连通器中水恰好不溢出为止.设甲水箱中水面的高度为y,注水时间为t,则y与t的函数图象大致为( )
A. B.
C. D.
4.(2024秋 长兴县期末)下列各曲线表示的y与x之间的关系中,y不是x的函数的是( )
A. B.
C. D.
5.(2024秋 南京期末)小明家、报亭、乒乓球馆在一条直线上.小明从家跑步到乒乓馆打球,再去报亭看报,最后回家.小明离家的距离y与时间x之间的函数关系如图所示.下列结论正确的是( )
A.小明从家到乒乓球馆的速度是250m/min
B.小明在报亭停留时间为10min
C.乒乓球馆在小明家与报亭之间
D.小明回家的速度是先慢后快
6.(2024秋 高陵区期末)下列属于定性数据的是( )
A.某市每年参加中考的人数
B.顾客对某超市服务的满意情况
C.高陵区12月1日的室外气温
D.高陵区居民月平均用电量
7.(2024秋 钱塘区期末)数学课上,李老师让同学们利用学习函数获得的经验去研究函数的图象特征.甲同学认为:该函数图象一定不经过第二象限.乙同学认为:该函数图象关于直线x=﹣1对称.以下对两位同学的看法判断正确的是( )
A.甲乙都正确 B.甲乙都错误
C.甲正确,乙错误 D.甲错误,乙正确
8.(2024秋 越城区校级期末)图1是变量y与变量x的函数关系图象,图2是变量z与变量y的函数关系图象,则变量z与变量x的函数关系图象可能是( )
A. B.
C. D.
9.(2024秋 柯桥区期末)如图,在等腰三角形ABC中,AB=AC,点D为BC中点,连结AD,若∠BAD=y,∠B=2x,则y与x之间的函数关系式是( )
A. B.
C. D.
10.(2024秋 嘉兴期末)材料:甲开汽车,乙骑自行车从A地沿一条笔直的公路匀速前往B地,乙比甲先出发.设乙行驶的时间为t(h),甲、乙两人之间的距离y(km)关于时间t(h)的函数图象如图所示.根据材料,获得正确的信息是( )
A.甲行驶的速度是20km/h
B.在甲出发后追上乙
C.A,B两地之间的距离为90km
D.甲比乙少行驶2小时
二.填空题(共5小题)
11.(2024秋 德化县期末)在实际情况中,我们都希望走的路程越短越好,如图,从A地到B地有三条路径,当然选择笔直的路线AB.若用数学知识解释,则其理由是 .
12.(2024秋 浦东新区期末)函数,则 .
13.(2024秋 浦东新区校级期末)已知函数,则f(﹣2)= .
14.(2024秋 普陀区期末)函数的定义域是 .
15.(2024秋 兴宁市期末)如图是1个纸杯和6个叠放在一起的相同纸杯的示意图.若设杯沿高为a(常量),杯子底部到杯沿底边高为b,写出杯子总高度h随着杯子数量n(自变量)的变化规律 .
三.解答题(共5小题)
16.(2024秋 苏州期末)某学校科技社团成员组装了一艘舰艇模型,并在一条笔直河道内进行往返航行测试,中途设置一个观测点P.他们根据测试结果绘制了如图所示的函数图象,其中t(min)表示航行时间,s(m)表示舰艇模型离出发点的距离.已知水流的速度为30m/min.
(1)根据图象回答:在OA段,舰艇模型是 水航行(填“顺”或“逆”);该舰艇模型在静水中的航行速度为 m/min;
(2)该舰艇模型先后两次经过观测点P的时间差为1.6min,求观察点P离出发点的距离.
17.(2024秋 高新区期末)为节省空间,工作人员常将购物车叠放在一起形成购物车列.如图1,表示一辆购物车的尺寸,如图2,表示3辆购物车叠放所形成的购物车列,长度为1.6米.购物车可以通过扶手电梯或直立电梯转运,直立电梯一次性最多能转运12辆购物车;如图3,扶手电梯一次性最多转运购物车时,需要在斜坡AC上预留CD=0.5m的安全距离.
(1)当x辆购物车按图2的方式叠放时,形成购物车列的长度为y米,则y与x的关系式是 ;
(2)若该超市扶手电梯水平距离BC为4m,高AB为3m,考虑安全距离,求扶手电梯一次性最多能转运的购物车数量,并比较哪种方式一次性转运的购物车数量多.
18.(2024秋 舟山期末)渔船常利用超声波来探测远处鱼群的方位,超声波的振幅h(m)与传输时间t(s)之间的关系如图所示.
(1)根据函数的定义,请判断变量h是否为关于t的函数?
(2)结合图象回答:
①当t=4s时,h的值是多少?
②在0≤t≤4内,当h随t的增大而增大,求t的取值范围.
19.(2024秋 浦东新区校级期末)某校科技节启用无人机航拍活动,在操控无人机时可调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是 ;
(2)无人机在75米高的上空停留的时间是 分钟;
(3)在上升或下降过程中,无人机的速度为 米/分;
(4)图中a表示的数是 ;b表示的数是 ;
(5)图中点A表示的实际意义是 .
20.(2024秋 云岩区期末)请用直观分析策略解答下面问题.
如图所示,一辆汽车以20m/s的速度匀速驶向正前方的山崖,驾驶员在鸣笛若干秒后听到从山崖反射回来的回声,已知声音在空气中的传播速度为340m/s,汽车鸣笛时与山崖的距离为540m.请想象一下汽车发出鸣笛声到反射传回驾驶员耳中的过程,用示意图直观地表示这一过程,并列出方程.
2025年中考数学高频易错考前冲刺:函数基础知识
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D D B B C B D C
一.选择题(共10小题)
1.(2024秋 福田区期末)作为“新质生产力”和“低空经济主角”的无人机在快递配送领域,悄然改变了我们获取快递的方式.现在一条笔直的公路旁依次有A,C,B三个快递驿站(如图1),甲、乙两架无人机分别从A,B两个快递驿站同时出发,沿公路匀速飞行,运输冷链包裹至快递驿站C.已知甲、乙两架无人机到驿站C的距离S1,S2(km)与飞行时间t(min)之间的函数关系如图2所示.若甲、乙两架无人机同时到达驿站C,则驿站B离驿站C的距离是( )
A.13km B.14km C.15km D.16km
【考点】函数的图象.
【专题】函数及其图象;应用意识.
【答案】C
【分析】根据A到C的距离大于B到C的距离,得到A到C的距离为20千米,甲2小时行了12千米,乙2小时行了9千米.再根据两架无人机用的时间相同,即可解答.
【解答】解:根据图中信息,得到A到C的距离为20千米,甲2小时行了12千米,乙2小时行了9千米.
甲从A到C用的时间:(小时),
乙从B到C的距离:915(千米),
故选:C.
【点评】本题考查了函数的图象,解题的关键是从图中获取信息来解答.
2.(2024秋 二七区期末)在测浮力的实验中,将一长方体铁块由玻璃器皿的上方,向下缓慢移动浸入水里的过程中,弹簧测力计的示数F(N)与铁块下降的高度h(cm)之间的关系如图所示.则以下说法正确的是( )
A.当铁块下降3cm时,此时铁块在水里
B.当5≤h≤10时,F(N)与h(cm)之间的函数表达式为
C.当弹簧测力计的示数为8N时,此时铁块底面距离水底8.5cm
D.当铁块下降高度为6cm时,此时弹簧测力计的示数是11.5N
【考点】动点问题的函数图象.
【专题】动点型;应用意识.
【答案】C
【分析】根据函数图象待定系数法求得线段AB的解析式,进而逐项分析判断即可求解.
【解答】解:A、由题图可知,石块下降到5cm时,石块正好接触水面,故选项A错误;
B、当5≤x≤10时,设AB所在直线的函数表达式为:F=kh+b(k≠0),
则,
解得,
∴Fh+20,故选项B错误;
C、当F=8N时,h+20=8,
解得h=7.5,
∴16﹣7.5=8.5(cm),
∴当弹簧测力计的示数为8N时,铁块底面距离水底8.5cm,故C正确;
D、当石块下降的高度为6cm时,即h=6时,
F6+20=10.4(N),
∴当铁块下降高度为6cm时,此时弹簧测力计的示数是10.4N,故D错误.
故选:C.
【点评】本题考查了动点问题的函数图象和一次函数的应用,求得函数解析式,数形结合是解题的关键.
3.(2024秋 济南期末)坎儿井是新疆吐鲁番盆地的一种特殊灌溉系统,主要是利用了连通器原理.如图是一个H型连通器模型,甲水箱、乙水箱是两个等高的圆柱体,甲水箱的底面面积是乙水箱底面面积的2倍,连接管在两个水箱的中间处(体积忽略不计),现用水管往甲水箱中持续匀速注水,直到连通器中水恰好不溢出为止.设甲水箱中水面的高度为y,注水时间为t,则y与t的函数图象大致为( )
A.
B.
C.
D.
【考点】函数的图象.
【专题】函数及其图象.
【答案】D
【分析】由连通器的原理可知,整个过程分为三个阶段:甲水面上升,乙水面上升,甲、乙水面一起上升,再根据甲、乙底面积的关系求出2的关系即可得到结论.
【解答】解:由连通器的原理可知,整个过程分为三个阶段,第一阶段为甲水箱中的水面随着时间的推移逐渐上升,直至到达连通器的入口,第二阶段为甲水箱中的水面不上升,注入的水通过连通器流入乙中,使乙水箱中的水面上升,直至到达连通器的入口,第三阶段为甲、乙两个水箱中的水以相同的速度上升(上升速度比第一阶段慢),
设单位时间内注水体积为V,甲水箱的底面积为2S,则乙水箱的底面积为S,
则连通器的高度为,
∴,
∴;
四个选项中,只有D选项中的函数图象符合题意,
故选:D.
【点评】本题考查了函数的图象,解题的关键是根据题意,结合图象来解答.
4.(2024秋 长兴县期末)下列各曲线表示的y与x之间的关系中,y不是x的函数的是( )
A. B.
C. D.
【考点】函数的概念.
【专题】函数及其图象;运算能力.
【答案】D
【分析】根据函数的概念:对于自变量x的每一个值,因变量y都有唯一的值与它对应,逐一判断即可解答.
【解答】解:A、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故A不符合题意;
B、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故B不符合题意;
C、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故C不符合题意;
D、对于自变量x的每一个值,因变量y不是都有唯一的值与它对应,所以y不是x的函数,故D符合题意;
故选:D.
【点评】本题考查了函数的概念,熟练掌握对于自变量x的每一个值,因变量y都有唯一的值与它对应是解题的关键.
5.(2024秋 南京期末)小明家、报亭、乒乓球馆在一条直线上.小明从家跑步到乒乓馆打球,再去报亭看报,最后回家.小明离家的距离y与时间x之间的函数关系如图所示.下列结论正确的是( )
A.小明从家到乒乓球馆的速度是250m/min
B.小明在报亭停留时间为10min
C.乒乓球馆在小明家与报亭之间
D.小明回家的速度是先慢后快
【考点】函数的图象.
【专题】函数及其图象;推理能力.
【答案】B
【分析】根据函数图象中每一段所表示关系,对各选项进行判断,即可得到结果.
【解答】解:∵根据函数图象,小明家到乒乓球馆的距离是1200m,用时为5 min,
∴小明从家到乒乓球馆的速度是1200÷5=240m/min,
故选项A错误,不符合题意;
∵图象中第二段与x轴平行的图象,表示在报亭停留时间,
∴对应的x轴上用时从39到49,用时为10min,
故选项B正确,符合题意;
根据函数图象,小明先到乒乓球馆,再往回走到报亭,再回到家,
∴乒乓球馆不在小明家与报亭之间,
故选项C错误,不符合题意;
∵小明从球馆出来到报亭用时4min,走了360m,速度为90m/min,
从报亭回到家用时14min,走了840m,速度为60m/min,
∴小明回家的速度是先快后慢,
故选项D错误,不符合题意,
故选:B.
【点评】本题考查了函数图象的应用,熟练看懂函数图象是解题的关键.
6.(2024秋 高陵区期末)下列属于定性数据的是( )
A.某市每年参加中考的人数
B.顾客对某超市服务的满意情况
C.高陵区12月1日的室外气温
D.高陵区居民月平均用电量
【考点】常量与变量.
【专题】数与式;应用意识.
【答案】B
【分析】根据定量数据与定性数据的定义解答即可.
【解答】解:A、某市每年参加中考的人数是定量数据,不符合题意;
B、顾客对某超市服务的满意情况是定性数据,符合题意;
C、高陵区12月1日的室外气温是定量数据,符合题意;
D、高陵区居民月平均用电量是定量数据,不符合题意;
故选:B.
【点评】本题考查了定量数据与定性数据,熟练掌握定量数据与定性数据的定义是解题的关键.
7.(2024秋 钱塘区期末)数学课上,李老师让同学们利用学习函数获得的经验去研究函数的图象特征.甲同学认为:该函数图象一定不经过第二象限.乙同学认为:该函数图象关于直线x=﹣1对称.以下对两位同学的看法判断正确的是( )
A.甲乙都正确 B.甲乙都错误
C.甲正确,乙错误 D.甲错误,乙正确
【考点】函数的图象.
【专题】推理能力.
【答案】C
【分析】根据所给函数解析式,分别对甲、乙两位同学的结论作出判断即可.
【解答】解:由题知,
因为函数解析式为,
所以当x<0(x≠﹣1)时,y一定小于零,
所以该函数图象一定不经过第二象限.
故甲正确.
当x=0时,y=0,
即该函数图象经过点(0,0).
点(0,0)关于直线x=﹣1的对称点坐标为(﹣2,0).
当x=﹣2时,y=﹣4≠0,
所以(﹣2,0)不在此函数图象上,
所以该函数图象不关于直线x=﹣1对称.
故乙错误.
故选:C.
【点评】本题主要考查了函数的图象,能对所给函数解析式进行正确的分析是解题的关键.
8.(2024秋 越城区校级期末)图1是变量y与变量x的函数关系图象,图2是变量z与变量y的函数关系图象,则变量z与变量x的函数关系图象可能是( )
A. B.
C. D.
【考点】函数的图象;函数自变量的取值范围.
【专题】函数及其图象;几何直观.
【答案】B
【分析】根据所给函数图象,分别设出一次函数及正比例函数的解析式,得出各系数的正负,最后得出z与x之间的关系式即可解决问题.
【解答】解:由题知,
令图1中直线的函数解析式为y=kx+b,
则k>0,b<0.
令图2中的直线的函数解析式为z=my,
则m<0,
所以z=m(kx+b)=mkx+mb.
因为mk<0,mb>0,
所以只有B选项符合题意.
故选:B.
【点评】本题主要考查了函数的图象及函数自变量的取值范围,能根据题意得出一次函数及正比例函数解析式中各系数的正负是解题的关键.
9.(2024秋 柯桥区期末)如图,在等腰三角形ABC中,AB=AC,点D为BC中点,连结AD,若∠BAD=y,∠B=2x,则y与x之间的函数关系式是( )
A. B.
C. D.
【考点】函数的图象;等腰三角形的性质;直角三角形的性质.
【专题】函数及其图象;几何直观.
【答案】D
【分析】根据题意,先得出y与x的函数关系式,再结合x的取值范围进行判断即可.
【解答】解:由题知,
因为AD⊥BC,
所以∠BAD+∠B=90°,
即y+2x=90°,
所以y=﹣2x+90°.
因为0°<﹣2x+90°<90°,
所以0°<x<45°,
显然D选项符合题意.
故选:D.
【点评】本题主要考查了函数的图象、等腰三角形的性质及直角三角形的性质,熟知等腰三角形的性质及直角三角形的性质是解题的关键.
10.(2024秋 嘉兴期末)材料:甲开汽车,乙骑自行车从A地沿一条笔直的公路匀速前往B地,乙比甲先出发.设乙行驶的时间为t(h),甲、乙两人之间的距离y(km)关于时间t(h)的函数图象如图所示.根据材料,获得正确的信息是( )
A.甲行驶的速度是20km/h
B.在甲出发后追上乙
C.A,B两地之间的距离为90km
D.甲比乙少行驶2小时
【考点】函数的图象.
【专题】函数及其图象;应用意识.
【答案】C
【分析】根据函数图象结合速度,时间,路程之间的关系逐项判断即可.
【解答】解:由图象可知,乙行驶的速度为20÷1=20(km/h),
∴甲行驶的速度为60(km/h),
故A错误;
由图象可知,当乙出发后追上甲,
故B错误;
A,B两地之间的距离为2090(km),
故C正确;
甲行驶的时间为1(h),乙行驶的时间为小时,
∴甲比乙少行驶3(h),
故D错误;
故选:C.
【点评】本题考查了函数图象,根据函数图象得出相关信息是解题关键.
二.填空题(共5小题)
11.(2024秋 德化县期末)在实际情况中,我们都希望走的路程越短越好,如图,从A地到B地有三条路径,当然选择笔直的路线AB.若用数学知识解释,则其理由是 两点之间,线段最短 .
【考点】函数的图象;线段的性质:两点之间线段最短.
【专题】线段、角、相交线与平行线;应用意识.
【答案】两点之间,线段最短.
【分析】根据两点之间线段最短解答.
【解答】解:如图,从A地到B地有三条路径,当然选择笔直的路线AB.若用数学知识解释,则其理由是两点之间,线段最短.
故答案为:两点之间,线段最短.
【点评】本题考查了线段的性质,熟记两点之间,线段最短是解题的关键.
12.(2024秋 浦东新区期末)函数,则 22 .
【考点】函数值.
【专题】函数及其图象;运算能力.
【答案】22.
【分析】先代入再化简,即可得出答案.
【解答】解:原式22.
故答案为:22.
【点评】本题主要考查函数值,熟练掌握分母有理化是解题的关键.
13.(2024秋 浦东新区校级期末)已知函数,则f(﹣2)= .
【考点】函数值.
【专题】函数及其图象;运算能力.
【答案】.
【分析】把x=﹣2代入函数关系式即可求解.
【解答】解:当x=﹣2时,f(﹣2)
故答案为:.
【点评】本题考查了函数求值,分式求值,熟练掌握知识点的应用是解题的关键.
14.(2024秋 普陀区期末)函数的定义域是 且x≠2 .
【考点】函数自变量的取值范围.
【专题】函数及其图象;数感.
【答案】见试题解答内容
【分析】根据二次根式的被开方数为非负数以及分式的分母不能为0,列不等式组求解即可.
【解答】解:由可得,
解得且x≠2,
故答案为:且x≠2.
【点评】此题考查了函数的定义域,使函数解析式有意义的自变量的取值范围为定义域,解题的关键是列出不等式组,并正确求解.
15.(2024秋 兴宁市期末)如图是1个纸杯和6个叠放在一起的相同纸杯的示意图.若设杯沿高为a(常量),杯子底部到杯沿底边高为b,写出杯子总高度h随着杯子数量n(自变量)的变化规律 h=an+b .
【考点】常量与变量.
【专题】整式;函数及其图象;运算能力.
【答案】h=an+b.
【分析】根据总高度与杯沿高a,杯子底部到杯沿底边高b与杯子的数量n之间的关系进行计算即可.
【解答】解:由题意可知,h=an+b,
故答案为:h=an+b.
【点评】本题考查常量与变量,掌握“总高度与杯沿高a,杯子底部到杯沿底边高b与杯子的数量n之间的关系”是正确解答的关键.
三.解答题(共5小题)
16.(2024秋 苏州期末)某学校科技社团成员组装了一艘舰艇模型,并在一条笔直河道内进行往返航行测试,中途设置一个观测点P.他们根据测试结果绘制了如图所示的函数图象,其中t(min)表示航行时间,s(m)表示舰艇模型离出发点的距离.已知水流的速度为30m/min.
(1)根据图象回答:在OA段,舰艇模型是 顺 水航行(填“顺”或“逆”);该舰艇模型在静水中的航行速度为 120 m/min;
(2)该舰艇模型先后两次经过观测点P的时间差为1.6min,求观察点P离出发点的距离.
【考点】函数的图象.
【专题】函数及其图象;推理能力.
【答案】(1)顺,120;
(2)观察点P离出发点的距离为360米.
【分析】(1)设顺水速度为v顺,逆水速度为v逆,v顺=v静+v水,v逆=v静﹣v水,列方程即可求解;
(2)设从P点去程到终点用时t1min,从终点返程到P点用时t2min,根据题意列方程即可求解;
【解答】解:(1)设顺水速度为v顺,则逆水速度为v逆,v顺=v静+v水,v逆=v静﹣v水,
∴v顺>v逆,
根据图像可知,从起点到终点,即OA,用时3min,
从终点到起点,即AB,用时8﹣3=5min,
路程相同,时间越短,速度越大,
可知,在OA段,舰艇模型是顺水航行,
设v静=x m/min,v水=30m/min,
∴3(x+30)=5(x﹣30),
解得:x=120;
故该舰艇模型在静水中的航行速度为120m/min;
故答案为:顺,120;
(2)设P点距离出发点的距离为y m,
由(1)可知v120m/min,v水=30m/min,
去程用时3min,可以计算出起点与终点的距离为:3×(120+30)=3×150=450(m),
∴P点距离终点的路程为(450﹣y)m,
设从P点去程到终点用时t1min,从终点返程到P点用时t2min,
∴t1+t2=1.6,
∵t1,
t2,
∴1.6,
解得:y=360,
∴观察点P离出发点的距离为360米.
【点评】本题考查一元一次方程与实际问题,函数图象和性质,根据题意列方程是解题的关键.
17.(2024秋 高新区期末)为节省空间,工作人员常将购物车叠放在一起形成购物车列.如图1,表示一辆购物车的尺寸,如图2,表示3辆购物车叠放所形成的购物车列,长度为1.6米.购物车可以通过扶手电梯或直立电梯转运,直立电梯一次性最多能转运12辆购物车;如图3,扶手电梯一次性最多转运购物车时,需要在斜坡AC上预留CD=0.5m的安全距离.
(1)当x辆购物车按图2的方式叠放时,形成购物车列的长度为y米,则y与x的关系式是 y=0.2x+1 ;
(2)若该超市扶手电梯水平距离BC为4m,高AB为3m,考虑安全距离,求扶手电梯一次性最多能转运的购物车数量,并比较哪种方式一次性转运的购物车数量多.
【考点】函数关系式.
【专题】函数及其图象;运算能力.
【答案】(1)y=0.2x+1;
(2)17辆,扶手电梯.
【分析】(1)1辆购物车时长度为1.2m,每增加一辆长度增加0.2m,据此写出y与x的关系式即可;
(2)在Rt△ABC中利用勾股定理求出AC,根据题意列关于x的一元一次不等式并求解,比较x的最大值与12的大小关系即可得出结论.
【解答】解:(1)y=0.2(x﹣1)+1.2=0.2x+1,
∴y与x的关系式是y=0.2x+1.
故答案为:y=0.2x+1.
(2)在Rt△ABC中利用勾股定理,得AC5(m),
根据题意,得5﹣(0.2x+1)≥0.5,
解得x≤17.5,
∴扶手电梯一次性最多能转运17辆购物车,
∵17>12,
∴扶手电梯一次性转运的购物车数量多.
【点评】本题考查函数关系式,根据题意写出函数关系式、掌握一元一次不等式的解法是解题的关键.
18.(2024秋 舟山期末)渔船常利用超声波来探测远处鱼群的方位,超声波的振幅h(m)与传输时间t(s)之间的关系如图所示.
(1)根据函数的定义,请判断变量h是否为关于t的函数?
(2)结合图象回答:
①当t=4s时,h的值是多少?
②在0≤t≤4内,当h随t的增大而增大,求t的取值范围.
【考点】函数的图象;函数的概念;函数值.
【专题】函数及其图象;几何直观.
【答案】(1)变量h是关于t的函数;
(2)①h的值为4;②2≤t≤4.
【分析】(1)根据所给函数图象,结合函数的定义进行判断即可.
(2)利用所给函数图象即可解决问题.
【解答】解:(1)由所给函数图象可知,
对于t的每一个值,总有唯一的h与之对应,
所以变量h是关于t的函数.
(2)①由函数图象可知,
当t=4s时,h的值为4.
②由函数图象可知,
在0≤t≤4内,当h随t的增大而增大时,
t的取值范围是:2≤t≤4.
【点评】本题主要考查了函数的图象、函数的概念及函数值,熟知函数的定义及正确识别所给函数图象是解题的关键.
19.(2024秋 浦东新区校级期末)某校科技节启用无人机航拍活动,在操控无人机时可调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是 时间(或t) ;
(2)无人机在75米高的上空停留的时间是 5 分钟;
(3)在上升或下降过程中,无人机的速度为 25 米/分;
(4)图中a表示的数是 2 ;b表示的数是 15 ;
(5)图中点A表示的实际意义是 在第6分钟时,无人机的飞行高度为50米 .
【考点】函数的图象;常量与变量.
【专题】函数及其图象;应用意识.
【答案】(1)时间(或t); (2)5; (3)25; (4)2,15;(5)第6分钟时,无人机飞行的高度是50米.
【分析】(1)根据图象信息得出自变量;
(2)根据图象信息得出无人机在75米高的上空停留的时间12﹣7=5分钟即可;
(3)根据“速度=路程÷时间”计算即可;
(4)根据速度、时间与路程的关系列式计算解得即可;
(5)根据点的实际意义解答即可.
【解答】解:(1)横轴是时间,纵轴是高度,所以自变量是时间(或t),因变量是高度(或h);
故答案为:时间(或t);
(2)无人机在75米高的上空停留的时间是12﹣7=5(分钟);
故答案为:5;
(3)在上升或下降过程中,无人机的速度=25(米/分);
故答案为:25;
(4)图中a表示的数是(分钟);b表示的数是(分钟);
故答案为:2,15;
(5)图中点A表示在第6分钟时,无人机的飞行高度为50米;
故答案为:在第6分钟时,无人机的飞行高度为50米.
【点评】此题考查函数图象问题,从图象中获取信息是学习函数的基本功,要结合题意熟练掌握.
20.(2024秋 云岩区期末)请用直观分析策略解答下面问题.
如图所示,一辆汽车以20m/s的速度匀速驶向正前方的山崖,驾驶员在鸣笛若干秒后听到从山崖反射回来的回声,已知声音在空气中的传播速度为340m/s,汽车鸣笛时与山崖的距离为540m.请想象一下汽车发出鸣笛声到反射传回驾驶员耳中的过程,用示意图直观地表示这一过程,并列出方程.
【考点】函数的图象;由实际问题抽象出一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】设驾驶员鸣笛x秒后听到从山崖反射回来的回声,方程为20x+340×20=2×540;图形示意图见解析过程.
【分析】设驾驶员鸣笛x秒后听到从山崖反射回来的回声,根据题意得出汽车x秒所走路程加上声音x秒传播的路程之和为2倍的540m,据此可解决问题.
【解答】解:设驾驶员鸣笛x秒后听到从山崖反射回来的回声,
如图所示,
根据汽车x秒所走路程加上声音x秒传播的路程之和为2倍的540m得,
20x+340×20=2×540.
【点评】本题主要考查了函数的图象及由实际问题抽象出一元一次方程,能根据题意得出汽车x秒所走路程加上声音x秒传播的路程之和为2倍的540m是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
