【中考押题卷】2025年中考数学高频易错考前冲刺:三角形(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:三角形(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
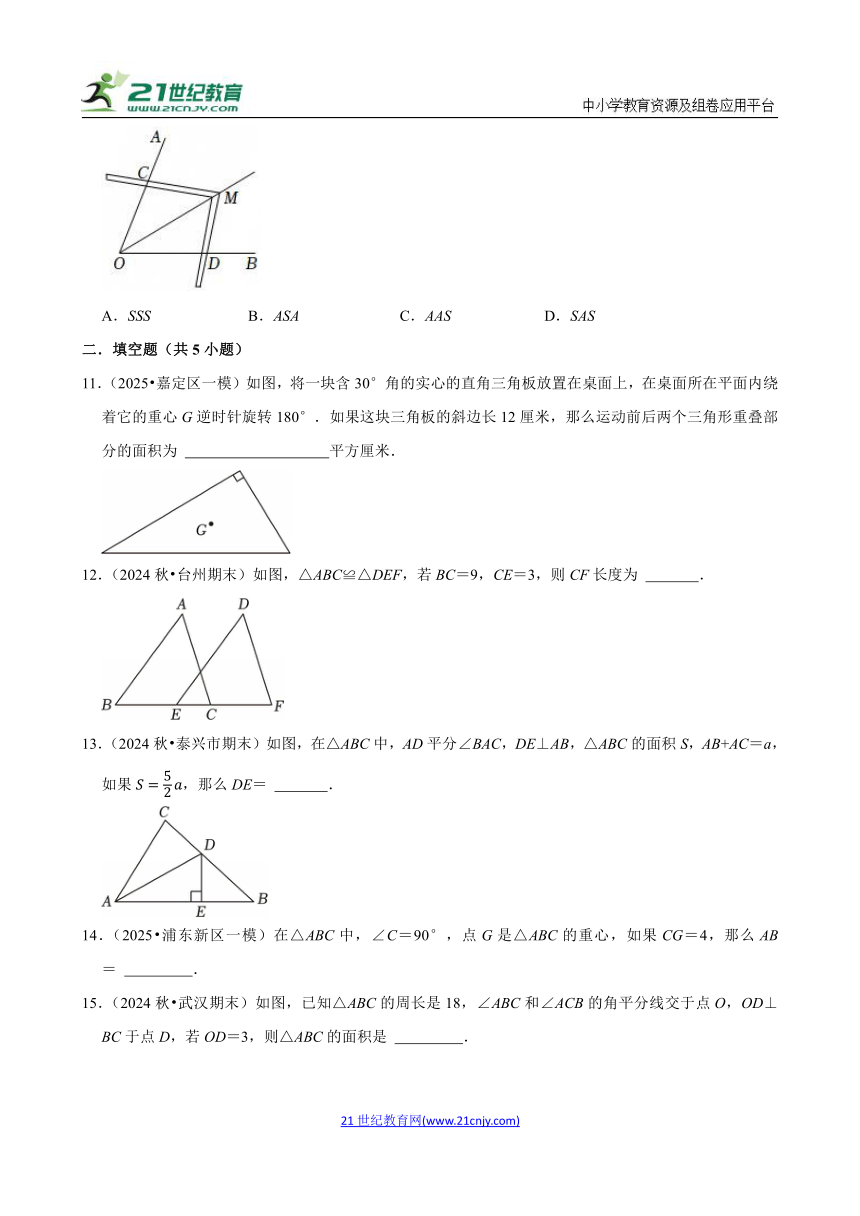
| 更新时间 | 2025-05-12 00:00:00 | ||
图片预览


文档简介
2025年中考数学高频易错考前冲刺:三角形
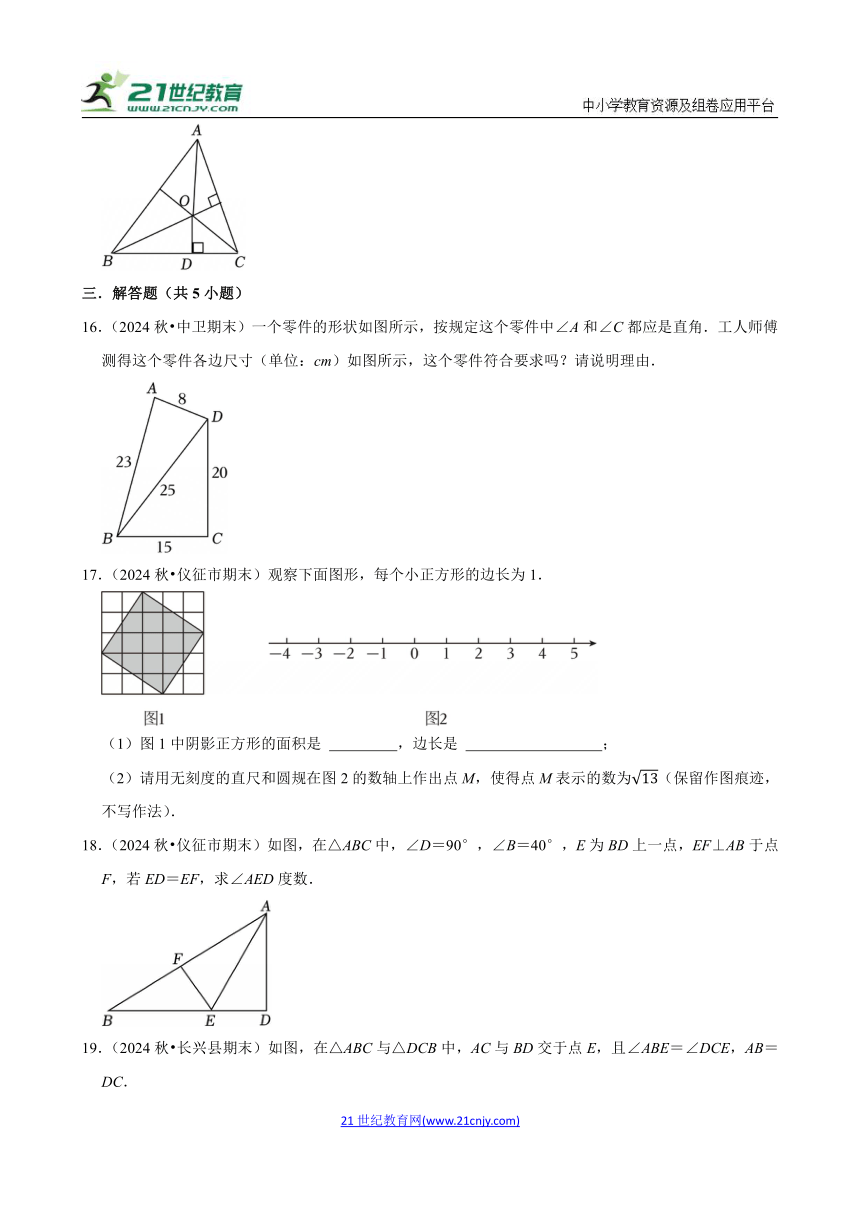
一.选择题(共10小题)
1.(2024秋 台州期末)若三角形的两边长分别为5,8,则第三条边的边长可能为( )
A.2.5 B.3 C.7 D.13
2.(2024秋 大理州期末)如图,△ABC≌△DEC,B、C、D三点在同一条直线上,CE=3,AC=4,则BD的长为( )
A.8 B.7 C.6 D.5
3.(2024秋 嘉兴期末)在下列条件中,不能判断△ABC是直角三角形的是( )
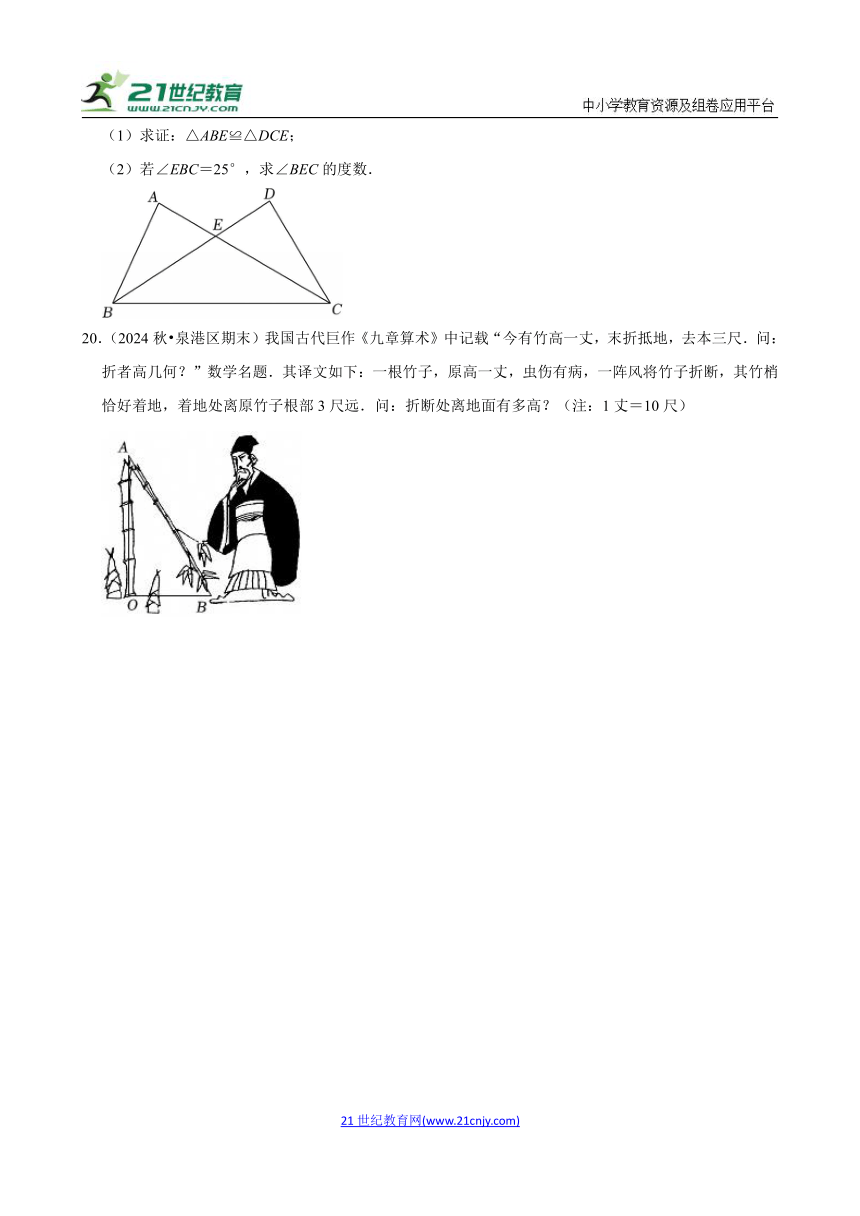
A.∠A=40°,∠B=50° B.AB=3,BC=4,
C.AB=AC,∠B=45° D.∠A=30°,
4.(2024秋 兴宁市期末)某次数学综合实践课上,小明将一副三角板摆成如图所示的样子,则∠1的大小为( )
A.70 B.75 C.80 D.85
5.(2024秋 大兴区期末)如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有( )
A.0个 B.1个 C.2个 D.3个
6.(2024秋 汕尾期末)如图,∠MON=30°,A为∠MON的平分线OP上一点,过点A作AB∥OM交ON于点B,过点A作AC⊥OM于点C,若AC=2,则AB=( )
A.3 B.4 C.6 D.7
7.(2024秋 长兴县期末)如图,在△ABC中,AB=AC,BC=10,AD是△ABC的角平分线,则CD的长是( )
A.6 B.5 C.4 D.无法确定
8.(2024秋 泉港区期末)下列各组数中,属于“勾股数”的是( )
A.2,4,6 B.4,6,8 C.6,8,10 D.8,10,12
9.(2024秋 门头沟区期末)如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,延长AC到点E,使CE=CD,连接BE交AD的延长线于点F.给出下面四个结论:①AD=BE;②BE=2BF;③AB=AC+CD;④△ABD的面积是△ACD的面积的2倍;上述结论中,所有正确结论的序号是( )
A.①② B.①②③ C.①③④ D.①②③④
10.(2024秋 武汉期末)工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA、OB上分别在取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线,这里构造全等三角形的依据是( )
A.SSS B.ASA C.AAS D.SAS
二.填空题(共5小题)
11.(2025 嘉定区一模)如图,将一块含30°角的实心的直角三角板放置在桌面上,在桌面所在平面内绕着它的重心G逆时针旋转180°.如果这块三角板的斜边长12厘米,那么运动前后两个三角形重叠部分的面积为 平方厘米.
12.(2024秋 台州期末)如图,△ABC≌△DEF,若BC=9,CE=3,则CF长度为 .
13.(2024秋 泰兴市期末)如图,在△ABC中,AD平分∠BAC,DE⊥AB,△ABC的面积S,AB+AC=a,如果,那么DE= .
14.(2025 浦东新区一模)在△ABC中,∠C=90°,点G是△ABC的重心,如果CG=4,那么AB= .
15.(2024秋 武汉期末)如图,已知△ABC的周长是18,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3,则△ABC的面积是 .
三.解答题(共5小题)
16.(2024秋 中卫期末)一个零件的形状如图所示,按规定这个零件中∠A和∠C都应是直角.工人师傅测得这个零件各边尺寸(单位:cm)如图所示,这个零件符合要求吗?请说明理由.
17.(2024秋 仪征市期末)观察下面图形,每个小正方形的边长为1.
(1)图1中阴影正方形的面积是 ,边长是 ;
(2)请用无刻度的直尺和圆规在图2的数轴上作出点M,使得点M表示的数为(保留作图痕迹,不写作法).
18.(2024秋 仪征市期末)如图,在△ABC中,∠D=90°,∠B=40°,E为BD上一点,EF⊥AB于点F,若ED=EF,求∠AED度数.
19.(2024秋 长兴县期末)如图,在△ABC与△DCB中,AC与BD交于点E,且∠ABE=∠DCE,AB=DC.
(1)求证:△ABE≌△DCE;
(2)若∠EBC=25°,求∠BEC的度数.
20.(2024秋 泉港区期末)我国古代巨作《九章算术》中记载“今有竹高一丈,末折抵地,去本三尺.问:折者高几何?”数学名题.其译文如下:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部3尺远.问:折断处离地面有多高?(注:1丈=10尺)
2025年中考数学高频易错考前冲刺:三角形
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D B D B B C B A
一.选择题(共10小题)
1.(2024秋 台州期末)若三角形的两边长分别为5,8,则第三条边的边长可能为( )
A.2.5 B.3 C.7 D.13
【考点】三角形三边关系.
【专题】三角形;推理能力.
【答案】C
【分析】根据两边之和大于第三边,两边之差小于第三边列式计算求解即可.
【解答】解:设第三边长为x,
∵三角形的两边长分别为5,8,
∴8﹣5<x<8+5,
解得3<x<13,
∴第三条边长可能为:7,
故选:C.
【点评】本题考查三角形三边关系,熟知三角形两边之和大于第三边;三角形的两边差小于第三边是解题的关键.
2.(2024秋 大理州期末)如图,△ABC≌△DEC,B、C、D三点在同一条直线上,CE=3,AC=4,则BD的长为( )
A.8 B.7 C.6 D.5
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】B
【分析】根据全等三角形的性质得出对应边相等,进而解答即可.
【解答】解:∵△ABC≌△DEC,B、C、D三点在同一条直线上,
∴BC=CE,CD=AC,
∵CE=3,AC=4,
∴BC=CE=3,CD=AC=4,
∴BD=BC+CD=3+4=7.
故选:B.
【点评】此题考查全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.
3.(2024秋 嘉兴期末)在下列条件中,不能判断△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.AB=3,BC=4,
C.AB=AC,∠B=45° D.∠A=30°,
【考点】勾股定理的逆定理;三角形内角和定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】D
【分析】根据三角形内角和定理,勾股定理的逆定理一一判断即可.
【解答】解:A、∵∠A=40°,∠B=50°,
∴∠C=180°﹣40°﹣50°=90°,
∴△ABC是直角三角形,不符合题意;
B、∵AB=3,BC=4,,
∴AB2+AC2=BC2,
∴∠A=90°,
∴△ABC是直角三角形,不符合题意;
C、∵AB=AC,∠B=45°,
∴∠B=∠C=45°,
∴∠A=90°,
∴△ABC是直角三角形,不符合题意.
D、不能得出△ABC是直角三角形,符合题意,
故选:D.
【点评】本题考查勾股定理的逆定理,三角形内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
4.(2024秋 兴宁市期末)某次数学综合实践课上,小明将一副三角板摆成如图所示的样子,则∠1的大小为( )
A.70 B.75 C.80 D.85
【考点】三角形的外角性质.
【专题】三角形;推理能力.
【答案】B
【分析】三角形的一个外角等于和它不相邻的两个内角的和,由此即可计算.
【解答】解:∵∠2=45°,∠3=30°,
∴∠1=∠2+∠3=75°.
故选:B.
【点评】本题考查三角形的外角性质,关键是掌握三角形的一个外角等于和它不相邻的两个内角的和.
5.(2024秋 大兴区期末)如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有( )
A.0个 B.1个 C.2个 D.3个
【考点】等腰三角形的判定;三角形的外角性质.
【专题】三角形;几何直观.
【答案】D
【分析】先计算出∠BDC,再计算出∠ABC,然后等腰三角形的判定方法对图形中的三角形进行判断.
【解答】解:∵∠BDC=180°﹣∠C﹣∠DBC=180°﹣72°﹣36°=72°,
∴∠BDC=∠C,
∴△BDC为等腰三角形,
∵∠BDC=∠A+∠ABD,
∴∠ABD=36°,
∴∠ABD=∠A,
∴△ABD为等腰三角形,
∵∠ABC=180°﹣∠A﹣∠C=72°,
∴∠ABC=∠C,
∴△ABC为等腰三角形.
故选:D.
【点评】本题考查了等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
6.(2024秋 汕尾期末)如图,∠MON=30°,A为∠MON的平分线OP上一点,过点A作AB∥OM交ON于点B,过点A作AC⊥OM于点C,若AC=2,则AB=( )
A.3 B.4 C.6 D.7
【考点】角平分线的性质;等腰三角形的判定与性质;含30度角的直角三角形;平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】过点A作AD⊥ON于点D,根据角平分线的性质可知AD=AC=2,再根据平行线的性质可知∠ABD=30°,然后根据“直角三角形中30度角所对的直角边等于斜边的一半”即可得答案.
【解答】解:如图,过点A作AD⊥ON于点D,
∵OP是∠MON的平分线,∠MON=30°,AC⊥OM,AD⊥ON,AC=2,
∴AD=AC=2,
∵AB∥OM,
∴∠ABD=∠MON=30°,
∵AD⊥ON,
∴AB=2AD=2×2=4.
故选:B.
【点评】本题主要考查了角平分线的性质、平行线的性质、直角三角形中30度角所对的直角边等于斜边的一半等知识,解题关键是熟练运用角平分线的性质、直角三角形中30度角所对的直角边等于斜边的一半.
7.(2024秋 长兴县期末)如图,在△ABC中,AB=AC,BC=10,AD是△ABC的角平分线,则CD的长是( )
A.6 B.5 C.4 D.无法确定
【考点】等腰三角形的性质.
【专题】等腰三角形与直角三角形;运算能力.
【答案】B
【分析】根据等腰三角形的三线合一性质进行计算,即可解答.
【解答】解:∵AB=AC,AD是△ABC的角平分线,
∴CDBC=5,
故选:B.
【点评】本题考查了等腰三角形的性质,熟练掌握等腰三角形的性质是解题的关键.
8.(2024秋 泉港区期末)下列各组数中,属于“勾股数”的是( )
A.2,4,6 B.4,6,8 C.6,8,10 D.8,10,12
【考点】勾股数.
【专题】实数;运算能力.
【答案】C
【分析】根据勾股数的定义对各选项进行逐一分析即可.
【解答】解:A、∵22+42≠62,
∴不是勾股数,不符合题意;
B、∵42+62≠82,
∴不是勾股数,不符合题意;
C、∵62+82=102,
∴是勾股数,符合题意;
D、∵82+102≠122,
∴不是勾股数,不符合题意,
故选:C.
【点评】本题考查的是勾股数,熟知满足a2+b2=c2 的三个正整数,称为勾股数是解题的关键.
9.(2024秋 门头沟区期末)如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,延长AC到点E,使CE=CD,连接BE交AD的延长线于点F.给出下面四个结论:①AD=BE;②BE=2BF;③AB=AC+CD;④△ABD的面积是△ACD的面积的2倍;上述结论中,所有正确结论的序号是( )
A.①② B.①②③ C.①③④ D.①②③④
【考点】全等三角形的判定与性质;等腰直角三角形.
【专题】图形的全等;推理能力.
【答案】B
【分析】根据全等三角形的判定与性质、三角形面积公式判断求解即可.
【解答】解:∵∠ACB=90°,
∴∠BCE=180°﹣∠ACB=90°,
在△ADC和△BEC中,
,
∴△ADC≌△BEC(SAS),
∴AD=BE,∠CAD=∠CBE,
故①正确,符合题意;
∵∠ADC=∠BDF,∠CAD=∠CBE,
∴∠ACD=∠BFD=90°,
∴AF⊥BE,
∵AD平分∠BAC,
∴∠EAF=BAF,
在△AEF和△ABF中,
,
∴△AEF和≌△ABF(ASA),
∴EF=BF,AE=AB,
∴BE=2BF,
故②正确,符合题意;
∵AE=AC+CE,AE=AB,CE=CD,
∴AB=AC+CD;
故③正确,符合题意;
根据三角形面积公式得,只有BD=2CD时,△ABD的面积是△ACD的面积的2倍,
故④错误,不符合题意;
故选:B.
【点评】此题考查了全等三角形的判定与性质,熟记全等三角形的判定定理与性质定理是解题的关键.
10.(2024秋 武汉期末)工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA、OB上分别在取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线,这里构造全等三角形的依据是( )
A.SSS B.ASA C.AAS D.SAS
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】A
【分析】根据题目中的条件,可以得到OC=OD,MC=MD,再根据OM=OM,即可得到△OMC≌△OMD,并写出依据即可.
【解答】解:由题意可得,
OC=OD,MC=MD,
又∵OM=OM,
∴△OMC≌△OMD(SSS),
故选:A.
【点评】本题考查全等三角形的判定,解答本题的关键是明确全等三角形的判定方法.
二.填空题(共5小题)
11.(2025 嘉定区一模)如图,将一块含30°角的实心的直角三角板放置在桌面上,在桌面所在平面内绕着它的重心G逆时针旋转180°.如果这块三角板的斜边长12厘米,那么运动前后两个三角形重叠部分的面积为 平方厘米.
【考点】三角形的重心;含30度角的直角三角形;生活中的旋转现象;三角形的面积.
【专题】等腰三角形与直角三角形;推理能力.
【答案】.
【分析】根据含30度角的直角三角形的性质,求出△ABC的面积,旋转的性质,重心的性质,推出△ADE﹣△ABC且相似比为1:3,利用△ABC的面积减去三个小三角形的面积求出重叠部分的面积即可.
【解答】解:如图,∠BAC=90°.∠B=30°,BC=12cm,
∴,
∴,
∵G为重心,
∴AG:GN=2:1,
∵△ABC绕点G旋转180度,
∴AB∥A′B′,BC∥B′C′,A′C′∥AC,AG=A′G,MG=NG,
∴AM:MG:GM=1:1:1,
∴AM:AN=1:3,
∵BC∥B′C′,
∴△ADE∽△ABC,
∴,
∴,
同理:,
∴重叠部分的面积为:,
故答案为:.
【点评】本题考查相似三角形的判定和性质,旋转的性质,重心的性质,掌握相似三角形的性质与判定是解题的关键.
12.(2024秋 台州期末)如图,△ABC≌△DEF,若BC=9,CE=3,则CF长度为 6 .
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】6.
【分析】根据全等三角形的性质可得EF=BC=9,进而可得答案.
【解答】解:∵△ABC≌△DEF,
∴EF=BC,
∵BC=9,CE=3,
∴EF=BC=9,
∴CF=EF﹣CE=9﹣3=6.
故答案为:6.
【点评】此题主要考查了全等三角形的性质.关键是掌握全等三角形的对应边相等.
13.(2024秋 泰兴市期末)如图,在△ABC中,AD平分∠BAC,DE⊥AB,△ABC的面积S,AB+AC=a,如果,那么DE= 5 .
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】5.
【分析】过点D作DF⊥AC,交AC于点F,利用角平分线的性质得出DF=DE,根据即可求解.
【解答】解:过点D作DF⊥AC于点F,
∵AD平分∠BAC,DE⊥AB,
∴DF=DE,
又∵△ABC的面积S,AB+AC=a,,
∴.即,
∴DE=5.
故答案为:5.
【点评】本题主要考查角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解题的关键.
14.(2025 浦东新区一模)在△ABC中,∠C=90°,点G是△ABC的重心,如果CG=4,那么AB= 12 .
【考点】三角形的重心.
【专题】三角形;几何直观;运算能力.
【答案】12.
【分析】连接AG并延长交BC于点F,连接CG并延长交AB于点E,在CE的延长线上取一点H,使EH=EG,连接AH,BH,BG,证明四边形AGBH是平行四边形得BH∥AG,进而得GF是△CHB的中位线,则CG=GH=2GE,据此得GE=2,则CE=6,再根据直角三角形斜边中线的性质可得出AB的长.
【解答】解:连接AG并延长交BC于点F,连接CG并延长交AB于点E,在CE的延长线上取一点H,使EH=EG,连接AH,BH,BG,如图所示:
∵G是△ABC的重心,
∴CE,BF是△ABC的中线,
∴AE=BE,BF=CF,
∵EH=EG,
∴四边形AGBH是平行四边形,
∴BH∥AG,
∵BF=CF,
∴GF是△CHB的中位线,
∴CG=GH=2GE,
∵CG=4,
∴GECG=2,
∴CE=CG+GE=6,
∵∠ACB=90°,
∴CE是Rt△ACB斜边AB上的中线,
∴AB=2CE=12.
故答案为:12.
【点评】此题主要考查了三角形的重心,熟练掌握三角形重心的性质是解决问题的关键.
15.(2024秋 武汉期末)如图,已知△ABC的周长是18,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3,则△ABC的面积是 27 .
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】27.
【分析】过点O作OE⊥AB于点E,过点O作OF⊥AC于点F,连接OA,根据角平分线的性质可得OE=OD=OF,进一步求△ABC的面积即可.
【解答】解:过点O作OE⊥AB于点E,过点O作OF⊥AC于点F,连接OA,如图所示:
∵点O为∠ABC与∠ACB的平分线的交点,且OD⊥BC,
∴OE=OD=OF,
∵OD=3,△ABC的周长为18,
∴△ABC的面积=S△AOB+S△AOC+S△BOC
18×3
=27,
故答案为:27.
【点评】本题考查了角平分线的性质,熟练掌握角平分线的性质并灵活运用是解题的关键.
三.解答题(共5小题)
16.(2024秋 中卫期末)一个零件的形状如图所示,按规定这个零件中∠A和∠C都应是直角.工人师傅测得这个零件各边尺寸(单位:cm)如图所示,这个零件符合要求吗?请说明理由.
【考点】勾股定理的逆定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】这个零件不符合要求,理由见解析
【分析】利用勾股定理的逆定理加以判断即可.
【解答】解:这个零件不符合要求,理由如下:
由图可知:AD=8cm,AB=23cm,BD=25cm,
∴AB2+AD2=529+64=593≠625=252=BD2,
∴△ABD不是直角三角形、
∴∠A≠90°,
∵DC=20cm,BC=15cm,BC2+DC2=152+202=625=252=BD2,
∴△BDC是直角三角形,
∴∠C=90°,
∴这个零件不符合要求.
【点评】本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解题关键.
17.(2024秋 仪征市期末)观察下面图形,每个小正方形的边长为1.
(1)图1中阴影正方形的面积是 13 ,边长是 ;
(2)请用无刻度的直尺和圆规在图2的数轴上作出点M,使得点M表示的数为(保留作图痕迹,不写作法).
【考点】勾股定理;实数与数轴.
【专题】等腰三角形与直角三角形;运算能力.
【答案】(1)13;;
(2)见解析.
【分析】(1)用大正方形面积减去四个面积相等的小三角形即可求解;利用算术平方根即可求得正方形的边长;
(2)构造两直角边分别为2与3的直角△OAB,由勾股定理得斜边,再在数轴上以O为圆心,为半径,在数轴上原点右边截取线段即可.
【解答】解:(1)阴影正方形的面积为;
阴影正方形的边长为:;
故答案为:13;;
(2)构造两直角边分别为2与3的直角△OAB,由勾股定理得斜边,再在数轴上以O为圆心,为半径,在数轴上原点右边截取线段OM,点M表示的数为.
【点评】本题考查了算术平方根,割补法求网格中图形面积,勾股定理与无理数,尺规作图等知识,掌握这些知识是关键.
18.(2024秋 仪征市期末)如图,在△ABC中,∠D=90°,∠B=40°,E为BD上一点,EF⊥AB于点F,若ED=EF,求∠AED度数.
【考点】全等三角形的判定与性质.
【专题】图形的全等;几何直观;推理能力.
【答案】65°.
【分析】根据EF⊥AB于点F,∠D=90°,ED=EF,证明△AFE≌△ADE(HL),因为∠B=40°,则,即可作答.
【解答】解:∵EF⊥AB于点F,
∴∠AFE=∠D=90°,
∴△AFE和△ADE是直角三角形,
在Rt△AFE和Rt△ADE中,
,
∴Rt△AFE≌Rt△ADE(HL),
∴∠FAE=∠DAE,
∵∠D=90°,∠B=40°,
∴,
∴∠AED=180°﹣90°﹣25°=65°.
【点评】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题的关键.
19.(2024秋 长兴县期末)如图,在△ABC与△DCB中,AC与BD交于点E,且∠ABE=∠DCE,AB=DC.
(1)求证:△ABE≌△DCE;
(2)若∠EBC=25°,求∠BEC的度数.
【考点】全等三角形的判定与性质;等腰三角形的性质;三角形内角和定理.
【专题】图形的全等;等腰三角形与直角三角形;推理能力.
【答案】(1)证明见解答过程;
(2)130°.
【分析】(1)利用AAS即可证明△ABE≌△DCE;
(2)根据全等三角形的性质求出BE=CE,根据等腰三角形的性质求出∠EBC=∠ECB=25°,再根据三角形内角和定理求解即可.
【解答】(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS);
(2)解:由(1)得:△ABE≌△DCE,
∴BE=CE,
∴∠EBC=∠ECB=25°,
∴∠BEC=180°﹣25°×2=130°.
【点评】此题考查了全等三角形的判定与性质、三角形内角和定理、等腰三角形的性质,熟记全等三角形的判定定理与性质定理是解题的关键.
20.(2024秋 泉港区期末)我国古代巨作《九章算术》中记载“今有竹高一丈,末折抵地,去本三尺.问:折者高几何?”数学名题.其译文如下:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部3尺远.问:折断处离地面有多高?(注:1丈=10尺)
【考点】勾股定理的应用;数学常识.
【专题】等腰三角形与直角三角形;应用意识.
【答案】竹子折断处离地面高4.55尺.
【分析】设折断处离地面x尺高,则折断的竹子长(10﹣x)尺,根据勾股定理列方程即可得到结论.
【解答】解:设折断处离地面x尺高,则折断的竹子长(10﹣x)尺,
在Rt△AOB中,OA2+OB2=AB2,
∴x2+32=(10﹣x)2,
解得x=4.55,
答:竹子折断处离地面高4.55尺.
【点评】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 台州期末)若三角形的两边长分别为5,8,则第三条边的边长可能为( )
A.2.5 B.3 C.7 D.13
2.(2024秋 大理州期末)如图,△ABC≌△DEC,B、C、D三点在同一条直线上,CE=3,AC=4,则BD的长为( )
A.8 B.7 C.6 D.5
3.(2024秋 嘉兴期末)在下列条件中,不能判断△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.AB=3,BC=4,
C.AB=AC,∠B=45° D.∠A=30°,
4.(2024秋 兴宁市期末)某次数学综合实践课上,小明将一副三角板摆成如图所示的样子,则∠1的大小为( )
A.70 B.75 C.80 D.85
5.(2024秋 大兴区期末)如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有( )
A.0个 B.1个 C.2个 D.3个
6.(2024秋 汕尾期末)如图,∠MON=30°,A为∠MON的平分线OP上一点,过点A作AB∥OM交ON于点B,过点A作AC⊥OM于点C,若AC=2,则AB=( )
A.3 B.4 C.6 D.7
7.(2024秋 长兴县期末)如图,在△ABC中,AB=AC,BC=10,AD是△ABC的角平分线,则CD的长是( )
A.6 B.5 C.4 D.无法确定
8.(2024秋 泉港区期末)下列各组数中,属于“勾股数”的是( )
A.2,4,6 B.4,6,8 C.6,8,10 D.8,10,12
9.(2024秋 门头沟区期末)如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,延长AC到点E,使CE=CD,连接BE交AD的延长线于点F.给出下面四个结论:①AD=BE;②BE=2BF;③AB=AC+CD;④△ABD的面积是△ACD的面积的2倍;上述结论中,所有正确结论的序号是( )
A.①② B.①②③ C.①③④ D.①②③④
10.(2024秋 武汉期末)工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA、OB上分别在取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线,这里构造全等三角形的依据是( )
A.SSS B.ASA C.AAS D.SAS
二.填空题(共5小题)
11.(2025 嘉定区一模)如图,将一块含30°角的实心的直角三角板放置在桌面上,在桌面所在平面内绕着它的重心G逆时针旋转180°.如果这块三角板的斜边长12厘米,那么运动前后两个三角形重叠部分的面积为 平方厘米.
12.(2024秋 台州期末)如图,△ABC≌△DEF,若BC=9,CE=3,则CF长度为 .
13.(2024秋 泰兴市期末)如图,在△ABC中,AD平分∠BAC,DE⊥AB,△ABC的面积S,AB+AC=a,如果,那么DE= .
14.(2025 浦东新区一模)在△ABC中,∠C=90°,点G是△ABC的重心,如果CG=4,那么AB= .
15.(2024秋 武汉期末)如图,已知△ABC的周长是18,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3,则△ABC的面积是 .
三.解答题(共5小题)
16.(2024秋 中卫期末)一个零件的形状如图所示,按规定这个零件中∠A和∠C都应是直角.工人师傅测得这个零件各边尺寸(单位:cm)如图所示,这个零件符合要求吗?请说明理由.
17.(2024秋 仪征市期末)观察下面图形,每个小正方形的边长为1.
(1)图1中阴影正方形的面积是 ,边长是 ;
(2)请用无刻度的直尺和圆规在图2的数轴上作出点M,使得点M表示的数为(保留作图痕迹,不写作法).
18.(2024秋 仪征市期末)如图,在△ABC中,∠D=90°,∠B=40°,E为BD上一点,EF⊥AB于点F,若ED=EF,求∠AED度数.
19.(2024秋 长兴县期末)如图,在△ABC与△DCB中,AC与BD交于点E,且∠ABE=∠DCE,AB=DC.
(1)求证:△ABE≌△DCE;
(2)若∠EBC=25°,求∠BEC的度数.
20.(2024秋 泉港区期末)我国古代巨作《九章算术》中记载“今有竹高一丈,末折抵地,去本三尺.问:折者高几何?”数学名题.其译文如下:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部3尺远.问:折断处离地面有多高?(注:1丈=10尺)
2025年中考数学高频易错考前冲刺:三角形
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D B D B B C B A
一.选择题(共10小题)
1.(2024秋 台州期末)若三角形的两边长分别为5,8,则第三条边的边长可能为( )
A.2.5 B.3 C.7 D.13
【考点】三角形三边关系.
【专题】三角形;推理能力.
【答案】C
【分析】根据两边之和大于第三边,两边之差小于第三边列式计算求解即可.
【解答】解:设第三边长为x,
∵三角形的两边长分别为5,8,
∴8﹣5<x<8+5,
解得3<x<13,
∴第三条边长可能为:7,
故选:C.
【点评】本题考查三角形三边关系,熟知三角形两边之和大于第三边;三角形的两边差小于第三边是解题的关键.
2.(2024秋 大理州期末)如图,△ABC≌△DEC,B、C、D三点在同一条直线上,CE=3,AC=4,则BD的长为( )
A.8 B.7 C.6 D.5
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】B
【分析】根据全等三角形的性质得出对应边相等,进而解答即可.
【解答】解:∵△ABC≌△DEC,B、C、D三点在同一条直线上,
∴BC=CE,CD=AC,
∵CE=3,AC=4,
∴BC=CE=3,CD=AC=4,
∴BD=BC+CD=3+4=7.
故选:B.
【点评】此题考查全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.
3.(2024秋 嘉兴期末)在下列条件中,不能判断△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.AB=3,BC=4,
C.AB=AC,∠B=45° D.∠A=30°,
【考点】勾股定理的逆定理;三角形内角和定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】D
【分析】根据三角形内角和定理,勾股定理的逆定理一一判断即可.
【解答】解:A、∵∠A=40°,∠B=50°,
∴∠C=180°﹣40°﹣50°=90°,
∴△ABC是直角三角形,不符合题意;
B、∵AB=3,BC=4,,
∴AB2+AC2=BC2,
∴∠A=90°,
∴△ABC是直角三角形,不符合题意;
C、∵AB=AC,∠B=45°,
∴∠B=∠C=45°,
∴∠A=90°,
∴△ABC是直角三角形,不符合题意.
D、不能得出△ABC是直角三角形,符合题意,
故选:D.
【点评】本题考查勾股定理的逆定理,三角形内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
4.(2024秋 兴宁市期末)某次数学综合实践课上,小明将一副三角板摆成如图所示的样子,则∠1的大小为( )
A.70 B.75 C.80 D.85
【考点】三角形的外角性质.
【专题】三角形;推理能力.
【答案】B
【分析】三角形的一个外角等于和它不相邻的两个内角的和,由此即可计算.
【解答】解:∵∠2=45°,∠3=30°,
∴∠1=∠2+∠3=75°.
故选:B.
【点评】本题考查三角形的外角性质,关键是掌握三角形的一个外角等于和它不相邻的两个内角的和.
5.(2024秋 大兴区期末)如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有( )
A.0个 B.1个 C.2个 D.3个
【考点】等腰三角形的判定;三角形的外角性质.
【专题】三角形;几何直观.
【答案】D
【分析】先计算出∠BDC,再计算出∠ABC,然后等腰三角形的判定方法对图形中的三角形进行判断.
【解答】解:∵∠BDC=180°﹣∠C﹣∠DBC=180°﹣72°﹣36°=72°,
∴∠BDC=∠C,
∴△BDC为等腰三角形,
∵∠BDC=∠A+∠ABD,
∴∠ABD=36°,
∴∠ABD=∠A,
∴△ABD为等腰三角形,
∵∠ABC=180°﹣∠A﹣∠C=72°,
∴∠ABC=∠C,
∴△ABC为等腰三角形.
故选:D.
【点评】本题考查了等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
6.(2024秋 汕尾期末)如图,∠MON=30°,A为∠MON的平分线OP上一点,过点A作AB∥OM交ON于点B,过点A作AC⊥OM于点C,若AC=2,则AB=( )
A.3 B.4 C.6 D.7
【考点】角平分线的性质;等腰三角形的判定与性质;含30度角的直角三角形;平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】过点A作AD⊥ON于点D,根据角平分线的性质可知AD=AC=2,再根据平行线的性质可知∠ABD=30°,然后根据“直角三角形中30度角所对的直角边等于斜边的一半”即可得答案.
【解答】解:如图,过点A作AD⊥ON于点D,
∵OP是∠MON的平分线,∠MON=30°,AC⊥OM,AD⊥ON,AC=2,
∴AD=AC=2,
∵AB∥OM,
∴∠ABD=∠MON=30°,
∵AD⊥ON,
∴AB=2AD=2×2=4.
故选:B.
【点评】本题主要考查了角平分线的性质、平行线的性质、直角三角形中30度角所对的直角边等于斜边的一半等知识,解题关键是熟练运用角平分线的性质、直角三角形中30度角所对的直角边等于斜边的一半.
7.(2024秋 长兴县期末)如图,在△ABC中,AB=AC,BC=10,AD是△ABC的角平分线,则CD的长是( )
A.6 B.5 C.4 D.无法确定
【考点】等腰三角形的性质.
【专题】等腰三角形与直角三角形;运算能力.
【答案】B
【分析】根据等腰三角形的三线合一性质进行计算,即可解答.
【解答】解:∵AB=AC,AD是△ABC的角平分线,
∴CDBC=5,
故选:B.
【点评】本题考查了等腰三角形的性质,熟练掌握等腰三角形的性质是解题的关键.
8.(2024秋 泉港区期末)下列各组数中,属于“勾股数”的是( )
A.2,4,6 B.4,6,8 C.6,8,10 D.8,10,12
【考点】勾股数.
【专题】实数;运算能力.
【答案】C
【分析】根据勾股数的定义对各选项进行逐一分析即可.
【解答】解:A、∵22+42≠62,
∴不是勾股数,不符合题意;
B、∵42+62≠82,
∴不是勾股数,不符合题意;
C、∵62+82=102,
∴是勾股数,符合题意;
D、∵82+102≠122,
∴不是勾股数,不符合题意,
故选:C.
【点评】本题考查的是勾股数,熟知满足a2+b2=c2 的三个正整数,称为勾股数是解题的关键.
9.(2024秋 门头沟区期末)如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,延长AC到点E,使CE=CD,连接BE交AD的延长线于点F.给出下面四个结论:①AD=BE;②BE=2BF;③AB=AC+CD;④△ABD的面积是△ACD的面积的2倍;上述结论中,所有正确结论的序号是( )
A.①② B.①②③ C.①③④ D.①②③④
【考点】全等三角形的判定与性质;等腰直角三角形.
【专题】图形的全等;推理能力.
【答案】B
【分析】根据全等三角形的判定与性质、三角形面积公式判断求解即可.
【解答】解:∵∠ACB=90°,
∴∠BCE=180°﹣∠ACB=90°,
在△ADC和△BEC中,
,
∴△ADC≌△BEC(SAS),
∴AD=BE,∠CAD=∠CBE,
故①正确,符合题意;
∵∠ADC=∠BDF,∠CAD=∠CBE,
∴∠ACD=∠BFD=90°,
∴AF⊥BE,
∵AD平分∠BAC,
∴∠EAF=BAF,
在△AEF和△ABF中,
,
∴△AEF和≌△ABF(ASA),
∴EF=BF,AE=AB,
∴BE=2BF,
故②正确,符合题意;
∵AE=AC+CE,AE=AB,CE=CD,
∴AB=AC+CD;
故③正确,符合题意;
根据三角形面积公式得,只有BD=2CD时,△ABD的面积是△ACD的面积的2倍,
故④错误,不符合题意;
故选:B.
【点评】此题考查了全等三角形的判定与性质,熟记全等三角形的判定定理与性质定理是解题的关键.
10.(2024秋 武汉期末)工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA、OB上分别在取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线,这里构造全等三角形的依据是( )
A.SSS B.ASA C.AAS D.SAS
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】A
【分析】根据题目中的条件,可以得到OC=OD,MC=MD,再根据OM=OM,即可得到△OMC≌△OMD,并写出依据即可.
【解答】解:由题意可得,
OC=OD,MC=MD,
又∵OM=OM,
∴△OMC≌△OMD(SSS),
故选:A.
【点评】本题考查全等三角形的判定,解答本题的关键是明确全等三角形的判定方法.
二.填空题(共5小题)
11.(2025 嘉定区一模)如图,将一块含30°角的实心的直角三角板放置在桌面上,在桌面所在平面内绕着它的重心G逆时针旋转180°.如果这块三角板的斜边长12厘米,那么运动前后两个三角形重叠部分的面积为 平方厘米.
【考点】三角形的重心;含30度角的直角三角形;生活中的旋转现象;三角形的面积.
【专题】等腰三角形与直角三角形;推理能力.
【答案】.
【分析】根据含30度角的直角三角形的性质,求出△ABC的面积,旋转的性质,重心的性质,推出△ADE﹣△ABC且相似比为1:3,利用△ABC的面积减去三个小三角形的面积求出重叠部分的面积即可.
【解答】解:如图,∠BAC=90°.∠B=30°,BC=12cm,
∴,
∴,
∵G为重心,
∴AG:GN=2:1,
∵△ABC绕点G旋转180度,
∴AB∥A′B′,BC∥B′C′,A′C′∥AC,AG=A′G,MG=NG,
∴AM:MG:GM=1:1:1,
∴AM:AN=1:3,
∵BC∥B′C′,
∴△ADE∽△ABC,
∴,
∴,
同理:,
∴重叠部分的面积为:,
故答案为:.
【点评】本题考查相似三角形的判定和性质,旋转的性质,重心的性质,掌握相似三角形的性质与判定是解题的关键.
12.(2024秋 台州期末)如图,△ABC≌△DEF,若BC=9,CE=3,则CF长度为 6 .
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】6.
【分析】根据全等三角形的性质可得EF=BC=9,进而可得答案.
【解答】解:∵△ABC≌△DEF,
∴EF=BC,
∵BC=9,CE=3,
∴EF=BC=9,
∴CF=EF﹣CE=9﹣3=6.
故答案为:6.
【点评】此题主要考查了全等三角形的性质.关键是掌握全等三角形的对应边相等.
13.(2024秋 泰兴市期末)如图,在△ABC中,AD平分∠BAC,DE⊥AB,△ABC的面积S,AB+AC=a,如果,那么DE= 5 .
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】5.
【分析】过点D作DF⊥AC,交AC于点F,利用角平分线的性质得出DF=DE,根据即可求解.
【解答】解:过点D作DF⊥AC于点F,
∵AD平分∠BAC,DE⊥AB,
∴DF=DE,
又∵△ABC的面积S,AB+AC=a,,
∴.即,
∴DE=5.
故答案为:5.
【点评】本题主要考查角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解题的关键.
14.(2025 浦东新区一模)在△ABC中,∠C=90°,点G是△ABC的重心,如果CG=4,那么AB= 12 .
【考点】三角形的重心.
【专题】三角形;几何直观;运算能力.
【答案】12.
【分析】连接AG并延长交BC于点F,连接CG并延长交AB于点E,在CE的延长线上取一点H,使EH=EG,连接AH,BH,BG,证明四边形AGBH是平行四边形得BH∥AG,进而得GF是△CHB的中位线,则CG=GH=2GE,据此得GE=2,则CE=6,再根据直角三角形斜边中线的性质可得出AB的长.
【解答】解:连接AG并延长交BC于点F,连接CG并延长交AB于点E,在CE的延长线上取一点H,使EH=EG,连接AH,BH,BG,如图所示:
∵G是△ABC的重心,
∴CE,BF是△ABC的中线,
∴AE=BE,BF=CF,
∵EH=EG,
∴四边形AGBH是平行四边形,
∴BH∥AG,
∵BF=CF,
∴GF是△CHB的中位线,
∴CG=GH=2GE,
∵CG=4,
∴GECG=2,
∴CE=CG+GE=6,
∵∠ACB=90°,
∴CE是Rt△ACB斜边AB上的中线,
∴AB=2CE=12.
故答案为:12.
【点评】此题主要考查了三角形的重心,熟练掌握三角形重心的性质是解决问题的关键.
15.(2024秋 武汉期末)如图,已知△ABC的周长是18,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3,则△ABC的面积是 27 .
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】27.
【分析】过点O作OE⊥AB于点E,过点O作OF⊥AC于点F,连接OA,根据角平分线的性质可得OE=OD=OF,进一步求△ABC的面积即可.
【解答】解:过点O作OE⊥AB于点E,过点O作OF⊥AC于点F,连接OA,如图所示:
∵点O为∠ABC与∠ACB的平分线的交点,且OD⊥BC,
∴OE=OD=OF,
∵OD=3,△ABC的周长为18,
∴△ABC的面积=S△AOB+S△AOC+S△BOC
18×3
=27,
故答案为:27.
【点评】本题考查了角平分线的性质,熟练掌握角平分线的性质并灵活运用是解题的关键.
三.解答题(共5小题)
16.(2024秋 中卫期末)一个零件的形状如图所示,按规定这个零件中∠A和∠C都应是直角.工人师傅测得这个零件各边尺寸(单位:cm)如图所示,这个零件符合要求吗?请说明理由.
【考点】勾股定理的逆定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】这个零件不符合要求,理由见解析
【分析】利用勾股定理的逆定理加以判断即可.
【解答】解:这个零件不符合要求,理由如下:
由图可知:AD=8cm,AB=23cm,BD=25cm,
∴AB2+AD2=529+64=593≠625=252=BD2,
∴△ABD不是直角三角形、
∴∠A≠90°,
∵DC=20cm,BC=15cm,BC2+DC2=152+202=625=252=BD2,
∴△BDC是直角三角形,
∴∠C=90°,
∴这个零件不符合要求.
【点评】本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解题关键.
17.(2024秋 仪征市期末)观察下面图形,每个小正方形的边长为1.
(1)图1中阴影正方形的面积是 13 ,边长是 ;
(2)请用无刻度的直尺和圆规在图2的数轴上作出点M,使得点M表示的数为(保留作图痕迹,不写作法).
【考点】勾股定理;实数与数轴.
【专题】等腰三角形与直角三角形;运算能力.
【答案】(1)13;;
(2)见解析.
【分析】(1)用大正方形面积减去四个面积相等的小三角形即可求解;利用算术平方根即可求得正方形的边长;
(2)构造两直角边分别为2与3的直角△OAB,由勾股定理得斜边,再在数轴上以O为圆心,为半径,在数轴上原点右边截取线段即可.
【解答】解:(1)阴影正方形的面积为;
阴影正方形的边长为:;
故答案为:13;;
(2)构造两直角边分别为2与3的直角△OAB,由勾股定理得斜边,再在数轴上以O为圆心,为半径,在数轴上原点右边截取线段OM,点M表示的数为.
【点评】本题考查了算术平方根,割补法求网格中图形面积,勾股定理与无理数,尺规作图等知识,掌握这些知识是关键.
18.(2024秋 仪征市期末)如图,在△ABC中,∠D=90°,∠B=40°,E为BD上一点,EF⊥AB于点F,若ED=EF,求∠AED度数.
【考点】全等三角形的判定与性质.
【专题】图形的全等;几何直观;推理能力.
【答案】65°.
【分析】根据EF⊥AB于点F,∠D=90°,ED=EF,证明△AFE≌△ADE(HL),因为∠B=40°,则,即可作答.
【解答】解:∵EF⊥AB于点F,
∴∠AFE=∠D=90°,
∴△AFE和△ADE是直角三角形,
在Rt△AFE和Rt△ADE中,
,
∴Rt△AFE≌Rt△ADE(HL),
∴∠FAE=∠DAE,
∵∠D=90°,∠B=40°,
∴,
∴∠AED=180°﹣90°﹣25°=65°.
【点评】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题的关键.
19.(2024秋 长兴县期末)如图,在△ABC与△DCB中,AC与BD交于点E,且∠ABE=∠DCE,AB=DC.
(1)求证:△ABE≌△DCE;
(2)若∠EBC=25°,求∠BEC的度数.
【考点】全等三角形的判定与性质;等腰三角形的性质;三角形内角和定理.
【专题】图形的全等;等腰三角形与直角三角形;推理能力.
【答案】(1)证明见解答过程;
(2)130°.
【分析】(1)利用AAS即可证明△ABE≌△DCE;
(2)根据全等三角形的性质求出BE=CE,根据等腰三角形的性质求出∠EBC=∠ECB=25°,再根据三角形内角和定理求解即可.
【解答】(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS);
(2)解:由(1)得:△ABE≌△DCE,
∴BE=CE,
∴∠EBC=∠ECB=25°,
∴∠BEC=180°﹣25°×2=130°.
【点评】此题考查了全等三角形的判定与性质、三角形内角和定理、等腰三角形的性质,熟记全等三角形的判定定理与性质定理是解题的关键.
20.(2024秋 泉港区期末)我国古代巨作《九章算术》中记载“今有竹高一丈,末折抵地,去本三尺.问:折者高几何?”数学名题.其译文如下:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部3尺远.问:折断处离地面有多高?(注:1丈=10尺)
【考点】勾股定理的应用;数学常识.
【专题】等腰三角形与直角三角形;应用意识.
【答案】竹子折断处离地面高4.55尺.
【分析】设折断处离地面x尺高,则折断的竹子长(10﹣x)尺,根据勾股定理列方程即可得到结论.
【解答】解:设折断处离地面x尺高,则折断的竹子长(10﹣x)尺,
在Rt△AOB中,OA2+OB2=AB2,
∴x2+32=(10﹣x)2,
解得x=4.55,
答:竹子折断处离地面高4.55尺.
【点评】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
