【中考押题卷】2025年中考数学高频易错考前冲刺:数据收集与处理(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:数据收集与处理(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 08:20:15 | ||
图片预览



文档简介
2025年中考数学高频易错考前冲刺:数据收集与处理
一.选择题(共10小题)
1.(2024秋 德化县期末)某校开展“阅读助成长,课程蕴书香”活动,对全校学生每天的课外阅读时间进行了全面调查,根据收集的相关数据绘制成如图所示的扇形统计图.下列说法错误的是( )
A.每天阅读不足30分钟的学生人数最多
B.每天阅读30分钟以上的学生人数超过50%
C.每天阅读1小时以上的学生人数占20%
D.每天阅读30分钟至2小时的学生人数占50%
2.(2024秋 温江区校级期末)以下说法中,正确的是( )
A.为了解全体学生的视力,对每位学生都进行视力检查是普查
B.全校学生上学的交通方式是定量数据
C.为调查小区1500户家庭用水情况,抽取该小区100户家庭,样本容量为1500
D.射线AB和射线BA表示同一条射线
3.(2024秋 新城区校级期末)下列说法中,正确的是( )
A.西安市每年参加中考的人数是定性数据
B.了解航天飞机升空前的安全检查,采用抽样调查
C.了解西安市的中学生保护水资源的意识,采用抽样调查
D.了解西安市民乘坐地铁8号线的情况,采用全面调查
4.(2024秋 泉港区期末)为了解动车经过各站后,乘车人数的变化情况,最适合使用的统计图是( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.以上三种都可以
5.(2024秋 永春县期末)在数字“82003018”中,数字“8”出现的频率为( )
A. B. C. D.2
6.(2024秋 兰州期末)在一个不透明的口袋中,放置2个黄球,1个白球,1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了蓝球出现的频率(如图所示),则n的值最可能是( )
A.4 B.5 C.6 D.7
7.(2024秋 市北区期末)下列说法正确的是( )
A.全班同学的上学交通方式是定量数据
B.某池塘中现有鱼的数量是定性数据
C.全班同学家养宠物的种类是定量数据
D.某公司职工的学历是定性数据
8.(2024秋 瑶海区期末)下列说法最恰当的是( )
A.某校对学生进行体育达标测试,应采用抽样调查法
B.了解我省中学生的身高状况采用抽样调查法
C.要了解某班级学生期中数学测试成绩采用抽样调查法
D.某工厂质检人员检测灯泡的使用寿命采用普查法
9.(2024秋 海伦市期末)某小学六年级有学生800人,每人只能参加一项延时服务,根据如图扇形统计图,求出参加绘画组的有( )人.
A.120 B.160 C.180 D.324
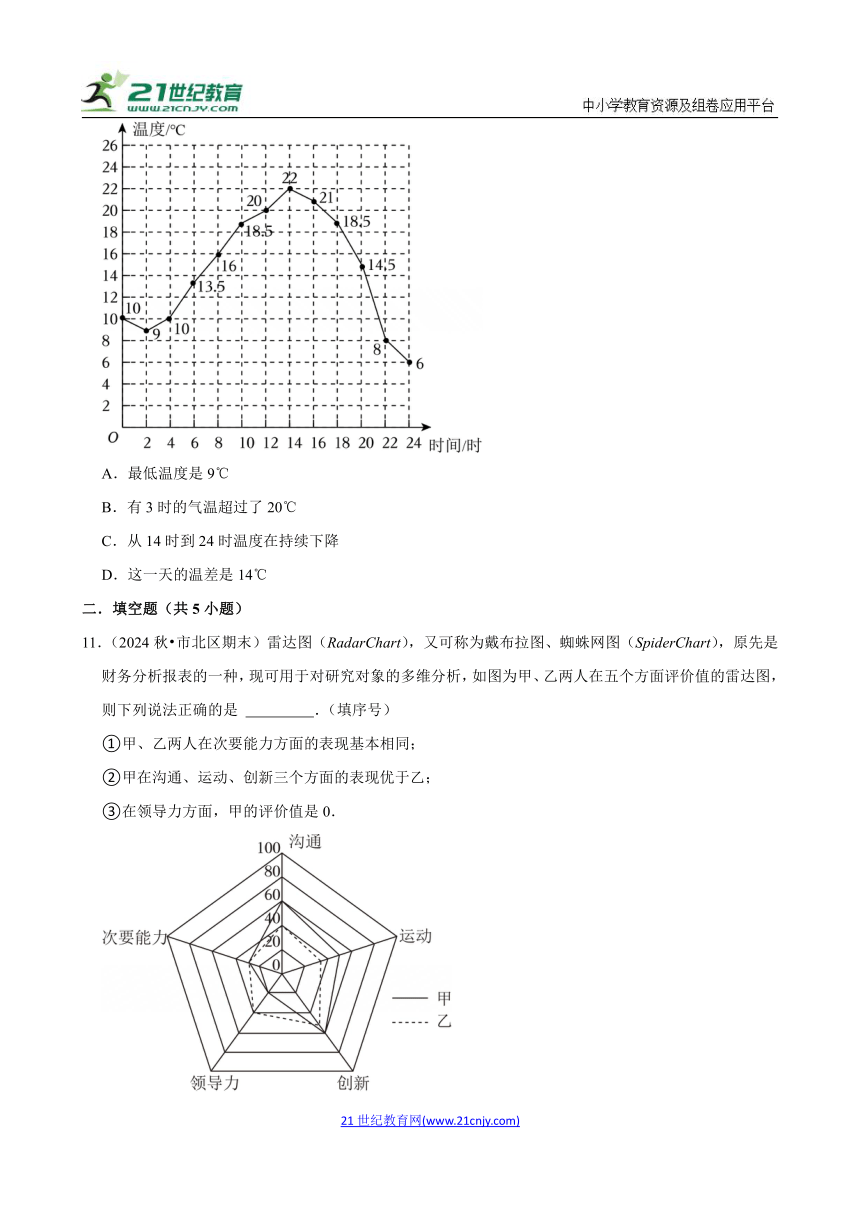
10.(2024秋 紫金县期末)如图是某地某天气温变化情况的折线图,下列描述正确的是( )
A.最低温度是9℃
B.有3时的气温超过了20℃
C.从14时到24时温度在持续下降
D.这一天的温差是14℃
二.填空题(共5小题)
11.(2024秋 市北区期末)雷达图(RadarChart),又可称为戴布拉图、蜘蛛网图(SpiderChart),原先是财务分析报表的一种,现可用于对研究对象的多维分析,如图为甲、乙两人在五个方面评价值的雷达图,则下列说法正确的是 .(填序号)
①甲、乙两人在次要能力方面的表现基本相同;
②甲在沟通、运动、创新三个方面的表现优于乙;
③在领导力方面,甲的评价值是0.
12.(2024秋 鲤城区校级期末)在英文“We like math”句中,字母“e”出现的频率为 .
13.(2024秋 建湖县期末)已知一个样本中,50个数据分别落在5个组内,第一、二、四、五组数据的个数分别为2,8,20,5,则第三组的频率为 .
14.(2024秋 泉港区期末)小明在抛一枚正六面体骰子的实验中,共抛了10次骰子,掷得3次“六点”向上.则该实验中,掷得“六点”向上的频率是 .
15.(2024秋 四平期末)某林业局将一种树苗移植成活的情况绘制成如图所示的折线统计图,由此可估计这种树苗移植1200棵,成活的大约有 棵.
三.解答题(共5小题)
16.(2024秋 沙坪坝区校级期末)为推动《关于全面实施学校美育浸润行动》,强化中小学美育育人工作,重庆市教育督导委员会开展了中小学艺术测评工作.督导组在某中学的艺术测评成绩中随机抽取了七、八年级各25名学生的艺术测评成绩(百分制),并对其数据进行整理、描述、分析.所有评分均不低于60分,且没有满分(评分分数用x表示,共分为四组:A:90≤x<100,B:80≤x<90,C:70≤x<80,D:60≤x<70),90分及以上评为优秀.下面给出部分信息:
抽取的七年级学生的艺术测评成绩为:
66,68,71,71,73,76,79,82,84,84,85,85,85,85,86,88,88,89,89,89,93,95,96,96,97.
抽取的八年级学生的艺术测评成绩中,B组包含的所有数据为:80,82,85,85,86,87,87,87,87,87,87,87.
抽取的七、八年级学生的艺术测评成绩统计表:
年级 平均数 中位数 众数 优秀率
七年级 84 85 a 20%
八年级 84 b 87 m%
(1)填空并补全条形统计图:a= ,b= ,m= .
(2)根据以上数据,你认为哪个年级的美育教育推动得更好?说明理由(写出一条即可);
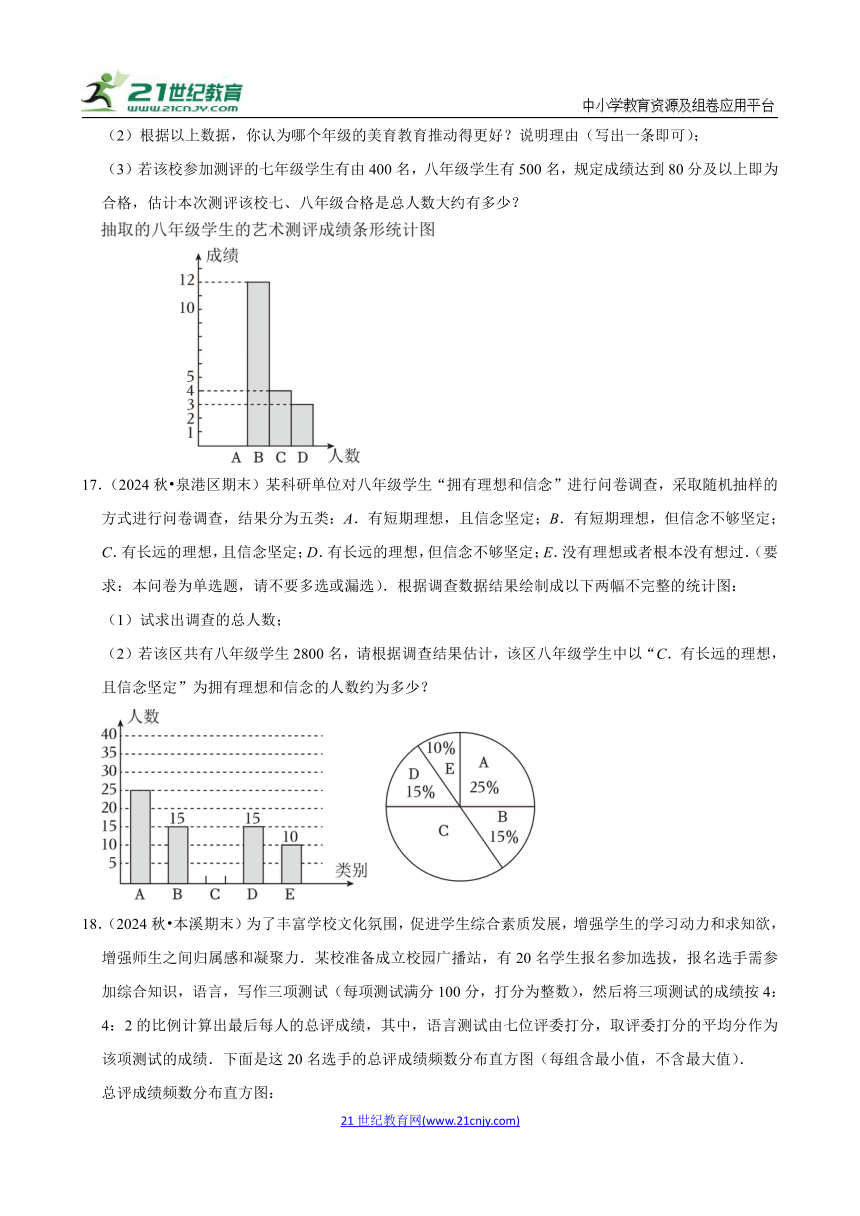
(3)若该校参加测评的七年级学生有由400名,八年级学生有500名,规定成绩达到80分及以上即为合格,估计本次测评该校七、八年级合格是总人数大约有多少?
17.(2024秋 泉港区期末)某科研单位对八年级学生“拥有理想和信念”进行问卷调查,采取随机抽样的方式进行问卷调查,结果分为五类:A.有短期理想,且信念坚定;B.有短期理想,但信念不够坚定;C.有长远的理想,且信念坚定;D.有长远的理想,但信念不够坚定;E.没有理想或者根本没有想过.(要求:本问卷为单选题,请不要多选或漏选).根据调查数据结果绘制成以下两幅不完整的统计图:
(1)试求出调查的总人数;
(2)若该区共有八年级学生2800名,请根据调查结果估计,该区八年级学生中以“C.有长远的理想,且信念坚定”为拥有理想和信念的人数约为多少?
18.(2024秋 本溪期末)为了丰富学校文化氛围,促进学生综合素质发展,增强学生的学习动力和求知欲,增强师生之间归属感和凝聚力.某校准备成立校园广播站,有20名学生报名参加选拔,报名选手需参加综合知识,语言,写作三项测试(每项测试满分100分,打分为整数),然后将三项测试的成绩按4:4:2的比例计算出最后每人的总评成绩,其中,语言测试由七位评委打分,取评委打分的平均分作为该项测试的成绩.下面是这20名选手的总评成绩频数分布直方图(每组含最小值,不含最大值).
总评成绩频数分布直方图:
小明和小亮两位选手的三项测试成绩如下表:
选手 测试成绩/分 总评成绩/分
综合知识 语言 写作
小明 83 72 80 78
小亮 86 84
(1)在语言测试中,七位评委给小亮打出的分数(单位:分)如下:67,72,68,69,74,69,71.求这组数据的中位数;
(2)请你计算小亮的总评成绩;
(3)学校决定根据总评成绩择优选拔10名广播员,试分析小明,小亮能否入选?并说明理由.
19.(2024秋 长沙期末)“双减”政策实施后,某校为丰富学生的课余生活,开设了A篮球,B足球,C绘画,D舞蹈四类兴趣班.为了解学生对这四类兴趣班的喜爱情况,随机抽取该校部分学生进行了问卷调查,并将调查结果整理后绘制成两幅不完整的统计图.请根据统计图信息回答下列问题.
(1)本次抽取调查学生共有 人,估计该校3000名学生喜爱“舞蹈”兴趣班的人数约为 人.
(2)请将如图两个统计图补充完整.
(3)甲、乙两名学生要选择参加兴趣班,若他们每人从A,B,C,D四类兴趣班中随机选取一类,请用画树状图或列表法,求两人恰好选择同一类的概率.
20.(2024秋 济南期末)蔬菜种植是农业经济的重要组成部分,其产量的数据分析可优化农业种植决策,促进农业的可持续发展.某社团对2024年上半年20个地区蔬菜产量进行了调查,获得了各地区蔬菜产量(蔬菜产量用m表示,单位:万吨)的数据,并对数据进行统计整理.数据分成5组:A组:30≤m<40;B组:40≤m<50;C组:50≤m<60;D组:60≤m<70;E组:70≤m<80.
下面给出了部分信息:
a.C组的数据:51,56,56,54,55,58.
b.不完整的2024年上半年蔬菜产量的频数分布直方图和扇形统计图如下:
请根据以上信息完成下列问题:
(1)请补全频数分布直方图;
(2)C组数据的众数是 ;
(3)这20个地区2024年上半年蔬菜产量的中位数是 ;
(4)2024年上半年各组蔬菜平均产量如表:
组别 A.30≤m<40 B.40≤m<50 C.50≤m<60 D.60≤m<70 E.70≤m<80
平均产量(万吨) 35 43 55 68 74
求这20个地区2024年上半年蔬菜的平均产量.
2025年中考数学高频易错考前冲刺:数据收集与处理
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C C A C D B B C
一.选择题(共10小题)
1.(2024秋 德化县期末)某校开展“阅读助成长,课程蕴书香”活动,对全校学生每天的课外阅读时间进行了全面调查,根据收集的相关数据绘制成如图所示的扇形统计图.下列说法错误的是( )
A.每天阅读不足30分钟的学生人数最多
B.每天阅读30分钟以上的学生人数超过50%
C.每天阅读1小时以上的学生人数占20%
D.每天阅读30分钟至2小时的学生人数占50%
【考点】扇形统计图.
【专题】统计的应用;数据分析观念.
【答案】C
【分析】从扇形图中获取信息逐一分析判断即可.
【解答】解:A、每天阅读不足30分钟的学生人数最多,占总人数的40%,原说法正确,故选项不符合题意;
B、每天阅读30分钟以上的学生人数占60%,超过50%,原说法正确,故选项不符合题意;
C、每天阅读1小时以上的学生人数占10%+20%=30%,原说法错误,故选项符合题意;
D、每天阅读30分钟至2小时的学生人数占50%,原说法正确,故选项不符合题意.
故选:C.
【点评】本题考查了扇形统计图,解题的关键是正确从扇形图中获取信息.
2.(2024秋 温江区校级期末)以下说法中,正确的是( )
A.为了解全体学生的视力,对每位学生都进行视力检查是普查
B.全校学生上学的交通方式是定量数据
C.为调查小区1500户家庭用水情况,抽取该小区100户家庭,样本容量为1500
D.射线AB和射线BA表示同一条射线
【考点】全面调查与抽样调查.
【专题】数据的收集与整理;线段、角、相交线与平行线;应用意识.
【答案】A
【分析】分别根据全面调查与抽样调查,定量数据与定性数据,样本容量和射线的定义判断即可.
【解答】解:A、为了解全体学生的视力,对每位学生都进行视力检查是普查,故符合题意;
B、全校学生上学的交通方式是定性数据,故不符合题意;
C、样本容量为100,故不符合题意;
D、射线AB和射线BA表示不同的射线,故不符合题意;
故选:A.
【点评】本题考查了全面调查与抽样调查,定量数据与定性数据,样本容量和射线,掌握相关概念是解题的关键.
3.(2024秋 新城区校级期末)下列说法中,正确的是( )
A.西安市每年参加中考的人数是定性数据
B.了解航天飞机升空前的安全检查,采用抽样调查
C.了解西安市的中学生保护水资源的意识,采用抽样调查
D.了解西安市民乘坐地铁8号线的情况,采用全面调查
【考点】全面调查与抽样调查.
【专题】统计的应用;数据分析观念.
【答案】C
【分析】根据定性数据与定量数据的定义判断A选项;由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.再根据问卷调查方法即可判断B、C、D选项.
【解答】解:A.西安市每年参加中考的人数是定量数据,故本选项不符合题意;
B.了解航天飞机升空前的安全检查,采用全面调查,故本选项不符合题意;
C.了解西安市的中学生保护水资源的意识,采用抽样调查,故本选项符合题意;
D.了解西安市民乘坐地铁8号线的情况,采用抽样调查,故本选项不符合题意.
故选:C.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.(2024秋 泉港区期末)为了解动车经过各站后,乘车人数的变化情况,最适合使用的统计图是( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.以上三种都可以
【考点】统计图的选择.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目;频数分布直方图,清楚显示在各个不同区间内取值,各组频数分布情况,易于显示各组之间频数的差别.
【解答】解:为了解动车经过各站后,乘车人数的变化情况,最适合使用的统计图是折线统计图.
故选:C.
【点评】本题考查了统计图的选择,掌握各种统计图的特点是解答本题的关键.
5.(2024秋 永春县期末)在数字“82003018”中,数字“8”出现的频率为( )
A. B. C. D.2
【考点】频数与频率.
【专题】统计的应用;运算能力.
【答案】A
【分析】根据频率的计算公式:频率=频数÷总数,进行计算即可.
【解答】解:由题意知,数字“8”出现的频率是.
故选:A.
【点评】本题主要考查了频数与频率,掌握频率的计算方法.
6.(2024秋 兰州期末)在一个不透明的口袋中,放置2个黄球,1个白球,1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了蓝球出现的频率(如图所示),则n的值最可能是( )
A.4 B.5 C.6 D.7
【考点】频数(率)分布折线图.
【专题】概率及其应用;数据分析观念.
【答案】C
【分析】利用频率估计概率,由概率列方程求解即可.
【解答】解:由频率分布图可知,当实验的次数逐渐增大时,摸到蓝球的频率越稳定在0.6附近,
因此摸到蓝球的概率为0.6,
所以有0.6,
解得n=6.
经检验,n=6是原方程的解,
因此n最可能有6.
故选:C.
【点评】本题考查频率估计概率,理解频率、概率的意义和相互关系是正确解答的关键.
7.(2024秋 市北区期末)下列说法正确的是( )
A.全班同学的上学交通方式是定量数据
B.某池塘中现有鱼的数量是定性数据
C.全班同学家养宠物的种类是定量数据
D.某公司职工的学历是定性数据
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;数据分析观念.
【答案】D
【分析】利用定量数据和定性数据的意义进行判断即可.
【解答】解:A、全班同学的上学交通方式是定性数据,故不符合题意;
B、某池塘中现有鱼的数量是定量数据,故不符合题意;
C、全班同学家养宠物的种类是定性数据,故不符合题意;
D、某公司职工的学历是定性数据,故符合题意.
故选:D.
【点评】本题考查了调查收集数据的过程与方程:正确理解定量数据和定性数据是解决问题的关键.
8.(2024秋 瑶海区期末)下列说法最恰当的是( )
A.某校对学生进行体育达标测试,应采用抽样调查法
B.了解我省中学生的身高状况采用抽样调查法
C.要了解某班级学生期中数学测试成绩采用抽样调查法
D.某工厂质检人员检测灯泡的使用寿命采用普查法
【考点】全面调查与抽样调查.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】一些调查项目并不适合普查,其一,调查者能力有限,不能进行普查;其二,调查过程带有破坏性;其三,有些被调查的对象无法进行普查.
【解答】解:A、某校对学生进行体育达标测试,应采用全面调查法,故本选项说法不恰当,不符合题意;
B、了解我省中学生的身高状况采用抽样调查法,本选项说法恰当,符合题意;
C、要了解某班级学生期中数学测试成绩采用全面调查法,故本选项说法不恰当,不符合题意;
D、某工厂质检人员检测灯泡的使用寿命采用抽样调查法,故本选项说法不恰当,不符合题意;
故选:B.
【点评】本题考查的是抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
9.(2024秋 海伦市期末)某小学六年级有学生800人,每人只能参加一项延时服务,根据如图扇形统计图,求出参加绘画组的有( )人.
A.120 B.160 C.180 D.324
【考点】扇形统计图.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】根据有学生800人和绘画组所占的百分比即可得出答案.
【解答】解:参加绘画组的有:800×(1﹣54%﹣26%)=160(人),
故选:B.
【点评】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
10.(2024秋 紫金县期末)如图是某地某天气温变化情况的折线图,下列描述正确的是( )
A.最低温度是9℃
B.有3时的气温超过了20℃
C.从14时到24时温度在持续下降
D.这一天的温差是14℃
【考点】折线统计图.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】从折线图中有效的获取信息,逐一进行判断即可.
【解答】解:A、最低温度是6℃,不是9℃,原选项说法错误,不符合题意;
B、小于3时的气温超过了20,原选项说法错误,不符合题意;
C、原选项说法正确,符合题意;
D、温差是用最高温度减去最低温度可得:22﹣6=16℃,原选项说法错误,不符合题意;
故选:C.
【点评】本题考查折线统计图,正确记忆相关知识点是解题关键.
二.填空题(共5小题)
11.(2024秋 市北区期末)雷达图(RadarChart),又可称为戴布拉图、蜘蛛网图(SpiderChart),原先是财务分析报表的一种,现可用于对研究对象的多维分析,如图为甲、乙两人在五个方面评价值的雷达图,则下列说法正确的是 ①② .(填序号)
①甲、乙两人在次要能力方面的表现基本相同;
②甲在沟通、运动、创新三个方面的表现优于乙;
③在领导力方面,甲的评价值是0.
【考点】其他统计图.
【专题】统计的应用;数据分析观念.
【答案】①②.
【分析】实线代表甲的能力数值,虚线代表乙的能力数值,越往外圈能力数值越大,分别比较甲乙两人在次要能力、沟通、运动、创新、领导力的数值情况即可得到答案.
【解答】解:从图中可以看出甲、乙两人在次要能力方面的表现基本相同;
甲在沟通、运动、创新三个方面的表现优于乙;
在领导力方面,甲的评价值是20,
故答案为:①②.
【点评】本题考查了其它统计图,对数据的分析处理能力及进行简单的合情推理是解题的关键.
12.(2024秋 鲤城区校级期末)在英文“We like math”句中,字母“e”出现的频率为 0.2 .
【考点】频数与频率.
【专题】统计的应用;运算能力.
【答案】0.2.
【分析】用字母“e”出现的个数除以总的字母个数即可得出答案.
【解答】解:∵字母“e”出现的次数为2,总共10个字母,
∴字母“e”出现的频率为0.2.
故答案为:0.2.
【点评】此题主要考查了频数与频率,关键是掌握频率的定义,频率=频数÷数据总数.
13.(2024秋 建湖县期末)已知一个样本中,50个数据分别落在5个组内,第一、二、四、五组数据的个数分别为2,8,20,5,则第三组的频率为 0.3 .
【考点】频数与频率.
【专题】统计的应用;运算能力.
【答案】0.3.
【分析】根据频率=频数÷总数进行计算即可.
【解答】解:∵第三组的频数为50﹣2﹣8﹣20﹣5=15,
∴第三组的频率0.3.
故答案为:0.3.
【点评】本题考查了频数与频率,解答本题的关键是掌握频数、总数与频率的关系.
14.(2024秋 泉港区期末)小明在抛一枚正六面体骰子的实验中,共抛了10次骰子,掷得3次“六点”向上.则该实验中,掷得“六点”向上的频率是 0.3 .
【考点】频数与频率.
【专题】统计的应用;数据分析观念.
【答案】0.3.
【分析】根据频率的概念计算即可.
【解答】解:∵共抛了10次骰子,掷得3次“六点”向上,
∴掷得“六点”向上的频率是:3÷10=0.3,
故答案为:0.3.
【点评】本题考查的是频数与频率,频率是指每个对象出现的次数与总次数的比值.
15.(2024秋 四平期末)某林业局将一种树苗移植成活的情况绘制成如图所示的折线统计图,由此可估计这种树苗移植1200棵,成活的大约有 960 棵.
【考点】折线统计图;用样本估计总体.
【专题】统计与概率;数据分析观念.
【答案】见试题解答内容
【分析】根据图形可以发现,在0.8附近波动,从而可以估计这种树苗移植成活的概率,再根据概率总体数量即可.
【解答】解:这种树苗移植1200棵,成活的大约有:1200×0.8=960(棵),
故答案为:960.
【点评】本题考查折线统计图,利用样本的频率估计总体,正确记忆相关知识点是解题关键.
三.解答题(共5小题)
16.(2024秋 沙坪坝区校级期末)为推动《关于全面实施学校美育浸润行动》,强化中小学美育育人工作,重庆市教育督导委员会开展了中小学艺术测评工作.督导组在某中学的艺术测评成绩中随机抽取了七、八年级各25名学生的艺术测评成绩(百分制),并对其数据进行整理、描述、分析.所有评分均不低于60分,且没有满分(评分分数用x表示,共分为四组:A:90≤x<100,B:80≤x<90,C:70≤x<80,D:60≤x<70),90分及以上评为优秀.下面给出部分信息:
抽取的七年级学生的艺术测评成绩为:
66,68,71,71,73,76,79,82,84,84,85,85,85,85,86,88,88,89,89,89,93,95,96,96,97.
抽取的八年级学生的艺术测评成绩中,B组包含的所有数据为:80,82,85,85,86,87,87,87,87,87,87,87.
抽取的七、八年级学生的艺术测评成绩统计表:
年级 平均数 中位数 众数 优秀率
七年级 84 85 a 20%
八年级 84 b 87 m%
(1)填空并补全条形统计图:a= 85 ,b= 87 ,m= 24 .
(2)根据以上数据,你认为哪个年级的美育教育推动得更好?说明理由(写出一条即可);
(3)若该校参加测评的七年级学生有由400名,八年级学生有500名,规定成绩达到80分及以上即为合格,估计本次测评该校七、八年级合格是总人数大约有多少?
【考点】频数(率)分布直方图;中位数;众数;用样本估计总体.
【专题】统计的应用;数据分析观念.
【答案】(1)85,87,24;
(2)八年级的美育教育推动得更好;
(3)648人.
【分析】(1)根据众数和中位数的定义即可求出a、b,根据优秀率的计算公式即可求出m;
(2)根据中位数、众数以及优秀率的意义分析即可;
(3)用样本估计总体即可.
【解答】解:(1)∵七年级学生的艺术测评成绩中85出现的次数最多,
∴众数a=85,
∵样本容量为25,八年级学生的艺术测评成绩中最中间的数据为87,
∴中位数b=87,
八年级学生的艺术测评成绩高于90分的人数:25﹣12﹣4﹣3=6(人),
∴m%100%=24%,
∴m=24.
故答案为:85,87,24;
(2)八年级的美育教育推动得更好.
理由:∵两个年级的平均数相同,而八年级的优秀率高于七年级,
∴八年级的美育教育推动得更好;
(3)400500648(人),
答:估计本次测评该校七、八年级合格是总人数大约有648人.
【点评】本题考查条形统计图与扇形统计图,中位数,众数,用样本估计总体,从统计图获取有用的信息是解题的关键.
17.(2024秋 泉港区期末)某科研单位对八年级学生“拥有理想和信念”进行问卷调查,采取随机抽样的方式进行问卷调查,结果分为五类:A.有短期理想,且信念坚定;B.有短期理想,但信念不够坚定;C.有长远的理想,且信念坚定;D.有长远的理想,但信念不够坚定;E.没有理想或者根本没有想过.(要求:本问卷为单选题,请不要多选或漏选).根据调查数据结果绘制成以下两幅不完整的统计图:
(1)试求出调查的总人数;
(2)若该区共有八年级学生2800名,请根据调查结果估计,该区八年级学生中以“C.有长远的理想,且信念坚定”为拥有理想和信念的人数约为多少?
【考点】条形统计图;用样本估计总体;扇形统计图.
【专题】统计的应用;数据分析观念.
【答案】(1)100人;(2)980人.
【分析】(1)由B类的人数除以所占的百分比,即可求解;
(2)求出C类的占比,用八年级总人数乘以C类占比即可.
【解答】解:(1)15÷15%=100(人),
答:调查的总人数为100人;
(2)1﹣25%﹣15%﹣15%﹣10%=35%,
2800×35%=980(人),
答:以选择“C.有长远的理想,且信念坚定”的人数约为980人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
18.(2024秋 本溪期末)为了丰富学校文化氛围,促进学生综合素质发展,增强学生的学习动力和求知欲,增强师生之间归属感和凝聚力.某校准备成立校园广播站,有20名学生报名参加选拔,报名选手需参加综合知识,语言,写作三项测试(每项测试满分100分,打分为整数),然后将三项测试的成绩按4:4:2的比例计算出最后每人的总评成绩,其中,语言测试由七位评委打分,取评委打分的平均分作为该项测试的成绩.下面是这20名选手的总评成绩频数分布直方图(每组含最小值,不含最大值).
总评成绩频数分布直方图:
小明和小亮两位选手的三项测试成绩如下表:
选手 测试成绩/分 总评成绩/分
综合知识 语言 写作
小明 83 72 80 78
小亮 86 84
(1)在语言测试中,七位评委给小亮打出的分数(单位:分)如下:67,72,68,69,74,69,71.求这组数据的中位数;
(2)请你计算小亮的总评成绩;
(3)学校决定根据总评成绩择优选拔10名广播员,试分析小明,小亮能否入选?并说明理由.
【考点】频数(率)分布直方图;加权平均数;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)69分;
(2)81分;
(3)小亮总评成绩超过80分,能够入选;小明总评成绩没超过80分,不能入选.
【分析】(1)分别根据中位数的定义即可求出答案;
(2)根据加权平均数公式计算即可求解;
(3)根据20名学生的总评成绩频数分布直方图即可得出答案.
【解答】解:(1)将七位评委的分数从小到大排序:67,68,69,69,71,72,74,
排序后处在中间位置的数据是69分,
答:这组数据的中位数是69分;
(2)小亮语言这项测试的得分为:(67+68+69+69+71+72+74)=70(分),
∴(分).
答:小亮的总评成绩为81分;
(3)小明不能入选,小亮能入选.
∵由这20名选手的总评成绩频数分布直方图可知,分数小于80分的有10人,
又∵学校准备根据总评成绩择优选拔10名广播员,
∴小亮总评成绩超过80分,能够入选;小明总评成绩没超过80分,不能入选.
【点评】本题考查了频数分布直方图,加权平均数,中位数,解题的关键在于熟练掌握加权平均数,中位数的计算方法.
19.(2024秋 长沙期末)“双减”政策实施后,某校为丰富学生的课余生活,开设了A篮球,B足球,C绘画,D舞蹈四类兴趣班.为了解学生对这四类兴趣班的喜爱情况,随机抽取该校部分学生进行了问卷调查,并将调查结果整理后绘制成两幅不完整的统计图.请根据统计图信息回答下列问题.
(1)本次抽取调查学生共有 50 人,估计该校3000名学生喜爱“舞蹈”兴趣班的人数约为 300 人.
(2)请将如图两个统计图补充完整.
(3)甲、乙两名学生要选择参加兴趣班,若他们每人从A,B,C,D四类兴趣班中随机选取一类,请用画树状图或列表法,求两人恰好选择同一类的概率.
【考点】条形统计图;概率公式;列表法与树状图法;用样本估计总体;扇形统计图.
【答案】(1)50、300;(2)见解答;(3).
【分析】(1)根据B类型的人数及其占总人数的百分比可得被调查的总人数,用总人数乘以样本中D类型人数占被调查的总人数的百分比可得答案;
(2)用总人数乘以A类型对应的百分比可得其人数,据此可补全条形图,分别用C、D类型人数除以总人数求出其所占百分比即可补全扇形图;
(3)画树状图列出所有等可能结果,并从中找到两人恰好选择同一类的结果数,再根据概率公式求解即可.
【解答】解:(1)本次抽取调查学生共有15÷30%=50(人),
估计该校3000名学生喜爱“舞蹈”兴趣班的人数约为3000300(人),
故答案为:50、300;
(2)A类型人数为50×36%=18(人),C类型人数所占百分比为100%=24%,
补全图形如下:
(3)画树状图为:
共有16种等可能的结果数,其中两人恰好选中同一类的结果数为4,
所以两人恰好选择同一类的概率为.
【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.也考查了统计图.
20.(2024秋 济南期末)蔬菜种植是农业经济的重要组成部分,其产量的数据分析可优化农业种植决策,促进农业的可持续发展.某社团对2024年上半年20个地区蔬菜产量进行了调查,获得了各地区蔬菜产量(蔬菜产量用m表示,单位:万吨)的数据,并对数据进行统计整理.数据分成5组:A组:30≤m<40;B组:40≤m<50;C组:50≤m<60;D组:60≤m<70;E组:70≤m<80.
下面给出了部分信息:
a.C组的数据:51,56,56,54,55,58.
b.不完整的2024年上半年蔬菜产量的频数分布直方图和扇形统计图如下:
请根据以上信息完成下列问题:
(1)请补全频数分布直方图;
(2)C组数据的众数是 56 ;
(3)这20个地区2024年上半年蔬菜产量的中位数是 56 ;
(4)2024年上半年各组蔬菜平均产量如表:
组别 A.30≤m<40 B.40≤m<50 C.50≤m<60 D.60≤m<70 E.70≤m<80
平均产量(万吨) 35 43 55 68 74
求这20个地区2024年上半年蔬菜的平均产量.
【考点】频数(率)分布直方图;扇形统计图;加权平均数;中位数;众数.
【专题】统计的应用;数据分析观念.
【答案】(1)见解析;
(2)56;
(3)56;
(4)56.4万吨.
【分析】(1)求出B组和D组的频数,从而补全图形;
(2)根据众数的定义求解即可;
(3)根据中位数的定义求解即可;
(4)根据加权平均数的定义求解即可.
【解答】解:(1)B组的频数为204,
D组的频数为20﹣2﹣4﹣6﹣2=6,
补全图形如下:
(2)C组数据的众数是56,
故答案为:56;
(3)这20个地区2024年上半年蔬菜产量的中位数是56,
故答案为:56;
(4)(35×2+43×4+55×6+68×6+74×2)=56.4(万吨),
答:这20个地区2024年上半年蔬菜的平均产量是56.4万吨.
【点评】本题考查频数分布直方图、加权平均数、众数、中位数、扇形统计图等知识,掌握相关知识,利用数形结合思想是解题关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 德化县期末)某校开展“阅读助成长,课程蕴书香”活动,对全校学生每天的课外阅读时间进行了全面调查,根据收集的相关数据绘制成如图所示的扇形统计图.下列说法错误的是( )
A.每天阅读不足30分钟的学生人数最多
B.每天阅读30分钟以上的学生人数超过50%
C.每天阅读1小时以上的学生人数占20%
D.每天阅读30分钟至2小时的学生人数占50%
2.(2024秋 温江区校级期末)以下说法中,正确的是( )
A.为了解全体学生的视力,对每位学生都进行视力检查是普查
B.全校学生上学的交通方式是定量数据
C.为调查小区1500户家庭用水情况,抽取该小区100户家庭,样本容量为1500
D.射线AB和射线BA表示同一条射线
3.(2024秋 新城区校级期末)下列说法中,正确的是( )
A.西安市每年参加中考的人数是定性数据
B.了解航天飞机升空前的安全检查,采用抽样调查
C.了解西安市的中学生保护水资源的意识,采用抽样调查
D.了解西安市民乘坐地铁8号线的情况,采用全面调查
4.(2024秋 泉港区期末)为了解动车经过各站后,乘车人数的变化情况,最适合使用的统计图是( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.以上三种都可以
5.(2024秋 永春县期末)在数字“82003018”中,数字“8”出现的频率为( )
A. B. C. D.2
6.(2024秋 兰州期末)在一个不透明的口袋中,放置2个黄球,1个白球,1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了蓝球出现的频率(如图所示),则n的值最可能是( )
A.4 B.5 C.6 D.7
7.(2024秋 市北区期末)下列说法正确的是( )
A.全班同学的上学交通方式是定量数据
B.某池塘中现有鱼的数量是定性数据
C.全班同学家养宠物的种类是定量数据
D.某公司职工的学历是定性数据
8.(2024秋 瑶海区期末)下列说法最恰当的是( )
A.某校对学生进行体育达标测试,应采用抽样调查法
B.了解我省中学生的身高状况采用抽样调查法
C.要了解某班级学生期中数学测试成绩采用抽样调查法
D.某工厂质检人员检测灯泡的使用寿命采用普查法
9.(2024秋 海伦市期末)某小学六年级有学生800人,每人只能参加一项延时服务,根据如图扇形统计图,求出参加绘画组的有( )人.
A.120 B.160 C.180 D.324
10.(2024秋 紫金县期末)如图是某地某天气温变化情况的折线图,下列描述正确的是( )
A.最低温度是9℃
B.有3时的气温超过了20℃
C.从14时到24时温度在持续下降
D.这一天的温差是14℃
二.填空题(共5小题)
11.(2024秋 市北区期末)雷达图(RadarChart),又可称为戴布拉图、蜘蛛网图(SpiderChart),原先是财务分析报表的一种,现可用于对研究对象的多维分析,如图为甲、乙两人在五个方面评价值的雷达图,则下列说法正确的是 .(填序号)
①甲、乙两人在次要能力方面的表现基本相同;
②甲在沟通、运动、创新三个方面的表现优于乙;
③在领导力方面,甲的评价值是0.
12.(2024秋 鲤城区校级期末)在英文“We like math”句中,字母“e”出现的频率为 .
13.(2024秋 建湖县期末)已知一个样本中,50个数据分别落在5个组内,第一、二、四、五组数据的个数分别为2,8,20,5,则第三组的频率为 .
14.(2024秋 泉港区期末)小明在抛一枚正六面体骰子的实验中,共抛了10次骰子,掷得3次“六点”向上.则该实验中,掷得“六点”向上的频率是 .
15.(2024秋 四平期末)某林业局将一种树苗移植成活的情况绘制成如图所示的折线统计图,由此可估计这种树苗移植1200棵,成活的大约有 棵.
三.解答题(共5小题)
16.(2024秋 沙坪坝区校级期末)为推动《关于全面实施学校美育浸润行动》,强化中小学美育育人工作,重庆市教育督导委员会开展了中小学艺术测评工作.督导组在某中学的艺术测评成绩中随机抽取了七、八年级各25名学生的艺术测评成绩(百分制),并对其数据进行整理、描述、分析.所有评分均不低于60分,且没有满分(评分分数用x表示,共分为四组:A:90≤x<100,B:80≤x<90,C:70≤x<80,D:60≤x<70),90分及以上评为优秀.下面给出部分信息:
抽取的七年级学生的艺术测评成绩为:
66,68,71,71,73,76,79,82,84,84,85,85,85,85,86,88,88,89,89,89,93,95,96,96,97.
抽取的八年级学生的艺术测评成绩中,B组包含的所有数据为:80,82,85,85,86,87,87,87,87,87,87,87.
抽取的七、八年级学生的艺术测评成绩统计表:
年级 平均数 中位数 众数 优秀率
七年级 84 85 a 20%
八年级 84 b 87 m%
(1)填空并补全条形统计图:a= ,b= ,m= .
(2)根据以上数据,你认为哪个年级的美育教育推动得更好?说明理由(写出一条即可);
(3)若该校参加测评的七年级学生有由400名,八年级学生有500名,规定成绩达到80分及以上即为合格,估计本次测评该校七、八年级合格是总人数大约有多少?
17.(2024秋 泉港区期末)某科研单位对八年级学生“拥有理想和信念”进行问卷调查,采取随机抽样的方式进行问卷调查,结果分为五类:A.有短期理想,且信念坚定;B.有短期理想,但信念不够坚定;C.有长远的理想,且信念坚定;D.有长远的理想,但信念不够坚定;E.没有理想或者根本没有想过.(要求:本问卷为单选题,请不要多选或漏选).根据调查数据结果绘制成以下两幅不完整的统计图:
(1)试求出调查的总人数;
(2)若该区共有八年级学生2800名,请根据调查结果估计,该区八年级学生中以“C.有长远的理想,且信念坚定”为拥有理想和信念的人数约为多少?
18.(2024秋 本溪期末)为了丰富学校文化氛围,促进学生综合素质发展,增强学生的学习动力和求知欲,增强师生之间归属感和凝聚力.某校准备成立校园广播站,有20名学生报名参加选拔,报名选手需参加综合知识,语言,写作三项测试(每项测试满分100分,打分为整数),然后将三项测试的成绩按4:4:2的比例计算出最后每人的总评成绩,其中,语言测试由七位评委打分,取评委打分的平均分作为该项测试的成绩.下面是这20名选手的总评成绩频数分布直方图(每组含最小值,不含最大值).
总评成绩频数分布直方图:
小明和小亮两位选手的三项测试成绩如下表:
选手 测试成绩/分 总评成绩/分
综合知识 语言 写作
小明 83 72 80 78
小亮 86 84
(1)在语言测试中,七位评委给小亮打出的分数(单位:分)如下:67,72,68,69,74,69,71.求这组数据的中位数;
(2)请你计算小亮的总评成绩;
(3)学校决定根据总评成绩择优选拔10名广播员,试分析小明,小亮能否入选?并说明理由.
19.(2024秋 长沙期末)“双减”政策实施后,某校为丰富学生的课余生活,开设了A篮球,B足球,C绘画,D舞蹈四类兴趣班.为了解学生对这四类兴趣班的喜爱情况,随机抽取该校部分学生进行了问卷调查,并将调查结果整理后绘制成两幅不完整的统计图.请根据统计图信息回答下列问题.
(1)本次抽取调查学生共有 人,估计该校3000名学生喜爱“舞蹈”兴趣班的人数约为 人.
(2)请将如图两个统计图补充完整.
(3)甲、乙两名学生要选择参加兴趣班,若他们每人从A,B,C,D四类兴趣班中随机选取一类,请用画树状图或列表法,求两人恰好选择同一类的概率.
20.(2024秋 济南期末)蔬菜种植是农业经济的重要组成部分,其产量的数据分析可优化农业种植决策,促进农业的可持续发展.某社团对2024年上半年20个地区蔬菜产量进行了调查,获得了各地区蔬菜产量(蔬菜产量用m表示,单位:万吨)的数据,并对数据进行统计整理.数据分成5组:A组:30≤m<40;B组:40≤m<50;C组:50≤m<60;D组:60≤m<70;E组:70≤m<80.
下面给出了部分信息:
a.C组的数据:51,56,56,54,55,58.
b.不完整的2024年上半年蔬菜产量的频数分布直方图和扇形统计图如下:
请根据以上信息完成下列问题:
(1)请补全频数分布直方图;
(2)C组数据的众数是 ;
(3)这20个地区2024年上半年蔬菜产量的中位数是 ;
(4)2024年上半年各组蔬菜平均产量如表:
组别 A.30≤m<40 B.40≤m<50 C.50≤m<60 D.60≤m<70 E.70≤m<80
平均产量(万吨) 35 43 55 68 74
求这20个地区2024年上半年蔬菜的平均产量.
2025年中考数学高频易错考前冲刺:数据收集与处理
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C C A C D B B C
一.选择题(共10小题)
1.(2024秋 德化县期末)某校开展“阅读助成长,课程蕴书香”活动,对全校学生每天的课外阅读时间进行了全面调查,根据收集的相关数据绘制成如图所示的扇形统计图.下列说法错误的是( )
A.每天阅读不足30分钟的学生人数最多
B.每天阅读30分钟以上的学生人数超过50%
C.每天阅读1小时以上的学生人数占20%
D.每天阅读30分钟至2小时的学生人数占50%
【考点】扇形统计图.
【专题】统计的应用;数据分析观念.
【答案】C
【分析】从扇形图中获取信息逐一分析判断即可.
【解答】解:A、每天阅读不足30分钟的学生人数最多,占总人数的40%,原说法正确,故选项不符合题意;
B、每天阅读30分钟以上的学生人数占60%,超过50%,原说法正确,故选项不符合题意;
C、每天阅读1小时以上的学生人数占10%+20%=30%,原说法错误,故选项符合题意;
D、每天阅读30分钟至2小时的学生人数占50%,原说法正确,故选项不符合题意.
故选:C.
【点评】本题考查了扇形统计图,解题的关键是正确从扇形图中获取信息.
2.(2024秋 温江区校级期末)以下说法中,正确的是( )
A.为了解全体学生的视力,对每位学生都进行视力检查是普查
B.全校学生上学的交通方式是定量数据
C.为调查小区1500户家庭用水情况,抽取该小区100户家庭,样本容量为1500
D.射线AB和射线BA表示同一条射线
【考点】全面调查与抽样调查.
【专题】数据的收集与整理;线段、角、相交线与平行线;应用意识.
【答案】A
【分析】分别根据全面调查与抽样调查,定量数据与定性数据,样本容量和射线的定义判断即可.
【解答】解:A、为了解全体学生的视力,对每位学生都进行视力检查是普查,故符合题意;
B、全校学生上学的交通方式是定性数据,故不符合题意;
C、样本容量为100,故不符合题意;
D、射线AB和射线BA表示不同的射线,故不符合题意;
故选:A.
【点评】本题考查了全面调查与抽样调查,定量数据与定性数据,样本容量和射线,掌握相关概念是解题的关键.
3.(2024秋 新城区校级期末)下列说法中,正确的是( )
A.西安市每年参加中考的人数是定性数据
B.了解航天飞机升空前的安全检查,采用抽样调查
C.了解西安市的中学生保护水资源的意识,采用抽样调查
D.了解西安市民乘坐地铁8号线的情况,采用全面调查
【考点】全面调查与抽样调查.
【专题】统计的应用;数据分析观念.
【答案】C
【分析】根据定性数据与定量数据的定义判断A选项;由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.再根据问卷调查方法即可判断B、C、D选项.
【解答】解:A.西安市每年参加中考的人数是定量数据,故本选项不符合题意;
B.了解航天飞机升空前的安全检查,采用全面调查,故本选项不符合题意;
C.了解西安市的中学生保护水资源的意识,采用抽样调查,故本选项符合题意;
D.了解西安市民乘坐地铁8号线的情况,采用抽样调查,故本选项不符合题意.
故选:C.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.(2024秋 泉港区期末)为了解动车经过各站后,乘车人数的变化情况,最适合使用的统计图是( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.以上三种都可以
【考点】统计图的选择.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目;频数分布直方图,清楚显示在各个不同区间内取值,各组频数分布情况,易于显示各组之间频数的差别.
【解答】解:为了解动车经过各站后,乘车人数的变化情况,最适合使用的统计图是折线统计图.
故选:C.
【点评】本题考查了统计图的选择,掌握各种统计图的特点是解答本题的关键.
5.(2024秋 永春县期末)在数字“82003018”中,数字“8”出现的频率为( )
A. B. C. D.2
【考点】频数与频率.
【专题】统计的应用;运算能力.
【答案】A
【分析】根据频率的计算公式:频率=频数÷总数,进行计算即可.
【解答】解:由题意知,数字“8”出现的频率是.
故选:A.
【点评】本题主要考查了频数与频率,掌握频率的计算方法.
6.(2024秋 兰州期末)在一个不透明的口袋中,放置2个黄球,1个白球,1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了蓝球出现的频率(如图所示),则n的值最可能是( )
A.4 B.5 C.6 D.7
【考点】频数(率)分布折线图.
【专题】概率及其应用;数据分析观念.
【答案】C
【分析】利用频率估计概率,由概率列方程求解即可.
【解答】解:由频率分布图可知,当实验的次数逐渐增大时,摸到蓝球的频率越稳定在0.6附近,
因此摸到蓝球的概率为0.6,
所以有0.6,
解得n=6.
经检验,n=6是原方程的解,
因此n最可能有6.
故选:C.
【点评】本题考查频率估计概率,理解频率、概率的意义和相互关系是正确解答的关键.
7.(2024秋 市北区期末)下列说法正确的是( )
A.全班同学的上学交通方式是定量数据
B.某池塘中现有鱼的数量是定性数据
C.全班同学家养宠物的种类是定量数据
D.某公司职工的学历是定性数据
【考点】调查收集数据的过程与方法.
【专题】数据的收集与整理;数据分析观念.
【答案】D
【分析】利用定量数据和定性数据的意义进行判断即可.
【解答】解:A、全班同学的上学交通方式是定性数据,故不符合题意;
B、某池塘中现有鱼的数量是定量数据,故不符合题意;
C、全班同学家养宠物的种类是定性数据,故不符合题意;
D、某公司职工的学历是定性数据,故符合题意.
故选:D.
【点评】本题考查了调查收集数据的过程与方程:正确理解定量数据和定性数据是解决问题的关键.
8.(2024秋 瑶海区期末)下列说法最恰当的是( )
A.某校对学生进行体育达标测试,应采用抽样调查法
B.了解我省中学生的身高状况采用抽样调查法
C.要了解某班级学生期中数学测试成绩采用抽样调查法
D.某工厂质检人员检测灯泡的使用寿命采用普查法
【考点】全面调查与抽样调查.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】一些调查项目并不适合普查,其一,调查者能力有限,不能进行普查;其二,调查过程带有破坏性;其三,有些被调查的对象无法进行普查.
【解答】解:A、某校对学生进行体育达标测试,应采用全面调查法,故本选项说法不恰当,不符合题意;
B、了解我省中学生的身高状况采用抽样调查法,本选项说法恰当,符合题意;
C、要了解某班级学生期中数学测试成绩采用全面调查法,故本选项说法不恰当,不符合题意;
D、某工厂质检人员检测灯泡的使用寿命采用抽样调查法,故本选项说法不恰当,不符合题意;
故选:B.
【点评】本题考查的是抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
9.(2024秋 海伦市期末)某小学六年级有学生800人,每人只能参加一项延时服务,根据如图扇形统计图,求出参加绘画组的有( )人.
A.120 B.160 C.180 D.324
【考点】扇形统计图.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】根据有学生800人和绘画组所占的百分比即可得出答案.
【解答】解:参加绘画组的有:800×(1﹣54%﹣26%)=160(人),
故选:B.
【点评】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
10.(2024秋 紫金县期末)如图是某地某天气温变化情况的折线图,下列描述正确的是( )
A.最低温度是9℃
B.有3时的气温超过了20℃
C.从14时到24时温度在持续下降
D.这一天的温差是14℃
【考点】折线统计图.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】从折线图中有效的获取信息,逐一进行判断即可.
【解答】解:A、最低温度是6℃,不是9℃,原选项说法错误,不符合题意;
B、小于3时的气温超过了20,原选项说法错误,不符合题意;
C、原选项说法正确,符合题意;
D、温差是用最高温度减去最低温度可得:22﹣6=16℃,原选项说法错误,不符合题意;
故选:C.
【点评】本题考查折线统计图,正确记忆相关知识点是解题关键.
二.填空题(共5小题)
11.(2024秋 市北区期末)雷达图(RadarChart),又可称为戴布拉图、蜘蛛网图(SpiderChart),原先是财务分析报表的一种,现可用于对研究对象的多维分析,如图为甲、乙两人在五个方面评价值的雷达图,则下列说法正确的是 ①② .(填序号)
①甲、乙两人在次要能力方面的表现基本相同;
②甲在沟通、运动、创新三个方面的表现优于乙;
③在领导力方面,甲的评价值是0.
【考点】其他统计图.
【专题】统计的应用;数据分析观念.
【答案】①②.
【分析】实线代表甲的能力数值,虚线代表乙的能力数值,越往外圈能力数值越大,分别比较甲乙两人在次要能力、沟通、运动、创新、领导力的数值情况即可得到答案.
【解答】解:从图中可以看出甲、乙两人在次要能力方面的表现基本相同;
甲在沟通、运动、创新三个方面的表现优于乙;
在领导力方面,甲的评价值是20,
故答案为:①②.
【点评】本题考查了其它统计图,对数据的分析处理能力及进行简单的合情推理是解题的关键.
12.(2024秋 鲤城区校级期末)在英文“We like math”句中,字母“e”出现的频率为 0.2 .
【考点】频数与频率.
【专题】统计的应用;运算能力.
【答案】0.2.
【分析】用字母“e”出现的个数除以总的字母个数即可得出答案.
【解答】解:∵字母“e”出现的次数为2,总共10个字母,
∴字母“e”出现的频率为0.2.
故答案为:0.2.
【点评】此题主要考查了频数与频率,关键是掌握频率的定义,频率=频数÷数据总数.
13.(2024秋 建湖县期末)已知一个样本中,50个数据分别落在5个组内,第一、二、四、五组数据的个数分别为2,8,20,5,则第三组的频率为 0.3 .
【考点】频数与频率.
【专题】统计的应用;运算能力.
【答案】0.3.
【分析】根据频率=频数÷总数进行计算即可.
【解答】解:∵第三组的频数为50﹣2﹣8﹣20﹣5=15,
∴第三组的频率0.3.
故答案为:0.3.
【点评】本题考查了频数与频率,解答本题的关键是掌握频数、总数与频率的关系.
14.(2024秋 泉港区期末)小明在抛一枚正六面体骰子的实验中,共抛了10次骰子,掷得3次“六点”向上.则该实验中,掷得“六点”向上的频率是 0.3 .
【考点】频数与频率.
【专题】统计的应用;数据分析观念.
【答案】0.3.
【分析】根据频率的概念计算即可.
【解答】解:∵共抛了10次骰子,掷得3次“六点”向上,
∴掷得“六点”向上的频率是:3÷10=0.3,
故答案为:0.3.
【点评】本题考查的是频数与频率,频率是指每个对象出现的次数与总次数的比值.
15.(2024秋 四平期末)某林业局将一种树苗移植成活的情况绘制成如图所示的折线统计图,由此可估计这种树苗移植1200棵,成活的大约有 960 棵.
【考点】折线统计图;用样本估计总体.
【专题】统计与概率;数据分析观念.
【答案】见试题解答内容
【分析】根据图形可以发现,在0.8附近波动,从而可以估计这种树苗移植成活的概率,再根据概率总体数量即可.
【解答】解:这种树苗移植1200棵,成活的大约有:1200×0.8=960(棵),
故答案为:960.
【点评】本题考查折线统计图,利用样本的频率估计总体,正确记忆相关知识点是解题关键.
三.解答题(共5小题)
16.(2024秋 沙坪坝区校级期末)为推动《关于全面实施学校美育浸润行动》,强化中小学美育育人工作,重庆市教育督导委员会开展了中小学艺术测评工作.督导组在某中学的艺术测评成绩中随机抽取了七、八年级各25名学生的艺术测评成绩(百分制),并对其数据进行整理、描述、分析.所有评分均不低于60分,且没有满分(评分分数用x表示,共分为四组:A:90≤x<100,B:80≤x<90,C:70≤x<80,D:60≤x<70),90分及以上评为优秀.下面给出部分信息:
抽取的七年级学生的艺术测评成绩为:
66,68,71,71,73,76,79,82,84,84,85,85,85,85,86,88,88,89,89,89,93,95,96,96,97.
抽取的八年级学生的艺术测评成绩中,B组包含的所有数据为:80,82,85,85,86,87,87,87,87,87,87,87.
抽取的七、八年级学生的艺术测评成绩统计表:
年级 平均数 中位数 众数 优秀率
七年级 84 85 a 20%
八年级 84 b 87 m%
(1)填空并补全条形统计图:a= 85 ,b= 87 ,m= 24 .
(2)根据以上数据,你认为哪个年级的美育教育推动得更好?说明理由(写出一条即可);
(3)若该校参加测评的七年级学生有由400名,八年级学生有500名,规定成绩达到80分及以上即为合格,估计本次测评该校七、八年级合格是总人数大约有多少?
【考点】频数(率)分布直方图;中位数;众数;用样本估计总体.
【专题】统计的应用;数据分析观念.
【答案】(1)85,87,24;
(2)八年级的美育教育推动得更好;
(3)648人.
【分析】(1)根据众数和中位数的定义即可求出a、b,根据优秀率的计算公式即可求出m;
(2)根据中位数、众数以及优秀率的意义分析即可;
(3)用样本估计总体即可.
【解答】解:(1)∵七年级学生的艺术测评成绩中85出现的次数最多,
∴众数a=85,
∵样本容量为25,八年级学生的艺术测评成绩中最中间的数据为87,
∴中位数b=87,
八年级学生的艺术测评成绩高于90分的人数:25﹣12﹣4﹣3=6(人),
∴m%100%=24%,
∴m=24.
故答案为:85,87,24;
(2)八年级的美育教育推动得更好.
理由:∵两个年级的平均数相同,而八年级的优秀率高于七年级,
∴八年级的美育教育推动得更好;
(3)400500648(人),
答:估计本次测评该校七、八年级合格是总人数大约有648人.
【点评】本题考查条形统计图与扇形统计图,中位数,众数,用样本估计总体,从统计图获取有用的信息是解题的关键.
17.(2024秋 泉港区期末)某科研单位对八年级学生“拥有理想和信念”进行问卷调查,采取随机抽样的方式进行问卷调查,结果分为五类:A.有短期理想,且信念坚定;B.有短期理想,但信念不够坚定;C.有长远的理想,且信念坚定;D.有长远的理想,但信念不够坚定;E.没有理想或者根本没有想过.(要求:本问卷为单选题,请不要多选或漏选).根据调查数据结果绘制成以下两幅不完整的统计图:
(1)试求出调查的总人数;
(2)若该区共有八年级学生2800名,请根据调查结果估计,该区八年级学生中以“C.有长远的理想,且信念坚定”为拥有理想和信念的人数约为多少?
【考点】条形统计图;用样本估计总体;扇形统计图.
【专题】统计的应用;数据分析观念.
【答案】(1)100人;(2)980人.
【分析】(1)由B类的人数除以所占的百分比,即可求解;
(2)求出C类的占比,用八年级总人数乘以C类占比即可.
【解答】解:(1)15÷15%=100(人),
答:调查的总人数为100人;
(2)1﹣25%﹣15%﹣15%﹣10%=35%,
2800×35%=980(人),
答:以选择“C.有长远的理想,且信念坚定”的人数约为980人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
18.(2024秋 本溪期末)为了丰富学校文化氛围,促进学生综合素质发展,增强学生的学习动力和求知欲,增强师生之间归属感和凝聚力.某校准备成立校园广播站,有20名学生报名参加选拔,报名选手需参加综合知识,语言,写作三项测试(每项测试满分100分,打分为整数),然后将三项测试的成绩按4:4:2的比例计算出最后每人的总评成绩,其中,语言测试由七位评委打分,取评委打分的平均分作为该项测试的成绩.下面是这20名选手的总评成绩频数分布直方图(每组含最小值,不含最大值).
总评成绩频数分布直方图:
小明和小亮两位选手的三项测试成绩如下表:
选手 测试成绩/分 总评成绩/分
综合知识 语言 写作
小明 83 72 80 78
小亮 86 84
(1)在语言测试中,七位评委给小亮打出的分数(单位:分)如下:67,72,68,69,74,69,71.求这组数据的中位数;
(2)请你计算小亮的总评成绩;
(3)学校决定根据总评成绩择优选拔10名广播员,试分析小明,小亮能否入选?并说明理由.
【考点】频数(率)分布直方图;加权平均数;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)69分;
(2)81分;
(3)小亮总评成绩超过80分,能够入选;小明总评成绩没超过80分,不能入选.
【分析】(1)分别根据中位数的定义即可求出答案;
(2)根据加权平均数公式计算即可求解;
(3)根据20名学生的总评成绩频数分布直方图即可得出答案.
【解答】解:(1)将七位评委的分数从小到大排序:67,68,69,69,71,72,74,
排序后处在中间位置的数据是69分,
答:这组数据的中位数是69分;
(2)小亮语言这项测试的得分为:(67+68+69+69+71+72+74)=70(分),
∴(分).
答:小亮的总评成绩为81分;
(3)小明不能入选,小亮能入选.
∵由这20名选手的总评成绩频数分布直方图可知,分数小于80分的有10人,
又∵学校准备根据总评成绩择优选拔10名广播员,
∴小亮总评成绩超过80分,能够入选;小明总评成绩没超过80分,不能入选.
【点评】本题考查了频数分布直方图,加权平均数,中位数,解题的关键在于熟练掌握加权平均数,中位数的计算方法.
19.(2024秋 长沙期末)“双减”政策实施后,某校为丰富学生的课余生活,开设了A篮球,B足球,C绘画,D舞蹈四类兴趣班.为了解学生对这四类兴趣班的喜爱情况,随机抽取该校部分学生进行了问卷调查,并将调查结果整理后绘制成两幅不完整的统计图.请根据统计图信息回答下列问题.
(1)本次抽取调查学生共有 50 人,估计该校3000名学生喜爱“舞蹈”兴趣班的人数约为 300 人.
(2)请将如图两个统计图补充完整.
(3)甲、乙两名学生要选择参加兴趣班,若他们每人从A,B,C,D四类兴趣班中随机选取一类,请用画树状图或列表法,求两人恰好选择同一类的概率.
【考点】条形统计图;概率公式;列表法与树状图法;用样本估计总体;扇形统计图.
【答案】(1)50、300;(2)见解答;(3).
【分析】(1)根据B类型的人数及其占总人数的百分比可得被调查的总人数,用总人数乘以样本中D类型人数占被调查的总人数的百分比可得答案;
(2)用总人数乘以A类型对应的百分比可得其人数,据此可补全条形图,分别用C、D类型人数除以总人数求出其所占百分比即可补全扇形图;
(3)画树状图列出所有等可能结果,并从中找到两人恰好选择同一类的结果数,再根据概率公式求解即可.
【解答】解:(1)本次抽取调查学生共有15÷30%=50(人),
估计该校3000名学生喜爱“舞蹈”兴趣班的人数约为3000300(人),
故答案为:50、300;
(2)A类型人数为50×36%=18(人),C类型人数所占百分比为100%=24%,
补全图形如下:
(3)画树状图为:
共有16种等可能的结果数,其中两人恰好选中同一类的结果数为4,
所以两人恰好选择同一类的概率为.
【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.也考查了统计图.
20.(2024秋 济南期末)蔬菜种植是农业经济的重要组成部分,其产量的数据分析可优化农业种植决策,促进农业的可持续发展.某社团对2024年上半年20个地区蔬菜产量进行了调查,获得了各地区蔬菜产量(蔬菜产量用m表示,单位:万吨)的数据,并对数据进行统计整理.数据分成5组:A组:30≤m<40;B组:40≤m<50;C组:50≤m<60;D组:60≤m<70;E组:70≤m<80.
下面给出了部分信息:
a.C组的数据:51,56,56,54,55,58.
b.不完整的2024年上半年蔬菜产量的频数分布直方图和扇形统计图如下:
请根据以上信息完成下列问题:
(1)请补全频数分布直方图;
(2)C组数据的众数是 56 ;
(3)这20个地区2024年上半年蔬菜产量的中位数是 56 ;
(4)2024年上半年各组蔬菜平均产量如表:
组别 A.30≤m<40 B.40≤m<50 C.50≤m<60 D.60≤m<70 E.70≤m<80
平均产量(万吨) 35 43 55 68 74
求这20个地区2024年上半年蔬菜的平均产量.
【考点】频数(率)分布直方图;扇形统计图;加权平均数;中位数;众数.
【专题】统计的应用;数据分析观念.
【答案】(1)见解析;
(2)56;
(3)56;
(4)56.4万吨.
【分析】(1)求出B组和D组的频数,从而补全图形;
(2)根据众数的定义求解即可;
(3)根据中位数的定义求解即可;
(4)根据加权平均数的定义求解即可.
【解答】解:(1)B组的频数为204,
D组的频数为20﹣2﹣4﹣6﹣2=6,
补全图形如下:
(2)C组数据的众数是56,
故答案为:56;
(3)这20个地区2024年上半年蔬菜产量的中位数是56,
故答案为:56;
(4)(35×2+43×4+55×6+68×6+74×2)=56.4(万吨),
答:这20个地区2024年上半年蔬菜的平均产量是56.4万吨.
【点评】本题考查频数分布直方图、加权平均数、众数、中位数、扇形统计图等知识,掌握相关知识,利用数形结合思想是解题关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
