【中考押题卷】2025年中考数学高频易错考前冲刺:四边形(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学高频易错考前冲刺:四边形(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 00:00:00 | ||
图片预览




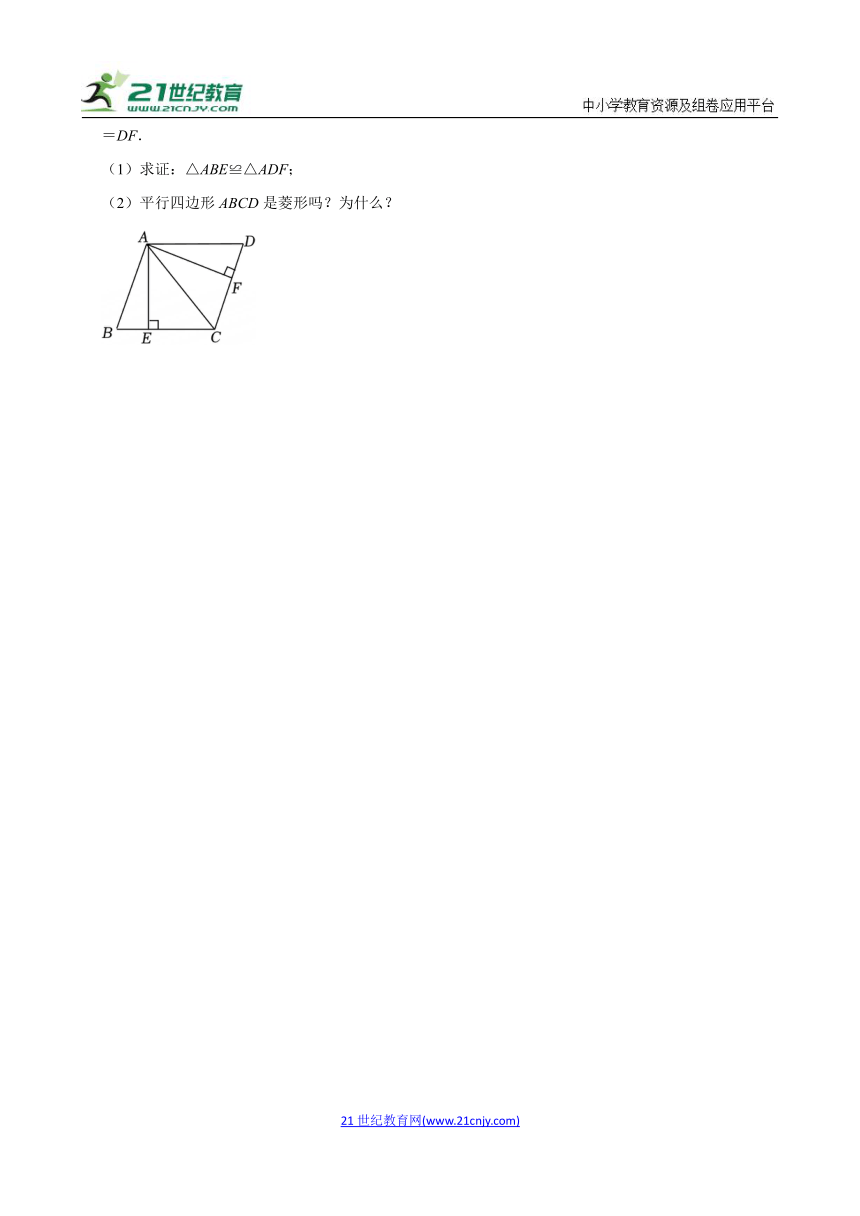
文档简介
2025年中考数学高频易错考前冲刺:四边形
一.选择题(共10小题)
1.(2024秋 南宁期末)“方寸之间,别有洞天”,我国古代建筑常采用花窗框景,让风景如同镶嵌在画框中的风景画.如图所示的窗框的外框形状是正八边形,则这个正八边形的内角和为( )
A.360° B.540° C.720° D.1080°
2.(2024秋 泰兴市期末)如图,把直角三角形拆解为一个正方形与两对全等的直角三角形.下面给出的条件中,一定能求出该直角三角形的面积的是( )
A.AD BD B.AI BD C.BI AD D.AI BI
3.(2024秋 宁波期末)由四个全等的直角三角形和一个小正方形组成的大正方形ABCD(如图所示),连结DF并延长交BC于点I,若,则tan∠BAE的值为( )
A. B. C. D.
4.(2025 嘉定区一模)如图,在直角梯形ABCD中,AD∥BC,∠D=90°,如果对角线AC⊥AB,那么的值是( )
A.sinB B.cosB C.tanB D.cotB
5.(2024秋 河西区期末)一个矩形的长和宽相差3cm,面积是4cm2,则这个矩形的周长为( )
A.6cm B.8cm C.10cm D.12cm
6.(2024秋 西山区期末)正八边形的内角和为( )
A.180° B.360° C.720° D.1080°
7.(2024秋 天府新区期末)矩形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角
8.(2024秋 英德市期末)如图,在矩形ABCD中,对角线AC,BD相交于点O,若AO=3,则BD的长为( )
A.3 B.4 C.5 D.6
9.(2024秋 郑州期末)下列说法中不正确的是( )
A.对角线相等的四边形是矩形
B.菱形既是轴对称图形又是中心对称图形
C.对角线互相垂直平分的四边形是菱形
D.正方形的四条边都相等
10.(2024秋 市北区期末)过某多边形一个顶点的所有对角线,将这个多边形分成4个三角形,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
二.填空题(共5小题)
11.(2024秋 本溪期末)过六边形的一个顶点能画出对角线的条数是 .
12.(2024秋 新城区校级期末)过一个多边形的一个顶点出发有4条对角线,这些对角线将这个多边形分成 个三角形.
13.(2024秋 东城区期末)已知正方形ABCD的边长为30cm.
(1)如图1,正方形ABCD各边的中点分别为E,F,G,H,依次连接四个中点,得到阴影部分.该阴影部分的面积为 cm2;
(2)如图2,点P1在边AB上,且.在正方形ABCD的四条边上截取BP2=BP3=CP4=CP5=DP6=DP7=AP8=AP1.连接P2P3,P4P5,P6P7,P8P1,得到阴影部分.设P1P2=x cm,则阴影部分的面积为 cm2(用含x的代数式表示).
14.(2024秋 汕尾期末)一个多边形的内角和等于1080°,这个多边形是 边形.
15.(2024秋 门头沟区期末)如果一个多边形的内角和等于外角和,那么该多边形的边数是 .
三.解答题(共5小题)
16.(2024秋 本溪期末)如图,△ABC中,AC=2AB,AD平分∠BAC,过点C作CE⊥AD交AD延长线于点E,点F是AC中点,连接EF,EB.
(1)证明:四边形ABEF是菱形;
(2)若∠BAC=120°,,求边BC的长.
17.(2024秋 贵阳期末)如图,在矩形ABCD中,AB=6,AD=4,点E是边BC上任意一点,连接AE,将△ABE沿直线AE折叠,点B的对应点B'恰好落在矩形的边CD上.
(1)直接写出图中AB',B′D的长;
(2)连接BB',判断AE与BB'的位置关系,并说明理由;
(3)在(2)的条件下,求的值.
18.(2024秋 高坪区期末)(1)如图1,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°.E、F两点分别是BC、CD上的点,且EF=BE+FD,试探究图中∠EAF与∠BAD的数量关系.
小王同学探究此题的方法是作辅助线:延长FD到点G,使DG=BE,连接AG.然后顺利的完成了此题的解答.请你按照他的方法写出解答过程.
(2)如图2,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD.若E、F分别在CB、CD的延长线上,且仍然满足EF=BE+FD,请直接写出∠EAF与∠BAD的数量关系.
19.(2025 浦东新区一模)在平行四边形ABCD中,对角线AC、BD交于点O,P是线段OC上一个动点(不与点O、点C重合),过点P分别作AD、CD的平行线,交CD于点E,交BC、BD于点F、G,联结EG.
(1)如图1,如果PC=2OP,求证:EG∥AC;
(2)如图2,如果∠ABC=90°,,且△DGE与△PCF相似,请补全图形,并求的值;
(3)如图3,如果BA=BG=BC,且射线EG过点A.请补全图形,并求∠ABC的度数.
20.(2024秋 贵阳期末)如图,在平行四边形ABCD中,AE⊥BC,AF⊥DC,垂足分别为E,F,且BE=DF.
(1)求证:△ABE≌△ADF;
(2)平行四边形ABCD是菱形吗?为什么?
2025年中考数学高频易错考前冲刺:四边形
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B A C D C D A C
一.选择题(共10小题)
1.(2024秋 南宁期末)“方寸之间,别有洞天”,我国古代建筑常采用花窗框景,让风景如同镶嵌在画框中的风景画.如图所示的窗框的外框形状是正八边形,则这个正八边形的内角和为( )
A.360° B.540° C.720° D.1080°
【考点】平面镶嵌(密铺);多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】D
【分析】根据多边形的内角和公式(n﹣2) 180°,列式进行计算即可得解.
【解答】解:内角和为(8﹣2) 180°=1080°.
故选:D.
【点评】本题考查了多边形的内角和,熟记内角和公式是解题的关键.
2.(2024秋 泰兴市期末)如图,把直角三角形拆解为一个正方形与两对全等的直角三角形.下面给出的条件中,一定能求出该直角三角形的面积的是( )
A.AD BD B.AI BD C.BI AD D.AI BI
【考点】正方形的性质;解直角三角形;三角形的面积;直角三角形全等的判定.
【专题】运算能力.
【答案】A
【分析】由题意可得:△ADI≌△AFI,△BDI≌△BEI,四边形IFCE是正方形,则AF=AD,BD=BE,IE=IF=EC=FC,设IE=IF=EC=FC=x,然后根据勾股定理列方程并整理可得x2+(AD+BD)x=AD BD,又该直角三角形的面积的是,整理得,将x2+(AD+BD)x=AD BD整体代入可得该直角三角形的面积的是AD BD,再结合选项即可解答.
【解答】解:由题意可得:△ADI≌△AFI,△BDI≌△BEI,四边形IFCE是正方形,
∴AF=AD,BD=BE,IE=IF=EC=FC,
设IE=IF=EC=FC=x,则AC=AF+x=AD+x,BC=BE+x=BD+x,AB=AD+BD,
∵AB2=BC2+AC2,
∴(AD+BD)2=(BD+x)2+(AD+x)2,整理为:x2+(AD+BD)x=AD BD,
∵直角三角形的面积是:
=AD BD.
∴当AD BD确定时,一定能求出该直角三角形的面积.
故选:A.
【点评】本题主要考查全等三角形的性质、正方形的性质、勾股定理等知识点,正确进行分析、推理成为解题的关键.
3.(2024秋 宁波期末)由四个全等的直角三角形和一个小正方形组成的大正方形ABCD(如图所示),连结DF并延长交BC于点I,若,则tan∠BAE的值为( )
A. B. C. D.
【考点】正方形的性质;相似三角形的判定与性质;解直角三角形;全等三角形的判定与性质.
【专题】图形的全等;矩形 菱形 正方形;图形的相似;几何直观;运算能力;推理能力.
【答案】B
【分析】过点I作IM⊥CF于点M,根据2,设BI=2a,IC=k,则BC=3k,依题意得DH∥BF∥IM,则△ICM和△BCF相似,进而得,设CM=a,IM=b,则BF=3b,CF=3a,BE=CF=DG=3a,FM=2a,EF=GF=3b﹣3a,再根据△IMF和△DGF相似得,则,由此得2a=b,a=﹣b(不合题意,舍去),则BE=3a,AE=BF=3b=6a,然后在Rt△ABE中,根据正切函数的定义即可得tan∠BAE的值.
【解答】解:过点I作IM⊥CF于点M,如图所示:
∵2,
设BI=2a,IC=k,
∴BC=BI+IC=3k,
依题意得:∠FGD=∠BFC=∠IMC=90°,
∴DH∥BF∥IM,
∴△ICM∽△BCF,
∴,
设CM=a,IM=b,则BF=3b,CF=3a,
∴BE=CF=DG=3a,FM=CF﹣CM=3a﹣a=2a,
∴EF=GF=BF﹣BE=3b﹣3a,
∵DH∥IM,
∴△IMF∽△DGF,
∴,
∴,
整理得:2a2+ab﹣b2=0,
∴(2a﹣b)(a+b)=0,
∴2a=b,a=﹣b(不合题意,舍去),
∴BE=3a,AE=BF=3b=6a,
在Rt△ABE中,tan∠BAE.
故选:B.
【点评】此题主要考查了正方形的性质,全等三角形的性质,相似三角形的判定与性质,解直角三角形,理解正方形的性质,全等三角形的性质,熟练掌握相似三角形的判定与性质,锐角三角函数的定义是解决问题的关键.
4.(2025 嘉定区一模)如图,在直角梯形ABCD中,AD∥BC,∠D=90°,如果对角线AC⊥AB,那么的值是( )
A.sinB B.cosB C.tanB D.cotB
【考点】直角梯形;相似三角形的判定与性质;解直角三角形;平行线的性质.
【专题】梯形;推理能力.
【答案】A
【分析】根据直角梯形得出∠D=90°,根据AD∥BC得出∠DAC=∠BCA,进而得出△ADC与△BAC相似,利用相似三角形的性质解答即可.
【解答】解:∵直角梯形ABCD,
∴∠D=90°,
∵AC⊥AB,
∴∠BAC=90°,
∵AD∥BC,
∴∠DAC=∠BCA,
∴△ADC∽△BAC,
∴,
故选:A.
【点评】此题考查直角梯形,关键是根据直角梯形得出∠D=90°解答.
5.(2024秋 河西区期末)一个矩形的长和宽相差3cm,面积是4cm2,则这个矩形的周长为( )
A.6cm B.8cm C.10cm D.12cm
【考点】矩形的性质;一元二次方程的应用.
【专题】一元二次方程及应用;矩形 菱形 正方形;应用意识.
【答案】C
【分析】设矩形的宽为x cm,则长为(x+3)cm,根据矩形的面积计算公式列出方程求出x的值,进而根据矩形的周长公式计算即可.
【解答】解:设矩形的宽为x cm,则长为(x+3)cm,
根据题意,得x(x+3)=4,
解得:x1=﹣4(不合题意,舍去),x2=1,
所以x=1,x+3=4,
则这个矩形的周长为2(4+1)=10(cm).
答:这个矩形的周长为10cm.
故选:C.
【点评】此题主要考查了矩形的性质,一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
6.(2024秋 西山区期末)正八边形的内角和为( )
A.180° B.360° C.720° D.1080°
【考点】多边形内角与外角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】根据多边形的内角和公式:(n﹣2) 180°计算即可.
【解答】解:正八边形的内角和为(8﹣2)×180°=1080°,
故选:D.
【点评】本题考查了多边形的内角与外角,掌握多边形的内角和公式:(n﹣2) 180°是解题的关键.
7.(2024秋 天府新区期末)矩形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角
【考点】矩形的性质;菱形的性质.
【专题】矩形 菱形 正方形;推理能力.
【答案】C
【分析】利用矩形与菱形的性质即可解答本题.
【解答】解:矩形具有而菱形不一定具有的性质是对角线相等,
故选:C.
【点评】本题考查了矩形与菱形的性质,中心对称图形,解题的关键是熟练掌握矩形与菱形的性质.
8.(2024秋 英德市期末)如图,在矩形ABCD中,对角线AC,BD相交于点O,若AO=3,则BD的长为( )
A.3 B.4 C.5 D.6
【考点】矩形的性质.
【专题】矩形 菱形 正方形;推理能力.
【答案】D
【分析】根据矩形的性质得出AC=BD,AO=CO,求出AC,再求出BD即可.
【解答】解:∵四边形ABCD是矩形,
∴AC=BD,AO=CO,
∵AO=3,
∴CO=3,
∴AC=3+3=6,
∴BD=AC=6,
故选:D.
【点评】本题考查了矩形的性质,能熟记矩形的对角线互相平分且相等是解此题的关键.
9.(2024秋 郑州期末)下列说法中不正确的是( )
A.对角线相等的四边形是矩形
B.菱形既是轴对称图形又是中心对称图形
C.对角线互相垂直平分的四边形是菱形
D.正方形的四条边都相等
【考点】矩形的判定;正方形的性质;菱形的判定.
【专题】矩形 菱形 正方形;推理能力.
【答案】A
【分析】根据矩形的判定方法、菱形的性质、菱形的判定方法以及正方形的性质进行解答即可.
【解答】解:A、对角线相等的平行四边形是矩形,原说法不正确;
B、菱形既是轴对称图形又是中心对称图形,原说法正确;
C、对角线互相垂直平分的四边形是菱形,原说法正确;
D、正方形的四条边都相等,原说法正确;
故选:A.
【点评】本题主要考查了矩形的判定方法、菱形的性质、菱形的判定方法以及正方形的性质,属于基础题.
10.(2024秋 市北区期末)过某多边形一个顶点的所有对角线,将这个多边形分成4个三角形,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
【考点】多边形的对角线;多边形.
【专题】多边形与平行四边形;运算能力.
【答案】C
【分析】根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成(n﹣2)个三角形,依此可得n的值.
【解答】解:设这个多边形是n边形,
由题意得,n﹣2=4,
解得:n=6,
即这个多边形是六边形,
故选:C.
【点评】本题考查了多边形的对角线,解题的关键是掌握n边形从一个顶点出发可引出(n﹣3)条对角线,可组成(n﹣2)个三角形.
二.填空题(共5小题)
11.(2024秋 本溪期末)过六边形的一个顶点能画出对角线的条数是 3 .
【考点】多边形的对角线.
【专题】多边形与平行四边形;推理能力.
【答案】3.
【分析】根据从一个n边形一个顶点出发,可以连的对角线的条数是(n﹣3)进行计算即可.
【解答】解:根据题意,引对角线的数量为:6﹣3=3 (条),
所以从六边形的一个顶点能画出对角线的条数是3,
故答案为:3.
【点评】本题主要考查了多边形的对角线,解答此类题目的关键是正确记忆一个n边形一个顶点出发,可以连的对角线的条数是n﹣3.
12.(2024秋 新城区校级期末)过一个多边形的一个顶点出发有4条对角线,这些对角线将这个多边形分成 5 个三角形.
【考点】多边形的对角线.
【专题】多边形与平行四边形;运算能力.
【答案】5.
【分析】根据过n边形的一个顶点,可以引出(n﹣3)条对角线,这些对角线把该多边形分成(n﹣2)个三角形,即可求解.
【解答】解:由题意可得:该多边形的边数为4+3=7,
∴这些对角线将这个多边形分成三角形的个数为7﹣2=5(个).
故答案为:5.
【点评】本题考查多边形对角线,解题关键是熟练掌握过n边形一个顶点有(n﹣3)条对角线,这些对角线将这个n边形分成(n﹣2)个三角形.
13.(2024秋 东城区期末)已知正方形ABCD的边长为30cm.
(1)如图1,正方形ABCD各边的中点分别为E,F,G,H,依次连接四个中点,得到阴影部分.该阴影部分的面积为 450 cm2;
(2)如图2,点P1在边AB上,且.在正方形ABCD的四条边上截取BP2=BP3=CP4=CP5=DP6=DP7=AP8=AP1.连接P2P3,P4P5,P6P7,P8P1,得到阴影部分.设P1P2=x cm,则阴影部分的面积为 cm2(用含x的代数式表示).
【考点】中点四边形;列代数式.
【专题】实数;运算能力.
【答案】450;.
【分析】(1)利用正方形ABCD的面积减去四个三角形面积即可得到阴影部分的面积;
(2)利用正方形ABCD的面积减去四个三角形面积即可得到阴影部分的面积.
【解答】解:(1)根据题意可知:AE=BE=BF=CF=CG=DG=DH=AH=5×30=15cm,
∴阴影部分的面积为:,
故答案为:450;
(2)根据题意可知:
,
∴阴影部分的面积为:,
故答案为:.
【点评】本题主要考查了中点四边形、四则混合运算的实际应用、列代数式等知识点,根据题中的面积关系正确列出算式或代数式是解题的关键.
14.(2024秋 汕尾期末)一个多边形的内角和等于1080°,这个多边形是 8 边形.
【考点】多边形内角与外角.
【答案】见试题解答内容
【分析】多边形的内角和可以表示成(n﹣2) 180°,依此列方程可求解.
【解答】解:设所求正n边形边数为n,
则1080°=(n﹣2) 180°,解得n=8.
故答案为:8.
【点评】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
15.(2024秋 门头沟区期末)如果一个多边形的内角和等于外角和,那么该多边形的边数是 4 .
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】4.
【分析】根据多边形内角和与外角和的关系列方程求解即可.
【解答】解:设这个多边形为n边形,由题意得,
(n﹣2)×180°=360°,
解得n=4,
故答案为:4.
【点评】本题考查多边形的内角与外角,掌握多边形内角和的计算方法是正确解答的关键.
三.解答题(共5小题)
16.(2024秋 本溪期末)如图,△ABC中,AC=2AB,AD平分∠BAC,过点C作CE⊥AD交AD延长线于点E,点F是AC中点,连接EF,EB.
(1)证明:四边形ABEF是菱形;
(2)若∠BAC=120°,,求边BC的长.
【考点】菱形的判定与性质;角平分线的性质;等腰三角形的判定与性质;直角三角形斜边上的中线;三角形中位线定理.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;运算能力;推理能力.
【答案】(1)证明见解析;
(2)BC=14.
【分析】(1)由直角三角形的性质得,则∠FAE=∠FEA,又AC=2AB,则AB=AF=EF,从而证明BA∥EF,即可证明四边形ABEF是平行四边形,再由菱形的判定方法即可求证;
(2)作BH⊥AC交CA延长线于点H,则∠AHB=90°,通过勾股定理即可求解.
【解答】(1)证明:∵CE⊥AE,
∴∠AEC=90°,
∵点F是AC中点,
∴,
∴∠FAE=∠FEA,
∵AC=2AB,
∴AB=AF=EF,
∵AD平分∠BAC,
∴∠BAE=∠FAE,
∴∠BAE=∠FEA,
∴BA∥EF,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形;
(2)解:作BH⊥AC交CA延长线于点H,则∠AHB=90°,
∵∠BAC=120°,
∴∠BAH=60°,
∴∠ABH=30°,
∴,
∵AC=2AB,
∴,
∴,
∴由勾股定理得:,
在Rt△BCH中,由勾股定理得:,
∴BC的长为14.
【点评】本题考查了平行四边形的判定,菱形的判定,等角对等边,直角三角形的性质,勾股定理,掌握知识点的应用是解题的关键.
17.(2024秋 贵阳期末)如图,在矩形ABCD中,AB=6,AD=4,点E是边BC上任意一点,连接AE,将△ABE沿直线AE折叠,点B的对应点B'恰好落在矩形的边CD上.
(1)直接写出图中AB',B′D的长;
(2)连接BB',判断AE与BB'的位置关系,并说明理由;
(3)在(2)的条件下,求的值.
【考点】四边形综合题.
【专题】几何综合题;运算能力;推理能力.
【答案】(1)2;
(2)AE⊥BB′,理由见解析;
(3).
【分析】(1)根据矩形的性质的∠D=90°,根据折叠的性质得到AB=AB′=6,根据勾股定理得到DB′2;
(2)如图,连接BB′交AE于H,根据折叠的性质得到AB=AB′,∠BAH=∠B′AH,根据全等三角形的性质得到∠AHB=∠AHB′,根据垂直的定义得到AE⊥BB′;
(3)根据矩形的性质得到∠C=∠ABE=90°,求得∠BAE=∠CBB′,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:(1)∵四边形ABCD是矩形,
∴∠D=90°,
∵将△ABE沿直线AE折叠,
∴AB=AB′=6,
∴DB′2;
(2)AE⊥BB′,
理由:如图,连接BB′交AE于H,
∵将△ABE沿直线AE折叠,
∴AB=AB′,∠BAH=∠B′AH,
在△ABH与△AB′H中,
,
∴∠AHB=∠AHB′,
∵∠AHB+∠AHB′=180°,
∴∠AHB=90°,
∴AE⊥BB′;
(3)∵四边形ABCD是矩形,
∴∠C=∠ABE=90°,
∵∠AHB=90°,
∴∠BAH+∠ABH=∠ABH+∠CBH=90°,
∴∠BAE=∠CBB′,
∴△ABE∽△BCB′,
∴.
【点评】本题是四边形的综合题,考查了全等三角形的判定和性质,折叠的性质,矩形的性质,相似三角形的判定和性质,熟练掌握各知识点是解题的关键.
18.(2024秋 高坪区期末)(1)如图1,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°.E、F两点分别是BC、CD上的点,且EF=BE+FD,试探究图中∠EAF与∠BAD的数量关系.
小王同学探究此题的方法是作辅助线:延长FD到点G,使DG=BE,连接AG.然后顺利的完成了此题的解答.请你按照他的方法写出解答过程.
(2)如图2,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD.若E、F分别在CB、CD的延长线上,且仍然满足EF=BE+FD,请直接写出∠EAF与∠BAD的数量关系.
【考点】四边形综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)∠BAD=2∠EAF;理由见解答过程;
(2)∠BAD=360°﹣2∠EAF;理由见解答过程.
【分析】(1)延长FD到点G,使DG=BE,连接AG,可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF,据此得出结论;
(2)在DC延长线上取一点G,使得DG=BE,连接AG,先判定△ADG≌△ABE,再判定△AEF≌△AGF,得出∠FAE=∠FAG,最后根据∠FAE+∠FAG+∠GAE=360°,推导得到2∠FAE+∠DAB=360°,即可得出结论.
【解答】解:(1)∠BAD=2∠EAF;理由如下:
在四边形ABCD中,AB=AD,如图1,延长FD到点G,使DG=BE,连接AG,
在△ABE和△ADG中,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,AE=AG,
∵EF=BE+DF,DG=BE,
∴EF=BE+DF=DG+DF=GF,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SSS),
∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF,
∴∠BAD=2∠EAF;
(2)∠BAD=360°﹣2∠EAF;理由如下:
如图2,在DC延长线上取一点G,使得DG=BE,连接AG,
∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∴∠ADC=∠ABE,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AG=AE,∠DAG=∠BAE,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SSS),
∴∠FAE=∠FAG,
∵∠FAE+∠FAG+∠GAE=360°
∴2∠FAE+(∠GAB+∠BAE)=360°,
∴2∠FAE+(∠GAB+∠DAG)=360°,
即2∠FAE+∠BAD=360°,
∴∠BAD=360°﹣2∠EAF.
【点评】本题属于四边形综合题,主要考查了全等三角形的判定以及全等三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应角相等进行推导变形.解题时注意:同角的补角相等.
19.(2025 浦东新区一模)在平行四边形ABCD中,对角线AC、BD交于点O,P是线段OC上一个动点(不与点O、点C重合),过点P分别作AD、CD的平行线,交CD于点E,交BC、BD于点F、G,联结EG.
(1)如图1,如果PC=2OP,求证:EG∥AC;
(2)如图2,如果∠ABC=90°,,且△DGE与△PCF相似,请补全图形,并求的值;
(3)如图3,如果BA=BG=BC,且射线EG过点A.请补全图形,并求∠ABC的度数.
【考点】四边形综合题.
【专题】多边形与平行四边形;矩形 菱形 正方形;图形的相似;推理能力.
【答案】(1)证明见解析;
(2);
(3)72°.
【分析】(1)由平行四边形的性质证出,得出,则可得出结论;
(2)证明△DGE∽△PFC∽△ABC,设CE=4k,那么PE=6k,PG=9k,得出,DE=13k.求出,则可得出答案;
(3)由题意画出图形,证明平行四边形ABCD为菱形.设FB=FG=a,PF=FC=CE=b,求出,得出,证明△DGA∽△DAB.设∠DAG=∠DBA=∠ADB=α,那么∠BAG=∠BGA=2α.求出α=36°,则可得出答案.
【解答】(1)证明:∵PC=2PO,PG∥CD,
∴,
在平行四边形ABCD中,OA=OC,
∴,
又∵PE∥AD,
∴,
∴,
∴EG∥OC;
(2)解:如图2,
∵∠ABC=90°,
∴平行四边形ABCD为矩形.
∴OC=OD,
∴∠GDE=∠PCE=∠CPF,
又∵∠CFP=∠ABC=90°,且∠DEG<90°,
∴只能∠DGE=90°,∠DEG=∠PGE=∠PCF.
∴此时有:△DGE∽△PFC∽△ABC,
设CE=4k,那么PE=6k,PG=9k,
∴EG3k,DE=13k.
∴,
∴;
(3)解:补全图形如下,
∵BA=BC,
∴平行四边形ABCD为菱形.
设FB=FG=a,PF=FC=CE=b,
∴GP=a﹣b.
∵GP∥CE,
∴,
∴,
∴a2﹣ab﹣b2=0,
∴,
∴(负根已舍).
∴,
∴,
∴,
又∵∠ADG=∠BDA,
∴△DGA∽△DAB.
∴设∠DAG=∠DBA=∠ADB=α,那么∠BAG=∠BGA=2α.
∴5α=180°,
∴α=36°,
∴∠ABC=72°.
【点评】本题属于四边形综合题,考查了矩形的判定与性质,平行四边形的性质,菱形的判定与性质,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,属于中考压轴题.
20.(2024秋 贵阳期末)如图,在平行四边形ABCD中,AE⊥BC,AF⊥DC,垂足分别为E,F,且BE=DF.
(1)求证:△ABE≌△ADF;
(2)平行四边形ABCD是菱形吗?为什么?
【考点】菱形的判定;全等三角形的判定与性质;平行四边形的性质.
【专题】图形的全等;多边形与平行四边形;矩形 菱形 正方形;推理能力.
【答案】(1)证明见解答;
(2)平行四边形ABCD是菱形,理由见解答.
【分析】(1)由平行四边形的性质得∠B=∠D,由AE⊥BC于点E,AF⊥DC于点F,得∠AEB=∠AFD=90°,而BE=DF,即可根据“ASA”证明△ABE≌△ADF;
(2)由全等三角形的性质得AB=AD,而四边形ABCD是平行四边形,即可根据菱形的定义证明平行四边形ABCD是菱形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC于点E,AF⊥DC于点F,
∴∠AEB=∠AFD=90°,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA).
(2)解:平行四边形ABCD是菱形,
理由:由(1)得△ABE≌△ADF,
∴AB=AD,
∵四边形ABCD是平行四边形,且AB=AD,
∴平行四边形ABCD是菱形.
【点评】此题重点考查平行四边形的性质、全等三角形的判定与性质、菱形的定义等知识,推导出∠B=∠D,∠AEB=∠AFD,进而证明△ABE≌△ADF是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2024秋 南宁期末)“方寸之间,别有洞天”,我国古代建筑常采用花窗框景,让风景如同镶嵌在画框中的风景画.如图所示的窗框的外框形状是正八边形,则这个正八边形的内角和为( )
A.360° B.540° C.720° D.1080°
2.(2024秋 泰兴市期末)如图,把直角三角形拆解为一个正方形与两对全等的直角三角形.下面给出的条件中,一定能求出该直角三角形的面积的是( )
A.AD BD B.AI BD C.BI AD D.AI BI
3.(2024秋 宁波期末)由四个全等的直角三角形和一个小正方形组成的大正方形ABCD(如图所示),连结DF并延长交BC于点I,若,则tan∠BAE的值为( )
A. B. C. D.
4.(2025 嘉定区一模)如图,在直角梯形ABCD中,AD∥BC,∠D=90°,如果对角线AC⊥AB,那么的值是( )
A.sinB B.cosB C.tanB D.cotB
5.(2024秋 河西区期末)一个矩形的长和宽相差3cm,面积是4cm2,则这个矩形的周长为( )
A.6cm B.8cm C.10cm D.12cm
6.(2024秋 西山区期末)正八边形的内角和为( )
A.180° B.360° C.720° D.1080°
7.(2024秋 天府新区期末)矩形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角
8.(2024秋 英德市期末)如图,在矩形ABCD中,对角线AC,BD相交于点O,若AO=3,则BD的长为( )
A.3 B.4 C.5 D.6
9.(2024秋 郑州期末)下列说法中不正确的是( )
A.对角线相等的四边形是矩形
B.菱形既是轴对称图形又是中心对称图形
C.对角线互相垂直平分的四边形是菱形
D.正方形的四条边都相等
10.(2024秋 市北区期末)过某多边形一个顶点的所有对角线,将这个多边形分成4个三角形,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
二.填空题(共5小题)
11.(2024秋 本溪期末)过六边形的一个顶点能画出对角线的条数是 .
12.(2024秋 新城区校级期末)过一个多边形的一个顶点出发有4条对角线,这些对角线将这个多边形分成 个三角形.
13.(2024秋 东城区期末)已知正方形ABCD的边长为30cm.
(1)如图1,正方形ABCD各边的中点分别为E,F,G,H,依次连接四个中点,得到阴影部分.该阴影部分的面积为 cm2;
(2)如图2,点P1在边AB上,且.在正方形ABCD的四条边上截取BP2=BP3=CP4=CP5=DP6=DP7=AP8=AP1.连接P2P3,P4P5,P6P7,P8P1,得到阴影部分.设P1P2=x cm,则阴影部分的面积为 cm2(用含x的代数式表示).
14.(2024秋 汕尾期末)一个多边形的内角和等于1080°,这个多边形是 边形.
15.(2024秋 门头沟区期末)如果一个多边形的内角和等于外角和,那么该多边形的边数是 .
三.解答题(共5小题)
16.(2024秋 本溪期末)如图,△ABC中,AC=2AB,AD平分∠BAC,过点C作CE⊥AD交AD延长线于点E,点F是AC中点,连接EF,EB.
(1)证明:四边形ABEF是菱形;
(2)若∠BAC=120°,,求边BC的长.
17.(2024秋 贵阳期末)如图,在矩形ABCD中,AB=6,AD=4,点E是边BC上任意一点,连接AE,将△ABE沿直线AE折叠,点B的对应点B'恰好落在矩形的边CD上.
(1)直接写出图中AB',B′D的长;
(2)连接BB',判断AE与BB'的位置关系,并说明理由;
(3)在(2)的条件下,求的值.
18.(2024秋 高坪区期末)(1)如图1,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°.E、F两点分别是BC、CD上的点,且EF=BE+FD,试探究图中∠EAF与∠BAD的数量关系.
小王同学探究此题的方法是作辅助线:延长FD到点G,使DG=BE,连接AG.然后顺利的完成了此题的解答.请你按照他的方法写出解答过程.
(2)如图2,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD.若E、F分别在CB、CD的延长线上,且仍然满足EF=BE+FD,请直接写出∠EAF与∠BAD的数量关系.
19.(2025 浦东新区一模)在平行四边形ABCD中,对角线AC、BD交于点O,P是线段OC上一个动点(不与点O、点C重合),过点P分别作AD、CD的平行线,交CD于点E,交BC、BD于点F、G,联结EG.
(1)如图1,如果PC=2OP,求证:EG∥AC;
(2)如图2,如果∠ABC=90°,,且△DGE与△PCF相似,请补全图形,并求的值;
(3)如图3,如果BA=BG=BC,且射线EG过点A.请补全图形,并求∠ABC的度数.
20.(2024秋 贵阳期末)如图,在平行四边形ABCD中,AE⊥BC,AF⊥DC,垂足分别为E,F,且BE=DF.
(1)求证:△ABE≌△ADF;
(2)平行四边形ABCD是菱形吗?为什么?
2025年中考数学高频易错考前冲刺:四边形
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B A C D C D A C
一.选择题(共10小题)
1.(2024秋 南宁期末)“方寸之间,别有洞天”,我国古代建筑常采用花窗框景,让风景如同镶嵌在画框中的风景画.如图所示的窗框的外框形状是正八边形,则这个正八边形的内角和为( )
A.360° B.540° C.720° D.1080°
【考点】平面镶嵌(密铺);多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】D
【分析】根据多边形的内角和公式(n﹣2) 180°,列式进行计算即可得解.
【解答】解:内角和为(8﹣2) 180°=1080°.
故选:D.
【点评】本题考查了多边形的内角和,熟记内角和公式是解题的关键.
2.(2024秋 泰兴市期末)如图,把直角三角形拆解为一个正方形与两对全等的直角三角形.下面给出的条件中,一定能求出该直角三角形的面积的是( )
A.AD BD B.AI BD C.BI AD D.AI BI
【考点】正方形的性质;解直角三角形;三角形的面积;直角三角形全等的判定.
【专题】运算能力.
【答案】A
【分析】由题意可得:△ADI≌△AFI,△BDI≌△BEI,四边形IFCE是正方形,则AF=AD,BD=BE,IE=IF=EC=FC,设IE=IF=EC=FC=x,然后根据勾股定理列方程并整理可得x2+(AD+BD)x=AD BD,又该直角三角形的面积的是,整理得,将x2+(AD+BD)x=AD BD整体代入可得该直角三角形的面积的是AD BD,再结合选项即可解答.
【解答】解:由题意可得:△ADI≌△AFI,△BDI≌△BEI,四边形IFCE是正方形,
∴AF=AD,BD=BE,IE=IF=EC=FC,
设IE=IF=EC=FC=x,则AC=AF+x=AD+x,BC=BE+x=BD+x,AB=AD+BD,
∵AB2=BC2+AC2,
∴(AD+BD)2=(BD+x)2+(AD+x)2,整理为:x2+(AD+BD)x=AD BD,
∵直角三角形的面积是:
=AD BD.
∴当AD BD确定时,一定能求出该直角三角形的面积.
故选:A.
【点评】本题主要考查全等三角形的性质、正方形的性质、勾股定理等知识点,正确进行分析、推理成为解题的关键.
3.(2024秋 宁波期末)由四个全等的直角三角形和一个小正方形组成的大正方形ABCD(如图所示),连结DF并延长交BC于点I,若,则tan∠BAE的值为( )
A. B. C. D.
【考点】正方形的性质;相似三角形的判定与性质;解直角三角形;全等三角形的判定与性质.
【专题】图形的全等;矩形 菱形 正方形;图形的相似;几何直观;运算能力;推理能力.
【答案】B
【分析】过点I作IM⊥CF于点M,根据2,设BI=2a,IC=k,则BC=3k,依题意得DH∥BF∥IM,则△ICM和△BCF相似,进而得,设CM=a,IM=b,则BF=3b,CF=3a,BE=CF=DG=3a,FM=2a,EF=GF=3b﹣3a,再根据△IMF和△DGF相似得,则,由此得2a=b,a=﹣b(不合题意,舍去),则BE=3a,AE=BF=3b=6a,然后在Rt△ABE中,根据正切函数的定义即可得tan∠BAE的值.
【解答】解:过点I作IM⊥CF于点M,如图所示:
∵2,
设BI=2a,IC=k,
∴BC=BI+IC=3k,
依题意得:∠FGD=∠BFC=∠IMC=90°,
∴DH∥BF∥IM,
∴△ICM∽△BCF,
∴,
设CM=a,IM=b,则BF=3b,CF=3a,
∴BE=CF=DG=3a,FM=CF﹣CM=3a﹣a=2a,
∴EF=GF=BF﹣BE=3b﹣3a,
∵DH∥IM,
∴△IMF∽△DGF,
∴,
∴,
整理得:2a2+ab﹣b2=0,
∴(2a﹣b)(a+b)=0,
∴2a=b,a=﹣b(不合题意,舍去),
∴BE=3a,AE=BF=3b=6a,
在Rt△ABE中,tan∠BAE.
故选:B.
【点评】此题主要考查了正方形的性质,全等三角形的性质,相似三角形的判定与性质,解直角三角形,理解正方形的性质,全等三角形的性质,熟练掌握相似三角形的判定与性质,锐角三角函数的定义是解决问题的关键.
4.(2025 嘉定区一模)如图,在直角梯形ABCD中,AD∥BC,∠D=90°,如果对角线AC⊥AB,那么的值是( )
A.sinB B.cosB C.tanB D.cotB
【考点】直角梯形;相似三角形的判定与性质;解直角三角形;平行线的性质.
【专题】梯形;推理能力.
【答案】A
【分析】根据直角梯形得出∠D=90°,根据AD∥BC得出∠DAC=∠BCA,进而得出△ADC与△BAC相似,利用相似三角形的性质解答即可.
【解答】解:∵直角梯形ABCD,
∴∠D=90°,
∵AC⊥AB,
∴∠BAC=90°,
∵AD∥BC,
∴∠DAC=∠BCA,
∴△ADC∽△BAC,
∴,
故选:A.
【点评】此题考查直角梯形,关键是根据直角梯形得出∠D=90°解答.
5.(2024秋 河西区期末)一个矩形的长和宽相差3cm,面积是4cm2,则这个矩形的周长为( )
A.6cm B.8cm C.10cm D.12cm
【考点】矩形的性质;一元二次方程的应用.
【专题】一元二次方程及应用;矩形 菱形 正方形;应用意识.
【答案】C
【分析】设矩形的宽为x cm,则长为(x+3)cm,根据矩形的面积计算公式列出方程求出x的值,进而根据矩形的周长公式计算即可.
【解答】解:设矩形的宽为x cm,则长为(x+3)cm,
根据题意,得x(x+3)=4,
解得:x1=﹣4(不合题意,舍去),x2=1,
所以x=1,x+3=4,
则这个矩形的周长为2(4+1)=10(cm).
答:这个矩形的周长为10cm.
故选:C.
【点评】此题主要考查了矩形的性质,一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
6.(2024秋 西山区期末)正八边形的内角和为( )
A.180° B.360° C.720° D.1080°
【考点】多边形内角与外角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】根据多边形的内角和公式:(n﹣2) 180°计算即可.
【解答】解:正八边形的内角和为(8﹣2)×180°=1080°,
故选:D.
【点评】本题考查了多边形的内角与外角,掌握多边形的内角和公式:(n﹣2) 180°是解题的关键.
7.(2024秋 天府新区期末)矩形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角
【考点】矩形的性质;菱形的性质.
【专题】矩形 菱形 正方形;推理能力.
【答案】C
【分析】利用矩形与菱形的性质即可解答本题.
【解答】解:矩形具有而菱形不一定具有的性质是对角线相等,
故选:C.
【点评】本题考查了矩形与菱形的性质,中心对称图形,解题的关键是熟练掌握矩形与菱形的性质.
8.(2024秋 英德市期末)如图,在矩形ABCD中,对角线AC,BD相交于点O,若AO=3,则BD的长为( )
A.3 B.4 C.5 D.6
【考点】矩形的性质.
【专题】矩形 菱形 正方形;推理能力.
【答案】D
【分析】根据矩形的性质得出AC=BD,AO=CO,求出AC,再求出BD即可.
【解答】解:∵四边形ABCD是矩形,
∴AC=BD,AO=CO,
∵AO=3,
∴CO=3,
∴AC=3+3=6,
∴BD=AC=6,
故选:D.
【点评】本题考查了矩形的性质,能熟记矩形的对角线互相平分且相等是解此题的关键.
9.(2024秋 郑州期末)下列说法中不正确的是( )
A.对角线相等的四边形是矩形
B.菱形既是轴对称图形又是中心对称图形
C.对角线互相垂直平分的四边形是菱形
D.正方形的四条边都相等
【考点】矩形的判定;正方形的性质;菱形的判定.
【专题】矩形 菱形 正方形;推理能力.
【答案】A
【分析】根据矩形的判定方法、菱形的性质、菱形的判定方法以及正方形的性质进行解答即可.
【解答】解:A、对角线相等的平行四边形是矩形,原说法不正确;
B、菱形既是轴对称图形又是中心对称图形,原说法正确;
C、对角线互相垂直平分的四边形是菱形,原说法正确;
D、正方形的四条边都相等,原说法正确;
故选:A.
【点评】本题主要考查了矩形的判定方法、菱形的性质、菱形的判定方法以及正方形的性质,属于基础题.
10.(2024秋 市北区期末)过某多边形一个顶点的所有对角线,将这个多边形分成4个三角形,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
【考点】多边形的对角线;多边形.
【专题】多边形与平行四边形;运算能力.
【答案】C
【分析】根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成(n﹣2)个三角形,依此可得n的值.
【解答】解:设这个多边形是n边形,
由题意得,n﹣2=4,
解得:n=6,
即这个多边形是六边形,
故选:C.
【点评】本题考查了多边形的对角线,解题的关键是掌握n边形从一个顶点出发可引出(n﹣3)条对角线,可组成(n﹣2)个三角形.
二.填空题(共5小题)
11.(2024秋 本溪期末)过六边形的一个顶点能画出对角线的条数是 3 .
【考点】多边形的对角线.
【专题】多边形与平行四边形;推理能力.
【答案】3.
【分析】根据从一个n边形一个顶点出发,可以连的对角线的条数是(n﹣3)进行计算即可.
【解答】解:根据题意,引对角线的数量为:6﹣3=3 (条),
所以从六边形的一个顶点能画出对角线的条数是3,
故答案为:3.
【点评】本题主要考查了多边形的对角线,解答此类题目的关键是正确记忆一个n边形一个顶点出发,可以连的对角线的条数是n﹣3.
12.(2024秋 新城区校级期末)过一个多边形的一个顶点出发有4条对角线,这些对角线将这个多边形分成 5 个三角形.
【考点】多边形的对角线.
【专题】多边形与平行四边形;运算能力.
【答案】5.
【分析】根据过n边形的一个顶点,可以引出(n﹣3)条对角线,这些对角线把该多边形分成(n﹣2)个三角形,即可求解.
【解答】解:由题意可得:该多边形的边数为4+3=7,
∴这些对角线将这个多边形分成三角形的个数为7﹣2=5(个).
故答案为:5.
【点评】本题考查多边形对角线,解题关键是熟练掌握过n边形一个顶点有(n﹣3)条对角线,这些对角线将这个n边形分成(n﹣2)个三角形.
13.(2024秋 东城区期末)已知正方形ABCD的边长为30cm.
(1)如图1,正方形ABCD各边的中点分别为E,F,G,H,依次连接四个中点,得到阴影部分.该阴影部分的面积为 450 cm2;
(2)如图2,点P1在边AB上,且.在正方形ABCD的四条边上截取BP2=BP3=CP4=CP5=DP6=DP7=AP8=AP1.连接P2P3,P4P5,P6P7,P8P1,得到阴影部分.设P1P2=x cm,则阴影部分的面积为 cm2(用含x的代数式表示).
【考点】中点四边形;列代数式.
【专题】实数;运算能力.
【答案】450;.
【分析】(1)利用正方形ABCD的面积减去四个三角形面积即可得到阴影部分的面积;
(2)利用正方形ABCD的面积减去四个三角形面积即可得到阴影部分的面积.
【解答】解:(1)根据题意可知:AE=BE=BF=CF=CG=DG=DH=AH=5×30=15cm,
∴阴影部分的面积为:,
故答案为:450;
(2)根据题意可知:
,
∴阴影部分的面积为:,
故答案为:.
【点评】本题主要考查了中点四边形、四则混合运算的实际应用、列代数式等知识点,根据题中的面积关系正确列出算式或代数式是解题的关键.
14.(2024秋 汕尾期末)一个多边形的内角和等于1080°,这个多边形是 8 边形.
【考点】多边形内角与外角.
【答案】见试题解答内容
【分析】多边形的内角和可以表示成(n﹣2) 180°,依此列方程可求解.
【解答】解:设所求正n边形边数为n,
则1080°=(n﹣2) 180°,解得n=8.
故答案为:8.
【点评】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
15.(2024秋 门头沟区期末)如果一个多边形的内角和等于外角和,那么该多边形的边数是 4 .
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】4.
【分析】根据多边形内角和与外角和的关系列方程求解即可.
【解答】解:设这个多边形为n边形,由题意得,
(n﹣2)×180°=360°,
解得n=4,
故答案为:4.
【点评】本题考查多边形的内角与外角,掌握多边形内角和的计算方法是正确解答的关键.
三.解答题(共5小题)
16.(2024秋 本溪期末)如图,△ABC中,AC=2AB,AD平分∠BAC,过点C作CE⊥AD交AD延长线于点E,点F是AC中点,连接EF,EB.
(1)证明:四边形ABEF是菱形;
(2)若∠BAC=120°,,求边BC的长.
【考点】菱形的判定与性质;角平分线的性质;等腰三角形的判定与性质;直角三角形斜边上的中线;三角形中位线定理.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;运算能力;推理能力.
【答案】(1)证明见解析;
(2)BC=14.
【分析】(1)由直角三角形的性质得,则∠FAE=∠FEA,又AC=2AB,则AB=AF=EF,从而证明BA∥EF,即可证明四边形ABEF是平行四边形,再由菱形的判定方法即可求证;
(2)作BH⊥AC交CA延长线于点H,则∠AHB=90°,通过勾股定理即可求解.
【解答】(1)证明:∵CE⊥AE,
∴∠AEC=90°,
∵点F是AC中点,
∴,
∴∠FAE=∠FEA,
∵AC=2AB,
∴AB=AF=EF,
∵AD平分∠BAC,
∴∠BAE=∠FAE,
∴∠BAE=∠FEA,
∴BA∥EF,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形;
(2)解:作BH⊥AC交CA延长线于点H,则∠AHB=90°,
∵∠BAC=120°,
∴∠BAH=60°,
∴∠ABH=30°,
∴,
∵AC=2AB,
∴,
∴,
∴由勾股定理得:,
在Rt△BCH中,由勾股定理得:,
∴BC的长为14.
【点评】本题考查了平行四边形的判定,菱形的判定,等角对等边,直角三角形的性质,勾股定理,掌握知识点的应用是解题的关键.
17.(2024秋 贵阳期末)如图,在矩形ABCD中,AB=6,AD=4,点E是边BC上任意一点,连接AE,将△ABE沿直线AE折叠,点B的对应点B'恰好落在矩形的边CD上.
(1)直接写出图中AB',B′D的长;
(2)连接BB',判断AE与BB'的位置关系,并说明理由;
(3)在(2)的条件下,求的值.
【考点】四边形综合题.
【专题】几何综合题;运算能力;推理能力.
【答案】(1)2;
(2)AE⊥BB′,理由见解析;
(3).
【分析】(1)根据矩形的性质的∠D=90°,根据折叠的性质得到AB=AB′=6,根据勾股定理得到DB′2;
(2)如图,连接BB′交AE于H,根据折叠的性质得到AB=AB′,∠BAH=∠B′AH,根据全等三角形的性质得到∠AHB=∠AHB′,根据垂直的定义得到AE⊥BB′;
(3)根据矩形的性质得到∠C=∠ABE=90°,求得∠BAE=∠CBB′,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:(1)∵四边形ABCD是矩形,
∴∠D=90°,
∵将△ABE沿直线AE折叠,
∴AB=AB′=6,
∴DB′2;
(2)AE⊥BB′,
理由:如图,连接BB′交AE于H,
∵将△ABE沿直线AE折叠,
∴AB=AB′,∠BAH=∠B′AH,
在△ABH与△AB′H中,
,
∴∠AHB=∠AHB′,
∵∠AHB+∠AHB′=180°,
∴∠AHB=90°,
∴AE⊥BB′;
(3)∵四边形ABCD是矩形,
∴∠C=∠ABE=90°,
∵∠AHB=90°,
∴∠BAH+∠ABH=∠ABH+∠CBH=90°,
∴∠BAE=∠CBB′,
∴△ABE∽△BCB′,
∴.
【点评】本题是四边形的综合题,考查了全等三角形的判定和性质,折叠的性质,矩形的性质,相似三角形的判定和性质,熟练掌握各知识点是解题的关键.
18.(2024秋 高坪区期末)(1)如图1,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°.E、F两点分别是BC、CD上的点,且EF=BE+FD,试探究图中∠EAF与∠BAD的数量关系.
小王同学探究此题的方法是作辅助线:延长FD到点G,使DG=BE,连接AG.然后顺利的完成了此题的解答.请你按照他的方法写出解答过程.
(2)如图2,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD.若E、F分别在CB、CD的延长线上,且仍然满足EF=BE+FD,请直接写出∠EAF与∠BAD的数量关系.
【考点】四边形综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)∠BAD=2∠EAF;理由见解答过程;
(2)∠BAD=360°﹣2∠EAF;理由见解答过程.
【分析】(1)延长FD到点G,使DG=BE,连接AG,可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF,据此得出结论;
(2)在DC延长线上取一点G,使得DG=BE,连接AG,先判定△ADG≌△ABE,再判定△AEF≌△AGF,得出∠FAE=∠FAG,最后根据∠FAE+∠FAG+∠GAE=360°,推导得到2∠FAE+∠DAB=360°,即可得出结论.
【解答】解:(1)∠BAD=2∠EAF;理由如下:
在四边形ABCD中,AB=AD,如图1,延长FD到点G,使DG=BE,连接AG,
在△ABE和△ADG中,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,AE=AG,
∵EF=BE+DF,DG=BE,
∴EF=BE+DF=DG+DF=GF,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SSS),
∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF,
∴∠BAD=2∠EAF;
(2)∠BAD=360°﹣2∠EAF;理由如下:
如图2,在DC延长线上取一点G,使得DG=BE,连接AG,
∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∴∠ADC=∠ABE,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AG=AE,∠DAG=∠BAE,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SSS),
∴∠FAE=∠FAG,
∵∠FAE+∠FAG+∠GAE=360°
∴2∠FAE+(∠GAB+∠BAE)=360°,
∴2∠FAE+(∠GAB+∠DAG)=360°,
即2∠FAE+∠BAD=360°,
∴∠BAD=360°﹣2∠EAF.
【点评】本题属于四边形综合题,主要考查了全等三角形的判定以及全等三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应角相等进行推导变形.解题时注意:同角的补角相等.
19.(2025 浦东新区一模)在平行四边形ABCD中,对角线AC、BD交于点O,P是线段OC上一个动点(不与点O、点C重合),过点P分别作AD、CD的平行线,交CD于点E,交BC、BD于点F、G,联结EG.
(1)如图1,如果PC=2OP,求证:EG∥AC;
(2)如图2,如果∠ABC=90°,,且△DGE与△PCF相似,请补全图形,并求的值;
(3)如图3,如果BA=BG=BC,且射线EG过点A.请补全图形,并求∠ABC的度数.
【考点】四边形综合题.
【专题】多边形与平行四边形;矩形 菱形 正方形;图形的相似;推理能力.
【答案】(1)证明见解析;
(2);
(3)72°.
【分析】(1)由平行四边形的性质证出,得出,则可得出结论;
(2)证明△DGE∽△PFC∽△ABC,设CE=4k,那么PE=6k,PG=9k,得出,DE=13k.求出,则可得出答案;
(3)由题意画出图形,证明平行四边形ABCD为菱形.设FB=FG=a,PF=FC=CE=b,求出,得出,证明△DGA∽△DAB.设∠DAG=∠DBA=∠ADB=α,那么∠BAG=∠BGA=2α.求出α=36°,则可得出答案.
【解答】(1)证明:∵PC=2PO,PG∥CD,
∴,
在平行四边形ABCD中,OA=OC,
∴,
又∵PE∥AD,
∴,
∴,
∴EG∥OC;
(2)解:如图2,
∵∠ABC=90°,
∴平行四边形ABCD为矩形.
∴OC=OD,
∴∠GDE=∠PCE=∠CPF,
又∵∠CFP=∠ABC=90°,且∠DEG<90°,
∴只能∠DGE=90°,∠DEG=∠PGE=∠PCF.
∴此时有:△DGE∽△PFC∽△ABC,
设CE=4k,那么PE=6k,PG=9k,
∴EG3k,DE=13k.
∴,
∴;
(3)解:补全图形如下,
∵BA=BC,
∴平行四边形ABCD为菱形.
设FB=FG=a,PF=FC=CE=b,
∴GP=a﹣b.
∵GP∥CE,
∴,
∴,
∴a2﹣ab﹣b2=0,
∴,
∴(负根已舍).
∴,
∴,
∴,
又∵∠ADG=∠BDA,
∴△DGA∽△DAB.
∴设∠DAG=∠DBA=∠ADB=α,那么∠BAG=∠BGA=2α.
∴5α=180°,
∴α=36°,
∴∠ABC=72°.
【点评】本题属于四边形综合题,考查了矩形的判定与性质,平行四边形的性质,菱形的判定与性质,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,属于中考压轴题.
20.(2024秋 贵阳期末)如图,在平行四边形ABCD中,AE⊥BC,AF⊥DC,垂足分别为E,F,且BE=DF.
(1)求证:△ABE≌△ADF;
(2)平行四边形ABCD是菱形吗?为什么?
【考点】菱形的判定;全等三角形的判定与性质;平行四边形的性质.
【专题】图形的全等;多边形与平行四边形;矩形 菱形 正方形;推理能力.
【答案】(1)证明见解答;
(2)平行四边形ABCD是菱形,理由见解答.
【分析】(1)由平行四边形的性质得∠B=∠D,由AE⊥BC于点E,AF⊥DC于点F,得∠AEB=∠AFD=90°,而BE=DF,即可根据“ASA”证明△ABE≌△ADF;
(2)由全等三角形的性质得AB=AD,而四边形ABCD是平行四边形,即可根据菱形的定义证明平行四边形ABCD是菱形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC于点E,AF⊥DC于点F,
∴∠AEB=∠AFD=90°,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA).
(2)解:平行四边形ABCD是菱形,
理由:由(1)得△ABE≌△ADF,
∴AB=AD,
∵四边形ABCD是平行四边形,且AB=AD,
∴平行四边形ABCD是菱形.
【点评】此题重点考查平行四边形的性质、全等三角形的判定与性质、菱形的定义等知识,推导出∠B=∠D,∠AEB=∠AFD,进而证明△ABE≌△ADF是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
