小学毕业数学总复习第五章图形与几何第1课时图形的认识课件(共68张PPT)
文档属性
| 名称 | 小学毕业数学总复习第五章图形与几何第1课时图形的认识课件(共68张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 15:53:06 | ||
图片预览










文档简介
(共68张PPT)
第五章 图形与几何
考点知识梳理
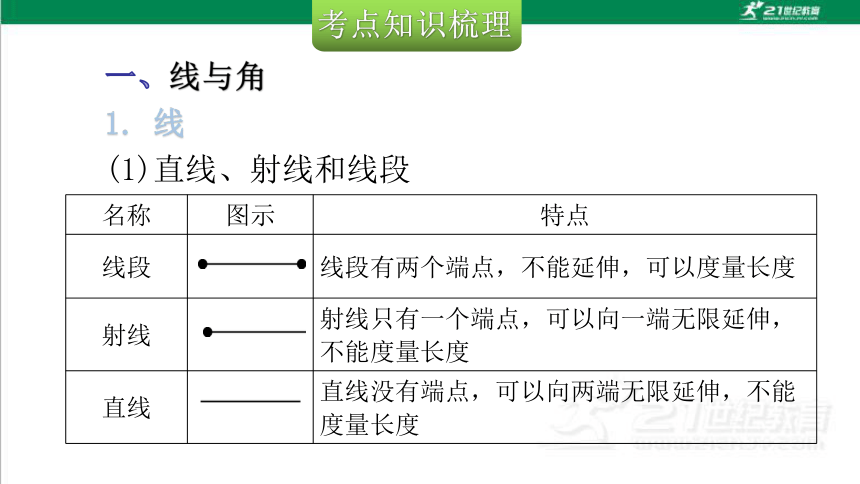
名称 图示 特点
线段 线段有两个端点,不能延伸,可以度量长度
射线 射线只有一个端点,可以向一端无限延伸,不能度量长度
直线 直线没有端点,可以向两端无限延伸,不能度量长度
①在两点的所有连线中,线段最短,即两点之间,线段最短。
②过一点可以画无数条直线;过两点只能画一条直线,即两点确定一条直线。
(2)垂直与平行
①垂直:两条直线相交成直角时,这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
②平行线:在同一平面内,不相交的两条直线叫做平行线。平行线之间的距离处处相等。
③点到直线的距离:从直线外一点到这条直线所画的垂直线段的长,叫做这个点到直线的距离。④同一平面内的两条直线不是平行就是相交(垂直是相交的特例)。
(3)垂线的基本性质
①过直线上或直线外一点,有且只有一条直线和已知直线垂直。
②从直线外一点到这条直线上各点所连的线段中,垂线段最短。
2. 角
(1)角的定义:从一点引出的两条射线所组成的图形叫做角。角的大小与两边的长短无关,与两边叉开的大小有关。
(2)计量角大小的单位计量角大小的单位是度,用符号“°”表示。
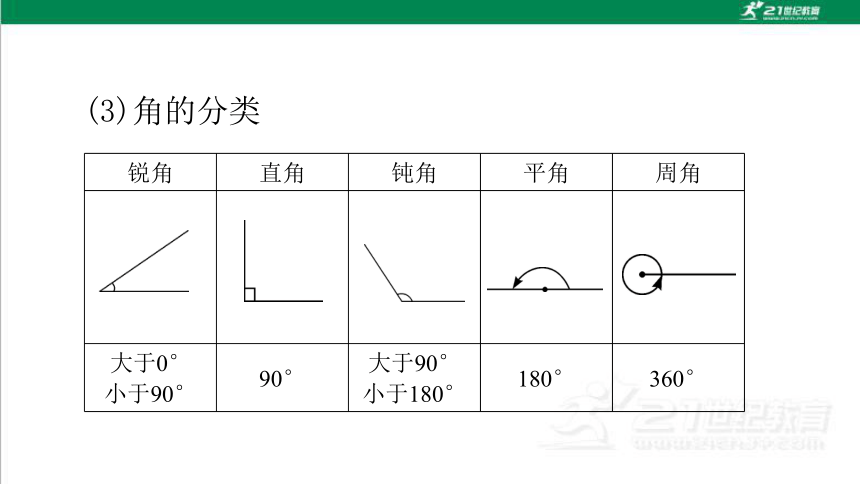
(3)角的分类
锐角 直角 钝角 平角 周角
大于0°
小于90° 90° 大于90°
小于180° 180° 360°
(3)从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。三角形有3条高。
(4)三角形的分类
(5)等边三角形是特殊的等腰三角形,它们的关系如右图。
(6)三角形的特征:
①三角形具有稳定性。
②三角形的内角和是180°。
(7)三角形三边之间的关系:三角形的任意两边之和大于第三边,任意两边之差小于第三边。
2. 四边形
(1)四边形的定义:在同一平面内,由不在同一条直线上的四条线段首尾顺次连接成的封闭图形叫做四边形。
(2)四边形的分类:
(3)四边形的特征:
①四边形具有不稳定性。
②四边形的内角和是360°。
3. 圆
(1)圆的认识:平面上的一种封闭曲线图形。①圆心:圆中心的一点叫做圆心,一般用字母O表示(如右图)。
②半径:连接圆心和圆上任意一点的
线段叫做半径,一般用r表示。
③在同一个圆里,有无数条半径,每条半径的长度都相等。
⑦圆心决定圆的位置,半径决定圆的大小。直径是圆中最长的线段。
⑧圆有无数条对称轴。
(2)圆的画法:把圆规的两脚分开,定好两脚间的距离(即半径);把有针尖的一只脚固定在一点(即圆心)上;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
4. 扇形
(1)扇形的定义:由一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,扇形是圆的一部分(如右图阴影部分图形)。
(2)如右图,圆上AB两点之间的部
分叫做弧,读作“弧AB”,
记作“AB”。
)
(3)长方体和正方体的关系:
名称 图形 相同点 不同点
顶点 棱 面 面的
形状 面的
大小 棱长
长方体 8个 12条 6个 6个面一般都是长方形,也可能有两个相对的面是正方形 相对的面面积相等 每一组互相平行的4条棱长度相等
正方体 6个面都是相同的正方形 6个面都是面积相等的正方形 12条棱长度都相等
名称 图形 底面 侧面 高
圆柱 可以由长方形沿一条边旋转得到 有2个底面,2个底面是完全一样的圆 是个曲面,沿高展开是个长方形(或正方形) 两个底面之间的距离叫做高,有无数条高
圆锥 可以由直角三角形沿一条直角边旋转得到 有1个底面,底面是个圆 是个曲面,侧面展开可以得到一个扇形 从圆锥的顶点到底面圆心的距离叫做高,只有1条高
典例精析及训练
【例1】下图中共有( )条直线、( )条射线和( )条线段。
题型一
精析:此题主要考查直线、射线和线段的特征。直线无端点,可以向两端无限延伸,图中有一条直线。射线只有一个端点,可以向一端无限延伸,所以图中的每一个点都可以看作是射线的端点,从一个点向左或向右延伸,分别得到两条射线,即一共有八条射线。线段有两个端点,任意两个端点间的一段都可以看作一条线段,以点A为左端点有AB,AC,AD三条线段,以点B为左端点有BC,BD两条线段,以点C为左端点有CD一条线段,即一共有六条线段。
答案:1 8 6
10
10
2. ( )可以看作射线。
A. 米尺的边线 B. 太阳的光线
C. 笔直的铁轨
B
14
6
(画图略)
【例2】直线a,b,c在同一平面内,a与b互相垂直,b与c互相垂直,那么a与c( )。
A. 垂直 B. 平行
C.平行或垂直
题型二
精析:此例题主要考查两直线在同一平面内的位置关系。根据之前所学,我们知道,在同一平面内,两直线的位置关系是相交或平行。本题中,三条直线在同一平面内,因为a与b互相垂直,b与c互相垂直,根据垂直于同一条直线的两直线平行,则可以判断a与c互相平行。因此答案选B。
答案:B
垂直
平行
无数
1
×
8. 下面有两条平行线,请你照着图中的样子再画3条垂线段,并量一量它们的长度。
我发现_____________________________________。
两条平行线之间的距离处处相等
(画图略)
【例3】已知∠1=75°,求∠2,∠3和∠4的度数。
题型三
精析:利用平角是180°以及图中各角之间的关系可以求得∠2=180°-∠1=180°-75°=105°,又根据两直线相交,所形成的对角相等,可得∠1=∠3=75°,∠2=∠4=105°。
答案:∠2=105°,∠3=75°,∠4=105°。
C
∠1=180°-35°=145°,∠2=90°-30°=60°,∠3=90°。
【例4】若一个三角形三个内角的度数比是6∶2∶1,则这个三角形是一个( )三角形。
题型四
精析:此题考查三角形内角和及分类。按角对三角形进行分类时,根据三角形中最大的内角的度数来判定这个三角形的形状。如果最大的角的度数大于90°,那么这个三角形是钝角三角形;如果等于90°,那么这个三角形是直角三角形;如果小于90°,那么这个三角形是锐角三角形。三角形的内角和是180°,而三个内角的度数比是6∶2∶1,则这个三角形中最大的内角是180°÷(6+2+1)×6=120°。因为120°大于90°,所以这个三角形是钝角三角形。
答案:钝角
30
直角
【例5】焊接一个长8 厘米、宽6 厘米、高2 厘米的长方体框架,至少要用( )厘米的铁丝。
题型五
精析:长方体有12条棱,相对的四条棱长度相等。按长度可分为三组,每一组有4条棱,至少需要多少铁丝就是求长方体的棱长总和,利用公式:长×4+宽×4+高×4=棱长总和。所以8×4+6×4+2×4=32+24+8=64(厘米)
答案:64
10
8
6
13. 用一根铁丝可以围成一个长100厘米、宽90厘米、高80厘米的长方体框架,这根铁丝的长度是( )厘米。如果这根铁丝刚好能围成一个正方体框架,那么这个正方体的棱长是
( )米。
1080
0.9
易错归纳及训练
【例1】判断:两条射线一定能组成一个角。( )
错解:√
分析:角是由两条有公共端点的射线组成的。本题容易出错的主要原因是对角的概念没有正确理解,还有一个原因是审题不仔细,没有深入思考,看到有两条射线就以为一定能组成一个角,而没有考虑到公共端点。
正解:×
类型一
√
【例2】丁丁早上7:25上学,分针刚好转了150°,他就到达学校,他上学用了( )分钟。
类型二
错解:45
分析:此题考查的是时间的计算和角的度量的综合运用。因为分针每小时转动360°,所以每分钟转动6°,丁丁出发到学校的时间内分针转了150°,列式可得150°÷6°=25。
正解:25
10
小考复习训练
4
2
1
锐角
无数
垂线段
2
1
无数
1
(m+n)
(m-n)
直
钝
360
210
116°
梯形
6
12
√
√
×
×
×
×
×
B
2. 把一个活动的长方形框架拉成平行四边形,那么它的( )不变,( )变了。
A.面积 B.周长
C.周长和面积 D. 周长或面积
B
A
D
A
B
D
画图略
(2)画一条比10厘米短4厘米的线段。
画图略
画图略
3. 如下图,从A,B两村各挖一条水渠与河相通,要使水渠最短,应怎样挖 请在图中画出来。
画图略
∠2=90°-∠1=90°-48°=42°
∠3=180°-∠2=180°-42°=138°
∠4=∠2=42°
∠5=90°
第五章 图形与几何
考点知识梳理
名称 图示 特点
线段 线段有两个端点,不能延伸,可以度量长度
射线 射线只有一个端点,可以向一端无限延伸,不能度量长度
直线 直线没有端点,可以向两端无限延伸,不能度量长度
①在两点的所有连线中,线段最短,即两点之间,线段最短。
②过一点可以画无数条直线;过两点只能画一条直线,即两点确定一条直线。
(2)垂直与平行
①垂直:两条直线相交成直角时,这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
②平行线:在同一平面内,不相交的两条直线叫做平行线。平行线之间的距离处处相等。
③点到直线的距离:从直线外一点到这条直线所画的垂直线段的长,叫做这个点到直线的距离。④同一平面内的两条直线不是平行就是相交(垂直是相交的特例)。
(3)垂线的基本性质
①过直线上或直线外一点,有且只有一条直线和已知直线垂直。
②从直线外一点到这条直线上各点所连的线段中,垂线段最短。
2. 角
(1)角的定义:从一点引出的两条射线所组成的图形叫做角。角的大小与两边的长短无关,与两边叉开的大小有关。
(2)计量角大小的单位计量角大小的单位是度,用符号“°”表示。
(3)角的分类
锐角 直角 钝角 平角 周角
大于0°
小于90° 90° 大于90°
小于180° 180° 360°
(3)从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。三角形有3条高。
(4)三角形的分类
(5)等边三角形是特殊的等腰三角形,它们的关系如右图。
(6)三角形的特征:
①三角形具有稳定性。
②三角形的内角和是180°。
(7)三角形三边之间的关系:三角形的任意两边之和大于第三边,任意两边之差小于第三边。
2. 四边形
(1)四边形的定义:在同一平面内,由不在同一条直线上的四条线段首尾顺次连接成的封闭图形叫做四边形。
(2)四边形的分类:
(3)四边形的特征:
①四边形具有不稳定性。
②四边形的内角和是360°。
3. 圆
(1)圆的认识:平面上的一种封闭曲线图形。①圆心:圆中心的一点叫做圆心,一般用字母O表示(如右图)。
②半径:连接圆心和圆上任意一点的
线段叫做半径,一般用r表示。
③在同一个圆里,有无数条半径,每条半径的长度都相等。
⑦圆心决定圆的位置,半径决定圆的大小。直径是圆中最长的线段。
⑧圆有无数条对称轴。
(2)圆的画法:把圆规的两脚分开,定好两脚间的距离(即半径);把有针尖的一只脚固定在一点(即圆心)上;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
4. 扇形
(1)扇形的定义:由一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,扇形是圆的一部分(如右图阴影部分图形)。
(2)如右图,圆上AB两点之间的部
分叫做弧,读作“弧AB”,
记作“AB”。
)
(3)长方体和正方体的关系:
名称 图形 相同点 不同点
顶点 棱 面 面的
形状 面的
大小 棱长
长方体 8个 12条 6个 6个面一般都是长方形,也可能有两个相对的面是正方形 相对的面面积相等 每一组互相平行的4条棱长度相等
正方体 6个面都是相同的正方形 6个面都是面积相等的正方形 12条棱长度都相等
名称 图形 底面 侧面 高
圆柱 可以由长方形沿一条边旋转得到 有2个底面,2个底面是完全一样的圆 是个曲面,沿高展开是个长方形(或正方形) 两个底面之间的距离叫做高,有无数条高
圆锥 可以由直角三角形沿一条直角边旋转得到 有1个底面,底面是个圆 是个曲面,侧面展开可以得到一个扇形 从圆锥的顶点到底面圆心的距离叫做高,只有1条高
典例精析及训练
【例1】下图中共有( )条直线、( )条射线和( )条线段。
题型一
精析:此题主要考查直线、射线和线段的特征。直线无端点,可以向两端无限延伸,图中有一条直线。射线只有一个端点,可以向一端无限延伸,所以图中的每一个点都可以看作是射线的端点,从一个点向左或向右延伸,分别得到两条射线,即一共有八条射线。线段有两个端点,任意两个端点间的一段都可以看作一条线段,以点A为左端点有AB,AC,AD三条线段,以点B为左端点有BC,BD两条线段,以点C为左端点有CD一条线段,即一共有六条线段。
答案:1 8 6
10
10
2. ( )可以看作射线。
A. 米尺的边线 B. 太阳的光线
C. 笔直的铁轨
B
14
6
(画图略)
【例2】直线a,b,c在同一平面内,a与b互相垂直,b与c互相垂直,那么a与c( )。
A. 垂直 B. 平行
C.平行或垂直
题型二
精析:此例题主要考查两直线在同一平面内的位置关系。根据之前所学,我们知道,在同一平面内,两直线的位置关系是相交或平行。本题中,三条直线在同一平面内,因为a与b互相垂直,b与c互相垂直,根据垂直于同一条直线的两直线平行,则可以判断a与c互相平行。因此答案选B。
答案:B
垂直
平行
无数
1
×
8. 下面有两条平行线,请你照着图中的样子再画3条垂线段,并量一量它们的长度。
我发现_____________________________________。
两条平行线之间的距离处处相等
(画图略)
【例3】已知∠1=75°,求∠2,∠3和∠4的度数。
题型三
精析:利用平角是180°以及图中各角之间的关系可以求得∠2=180°-∠1=180°-75°=105°,又根据两直线相交,所形成的对角相等,可得∠1=∠3=75°,∠2=∠4=105°。
答案:∠2=105°,∠3=75°,∠4=105°。
C
∠1=180°-35°=145°,∠2=90°-30°=60°,∠3=90°。
【例4】若一个三角形三个内角的度数比是6∶2∶1,则这个三角形是一个( )三角形。
题型四
精析:此题考查三角形内角和及分类。按角对三角形进行分类时,根据三角形中最大的内角的度数来判定这个三角形的形状。如果最大的角的度数大于90°,那么这个三角形是钝角三角形;如果等于90°,那么这个三角形是直角三角形;如果小于90°,那么这个三角形是锐角三角形。三角形的内角和是180°,而三个内角的度数比是6∶2∶1,则这个三角形中最大的内角是180°÷(6+2+1)×6=120°。因为120°大于90°,所以这个三角形是钝角三角形。
答案:钝角
30
直角
【例5】焊接一个长8 厘米、宽6 厘米、高2 厘米的长方体框架,至少要用( )厘米的铁丝。
题型五
精析:长方体有12条棱,相对的四条棱长度相等。按长度可分为三组,每一组有4条棱,至少需要多少铁丝就是求长方体的棱长总和,利用公式:长×4+宽×4+高×4=棱长总和。所以8×4+6×4+2×4=32+24+8=64(厘米)
答案:64
10
8
6
13. 用一根铁丝可以围成一个长100厘米、宽90厘米、高80厘米的长方体框架,这根铁丝的长度是( )厘米。如果这根铁丝刚好能围成一个正方体框架,那么这个正方体的棱长是
( )米。
1080
0.9
易错归纳及训练
【例1】判断:两条射线一定能组成一个角。( )
错解:√
分析:角是由两条有公共端点的射线组成的。本题容易出错的主要原因是对角的概念没有正确理解,还有一个原因是审题不仔细,没有深入思考,看到有两条射线就以为一定能组成一个角,而没有考虑到公共端点。
正解:×
类型一
√
【例2】丁丁早上7:25上学,分针刚好转了150°,他就到达学校,他上学用了( )分钟。
类型二
错解:45
分析:此题考查的是时间的计算和角的度量的综合运用。因为分针每小时转动360°,所以每分钟转动6°,丁丁出发到学校的时间内分针转了150°,列式可得150°÷6°=25。
正解:25
10
小考复习训练
4
2
1
锐角
无数
垂线段
2
1
无数
1
(m+n)
(m-n)
直
钝
360
210
116°
梯形
6
12
√
√
×
×
×
×
×
B
2. 把一个活动的长方形框架拉成平行四边形,那么它的( )不变,( )变了。
A.面积 B.周长
C.周长和面积 D. 周长或面积
B
A
D
A
B
D
画图略
(2)画一条比10厘米短4厘米的线段。
画图略
画图略
3. 如下图,从A,B两村各挖一条水渠与河相通,要使水渠最短,应怎样挖 请在图中画出来。
画图略
∠2=90°-∠1=90°-48°=42°
∠3=180°-∠2=180°-42°=138°
∠4=∠2=42°
∠5=90°
同课章节目录
