小学毕业数学总复习第五章图形与几何第2课时图形的测量课件(共70张PPT)
文档属性
| 名称 | 小学毕业数学总复习第五章图形与几何第2课时图形的测量课件(共70张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 15:54:07 | ||
图片预览







文档简介
(共70张PPT)
第五章 图形与几何
考点知识梳理
1. 平面图形的周长与面积
周长:封闭图形一周的长度叫做周长。
面积:物体表面或围成的平面图形的大小叫做面积。
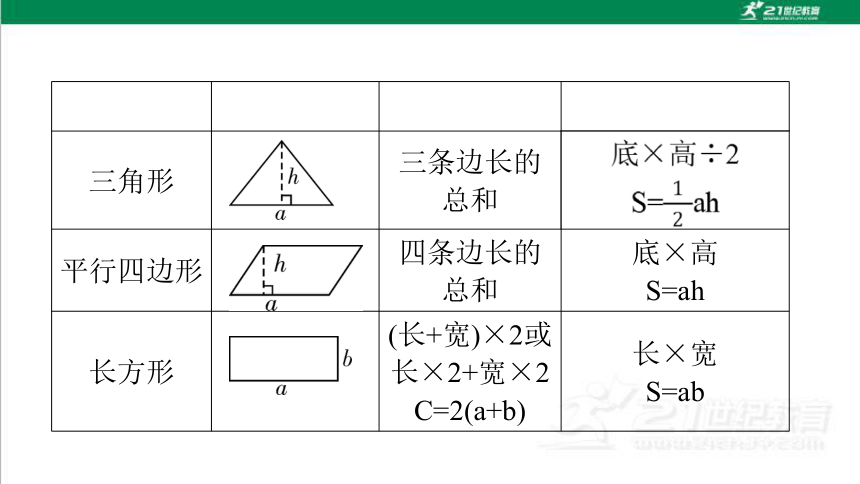
名称 图形 周长 面积
三角形 三条边长的总和
平行四边形 四条边长的总和 底×高
S=ah
长方形 (长+宽)×2或长×2+宽×2
C=2(a+b) 长×宽
S=ab
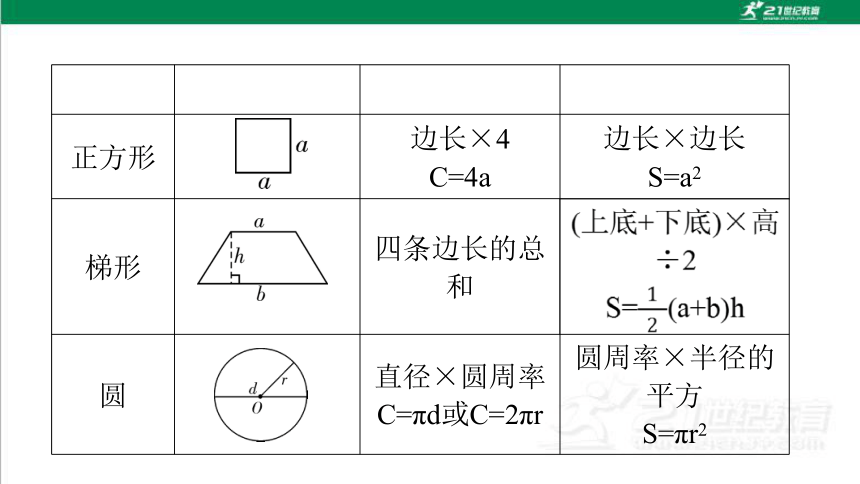
名称 图形 周长 面积
正方形 边长×4
C=4a 边长×边长
S=a2
梯形 四条边长的总和
圆 直径×圆周率C=πd或C=2πr 圆周率×半径的平方
S=πr2
名称 图形 周长 面积
半圆 圆周长的一半+直径
C=πr+d或C=πr+2r
圆环 — 大圆的面积-小圆的面积
S环=π(R2-r2)
2. 立体图形的表面积与体积
(1)表面积:物体表面面积的总和,叫做物体的表面积。
(2)体积:物体所占空间的大小,叫做物体的体积。
(3)容积:箱子、油桶、仓库等所能容纳物体的体积,叫做它们的容积或容量。常用的容积单位是升、毫升。
(4)体积和容积单位之间的换算:
1立方分米=1升;1立方厘米=1毫升。
名称 图形 棱长总和 表面积 体积
长方体 (长+宽+高)×4
L=4(a+b+h) (长×宽+长×高+宽×高)
×2
S表=2(ab+
ah+bh) 长×宽×高
V=abh
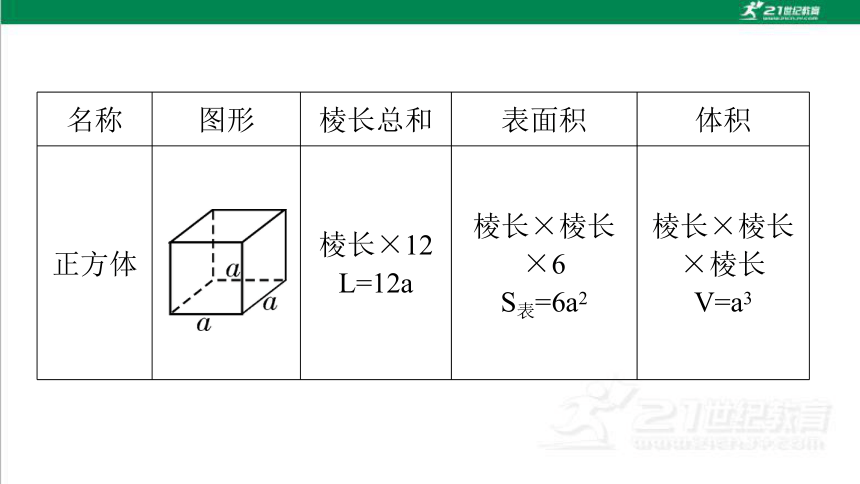
名称 图形 棱长总和 表面积 体积
正方体 棱长×12
L=12a 棱长×棱长×6
S表=6a2 棱长×棱长×棱长
V=a3
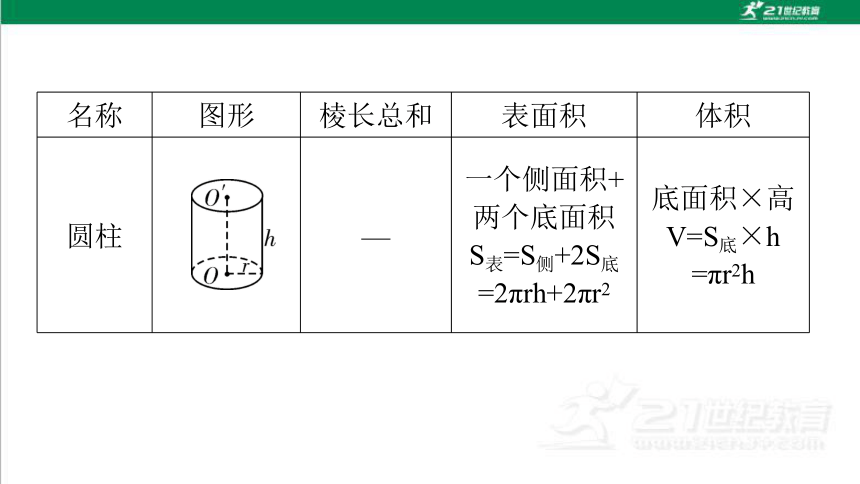
名称 图形 棱长总和 表面积 体积
圆柱 — 一个侧面积+两个底面积
S表=S侧+2S底
=2πrh+2πr2 底面积×高
V=S底×h
=πr2h
名称 图形 棱长总和 表面积 体积
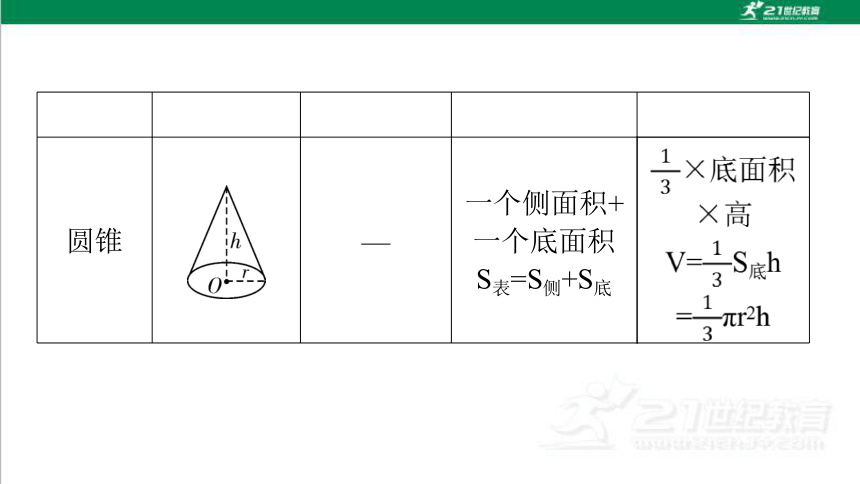
圆锥 — 一个侧面积+一个底面积
S表=S侧+S底
3. 图形间的关系
(1)面积相等的长方形(或平行四边形)和三角形,当它们等底时,三角形的高是长方形(或平行四边形)的高的2倍。
(2)长方体的棱长总和一定时,长、宽、高越接近,长方体的体积就越大,表面积也就越大。
(3)当圆柱和圆锥等底等高时,圆柱的体积是圆锥的体积的3倍;
当圆柱和圆锥等底等体积时,圆锥的高是圆柱的高的3倍;
当圆柱和圆锥等高等体积时,圆锥的底面积是圆柱的底面积的3倍。
典例精析及训练
【例1】用一张边长为10厘米的正方形纸,剪一个最大的圆,所剪的圆的面积是( )。
题型一
精析:此题考查“外方内圆”中圆面积的求法,如右图。用正方形纸剪的最大的圆的直径等于正方形的边长,所以所剪的最大的圆的面积为π(10÷2)2=25π=78.5(平方厘米)。
答案:78.5平方厘米
圆的周长:3.14×12=37.68(厘米)
圆的面积:3.14×(12÷2)2
=3.14×62
=3.14×36
=113.04(平方厘米)
答:这个圆的周长是37.68厘米,面积是113.04平方厘米。
18.84÷3.14×4=24(厘米)
答:正方形的周长是24厘米。
答:正方形的面积约占圆面积的63.7%。
【例2】一个长方体形状的露天水池,长20米,宽10米,深4米。如果在这个水池的四周和底面铺上边长是2分米的正方形瓷砖,至少需要多少块瓷砖?
题型二
精析:由于水池无盖,所以贴瓷砖的部分是这个长方体的一个底面和4个侧面的总面积,根据无盖长方体的表面积公式S=ab+(ah+bh)×2,求出贴瓷砖的面积,再根据正方形的面积公式S=a2,求出每块瓷砖的面积,然后再用贴瓷砖的面积除以每块瓷砖的面积即可。
答案:2分米=0.2米[20×10+(20×4+10×4)×2]÷(0.2×0.2)
=[200+(80+40)×2]÷0.04
=(200+120×2)÷0.04
=(200+240)÷0.04
=440÷0.04
=11000(块)
答:至少需要11000块瓷砖。
76
236
表面积:5×5×6=150(平方厘米)
体积:5×5×5=125(立方厘米)
答:这个正方体的表面积是
150平方厘米,体积是125立方厘米。
【例3】一个高为20厘米的圆柱体,如果它的高增加2厘米,那么它的表面积就增加62.8平方厘米。求这个圆柱的体积。
题型三
精析:圆柱的高增加2厘米时,增加的表面积就等于底面积不变、高为2厘米的圆柱的侧面积,用侧面积÷2算出底面的周长,再算出其半径,然后算出底面积,就可以求出圆柱的体积了。
答案:底面半径为62.8÷2÷3.14÷2=5(厘米)
圆柱体积为3.14×52×20=1570(立方厘米)
答:这个圆柱的体积为1570立方厘米。
3000
6280
94.2÷3÷3.14÷2=5(厘米)
3.14×52×3=235.5(立方厘米)
答:这个圆柱体的体积减少了235.5立方厘米。
【例4】在一个棱长为10厘米的正方体容器中放入一个圆锥形铁块,铁块完全浸没后发现水面由原来的6厘米上升到8厘米,求这个圆锥形铁块的体积是多少立方厘米。
题型四
精析:这是等积变形的一类题,要求圆锥形铁块的体积,就是求水面上升的高度对应水的体积。
答案:10×10×(8-6)=200(立方厘米)
答:这个圆锥形铁块的体积是200立方厘米。
10
40÷2=20(厘米)
3.14×20×20×3=3768(立方厘米)
20÷2=10(厘米)
3768×3÷(3.14×10×10)=36(厘米)
答:这个圆锥体的高为36厘米。
3.14×(16÷2)2×(18-15)
=3.14×64×3
=602.88(立方厘米)
答:这块石头的体积是602.88立方厘米。
易错归纳及训练
【例1】一座大钟分针长3分米,它的尖端在一昼夜里走过的路程是多少分米?
错解:2×3.14×3×12
=18.84×12
=226.08(分米)
答:它的尖端在一昼夜里走过的路程是226.08分米。
类型一
分析:只知道利用求圆的周长的知识来解决,但对“一昼夜”这个词不理解或是没仔细审题,所以只计算出了一个白天所走过的周长,忽视了一昼夜是24小时。
正解:2×3.14×3×24
=18.84×24
=452.16(分米)
答:它的尖端在一昼夜里走过的路程是452.16分米。
圆
半径
24
【例2】一圆柱形水池,底面半径为5米,高为4米,沿这个水池的四周及底部抹水泥。如果每千克水泥可涂0.5平方米,共需多少千克水泥?
类型二
错解:2×3.14×52=157(平方米)
2×5×3.14×4=125.6(平方米)
157+125.6=282.6(平方米)
282.6÷0.5=565.2(千克)
答:共需565.2千克水泥。
分析:此题主要是错在没有考虑到水池是没有上面的盖的,只要给一个底面加一个侧面抹水泥就行了,考虑问题欠周到。
正解:3.14×52=78.5(平方米)
2×5×3.14×4=125.6(平方米)
78.5+125.6=204.1(平方米)
204.1÷0.5=408.2(千克)
答:共需408.2千克水泥。
8×4=32(平方米)
32+(8×3+4×3)×2=104(平方米)
4×8×3=96(立方米)
答:这个蓄水池占地面积是32平方米,抹水泥的面积是104平方米,水池的最大蓄水量是96立方米。
【例3】将一根长1米的圆木沿着直径劈成相等的两半,表面积增加了0.8平方米。原来这根圆木的表面积是多少平方米?
类型三
错解:0.8÷2÷1=0.4(米)
0.4×3.14×1+3.14×0.42×2=2.2608(平方米)
答:原来这根圆木的表面积是2.2608平方米。
分析:由于学生空间想象能力的差异,有些学生无法想象沿着直径劈成两半或沿着横截面切成几段各自增加的表面是什么形状的,无法想象问题的具体表象而出错。
正解:0.8÷2÷1÷2=0.2(米)
0.2×2×3.14×1+3.14×0.22×2=1.5072(平方米)答:原来这根圆木的表面积是1.5072平方米。
锯下的正方体的一个面的面积:
(98-78)÷4=20÷4=5(平方厘米)
锯下的正方体的表面积:5×6=30(平方厘米)
答:锯下的正方体的表面积是30平方厘米。
小考复习训练
66
5
3
9
27
25.12
27
9
352
384
314
86
34.54
6.28
6.0288
√
√
×
√
√
×
√
×
D
D
C
D
C
画图略
(20+7+3)×2=60(厘米)
(1)表面积:(20×10+20×9+10×9)×2=940(平方厘米)
体积:20×10×9=1800(立方厘米)
(2)
(1)3.14×3×2+3×4=30.84(厘米)
答:需要铝边长30.84厘米。
(2)3.14×3×3+3×3=37.26(平方厘米)
答:这个模型的面积是37.26平方厘米。
答:可以铺0.0314米厚。
(30-1.74)÷10÷3.14
=28.26÷10÷3.14
=2.826÷3.14
=0.9(米)
答:这棵树干的直径大约是0.9米。
底面半径:96÷2÷12=4(厘米)
圆柱体积:3.14×42×12=
602.88(立方厘米)
答:这个圆柱的体积是602.88立方厘米。
40×12+40×12=
960(平方厘米)
113.04-28.26=84.78(平方厘米)
1.505(平方厘米)
=45.76(平方厘米)
第五章 图形与几何
考点知识梳理
1. 平面图形的周长与面积
周长:封闭图形一周的长度叫做周长。
面积:物体表面或围成的平面图形的大小叫做面积。
名称 图形 周长 面积
三角形 三条边长的总和
平行四边形 四条边长的总和 底×高
S=ah
长方形 (长+宽)×2或长×2+宽×2
C=2(a+b) 长×宽
S=ab
名称 图形 周长 面积
正方形 边长×4
C=4a 边长×边长
S=a2
梯形 四条边长的总和
圆 直径×圆周率C=πd或C=2πr 圆周率×半径的平方
S=πr2
名称 图形 周长 面积
半圆 圆周长的一半+直径
C=πr+d或C=πr+2r
圆环 — 大圆的面积-小圆的面积
S环=π(R2-r2)
2. 立体图形的表面积与体积
(1)表面积:物体表面面积的总和,叫做物体的表面积。
(2)体积:物体所占空间的大小,叫做物体的体积。
(3)容积:箱子、油桶、仓库等所能容纳物体的体积,叫做它们的容积或容量。常用的容积单位是升、毫升。
(4)体积和容积单位之间的换算:
1立方分米=1升;1立方厘米=1毫升。
名称 图形 棱长总和 表面积 体积
长方体 (长+宽+高)×4
L=4(a+b+h) (长×宽+长×高+宽×高)
×2
S表=2(ab+
ah+bh) 长×宽×高
V=abh
名称 图形 棱长总和 表面积 体积
正方体 棱长×12
L=12a 棱长×棱长×6
S表=6a2 棱长×棱长×棱长
V=a3
名称 图形 棱长总和 表面积 体积
圆柱 — 一个侧面积+两个底面积
S表=S侧+2S底
=2πrh+2πr2 底面积×高
V=S底×h
=πr2h
名称 图形 棱长总和 表面积 体积
圆锥 — 一个侧面积+一个底面积
S表=S侧+S底
3. 图形间的关系
(1)面积相等的长方形(或平行四边形)和三角形,当它们等底时,三角形的高是长方形(或平行四边形)的高的2倍。
(2)长方体的棱长总和一定时,长、宽、高越接近,长方体的体积就越大,表面积也就越大。
(3)当圆柱和圆锥等底等高时,圆柱的体积是圆锥的体积的3倍;
当圆柱和圆锥等底等体积时,圆锥的高是圆柱的高的3倍;
当圆柱和圆锥等高等体积时,圆锥的底面积是圆柱的底面积的3倍。
典例精析及训练
【例1】用一张边长为10厘米的正方形纸,剪一个最大的圆,所剪的圆的面积是( )。
题型一
精析:此题考查“外方内圆”中圆面积的求法,如右图。用正方形纸剪的最大的圆的直径等于正方形的边长,所以所剪的最大的圆的面积为π(10÷2)2=25π=78.5(平方厘米)。
答案:78.5平方厘米
圆的周长:3.14×12=37.68(厘米)
圆的面积:3.14×(12÷2)2
=3.14×62
=3.14×36
=113.04(平方厘米)
答:这个圆的周长是37.68厘米,面积是113.04平方厘米。
18.84÷3.14×4=24(厘米)
答:正方形的周长是24厘米。
答:正方形的面积约占圆面积的63.7%。
【例2】一个长方体形状的露天水池,长20米,宽10米,深4米。如果在这个水池的四周和底面铺上边长是2分米的正方形瓷砖,至少需要多少块瓷砖?
题型二
精析:由于水池无盖,所以贴瓷砖的部分是这个长方体的一个底面和4个侧面的总面积,根据无盖长方体的表面积公式S=ab+(ah+bh)×2,求出贴瓷砖的面积,再根据正方形的面积公式S=a2,求出每块瓷砖的面积,然后再用贴瓷砖的面积除以每块瓷砖的面积即可。
答案:2分米=0.2米[20×10+(20×4+10×4)×2]÷(0.2×0.2)
=[200+(80+40)×2]÷0.04
=(200+120×2)÷0.04
=(200+240)÷0.04
=440÷0.04
=11000(块)
答:至少需要11000块瓷砖。
76
236
表面积:5×5×6=150(平方厘米)
体积:5×5×5=125(立方厘米)
答:这个正方体的表面积是
150平方厘米,体积是125立方厘米。
【例3】一个高为20厘米的圆柱体,如果它的高增加2厘米,那么它的表面积就增加62.8平方厘米。求这个圆柱的体积。
题型三
精析:圆柱的高增加2厘米时,增加的表面积就等于底面积不变、高为2厘米的圆柱的侧面积,用侧面积÷2算出底面的周长,再算出其半径,然后算出底面积,就可以求出圆柱的体积了。
答案:底面半径为62.8÷2÷3.14÷2=5(厘米)
圆柱体积为3.14×52×20=1570(立方厘米)
答:这个圆柱的体积为1570立方厘米。
3000
6280
94.2÷3÷3.14÷2=5(厘米)
3.14×52×3=235.5(立方厘米)
答:这个圆柱体的体积减少了235.5立方厘米。
【例4】在一个棱长为10厘米的正方体容器中放入一个圆锥形铁块,铁块完全浸没后发现水面由原来的6厘米上升到8厘米,求这个圆锥形铁块的体积是多少立方厘米。
题型四
精析:这是等积变形的一类题,要求圆锥形铁块的体积,就是求水面上升的高度对应水的体积。
答案:10×10×(8-6)=200(立方厘米)
答:这个圆锥形铁块的体积是200立方厘米。
10
40÷2=20(厘米)
3.14×20×20×3=3768(立方厘米)
20÷2=10(厘米)
3768×3÷(3.14×10×10)=36(厘米)
答:这个圆锥体的高为36厘米。
3.14×(16÷2)2×(18-15)
=3.14×64×3
=602.88(立方厘米)
答:这块石头的体积是602.88立方厘米。
易错归纳及训练
【例1】一座大钟分针长3分米,它的尖端在一昼夜里走过的路程是多少分米?
错解:2×3.14×3×12
=18.84×12
=226.08(分米)
答:它的尖端在一昼夜里走过的路程是226.08分米。
类型一
分析:只知道利用求圆的周长的知识来解决,但对“一昼夜”这个词不理解或是没仔细审题,所以只计算出了一个白天所走过的周长,忽视了一昼夜是24小时。
正解:2×3.14×3×24
=18.84×24
=452.16(分米)
答:它的尖端在一昼夜里走过的路程是452.16分米。
圆
半径
24
【例2】一圆柱形水池,底面半径为5米,高为4米,沿这个水池的四周及底部抹水泥。如果每千克水泥可涂0.5平方米,共需多少千克水泥?
类型二
错解:2×3.14×52=157(平方米)
2×5×3.14×4=125.6(平方米)
157+125.6=282.6(平方米)
282.6÷0.5=565.2(千克)
答:共需565.2千克水泥。
分析:此题主要是错在没有考虑到水池是没有上面的盖的,只要给一个底面加一个侧面抹水泥就行了,考虑问题欠周到。
正解:3.14×52=78.5(平方米)
2×5×3.14×4=125.6(平方米)
78.5+125.6=204.1(平方米)
204.1÷0.5=408.2(千克)
答:共需408.2千克水泥。
8×4=32(平方米)
32+(8×3+4×3)×2=104(平方米)
4×8×3=96(立方米)
答:这个蓄水池占地面积是32平方米,抹水泥的面积是104平方米,水池的最大蓄水量是96立方米。
【例3】将一根长1米的圆木沿着直径劈成相等的两半,表面积增加了0.8平方米。原来这根圆木的表面积是多少平方米?
类型三
错解:0.8÷2÷1=0.4(米)
0.4×3.14×1+3.14×0.42×2=2.2608(平方米)
答:原来这根圆木的表面积是2.2608平方米。
分析:由于学生空间想象能力的差异,有些学生无法想象沿着直径劈成两半或沿着横截面切成几段各自增加的表面是什么形状的,无法想象问题的具体表象而出错。
正解:0.8÷2÷1÷2=0.2(米)
0.2×2×3.14×1+3.14×0.22×2=1.5072(平方米)答:原来这根圆木的表面积是1.5072平方米。
锯下的正方体的一个面的面积:
(98-78)÷4=20÷4=5(平方厘米)
锯下的正方体的表面积:5×6=30(平方厘米)
答:锯下的正方体的表面积是30平方厘米。
小考复习训练
66
5
3
9
27
25.12
27
9
352
384
314
86
34.54
6.28
6.0288
√
√
×
√
√
×
√
×
D
D
C
D
C
画图略
(20+7+3)×2=60(厘米)
(1)表面积:(20×10+20×9+10×9)×2=940(平方厘米)
体积:20×10×9=1800(立方厘米)
(2)
(1)3.14×3×2+3×4=30.84(厘米)
答:需要铝边长30.84厘米。
(2)3.14×3×3+3×3=37.26(平方厘米)
答:这个模型的面积是37.26平方厘米。
答:可以铺0.0314米厚。
(30-1.74)÷10÷3.14
=28.26÷10÷3.14
=2.826÷3.14
=0.9(米)
答:这棵树干的直径大约是0.9米。
底面半径:96÷2÷12=4(厘米)
圆柱体积:3.14×42×12=
602.88(立方厘米)
答:这个圆柱的体积是602.88立方厘米。
40×12+40×12=
960(平方厘米)
113.04-28.26=84.78(平方厘米)
1.505(平方厘米)
=45.76(平方厘米)
同课章节目录
