【高考押题卷】2025年高考数学高频易错题考前冲刺:幂函数、指数函数、对数函数(含解析)
文档属性
| 名称 | 【高考押题卷】2025年高考数学高频易错题考前冲刺:幂函数、指数函数、对数函数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 219.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 22:15:58 | ||
图片预览




文档简介
2025年高考数学高频易错考前冲刺:幂函数、指数函数、对数函数
一.选择题(共8小题)
1.(2024秋 道里区校级期末)已知集合,B={y|y=2x+1},则A∩B=( )
A.[1,2] B.(1,2] C.[﹣2,+∞) D.(1,2)
2.(2024秋 清远期末)下列说法正确的是( )
A.若a>0,则
B.若a>0,则
C.若a>0且a≠1,则
D.若log3(log4x)=0,则x=4
3.(2024秋 铜仁市期末)已知幂函数f(x)的图象过点(8,2),则( )
A.f(x)=x B.f(x)=x
C.f(x)=x D.f(x)=x
4.(2024秋 鄂尔多斯期末)设a=30.1,b=log0.71.1,c=log32,则a,b,c的大小关系是( )
A.a>b>c B.a>c>b C.b>a>c D.c>b>a
5.(2024秋 鄂尔多斯期末)已知某种蔬菜的保鲜时间y(单位:小时)与储藏温度x(单位:℃)近似满足函数关系y=ekx+b(k,b为常数,e为自然对数底数),若该品种蔬菜在5℃时的保鲜时间为216小时,在25℃时的保鲜时间为24小时,则在15℃时,该品种蔬菜的保鲜时间大约为( )
A.120小时 B.96小时 C.72小时 D.64小时
6.(2024秋 朝阳区校级期末)已知关于x的函数在[﹣4,﹣3]上单调递增,则实数a的取值范围是( )
A.a≤4 B.a<4 C.a≤6 D.a<6
7.(2024秋 张家界期末)使式子log(2x﹣1)(3﹣x)有意义的x的取值范围是( )
A.x>3 B.x<3
C. D.且x≠1
8.(2024秋 重庆期末)某食品的保鲜时间y(单位:天)与储存温度x(单位:℃)满足函数关系y=ekx+m(e为自然对数的底数,k,m为常数).若该食品在0℃的保鲜时间是14天,在10℃的保鲜时间是7天,则该食品在20℃的保鲜时间是( )
A.48小时 B.60小时 C.72小时 D.84小时
二.多选题(共4小题)
(多选)9.(2024秋 丽水期末)下列函数中,为幂函数的是( )
A.f(x)=x3 B.f(x)=2x2 C.f(x)=x﹣1 D.f(x)=2x
(多选)10.(2025 柳州二模)已知x,y∈R,15x=3,15y=5,则( )
A.y>x B.x+y>1 C. D.
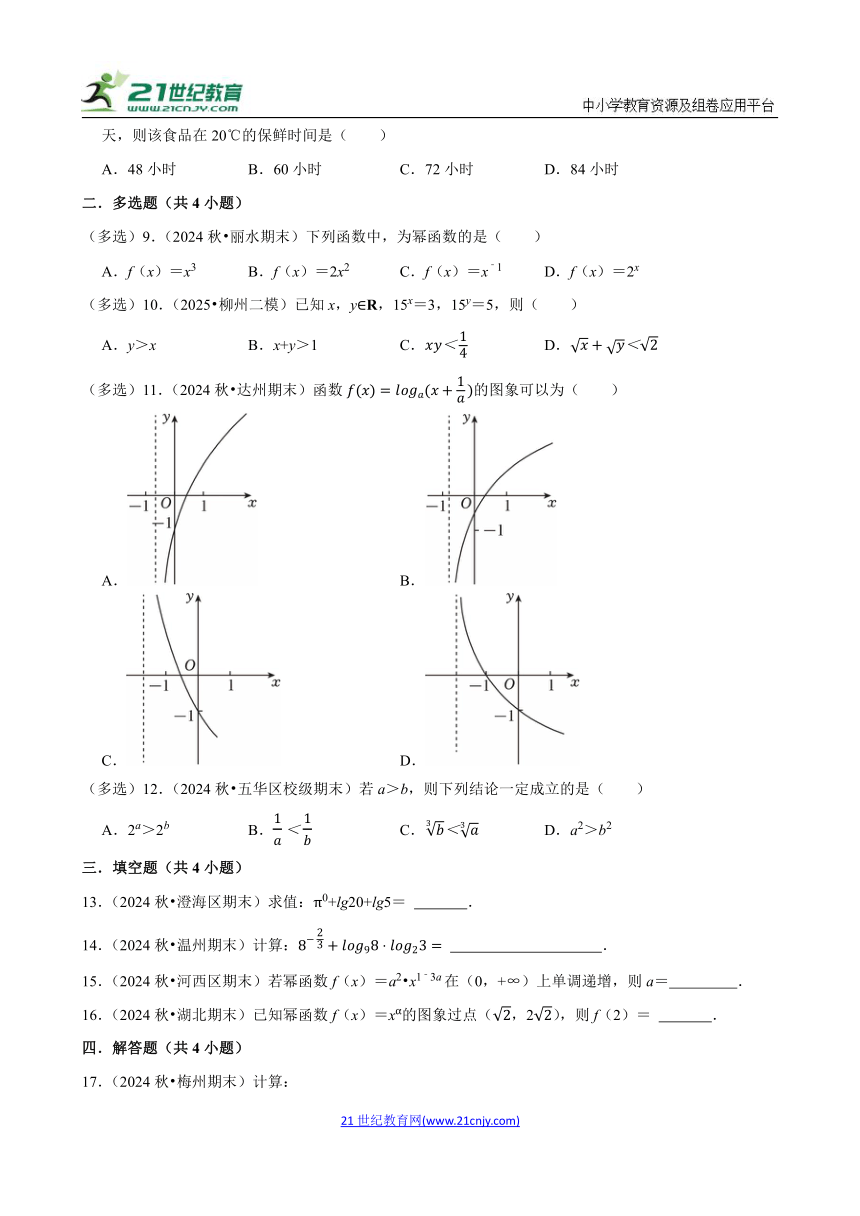
(多选)11.(2024秋 达州期末)函数的图象可以为( )
A. B.
C. D.
(多选)12.(2024秋 五华区校级期末)若a>b,则下列结论一定成立的是( )
A.2a>2b B. C. D.a2>b2
三.填空题(共4小题)
13.(2024秋 澄海区期末)求值:π0+lg20+lg5= .
14.(2024秋 温州期末)计算: .
15.(2024秋 河西区期末)若幂函数f(x)=a2 x1﹣3a在(0,+∞)上单调递增,则a= .
16.(2024秋 湖北期末)已知幂函数f(x)=xα的图象过点(,2),则f(2)= .
四.解答题(共4小题)
17.(2024秋 梅州期末)计算:
(1);
(2)log216﹣log42+log26﹣log23.
18.(2024秋 丽水期末)已知函数.
(1)求函数f(x)的定义域;
(2)若f(x)=2,求x的值.
19.(2024秋 西城区校级期末)已知函数f(x)=log4(x+2),g(x)=log2x.
(Ⅰ)当f(x)>g(x)时,求x的取值范围;
(Ⅱ)若函数在[1,8]上的最大值为6,求实数m的值;
(Ⅲ)通过软件作图发现,当x∈(﹣1,0)时,f(x)<x+1<g(x+2).试利用上述结论证明:1.1<20.2<1.2.
20.(2024秋 宝山区校级期末)已知a∈R,函数f(x)=log2[(a﹣3)x+3a﹣4].
(1)当a=2时,解不等式;
(2)若函数y=f(x2﹣4x)的值域为R,求a的取值范围.
2025年高考数学高频易错考前冲刺:幂函数、指数函数、对数函数
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 道里区校级期末)已知集合,B={y|y=2x+1},则A∩B=( )
A.[1,2] B.(1,2] C.[﹣2,+∞) D.(1,2)
【考点】指数函数的值域;求集合的交集;复合函数的定义域.
【专题】计算题;转化思想;分析法;函数的性质及应用;集合;运算求解.
【答案】B
【分析】结合函数定义域和指数函数值域求解.
【解答】解:对于集合A,有4﹣x2≥0,解得x∈[﹣2,2],故A={x|﹣2≤x≤2};
对于集合B,有2x+1>1,故B={y|y>1},
故A∩B=(1,2].
故选:B.
【点评】本题考查函数定义域与指数函数值域,集合的运算,属于基础题.
2.(2024秋 清远期末)下列说法正确的是( )
A.若a>0,则
B.若a>0,则
C.若a>0且a≠1,则
D.若log3(log4x)=0,则x=4
【考点】对数运算求值;有理数指数幂及根式化简运算求值.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】D
【分析】结合指数幂、对数的运算法则,即可求解.
【解答】解:若a>0,则,故A错误;
若a>0,则,故B错误;
若a>0且a≠1,则,故C错误;
若log3(log4x)=0,
则log4x=1,解得x=4.
故选:D.
【点评】本题主要考查指数幂、对数的运算法则,属于基础题.
3.(2024秋 铜仁市期末)已知幂函数f(x)的图象过点(8,2),则( )
A.f(x)=x B.f(x)=x
C.f(x)=x D.f(x)=x
【考点】幂函数的概念.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】D
【分析】设出幂函数,将点代入,即可求解.
【解答】解:设幂函数f(x)=xα,
幂函数f(x)的图象过点(8,2),
则8α=2,解得,
故f(x).
故选:D.
【点评】本题主要考查幂函数的概念,属于基础题.
4.(2024秋 鄂尔多斯期末)设a=30.1,b=log0.71.1,c=log32,则a,b,c的大小关系是( )
A.a>b>c B.a>c>b C.b>a>c D.c>b>a
【考点】对数函数的单调性与最值;指数函数的单调性与最值.
【答案】B
【分析】通过构造指数函数和对数函数比较大小.
【解答】解:因为函数y=3x在R上单调递增,且0.1>0,所以a=30.1>1,
因为函数y=log0.7x在(0,+∞)上单调递减,所以log0.71.1<log0.71=0,即b<0;
因为函数y=log3x在(0,+∞)上单调递增,且1<2<3,所以log31<log32<log33,即0<c<1;
所以a>c>b.
故选:B.
【点评】本题主要考查了指数函数及对数函数单调性在函数值大小比较中的应用,属于基础题.
5.(2024秋 鄂尔多斯期末)已知某种蔬菜的保鲜时间y(单位:小时)与储藏温度x(单位:℃)近似满足函数关系y=ekx+b(k,b为常数,e为自然对数底数),若该品种蔬菜在5℃时的保鲜时间为216小时,在25℃时的保鲜时间为24小时,则在15℃时,该品种蔬菜的保鲜时间大约为( )
A.120小时 B.96小时 C.72小时 D.64小时
【考点】指数函数的实际应用.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】C
【分析】根据已知类型函数式,代入条件,结合指数幂的运算,即可直接求解所求结果.
【解答】解:由题意得:,
两式相除得:e﹣20k=9,
则,
即该品种蔬菜的保鲜时间大约为72小时.
故选:C.
【点评】本题主要考查了函数的实际应用,属于基础题.
6.(2024秋 朝阳区校级期末)已知关于x的函数在[﹣4,﹣3]上单调递增,则实数a的取值范围是( )
A.a≤4 B.a<4 C.a≤6 D.a<6
【考点】由对数函数的单调性求解参数;求对数函数及对数型复合函数的单调性.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】B
【分析】根据复合函数的单调性及对数函数的定义域求解即可.
【解答】解:因为在[﹣4,﹣3]上单调递增,
函数y=x2+ax+a﹣1在[﹣4,﹣3]上单调递减,且x2+ax+a﹣1>0对于x∈[﹣4,﹣3]恒成立,
则,解得a<4.
故选:B.
【点评】本题主要考查了对数函数与二次函数复合而成的复合函数单调性的应用,属于中档题.
7.(2024秋 张家界期末)使式子log(2x﹣1)(3﹣x)有意义的x的取值范围是( )
A.x>3 B.x<3
C. D.且x≠1
【考点】求对数函数的定义域.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】D
【分析】结合对数函数的定义,即可求解.
【解答】解:log(2x﹣1)(3﹣x),
则,解得且x≠1.
故选:D.
【点评】本题主要考查对数函数定义域的求解,属于基础题.
8.(2024秋 重庆期末)某食品的保鲜时间y(单位:天)与储存温度x(单位:℃)满足函数关系y=ekx+m(e为自然对数的底数,k,m为常数).若该食品在0℃的保鲜时间是14天,在10℃的保鲜时间是7天,则该食品在20℃的保鲜时间是( )
A.48小时 B.60小时 C.72小时 D.84小时
【考点】有理数指数幂及根式化简运算求值.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】D
【分析】由已知结合指数运算性质即可求解.
【解答】解:因为y=ekx+m,
若该食品在0℃的保鲜时间是14天,在10℃的保鲜时间是7天,则,
所以e10k,
所以该食品在20℃的保鲜时间是y=e20k+m=e20k em天,即84小时.
故选:D.
【点评】本题主要考查了指数运算性质应用,属于基础题.
二.多选题(共4小题)
(多选)9.(2024秋 丽水期末)下列函数中,为幂函数的是( )
A.f(x)=x3 B.f(x)=2x2 C.f(x)=x﹣1 D.f(x)=2x
【考点】幂函数的概念.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】AC
【分析】结合幂函数的概念,即可求解.
【解答】解:幂函数的形式为y=xα(α≠0),故AC符合题意.
故选:AC.
【点评】本题主要考查幂函数的概念,属于基础题.
(多选)10.(2025 柳州二模)已知x,y∈R,15x=3,15y=5,则( )
A.y>x B.x+y>1 C. D.
【考点】对数值大小的比较.
【专题】整体思想;综合法;函数的性质及应用;不等式;运算求解.
【答案】ACD
【分析】由已知结合指数与对数的转化检验选项A,结合对数运算性质检验选项B,结合基本不等式检验选项CD.
【解答】解:因为15x=3,15y=5,
所以x=log153,y=log155,
所以y>x,A正确;
因为x+y=log153+log155=log1515=1,B错误;
xy,C正确;
()2=x+y+21+22,
故,D正确.
故选:ACD.
【点评】本题主要考查了对数运算性质,基本不等式的应用,属于基础题.
(多选)11.(2024秋 达州期末)函数的图象可以为( )
A. B.
C. D.
【考点】对数函数图象特征与底数的关系;由函数解析式求解函数图象.
【专题】数形结合;分类讨论;综合法;函数的性质及应用;数学抽象.
【答案】ACD
【分析】由已知结合对数函数的性质及函数图象的平移变换检验各选项.
【解答】解:由题意可得,a>0且a≠1,
故f(x)的图象可看着由y=logax的图象向左平移个单位,
因为f(0)=loga1,当y=0时,x=1,
当a>1时,选项A符合题意,B错误;
当0<a<1时,x=10,CD都符合题意.
故选:ACD.
【点评】本题主要考查了对数函数的图象变换的应用,属于基础题.
(多选)12.(2024秋 五华区校级期末)若a>b,则下列结论一定成立的是( )
A.2a>2b B. C. D.a2>b2
【考点】指数函数的单调性与最值;幂函数的单调性与最值.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】AC
【分析】根据指数函数和幂函数的单调性即可判断AC;举例说明即可判断BD.
【解答】解:因为a>b,且y=2x在R上是增函数,所以2a>2b,故A正确;
当a=1,b=﹣1时,满足a>b,但,故B错误;
因为a>b,且在R上是增函数,所以,故C正确;
当a=0,b=﹣1时,a2<b2,故D错误.
故选:AC.
【点评】本题主要考查函数的单调性,以及不等式的性质,属于基础题.
三.填空题(共4小题)
13.(2024秋 澄海区期末)求值:π0+lg20+lg5= 3 .
【考点】对数运算求值.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】3.
【分析】结合指数幂、对数的运算法则,即可求解.
【解答】解:π0+lg20+lg5=1+lg100=1+lg102=1+2=3.
故答案为:3.
【点评】本题主要考查指数幂、对数的运算法则,属于基础题.
14.(2024秋 温州期末)计算: .
【考点】对数的运算性质.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】.
【分析】由已知结合指数及对数运算性质即可求解.
【解答】解:
.
故答案为:.
【点评】本题主要考查了指数及对数运算性质的应用,属于基础题.
15.(2024秋 河西区期末)若幂函数f(x)=a2 x1﹣3a在(0,+∞)上单调递增,则a= ﹣1 .
【考点】由幂函数的单调性求解参数.
【专题】转化思想;综合法;函数的性质及应用;运算求解.
【答案】﹣1.
【分析】由幂函数定义和性质列出关于a的方程和不等式即可求解.
【解答】解:根据题意,幂函数f(x)=a2 x1﹣3a在(0,+∞)上单调递增,
则.
故答案为:﹣1.
【点评】本题考查了幂函数定义和性质,属于基础题.
16.(2024秋 湖北期末)已知幂函数f(x)=xα的图象过点(,2),则f(2)= 8 .
【考点】求幂函数的解析式.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】8.
【分析】先求出函数解析式,再将x=2代入,即可求解.
【解答】解:幂函数f(x)=xα的图象过点(,2),
则,解得α=3,
故f(x)=x3,
所以f(2)=23=8.
【点评】本题主要考查函数解析式的求解,属于基础题.
四.解答题(共4小题)
17.(2024秋 梅州期末)计算:
(1);
(2)log216﹣log42+log26﹣log23.
【考点】对数运算求值;有理数指数幂及根式化简运算求值.
【专题】函数思想;定义法;函数的性质及应用;运算求解.
【答案】(1);(2).
【分析】(1)利用指数的性质、运算法则求解;
(2)利用对数的性质、运算法则求解.
【解答】解:(1)
=1﹣9﹣9
.
(2)log216﹣log42+log26﹣log23
=41
.
【点评】本题考查指数、对数的性质、运算法则等基础知识,考查运算求解能力,是基础题.
18.(2024秋 丽水期末)已知函数.
(1)求函数f(x)的定义域;
(2)若f(x)=2,求x的值.
【考点】对数的运算性质;函数的定义域及其求法.
【专题】函数思想;定义法;函数的性质及应用;运算求解.
【答案】(1)(﹣1,1);(2).
【分析】(1)由0,能求出函数f(x)的定义域.
(2)f(x)=2时,,由此能求出x的值.
【解答】解:(1)函数.
,
∴函数f(x)的定义域是(﹣1,1).
(2),
∴若f(x)=2,则x的值为.
【点评】本题考查对数函数的定义域、性质等基础知识,考查运算求解能力,是基础题.
19.(2024秋 西城区校级期末)已知函数f(x)=log4(x+2),g(x)=log2x.
(Ⅰ)当f(x)>g(x)时,求x的取值范围;
(Ⅱ)若函数在[1,8]上的最大值为6,求实数m的值;
(Ⅲ)通过软件作图发现,当x∈(﹣1,0)时,f(x)<x+1<g(x+2).试利用上述结论证明:1.1<20.2<1.2.
【考点】求对数函数及对数型复合函数的最值;指、对数不等式的解法.
【专题】计算题;证明题;转化思想;综合法;函数的性质及应用;逻辑思维;运算求解.
【答案】(Ⅰ)x的取值范围为(0,2);
(Ⅱ)实数m的值为或1;
(Ⅲ)证明见解析.
【分析】(Ⅰ)根据对数函数的单调性求解不等式;
(Ⅱ)代入函数表达式后分类讨论;
(Ⅲ)根据题目已知结论证明.
【解答】解:(Ⅰ)由题意函数f(x)的定义域为(﹣2,+∞),g(x)的定义域为(0,+∞),
由f(x)>g(x)得,
故x+2>x2,得﹣1<x<2,又x>0,
故x的取值范围为(0,2).
(Ⅱ),
设t=log2x,因x∈[1,8],故0≤t≤3,
则,
当,即时,当t=3时,取得最大值6,故(log2m+3)(3﹣1)=6,得m=1,
当即时,当t=0时,取得最大值6,故(log2m+0)(0﹣1)=6,得,
故实数m的值为或1.
(Ⅲ)证明:当x=﹣0.9时,由f(x)<x+1可得log41.1<0.1,故1.1<40.1=20.2,
当x=﹣0.8时,由x+1<g(x+2)可得0.2<log21.2,故20.2<1.2,故1.1<20.2<1.2.
【点评】本题考查指数函数与对数函数的性质及其对数不等式的解法,属于较难题.
20.(2024秋 宝山区校级期末)已知a∈R,函数f(x)=log2[(a﹣3)x+3a﹣4].
(1)当a=2时,解不等式;
(2)若函数y=f(x2﹣4x)的值域为R,求a的取值范围.
【考点】求对数函数及对数型复合函数的单调性.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】(1);
(2)[8,+∞).
【分析】(1)由题意得到对数不等式,求解不等式即可;
(2)将原问题转化为二次函数的问题,结合二次函数的开口方向和判别式可得关于实数a的不等式,求解即可.
【解答】解:(1)a=2 时,f(x)=log2(﹣x+2),
不等式 等价于 ,
所以 ,解得,
所以不等式 的解集为.
(2)因为函数 y=f(x2﹣4x)的值域为R,
即的值域为R,
故(a﹣3)x2﹣4(a﹣3)x+3a﹣4 能取到一切正数,
当a=3时,(a﹣3)x2﹣4(a﹣3)x+3a﹣4=5,不符合题意;
当 a<3 时,(a﹣3)x2﹣4(a﹣3)x+3a﹣4=(a﹣3)(x﹣2)2+8﹣a≤8﹣a,不符合题意;
当 a>3 时,根据二次函数的图象和性质可得Δ=16(a﹣3)2﹣4(a﹣3)(3a﹣4)≥0,解得a≤3或a≥8,所以a≥8;
综上所述:a的取值范围是[8,+∞).
【点评】本题主要考查了函数的性质的综合应用,属于中档题.
21世纪教育网(www.21cnjy.com)
一.选择题(共8小题)
1.(2024秋 道里区校级期末)已知集合,B={y|y=2x+1},则A∩B=( )
A.[1,2] B.(1,2] C.[﹣2,+∞) D.(1,2)
2.(2024秋 清远期末)下列说法正确的是( )
A.若a>0,则
B.若a>0,则
C.若a>0且a≠1,则
D.若log3(log4x)=0,则x=4
3.(2024秋 铜仁市期末)已知幂函数f(x)的图象过点(8,2),则( )
A.f(x)=x B.f(x)=x
C.f(x)=x D.f(x)=x
4.(2024秋 鄂尔多斯期末)设a=30.1,b=log0.71.1,c=log32,则a,b,c的大小关系是( )
A.a>b>c B.a>c>b C.b>a>c D.c>b>a
5.(2024秋 鄂尔多斯期末)已知某种蔬菜的保鲜时间y(单位:小时)与储藏温度x(单位:℃)近似满足函数关系y=ekx+b(k,b为常数,e为自然对数底数),若该品种蔬菜在5℃时的保鲜时间为216小时,在25℃时的保鲜时间为24小时,则在15℃时,该品种蔬菜的保鲜时间大约为( )
A.120小时 B.96小时 C.72小时 D.64小时
6.(2024秋 朝阳区校级期末)已知关于x的函数在[﹣4,﹣3]上单调递增,则实数a的取值范围是( )
A.a≤4 B.a<4 C.a≤6 D.a<6
7.(2024秋 张家界期末)使式子log(2x﹣1)(3﹣x)有意义的x的取值范围是( )
A.x>3 B.x<3
C. D.且x≠1
8.(2024秋 重庆期末)某食品的保鲜时间y(单位:天)与储存温度x(单位:℃)满足函数关系y=ekx+m(e为自然对数的底数,k,m为常数).若该食品在0℃的保鲜时间是14天,在10℃的保鲜时间是7天,则该食品在20℃的保鲜时间是( )
A.48小时 B.60小时 C.72小时 D.84小时
二.多选题(共4小题)
(多选)9.(2024秋 丽水期末)下列函数中,为幂函数的是( )
A.f(x)=x3 B.f(x)=2x2 C.f(x)=x﹣1 D.f(x)=2x
(多选)10.(2025 柳州二模)已知x,y∈R,15x=3,15y=5,则( )
A.y>x B.x+y>1 C. D.
(多选)11.(2024秋 达州期末)函数的图象可以为( )
A. B.
C. D.
(多选)12.(2024秋 五华区校级期末)若a>b,则下列结论一定成立的是( )
A.2a>2b B. C. D.a2>b2
三.填空题(共4小题)
13.(2024秋 澄海区期末)求值:π0+lg20+lg5= .
14.(2024秋 温州期末)计算: .
15.(2024秋 河西区期末)若幂函数f(x)=a2 x1﹣3a在(0,+∞)上单调递增,则a= .
16.(2024秋 湖北期末)已知幂函数f(x)=xα的图象过点(,2),则f(2)= .
四.解答题(共4小题)
17.(2024秋 梅州期末)计算:
(1);
(2)log216﹣log42+log26﹣log23.
18.(2024秋 丽水期末)已知函数.
(1)求函数f(x)的定义域;
(2)若f(x)=2,求x的值.
19.(2024秋 西城区校级期末)已知函数f(x)=log4(x+2),g(x)=log2x.
(Ⅰ)当f(x)>g(x)时,求x的取值范围;
(Ⅱ)若函数在[1,8]上的最大值为6,求实数m的值;
(Ⅲ)通过软件作图发现,当x∈(﹣1,0)时,f(x)<x+1<g(x+2).试利用上述结论证明:1.1<20.2<1.2.
20.(2024秋 宝山区校级期末)已知a∈R,函数f(x)=log2[(a﹣3)x+3a﹣4].
(1)当a=2时,解不等式;
(2)若函数y=f(x2﹣4x)的值域为R,求a的取值范围.
2025年高考数学高频易错考前冲刺:幂函数、指数函数、对数函数
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 道里区校级期末)已知集合,B={y|y=2x+1},则A∩B=( )
A.[1,2] B.(1,2] C.[﹣2,+∞) D.(1,2)
【考点】指数函数的值域;求集合的交集;复合函数的定义域.
【专题】计算题;转化思想;分析法;函数的性质及应用;集合;运算求解.
【答案】B
【分析】结合函数定义域和指数函数值域求解.
【解答】解:对于集合A,有4﹣x2≥0,解得x∈[﹣2,2],故A={x|﹣2≤x≤2};
对于集合B,有2x+1>1,故B={y|y>1},
故A∩B=(1,2].
故选:B.
【点评】本题考查函数定义域与指数函数值域,集合的运算,属于基础题.
2.(2024秋 清远期末)下列说法正确的是( )
A.若a>0,则
B.若a>0,则
C.若a>0且a≠1,则
D.若log3(log4x)=0,则x=4
【考点】对数运算求值;有理数指数幂及根式化简运算求值.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】D
【分析】结合指数幂、对数的运算法则,即可求解.
【解答】解:若a>0,则,故A错误;
若a>0,则,故B错误;
若a>0且a≠1,则,故C错误;
若log3(log4x)=0,
则log4x=1,解得x=4.
故选:D.
【点评】本题主要考查指数幂、对数的运算法则,属于基础题.
3.(2024秋 铜仁市期末)已知幂函数f(x)的图象过点(8,2),则( )
A.f(x)=x B.f(x)=x
C.f(x)=x D.f(x)=x
【考点】幂函数的概念.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】D
【分析】设出幂函数,将点代入,即可求解.
【解答】解:设幂函数f(x)=xα,
幂函数f(x)的图象过点(8,2),
则8α=2,解得,
故f(x).
故选:D.
【点评】本题主要考查幂函数的概念,属于基础题.
4.(2024秋 鄂尔多斯期末)设a=30.1,b=log0.71.1,c=log32,则a,b,c的大小关系是( )
A.a>b>c B.a>c>b C.b>a>c D.c>b>a
【考点】对数函数的单调性与最值;指数函数的单调性与最值.
【答案】B
【分析】通过构造指数函数和对数函数比较大小.
【解答】解:因为函数y=3x在R上单调递增,且0.1>0,所以a=30.1>1,
因为函数y=log0.7x在(0,+∞)上单调递减,所以log0.71.1<log0.71=0,即b<0;
因为函数y=log3x在(0,+∞)上单调递增,且1<2<3,所以log31<log32<log33,即0<c<1;
所以a>c>b.
故选:B.
【点评】本题主要考查了指数函数及对数函数单调性在函数值大小比较中的应用,属于基础题.
5.(2024秋 鄂尔多斯期末)已知某种蔬菜的保鲜时间y(单位:小时)与储藏温度x(单位:℃)近似满足函数关系y=ekx+b(k,b为常数,e为自然对数底数),若该品种蔬菜在5℃时的保鲜时间为216小时,在25℃时的保鲜时间为24小时,则在15℃时,该品种蔬菜的保鲜时间大约为( )
A.120小时 B.96小时 C.72小时 D.64小时
【考点】指数函数的实际应用.
【专题】函数思想;综合法;函数的性质及应用;运算求解.
【答案】C
【分析】根据已知类型函数式,代入条件,结合指数幂的运算,即可直接求解所求结果.
【解答】解:由题意得:,
两式相除得:e﹣20k=9,
则,
即该品种蔬菜的保鲜时间大约为72小时.
故选:C.
【点评】本题主要考查了函数的实际应用,属于基础题.
6.(2024秋 朝阳区校级期末)已知关于x的函数在[﹣4,﹣3]上单调递增,则实数a的取值范围是( )
A.a≤4 B.a<4 C.a≤6 D.a<6
【考点】由对数函数的单调性求解参数;求对数函数及对数型复合函数的单调性.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】B
【分析】根据复合函数的单调性及对数函数的定义域求解即可.
【解答】解:因为在[﹣4,﹣3]上单调递增,
函数y=x2+ax+a﹣1在[﹣4,﹣3]上单调递减,且x2+ax+a﹣1>0对于x∈[﹣4,﹣3]恒成立,
则,解得a<4.
故选:B.
【点评】本题主要考查了对数函数与二次函数复合而成的复合函数单调性的应用,属于中档题.
7.(2024秋 张家界期末)使式子log(2x﹣1)(3﹣x)有意义的x的取值范围是( )
A.x>3 B.x<3
C. D.且x≠1
【考点】求对数函数的定义域.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】D
【分析】结合对数函数的定义,即可求解.
【解答】解:log(2x﹣1)(3﹣x),
则,解得且x≠1.
故选:D.
【点评】本题主要考查对数函数定义域的求解,属于基础题.
8.(2024秋 重庆期末)某食品的保鲜时间y(单位:天)与储存温度x(单位:℃)满足函数关系y=ekx+m(e为自然对数的底数,k,m为常数).若该食品在0℃的保鲜时间是14天,在10℃的保鲜时间是7天,则该食品在20℃的保鲜时间是( )
A.48小时 B.60小时 C.72小时 D.84小时
【考点】有理数指数幂及根式化简运算求值.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】D
【分析】由已知结合指数运算性质即可求解.
【解答】解:因为y=ekx+m,
若该食品在0℃的保鲜时间是14天,在10℃的保鲜时间是7天,则,
所以e10k,
所以该食品在20℃的保鲜时间是y=e20k+m=e20k em天,即84小时.
故选:D.
【点评】本题主要考查了指数运算性质应用,属于基础题.
二.多选题(共4小题)
(多选)9.(2024秋 丽水期末)下列函数中,为幂函数的是( )
A.f(x)=x3 B.f(x)=2x2 C.f(x)=x﹣1 D.f(x)=2x
【考点】幂函数的概念.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】AC
【分析】结合幂函数的概念,即可求解.
【解答】解:幂函数的形式为y=xα(α≠0),故AC符合题意.
故选:AC.
【点评】本题主要考查幂函数的概念,属于基础题.
(多选)10.(2025 柳州二模)已知x,y∈R,15x=3,15y=5,则( )
A.y>x B.x+y>1 C. D.
【考点】对数值大小的比较.
【专题】整体思想;综合法;函数的性质及应用;不等式;运算求解.
【答案】ACD
【分析】由已知结合指数与对数的转化检验选项A,结合对数运算性质检验选项B,结合基本不等式检验选项CD.
【解答】解:因为15x=3,15y=5,
所以x=log153,y=log155,
所以y>x,A正确;
因为x+y=log153+log155=log1515=1,B错误;
xy,C正确;
()2=x+y+21+22,
故,D正确.
故选:ACD.
【点评】本题主要考查了对数运算性质,基本不等式的应用,属于基础题.
(多选)11.(2024秋 达州期末)函数的图象可以为( )
A. B.
C. D.
【考点】对数函数图象特征与底数的关系;由函数解析式求解函数图象.
【专题】数形结合;分类讨论;综合法;函数的性质及应用;数学抽象.
【答案】ACD
【分析】由已知结合对数函数的性质及函数图象的平移变换检验各选项.
【解答】解:由题意可得,a>0且a≠1,
故f(x)的图象可看着由y=logax的图象向左平移个单位,
因为f(0)=loga1,当y=0时,x=1,
当a>1时,选项A符合题意,B错误;
当0<a<1时,x=10,CD都符合题意.
故选:ACD.
【点评】本题主要考查了对数函数的图象变换的应用,属于基础题.
(多选)12.(2024秋 五华区校级期末)若a>b,则下列结论一定成立的是( )
A.2a>2b B. C. D.a2>b2
【考点】指数函数的单调性与最值;幂函数的单调性与最值.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】AC
【分析】根据指数函数和幂函数的单调性即可判断AC;举例说明即可判断BD.
【解答】解:因为a>b,且y=2x在R上是增函数,所以2a>2b,故A正确;
当a=1,b=﹣1时,满足a>b,但,故B错误;
因为a>b,且在R上是增函数,所以,故C正确;
当a=0,b=﹣1时,a2<b2,故D错误.
故选:AC.
【点评】本题主要考查函数的单调性,以及不等式的性质,属于基础题.
三.填空题(共4小题)
13.(2024秋 澄海区期末)求值:π0+lg20+lg5= 3 .
【考点】对数运算求值.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】3.
【分析】结合指数幂、对数的运算法则,即可求解.
【解答】解:π0+lg20+lg5=1+lg100=1+lg102=1+2=3.
故答案为:3.
【点评】本题主要考查指数幂、对数的运算法则,属于基础题.
14.(2024秋 温州期末)计算: .
【考点】对数的运算性质.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】.
【分析】由已知结合指数及对数运算性质即可求解.
【解答】解:
.
故答案为:.
【点评】本题主要考查了指数及对数运算性质的应用,属于基础题.
15.(2024秋 河西区期末)若幂函数f(x)=a2 x1﹣3a在(0,+∞)上单调递增,则a= ﹣1 .
【考点】由幂函数的单调性求解参数.
【专题】转化思想;综合法;函数的性质及应用;运算求解.
【答案】﹣1.
【分析】由幂函数定义和性质列出关于a的方程和不等式即可求解.
【解答】解:根据题意,幂函数f(x)=a2 x1﹣3a在(0,+∞)上单调递增,
则.
故答案为:﹣1.
【点评】本题考查了幂函数定义和性质,属于基础题.
16.(2024秋 湖北期末)已知幂函数f(x)=xα的图象过点(,2),则f(2)= 8 .
【考点】求幂函数的解析式.
【专题】转化思想;转化法;函数的性质及应用;运算求解.
【答案】8.
【分析】先求出函数解析式,再将x=2代入,即可求解.
【解答】解:幂函数f(x)=xα的图象过点(,2),
则,解得α=3,
故f(x)=x3,
所以f(2)=23=8.
【点评】本题主要考查函数解析式的求解,属于基础题.
四.解答题(共4小题)
17.(2024秋 梅州期末)计算:
(1);
(2)log216﹣log42+log26﹣log23.
【考点】对数运算求值;有理数指数幂及根式化简运算求值.
【专题】函数思想;定义法;函数的性质及应用;运算求解.
【答案】(1);(2).
【分析】(1)利用指数的性质、运算法则求解;
(2)利用对数的性质、运算法则求解.
【解答】解:(1)
=1﹣9﹣9
.
(2)log216﹣log42+log26﹣log23
=41
.
【点评】本题考查指数、对数的性质、运算法则等基础知识,考查运算求解能力,是基础题.
18.(2024秋 丽水期末)已知函数.
(1)求函数f(x)的定义域;
(2)若f(x)=2,求x的值.
【考点】对数的运算性质;函数的定义域及其求法.
【专题】函数思想;定义法;函数的性质及应用;运算求解.
【答案】(1)(﹣1,1);(2).
【分析】(1)由0,能求出函数f(x)的定义域.
(2)f(x)=2时,,由此能求出x的值.
【解答】解:(1)函数.
,
∴函数f(x)的定义域是(﹣1,1).
(2),
∴若f(x)=2,则x的值为.
【点评】本题考查对数函数的定义域、性质等基础知识,考查运算求解能力,是基础题.
19.(2024秋 西城区校级期末)已知函数f(x)=log4(x+2),g(x)=log2x.
(Ⅰ)当f(x)>g(x)时,求x的取值范围;
(Ⅱ)若函数在[1,8]上的最大值为6,求实数m的值;
(Ⅲ)通过软件作图发现,当x∈(﹣1,0)时,f(x)<x+1<g(x+2).试利用上述结论证明:1.1<20.2<1.2.
【考点】求对数函数及对数型复合函数的最值;指、对数不等式的解法.
【专题】计算题;证明题;转化思想;综合法;函数的性质及应用;逻辑思维;运算求解.
【答案】(Ⅰ)x的取值范围为(0,2);
(Ⅱ)实数m的值为或1;
(Ⅲ)证明见解析.
【分析】(Ⅰ)根据对数函数的单调性求解不等式;
(Ⅱ)代入函数表达式后分类讨论;
(Ⅲ)根据题目已知结论证明.
【解答】解:(Ⅰ)由题意函数f(x)的定义域为(﹣2,+∞),g(x)的定义域为(0,+∞),
由f(x)>g(x)得,
故x+2>x2,得﹣1<x<2,又x>0,
故x的取值范围为(0,2).
(Ⅱ),
设t=log2x,因x∈[1,8],故0≤t≤3,
则,
当,即时,当t=3时,取得最大值6,故(log2m+3)(3﹣1)=6,得m=1,
当即时,当t=0时,取得最大值6,故(log2m+0)(0﹣1)=6,得,
故实数m的值为或1.
(Ⅲ)证明:当x=﹣0.9时,由f(x)<x+1可得log41.1<0.1,故1.1<40.1=20.2,
当x=﹣0.8时,由x+1<g(x+2)可得0.2<log21.2,故20.2<1.2,故1.1<20.2<1.2.
【点评】本题考查指数函数与对数函数的性质及其对数不等式的解法,属于较难题.
20.(2024秋 宝山区校级期末)已知a∈R,函数f(x)=log2[(a﹣3)x+3a﹣4].
(1)当a=2时,解不等式;
(2)若函数y=f(x2﹣4x)的值域为R,求a的取值范围.
【考点】求对数函数及对数型复合函数的单调性.
【专题】整体思想;综合法;函数的性质及应用;运算求解.
【答案】(1);
(2)[8,+∞).
【分析】(1)由题意得到对数不等式,求解不等式即可;
(2)将原问题转化为二次函数的问题,结合二次函数的开口方向和判别式可得关于实数a的不等式,求解即可.
【解答】解:(1)a=2 时,f(x)=log2(﹣x+2),
不等式 等价于 ,
所以 ,解得,
所以不等式 的解集为.
(2)因为函数 y=f(x2﹣4x)的值域为R,
即的值域为R,
故(a﹣3)x2﹣4(a﹣3)x+3a﹣4 能取到一切正数,
当a=3时,(a﹣3)x2﹣4(a﹣3)x+3a﹣4=5,不符合题意;
当 a<3 时,(a﹣3)x2﹣4(a﹣3)x+3a﹣4=(a﹣3)(x﹣2)2+8﹣a≤8﹣a,不符合题意;
当 a>3 时,根据二次函数的图象和性质可得Δ=16(a﹣3)2﹣4(a﹣3)(3a﹣4)≥0,解得a≤3或a≥8,所以a≥8;
综上所述:a的取值范围是[8,+∞).
【点评】本题主要考查了函数的性质的综合应用,属于中档题.
21世纪教育网(www.21cnjy.com)
同课章节目录
