小学毕业数学总复习第二章数的运算第2课时运算定律及简便运算课件(共62张PPT)
文档属性
| 名称 | 小学毕业数学总复习第二章数的运算第2课时运算定律及简便运算课件(共62张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 17:02:43 | ||
图片预览










文档简介
(共62张PPT)
第二章 数的运算
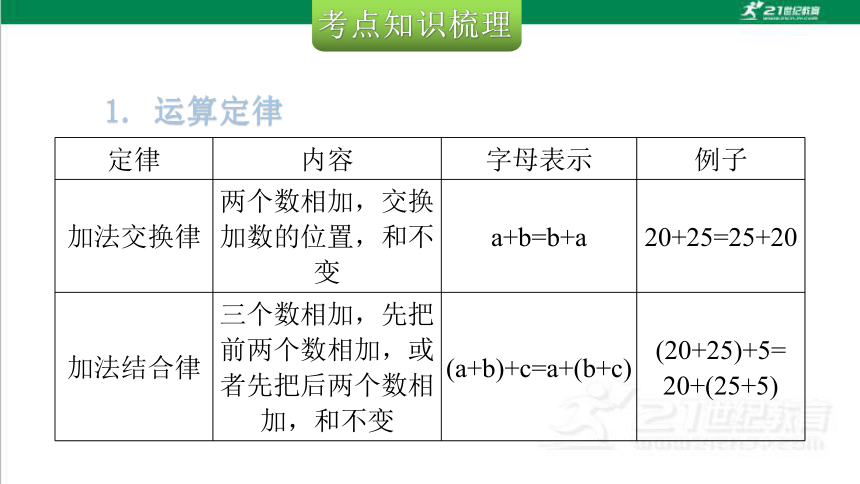
考点知识梳理
定律 内容 字母表示 例子
加法交换律 两个数相加,交换加数的位置,和不变 a+b=b+a 20+25=25+20
加法结合律 三个数相加,先把前两个数相加,或者先把后两个数相加,和不变 (a+b)+c=a+(b+c) (20+25)+5=
20+(25+5)
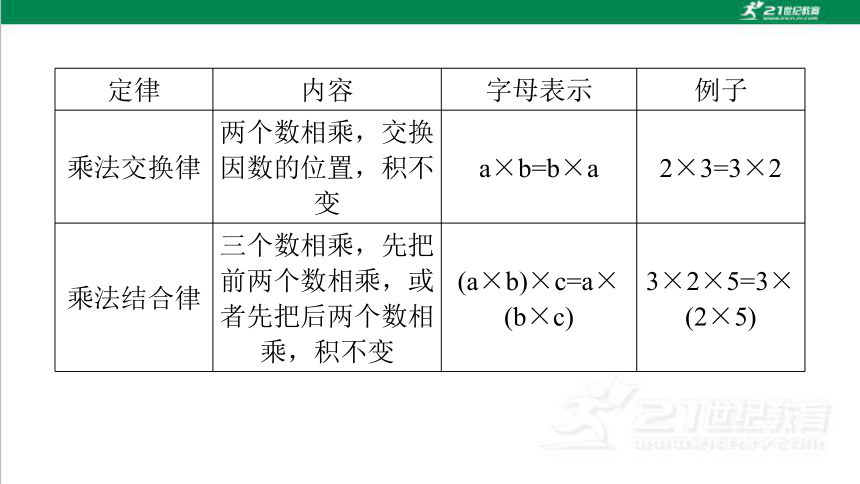
定律 内容 字母表示 例子
乘法交换律 两个数相乘,交换因数的位置,积不变 a×b=b×a 2×3=3×2
乘法结合律 三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变 (a×b)×c=a×(b×c) 3×2×5=3×(2×5)
定律 内容 字母表示 例子
乘法分配律 两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再把积相加,结果不变 (a+b)×c=a×c+b×c (2+3)×5=2×5+3×5
名称 内容 字母表示及推广
减法性质 一个数连续减去两个数,等于这个数减去这两个数的和 a-b-c=a-(b+c)
a-(b+c)=a-b-c
一个数减去两个数的差,等于先从这个数中减去差里的被减数,然后加上减数 a-(b-c)=a-b+c
a-b+c=a-(b-c)
a+b-c=a+(b-c)
名称 内容 字母表示及推广
除法性质 一个数连续除以几个数(0除外),可以用这个数除以所有除数的积 a÷(b×c)=a÷b÷c
a÷b÷c=a÷(b×c)
a÷(b÷c)=a÷b×c
积不变的规律 当一个因数乘(或除以)一个数(0除外),另一个因数除以(或乘)同一个数时,它们的积不变 a×b=(a×c)×(b÷c)(c≠0)
注意:在有余数的整数除法中,利用商不变的性质时,商是不变的,但余数会扩大或缩小相同的倍数。
例如:25÷4=6……1
2500÷400=6……100
3. 简便运算
(1)一般情况下,四则运算的计算顺序:有括号时,先算括号里面的;没有括号时,先算乘除法,再算加减法;只有同一级运算时,按从左往右的顺序计算。
(2)由于有的计算题具有它自身的特征,这时运用运算定律,可以使计算过程简便,同时又不容易出错。
4. 常见的简便运算方法
(1)把数化整。为了便于简算,能凑成整十、整百、整千的数,要把一些数交换,结合在一起先算。
(2)改变运算顺序,把能简算的步骤按定律、性质等规定改变原来的运算顺序或形式(有时需要去括号或添括号)。
(3)把已知数适当进行分解,可使计算简便。
(4)把算式中某些具有相同特点的数,结合在一起再计算,可使计算简便。
典例精析及训练
【例1】用简便方法计算。
(1)1.24+0.78+8.76 (2)7.05-3.84-0.16
精析:(1)①加法交换律: a+b=b+a。②加法结合律:(a+b)+c=a+(b+c)。(2)减法的运算性质: a-b-c=a-(b+c)。
题型一
答案:(1)1.24+0.78+8.76
=(1.24+8.76)+0.78
=10+0.78
=10.78
(2)7.05-3.84-0.16
=7.05-(3.84+0.16)
=7.05-4
=3.05
=(0.21+0.79)+(12.3+7.7)
=1+20
=21
=(6.51-3.51)+(2.74+7.26)
=3+10
=13
1592+3698+408+302
=(1592+408)+(3698+302)
=2000+4000
=6000
=80
题型二
【例2】用简便方法计算。
(1)2.5×12.5×4×8 (2)48×
精析:①乘法交换律: a×b=b×a。②乘法结合律:(a×b)×c=a×(b×c)。③乘法分配律:(a+b)×c=a×c+b×c。④两组特殊算式的乘积:25×4=100,125×8=1000。
答案:(1)2.5×12.5×4×8
=(2.5×4)×(12.5×8)
=10×100
=1000
=(2.5×4)×6
=10×6
=60
=0.25×40×19
=10×19
=190
90.5×99+90.5 7.7×7+7.7+2×7.7
=90.5×(99+1)
=90.5×100
=9050
=7.7×(7+2+1)
=7.7×10
=77
【例3】计算:(1)9999×1001 (2)1.71×99
精析:(1)此题把1001看成1000+1,然后根据乘法分配律去简算。(2)把99看成100-1,然后根据乘法分配律进行计算。
题型三
答案:(1)9999×1001 (2)1.71×99
=9999×(1000+1)
=9999×1000+9999×1
=9999000+9999
=10008999
=1.71×(100-1)
=1.71×100-1.71×1
=171-1.71
=169.29
=1.25×(800+8)
=1.25×800+1.25×8
=1000+10
=1010
=25×(40+1)
=25×40+25×1
=1000+25
=1025
11×49 23×99
=(10+1)×49
=10×49+1×49
=490+49
=539
=23×(100-1)
=23×100-23×1
=2300-23
=2277
205×7 63×10.1
=(200+5)×7
=200×7+5×7
=1400+35
=1435
=63×(10+0.1)
=63×10+63×0.1
=630+6.3
=636.3
【例4】计算:7.2÷(0.2×6)。
精析:此题可应用除法的性质:一个数除以两个数的积,等于这个数依次除以积里面的两个因数来计算。
题型四
答案:7.2÷(0.2×6)
=7.2÷0.2÷6
=36÷6
=6
0.406
×
=3.25÷(2.5×4)
=3.25÷10
=0.325
=125÷50×8
=125×8÷50
=1000÷50
=20
350÷(35×2)
=350÷35÷2
=10÷2
=5
易错归纳及训练
【例1】计算:493-255-145。
错解:493-255-145
=493-(255-145)
=493-110
=383
类型一
分析:添括号后,括号前面是“-”的,移进括号后“-”变“+”,“+”变“-”。在简便运算过程中,需要添括号或去括号时,一定要注意括号前面原来是“+”还是“-”,如果是“+”,添、去括号后原来的数不变号,如果是“-”,添、去括号后原来的数“-”变“+”,“+”变“-”。
正解:493-255-145
=493-(255+145)
=493-400
=93
4.3-2.45+5.7-6.55 35.01-3.03-16.97
=(4.3+5.7)-(2.45+6.55)
=10-9
=1
=35.01-(3.03+16.97)
=35.01-20
=15.01
【例2】用简便方法计算。
(125-40)×8 860÷(86×5)
错解:(125-40)×8 860÷(86×5)
=125×8-40 =860÷86×5
=1000-40 =10×5
=960 =50
类型二
分析:运用乘法分配律时,括号外面的数应和括号里面的每一个数都相乘再相加、减。运用运算性质时,要注意括号及运算符号的使用。
正解:(125-40)×8 860÷(86×5)
=125×8-40×8 =860÷86÷5
=1000-320 =10÷5
=680 =2
4.2×101-4.2
=4.2×101-4.2×1
=(101-1)×4.2
=100×4.2
=420
小考复习训练
3
÷
÷
5
×
4
×
4
(答案不唯一)
(69+31)
加法结合律
(a+b)+c=a+(b+c)
(32+68)
乘法分配律
a×(b+c)=ab+ac
=
<
<
>
2400
42
C
C
C
B
A
B
77.49
33.852
128.625
0.27
(竖式略)
=85×(156-56)
=85×100
=8500
=15×(10-0.1)
=15×10-15×0.1
=150-1.5
=148.5
159×68+159×33-159
=159×(68+33-1)
=159×100
=15900
3.7×5.4+0.37×46
=3.7×(5.4+4.6)
=3.7×10
=37
15.43-(2.6+5.43)
=15.43-5.43-2.6
=10-2.6
=7.4
2000÷12.5÷0.8
=2000÷(12.5×0.8)
=2000÷10
=200
104×0.25
=(100+4)×0.25
=100×0.25+4×0.25
=25+1
=26
45÷(15÷11) 72×101-72
=45÷15×11
=3×11
=33
=72×(101-1)
=72×100
=7200
138+97+3+42
=(138+42)+(97+3)
=180+100
=280
第二章 数的运算
考点知识梳理
定律 内容 字母表示 例子
加法交换律 两个数相加,交换加数的位置,和不变 a+b=b+a 20+25=25+20
加法结合律 三个数相加,先把前两个数相加,或者先把后两个数相加,和不变 (a+b)+c=a+(b+c) (20+25)+5=
20+(25+5)
定律 内容 字母表示 例子
乘法交换律 两个数相乘,交换因数的位置,积不变 a×b=b×a 2×3=3×2
乘法结合律 三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变 (a×b)×c=a×(b×c) 3×2×5=3×(2×5)
定律 内容 字母表示 例子
乘法分配律 两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再把积相加,结果不变 (a+b)×c=a×c+b×c (2+3)×5=2×5+3×5
名称 内容 字母表示及推广
减法性质 一个数连续减去两个数,等于这个数减去这两个数的和 a-b-c=a-(b+c)
a-(b+c)=a-b-c
一个数减去两个数的差,等于先从这个数中减去差里的被减数,然后加上减数 a-(b-c)=a-b+c
a-b+c=a-(b-c)
a+b-c=a+(b-c)
名称 内容 字母表示及推广
除法性质 一个数连续除以几个数(0除外),可以用这个数除以所有除数的积 a÷(b×c)=a÷b÷c
a÷b÷c=a÷(b×c)
a÷(b÷c)=a÷b×c
积不变的规律 当一个因数乘(或除以)一个数(0除外),另一个因数除以(或乘)同一个数时,它们的积不变 a×b=(a×c)×(b÷c)(c≠0)
注意:在有余数的整数除法中,利用商不变的性质时,商是不变的,但余数会扩大或缩小相同的倍数。
例如:25÷4=6……1
2500÷400=6……100
3. 简便运算
(1)一般情况下,四则运算的计算顺序:有括号时,先算括号里面的;没有括号时,先算乘除法,再算加减法;只有同一级运算时,按从左往右的顺序计算。
(2)由于有的计算题具有它自身的特征,这时运用运算定律,可以使计算过程简便,同时又不容易出错。
4. 常见的简便运算方法
(1)把数化整。为了便于简算,能凑成整十、整百、整千的数,要把一些数交换,结合在一起先算。
(2)改变运算顺序,把能简算的步骤按定律、性质等规定改变原来的运算顺序或形式(有时需要去括号或添括号)。
(3)把已知数适当进行分解,可使计算简便。
(4)把算式中某些具有相同特点的数,结合在一起再计算,可使计算简便。
典例精析及训练
【例1】用简便方法计算。
(1)1.24+0.78+8.76 (2)7.05-3.84-0.16
精析:(1)①加法交换律: a+b=b+a。②加法结合律:(a+b)+c=a+(b+c)。(2)减法的运算性质: a-b-c=a-(b+c)。
题型一
答案:(1)1.24+0.78+8.76
=(1.24+8.76)+0.78
=10+0.78
=10.78
(2)7.05-3.84-0.16
=7.05-(3.84+0.16)
=7.05-4
=3.05
=(0.21+0.79)+(12.3+7.7)
=1+20
=21
=(6.51-3.51)+(2.74+7.26)
=3+10
=13
1592+3698+408+302
=(1592+408)+(3698+302)
=2000+4000
=6000
=80
题型二
【例2】用简便方法计算。
(1)2.5×12.5×4×8 (2)48×
精析:①乘法交换律: a×b=b×a。②乘法结合律:(a×b)×c=a×(b×c)。③乘法分配律:(a+b)×c=a×c+b×c。④两组特殊算式的乘积:25×4=100,125×8=1000。
答案:(1)2.5×12.5×4×8
=(2.5×4)×(12.5×8)
=10×100
=1000
=(2.5×4)×6
=10×6
=60
=0.25×40×19
=10×19
=190
90.5×99+90.5 7.7×7+7.7+2×7.7
=90.5×(99+1)
=90.5×100
=9050
=7.7×(7+2+1)
=7.7×10
=77
【例3】计算:(1)9999×1001 (2)1.71×99
精析:(1)此题把1001看成1000+1,然后根据乘法分配律去简算。(2)把99看成100-1,然后根据乘法分配律进行计算。
题型三
答案:(1)9999×1001 (2)1.71×99
=9999×(1000+1)
=9999×1000+9999×1
=9999000+9999
=10008999
=1.71×(100-1)
=1.71×100-1.71×1
=171-1.71
=169.29
=1.25×(800+8)
=1.25×800+1.25×8
=1000+10
=1010
=25×(40+1)
=25×40+25×1
=1000+25
=1025
11×49 23×99
=(10+1)×49
=10×49+1×49
=490+49
=539
=23×(100-1)
=23×100-23×1
=2300-23
=2277
205×7 63×10.1
=(200+5)×7
=200×7+5×7
=1400+35
=1435
=63×(10+0.1)
=63×10+63×0.1
=630+6.3
=636.3
【例4】计算:7.2÷(0.2×6)。
精析:此题可应用除法的性质:一个数除以两个数的积,等于这个数依次除以积里面的两个因数来计算。
题型四
答案:7.2÷(0.2×6)
=7.2÷0.2÷6
=36÷6
=6
0.406
×
=3.25÷(2.5×4)
=3.25÷10
=0.325
=125÷50×8
=125×8÷50
=1000÷50
=20
350÷(35×2)
=350÷35÷2
=10÷2
=5
易错归纳及训练
【例1】计算:493-255-145。
错解:493-255-145
=493-(255-145)
=493-110
=383
类型一
分析:添括号后,括号前面是“-”的,移进括号后“-”变“+”,“+”变“-”。在简便运算过程中,需要添括号或去括号时,一定要注意括号前面原来是“+”还是“-”,如果是“+”,添、去括号后原来的数不变号,如果是“-”,添、去括号后原来的数“-”变“+”,“+”变“-”。
正解:493-255-145
=493-(255+145)
=493-400
=93
4.3-2.45+5.7-6.55 35.01-3.03-16.97
=(4.3+5.7)-(2.45+6.55)
=10-9
=1
=35.01-(3.03+16.97)
=35.01-20
=15.01
【例2】用简便方法计算。
(125-40)×8 860÷(86×5)
错解:(125-40)×8 860÷(86×5)
=125×8-40 =860÷86×5
=1000-40 =10×5
=960 =50
类型二
分析:运用乘法分配律时,括号外面的数应和括号里面的每一个数都相乘再相加、减。运用运算性质时,要注意括号及运算符号的使用。
正解:(125-40)×8 860÷(86×5)
=125×8-40×8 =860÷86÷5
=1000-320 =10÷5
=680 =2
4.2×101-4.2
=4.2×101-4.2×1
=(101-1)×4.2
=100×4.2
=420
小考复习训练
3
÷
÷
5
×
4
×
4
(答案不唯一)
(69+31)
加法结合律
(a+b)+c=a+(b+c)
(32+68)
乘法分配律
a×(b+c)=ab+ac
=
<
<
>
2400
42
C
C
C
B
A
B
77.49
33.852
128.625
0.27
(竖式略)
=85×(156-56)
=85×100
=8500
=15×(10-0.1)
=15×10-15×0.1
=150-1.5
=148.5
159×68+159×33-159
=159×(68+33-1)
=159×100
=15900
3.7×5.4+0.37×46
=3.7×(5.4+4.6)
=3.7×10
=37
15.43-(2.6+5.43)
=15.43-5.43-2.6
=10-2.6
=7.4
2000÷12.5÷0.8
=2000÷(12.5×0.8)
=2000÷10
=200
104×0.25
=(100+4)×0.25
=100×0.25+4×0.25
=25+1
=26
45÷(15÷11) 72×101-72
=45÷15×11
=3×11
=33
=72×(101-1)
=72×100
=7200
138+97+3+42
=(138+42)+(97+3)
=180+100
=280
同课章节目录
