小学毕业数学总复习第三章式与方程第2课时比、比例和比例尺课件(共60张PPT)
文档属性
| 名称 | 小学毕业数学总复习第三章式与方程第2课时比、比例和比例尺课件(共60张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 17:05:04 | ||
图片预览










文档简介
(共60张PPT)
第三章 式与方程
考点知识梳理
②比值通常用分数表示,也可以用小数或整数表示。
注意:比的后项不能是零。
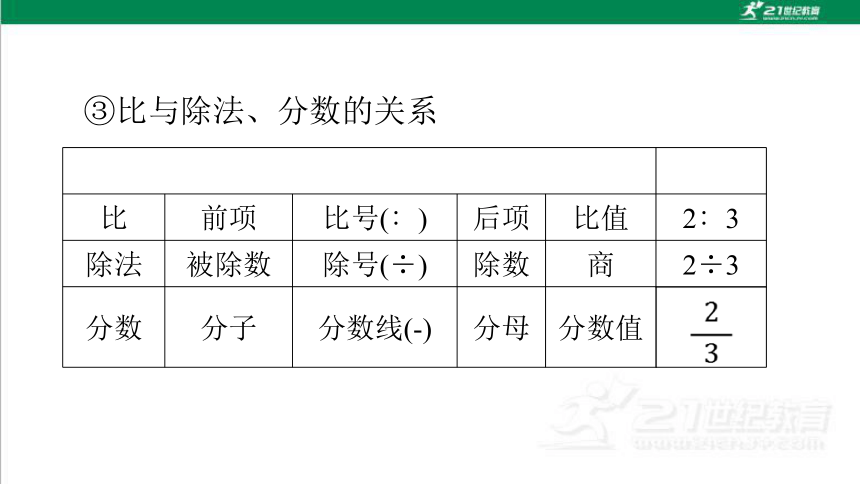
③比与除法、分数的关系
各部分名称 例子
比 前项 比号(∶) 后项 比值 2∶3
除法 被除数 除号(÷) 除数 商 2÷3
分数 分子 分数线(-) 分母 分数值
(2)比的基本性质比的前项和后项同时乘或者除以相同的数(0除外),比值不变,这叫做比的基本性质。
(3)求比值和化简比求比值的方法:用比的前项除以后项,它的结果是一个数值,这个数值可以是整数,也可以是小数或分数。
化简比:把一个比化成与它相等的最简整数比。(最简整数比是指前项和后项为互质数)
(4)比例尺
2. 比例的意义和性质
(1)比例的意义
表示两个比相等的式子叫做比例。组成比例的四个数,叫做比例的项,两端的两项叫做外项,中间的两项叫做内项。例如:
(2)比例的基本性质在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
(3)解比例根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。
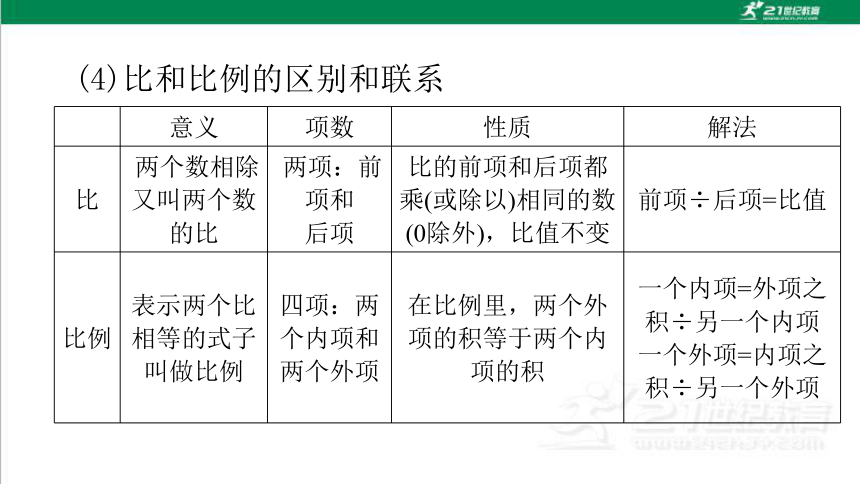
(4)比和比例的区别和联系
意义 项数 性质 解法
比 两个数相除又叫两个数的比 两项:前项和
后项 比的前项和后项都乘(或除以)相同的数(0除外),比值不变 前项÷后项=比值
比例 表示两个比相等的式子叫做比例 四项:两个内项和两个外项 在比例里,两个外项的积等于两个内项的积 一个内项=外项之积÷另一个内项
一个外项=内项之积÷另一个外项
3. 正比例和反比例
(1)正比例与反比例的区别和联系
关联 相同点 不同点 字母表示
成正比例的量 两种相关联的量,一种量变化,另一种量也随着变化 比值一定
成反比例的量 乘积一定 xy=k(一定)
(2)判断正反比例的方法
一找、二看、三判断。
找变量:分析数量关系,确定哪两种量是相关联的量。
看定量:分析这两种相关联的量,它们之间是商一定还是积一定。
判断:如果商一定就成正比例;如果积一定就成反比例;如果商和积都不一定,就不成比例。
典例精析及训练
题型一
30
12
八
1.8
(3) =45∶( )=1.25=
15÷( )=( )%
30
36
12
125
4×45=9×20
题型二
×
4∶3
3∶4
4∶7
C
C
【例3】在一张比例尺是1∶30000的地图上量得甲、乙两地的图上距离为6厘米,则甲、乙两地的实地距离是( )千米。
题型三
精析:根据题意我们可以列出比例式:6厘米∶( )=1∶30000,解比例式可得括号里应填180000厘米,注意题中是要填多少千米,所以还要将所得的180000厘米化成千米为单位,应是1.8千米,故题中的括号内应填1.8。
答案:1.8
3厘米∶480千米
=3厘米∶48000000厘米
=3∶48000000
=1∶16000000
答:这幅地图的比例尺是1∶16000000。
易错归纳及训练
【例1】两个正方体的棱长的比是1∶3,这两个正方体的表面积的比是( ),体积比是( )。
错解:1∶3 1∶9
类型一
分析:这道题目是考查学生根据正方体的棱长比求表面积的比和体积比。正方体的表面积和体积的计算公式是解题的关键。此题出错的原因是对比的意义不理解,认为表面积的比和棱长的比相等,而导致错误。
正解:1∶9 1∶27
49∶48
20∶100
1∶5
0.2
5∶4
1∶2
1∶2
4∶1
【例2】生产相同数目的一种零件,甲、乙两人的工作时间比是4∶5,甲、乙两人的工作效率比是
( )。
错解:4∶5
类型二
4∶6=6∶9
4
1.2
5
4
B
×
小考复习训练
35
14
87.5
20
100
24
192
3∶2
4250
正
8
7
1550
×
×
×
√
B
2. 圆的周长和直径( )。
A. 成正比例 B. 成反比例
C. 不成比例 D.无法确定
3. 如果一个三角形三个内角的度数比是1∶1∶2,那么这个三角形一定是( )。
A.锐角三角形 B.等边三角形
C.等腰直角三角形 D.钝角三角形
A
C
A
D
B
B
D
解:1.5x=9×5
x=30
解:1.2x=7.5×0.4
x=2.5
解:9x=1.8×2
x=0.4
解:24∶x=36∶18
36x=24×18
x=12
2.4平方米∶30平方分米=240∶30=8∶1
8∶1=8÷1=8
1.2吨∶300千克=1200∶300=4∶1
4∶1=4÷1=4
第三章 式与方程
考点知识梳理
②比值通常用分数表示,也可以用小数或整数表示。
注意:比的后项不能是零。
③比与除法、分数的关系
各部分名称 例子
比 前项 比号(∶) 后项 比值 2∶3
除法 被除数 除号(÷) 除数 商 2÷3
分数 分子 分数线(-) 分母 分数值
(2)比的基本性质比的前项和后项同时乘或者除以相同的数(0除外),比值不变,这叫做比的基本性质。
(3)求比值和化简比求比值的方法:用比的前项除以后项,它的结果是一个数值,这个数值可以是整数,也可以是小数或分数。
化简比:把一个比化成与它相等的最简整数比。(最简整数比是指前项和后项为互质数)
(4)比例尺
2. 比例的意义和性质
(1)比例的意义
表示两个比相等的式子叫做比例。组成比例的四个数,叫做比例的项,两端的两项叫做外项,中间的两项叫做内项。例如:
(2)比例的基本性质在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
(3)解比例根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。
(4)比和比例的区别和联系
意义 项数 性质 解法
比 两个数相除又叫两个数的比 两项:前项和
后项 比的前项和后项都乘(或除以)相同的数(0除外),比值不变 前项÷后项=比值
比例 表示两个比相等的式子叫做比例 四项:两个内项和两个外项 在比例里,两个外项的积等于两个内项的积 一个内项=外项之积÷另一个内项
一个外项=内项之积÷另一个外项
3. 正比例和反比例
(1)正比例与反比例的区别和联系
关联 相同点 不同点 字母表示
成正比例的量 两种相关联的量,一种量变化,另一种量也随着变化 比值一定
成反比例的量 乘积一定 xy=k(一定)
(2)判断正反比例的方法
一找、二看、三判断。
找变量:分析数量关系,确定哪两种量是相关联的量。
看定量:分析这两种相关联的量,它们之间是商一定还是积一定。
判断:如果商一定就成正比例;如果积一定就成反比例;如果商和积都不一定,就不成比例。
典例精析及训练
题型一
30
12
八
1.8
(3) =45∶( )=1.25=
15÷( )=( )%
30
36
12
125
4×45=9×20
题型二
×
4∶3
3∶4
4∶7
C
C
【例3】在一张比例尺是1∶30000的地图上量得甲、乙两地的图上距离为6厘米,则甲、乙两地的实地距离是( )千米。
题型三
精析:根据题意我们可以列出比例式:6厘米∶( )=1∶30000,解比例式可得括号里应填180000厘米,注意题中是要填多少千米,所以还要将所得的180000厘米化成千米为单位,应是1.8千米,故题中的括号内应填1.8。
答案:1.8
3厘米∶480千米
=3厘米∶48000000厘米
=3∶48000000
=1∶16000000
答:这幅地图的比例尺是1∶16000000。
易错归纳及训练
【例1】两个正方体的棱长的比是1∶3,这两个正方体的表面积的比是( ),体积比是( )。
错解:1∶3 1∶9
类型一
分析:这道题目是考查学生根据正方体的棱长比求表面积的比和体积比。正方体的表面积和体积的计算公式是解题的关键。此题出错的原因是对比的意义不理解,认为表面积的比和棱长的比相等,而导致错误。
正解:1∶9 1∶27
49∶48
20∶100
1∶5
0.2
5∶4
1∶2
1∶2
4∶1
【例2】生产相同数目的一种零件,甲、乙两人的工作时间比是4∶5,甲、乙两人的工作效率比是
( )。
错解:4∶5
类型二
4∶6=6∶9
4
1.2
5
4
B
×
小考复习训练
35
14
87.5
20
100
24
192
3∶2
4250
正
8
7
1550
×
×
×
√
B
2. 圆的周长和直径( )。
A. 成正比例 B. 成反比例
C. 不成比例 D.无法确定
3. 如果一个三角形三个内角的度数比是1∶1∶2,那么这个三角形一定是( )。
A.锐角三角形 B.等边三角形
C.等腰直角三角形 D.钝角三角形
A
C
A
D
B
B
D
解:1.5x=9×5
x=30
解:1.2x=7.5×0.4
x=2.5
解:9x=1.8×2
x=0.4
解:24∶x=36∶18
36x=24×18
x=12
2.4平方米∶30平方分米=240∶30=8∶1
8∶1=8÷1=8
1.2吨∶300千克=1200∶300=4∶1
4∶1=4÷1=4
同课章节目录
