2025学年华东师大版八年级数学下册期末真题练习(含解析)
文档属性
| 名称 | 2025学年华东师大版八年级数学下册期末真题练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 423.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 00:00:00 | ||
图片预览


文档简介
2025学年华东师大版八年级数学下册期末真题练习
一、选择题
1.(2024八下·西安期末)如图,平行四边形中,的平分线交于点E,的平分线交于点F,若,,则的长为( )
A.1 B.2 C.3 D.4
2.(2024八下·新昌期末)如图,在四边形中,,要使四边形是平行四边形,下列添加的条件正确的是( )
A. B. C. D.
3.(2024八下·杭州期末)如图,在正方形中,,点E、F分别是边、的中点,连接、,点M,N分别是、的中点,则的长为( )
A.5 B. C. D.2
4.(2025八下·江苏期末)如图,已知在正方形ABCD中,对角线AC与BD相交于点O,AE,DF分别是∠OAD与∠ODC的角平分线,AE的延长线与DF相交于点G,则下列结论:①AG⊥DF;②EFAB;③AB=AF;④AB=2EF.其中正确的有( )个.
A.1个 B.2个 C.3个 D.4个
5.(2025八下·江苏期末)在矩形ABCD中,E,F,G,H分别是边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,以下结论:
①存在且仅有一个四边形EFGH是菱形;
②存在无数个四边形EFGH是平行四边形;
③存在无数个四边形EFGH是矩形;
④除非矩形ABCD为正方形,否则不存在四边形EFGH是正方形.
其中正确的是( )
A.③④ B.①②③ C.②③④ D.①②④
6.(2024八下·赤坎期末)如图,在平行四边形中,,则的度数为( )
A. B. C. D.
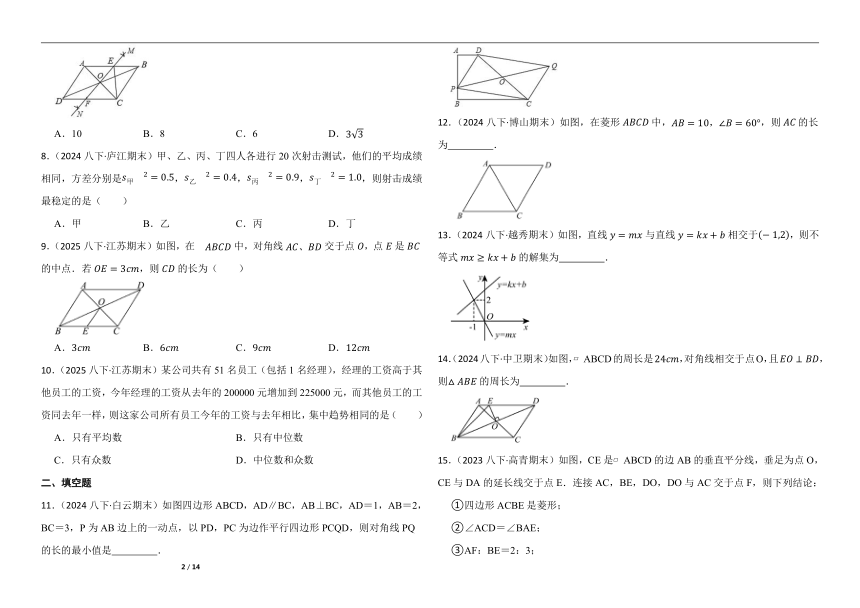
7.(2023八下·海拉尔期末)如图,中,、交于点O,分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于M、N两点,作直线,交于点E,交于点F,连接,若,的周长为14,则的长为( )
A.10 B.8 C.6 D.
8.(2024八下·庐江期末)甲、乙、丙、丁四人各进行20次射击测试,他们的平均成绩相同,方差分别是,,,,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
9.(2025八下·江苏期末)如图,在中,对角线交于点,点是的中点.若,则的长为( )
A. B. C. D.
10.(2025八下·江苏期末)某公司共有51名员工(包括1名经理),经理的工资高于其他员工的工资,今年经理的工资从去年的200000元增加到225000元,而其他员工的工资同去年一样,则这家公司所有员工今年的工资与去年相比,集中趋势相同的是( )
A.只有平均数 B.只有中位数
C.只有众数 D.中位数和众数
二、填空题
11.(2024八下·白云期末)如图四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,P为AB边上的一动点,以PD,PC为边作平行四边形PCQD,则对角线PQ的长的最小值是 .
12.(2024八下·博山期末)如图,在菱形中,,则的长为 .
13.(2024八下·越秀期末)如图,直线与直线相交于,则不等式的解集为 .
14.(2024八下·中卫期末)如图, ABCD的周长是,对角线相交于点O,且,则的周长为 .
15.(2023八下·高青期末)如图,CE是 ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
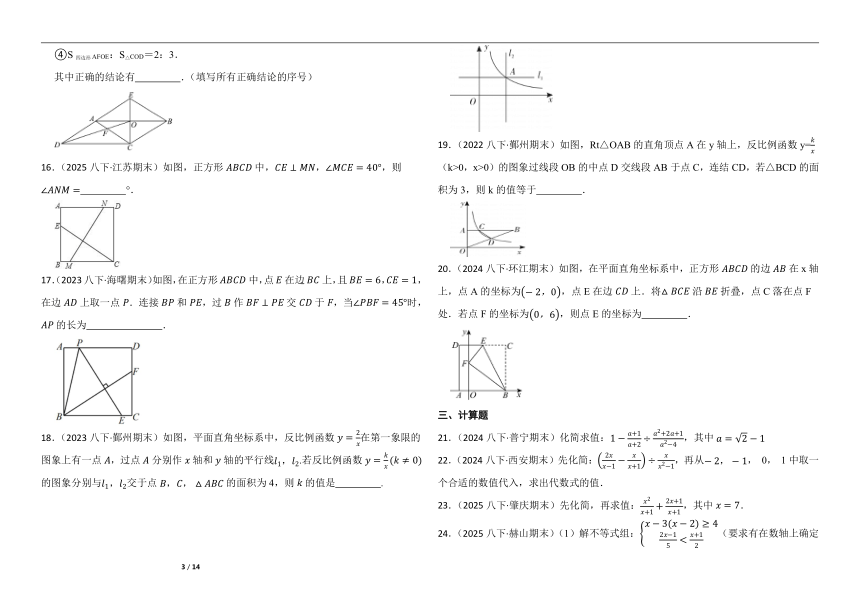
④S四边形AFOE:S△COD=2:3.
其中正确的结论有 .(填写所有正确结论的序号)
16.(2025八下·江苏期末)如图,正方形中,,,则 °.
17.(2023八下·海曙期末)如图,在正方形中,点在边上,且,,在边上取一点.连接和,过作交于,当时,的长为 .
18.(2023八下·鄞州期末)如图,平面直角坐标系中,反比例函数在第一象限的图象上有一点,过点分别作轴和轴的平行线.若反比例函数的图象分别与交于点的面积为4,则的值是 .
19.(2022八下·鄞州期末)如图,Rt△OAB的直角顶点A在y轴上,反比例函数y=(k>0,x>0)的图象过线段OB的中点D交线段AB于点C,连结CD,若△BCD的面积为3,则k的值等于 .
20.(2024八下·环江期末)如图,在平面直角坐标系中,正方形的边在x轴上,点A的坐标为,点E在边上.将沿折叠,点C落在点F处.若点F的坐标为,则点E的坐标为 .
三、计算题
21.(2024八下·普宁期末)化简求值:,其中
22.(2024八下·西安期末)先化简:,再从, 0, 1中取一个合适的数值代入,求出代数式的值.
23.(2025八下·肇庆期末)先化简,再求值:,其中.
24.(2025八下·赫山期末)(1)解不等式组:(要求有在数轴上确定解集的过程)
(2)解分式方程:.
四、证明题
25.(2023八下·巴楚期末)已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.
(1)求证:△AFD≌△CEB.
(2)求证:四边形ABCD是平行四边形.
26.(2024八下·北仑期末)如图,菱形的对角线与交于点O,,.
(1)求证:四边形是矩形;
(2)若 ,求四边形的周长.
五、实践探究题
27.(2024八下·温州期末)综合与实践:探索某款冷柜的日耗电量.
素材1:图1是某款冷柜,耗电功率为0.15千瓦.当内部温度为时,冷柜运行,当温度下降到时,停止运行,温度上升,到时,冷柜再次运行,如此循环.
素材2:冷柜内部温度与时间的关系如图2所示.
当时,是的一次函数;当时,是的反比例函数.
链接:冷柜每天耗电量(度)耗电功率(千瓦)每天运行时间(小时).
任务1:求时,关于的函数表达式.
任务2:求该冷柜一天的耗电量.
28.(2024八下·荣昌期末)如图,多边形是一个小型人工湖,多边形各边构成环湖路某班数学综合实践两个小组对部分环湖路进行了测量,数据包括:甲小组在点处测得点在正西方向,点在正北方向,点在东北方向,在点处测得点在正西方向,点在正南方向;乙小组测得米,米,米,米.(参考数据:)
(1)计算点与点的距离;
(2)某同学从去处回收测量工具,他有两条线路可以前往:①;②.请计算说明他选择线路①还是线路②路程更短.(计算结果保留到1米)
六、综合题
29.(2024八下·宿城期末)为打造书香校园,某中学计划选购甲、乙两种图书.已知甲图书每本价格比乙图书每本价格多30元,用1000元单独购买甲图书与用400元单独购买乙图书数量相同.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该校计划购买乙图书的本数比购买甲图书本数的3倍多4本,且用于购买甲、乙两种图书的总经费不超过850元,那么该中学最多可以购买多少本甲图书?
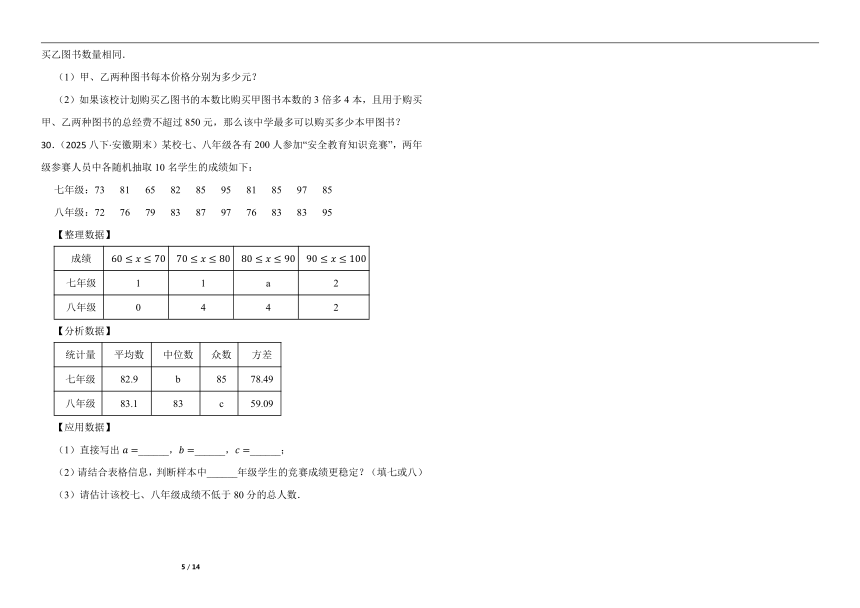
30.(2025八下·安徽期末)某校七、八年级各有200人参加“安全教育知识竞赛”,两年级参赛人员中各随机抽取10名学生的成绩如下:
七年级:73 81 65 82 85 95 81 85 97 85
八年级:72 76 79 83 87 97 76 83 83 95
【整理数据】
成绩
七年级 1 1 a 2
八年级 0 4 4 2
【分析数据】
统计量 平均数 中位数 众数 方差
七年级 82.9 b 85 78.49
八年级 83.1 83 c 59.09
【应用数据】
(1)直接写出______,______,______;
(2)请结合表格信息,判断样本中______年级学生的竞赛成绩更稳定?(填七或八)
(3)请估计该校七、八年级成绩不低于80分的总人数.
答案解析部分
1.【答案】D
【知识点】等腰三角形的判定;平行四边形的性质
2.【答案】D
【知识点】平行四边形的判定
【解析】【解答】解:由题意可知∵,
∴,
∵,
∴,
∴,
∵两组对边分别平行的四边形为平行四边形,
∴四边形是平行四边形,
故答案为:D.
【分析】根据平行四边形的判定定理解答即可.
3.【答案】B
【知识点】勾股定理;正方形的性质;三角形的中位线定理
【解析】【解答】解:连接,
∵四边形是正方形,
∴,,
∵点E、F分别是边、的中点,
∴,,
∴,
∵点M,N为别是、的中点,
∴是的中位线,
∴,
故选:B.
【分析】连接,利用正方形的性质和勾股定理求得长,再利用三角形中位线定理解答.
4.【答案】C
【知识点】正方形的判定与性质;两条直线被一组平行线所截,所得的对应线段成比例
5.【答案】C
【知识点】平行四边形的判定;菱形的判定;矩形的判定;正方形的判定
6.【答案】B
【知识点】平行四边形的性质
7.【答案】B
【知识点】线段垂直平分线的性质;平行四边形的性质;尺规作图-垂直平分线
【解析】【解答】解:由已知条件可知EF是AC的垂直平分线,所以EA=EC,
∵△BCE 的周长为14,
∴BC+CE+EB=14,
∴BC+EA+EB=14,
即BC+AB=14,
∵四边形ABCD为平行四边形,
∴DC=AB,BC=AD=6,
∴DC=14-BC=14-6=8,
故答案为:B.
【分析】由线段的垂直平分线的性质“线段的垂直平分线上的点到线段两端点的距离相等”可得EA=EC,再根据三角形BCE的周长等于三角形三边之和可求得AB的长,然后根据平行四边形的对边相等可求解 .
8.【答案】B
【知识点】方差
【解析】【解答】解:∵,,,,
,
∴最小.
∴乙的射击成绩最稳定.
故答案为:B.
【分析】根据方差的意义,方差越小数据越稳定即可求解.
9.【答案】B
【知识点】平行四边形的性质;三角形的中位线定理
10.【答案】D
【知识点】平均数及其计算;中位数;众数
11.【答案】4
【知识点】平行四边形的性质;三角形全等的判定-AAS;四边形的综合;四边形-动点问题
【解析】【解答】解:在平行四边形PCQD中,设对角线PQ与DC相交于点O,则O是DC的中点,
过点Q作QH⊥BC,交BC的延长线于H,
∵AD∥BC,
∴∠ADC=∠DCH,即∠ADP+∠PDC=∠DCQ+∠QCH,
∵PD∥CQ,
∴∠PDC=∠DCQ,
∴∠ADP=∠QCH,
又∵PD=CQ,
在Rt△ADP与Rt△HCQ中,
∴Rt△ADP≌Rt△HCQ(AAS),
∴AD=HC,
∵AD=1,BC=3,
∴BH=4,
∴当PQ⊥AB时,PQ的长最小,即为4.
故答案为:4.
【分析】过点Q作QH⊥BC,交BC的延长线于H,先利用“AAS”证出Rt△ADP≌Rt△HCQ,利用全等三角形的性质可得AD=HC,利用线段的和差求出BH=4,最后求出当PQ⊥AB时,PQ的长最小,即为4,从而得解.
12.【答案】10
【知识点】等边三角形的判定与性质;菱形的性质
【解析】【解答】解:∵四边形是菱形,
∴,
∵,
∴是等边三角形,
∴.
故答案为:10.
【分析】根据菱形的性质得到是等边三角形解题即可.
13.【答案】
【知识点】一次函数与不等式(组)的关系
【解析】【解答】解:∵直线与直线相交于,
∴不等式的解集为.
故答案为:.
【分析】结合函数图象,利用函数值大的图象在上方的原则求解即可.
14.【答案】
【知识点】线段垂直平分线的性质;平行四边形的性质
【解析】【解答】解:在中,
,相交于点,
为的中点,
,
是的垂直平分线,
,
∵的周长是,
∴,
的周长,
故答案为:.
【分析】
因为平行四边形的对角线互相平分,即O为BD中点,又EO垂直BD,则EO垂直平分BD,由线段垂直平分线的性质知ED等于EB,则的周长等于AB与AD的和,又平行四边形的对边分别相等,即的周长等于平行四边形ABCD周长的一半.
15.【答案】①②④
【知识点】平行四边形的性质;菱形的判定;两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的性质-对应边
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵EC垂直平分AB,
∴OA=OB=AB=DC,CD⊥CE,
∵OA∥DC,
∴=,
∴AE=AD,OE=OC,
∵OA=OB,OE=OC,
∴四边形ACBE是平行四边形,
∵AB⊥EC,
∴四边形ACBE是菱形,故①正确,
∵∠DCE=90°,DA=AE,
∴AC=AD=AE,
∴∠ACD=∠ADC=∠BAE,故②正确,
∵OA∥CD,
∴,
∴,故③错误,
设△AOF的面积为a,则△OFC的面积为2a,△CDF的面积为4a,△AOC的面积=△AOE的面积=3a,
∴四边形AFOE的面积为4a,△ODC的面积为6a
∴S四边形AFOE:S△COD=2:3.故④正确.
故答案是:①②④.
【分析】先证出四边形ACBE是平行四边形,再结合AB⊥EC,即可证出四边形ACBE是菱形,从而可判定①是否正确;再直角三角形斜边上中线的性质及等量代换可得AC=AD=AE,再利用等边对等角的性质可得∠ACD=∠ADC=∠BAE,从而可判断②是否正确;再利用平行线分线段成比例的性质及等量代换可得,从而可判断③是否正确;设△AOF的面积为a,再求出四边形AFOE的面积为4a,△ODC的面积为6a,最后求出S四边形AFOE:S△COD=2:3,从而可判断④是否正确,从而得解.
16.【答案】50
【知识点】正方形的性质
17.【答案】或
【知识点】正方形的性质;两条直线被一组平行线所截,所得的对应线段成比例;旋转的性质;等腰直角三角形
【解析】【解答】解:∵BE=6,CE=1,
∴BC=BE+CE=7.
∵四边形ABCD为正方形,
∴AB=BC=CD=DA=7,∠BAD=∠ABC=∠BCD=∠ADC=90°.
将△ABP绕点B顺时针旋转90°得到△CBQ,
∴AP=CQ,∠PBQ=90°,∠BCQ=∠BCD=90°,
∴△PBQ为等腰直角三角形,Q、C、D三点共线.
设AP=CQ=x,则PD=AD-AP=7-x,DQ=CD+CQ=7+x.
∵CE∥PD,
∴,
∴,
∴x=3+或3-,
经检验:x=3+,x=3-是分式方程的根且符合题意,
∴AP=3+或3-.
故答案为:3+或3-.
【分析】由已知条件可得BC=BE+CE=7,根据正方形的性质可得AB=BC=CD=DA=7,∠BAD=∠ABC=∠BCD=∠ADC=90°,将△ABP绕点B顺时针旋转90°得到△CBQ,可得AP=CQ,∠PBQ=90°,推出△PBQ为等腰直角三角形,Q、C、D三点共线,设AP=CQ=x,则PD=7-x,DQ=7+x,由平行线分线段成比例的性质可得,然后代入计算即可.
18.【答案】6或-2
【知识点】反比例函数系数k的几何意义;三角形的面积
【解析】【解答】解:设点A的坐标为(x0,),
由题意得,点B的坐标为(,),
点C的坐标为(x0,),AB=x0-kx02,AC=2x0-kx0,
∵S ABC=4 ,S ABC=12×AB×AC=12×x0-kx02×2x0-kx0,
∴12×x0-kx02×2x0-kx0=4,
解得k=6或k=-2.
故答案为:6或-2
【分析】先设点A的坐标为(x0,),根据题意,分别列出点B的坐标(,)和点C的坐标(x0,),表示出AB的长度x0-kx02 和AC的长度2x0-kx0 ,根据三角形的面积公式即可求出答案.
19.【答案】4
【知识点】反比例函数系数k的几何意义;三角形的面积;三角形的中位线定理
【解析】【解答】解:连接OC,过D作x轴的垂线交AB于E点,交x轴于F点,
∵S△CAO=S△DOF=|k|,
∵ D为线段OB的中点,
∴S△BDE=S△DOF=|k|,
∵DE是△AOB的中位线,
∴DE:OA=1:2,
∴S△BDE=S△AOB=S△CAO,
∴S△OBC=S△AOB-S△CAO=S△AOB,
∵ D为线段OB的中点,
∴S△OBC=2S△BCD=6=S△AOB,
∴S△AOB=8,
∴S△AOC=S△AOB=2= 12|k|,
∵k>0,
∴k=4.
故答案为:4.
【分析】连接OC,过D作x轴的垂线交AB于E点,交x轴于F点,根据反比例函数k的几何意义得出S△CAO=S△DOF,再由全等三角形的性质得出S△BDE=S△DOF,根据根据中位线定理推出S△BDE=S△AOB=S△CAO,从而得出S△OBC=S△AOB,再由同底等高得出S△OBC=2S△BCD=6,则可求出S△AOB=8,从而推出S△AOC=2=12|k|,即可解答.
20.【答案】
【知识点】坐标与图形性质;勾股定理;正方形的性质;翻折变换(折叠问题)
【解析】【解答】解∶设正方形的边长为a,与y轴相交于G,
则四边形是矩形,
∴,,,
∵折叠,
∴,,
∵点A的坐标为,点F的坐标为,
∴,,
∴,
在中,,
∴,
解得,
∴,,
在中,,
∴,
解得,
∴,
∴点E的坐标为,
故答案为:.
【分析】设正方形的边长为a,与y轴相交于G,即可得到是矩形,求出,,,利用折叠得到,,然后在中根据勾股定理求出a的值,再在中运用勾股定理得到长解题.
21.【答案】,
【知识点】分式的化简求值
22.【答案】解:
,
∵分式要有意义,
∴,
∴,
∴可取,此时原式.
【知识点】分式有无意义的条件;分式的化简求值-直接代入
【解析】【分析】先把小括号内的式子通分化简,再把除法变成乘法,后约分化简,接着再根据分式有意义的条件确定符合条件的x的值,并代值计算即可.
23.【答案】;8
【知识点】分式的化简求值
24.【答案】解:(1)
由①得:,即
由②得:,即,
把不等式①、②的解集在数轴上表示为
由图可知,两不等式解集的公共部分是,
所以这个不等式组的解集是.
(2)
在分式方程两边同乘最简公分母得:
解得:
检验:当时,
因此,是原方程的解.
【知识点】解分式方程;解一元一次不等式组;在数轴上表示不等式的解集
【解析】【分析】(1)根据解不等式的步骤,分别求出不等式组中每个不等式的解集,进而根据数轴上表示不等式解集的方法“大向右,小向左,实心等于,空心不等”将两个不等式的解集在数轴上表示出来,最后取两个不等式解集的公共部分,即可得到该不等式组的解集;
(2)在原方程两边同乘最简公分母(x+1)(x-1),约去分母,将分式方程转化为整式方程,解整式方程求出x的值,再检验即可得出原方程解的情况.
25.【答案】证明:(1)∵DF∥BE,
∴∠DFE=∠BEF.
又∵AF=CE,DF=BE,
∴△AFD≌△CEB(SAS).
(2)由(1)知△AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC,
∴AD∥BC.
∴四边形ABCD是平行四边形.
【知识点】平行四边形的判定;三角形全等的判定-SAS;全等三角形中对应边的关系;全等三角形中对应角的关系
【解析】【分析】(1)先根据平行线得到∠DFE=∠BEF,然后根据SAS证明两三角形全等即可;
(2)根据△AFD≌△CEB可得AD=BC且AD∥BC,然后根据平行四边形的判定定理解题即可.
26.【答案】(1)证明:,.
四边形是平行四边形,
又四边形是菱形,
,
,
平行四边形是矩形.
(2)解:四边形是菱形,
,,,
,
,
,
为等边三角形,则
,
,
四边形是矩形,
,
四边形的周长是.
【知识点】等边三角形的判定与性质;勾股定理;菱形的性质;矩形的判定与性质
【解析】【分析】本题考查菱形的性质、矩形的判定与性质、等边三角形的判定与性质、勾股定理,熟练掌握它们的性质和判定定理是解答的关键.
(1)先证四边形是平行四边形,再根据菱形的性质得到,根据有一个角是直角的平行四边形是矩形即证;
(2)由菱形的性质及可得∠ABC=60°,可证为等边三角形,根据等边三角形的性质得到,从而求出,,然后根据矩形的周长公式求解即可.
(1)证明:,.
四边形是平行四边形,
又四边形是菱形,
,
,
平行四边形是矩形.
(2)解:四边形是菱形,
,,,
,
,
,
为等边三角形,则
,则
,
四边形是矩形,
,
四边形的周长是.
27.【答案】任务1:设时,关于的函数表达式为,将点代入,可得,
∴时,关于的函数表达式为;
任务2:当时,可有,解得,
∵冷柜每20分钟为一个循环,
∴每天共有循环个数:(个),
∴冷柜每天运行的时间为分钟,
∴每天耗电量为:(度).
【知识点】反比例函数的实际应用
【解析】【分析】任务1:利用待定系数法求函数解析式即可;
任务2:得到冷柜每20分钟为一个循环,然后求出循环次数即可得到运行时间,利用公式解题即可.
28.【答案】(1)400米
(2)选择线路①路程更短
【知识点】勾股定理;矩形的判定与性质
29.【答案】(1)解:设乙图书每本价格为x元,则甲图书每本价格是元,
根据题意得:,
解得:,
经检验,x=20是所列方程的解,且符合题意,
∴x+30=20+30=50(元),
答:甲图书每本价格为50元,乙图书每本价格为20元;
(2)设该中学可以购买m本甲图书,则可以购买本乙图书,
由题意得:,
解得:,
答:该中学最多可以购买7本甲图书.
【知识点】分式方程的实际应用;一元一次不等式的应用
【解析】【分析】(1)设乙图书每本价格为x元,则甲图书每本价格是元,根据题意得等量关系: 1000元单独购买甲图书的数量=用400元单独购买乙图书的数量,据此列分式方程并求解即可.
(2)设该中学可以购买m本甲图书,则可以购买本乙图书,根据题意列出不等式求解即可得出答案.
30.【答案】(1)6;;83
(2)八
(3)估计该校七、八年级成绩不低于80分的总人数约为280人.
【知识点】中位数;方差;众数;用样本所占百分比估计总体数量
1 / 1
一、选择题
1.(2024八下·西安期末)如图,平行四边形中,的平分线交于点E,的平分线交于点F,若,,则的长为( )
A.1 B.2 C.3 D.4
2.(2024八下·新昌期末)如图,在四边形中,,要使四边形是平行四边形,下列添加的条件正确的是( )
A. B. C. D.
3.(2024八下·杭州期末)如图,在正方形中,,点E、F分别是边、的中点,连接、,点M,N分别是、的中点,则的长为( )
A.5 B. C. D.2
4.(2025八下·江苏期末)如图,已知在正方形ABCD中,对角线AC与BD相交于点O,AE,DF分别是∠OAD与∠ODC的角平分线,AE的延长线与DF相交于点G,则下列结论:①AG⊥DF;②EFAB;③AB=AF;④AB=2EF.其中正确的有( )个.
A.1个 B.2个 C.3个 D.4个
5.(2025八下·江苏期末)在矩形ABCD中,E,F,G,H分别是边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,以下结论:
①存在且仅有一个四边形EFGH是菱形;
②存在无数个四边形EFGH是平行四边形;
③存在无数个四边形EFGH是矩形;
④除非矩形ABCD为正方形,否则不存在四边形EFGH是正方形.
其中正确的是( )
A.③④ B.①②③ C.②③④ D.①②④
6.(2024八下·赤坎期末)如图,在平行四边形中,,则的度数为( )
A. B. C. D.
7.(2023八下·海拉尔期末)如图,中,、交于点O,分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于M、N两点,作直线,交于点E,交于点F,连接,若,的周长为14,则的长为( )
A.10 B.8 C.6 D.
8.(2024八下·庐江期末)甲、乙、丙、丁四人各进行20次射击测试,他们的平均成绩相同,方差分别是,,,,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
9.(2025八下·江苏期末)如图,在中,对角线交于点,点是的中点.若,则的长为( )
A. B. C. D.
10.(2025八下·江苏期末)某公司共有51名员工(包括1名经理),经理的工资高于其他员工的工资,今年经理的工资从去年的200000元增加到225000元,而其他员工的工资同去年一样,则这家公司所有员工今年的工资与去年相比,集中趋势相同的是( )
A.只有平均数 B.只有中位数
C.只有众数 D.中位数和众数
二、填空题
11.(2024八下·白云期末)如图四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,P为AB边上的一动点,以PD,PC为边作平行四边形PCQD,则对角线PQ的长的最小值是 .
12.(2024八下·博山期末)如图,在菱形中,,则的长为 .
13.(2024八下·越秀期末)如图,直线与直线相交于,则不等式的解集为 .
14.(2024八下·中卫期末)如图, ABCD的周长是,对角线相交于点O,且,则的周长为 .
15.(2023八下·高青期末)如图,CE是 ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四边形AFOE:S△COD=2:3.
其中正确的结论有 .(填写所有正确结论的序号)
16.(2025八下·江苏期末)如图,正方形中,,,则 °.
17.(2023八下·海曙期末)如图,在正方形中,点在边上,且,,在边上取一点.连接和,过作交于,当时,的长为 .
18.(2023八下·鄞州期末)如图,平面直角坐标系中,反比例函数在第一象限的图象上有一点,过点分别作轴和轴的平行线.若反比例函数的图象分别与交于点的面积为4,则的值是 .
19.(2022八下·鄞州期末)如图,Rt△OAB的直角顶点A在y轴上,反比例函数y=(k>0,x>0)的图象过线段OB的中点D交线段AB于点C,连结CD,若△BCD的面积为3,则k的值等于 .
20.(2024八下·环江期末)如图,在平面直角坐标系中,正方形的边在x轴上,点A的坐标为,点E在边上.将沿折叠,点C落在点F处.若点F的坐标为,则点E的坐标为 .
三、计算题
21.(2024八下·普宁期末)化简求值:,其中
22.(2024八下·西安期末)先化简:,再从, 0, 1中取一个合适的数值代入,求出代数式的值.
23.(2025八下·肇庆期末)先化简,再求值:,其中.
24.(2025八下·赫山期末)(1)解不等式组:(要求有在数轴上确定解集的过程)
(2)解分式方程:.
四、证明题
25.(2023八下·巴楚期末)已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.
(1)求证:△AFD≌△CEB.
(2)求证:四边形ABCD是平行四边形.
26.(2024八下·北仑期末)如图,菱形的对角线与交于点O,,.
(1)求证:四边形是矩形;
(2)若 ,求四边形的周长.
五、实践探究题
27.(2024八下·温州期末)综合与实践:探索某款冷柜的日耗电量.
素材1:图1是某款冷柜,耗电功率为0.15千瓦.当内部温度为时,冷柜运行,当温度下降到时,停止运行,温度上升,到时,冷柜再次运行,如此循环.
素材2:冷柜内部温度与时间的关系如图2所示.
当时,是的一次函数;当时,是的反比例函数.
链接:冷柜每天耗电量(度)耗电功率(千瓦)每天运行时间(小时).
任务1:求时,关于的函数表达式.
任务2:求该冷柜一天的耗电量.
28.(2024八下·荣昌期末)如图,多边形是一个小型人工湖,多边形各边构成环湖路某班数学综合实践两个小组对部分环湖路进行了测量,数据包括:甲小组在点处测得点在正西方向,点在正北方向,点在东北方向,在点处测得点在正西方向,点在正南方向;乙小组测得米,米,米,米.(参考数据:)
(1)计算点与点的距离;
(2)某同学从去处回收测量工具,他有两条线路可以前往:①;②.请计算说明他选择线路①还是线路②路程更短.(计算结果保留到1米)
六、综合题
29.(2024八下·宿城期末)为打造书香校园,某中学计划选购甲、乙两种图书.已知甲图书每本价格比乙图书每本价格多30元,用1000元单独购买甲图书与用400元单独购买乙图书数量相同.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该校计划购买乙图书的本数比购买甲图书本数的3倍多4本,且用于购买甲、乙两种图书的总经费不超过850元,那么该中学最多可以购买多少本甲图书?
30.(2025八下·安徽期末)某校七、八年级各有200人参加“安全教育知识竞赛”,两年级参赛人员中各随机抽取10名学生的成绩如下:
七年级:73 81 65 82 85 95 81 85 97 85
八年级:72 76 79 83 87 97 76 83 83 95
【整理数据】
成绩
七年级 1 1 a 2
八年级 0 4 4 2
【分析数据】
统计量 平均数 中位数 众数 方差
七年级 82.9 b 85 78.49
八年级 83.1 83 c 59.09
【应用数据】
(1)直接写出______,______,______;
(2)请结合表格信息,判断样本中______年级学生的竞赛成绩更稳定?(填七或八)
(3)请估计该校七、八年级成绩不低于80分的总人数.
答案解析部分
1.【答案】D
【知识点】等腰三角形的判定;平行四边形的性质
2.【答案】D
【知识点】平行四边形的判定
【解析】【解答】解:由题意可知∵,
∴,
∵,
∴,
∴,
∵两组对边分别平行的四边形为平行四边形,
∴四边形是平行四边形,
故答案为:D.
【分析】根据平行四边形的判定定理解答即可.
3.【答案】B
【知识点】勾股定理;正方形的性质;三角形的中位线定理
【解析】【解答】解:连接,
∵四边形是正方形,
∴,,
∵点E、F分别是边、的中点,
∴,,
∴,
∵点M,N为别是、的中点,
∴是的中位线,
∴,
故选:B.
【分析】连接,利用正方形的性质和勾股定理求得长,再利用三角形中位线定理解答.
4.【答案】C
【知识点】正方形的判定与性质;两条直线被一组平行线所截,所得的对应线段成比例
5.【答案】C
【知识点】平行四边形的判定;菱形的判定;矩形的判定;正方形的判定
6.【答案】B
【知识点】平行四边形的性质
7.【答案】B
【知识点】线段垂直平分线的性质;平行四边形的性质;尺规作图-垂直平分线
【解析】【解答】解:由已知条件可知EF是AC的垂直平分线,所以EA=EC,
∵△BCE 的周长为14,
∴BC+CE+EB=14,
∴BC+EA+EB=14,
即BC+AB=14,
∵四边形ABCD为平行四边形,
∴DC=AB,BC=AD=6,
∴DC=14-BC=14-6=8,
故答案为:B.
【分析】由线段的垂直平分线的性质“线段的垂直平分线上的点到线段两端点的距离相等”可得EA=EC,再根据三角形BCE的周长等于三角形三边之和可求得AB的长,然后根据平行四边形的对边相等可求解 .
8.【答案】B
【知识点】方差
【解析】【解答】解:∵,,,,
,
∴最小.
∴乙的射击成绩最稳定.
故答案为:B.
【分析】根据方差的意义,方差越小数据越稳定即可求解.
9.【答案】B
【知识点】平行四边形的性质;三角形的中位线定理
10.【答案】D
【知识点】平均数及其计算;中位数;众数
11.【答案】4
【知识点】平行四边形的性质;三角形全等的判定-AAS;四边形的综合;四边形-动点问题
【解析】【解答】解:在平行四边形PCQD中,设对角线PQ与DC相交于点O,则O是DC的中点,
过点Q作QH⊥BC,交BC的延长线于H,
∵AD∥BC,
∴∠ADC=∠DCH,即∠ADP+∠PDC=∠DCQ+∠QCH,
∵PD∥CQ,
∴∠PDC=∠DCQ,
∴∠ADP=∠QCH,
又∵PD=CQ,
在Rt△ADP与Rt△HCQ中,
∴Rt△ADP≌Rt△HCQ(AAS),
∴AD=HC,
∵AD=1,BC=3,
∴BH=4,
∴当PQ⊥AB时,PQ的长最小,即为4.
故答案为:4.
【分析】过点Q作QH⊥BC,交BC的延长线于H,先利用“AAS”证出Rt△ADP≌Rt△HCQ,利用全等三角形的性质可得AD=HC,利用线段的和差求出BH=4,最后求出当PQ⊥AB时,PQ的长最小,即为4,从而得解.
12.【答案】10
【知识点】等边三角形的判定与性质;菱形的性质
【解析】【解答】解:∵四边形是菱形,
∴,
∵,
∴是等边三角形,
∴.
故答案为:10.
【分析】根据菱形的性质得到是等边三角形解题即可.
13.【答案】
【知识点】一次函数与不等式(组)的关系
【解析】【解答】解:∵直线与直线相交于,
∴不等式的解集为.
故答案为:.
【分析】结合函数图象,利用函数值大的图象在上方的原则求解即可.
14.【答案】
【知识点】线段垂直平分线的性质;平行四边形的性质
【解析】【解答】解:在中,
,相交于点,
为的中点,
,
是的垂直平分线,
,
∵的周长是,
∴,
的周长,
故答案为:.
【分析】
因为平行四边形的对角线互相平分,即O为BD中点,又EO垂直BD,则EO垂直平分BD,由线段垂直平分线的性质知ED等于EB,则的周长等于AB与AD的和,又平行四边形的对边分别相等,即的周长等于平行四边形ABCD周长的一半.
15.【答案】①②④
【知识点】平行四边形的性质;菱形的判定;两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的性质-对应边
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵EC垂直平分AB,
∴OA=OB=AB=DC,CD⊥CE,
∵OA∥DC,
∴=,
∴AE=AD,OE=OC,
∵OA=OB,OE=OC,
∴四边形ACBE是平行四边形,
∵AB⊥EC,
∴四边形ACBE是菱形,故①正确,
∵∠DCE=90°,DA=AE,
∴AC=AD=AE,
∴∠ACD=∠ADC=∠BAE,故②正确,
∵OA∥CD,
∴,
∴,故③错误,
设△AOF的面积为a,则△OFC的面积为2a,△CDF的面积为4a,△AOC的面积=△AOE的面积=3a,
∴四边形AFOE的面积为4a,△ODC的面积为6a
∴S四边形AFOE:S△COD=2:3.故④正确.
故答案是:①②④.
【分析】先证出四边形ACBE是平行四边形,再结合AB⊥EC,即可证出四边形ACBE是菱形,从而可判定①是否正确;再直角三角形斜边上中线的性质及等量代换可得AC=AD=AE,再利用等边对等角的性质可得∠ACD=∠ADC=∠BAE,从而可判断②是否正确;再利用平行线分线段成比例的性质及等量代换可得,从而可判断③是否正确;设△AOF的面积为a,再求出四边形AFOE的面积为4a,△ODC的面积为6a,最后求出S四边形AFOE:S△COD=2:3,从而可判断④是否正确,从而得解.
16.【答案】50
【知识点】正方形的性质
17.【答案】或
【知识点】正方形的性质;两条直线被一组平行线所截,所得的对应线段成比例;旋转的性质;等腰直角三角形
【解析】【解答】解:∵BE=6,CE=1,
∴BC=BE+CE=7.
∵四边形ABCD为正方形,
∴AB=BC=CD=DA=7,∠BAD=∠ABC=∠BCD=∠ADC=90°.
将△ABP绕点B顺时针旋转90°得到△CBQ,
∴AP=CQ,∠PBQ=90°,∠BCQ=∠BCD=90°,
∴△PBQ为等腰直角三角形,Q、C、D三点共线.
设AP=CQ=x,则PD=AD-AP=7-x,DQ=CD+CQ=7+x.
∵CE∥PD,
∴,
∴,
∴x=3+或3-,
经检验:x=3+,x=3-是分式方程的根且符合题意,
∴AP=3+或3-.
故答案为:3+或3-.
【分析】由已知条件可得BC=BE+CE=7,根据正方形的性质可得AB=BC=CD=DA=7,∠BAD=∠ABC=∠BCD=∠ADC=90°,将△ABP绕点B顺时针旋转90°得到△CBQ,可得AP=CQ,∠PBQ=90°,推出△PBQ为等腰直角三角形,Q、C、D三点共线,设AP=CQ=x,则PD=7-x,DQ=7+x,由平行线分线段成比例的性质可得,然后代入计算即可.
18.【答案】6或-2
【知识点】反比例函数系数k的几何意义;三角形的面积
【解析】【解答】解:设点A的坐标为(x0,),
由题意得,点B的坐标为(,),
点C的坐标为(x0,),AB=x0-kx02,AC=2x0-kx0,
∵S ABC=4 ,S ABC=12×AB×AC=12×x0-kx02×2x0-kx0,
∴12×x0-kx02×2x0-kx0=4,
解得k=6或k=-2.
故答案为:6或-2
【分析】先设点A的坐标为(x0,),根据题意,分别列出点B的坐标(,)和点C的坐标(x0,),表示出AB的长度x0-kx02 和AC的长度2x0-kx0 ,根据三角形的面积公式即可求出答案.
19.【答案】4
【知识点】反比例函数系数k的几何意义;三角形的面积;三角形的中位线定理
【解析】【解答】解:连接OC,过D作x轴的垂线交AB于E点,交x轴于F点,
∵S△CAO=S△DOF=|k|,
∵ D为线段OB的中点,
∴S△BDE=S△DOF=|k|,
∵DE是△AOB的中位线,
∴DE:OA=1:2,
∴S△BDE=S△AOB=S△CAO,
∴S△OBC=S△AOB-S△CAO=S△AOB,
∵ D为线段OB的中点,
∴S△OBC=2S△BCD=6=S△AOB,
∴S△AOB=8,
∴S△AOC=S△AOB=2= 12|k|,
∵k>0,
∴k=4.
故答案为:4.
【分析】连接OC,过D作x轴的垂线交AB于E点,交x轴于F点,根据反比例函数k的几何意义得出S△CAO=S△DOF,再由全等三角形的性质得出S△BDE=S△DOF,根据根据中位线定理推出S△BDE=S△AOB=S△CAO,从而得出S△OBC=S△AOB,再由同底等高得出S△OBC=2S△BCD=6,则可求出S△AOB=8,从而推出S△AOC=2=12|k|,即可解答.
20.【答案】
【知识点】坐标与图形性质;勾股定理;正方形的性质;翻折变换(折叠问题)
【解析】【解答】解∶设正方形的边长为a,与y轴相交于G,
则四边形是矩形,
∴,,,
∵折叠,
∴,,
∵点A的坐标为,点F的坐标为,
∴,,
∴,
在中,,
∴,
解得,
∴,,
在中,,
∴,
解得,
∴,
∴点E的坐标为,
故答案为:.
【分析】设正方形的边长为a,与y轴相交于G,即可得到是矩形,求出,,,利用折叠得到,,然后在中根据勾股定理求出a的值,再在中运用勾股定理得到长解题.
21.【答案】,
【知识点】分式的化简求值
22.【答案】解:
,
∵分式要有意义,
∴,
∴,
∴可取,此时原式.
【知识点】分式有无意义的条件;分式的化简求值-直接代入
【解析】【分析】先把小括号内的式子通分化简,再把除法变成乘法,后约分化简,接着再根据分式有意义的条件确定符合条件的x的值,并代值计算即可.
23.【答案】;8
【知识点】分式的化简求值
24.【答案】解:(1)
由①得:,即
由②得:,即,
把不等式①、②的解集在数轴上表示为
由图可知,两不等式解集的公共部分是,
所以这个不等式组的解集是.
(2)
在分式方程两边同乘最简公分母得:
解得:
检验:当时,
因此,是原方程的解.
【知识点】解分式方程;解一元一次不等式组;在数轴上表示不等式的解集
【解析】【分析】(1)根据解不等式的步骤,分别求出不等式组中每个不等式的解集,进而根据数轴上表示不等式解集的方法“大向右,小向左,实心等于,空心不等”将两个不等式的解集在数轴上表示出来,最后取两个不等式解集的公共部分,即可得到该不等式组的解集;
(2)在原方程两边同乘最简公分母(x+1)(x-1),约去分母,将分式方程转化为整式方程,解整式方程求出x的值,再检验即可得出原方程解的情况.
25.【答案】证明:(1)∵DF∥BE,
∴∠DFE=∠BEF.
又∵AF=CE,DF=BE,
∴△AFD≌△CEB(SAS).
(2)由(1)知△AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC,
∴AD∥BC.
∴四边形ABCD是平行四边形.
【知识点】平行四边形的判定;三角形全等的判定-SAS;全等三角形中对应边的关系;全等三角形中对应角的关系
【解析】【分析】(1)先根据平行线得到∠DFE=∠BEF,然后根据SAS证明两三角形全等即可;
(2)根据△AFD≌△CEB可得AD=BC且AD∥BC,然后根据平行四边形的判定定理解题即可.
26.【答案】(1)证明:,.
四边形是平行四边形,
又四边形是菱形,
,
,
平行四边形是矩形.
(2)解:四边形是菱形,
,,,
,
,
,
为等边三角形,则
,
,
四边形是矩形,
,
四边形的周长是.
【知识点】等边三角形的判定与性质;勾股定理;菱形的性质;矩形的判定与性质
【解析】【分析】本题考查菱形的性质、矩形的判定与性质、等边三角形的判定与性质、勾股定理,熟练掌握它们的性质和判定定理是解答的关键.
(1)先证四边形是平行四边形,再根据菱形的性质得到,根据有一个角是直角的平行四边形是矩形即证;
(2)由菱形的性质及可得∠ABC=60°,可证为等边三角形,根据等边三角形的性质得到,从而求出,,然后根据矩形的周长公式求解即可.
(1)证明:,.
四边形是平行四边形,
又四边形是菱形,
,
,
平行四边形是矩形.
(2)解:四边形是菱形,
,,,
,
,
,
为等边三角形,则
,则
,
四边形是矩形,
,
四边形的周长是.
27.【答案】任务1:设时,关于的函数表达式为,将点代入,可得,
∴时,关于的函数表达式为;
任务2:当时,可有,解得,
∵冷柜每20分钟为一个循环,
∴每天共有循环个数:(个),
∴冷柜每天运行的时间为分钟,
∴每天耗电量为:(度).
【知识点】反比例函数的实际应用
【解析】【分析】任务1:利用待定系数法求函数解析式即可;
任务2:得到冷柜每20分钟为一个循环,然后求出循环次数即可得到运行时间,利用公式解题即可.
28.【答案】(1)400米
(2)选择线路①路程更短
【知识点】勾股定理;矩形的判定与性质
29.【答案】(1)解:设乙图书每本价格为x元,则甲图书每本价格是元,
根据题意得:,
解得:,
经检验,x=20是所列方程的解,且符合题意,
∴x+30=20+30=50(元),
答:甲图书每本价格为50元,乙图书每本价格为20元;
(2)设该中学可以购买m本甲图书,则可以购买本乙图书,
由题意得:,
解得:,
答:该中学最多可以购买7本甲图书.
【知识点】分式方程的实际应用;一元一次不等式的应用
【解析】【分析】(1)设乙图书每本价格为x元,则甲图书每本价格是元,根据题意得等量关系: 1000元单独购买甲图书的数量=用400元单独购买乙图书的数量,据此列分式方程并求解即可.
(2)设该中学可以购买m本甲图书,则可以购买本乙图书,根据题意列出不等式求解即可得出答案.
30.【答案】(1)6;;83
(2)八
(3)估计该校七、八年级成绩不低于80分的总人数约为280人.
【知识点】中位数;方差;众数;用样本所占百分比估计总体数量
1 / 1
同课章节目录
