【中考押题卷】2025年中考数学二轮复习考前预测:尺规作图(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学二轮复习考前预测:尺规作图(含解析) |

|
|
| 格式 | docx | ||
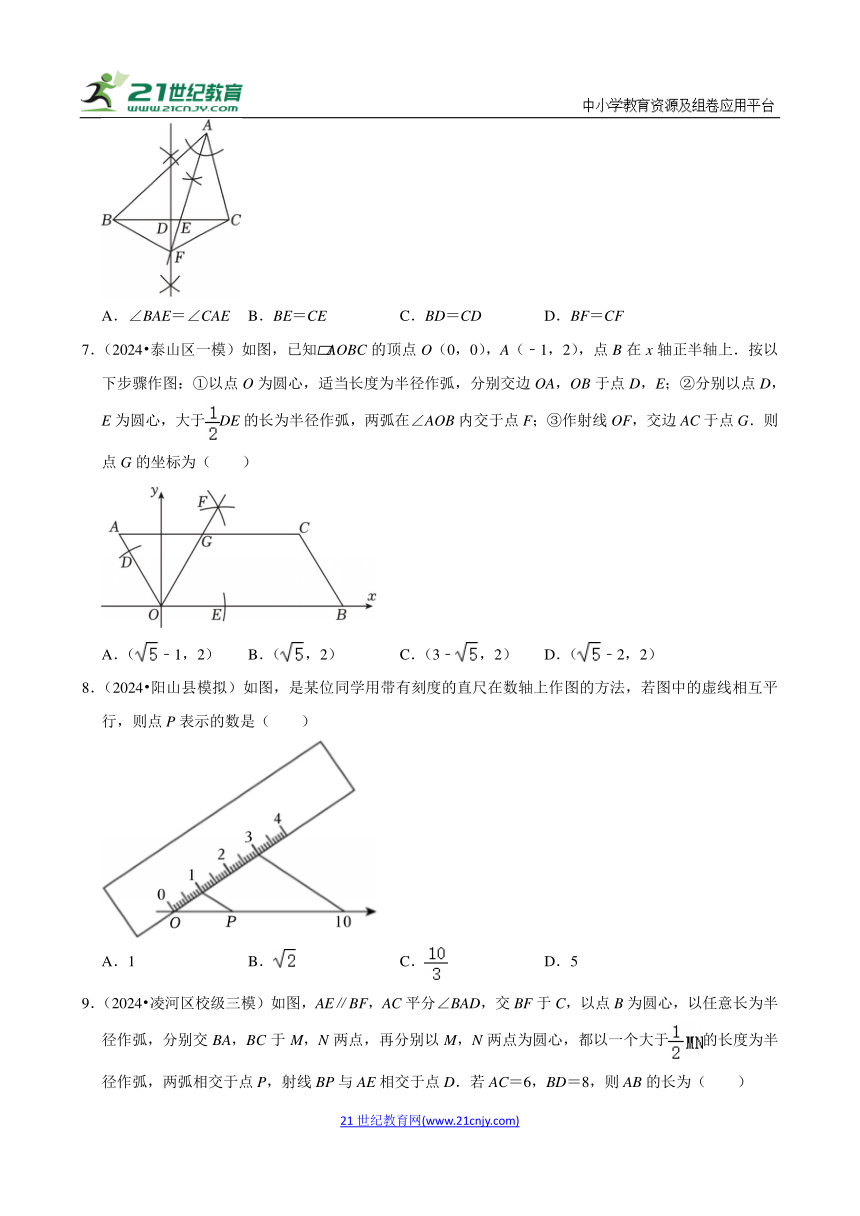
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 00:00:00 | ||
图片预览



文档简介
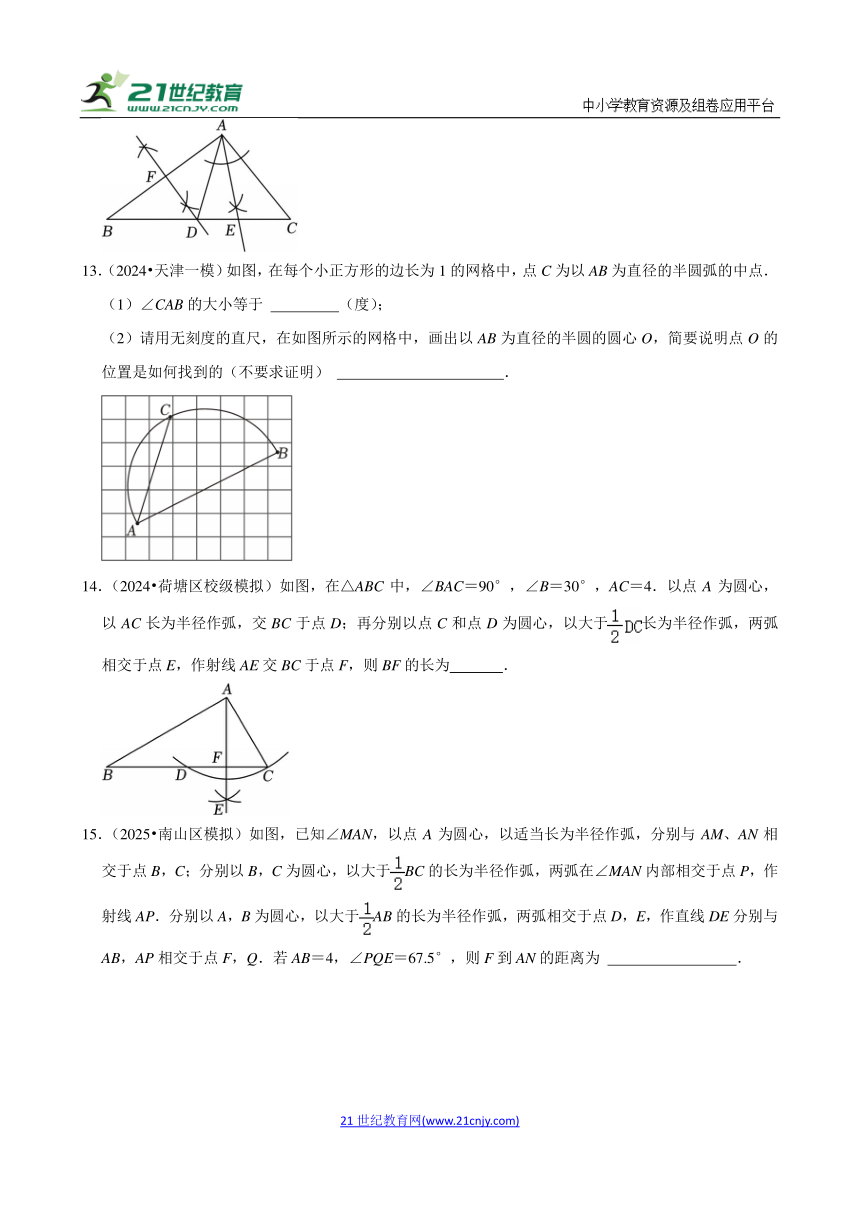
2025年中考数学二轮复习考前预测:尺规作图
一.选择题(共10小题)
1.(2025 济南模拟)如图,在平面直角坐标系中,正方形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,对角线AC和OB交于点D,作以下操作:(1)以点B为圆心,任意长为半径作弧,交BO于点M,交AB于点N;(2)分别以M,N为圆心,以大于的长为半径作弧,两弧交于点G;(3)作射线BG,交OA于点P,交AC于点Q.若OP=2,则点Q的坐标为( )
A. B. C. D.(3,1)
2.(2025 松江区一模)已知线段a、b、c,求作线段x,使.下列作图方法中(AB∥CD)不合理的是( )
A. B.
C. D.
3.(2025 石家庄校级模拟)如图,平面内有一点O,用尺规按①到③的步骤操作:①以点O为圆心,以任意长r为半径,画半圆O,直径为AB;②分别以点O,B为圆心,大于长为半径作弧,两弧交于点M,N,作直线MN,交半圆O于点C;③连接OC,以点C为圆心,以OC长为半径作弧,交半圆O于点E,连接AE,CE.
结论Ⅰ:点E为的中点;
结论Ⅱ:四边形AOCE为菱形.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
4.(2024 深圳模拟)如图,在△ABC中,AB=AC,∠BAC=36°,以点B为圆心,以BC为半径作弧交AB于点D,再分别以C,D为圆心,以大于长为半径作弧,两弧相交于点E,作射线BE交AC于点F,连接DF.以下结论不正确的是( )
A.AD=CF B.BC=AF C.∠ABE=36° D.∠CFD=108°
5.(2024 雨花台区模拟)如图,在Rt△ABC中,∠ACB=90°,根据尺规作图的痕迹,判断以下结论错误的是( )
A.∠BDE=∠BAC B.∠BAD=∠B C.DE=DC D.AE=AC
6.(2024 昌邑区校级三模)如图,在△ABC中,根据图中尺规作图的痕迹推断,以下结论不一定正确的是( )
A.∠BAE=∠CAE B.BE=CE C.BD=CD D.BF=CF
7.(2024 泰山区一模)如图,已知 AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上.按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.则点G的坐标为( )
A.(﹣1,2) B.(,2) C.(3﹣,2) D.(﹣2,2)
8.(2024 阳山县模拟)如图,是某位同学用带有刻度的直尺在数轴上作图的方法,若图中的虚线相互平行,则点P表示的数是( )
A.1 B. C. D.5
9.(2024 凌河区校级三模)如图,AE∥BF,AC平分∠BAD,交BF于C,以点B为圆心,以任意长为半径作弧,分别交BA,BC于M,N两点,再分别以M,N两点为圆心,都以一个大于的长度为半径作弧,两弧相交于点P,射线BP与AE相交于点D.若AC=6,BD=8,则AB的长为( )
A.3 B.4 C.5 D.6
10.(2024 长安区一模)对于题目“已知⊙O及圆外一点P,如何过点P作出⊙O的切线?”甲、乙的作法如图.
甲的作法 连接OP,作OP的垂直平分线交OP于点G,以点G为圆心,OG长为半径画弧交⊙O于M,作直线PM.直线PM即为所求. 乙的作法 连接PO并延长,交⊙O于B,C两点,分别以P,O为圆心,PO,BC长为半径作弧,两弧交于点D,连接OD,交⊙O于点M,作直线PM,直线PM即为所求.
下列说法正确的是( )
A.甲和乙的作法都正确
B.甲和乙的作法都错误
C.甲的作法正确,乙的作法错误
D.乙的作法正确,甲的作法错误
二.填空题(共5小题)
11.(2025 金山区一模)某校初三数学活动小组在利用尺规把线段AB分割成两条线段.
(1)过点B作BC⊥AB,使.
(2)联结AC,在线段CA上被取CD=CB.
(3)在线段AB上截取AE=AD.那么= .
12.(2024 坪山区校级一模)如图,在△ABC中,∠B=40°,∠C=50°.通过观察尺规作图的痕迹,可以求得∠DAE= 度.
13.(2024 天津一模)如图,在每个小正方形的边长为1的网格中,点C为以AB为直径的半圆弧的中点.
(1)∠CAB的大小等于 (度);
(2)请用无刻度的直尺,在如图所示的网格中,画出以AB为直径的半圆的圆心O,简要说明点O的位置是如何找到的(不要求证明) .
14.(2024 荷塘区校级模拟)如图,在△ABC中,∠BAC=90°,∠B=30°,AC=4.以点A为圆心,以AC长为半径作弧,交BC于点D;再分别以点C和点D为圆心,以大于长为半径作弧,两弧相交于点E,作射线AE交BC于点F,则BF的长为 .
15.(2025 南山区模拟)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B,C;分别以B,C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A,B为圆心,以大于AB的长为半径作弧,两弧相交于点D,E,作直线DE分别与AB,AP相交于点F,Q.若AB=4,∠PQE=67.5°,则F到AN的距离为 .
三.解答题(共5小题)
16.(2025 安阳模拟)已知在一些边长相同的小正方形组成的网格中,正方形ABCD的四个顶点都在小正方形的顶点上.点P为对角线BD上任意一点,连接PA,以PA,PD为邻边作平行四边形PAQD.
(1)当点P(在小正方形的顶点上)的位置如图所示时,请用直尺画出平行四边形PAQD;
(2)当PQ的最小值为时,求正方形ABCD的边长.
17.(2025 永寿县校级一模)如图,已知E是∠AOB的边AO上一点,EF∥OB.请用尺规作图的方法在EF上求作一点P,连接OP,使得.(保留作图痕迹,不写作法)
18.(2025 雁塔区校级一模)尺规作图(不写作法,保留作图痕迹):如图,AB为⊙O的直径,点C在⊙O上.在⊙O上作点D,使得线段DB=DC,且线段AD与BC相交.
19.(2025 旺苍县一模)如图这是一个残缺的圆形部件,已知A,B,C是该部件圆弧上的三点.
(1)利用尺规作图作出该部件的圆心;(保留作图痕迹)
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求该部件的半径R.
20.(2025 佛山一模)如图所示是广东醒狮,它是国家级非物质文化遗产之一,其中高桩醒狮更是由现代艺术演出转变而来的体育竞技.如图2,三根梅花桩AM,BP,CN垂直于地面放置,醒狮少年从点A跳跃到点B,随后纵身跃至点C,已知∠A=59°,∠C=45°,MP=0.25m,NP=1.35m.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
(1)在图2中,∠ABC= ;
(2)醒狮少年在某次演出时需要从点A直接腾跃至点C进行“采青”,请求出“采青”路径AC的长度;
(3)醒狮少年在休息时发现,在太阳光下梅花桩AM的影子顶端恰好落在点B处,梅花桩BP的影子顶端恰好与点N重合,请在图3中画出梅花桩AM,BP的影子并计算出BP的高度;
(4)如图4,保持BP不变,通过调整梅花桩AM的高度,使得AC+AB的值最小,请求出此时AM的高度(结果精确到0.01m).
2025年中考数学二轮复习考前预测:尺规作图
参考答案与试题解析
一.选择题(共10小题)
1.(2025 济南模拟)如图,在平面直角坐标系中,正方形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,对角线AC和OB交于点D,作以下操作:(1)以点B为圆心,任意长为半径作弧,交BO于点M,交AB于点N;(2)分别以M,N为圆心,以大于的长为半径作弧,两弧交于点G;(3)作射线BG,交OA于点P,交AC于点Q.若OP=2,则点Q的坐标为( )
A. B. C. D.(3,1)
【考点】作图—基本作图;坐标与图形性质;角平分线的性质;正方形的性质.
【专题】作图题;矩形 菱形 正方形;几何直观;运算能力;推理能力.
【答案】B
【分析】过点P作PT⊥OB于点T,过点Q作QK⊥AB于K,作QJ⊥OA于J,先在Rt△OPT中求出PT=,则OA=2+,进而再求出AD=+1,再证四边形AKQJ为正方形,设边长为a,则AQ=a,MD=MQ=a,据此得AD=a+a,据此可求出a的值,进而即可求出点Q的坐标.
【解答】解:过点P作PT⊥OB于点T,过点Q作QK⊥AB于K,作QJ⊥OA于J,
∵四边形OABC为正方形,
∴∠BOA=∠BAC=∠OAC=45°,∠OAB=90°,OB⊥AC,OD=AD,
∴△OPT为等腰直角三角形,
∵OP=2,
在Rt△OPT中,OT=PT,OP=2,
由勾股定理得:OT2+PT2=OP2,
即:2PT2=22,
∴PT=,
由作图可知:BP为∠OBA的平分线,
又PT⊥OB,∠OAB=90°,
∴PA=PT=,
∴OA=OP+PA=2+,
在Rt△OAD中,OD=AD,OA=2+,
由勾股定理得:OD2+AD2=OA2,
即:2AD2=(2+)2,
∴AD=+1,
∵∠BAC=∠OAC=45°,MQ⊥AB,MP⊥OA,
∴△AJQ和△AAQK均为等腰直角三角形,
∴JA=JQ,KA=KQ,
∵AC为∠OAB的平分线,QJ⊥AO,QK⊥AB,
∴QK=AK,
∴QJ=AJ=KQ=AK,
∴四边形AKQJ为正方形,
设JQ=a,则AQ=a,
∵BP为∠OBA的平分线,MQ⊥OB,QK⊥AB,
∴MQ=QK=a,
∴AD=AM+MD=a+a,
∴a+a=+1,
解得:a=1,
∴AJ=QJ=1,
∴OJ=OA﹣AJ=2+﹣1=+1,
∴点Q的坐标为(+1,1).
故选:B.
【点评】此题主要考查了正方形的判定和性质,基本作图——尺规作已知角的平分线,角平分线的性质,勾股定理等知识点,解答此题的关键是熟练掌握正方形的判定方法,理解正方形的性质和角平分线的性质.
2.(2025 松江区一模)已知线段a、b、c,求作线段x,使.下列作图方法中(AB∥CD)不合理的是( )
A. B.
C. D.
【考点】作图—复杂作图;平行线的性质.
【专题】作图题;几何直观.
【答案】B
【分析】利用图形得比例线段,再与已知式作对比,可以得出结论.
【解答】解:A、由图可得=,即x=,图形能画出,故此选项不符合题意;
B、由图可得=,即x=,图形不能画出,故此选项符合题意;
C、由图可得,图形能画出,故此选项不符合题意;
D、由图可得图形能画出,故此选项不符合题意.
故选:B.
【点评】本题考查作图﹣复杂作图,平行线的性质,解题的关键是掌握平行线分线段成比例定理.
3.(2025 石家庄校级模拟)如图,平面内有一点O,用尺规按①到③的步骤操作:①以点O为圆心,以任意长r为半径,画半圆O,直径为AB;②分别以点O,B为圆心,大于长为半径作弧,两弧交于点M,N,作直线MN,交半圆O于点C;③连接OC,以点C为圆心,以OC长为半径作弧,交半圆O于点E,连接AE,CE.
结论Ⅰ:点E为的中点;
结论Ⅱ:四边形AOCE为菱形.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
【考点】作图—复杂作图;线段垂直平分线的性质;菱形的判定;圆心角、弧、弦的关系.
【专题】矩形 菱形 正方形;圆的有关概念及性质;尺规作图;几何直观.
【答案】A
【分析】连接BC,OE,由作图过程可知,直线MN为线段OB的垂直平分线,CO=CE,可得△BOC为等边三角形,△COE为等边三角形,则∠BOC=60°,∠COE=∠ECO=60°,∠AOE=180°﹣∠COE﹣∠BOC=60°,可得∠COE=∠AOE,则,即点E为的中点;结合菱形的判定可得四边形AOCE为菱形.
【解答】解:连接BC,OE,
由作图过程可知,直线MN为线段OB的垂直平分线,
∴CO=CB.
∵OC=OB,
∴CO=CB=OB,
即△BOC为等边三角形,
∴∠BOC=60°.
由作图过程可知,CO=CE,
∵CO=OE,
∴CO=CE=OE,
即△COE为等边三角形,
∴∠COE=∠ECO=60°,
∴∠AOE=180°﹣∠COE﹣∠BOC=60°,
∴∠COE=∠AOE,
∴,
即点E为的中点.
故结论Ⅰ正确,符合题意;
∵∠ECO=∠BOC=60°,
∴CE∥AB.
∵CE=CO=OB=OA,
∴四边形AOCE为平行四边形.
∵CO=CE,
∴四边形AOCE为菱形.
故结论Ⅱ正确,符合题意.
故选:A.
【点评】本题考查作图—复杂作图、线段垂直平分线的性质、菱形的判定、圆心角、弧、弦的关系,解题的关键是理解题意,灵活运用所学知识解决问题.
4.(2024 深圳模拟)如图,在△ABC中,AB=AC,∠BAC=36°,以点B为圆心,以BC为半径作弧交AB于点D,再分别以C,D为圆心,以大于长为半径作弧,两弧相交于点E,作射线BE交AC于点F,连接DF.以下结论不正确的是( )
A.AD=CF B.BC=AF C.∠ABE=36° D.∠CFD=108°
【考点】作图—基本作图;角平分线的定义;等腰三角形的性质.
【专题】图形的全等;等腰三角形与直角三角形;尺规作图;几何直观.
【答案】D
【分析】由作图可知,BD=BC,BE为∠ABC的平分线.证明△BDF≌△BCF,可得DF=CF,∠BDF=∠BCF,结合等腰三角形的性质可得∠ABC=∠ACB=72°,则∠BDF=72°,进而可得∠BAC=∠AFD=36°,则AD=DF,即AD=CF,可判断A选项正确;根据等腰三角形的判定与性质可得AF=BF,BF=BC,则BC=AF,可判断B选项正确;根据∠ABE=∠CBE=ABC=36°,可判断C选项正确;由∠CFD=180°﹣∠AFD=144°,可判断D选项不正确.
【解答】解:由作图可知,BD=BC,BE为∠ABC的平分线,
∴∠ABE=∠CBE.
∵BF=BF,
∴△BDF≌△BCF(SAS),
∴DF=CF,∠BDF=∠BCF.
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°,
∴∠BDF=72°,
∴∠AFD=∠BDF﹣∠BAC=36°,
∴∠BAC=∠AFD,
∴AD=DF,
∴AD=CF,
故A选项正确,不符合题意;
∵∠ABE=∠CBE=ABC=36°,
∴∠BAC=∠ABE,
∴AF=BF,
∵∠BFC=180°﹣∠ACB﹣∠CBE=72°,
∴∠BFC=∠ACB,
∴BF=BC,
∴BC=AF,
故B选项正确,不符合题意,C选项正确,不符合题意;
∵∠CFD=180°﹣∠AFD,∠AFD=36°,
∴∠CFD=144°,
故D选项不正确,符合题意.
故选:D.
【点评】本题考查作图—基本作图、等腰三角形的性质、角平分线的定义、全等三角形的判定与性质,熟练掌握等腰三角形的性质、角平分线的定义、全等三角形的判定与性质是解答本题的关键.
5.(2024 雨花台区模拟)如图,在Rt△ABC中,∠ACB=90°,根据尺规作图的痕迹,判断以下结论错误的是( )
A.∠BDE=∠BAC B.∠BAD=∠B C.DE=DC D.AE=AC
【考点】作图—基本作图.
【专题】线段、角、相交线与平行线;图形的全等;尺规作图;推理能力.
【答案】B
【分析】由尺规作图的痕迹可得,DE⊥AB,AD是∠BAC的平分线,根据同角的余角相等可判断A,根据角平分线的性质可判断C,证得Rt△AED≌Rt△ACD可判定D,由于DE不是AB的垂直平分线,不能证明∠BAD=∠B.
【解答】解:根据尺规作图的痕迹可得,
∵DE可以理解成是平角∠AEB的角平分线,
∴DE⊥AB,AD是∠BAC的平分线,
∵∠C=90°,
∴DE=DC,∠B+∠BDE=∠B+∠BAC=90°,
∴∠BDE=∠BAC,
在Rt△AED和Rt△ACD中,
,
∴Rt△AED≌Rt△ACD(HL),
∴AE=AC,
∵DE不是AB的垂直平分线,故不能证明∠BAD=∠B,
综上所述:A,C,D不符合题意,B符合题意,
故选:B.
【点评】本题考查作图﹣基本作图,全等三角形的判定和性质,角平分线的性质,直角三角形的性质,解题的关键是根据尺规作图的痕迹可判断出DE⊥AB,AD是∠BAC的平分线.
6.(2024 昌邑区校级三模)如图,在△ABC中,根据图中尺规作图的痕迹推断,以下结论不一定正确的是( )
A.∠BAE=∠CAE B.BE=CE C.BD=CD D.BF=CF
【考点】作图—基本作图.
【专题】线段、角、相交线与平行线;尺规作图;几何直观;推理能力.
【答案】B
【分析】根据题意得到AF是∠BAC的角平分线,MN垂直平分BC,进而求解即可.
【解答】解:由作图知,AF是∠BAC的角平分线,
∴∠BAE=∠CAE,故A不符合题意;
由作图知MN垂直平分BC,
∴BD=CD,BF=CF,故C,D不符合题意;
无法证明BE=CE,故B符合题意,
故选:B.
【点评】本题考查作图﹣基本作图,熟知角平分线的作法和垂直平分线性质是解答此题的关键.
7.(2024 泰山区一模)如图,已知 AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上.按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.则点G的坐标为( )
A.(﹣1,2) B.(,2) C.(3﹣,2) D.(﹣2,2)
【考点】作图—基本作图;坐标与图形性质;平行四边形的性质.
【专题】尺规作图;几何直观.
【答案】A
【分析】分析题目,首先根据平行四边形的性质可得AC∥OB,接下来根据平行线的性质可得∠AGO=∠GOB;结合给出的作图步骤可知∠AOG=∠GOB,进而得到AG=AO,然后根据勾股定理求出OA的长,进而求出AG的长,问题便可解答.
【解答】解:∵四边形OACB是平行四边形,
∴AC∥OB,
∴∠AGO=∠GOB(两直线平行内错角相等).
由作图步骤可得∠AOG=∠GOB,
∴∠AGO=∠AOG,
∴AG=AO.
∵A(﹣1,2),
∴OA=,
∴AG=,
∴点G的坐标为(﹣1,2).
故选:A.
【点评】本题主要考查基本作图,掌握角平分线的做法是解题的关键.
8.(2024 阳山县模拟)如图,是某位同学用带有刻度的直尺在数轴上作图的方法,若图中的虚线相互平行,则点P表示的数是( )
A.1 B. C. D.5
【考点】作图—复杂作图;实数与数轴.
【专题】作图题;图形的相似;运算能力;推理能力.
【答案】C
【分析】根据平行线分线段成比例即可求解.
【解答】解:如图,OB=1,OA=3,OC=10,
∵PB∥AC,
∴,
∴=
∴OP=.
∴点P表示的数是.
故选:C.
【点评】本题考查平行线分线段成比例定理,熟练掌握平行线分线段成比例定理是解题的关键.
9.(2024 凌河区校级三模)如图,AE∥BF,AC平分∠BAD,交BF于C,以点B为圆心,以任意长为半径作弧,分别交BA,BC于M,N两点,再分别以M,N两点为圆心,都以一个大于的长度为半径作弧,两弧相交于点P,射线BP与AE相交于点D.若AC=6,BD=8,则AB的长为( )
A.3 B.4 C.5 D.6
【考点】作图—基本作图;角平分线的定义;平行线的性质;角平分线的性质;菱形的判定与性质.
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;矩形 菱形 正方形;推理能力.
【答案】C
【分析】根据角平分线的定义和平行线的性质证明四边形ABCD是菱形,由菱形的性质和勾股定理即可求出AB.
【解答】解:由基本作图可知BD是∠ABC的平分线,
∴∠ABD=∠CBD,
∵AE∥BF,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∵AC平分∠BAD,
∴∠BAC=∠DAC,
∵AE∥BF,
∴∠DAC=∠ACB,
∴∠BAC=∠ACB,
∴AB=BC,
∴AB=BC=AD,
∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形.
令AB与CD交于点O,
∴AO=CO=AC=×6=3,BO=DO=BD=×8=4,AC⊥BD,
在Rt△ABO中,
AB===5.
故选:C.
【点评】本题主要考查了角平分线的定义,平行线的性质,菱形的性质和判定,勾股定理,证明四边形ABCD是菱形是解决问题的关键.
10.(2024 长安区一模)对于题目“已知⊙O及圆外一点P,如何过点P作出⊙O的切线?”甲、乙的作法如图.
甲的作法 连接OP,作OP的垂直平分线交OP于点G,以点G为圆心,OG长为半径画弧交⊙O于M,作直线PM.直线PM即为所求. 乙的作法 连接PO并延长,交⊙O于B,C两点,分别以P,O为圆心,PO,BC长为半径作弧,两弧交于点D,连接OD,交⊙O于点M,作直线PM,直线PM即为所求.
下列说法正确的是( )
A.甲和乙的作法都正确
B.甲和乙的作法都错误
C.甲的作法正确,乙的作法错误
D.乙的作法正确,甲的作法错误
【考点】作图—复杂作图;线段垂直平分线的性质;切线的判定与性质.
【专题】作图题;几何直观;推理能力.
【答案】A
【分析】对于甲的作法,利用基本作图得到AB垂直平分OP,则OG=GP,再根据圆周角定理得到∠PMO=90°,然后根据切线的判定方法得到PM为⊙O的切线,于是可判断甲的作法正确;对于乙的作法:利用基本作图得到PD=PO,OD=BC,由于OM=BC,所以OM=DM,则根据等腰三角形的性质得到PM⊥OD,然后根据切线的判定方法得到PM为⊙O的切线,于是可判断乙的作法正确.
【解答】解:对于甲的作法:
由作法得AB垂直平分OP,
∴OG=GP,
∴点M为以OP为直径的圆与⊙O的交点,
∴∠PMO=90°,
∴OM⊥PM,
∴PM为⊙O的切线,所以甲的作法正确;
对于乙的作法:
由作法得PD=PO,OD=BC,
∵OM=BC,
∴OM=DM,
∴PM⊥OD,
∴PM为⊙O的切线,所以乙的作法正确;
故选:A.
【点评】本题考查了作图﹣复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的性质和切线的判定方法.
二.填空题(共5小题)
11.(2025 金山区一模)某校初三数学活动小组在利用尺规把线段AB分割成两条线段.
(1)过点B作BC⊥AB,使.
(2)联结AC,在线段CA上被取CD=CB.
(3)在线段AB上截取AE=AD.那么= .
【考点】作图—基本作图;含30度角的直角三角形.
【专题】作图题;几何直观;推理能力.
【答案】(1)见解析;
(2)见解析;
(3).
【分析】(1)作线段AB的垂直平分线得到线段AB的中点,作直线BC⊥AB于B,然后截取BC=AB即可;
(2)根据题意作出图形即可;
(3)根据勾股定理得到AC==AB,求得AD=AE=AC﹣CD=AB﹣AB,得到BE=AB﹣AE=AB﹣(AB﹣AB)=AB,于是得到结论.
【解答】解:(1)如图所示;点C即为所求;
(2)如图所示,点D即为所求;
(3)如图所示,点E即为所求.
∵BC=CD=,AC==AB,
∴AD=AE=AC﹣CD=AB﹣AB,
∴BE=AB﹣AE=AB﹣(AB﹣AB)=AB,
∴==,
故答案为:.
【点评】本题考查了作图﹣基本作图,熟练掌握基本作图的方法是解题的关键.
12.(2024 坪山区校级一模)如图,在△ABC中,∠B=40°,∠C=50°.通过观察尺规作图的痕迹,可以求得∠DAE= 25 度.
【考点】作图—基本作图;三角形内角和定理.
【专题】作图题;几何直观;推理能力.
【答案】25.
【分析】利用基本作图得到DF垂直平分AB,AE平分∠DAC,则DB=DA,∠DAE=∠DAC,所以∠DAB=∠B=40°,再利用三角形内角和计算出∠BAC=90°,则∠DAC=50°,从而得到∠DAE=25°.
【解答】解:由作图痕迹得DF垂直平分AB,AE平分∠DAC,
∴DB=DA,∠DAE=∠DAC,
∴∠DAB=∠B=40°,
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣40°﹣50°=90°,
∵∠DAC=∠BAC﹣∠DAB=90°﹣40°=50°,
∴∠DAE=×50°=25°.
故答案为:25.
【点评】本题考查了作图﹣基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了角平分线的性质和线段垂直平分线的性质.
13.(2024 天津一模)如图,在每个小正方形的边长为1的网格中,点C为以AB为直径的半圆弧的中点.
(1)∠CAB的大小等于 45 (度);
(2)请用无刻度的直尺,在如图所示的网格中,画出以AB为直径的半圆的圆心O,简要说明点O的位置是如何找到的(不要求证明) 取圆上两个格点M,N,再作MN的垂直平分线EF与AB的交点即为圆心O .
【考点】作图—复杂作图;垂径定理;圆周角定理.
【专题】作图题;与圆有关的计算;几何直观;推理能力.
【答案】(1)45;
(2)取圆上两个格点M,N,再作MN的垂直平分线EF与AB的交点即为圆心O.
【分析】(1)连接BC,证明△ABC是等腰直角三角形即可得到∠CAB=45°;
(2)取圆上两个格点M,N,再作MN的垂直平分线EF与AB的交点即为圆心O.
【解答】解:(1)连接BC,如图1,
∵点C为以AB为直径的半圆弧的中点,
∴CA=CB,∠ACB=90°
∴∠CAB=45°,
故答案为:45;
(2)取圆上两个格点M,N,再作MN的垂直平分线EF与AB的交点即为圆心O,依据垂径定理可知,O即为圆心,
如图2:
理由:∵EM=MF=FN=NE==,
∴四边形EMFN是菱形,
∴EF垂直平分MN,
EF与直径AB的交点O为圆心.
故答案为:取圆上两个格点M,N,再作MN的垂直平分线EF与AB的交点即为圆心O.
【点评】本题考查作图﹣复杂作图,垂径定理,圆周角定理,解题的关键是理解题意,灵活运用所学知识解决问题.
14.(2024 荷塘区校级模拟)如图,在△ABC中,∠BAC=90°,∠B=30°,AC=4.以点A为圆心,以AC长为半径作弧,交BC于点D;再分别以点C和点D为圆心,以大于长为半径作弧,两弧相交于点E,作射线AE交BC于点F,则BF的长为 6 .
【考点】作图—基本作图;含30度角的直角三角形.
【专题】作图题;等腰三角形与直角三角形;推理能力.
【答案】6.
【分析】根据直角三角形的性质和特殊角的三角函数即可得到结论.
【解答】解:由作图知,AF⊥BC,
∵∠BAC=90°,∠B=30°,AC=4.
∴AB=AC=4,
∵AF⊥BC,
∴∠AFB=90°,
∴,
故答案为:6.
【点评】本题考查了作图﹣基本作图,解决本题的关键是理解作图过程.
15.(2025 南山区模拟)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B,C;分别以B,C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A,B为圆心,以大于AB的长为半径作弧,两弧相交于点D,E,作直线DE分别与AB,AP相交于点F,Q.若AB=4,∠PQE=67.5°,则F到AN的距离为 .
【考点】作图—基本作图;角平分线的性质;线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;几何直观;推理能力.
【答案】见试题解答内容
【分析】如图,过F作FH⊥AC于H,证明∠BAP=∠CAP,DE⊥AB,,再证明∠FAH=45°,再结合勾股定理可得答案.
【解答】解:如图,过F作FH⊥AC于H,
由作图可得:∠BAP=∠CAP,DE⊥AB,,
∵∠PQE=67.5°,
∴∠AQF=67.5°,
∴∠BAP=∠CAP=90°﹣67.5°=22.5°,
∴∠FAH=45°,
∴,
∴F到AN的距离为;
故答案为:.
【点评】本题考查了作图﹣复杂作图:基本作图,三角形的内角和定理的应用,勾股定理的应用,等腰三角形的判定,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质,逐步操作.
三.解答题(共5小题)
16.(2025 安阳模拟)已知在一些边长相同的小正方形组成的网格中,正方形ABCD的四个顶点都在小正方形的顶点上.点P为对角线BD上任意一点,连接PA,以PA,PD为邻边作平行四边形PAQD.
(1)当点P(在小正方形的顶点上)的位置如图所示时,请用直尺画出平行四边形PAQD;
(2)当PQ的最小值为时,求正方形ABCD的边长.
【考点】作图—应用与设计作图;相似三角形的判定与性质;垂线段最短;平行四边形的判定与性质.
【专题】平移、旋转与对称;推理能力.
【答案】(1)见解析;
(2).
【分析】(1)根据平行四边形两组对比分别平行的性质画图即可;
(2)设PQ与AD交于点O,根据平行四边形的性质可知,OP=OQ,OA=OD,得出OP最短时,PQ最小,再过O作BD的垂线,垂足为P′,此时OP′最短,再得出△DOP′~△DAB,根据相似比求出正方形边长即可.
【解答】解:(1)如图所示,四边形PAQD即为所求;
(2)设PQ与AD交于点O,
∵PAQD为平行四边形,
∴OP=OQ,OA=OD,
∴OP最短时,PQ最小,
过O作BD的垂线,垂足为P′,此时OP′最短,
∵PQ的最小值为,
∴,
∵∠DP′O=∠DAB=90°,
∠ADB为公共角,
∴△DOP′~△DAB,
∴,
设正方形边长为a,
∴,
∴,
解得,
∴正方形ABCD的边长为.
【点评】本题主要考查平行四边形的性质,利用垂线段求最小值,相似三角形的判定与性质,熟练运用垂线段求最小值是解决本题的关键.
17.(2025 永寿县校级一模)如图,已知E是∠AOB的边AO上一点,EF∥OB.请用尺规作图的方法在EF上求作一点P,连接OP,使得.(保留作图痕迹,不写作法)
【考点】作图—复杂作图;平行线的性质.
【专题】线段、角、相交线与平行线;尺规作图;几何直观.
【答案】见解答.
【分析】结合平行线的性质,作∠AOB的平分线,交EF于点P,则点P即为所求.
【解答】解:如图,作∠AOB的平分线,交EF于点P,
可得.
∵EF∥OB,
∴∠AEF=∠AOB,
∴,
则点P即为所求.
【点评】本题考查作图—复杂作图、平行线的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
18.(2025 雁塔区校级一模)尺规作图(不写作法,保留作图痕迹):如图,AB为⊙O的直径,点C在⊙O上.在⊙O上作点D,使得线段DB=DC,且线段AD与BC相交.
【考点】作图—复杂作图;线段垂直平分线的性质.
【专题】作图题;几何直观.
【答案】见解析.
【分析】作线段BC的垂直平分线交优弧BC于点D,点D即为所求.
【解答】解:如图,点D即为所求.
【点评】本题考查作图﹣复杂作图,解题的关键是理解题意,正确作出图形.
19.(2025 旺苍县一模)如图这是一个残缺的圆形部件,已知A,B,C是该部件圆弧上的三点.
(1)利用尺规作图作出该部件的圆心;(保留作图痕迹)
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求该部件的半径R.
【考点】作图—应用与设计作图;等腰三角形的性质;垂径定理.
【专题】与圆有关的计算;几何直观;运算能力.
【答案】见试题解答内容
【分析】(1)作相等AB,AC的垂直平分线交于点O,以O为圆心,OA为半径作⊙O即可;
(2)利用垂径定理,勾股定理求解.
【解答】解:(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;
(2)连接AO,OB,BC,BC交OA于D.
∵AB=AC,
∴=,
∴OA⊥BC,
∴BD=DC,
∵BC=16cm,
∴BD=8(cm),
∵AB=10cm,
∴AD===6(cm),
设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,
∴R2=82+(R﹣6)2,
解得:,
∴圆片的半径R为.
【点评】本题考查作图﹣应用与设计作图,垂径定理,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
20.(2025 佛山一模)如图所示是广东醒狮,它是国家级非物质文化遗产之一,其中高桩醒狮更是由现代艺术演出转变而来的体育竞技.如图2,三根梅花桩AM,BP,CN垂直于地面放置,醒狮少年从点A跳跃到点B,随后纵身跃至点C,已知∠A=59°,∠C=45°,MP=0.25m,NP=1.35m.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
(1)在图2中,∠ABC= 104° ;
(2)醒狮少年在某次演出时需要从点A直接腾跃至点C进行“采青”,请求出“采青”路径AC的长度;
(3)醒狮少年在休息时发现,在太阳光下梅花桩AM的影子顶端恰好落在点B处,梅花桩BP的影子顶端恰好与点N重合,请在图3中画出梅花桩AM,BP的影子并计算出BP的高度;
(4)如图4,保持BP不变,通过调整梅花桩AM的高度,使得AC+AB的值最小,请求出此时AM的高度(结果精确到0.01m).
【考点】作图—应用与设计作图;轴对称﹣最短路线问题;解直角三角形的应用;平行投影.
【专题】解直角三角形及其应用;推理能力.
【答案】(1)104°;
(2)AC的长度约为2m;
(3)见解析,BP的高度约为0.81m;
(4)AM的高度约为0.99m.
【分析】(1)延长PB至H,根据平行线的性质可得∠ABH=∠A=59°,∠CBH=∠C=45°,即可得解;
(2)过点B作直线EF∥MN,分别交AM,CN于点E,F,过点A作直线AD∥MN,交CN于点D,连接AC,则四边形AMND,四边形AEFD,四边形EMPB,四边形BPNF均是矩形,由矩形的性质可得EB=MP=0.25m,BF=NP=1.35m,DF=AE,再解直角三角形结合勾股定理计算即可得解;
(3)线段MP,PB为梅花桩AM的影子,线段PN为梅花桩BP的影子.再利用相似三角形的性质求解即可;
(4)作点B关于AM的对称点B′,连接B′C交AM于A′,连接A′B,A′C,则A′B+A′C=A′B′+A′C=B′C,则B′C就是AC+AB的最小值,由(2)得CH=1.35m,由轴对称得B′G=BG=0.25m,再利用相似三角形的性质计算即可得解.
【解答】解:(1)如图:延长PB至H,
由题意可得:AM∥PH∥CN,
∴∠ABH=∠A=59°,∠CBH=∠C=45°,
∴∠ABC=∠ABH+∠CBH=104°,
故答案为:104°;
(2)如图,过点B作直线EF∥MN,分别交AM,CN于点E,F,过点A作直线AD∥MN,交CN于点D,连接AC.
由题意得∠EMN=∠FNM=∠MAD=∠ADN=∠MEF=∠NFE=∠BPM=∠BPN=90°,
∴四边形AMND,四边形AEFD,四边形EMPB,四边形BPNF均是矩形,
∴EB=MP=0.25m,BF=NP=1.35m,DF=AE,
∴AD=EF=1.6m.
∵∠EAB=59°,∠BCF=45°,
∴∠EBA=90°﹣59°=31°,∠CBF=90°﹣45°=45°=∠BCF,
∴AE=EB tan31°≈0.15m,CF=BF=1.35m,
∴CD=CF﹣DF=CF﹣AE=1.2m,
∵在Rt△ACD中,AD=1.6m,CD=1.2m,
AC2=AD2+CD2,
∴.
即“采青”路径AC的长度约为2m.
(3)如图,线段MP,PB为梅花桩AM的影子,线段PN为梅花桩BP的影子.
∵∠BPN=∠AMN=90°,∠BNP=∠ANM,
∴△BNP∽△ANM,
∴.
由(1)得AM≈0.15+BP,
∴,
∴1.6BP=0.2025+1.35BP,
∴0.25BP=0.2025,
∴BP=0.81m.
经检验BP=0.81且符合题意,所以BP的高度约为0.81米.
(4)如图,作点B关于AM的对称点B′,连接B′C交AM于A′,连接B′B并延长交CN于H,连接A′B,A′C,
∴A′B+A′C=A′B′+A′C=B′C,则B′C就是AC+AB的最小值,
由对称性质可知:B′B⊥AM,
同理(2)得CH=1.35m,
由轴对称得B′G=BG=0.25m,
∴B′H=1.85m.
∵A′G∥CH
∴△A′B′G′∽△CB′H,
∴.
即,
∴A'G=m,
∴A′M=0.18+GM=0.18+BP=0.99m,
∴此时AM的高度约为0.99m.
【点评】本题考查了平行线的性质、解直角三角形、相似三角形的判定与性质、勾股定理等知识点,熟练掌握以上知识点并灵活运用,添加适当的辅助线是解此题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2025 济南模拟)如图,在平面直角坐标系中,正方形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,对角线AC和OB交于点D,作以下操作:(1)以点B为圆心,任意长为半径作弧,交BO于点M,交AB于点N;(2)分别以M,N为圆心,以大于的长为半径作弧,两弧交于点G;(3)作射线BG,交OA于点P,交AC于点Q.若OP=2,则点Q的坐标为( )
A. B. C. D.(3,1)
2.(2025 松江区一模)已知线段a、b、c,求作线段x,使.下列作图方法中(AB∥CD)不合理的是( )
A. B.
C. D.
3.(2025 石家庄校级模拟)如图,平面内有一点O,用尺规按①到③的步骤操作:①以点O为圆心,以任意长r为半径,画半圆O,直径为AB;②分别以点O,B为圆心,大于长为半径作弧,两弧交于点M,N,作直线MN,交半圆O于点C;③连接OC,以点C为圆心,以OC长为半径作弧,交半圆O于点E,连接AE,CE.
结论Ⅰ:点E为的中点;
结论Ⅱ:四边形AOCE为菱形.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
4.(2024 深圳模拟)如图,在△ABC中,AB=AC,∠BAC=36°,以点B为圆心,以BC为半径作弧交AB于点D,再分别以C,D为圆心,以大于长为半径作弧,两弧相交于点E,作射线BE交AC于点F,连接DF.以下结论不正确的是( )
A.AD=CF B.BC=AF C.∠ABE=36° D.∠CFD=108°
5.(2024 雨花台区模拟)如图,在Rt△ABC中,∠ACB=90°,根据尺规作图的痕迹,判断以下结论错误的是( )
A.∠BDE=∠BAC B.∠BAD=∠B C.DE=DC D.AE=AC
6.(2024 昌邑区校级三模)如图,在△ABC中,根据图中尺规作图的痕迹推断,以下结论不一定正确的是( )
A.∠BAE=∠CAE B.BE=CE C.BD=CD D.BF=CF
7.(2024 泰山区一模)如图,已知 AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上.按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.则点G的坐标为( )
A.(﹣1,2) B.(,2) C.(3﹣,2) D.(﹣2,2)
8.(2024 阳山县模拟)如图,是某位同学用带有刻度的直尺在数轴上作图的方法,若图中的虚线相互平行,则点P表示的数是( )
A.1 B. C. D.5
9.(2024 凌河区校级三模)如图,AE∥BF,AC平分∠BAD,交BF于C,以点B为圆心,以任意长为半径作弧,分别交BA,BC于M,N两点,再分别以M,N两点为圆心,都以一个大于的长度为半径作弧,两弧相交于点P,射线BP与AE相交于点D.若AC=6,BD=8,则AB的长为( )
A.3 B.4 C.5 D.6
10.(2024 长安区一模)对于题目“已知⊙O及圆外一点P,如何过点P作出⊙O的切线?”甲、乙的作法如图.
甲的作法 连接OP,作OP的垂直平分线交OP于点G,以点G为圆心,OG长为半径画弧交⊙O于M,作直线PM.直线PM即为所求. 乙的作法 连接PO并延长,交⊙O于B,C两点,分别以P,O为圆心,PO,BC长为半径作弧,两弧交于点D,连接OD,交⊙O于点M,作直线PM,直线PM即为所求.
下列说法正确的是( )
A.甲和乙的作法都正确
B.甲和乙的作法都错误
C.甲的作法正确,乙的作法错误
D.乙的作法正确,甲的作法错误
二.填空题(共5小题)
11.(2025 金山区一模)某校初三数学活动小组在利用尺规把线段AB分割成两条线段.
(1)过点B作BC⊥AB,使.
(2)联结AC,在线段CA上被取CD=CB.
(3)在线段AB上截取AE=AD.那么= .
12.(2024 坪山区校级一模)如图,在△ABC中,∠B=40°,∠C=50°.通过观察尺规作图的痕迹,可以求得∠DAE= 度.
13.(2024 天津一模)如图,在每个小正方形的边长为1的网格中,点C为以AB为直径的半圆弧的中点.
(1)∠CAB的大小等于 (度);
(2)请用无刻度的直尺,在如图所示的网格中,画出以AB为直径的半圆的圆心O,简要说明点O的位置是如何找到的(不要求证明) .
14.(2024 荷塘区校级模拟)如图,在△ABC中,∠BAC=90°,∠B=30°,AC=4.以点A为圆心,以AC长为半径作弧,交BC于点D;再分别以点C和点D为圆心,以大于长为半径作弧,两弧相交于点E,作射线AE交BC于点F,则BF的长为 .
15.(2025 南山区模拟)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B,C;分别以B,C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A,B为圆心,以大于AB的长为半径作弧,两弧相交于点D,E,作直线DE分别与AB,AP相交于点F,Q.若AB=4,∠PQE=67.5°,则F到AN的距离为 .
三.解答题(共5小题)
16.(2025 安阳模拟)已知在一些边长相同的小正方形组成的网格中,正方形ABCD的四个顶点都在小正方形的顶点上.点P为对角线BD上任意一点,连接PA,以PA,PD为邻边作平行四边形PAQD.
(1)当点P(在小正方形的顶点上)的位置如图所示时,请用直尺画出平行四边形PAQD;
(2)当PQ的最小值为时,求正方形ABCD的边长.
17.(2025 永寿县校级一模)如图,已知E是∠AOB的边AO上一点,EF∥OB.请用尺规作图的方法在EF上求作一点P,连接OP,使得.(保留作图痕迹,不写作法)
18.(2025 雁塔区校级一模)尺规作图(不写作法,保留作图痕迹):如图,AB为⊙O的直径,点C在⊙O上.在⊙O上作点D,使得线段DB=DC,且线段AD与BC相交.
19.(2025 旺苍县一模)如图这是一个残缺的圆形部件,已知A,B,C是该部件圆弧上的三点.
(1)利用尺规作图作出该部件的圆心;(保留作图痕迹)
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求该部件的半径R.
20.(2025 佛山一模)如图所示是广东醒狮,它是国家级非物质文化遗产之一,其中高桩醒狮更是由现代艺术演出转变而来的体育竞技.如图2,三根梅花桩AM,BP,CN垂直于地面放置,醒狮少年从点A跳跃到点B,随后纵身跃至点C,已知∠A=59°,∠C=45°,MP=0.25m,NP=1.35m.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
(1)在图2中,∠ABC= ;
(2)醒狮少年在某次演出时需要从点A直接腾跃至点C进行“采青”,请求出“采青”路径AC的长度;
(3)醒狮少年在休息时发现,在太阳光下梅花桩AM的影子顶端恰好落在点B处,梅花桩BP的影子顶端恰好与点N重合,请在图3中画出梅花桩AM,BP的影子并计算出BP的高度;
(4)如图4,保持BP不变,通过调整梅花桩AM的高度,使得AC+AB的值最小,请求出此时AM的高度(结果精确到0.01m).
2025年中考数学二轮复习考前预测:尺规作图
参考答案与试题解析
一.选择题(共10小题)
1.(2025 济南模拟)如图,在平面直角坐标系中,正方形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,对角线AC和OB交于点D,作以下操作:(1)以点B为圆心,任意长为半径作弧,交BO于点M,交AB于点N;(2)分别以M,N为圆心,以大于的长为半径作弧,两弧交于点G;(3)作射线BG,交OA于点P,交AC于点Q.若OP=2,则点Q的坐标为( )
A. B. C. D.(3,1)
【考点】作图—基本作图;坐标与图形性质;角平分线的性质;正方形的性质.
【专题】作图题;矩形 菱形 正方形;几何直观;运算能力;推理能力.
【答案】B
【分析】过点P作PT⊥OB于点T,过点Q作QK⊥AB于K,作QJ⊥OA于J,先在Rt△OPT中求出PT=,则OA=2+,进而再求出AD=+1,再证四边形AKQJ为正方形,设边长为a,则AQ=a,MD=MQ=a,据此得AD=a+a,据此可求出a的值,进而即可求出点Q的坐标.
【解答】解:过点P作PT⊥OB于点T,过点Q作QK⊥AB于K,作QJ⊥OA于J,
∵四边形OABC为正方形,
∴∠BOA=∠BAC=∠OAC=45°,∠OAB=90°,OB⊥AC,OD=AD,
∴△OPT为等腰直角三角形,
∵OP=2,
在Rt△OPT中,OT=PT,OP=2,
由勾股定理得:OT2+PT2=OP2,
即:2PT2=22,
∴PT=,
由作图可知:BP为∠OBA的平分线,
又PT⊥OB,∠OAB=90°,
∴PA=PT=,
∴OA=OP+PA=2+,
在Rt△OAD中,OD=AD,OA=2+,
由勾股定理得:OD2+AD2=OA2,
即:2AD2=(2+)2,
∴AD=+1,
∵∠BAC=∠OAC=45°,MQ⊥AB,MP⊥OA,
∴△AJQ和△AAQK均为等腰直角三角形,
∴JA=JQ,KA=KQ,
∵AC为∠OAB的平分线,QJ⊥AO,QK⊥AB,
∴QK=AK,
∴QJ=AJ=KQ=AK,
∴四边形AKQJ为正方形,
设JQ=a,则AQ=a,
∵BP为∠OBA的平分线,MQ⊥OB,QK⊥AB,
∴MQ=QK=a,
∴AD=AM+MD=a+a,
∴a+a=+1,
解得:a=1,
∴AJ=QJ=1,
∴OJ=OA﹣AJ=2+﹣1=+1,
∴点Q的坐标为(+1,1).
故选:B.
【点评】此题主要考查了正方形的判定和性质,基本作图——尺规作已知角的平分线,角平分线的性质,勾股定理等知识点,解答此题的关键是熟练掌握正方形的判定方法,理解正方形的性质和角平分线的性质.
2.(2025 松江区一模)已知线段a、b、c,求作线段x,使.下列作图方法中(AB∥CD)不合理的是( )
A. B.
C. D.
【考点】作图—复杂作图;平行线的性质.
【专题】作图题;几何直观.
【答案】B
【分析】利用图形得比例线段,再与已知式作对比,可以得出结论.
【解答】解:A、由图可得=,即x=,图形能画出,故此选项不符合题意;
B、由图可得=,即x=,图形不能画出,故此选项符合题意;
C、由图可得,图形能画出,故此选项不符合题意;
D、由图可得图形能画出,故此选项不符合题意.
故选:B.
【点评】本题考查作图﹣复杂作图,平行线的性质,解题的关键是掌握平行线分线段成比例定理.
3.(2025 石家庄校级模拟)如图,平面内有一点O,用尺规按①到③的步骤操作:①以点O为圆心,以任意长r为半径,画半圆O,直径为AB;②分别以点O,B为圆心,大于长为半径作弧,两弧交于点M,N,作直线MN,交半圆O于点C;③连接OC,以点C为圆心,以OC长为半径作弧,交半圆O于点E,连接AE,CE.
结论Ⅰ:点E为的中点;
结论Ⅱ:四边形AOCE为菱形.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
【考点】作图—复杂作图;线段垂直平分线的性质;菱形的判定;圆心角、弧、弦的关系.
【专题】矩形 菱形 正方形;圆的有关概念及性质;尺规作图;几何直观.
【答案】A
【分析】连接BC,OE,由作图过程可知,直线MN为线段OB的垂直平分线,CO=CE,可得△BOC为等边三角形,△COE为等边三角形,则∠BOC=60°,∠COE=∠ECO=60°,∠AOE=180°﹣∠COE﹣∠BOC=60°,可得∠COE=∠AOE,则,即点E为的中点;结合菱形的判定可得四边形AOCE为菱形.
【解答】解:连接BC,OE,
由作图过程可知,直线MN为线段OB的垂直平分线,
∴CO=CB.
∵OC=OB,
∴CO=CB=OB,
即△BOC为等边三角形,
∴∠BOC=60°.
由作图过程可知,CO=CE,
∵CO=OE,
∴CO=CE=OE,
即△COE为等边三角形,
∴∠COE=∠ECO=60°,
∴∠AOE=180°﹣∠COE﹣∠BOC=60°,
∴∠COE=∠AOE,
∴,
即点E为的中点.
故结论Ⅰ正确,符合题意;
∵∠ECO=∠BOC=60°,
∴CE∥AB.
∵CE=CO=OB=OA,
∴四边形AOCE为平行四边形.
∵CO=CE,
∴四边形AOCE为菱形.
故结论Ⅱ正确,符合题意.
故选:A.
【点评】本题考查作图—复杂作图、线段垂直平分线的性质、菱形的判定、圆心角、弧、弦的关系,解题的关键是理解题意,灵活运用所学知识解决问题.
4.(2024 深圳模拟)如图,在△ABC中,AB=AC,∠BAC=36°,以点B为圆心,以BC为半径作弧交AB于点D,再分别以C,D为圆心,以大于长为半径作弧,两弧相交于点E,作射线BE交AC于点F,连接DF.以下结论不正确的是( )
A.AD=CF B.BC=AF C.∠ABE=36° D.∠CFD=108°
【考点】作图—基本作图;角平分线的定义;等腰三角形的性质.
【专题】图形的全等;等腰三角形与直角三角形;尺规作图;几何直观.
【答案】D
【分析】由作图可知,BD=BC,BE为∠ABC的平分线.证明△BDF≌△BCF,可得DF=CF,∠BDF=∠BCF,结合等腰三角形的性质可得∠ABC=∠ACB=72°,则∠BDF=72°,进而可得∠BAC=∠AFD=36°,则AD=DF,即AD=CF,可判断A选项正确;根据等腰三角形的判定与性质可得AF=BF,BF=BC,则BC=AF,可判断B选项正确;根据∠ABE=∠CBE=ABC=36°,可判断C选项正确;由∠CFD=180°﹣∠AFD=144°,可判断D选项不正确.
【解答】解:由作图可知,BD=BC,BE为∠ABC的平分线,
∴∠ABE=∠CBE.
∵BF=BF,
∴△BDF≌△BCF(SAS),
∴DF=CF,∠BDF=∠BCF.
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°,
∴∠BDF=72°,
∴∠AFD=∠BDF﹣∠BAC=36°,
∴∠BAC=∠AFD,
∴AD=DF,
∴AD=CF,
故A选项正确,不符合题意;
∵∠ABE=∠CBE=ABC=36°,
∴∠BAC=∠ABE,
∴AF=BF,
∵∠BFC=180°﹣∠ACB﹣∠CBE=72°,
∴∠BFC=∠ACB,
∴BF=BC,
∴BC=AF,
故B选项正确,不符合题意,C选项正确,不符合题意;
∵∠CFD=180°﹣∠AFD,∠AFD=36°,
∴∠CFD=144°,
故D选项不正确,符合题意.
故选:D.
【点评】本题考查作图—基本作图、等腰三角形的性质、角平分线的定义、全等三角形的判定与性质,熟练掌握等腰三角形的性质、角平分线的定义、全等三角形的判定与性质是解答本题的关键.
5.(2024 雨花台区模拟)如图,在Rt△ABC中,∠ACB=90°,根据尺规作图的痕迹,判断以下结论错误的是( )
A.∠BDE=∠BAC B.∠BAD=∠B C.DE=DC D.AE=AC
【考点】作图—基本作图.
【专题】线段、角、相交线与平行线;图形的全等;尺规作图;推理能力.
【答案】B
【分析】由尺规作图的痕迹可得,DE⊥AB,AD是∠BAC的平分线,根据同角的余角相等可判断A,根据角平分线的性质可判断C,证得Rt△AED≌Rt△ACD可判定D,由于DE不是AB的垂直平分线,不能证明∠BAD=∠B.
【解答】解:根据尺规作图的痕迹可得,
∵DE可以理解成是平角∠AEB的角平分线,
∴DE⊥AB,AD是∠BAC的平分线,
∵∠C=90°,
∴DE=DC,∠B+∠BDE=∠B+∠BAC=90°,
∴∠BDE=∠BAC,
在Rt△AED和Rt△ACD中,
,
∴Rt△AED≌Rt△ACD(HL),
∴AE=AC,
∵DE不是AB的垂直平分线,故不能证明∠BAD=∠B,
综上所述:A,C,D不符合题意,B符合题意,
故选:B.
【点评】本题考查作图﹣基本作图,全等三角形的判定和性质,角平分线的性质,直角三角形的性质,解题的关键是根据尺规作图的痕迹可判断出DE⊥AB,AD是∠BAC的平分线.
6.(2024 昌邑区校级三模)如图,在△ABC中,根据图中尺规作图的痕迹推断,以下结论不一定正确的是( )
A.∠BAE=∠CAE B.BE=CE C.BD=CD D.BF=CF
【考点】作图—基本作图.
【专题】线段、角、相交线与平行线;尺规作图;几何直观;推理能力.
【答案】B
【分析】根据题意得到AF是∠BAC的角平分线,MN垂直平分BC,进而求解即可.
【解答】解:由作图知,AF是∠BAC的角平分线,
∴∠BAE=∠CAE,故A不符合题意;
由作图知MN垂直平分BC,
∴BD=CD,BF=CF,故C,D不符合题意;
无法证明BE=CE,故B符合题意,
故选:B.
【点评】本题考查作图﹣基本作图,熟知角平分线的作法和垂直平分线性质是解答此题的关键.
7.(2024 泰山区一模)如图,已知 AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上.按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.则点G的坐标为( )
A.(﹣1,2) B.(,2) C.(3﹣,2) D.(﹣2,2)
【考点】作图—基本作图;坐标与图形性质;平行四边形的性质.
【专题】尺规作图;几何直观.
【答案】A
【分析】分析题目,首先根据平行四边形的性质可得AC∥OB,接下来根据平行线的性质可得∠AGO=∠GOB;结合给出的作图步骤可知∠AOG=∠GOB,进而得到AG=AO,然后根据勾股定理求出OA的长,进而求出AG的长,问题便可解答.
【解答】解:∵四边形OACB是平行四边形,
∴AC∥OB,
∴∠AGO=∠GOB(两直线平行内错角相等).
由作图步骤可得∠AOG=∠GOB,
∴∠AGO=∠AOG,
∴AG=AO.
∵A(﹣1,2),
∴OA=,
∴AG=,
∴点G的坐标为(﹣1,2).
故选:A.
【点评】本题主要考查基本作图,掌握角平分线的做法是解题的关键.
8.(2024 阳山县模拟)如图,是某位同学用带有刻度的直尺在数轴上作图的方法,若图中的虚线相互平行,则点P表示的数是( )
A.1 B. C. D.5
【考点】作图—复杂作图;实数与数轴.
【专题】作图题;图形的相似;运算能力;推理能力.
【答案】C
【分析】根据平行线分线段成比例即可求解.
【解答】解:如图,OB=1,OA=3,OC=10,
∵PB∥AC,
∴,
∴=
∴OP=.
∴点P表示的数是.
故选:C.
【点评】本题考查平行线分线段成比例定理,熟练掌握平行线分线段成比例定理是解题的关键.
9.(2024 凌河区校级三模)如图,AE∥BF,AC平分∠BAD,交BF于C,以点B为圆心,以任意长为半径作弧,分别交BA,BC于M,N两点,再分别以M,N两点为圆心,都以一个大于的长度为半径作弧,两弧相交于点P,射线BP与AE相交于点D.若AC=6,BD=8,则AB的长为( )
A.3 B.4 C.5 D.6
【考点】作图—基本作图;角平分线的定义;平行线的性质;角平分线的性质;菱形的判定与性质.
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;矩形 菱形 正方形;推理能力.
【答案】C
【分析】根据角平分线的定义和平行线的性质证明四边形ABCD是菱形,由菱形的性质和勾股定理即可求出AB.
【解答】解:由基本作图可知BD是∠ABC的平分线,
∴∠ABD=∠CBD,
∵AE∥BF,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∵AC平分∠BAD,
∴∠BAC=∠DAC,
∵AE∥BF,
∴∠DAC=∠ACB,
∴∠BAC=∠ACB,
∴AB=BC,
∴AB=BC=AD,
∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形.
令AB与CD交于点O,
∴AO=CO=AC=×6=3,BO=DO=BD=×8=4,AC⊥BD,
在Rt△ABO中,
AB===5.
故选:C.
【点评】本题主要考查了角平分线的定义,平行线的性质,菱形的性质和判定,勾股定理,证明四边形ABCD是菱形是解决问题的关键.
10.(2024 长安区一模)对于题目“已知⊙O及圆外一点P,如何过点P作出⊙O的切线?”甲、乙的作法如图.
甲的作法 连接OP,作OP的垂直平分线交OP于点G,以点G为圆心,OG长为半径画弧交⊙O于M,作直线PM.直线PM即为所求. 乙的作法 连接PO并延长,交⊙O于B,C两点,分别以P,O为圆心,PO,BC长为半径作弧,两弧交于点D,连接OD,交⊙O于点M,作直线PM,直线PM即为所求.
下列说法正确的是( )
A.甲和乙的作法都正确
B.甲和乙的作法都错误
C.甲的作法正确,乙的作法错误
D.乙的作法正确,甲的作法错误
【考点】作图—复杂作图;线段垂直平分线的性质;切线的判定与性质.
【专题】作图题;几何直观;推理能力.
【答案】A
【分析】对于甲的作法,利用基本作图得到AB垂直平分OP,则OG=GP,再根据圆周角定理得到∠PMO=90°,然后根据切线的判定方法得到PM为⊙O的切线,于是可判断甲的作法正确;对于乙的作法:利用基本作图得到PD=PO,OD=BC,由于OM=BC,所以OM=DM,则根据等腰三角形的性质得到PM⊥OD,然后根据切线的判定方法得到PM为⊙O的切线,于是可判断乙的作法正确.
【解答】解:对于甲的作法:
由作法得AB垂直平分OP,
∴OG=GP,
∴点M为以OP为直径的圆与⊙O的交点,
∴∠PMO=90°,
∴OM⊥PM,
∴PM为⊙O的切线,所以甲的作法正确;
对于乙的作法:
由作法得PD=PO,OD=BC,
∵OM=BC,
∴OM=DM,
∴PM⊥OD,
∴PM为⊙O的切线,所以乙的作法正确;
故选:A.
【点评】本题考查了作图﹣复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的性质和切线的判定方法.
二.填空题(共5小题)
11.(2025 金山区一模)某校初三数学活动小组在利用尺规把线段AB分割成两条线段.
(1)过点B作BC⊥AB,使.
(2)联结AC,在线段CA上被取CD=CB.
(3)在线段AB上截取AE=AD.那么= .
【考点】作图—基本作图;含30度角的直角三角形.
【专题】作图题;几何直观;推理能力.
【答案】(1)见解析;
(2)见解析;
(3).
【分析】(1)作线段AB的垂直平分线得到线段AB的中点,作直线BC⊥AB于B,然后截取BC=AB即可;
(2)根据题意作出图形即可;
(3)根据勾股定理得到AC==AB,求得AD=AE=AC﹣CD=AB﹣AB,得到BE=AB﹣AE=AB﹣(AB﹣AB)=AB,于是得到结论.
【解答】解:(1)如图所示;点C即为所求;
(2)如图所示,点D即为所求;
(3)如图所示,点E即为所求.
∵BC=CD=,AC==AB,
∴AD=AE=AC﹣CD=AB﹣AB,
∴BE=AB﹣AE=AB﹣(AB﹣AB)=AB,
∴==,
故答案为:.
【点评】本题考查了作图﹣基本作图,熟练掌握基本作图的方法是解题的关键.
12.(2024 坪山区校级一模)如图,在△ABC中,∠B=40°,∠C=50°.通过观察尺规作图的痕迹,可以求得∠DAE= 25 度.
【考点】作图—基本作图;三角形内角和定理.
【专题】作图题;几何直观;推理能力.
【答案】25.
【分析】利用基本作图得到DF垂直平分AB,AE平分∠DAC,则DB=DA,∠DAE=∠DAC,所以∠DAB=∠B=40°,再利用三角形内角和计算出∠BAC=90°,则∠DAC=50°,从而得到∠DAE=25°.
【解答】解:由作图痕迹得DF垂直平分AB,AE平分∠DAC,
∴DB=DA,∠DAE=∠DAC,
∴∠DAB=∠B=40°,
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣40°﹣50°=90°,
∵∠DAC=∠BAC﹣∠DAB=90°﹣40°=50°,
∴∠DAE=×50°=25°.
故答案为:25.
【点评】本题考查了作图﹣基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了角平分线的性质和线段垂直平分线的性质.
13.(2024 天津一模)如图,在每个小正方形的边长为1的网格中,点C为以AB为直径的半圆弧的中点.
(1)∠CAB的大小等于 45 (度);
(2)请用无刻度的直尺,在如图所示的网格中,画出以AB为直径的半圆的圆心O,简要说明点O的位置是如何找到的(不要求证明) 取圆上两个格点M,N,再作MN的垂直平分线EF与AB的交点即为圆心O .
【考点】作图—复杂作图;垂径定理;圆周角定理.
【专题】作图题;与圆有关的计算;几何直观;推理能力.
【答案】(1)45;
(2)取圆上两个格点M,N,再作MN的垂直平分线EF与AB的交点即为圆心O.
【分析】(1)连接BC,证明△ABC是等腰直角三角形即可得到∠CAB=45°;
(2)取圆上两个格点M,N,再作MN的垂直平分线EF与AB的交点即为圆心O.
【解答】解:(1)连接BC,如图1,
∵点C为以AB为直径的半圆弧的中点,
∴CA=CB,∠ACB=90°
∴∠CAB=45°,
故答案为:45;
(2)取圆上两个格点M,N,再作MN的垂直平分线EF与AB的交点即为圆心O,依据垂径定理可知,O即为圆心,
如图2:
理由:∵EM=MF=FN=NE==,
∴四边形EMFN是菱形,
∴EF垂直平分MN,
EF与直径AB的交点O为圆心.
故答案为:取圆上两个格点M,N,再作MN的垂直平分线EF与AB的交点即为圆心O.
【点评】本题考查作图﹣复杂作图,垂径定理,圆周角定理,解题的关键是理解题意,灵活运用所学知识解决问题.
14.(2024 荷塘区校级模拟)如图,在△ABC中,∠BAC=90°,∠B=30°,AC=4.以点A为圆心,以AC长为半径作弧,交BC于点D;再分别以点C和点D为圆心,以大于长为半径作弧,两弧相交于点E,作射线AE交BC于点F,则BF的长为 6 .
【考点】作图—基本作图;含30度角的直角三角形.
【专题】作图题;等腰三角形与直角三角形;推理能力.
【答案】6.
【分析】根据直角三角形的性质和特殊角的三角函数即可得到结论.
【解答】解:由作图知,AF⊥BC,
∵∠BAC=90°,∠B=30°,AC=4.
∴AB=AC=4,
∵AF⊥BC,
∴∠AFB=90°,
∴,
故答案为:6.
【点评】本题考查了作图﹣基本作图,解决本题的关键是理解作图过程.
15.(2025 南山区模拟)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B,C;分别以B,C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A,B为圆心,以大于AB的长为半径作弧,两弧相交于点D,E,作直线DE分别与AB,AP相交于点F,Q.若AB=4,∠PQE=67.5°,则F到AN的距离为 .
【考点】作图—基本作图;角平分线的性质;线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;几何直观;推理能力.
【答案】见试题解答内容
【分析】如图,过F作FH⊥AC于H,证明∠BAP=∠CAP,DE⊥AB,,再证明∠FAH=45°,再结合勾股定理可得答案.
【解答】解:如图,过F作FH⊥AC于H,
由作图可得:∠BAP=∠CAP,DE⊥AB,,
∵∠PQE=67.5°,
∴∠AQF=67.5°,
∴∠BAP=∠CAP=90°﹣67.5°=22.5°,
∴∠FAH=45°,
∴,
∴F到AN的距离为;
故答案为:.
【点评】本题考查了作图﹣复杂作图:基本作图,三角形的内角和定理的应用,勾股定理的应用,等腰三角形的判定,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质,逐步操作.
三.解答题(共5小题)
16.(2025 安阳模拟)已知在一些边长相同的小正方形组成的网格中,正方形ABCD的四个顶点都在小正方形的顶点上.点P为对角线BD上任意一点,连接PA,以PA,PD为邻边作平行四边形PAQD.
(1)当点P(在小正方形的顶点上)的位置如图所示时,请用直尺画出平行四边形PAQD;
(2)当PQ的最小值为时,求正方形ABCD的边长.
【考点】作图—应用与设计作图;相似三角形的判定与性质;垂线段最短;平行四边形的判定与性质.
【专题】平移、旋转与对称;推理能力.
【答案】(1)见解析;
(2).
【分析】(1)根据平行四边形两组对比分别平行的性质画图即可;
(2)设PQ与AD交于点O,根据平行四边形的性质可知,OP=OQ,OA=OD,得出OP最短时,PQ最小,再过O作BD的垂线,垂足为P′,此时OP′最短,再得出△DOP′~△DAB,根据相似比求出正方形边长即可.
【解答】解:(1)如图所示,四边形PAQD即为所求;
(2)设PQ与AD交于点O,
∵PAQD为平行四边形,
∴OP=OQ,OA=OD,
∴OP最短时,PQ最小,
过O作BD的垂线,垂足为P′,此时OP′最短,
∵PQ的最小值为,
∴,
∵∠DP′O=∠DAB=90°,
∠ADB为公共角,
∴△DOP′~△DAB,
∴,
设正方形边长为a,
∴,
∴,
解得,
∴正方形ABCD的边长为.
【点评】本题主要考查平行四边形的性质,利用垂线段求最小值,相似三角形的判定与性质,熟练运用垂线段求最小值是解决本题的关键.
17.(2025 永寿县校级一模)如图,已知E是∠AOB的边AO上一点,EF∥OB.请用尺规作图的方法在EF上求作一点P,连接OP,使得.(保留作图痕迹,不写作法)
【考点】作图—复杂作图;平行线的性质.
【专题】线段、角、相交线与平行线;尺规作图;几何直观.
【答案】见解答.
【分析】结合平行线的性质,作∠AOB的平分线,交EF于点P,则点P即为所求.
【解答】解:如图,作∠AOB的平分线,交EF于点P,
可得.
∵EF∥OB,
∴∠AEF=∠AOB,
∴,
则点P即为所求.
【点评】本题考查作图—复杂作图、平行线的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
18.(2025 雁塔区校级一模)尺规作图(不写作法,保留作图痕迹):如图,AB为⊙O的直径,点C在⊙O上.在⊙O上作点D,使得线段DB=DC,且线段AD与BC相交.
【考点】作图—复杂作图;线段垂直平分线的性质.
【专题】作图题;几何直观.
【答案】见解析.
【分析】作线段BC的垂直平分线交优弧BC于点D,点D即为所求.
【解答】解:如图,点D即为所求.
【点评】本题考查作图﹣复杂作图,解题的关键是理解题意,正确作出图形.
19.(2025 旺苍县一模)如图这是一个残缺的圆形部件,已知A,B,C是该部件圆弧上的三点.
(1)利用尺规作图作出该部件的圆心;(保留作图痕迹)
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求该部件的半径R.
【考点】作图—应用与设计作图;等腰三角形的性质;垂径定理.
【专题】与圆有关的计算;几何直观;运算能力.
【答案】见试题解答内容
【分析】(1)作相等AB,AC的垂直平分线交于点O,以O为圆心,OA为半径作⊙O即可;
(2)利用垂径定理,勾股定理求解.
【解答】解:(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;
(2)连接AO,OB,BC,BC交OA于D.
∵AB=AC,
∴=,
∴OA⊥BC,
∴BD=DC,
∵BC=16cm,
∴BD=8(cm),
∵AB=10cm,
∴AD===6(cm),
设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,
∴R2=82+(R﹣6)2,
解得:,
∴圆片的半径R为.
【点评】本题考查作图﹣应用与设计作图,垂径定理,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
20.(2025 佛山一模)如图所示是广东醒狮,它是国家级非物质文化遗产之一,其中高桩醒狮更是由现代艺术演出转变而来的体育竞技.如图2,三根梅花桩AM,BP,CN垂直于地面放置,醒狮少年从点A跳跃到点B,随后纵身跃至点C,已知∠A=59°,∠C=45°,MP=0.25m,NP=1.35m.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
(1)在图2中,∠ABC= 104° ;
(2)醒狮少年在某次演出时需要从点A直接腾跃至点C进行“采青”,请求出“采青”路径AC的长度;
(3)醒狮少年在休息时发现,在太阳光下梅花桩AM的影子顶端恰好落在点B处,梅花桩BP的影子顶端恰好与点N重合,请在图3中画出梅花桩AM,BP的影子并计算出BP的高度;
(4)如图4,保持BP不变,通过调整梅花桩AM的高度,使得AC+AB的值最小,请求出此时AM的高度(结果精确到0.01m).
【考点】作图—应用与设计作图;轴对称﹣最短路线问题;解直角三角形的应用;平行投影.
【专题】解直角三角形及其应用;推理能力.
【答案】(1)104°;
(2)AC的长度约为2m;
(3)见解析,BP的高度约为0.81m;
(4)AM的高度约为0.99m.
【分析】(1)延长PB至H,根据平行线的性质可得∠ABH=∠A=59°,∠CBH=∠C=45°,即可得解;
(2)过点B作直线EF∥MN,分别交AM,CN于点E,F,过点A作直线AD∥MN,交CN于点D,连接AC,则四边形AMND,四边形AEFD,四边形EMPB,四边形BPNF均是矩形,由矩形的性质可得EB=MP=0.25m,BF=NP=1.35m,DF=AE,再解直角三角形结合勾股定理计算即可得解;
(3)线段MP,PB为梅花桩AM的影子,线段PN为梅花桩BP的影子.再利用相似三角形的性质求解即可;
(4)作点B关于AM的对称点B′,连接B′C交AM于A′,连接A′B,A′C,则A′B+A′C=A′B′+A′C=B′C,则B′C就是AC+AB的最小值,由(2)得CH=1.35m,由轴对称得B′G=BG=0.25m,再利用相似三角形的性质计算即可得解.
【解答】解:(1)如图:延长PB至H,
由题意可得:AM∥PH∥CN,
∴∠ABH=∠A=59°,∠CBH=∠C=45°,
∴∠ABC=∠ABH+∠CBH=104°,
故答案为:104°;
(2)如图,过点B作直线EF∥MN,分别交AM,CN于点E,F,过点A作直线AD∥MN,交CN于点D,连接AC.
由题意得∠EMN=∠FNM=∠MAD=∠ADN=∠MEF=∠NFE=∠BPM=∠BPN=90°,
∴四边形AMND,四边形AEFD,四边形EMPB,四边形BPNF均是矩形,
∴EB=MP=0.25m,BF=NP=1.35m,DF=AE,
∴AD=EF=1.6m.
∵∠EAB=59°,∠BCF=45°,
∴∠EBA=90°﹣59°=31°,∠CBF=90°﹣45°=45°=∠BCF,
∴AE=EB tan31°≈0.15m,CF=BF=1.35m,
∴CD=CF﹣DF=CF﹣AE=1.2m,
∵在Rt△ACD中,AD=1.6m,CD=1.2m,
AC2=AD2+CD2,
∴.
即“采青”路径AC的长度约为2m.
(3)如图,线段MP,PB为梅花桩AM的影子,线段PN为梅花桩BP的影子.
∵∠BPN=∠AMN=90°,∠BNP=∠ANM,
∴△BNP∽△ANM,
∴.
由(1)得AM≈0.15+BP,
∴,
∴1.6BP=0.2025+1.35BP,
∴0.25BP=0.2025,
∴BP=0.81m.
经检验BP=0.81且符合题意,所以BP的高度约为0.81米.
(4)如图,作点B关于AM的对称点B′,连接B′C交AM于A′,连接B′B并延长交CN于H,连接A′B,A′C,
∴A′B+A′C=A′B′+A′C=B′C,则B′C就是AC+AB的最小值,
由对称性质可知:B′B⊥AM,
同理(2)得CH=1.35m,
由轴对称得B′G=BG=0.25m,
∴B′H=1.85m.
∵A′G∥CH
∴△A′B′G′∽△CB′H,
∴.
即,
∴A'G=m,
∴A′M=0.18+GM=0.18+BP=0.99m,
∴此时AM的高度约为0.99m.
【点评】本题考查了平行线的性质、解直角三角形、相似三角形的判定与性质、勾股定理等知识点,熟练掌握以上知识点并灵活运用,添加适当的辅助线是解此题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
