【中考押题卷】2025年中考数学二轮复习考前预测:二次函数(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学二轮复习考前预测:二次函数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 11:15:52 | ||
图片预览




文档简介
2025年中考数学二轮复习考前预测:二次函数
一.选择题(共10小题)
1.(2025 雁塔区校级模拟)已知二次函数y=ax2﹣2ax+2(a>0且﹣1≤x≤t﹣1),当x=﹣1时,函数取得最大值;当x=1时,函数取得最小值,则t的取值范围是( )
A.0<t≤2 B.0<t≤4 C.2≤t≤4 D.t≥2
2.(2024 历城区一模)阅读材料:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式计算.例如:求点P(﹣2,1)到直线y=x+1的距离.其中k=1,b=1.所以点P(﹣2,1)到直线y=x+1的距离为.
根据以上材料,有下列结论:
①点(2,0)到直线y=﹣2x的距离是;
②直线y=﹣2x和直线y=﹣2x+6的距离是;
③抛物线y=x2﹣4x+3上存在两个点到直线y=﹣2x的距离是;
④若点P是抛物线y=x2﹣4x+3上的点,则点P到直线y=﹣2x距离的最小值是.
其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
3.(2025 徐汇区一模)“数形结合”是研究函数的重要思想方法,如果抛物线y=x2+2x+m+5只经过两个象限,那么m的取值范围是( )
A.m≥﹣4 B.m<﹣4 C.m<﹣5 D.m≥﹣5
4.(2025 汕头校级模拟)已知二次函数y=ax2+bx+c,其中a<0,b<0,c>0,则该二次函数图象大致是( )
A. B.
C. D.
5.(2025 安阳模拟)如图,将抛物线y=x2先向左平移1个单位长度,再把所得新图象位于直线y=4上方的部分,以直线y=4为对称轴作对称,得到如图所示的图象G.当直线y=x+m与图象G只有四个交点时,m的取值范围是( )
A. B. C. D.
6.(2025 济南模拟)定义平面内任意两点P(x1,y1),Q(x2,y2)之间的距离dPQ=|x2﹣x1|+|y2﹣y1|,称为这两点间的曼哈顿距离(简称为曼距).例如,在平面直角坐标系中,点P(﹣3,﹣2)与点Q(2,2)之间的曼距dPQ=|﹣3﹣2|+|﹣2﹣2|=5+4=9,若点A在直线上,点B为抛物线y=x2+2x上一点,则曼距dAB的最小值( )
A. B. C. D.
7.(2025 雁塔区校级一模)若二次函数y=ax2+2ax+3a的图象过不同的三个点A(t,y1),B(1﹣t,y2),C(﹣1,y3),且y1>y2>y3,则t的取值范围是( )
A. B. C.t>且t≠2 D.
8.(2025 江北区模拟)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
A. B.4ac﹣b2>0 C.9a+3b+c<0 D.2a﹣b=0
9.(2025 永寿县校级一模)已知二次函数y=﹣x2+4ax+5(a>0),则下列说法正确的是( )
A.该函数的最大值为5
B.该函数的图象开口向上
C.该函数的图象一定经过点(2a,5)
D.该函数的图象对称轴在y轴右侧
10.(2025 佛山一模)在平面直角坐标系xOy中,点A的坐标为(3,4),点M是抛物线y=ax2+bx+2(a≠0)对称轴上的一个动点.小明经过探究发现:当的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定.若抛物线y=ax2+bx+2(a≠0)的对称轴上存在3个不同的点M,使△AOM为直角三角形,则的值是( )
A.﹣8 B.或﹣8 C.2 D.2或﹣8
二.填空题(共5小题)
11.(2025 福建模拟)把抛物线y=x2+1向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 .
12.(2025 旺苍县一模)已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=﹣(x﹣2)2+k的图象上,则y1,y2,y3的大小关系是 .
13.(2025 晋安区校级模拟)二次函数y=2x2﹣4x+1的顶点坐标为 .
14.(2025 登封市一模)在平面直角坐标系中,若将二次函数y=(x+1)(x﹣2023)﹣4的图象向上平移4个单位长度,则所得新函数的图象与x轴两交点之间的距离是 .
15.(2025 潍坊模拟)一种玻璃水杯的截面如图1所示,其左右轮廓线AC,BD为某一抛物线的一部分,杯口AB=8cm,杯底CD=4cm,且AB∥CD,杯深12cm,如图2若盛有部分水的水杯倾斜45°(即∠ABP=45°),水面正好经过点B,则此时点P到杯口AB的距离为 .
三.解答题(共5小题)
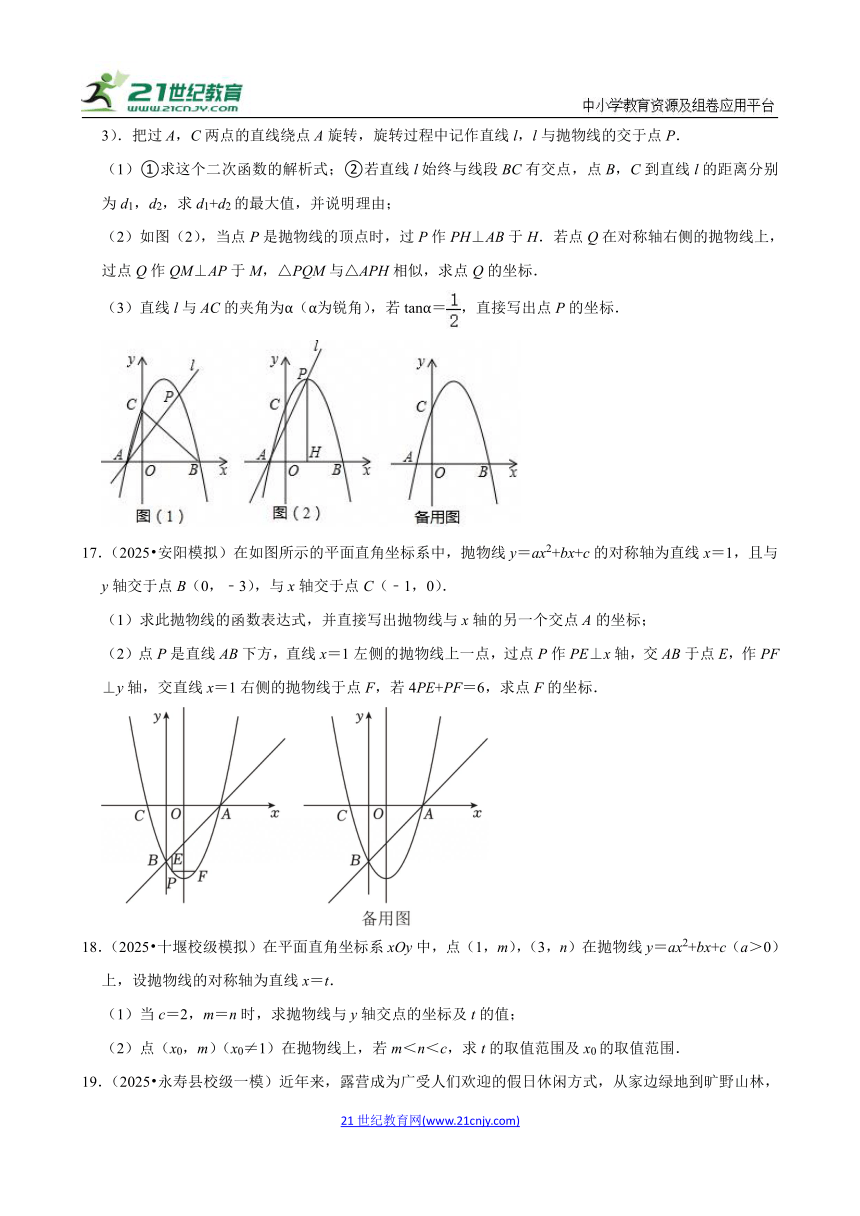
16.(2024 五莲县二模)如图(1),二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(3,0),C(0,3).把过A,C两点的直线绕点A旋转,旋转过程中记作直线l,l与抛物线的交于点P.
(1)①求这个二次函数的解析式;②若直线l始终与线段BC有交点,点B,C到直线l的距离分别为d1,d2,求d1+d2的最大值,并说明理由;
(2)如图(2),当点P是抛物线的顶点时,过P作PH⊥AB于H.若点Q在对称轴右侧的抛物线上,过点Q作QM⊥AP于M,△PQM与△APH相似,求点Q的坐标.
(3)直线l与AC的夹角为α(α为锐角),若tanα=,直接写出点P的坐标.
17.(2025 安阳模拟)在如图所示的平面直角坐标系中,抛物线y=ax2+bx+c的对称轴为直线x=1,且与y轴交于点B(0,﹣3),与x轴交于点C(﹣1,0).
(1)求此抛物线的函数表达式,并直接写出抛物线与x轴的另一个交点A的坐标;
(2)点P是直线AB下方,直线x=1左侧的抛物线上一点,过点P作PE⊥x轴,交AB于点E,作PF⊥y轴,交直线x=1右侧的抛物线于点F,若4PE+PF=6,求点F的坐标.
18.(2025 十堰校级模拟)在平面直角坐标系xOy中,点(1,m),(3,n)在抛物线y=ax2+bx+c(a>0)上,设抛物线的对称轴为直线x=t.
(1)当c=2,m=n时,求抛物线与y轴交点的坐标及t的值;
(2)点(x0,m)(x0≠1)在抛物线上,若m<n<c,求t的取值范围及x0的取值范围.
19.(2025 永寿县校级一模)近年来,露营成为广受人们欢迎的假日休闲方式,从家边绿地到旷野山林,各具特色的露营地吸引着大家前去体验,各式帐篷已成为户外活动的必要装备,其中抛物线型帐篷支架简单,携带方便,适合休闲旅行使用.如图1,这款帐篷搭建时张开的宽度AB=4m,顶部高度h=2m,在图1中以AB所在直线为x轴,AB的中点为原点,建立平面直角坐标系.
(1)求帐篷支架对应的抛物线的函数表达式;
(2)每款帐篷张开时的宽度和顶部高度都会影响其容纳椅子的数量,图2为一张椅子摆入这款帐篷后的简易视图,椅子高度CE=0.72m,宽度CD=0.5m,若在帐篷内沿AB所在的水平方向摆放一排这种椅子(椅子间的间隔忽略不计),求最多可摆放的椅子数量.
20.(2025 旺苍县一模)文旅发展促进经济增长的同时,也带动了电器销售.一电器商城销售某品牌空调,该空调每台进货价为2500元,已知该商店6月份售出75台空调,8月份售出108台空调.求该商城7、8两个月售出空调数的月平均增长率;调查发现,当该空调售价为3000元时,平均每天能售出8台;售价每降低50元,平均每天能多售出4台,该商城如何定价能使每天的利润最大?最大利润是多少?
2025年中考数学二轮复习考前预测:二次函数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 雁塔区校级模拟)已知二次函数y=ax2﹣2ax+2(a>0且﹣1≤x≤t﹣1),当x=﹣1时,函数取得最大值;当x=1时,函数取得最小值,则t的取值范围是( )
A.0<t≤2 B.0<t≤4 C.2≤t≤4 D.t≥2
【考点】二次函数的最值.
【专题】二次函数图象及其性质.
【答案】C
【分析】根据题意,结合二次函数的对称性和增减性建立关于t的不等式组即可解决问题.
【解答】解:因为y=ax2﹣2ax+2=a(x﹣1)2+2﹣a(a>0),
所以抛物线的对称轴为直线x=1,且顶点坐标为(1,2﹣a).
因为1﹣(﹣1)=3﹣1,
所以x=﹣1和x=3时的函数值相等,
因为﹣1≤x≤t﹣1,当x=﹣1时,函数取得最大值,
所以t﹣1≤3,
又因为当x=1时,函数取得最小值,
所以t﹣1≥1,
所以1≤t﹣1≤3,
解得2≤t≤4.
故选:C.
【点评】本题主要考查了二次函数的性质和二次函数的最值,熟知二次函数的图象和性质是解题的关键.
2.(2024 历城区一模)阅读材料:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式计算.例如:求点P(﹣2,1)到直线y=x+1的距离.其中k=1,b=1.所以点P(﹣2,1)到直线y=x+1的距离为.
根据以上材料,有下列结论:
①点(2,0)到直线y=﹣2x的距离是;
②直线y=﹣2x和直线y=﹣2x+6的距离是;
③抛物线y=x2﹣4x+3上存在两个点到直线y=﹣2x的距离是;
④若点P是抛物线y=x2﹣4x+3上的点,则点P到直线y=﹣2x距离的最小值是.
其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
【考点】二次函数图象上点的坐标特征;垂线段最短;一次函数的性质;一次函数图象上点的坐标特征.
【专题】一次函数及其应用;二次函数图象及其性质;运算能力.
【答案】D
【分析】①利用点到直线的距离公式求出即可;
②从直线y=﹣2x上找一个点(0,0),求出该点到y=﹣2x+6的距离,即为两条平行线的距离.
③利用点到直线的距离公式求出点的坐标,即可作出判断;
④求得直线y=﹣2x+m与抛物线有一个交点时的m的值,即可求得直线y=﹣2x+m的解析式,从直线y=﹣2x上找一个点(﹣,0),求出该点到y=﹣2x+m的距离,即为点P到直线y=﹣2x距离的最小值.
【解答】解:①直线y=﹣2x,
∴点(2,0)到直线y=﹣2x的距离是d==;故①正确;
②找出直线y=﹣2x上一点(0,0),
∴点(0,0)到直线y=﹣2x+6的距离d==,故②正确;
③设点P(x0,y0)是抛物线y=x2﹣4x+3的点,到直线y=﹣2x的距离是,
则,
∴|﹣2x0﹣y0|=5,
∴|﹣2x0﹣+4x0﹣3|=5,即|﹣+2x0﹣3|=5,
当﹣+2x0﹣3=5时,无解,
当﹣+2x0﹣3=﹣5时,解得x0=1+或x0=1﹣,
∴抛物线y=x2﹣4x+3上存在两个点到直线y=﹣2x的距离是;故③正确;
④设直线y=﹣2x向上平移m个单位与抛物线y=x2﹣4x+3有一个交点,则平移后的直线为y=﹣2x+m,
令﹣2x+m=x2﹣4x+3,则x2﹣2x+3﹣m=0,
∴Δ=0,即(﹣2)2﹣4(3﹣m)=0,
解得m=2,
∴平移后的直线为y=﹣2x+2,
找出直线y=﹣2x上一点(0,0),
∴点(0,0)到直线y=﹣2x+2的距离d==,
∴若点P是抛物线y=x2﹣4x+3上的点,则点P到直线y=﹣2x距离的最小值是,故④正确;
故选:D.
【点评】本题考查了一次函数的点与直线之间的距离公式的运用,由函数的解析式求点的坐标的运用,平行线的性质的运用,解答时掌握点到直线的距离公式是关键.
3.(2025 徐汇区一模)“数形结合”是研究函数的重要思想方法,如果抛物线y=x2+2x+m+5只经过两个象限,那么m的取值范围是( )
A.m≥﹣4 B.m<﹣4 C.m<﹣5 D.m≥﹣5
【考点】二次函数图象与系数的关系.
【专题】二次函数图象及其性质;应用意识.
【答案】A
【分析】根据抛物线抛物线y=x2+2x+m+5只经过两个象限,且抛物线开口向上,得出最小值大于等于0,得出结论.
【解答】解:∵y=x2+2x+m+5=(x+1)2+m+4,
∴抛物线开口向上,对称轴为直线x=﹣1,顶点坐标为(﹣1,m+4),
∵抛物线y=x2+2x+m+5只经过两个象限,
∴m+4≥0,
∴m≥﹣4,
故选:A.
【点评】本题考查二次函数图象与系数的关系,关键是利用数形结合的思想解答.
4.(2025 汕头校级模拟)已知二次函数y=ax2+bx+c,其中a<0,b<0,c>0,则该二次函数图象大致是( )
A. B.
C. D.
【考点】二次函数的图象.
【专题】二次函数图象及其性质;应用意识.
【答案】B
【分析】根据a<0,可知该函数图象开口向下,再根据左同右异,可知对称轴在y轴右侧,根据c<0,可知图象与y轴交于负半轴,然后即可判断哪个选项符合题意.
【解答】解:∵二次函数y=ax2+bx+c,a<0,b<0,c>0,
∴该函数图象开口向下,对称轴在y轴的左侧,与y轴交于正半轴,
故选:B.
【点评】本题考查二次函数的图象,解答本题的关键是明确题意,利用二次函数的性质解答.
5.(2025 安阳模拟)如图,将抛物线y=x2先向左平移1个单位长度,再把所得新图象位于直线y=4上方的部分,以直线y=4为对称轴作对称,得到如图所示的图象G.当直线y=x+m与图象G只有四个交点时,m的取值范围是( )
A. B. C. D.
【考点】二次函数图象与几何变换;一次函数图象与系数的关系;一次函数图象上点的坐标特征;二次函数的性质.
【专题】二次函数图象及其性质;运算能力.
【答案】C
【分析】首先求出抛物线y=x2先向左平移1个单位长度,得到抛物线为y=(x+1)2,然后求出当直线位于l1时m的值,当直线位于l2时,此时l2与函数y=(x+1)2 的图象有一个公共点,然后与抛物线联立,得到Δ=1﹣4(1﹣m)=0,求出,进而结合图象即可求出当直线y=x+m与图象G只有四个交点时,m的取值范围.
【解答】解:如图所示,
将抛物线y=x2先向左平移1个单位长度,得到抛物线为y=(x+1)2
令y=4,则4=(x+1)2,
解得x=﹣3或1,
∴A(1,4),
直线位于l1和l2时,它与新图象有三个不同的公共点.
①当直线位于l1时,此时l1过点A(1,4),
∴4=1+m,即m=3;
②当直线位于l2时,此时l2与抛物线的图象有一个公共点,
∴方程x+m=x2+2x+1,
即x2+x+1﹣m=0有两个相等实根,
∴Δ=1﹣4(1﹣m)=0,
即;
由以上分析可知若直线y=x+m与新图象只有四个交点,m的取值范围为.
故选:C.
【点评】本题主要考查了二次函数图象与几何变换、一次函数的性质、函数图象交点,解题的关键是正确分析图象.
6.(2025 济南模拟)定义平面内任意两点P(x1,y1),Q(x2,y2)之间的距离dPQ=|x2﹣x1|+|y2﹣y1|,称为这两点间的曼哈顿距离(简称为曼距).例如,在平面直角坐标系中,点P(﹣3,﹣2)与点Q(2,2)之间的曼距dPQ=|﹣3﹣2|+|﹣2﹣2|=5+4=9,若点A在直线上,点B为抛物线y=x2+2x上一点,则曼距dAB的最小值( )
A. B. C. D.
【考点】二次函数的最值;一次函数的性质;一次函数图象上点的坐标特征;二次函数图象上点的坐标特征.
【专题】新定义;二次函数图象及其性质;推理能力.
【答案】C
【分析】根据定义表示出曼距dAB,当A、B两点横坐标相等时,dAB取得最小值,求解即可.
【解答】解:由题意得:设,B(b,b2+2b),
∴,
当A、B两点横坐标相等时,dAB取得最小值,
∴,
∴曼距dAB的最小值为;
故选:C.
【点评】本题考查了二次函数与一次函数的综合应用,二次函数的最值,弄清题中的新定义是解本题的关键.
7.(2025 雁塔区校级一模)若二次函数y=ax2+2ax+3a的图象过不同的三个点A(t,y1),B(1﹣t,y2),C(﹣1,y3),且y1>y2>y3,则t的取值范围是( )
A. B. C.t>且t≠2 D.
【考点】二次函数图象上点的坐标特征.
【专题】二次函数图象及其性质;推理能力.
【答案】C
【分析】根据二次函数的解析式可得出二次函数的对称轴为直线x=﹣1,由题意推出二次项系数大于0,可找出函数的单调区间,再结合A、B点坐标的特点即可得出关于t的一元一次不等式,解不等式即可得出结论.
【解答】解:二次函数y=ax2+2ax+3a的对称轴为直线x=﹣=﹣1,
∵点A(t,y1),B(1﹣t,y2),C(﹣1,y3)在二次函数y=ax2+2ax+3a的图象上,且y1>y2>y3,
∴a>0,1﹣t≠﹣1,
∴二次函数图象在x<﹣1上单调递减,在x≥﹣1上单调递增.
∵点A(t,y1),B(1﹣t,y2)都在二次函数y=ax2+2ax+3a(a>0)的图象上,且y1>y2,
∴|﹣1﹣t|>|﹣1﹣1+t|,
解得:t且t≠2.
故选:C.
【点评】本题考查了二次函数图象上点的坐标特征,二次函数的性质.本题属于基础题,难度不大,解决该题型题目时,根据二次函数的性质结合二次函数的对称轴找出关于点的横坐标的不等式是关键.
8.(2025 江北区模拟)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
A. B.4ac﹣b2>0 C.9a+3b+c<0 D.2a﹣b=0
【考点】二次函数图象与系数的关系.
【专题】二次函数图象及其性质;推理能力.
【答案】C
【分析】根据所给二次函数图象,可得出a,b,c的正负,再结合抛物线的对称性及抛物线上点的坐标特征,依次对所给选项进行判断即可.
【解答】解:由函数图象可知,
a>0,b<0,c<0,
所以.
故A选项不符合题意.
因为抛物线与x轴有两个不同的交点,
所以方程ax2+bx+c=0有两个不相等的实数根,
则b2﹣4ac>0,
所以4ac﹣b2<0.
故B选项不符合题意.
因为抛物线的对称轴为直线x=1,
所以x=3时的函数值与x=﹣1时的函数值相等.
由函数图象可知,x=﹣1时函数值小于零,
所以x=3时函数值也小于零,
即9a+3b+c<0.
故C选项符合题意.
因为抛物线的对称轴为直线x=1,
所以,
即2a+b=0.
故D选项不符合题意.
故选:C.
【点评】本题主要考查了二次函数图象与系数的关系,熟知二次函数的图象与性质是解题的关键.
9.(2025 永寿县校级一模)已知二次函数y=﹣x2+4ax+5(a>0),则下列说法正确的是( )
A.该函数的最大值为5
B.该函数的图象开口向上
C.该函数的图象一定经过点(2a,5)
D.该函数的图象对称轴在y轴右侧
【考点】二次函数图象与系数的关系;二次函数图象上点的坐标特征;二次函数的最值.
【专题】二次函数图象及其性质;运算能力.
【答案】D
【分析】先把二次函数解析式化为顶点式,得到二次函数开口向下,顶点坐标为(2a,4a2+5),对称轴为直线x=2a,可判断B错误;结合a>0可判断A错误;把x=2a代入解析式可判断C错误;根据对称轴为直线x=2a,a>0可判断D正确.
【解答】解:将二次函数解析式配方得为y=﹣x2+4ax+5=﹣(x﹣2a)2+4a2+5,
∴二次函数开口向下,顶点坐标为(2a,4a2+5),对称轴为直线x=2a,故B错误,
∵a>0,
∴4a2+5>5,
∴该函数的最大值大于5,故A错误;
∵当x=2a时,y=4a2+5≠5,
∴该函数的图象不经过点(2a,5),故C错误;
∵a>0,
∴2a>0,
∴该函数的图象对称轴在y轴右侧,故D正确.
故选:D.
【点评】本题考查了二次函数图象的性质,熟练掌握该知识点是关键.
10.(2025 佛山一模)在平面直角坐标系xOy中,点A的坐标为(3,4),点M是抛物线y=ax2+bx+2(a≠0)对称轴上的一个动点.小明经过探究发现:当的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定.若抛物线y=ax2+bx+2(a≠0)的对称轴上存在3个不同的点M,使△AOM为直角三角形,则的值是( )
A.﹣8 B.或﹣8 C.2 D.2或﹣8
【考点】二次函数的应用;切线的判定与性质.
【专题】二次函数的应用;运算能力.
【答案】D
【分析】如图(见解析),分三种情况:①当∠AOM=90°时,则点M在与OA垂直的直线l1上运动(不含点O),②当∠OAM=90°时,则点M在与OA垂直的直线l2上运动(不含点A),③当∠OMA=90°时,则点M在以OA为直径的圆上运动,圆心为OA的中点P,判断出这个抛物线的对称轴(图中的l3和l4)与⊙P相切,由此计算即可得.
【解答】解:由题意可知,有以下三种情况:
①如图,当∠AOM=90°时,OA⊥OM,△AOM为直角三角形,
则点M在与OA垂直的直线l1上运动(不含点O),且M点是l1与抛物线对称轴的交点;
②当∠OAM=90°时,OA⊥AM,△AOM为直角三角形,
则点M在与OA垂直的直线l2上运动(不含点A),且M点是l2与抛物线对称轴的交点;
③当∠OMA=90°时,OM⊥AM,△AOM为直角三角形,
则点M在以OA为直径的圆上运动,圆心为OA的中点P;
∵O(0,0),A(3,4),
∴,⊙P的半径为,
抛物线的对称轴为直线,
∵抛物线的对称轴上存在3个不同的点M,使△AOM为直角三角形,
∴这个抛物线的对称轴(图中的l3和l4)与⊙P相切时,只有一个点M,使△AOM为直角三角形;
∴,
解得或,
∴或,
故选:D.
【点评】本题考查了二次函数的应用、圆的切线的性质等知识,综合性较强,有一定难度.正确分情况讨论,找出抛物线的对称轴的位置是解题关键.
二.填空题(共5小题)
11.(2025 福建模拟)把抛物线y=x2+1向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 y=(x+1)2+4 .
【考点】二次函数图象与几何变换.
【专题】二次函数图象及其性质;运算能力.
【答案】y=(x+1)2+4.
【分析】依据题意,根据抛物线平移的规律:左加右减,上加下减,即可判断得解.
【解答】解:由题意,抛物线y=x2+1向左平移1个单位,然后向上平移3个单位,
∴平移后抛物线的解析式为y=(x+1)2+1+3=(x+1)2+4.
故答案为:y=(x+1)2+4.
【点评】本题主要考查了二次函数图象与几何变换,解题时要熟练掌握并能灵活运用是关键.
12.(2025 旺苍县一模)已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=﹣(x﹣2)2+k的图象上,则y1,y2,y3的大小关系是 y3<y1<y2 .
【考点】二次函数图象上点的坐标特征.
【专题】计算题.
【答案】见试题解答内容
【分析】先利用顶点式得到抛物线对称轴为直线x=2,再比较点A、B、C到直线x=2的距离,然后根据二次函数的性质判断函数值的大小.
【解答】解:二次函数y=﹣(x﹣2)2+k的图象的对称轴为直线x=2,
因为点B(,y2)到直线x=2的距离最小,点C(﹣2,y3)到直线x=2的距离最大,
而抛物线的开口向下,
所以y3<y1<y2.
故答案为y3<y1<y2.
【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.熟练掌握二次函数的性质是解决本题的关键.
13.(2025 晋安区校级模拟)二次函数y=2x2﹣4x+1的顶点坐标为 (1,﹣1) .
【考点】二次函数的性质.
【专题】二次函数图象及其性质;运算能力.
【答案】(1,﹣1).
【分析】先,然后利用二次函数的性质解决问题.
【解答】解:把一般式配成顶点式得y=2(x﹣1)2﹣1,
∴抛物线的顶点坐标为(1,﹣1).
故答案为:(1,﹣1).
【点评】本题考查了二次函数的性质.熟练掌握该知识点是关键.
14.(2025 登封市一模)在平面直角坐标系中,若将二次函数y=(x+1)(x﹣2023)﹣4的图象向上平移4个单位长度,则所得新函数的图象与x轴两交点之间的距离是 2024 .
【考点】抛物线与x轴的交点;二次函数图象与几何变换.
【专题】二次函数图象及其性质;应用意识.
【答案】2024.
【分析】由题意得,所得新函数的解析式为y=(x+1)(x﹣2023),令(x+1)(x﹣2023)=0,解得x1=﹣1,x2=2023,则可得新函数的图象与x轴两交点之间的距离是2023﹣(﹣1)=2024.
【解答】解:将二次函数y=(x+1)(x﹣2023)﹣4的图象向上平移4个单位长度,所得新函数的解析式为y=(x+1)(x﹣2023),
令(x+1)(x﹣2023)=0,
解得x1=﹣1,x2=2023,
∴所得新函数的图象与x轴两交点之间的距离是2023﹣(﹣1)=2024.
故答案为:2024.
【点评】本题考查抛物线与x轴的交点、二次函数图象与几何变换,解题的关键是理解题意,灵活运用所学知识解决问题.
15.(2025 潍坊模拟)一种玻璃水杯的截面如图1所示,其左右轮廓线AC,BD为某一抛物线的一部分,杯口AB=8cm,杯底CD=4cm,且AB∥CD,杯深12cm,如图2若盛有部分水的水杯倾斜45°(即∠ABP=45°),水面正好经过点B,则此时点P到杯口AB的距离为 7 .
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】7.
【分析】建立合适的坐标系,求出抛物线的解析式,求P点坐标,就可求出点P到杯口AB的距离.
【解答】解:建立如图所示坐标系,作PE⊥x轴于点E,
各点坐标为:A(﹣4,0),B(4,0),C(﹣2,﹣12),D(2,﹣12).
设y=a(x+4)(x﹣4),
把点C坐标代入解析式得:﹣12=a(﹣2+4)(﹣2﹣4),
解得a=1,
∴y=(x+4)(x﹣4)=x2﹣16,
∵∠ABP=45°,∠PEB=90°,
∴∠BPE=45°,
∴∠EPB=∠EBP,
∴EP=EB,
设P(x,y),
∴BE=4﹣x,EP=﹣y,
∴﹣y=4﹣x,
即﹣(x2﹣16)=4﹣x,
解得x1=4(舍去),x2=﹣3,
∴y=9﹣16=﹣7,
∴PE=﹣y=7.
故答案为:7.
【点评】本题考查了二次函数的应用,关键是建立合适的坐标系,求出抛物线的解析式.
三.解答题(共5小题)
16.(2024 五莲县二模)如图(1),二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(3,0),C(0,3).把过A,C两点的直线绕点A旋转,旋转过程中记作直线l,l与抛物线的交于点P.
(1)①求这个二次函数的解析式;②若直线l始终与线段BC有交点,点B,C到直线l的距离分别为d1,d2,求d1+d2的最大值,并说明理由;
(2)如图(2),当点P是抛物线的顶点时,过P作PH⊥AB于H.若点Q在对称轴右侧的抛物线上,过点Q作QM⊥AP于M,△PQM与△APH相似,求点Q的坐标.
(3)直线l与AC的夹角为α(α为锐角),若tanα=,直接写出点P的坐标.
【考点】二次函数综合题.
【专题】压轴题.
【答案】见试题解答内容
【分析】(1)①利用待定系数法即可解决问题;
②如图1中,作BM⊥直线l于M,CN⊥直线l于N.则d1=BM≤BD,d2=CN≤CD,可得d1+d2≤CD+BD,推出d1+d2≤BC,即可解决问题;
(2)如图2中,延长PQ交x轴于N.首先证明AN=NP,设AN=NP=m,在Rt△PHN中,利用勾股定理求出m的值,再求出直线AN的解析式,构建方程组确定点P坐标即可;
(3)如图3中,设直线PA交y轴与D,作DE⊥AC于E.设DE=k.首先求出直线AP的解析式,利用方程组确定解得P坐标,再根据对称性,求出直线AP关于直线AC 的对称的直线AD′的解析式,利用方程组确定交点坐标即可;
【解答】解:(1)①把点A(﹣1,0),B(3,0),C(0,3)代入二次函数y=ax2+bx+c得到
,
解得,
∴二次函数的解析式为y=﹣x2+2x+3.
②如图1中,作BM⊥直线l于M,CN⊥直线l于N.
则d1=BM≤BD,d2=CN≤CD,
∴d1+d2≤CD+BD,
∴d1+d2≤BC,
∵OC=OB=3,
∴BC=3,
∴d1+d2的最大值为3.
(2)如图2中,延长PQ交x轴于N.由题意P(1,4).
∵△PQM与△APH相似,
观察图象可知,只有∠QPM=∠PAH,
∴NA=PN,设NA=PN=m,
在Rt△PNH中,∵PH2+NH2=PN2,
∴m2=42+(m﹣2)2,
解得m=5,
∴ON=4,
∴N(4,0),
∴直线PN的解析式为y=﹣x+,
由,解得或,
∴Q(,).
(3)如图3中,设直线PA交y轴与D,作DE⊥AC于E.设DE=k.
∵tan∠EAD=,tan∠DCE=,
∴AE=2k,EC=3k,
∴AC=5k,
∵AC==,
∴k=,
∴DE=,EC=,
∴CD==2,
∴D(0,1),
∴直线AP的解析式为y=x+1,
由,解得或,
∴P(2,3).
作点D关于直线AC的对称点D′,
∵E(﹣,),
∴D′(﹣,),
∴直线AD′的解析式为y=﹣7x﹣7,
由解得或,
∴P(10,﹣77),
综上所述,满足条件的点P坐标为(2,3)或(10,﹣77).
【点评】本题考查二次函数综合题、垂线段最短、一次函数的应用等知识,解题的关键是学会添加常用辅助线,学会利用参数构建方程解决问题,学会构建一次函数,利用方程组确定两个函数的交点坐标解决问题,属于中考压轴题.
17.(2025 安阳模拟)在如图所示的平面直角坐标系中,抛物线y=ax2+bx+c的对称轴为直线x=1,且与y轴交于点B(0,﹣3),与x轴交于点C(﹣1,0).
(1)求此抛物线的函数表达式,并直接写出抛物线与x轴的另一个交点A的坐标;
(2)点P是直线AB下方,直线x=1左侧的抛物线上一点,过点P作PE⊥x轴,交AB于点E,作PF⊥y轴,交直线x=1右侧的抛物线于点F,若4PE+PF=6,求点F的坐标.
【考点】二次函数综合题.
【专题】二次函数图象及其性质.
【答案】(1)y=x2﹣2x﹣3;A(3,0);
(2)点F坐标为.
【分析】(1)用待定系数法可得抛物线的函数表达式;令y=0,得x2﹣2x﹣3=0,解方程即可求解;
(2)先用待定系数法求出直线AB的解析式,再设P(m,m2﹣2m﹣3),则E(m,m﹣3),F(2﹣m,m2﹣2m﹣3),求出PE=﹣m2+3m,PF=2(1﹣m),再解方程求出m的值,并得出点F坐标.
【解答】解:(1)∵抛物线y=ax2+bx+c的对称轴为直线x=1,
∴,
把B(0,﹣3),C(﹣1,0)代入y=ax2+bx+c得:
,
解得,
∴抛物线的函数表达式为y=x2﹣2x﹣3;
令y=0,则x2﹣2x﹣3=0,
∴x1=3,x2=﹣1,
∴A(3,0);
(2)设直线AB解析式为y=kx+t,
把A(3,0),B(0,﹣3)代入y=kx+t得:
,
解得,
∴直线AB解析式为y=x﹣3,
设P(m,m2﹣2m﹣3),则E(m,m﹣3),F(2﹣m,m2﹣2m﹣3),
∴PE=﹣m2+3m,PF=2(1﹣m),
∵点P是直线AB下方,直线x=1左侧的抛物线上一点,
∴0<m<1,
∵4PE+PF=6,
∴4(﹣m2+3m)+2(1﹣m)=6,
整理得2m2﹣5m+2=0,
解得(舍),
∴当时,,
此时点F坐标为.
【点评】本题考查待定系数法求二次函数的解析式,抛物线与x轴的交点,二次函数与几何图形的综合等问题,关键是利用二次函数的性质求解.
18.(2025 十堰校级模拟)在平面直角坐标系xOy中,点(1,m),(3,n)在抛物线y=ax2+bx+c(a>0)上,设抛物线的对称轴为直线x=t.
(1)当c=2,m=n时,求抛物线与y轴交点的坐标及t的值;
(2)点(x0,m)(x0≠1)在抛物线上,若m<n<c,求t的取值范围及x0的取值范围.
【考点】二次函数的性质;二次函数图象上点的坐标特征.
【专题】二次函数图象及其性质;推理能力.
【答案】(1)抛物线与y轴交点的坐标为(0,2),t=2;(2)2<x0<3.
【分析】(1)将点(1,m),(3,n)代入抛物线解析式,再根据m=n得出b=﹣4a,再求对称轴即可;
(2)再根据m<n<c,可确定出对称轴的取值范围,进而可确定x0的取值范围.
【解答】解:(1)法一、将点(1,m),(3,n)代入抛物线解析式,
∴,
∵m=n,
∴a+b+c=9a+3b+c,整理得,b=﹣4a,
∴抛物线的对称轴为直线x=﹣=﹣=2;
∴t=2,
∵c=2,
∴抛物线与y轴交点的坐标为(0,2).
法二、当m=n时,点A(1,m),B(3,n)的纵坐标相等,
由抛物线的对称性可得,抛物线的对称轴为直线x=,
∴t=2,
∵c=2,
∴抛物线与y轴交点的坐标为(0,2).
(2)∵m<n<c,
∴a+b+c<9a+3b+c<c,
解得﹣4a<b<﹣3a,
∴3a<﹣b<4a,
∴<﹣<,即<t<2.
由题意可知,点(x0,m)与点(1,m)关于x=t对称;
∴t=;
当t=时,x0=2;
当t=2时,x0=3.
∴x0的取值范围2<x0<3.
综上,t的取值范围为:<t<2;x0的取值范围2<x0<3.
【点评】本题考查二次函数的性质,解题关键是根据数形结合求解.
19.(2025 永寿县校级一模)近年来,露营成为广受人们欢迎的假日休闲方式,从家边绿地到旷野山林,各具特色的露营地吸引着大家前去体验,各式帐篷已成为户外活动的必要装备,其中抛物线型帐篷支架简单,携带方便,适合休闲旅行使用.如图1,这款帐篷搭建时张开的宽度AB=4m,顶部高度h=2m,在图1中以AB所在直线为x轴,AB的中点为原点,建立平面直角坐标系.
(1)求帐篷支架对应的抛物线的函数表达式;
(2)每款帐篷张开时的宽度和顶部高度都会影响其容纳椅子的数量,图2为一张椅子摆入这款帐篷后的简易视图,椅子高度CE=0.72m,宽度CD=0.5m,若在帐篷内沿AB所在的水平方向摆放一排这种椅子(椅子间的间隔忽略不计),求最多可摆放的椅子数量.
【考点】二次函数的应用.
【专题】二次函数的应用;运算能力.
【答案】(1);
(2)6把.
【分析】(1)先求出A(﹣2,0),B(2,0),顶点坐标为(0,2),设抛物线的函数表达式为y=ax2+2,然后用待定系数法求解即可;
(2)将y=0.72代入,解出x1,x2的值,然后用两根之差除以椅子的宽度即可作答.
【解答】解:(1)由题意可得:A(﹣2,0),B(2,0),顶点坐标为(0,2).
设抛物线的函数表达式为y=ax2+2,
将A(﹣2,0)代入,得0=4a+2,
解得,
∴;
(2)∵椅子的高度CE=0.72m,宽度CD=0.5m,
∴将y=0.72代入,
得,
解得x1=1.6,x2=﹣1.6,
1.6﹣(﹣1.6)=3.2(m),
3.2÷0.5=6.4(把),
∴最多可撰放6把椅子.
【点评】本题考查了二次函数的应用,正确进行计算是解题关键.
20.(2025 旺苍县一模)文旅发展促进经济增长的同时,也带动了电器销售.一电器商城销售某品牌空调,该空调每台进货价为2500元,已知该商店6月份售出75台空调,8月份售出108台空调.求该商城7、8两个月售出空调数的月平均增长率;调查发现,当该空调售价为3000元时,平均每天能售出8台;售价每降低50元,平均每天能多售出4台,该商城如何定价能使每天的利润最大?最大利润是多少?
【考点】二次函数的应用;一元二次方程的应用.
【专题】二次函数的应用;运算能力.
【答案】(1)该商城7、8两个月售出空调数的月平均增长率为20%;
(2)该商城将空调定价为2800元时,每天的利润最大,最大利润是7200元.
【分析】(1)设该商城7、8两个月售出空调数的月平均增长率为x,根据题意列方程求解即可;
(2)设该商城每台空调降价m元,则每天可多售台,每天的利润为w元.
根据题意列出,然后根据二次函数的性质即可求解.
【解答】解(1)设月平均增长率为x,根据题意得:75(1+x)2=108,
解得:x1=0.2=20%,x2=﹣2.2(舍去).
答:该商城7、8两个月售出空调数的月平均增长率为20%;
(2)设该商城每台空调降价m元,则每天可多售台,每天的利润为w元,
根据题意得出:
=
=,
当m=200时,w最大=5000,
则3000﹣m=2800,
答:该商城将空调定价为2800元时,每天的利润最大,最大利润是7200元.
【点评】本题考查了一元二次方程的应用,二次函数的应用,解题的关键是理解题意,正确建立方程模型与函数模型解决问题.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2025 雁塔区校级模拟)已知二次函数y=ax2﹣2ax+2(a>0且﹣1≤x≤t﹣1),当x=﹣1时,函数取得最大值;当x=1时,函数取得最小值,则t的取值范围是( )
A.0<t≤2 B.0<t≤4 C.2≤t≤4 D.t≥2
2.(2024 历城区一模)阅读材料:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式计算.例如:求点P(﹣2,1)到直线y=x+1的距离.其中k=1,b=1.所以点P(﹣2,1)到直线y=x+1的距离为.
根据以上材料,有下列结论:
①点(2,0)到直线y=﹣2x的距离是;
②直线y=﹣2x和直线y=﹣2x+6的距离是;
③抛物线y=x2﹣4x+3上存在两个点到直线y=﹣2x的距离是;
④若点P是抛物线y=x2﹣4x+3上的点,则点P到直线y=﹣2x距离的最小值是.
其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
3.(2025 徐汇区一模)“数形结合”是研究函数的重要思想方法,如果抛物线y=x2+2x+m+5只经过两个象限,那么m的取值范围是( )
A.m≥﹣4 B.m<﹣4 C.m<﹣5 D.m≥﹣5
4.(2025 汕头校级模拟)已知二次函数y=ax2+bx+c,其中a<0,b<0,c>0,则该二次函数图象大致是( )
A. B.
C. D.
5.(2025 安阳模拟)如图,将抛物线y=x2先向左平移1个单位长度,再把所得新图象位于直线y=4上方的部分,以直线y=4为对称轴作对称,得到如图所示的图象G.当直线y=x+m与图象G只有四个交点时,m的取值范围是( )
A. B. C. D.
6.(2025 济南模拟)定义平面内任意两点P(x1,y1),Q(x2,y2)之间的距离dPQ=|x2﹣x1|+|y2﹣y1|,称为这两点间的曼哈顿距离(简称为曼距).例如,在平面直角坐标系中,点P(﹣3,﹣2)与点Q(2,2)之间的曼距dPQ=|﹣3﹣2|+|﹣2﹣2|=5+4=9,若点A在直线上,点B为抛物线y=x2+2x上一点,则曼距dAB的最小值( )
A. B. C. D.
7.(2025 雁塔区校级一模)若二次函数y=ax2+2ax+3a的图象过不同的三个点A(t,y1),B(1﹣t,y2),C(﹣1,y3),且y1>y2>y3,则t的取值范围是( )
A. B. C.t>且t≠2 D.
8.(2025 江北区模拟)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
A. B.4ac﹣b2>0 C.9a+3b+c<0 D.2a﹣b=0
9.(2025 永寿县校级一模)已知二次函数y=﹣x2+4ax+5(a>0),则下列说法正确的是( )
A.该函数的最大值为5
B.该函数的图象开口向上
C.该函数的图象一定经过点(2a,5)
D.该函数的图象对称轴在y轴右侧
10.(2025 佛山一模)在平面直角坐标系xOy中,点A的坐标为(3,4),点M是抛物线y=ax2+bx+2(a≠0)对称轴上的一个动点.小明经过探究发现:当的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定.若抛物线y=ax2+bx+2(a≠0)的对称轴上存在3个不同的点M,使△AOM为直角三角形,则的值是( )
A.﹣8 B.或﹣8 C.2 D.2或﹣8
二.填空题(共5小题)
11.(2025 福建模拟)把抛物线y=x2+1向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 .
12.(2025 旺苍县一模)已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=﹣(x﹣2)2+k的图象上,则y1,y2,y3的大小关系是 .
13.(2025 晋安区校级模拟)二次函数y=2x2﹣4x+1的顶点坐标为 .
14.(2025 登封市一模)在平面直角坐标系中,若将二次函数y=(x+1)(x﹣2023)﹣4的图象向上平移4个单位长度,则所得新函数的图象与x轴两交点之间的距离是 .
15.(2025 潍坊模拟)一种玻璃水杯的截面如图1所示,其左右轮廓线AC,BD为某一抛物线的一部分,杯口AB=8cm,杯底CD=4cm,且AB∥CD,杯深12cm,如图2若盛有部分水的水杯倾斜45°(即∠ABP=45°),水面正好经过点B,则此时点P到杯口AB的距离为 .
三.解答题(共5小题)
16.(2024 五莲县二模)如图(1),二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(3,0),C(0,3).把过A,C两点的直线绕点A旋转,旋转过程中记作直线l,l与抛物线的交于点P.
(1)①求这个二次函数的解析式;②若直线l始终与线段BC有交点,点B,C到直线l的距离分别为d1,d2,求d1+d2的最大值,并说明理由;
(2)如图(2),当点P是抛物线的顶点时,过P作PH⊥AB于H.若点Q在对称轴右侧的抛物线上,过点Q作QM⊥AP于M,△PQM与△APH相似,求点Q的坐标.
(3)直线l与AC的夹角为α(α为锐角),若tanα=,直接写出点P的坐标.
17.(2025 安阳模拟)在如图所示的平面直角坐标系中,抛物线y=ax2+bx+c的对称轴为直线x=1,且与y轴交于点B(0,﹣3),与x轴交于点C(﹣1,0).
(1)求此抛物线的函数表达式,并直接写出抛物线与x轴的另一个交点A的坐标;
(2)点P是直线AB下方,直线x=1左侧的抛物线上一点,过点P作PE⊥x轴,交AB于点E,作PF⊥y轴,交直线x=1右侧的抛物线于点F,若4PE+PF=6,求点F的坐标.
18.(2025 十堰校级模拟)在平面直角坐标系xOy中,点(1,m),(3,n)在抛物线y=ax2+bx+c(a>0)上,设抛物线的对称轴为直线x=t.
(1)当c=2,m=n时,求抛物线与y轴交点的坐标及t的值;
(2)点(x0,m)(x0≠1)在抛物线上,若m<n<c,求t的取值范围及x0的取值范围.
19.(2025 永寿县校级一模)近年来,露营成为广受人们欢迎的假日休闲方式,从家边绿地到旷野山林,各具特色的露营地吸引着大家前去体验,各式帐篷已成为户外活动的必要装备,其中抛物线型帐篷支架简单,携带方便,适合休闲旅行使用.如图1,这款帐篷搭建时张开的宽度AB=4m,顶部高度h=2m,在图1中以AB所在直线为x轴,AB的中点为原点,建立平面直角坐标系.
(1)求帐篷支架对应的抛物线的函数表达式;
(2)每款帐篷张开时的宽度和顶部高度都会影响其容纳椅子的数量,图2为一张椅子摆入这款帐篷后的简易视图,椅子高度CE=0.72m,宽度CD=0.5m,若在帐篷内沿AB所在的水平方向摆放一排这种椅子(椅子间的间隔忽略不计),求最多可摆放的椅子数量.
20.(2025 旺苍县一模)文旅发展促进经济增长的同时,也带动了电器销售.一电器商城销售某品牌空调,该空调每台进货价为2500元,已知该商店6月份售出75台空调,8月份售出108台空调.求该商城7、8两个月售出空调数的月平均增长率;调查发现,当该空调售价为3000元时,平均每天能售出8台;售价每降低50元,平均每天能多售出4台,该商城如何定价能使每天的利润最大?最大利润是多少?
2025年中考数学二轮复习考前预测:二次函数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 雁塔区校级模拟)已知二次函数y=ax2﹣2ax+2(a>0且﹣1≤x≤t﹣1),当x=﹣1时,函数取得最大值;当x=1时,函数取得最小值,则t的取值范围是( )
A.0<t≤2 B.0<t≤4 C.2≤t≤4 D.t≥2
【考点】二次函数的最值.
【专题】二次函数图象及其性质.
【答案】C
【分析】根据题意,结合二次函数的对称性和增减性建立关于t的不等式组即可解决问题.
【解答】解:因为y=ax2﹣2ax+2=a(x﹣1)2+2﹣a(a>0),
所以抛物线的对称轴为直线x=1,且顶点坐标为(1,2﹣a).
因为1﹣(﹣1)=3﹣1,
所以x=﹣1和x=3时的函数值相等,
因为﹣1≤x≤t﹣1,当x=﹣1时,函数取得最大值,
所以t﹣1≤3,
又因为当x=1时,函数取得最小值,
所以t﹣1≥1,
所以1≤t﹣1≤3,
解得2≤t≤4.
故选:C.
【点评】本题主要考查了二次函数的性质和二次函数的最值,熟知二次函数的图象和性质是解题的关键.
2.(2024 历城区一模)阅读材料:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式计算.例如:求点P(﹣2,1)到直线y=x+1的距离.其中k=1,b=1.所以点P(﹣2,1)到直线y=x+1的距离为.
根据以上材料,有下列结论:
①点(2,0)到直线y=﹣2x的距离是;
②直线y=﹣2x和直线y=﹣2x+6的距离是;
③抛物线y=x2﹣4x+3上存在两个点到直线y=﹣2x的距离是;
④若点P是抛物线y=x2﹣4x+3上的点,则点P到直线y=﹣2x距离的最小值是.
其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
【考点】二次函数图象上点的坐标特征;垂线段最短;一次函数的性质;一次函数图象上点的坐标特征.
【专题】一次函数及其应用;二次函数图象及其性质;运算能力.
【答案】D
【分析】①利用点到直线的距离公式求出即可;
②从直线y=﹣2x上找一个点(0,0),求出该点到y=﹣2x+6的距离,即为两条平行线的距离.
③利用点到直线的距离公式求出点的坐标,即可作出判断;
④求得直线y=﹣2x+m与抛物线有一个交点时的m的值,即可求得直线y=﹣2x+m的解析式,从直线y=﹣2x上找一个点(﹣,0),求出该点到y=﹣2x+m的距离,即为点P到直线y=﹣2x距离的最小值.
【解答】解:①直线y=﹣2x,
∴点(2,0)到直线y=﹣2x的距离是d==;故①正确;
②找出直线y=﹣2x上一点(0,0),
∴点(0,0)到直线y=﹣2x+6的距离d==,故②正确;
③设点P(x0,y0)是抛物线y=x2﹣4x+3的点,到直线y=﹣2x的距离是,
则,
∴|﹣2x0﹣y0|=5,
∴|﹣2x0﹣+4x0﹣3|=5,即|﹣+2x0﹣3|=5,
当﹣+2x0﹣3=5时,无解,
当﹣+2x0﹣3=﹣5时,解得x0=1+或x0=1﹣,
∴抛物线y=x2﹣4x+3上存在两个点到直线y=﹣2x的距离是;故③正确;
④设直线y=﹣2x向上平移m个单位与抛物线y=x2﹣4x+3有一个交点,则平移后的直线为y=﹣2x+m,
令﹣2x+m=x2﹣4x+3,则x2﹣2x+3﹣m=0,
∴Δ=0,即(﹣2)2﹣4(3﹣m)=0,
解得m=2,
∴平移后的直线为y=﹣2x+2,
找出直线y=﹣2x上一点(0,0),
∴点(0,0)到直线y=﹣2x+2的距离d==,
∴若点P是抛物线y=x2﹣4x+3上的点,则点P到直线y=﹣2x距离的最小值是,故④正确;
故选:D.
【点评】本题考查了一次函数的点与直线之间的距离公式的运用,由函数的解析式求点的坐标的运用,平行线的性质的运用,解答时掌握点到直线的距离公式是关键.
3.(2025 徐汇区一模)“数形结合”是研究函数的重要思想方法,如果抛物线y=x2+2x+m+5只经过两个象限,那么m的取值范围是( )
A.m≥﹣4 B.m<﹣4 C.m<﹣5 D.m≥﹣5
【考点】二次函数图象与系数的关系.
【专题】二次函数图象及其性质;应用意识.
【答案】A
【分析】根据抛物线抛物线y=x2+2x+m+5只经过两个象限,且抛物线开口向上,得出最小值大于等于0,得出结论.
【解答】解:∵y=x2+2x+m+5=(x+1)2+m+4,
∴抛物线开口向上,对称轴为直线x=﹣1,顶点坐标为(﹣1,m+4),
∵抛物线y=x2+2x+m+5只经过两个象限,
∴m+4≥0,
∴m≥﹣4,
故选:A.
【点评】本题考查二次函数图象与系数的关系,关键是利用数形结合的思想解答.
4.(2025 汕头校级模拟)已知二次函数y=ax2+bx+c,其中a<0,b<0,c>0,则该二次函数图象大致是( )
A. B.
C. D.
【考点】二次函数的图象.
【专题】二次函数图象及其性质;应用意识.
【答案】B
【分析】根据a<0,可知该函数图象开口向下,再根据左同右异,可知对称轴在y轴右侧,根据c<0,可知图象与y轴交于负半轴,然后即可判断哪个选项符合题意.
【解答】解:∵二次函数y=ax2+bx+c,a<0,b<0,c>0,
∴该函数图象开口向下,对称轴在y轴的左侧,与y轴交于正半轴,
故选:B.
【点评】本题考查二次函数的图象,解答本题的关键是明确题意,利用二次函数的性质解答.
5.(2025 安阳模拟)如图,将抛物线y=x2先向左平移1个单位长度,再把所得新图象位于直线y=4上方的部分,以直线y=4为对称轴作对称,得到如图所示的图象G.当直线y=x+m与图象G只有四个交点时,m的取值范围是( )
A. B. C. D.
【考点】二次函数图象与几何变换;一次函数图象与系数的关系;一次函数图象上点的坐标特征;二次函数的性质.
【专题】二次函数图象及其性质;运算能力.
【答案】C
【分析】首先求出抛物线y=x2先向左平移1个单位长度,得到抛物线为y=(x+1)2,然后求出当直线位于l1时m的值,当直线位于l2时,此时l2与函数y=(x+1)2 的图象有一个公共点,然后与抛物线联立,得到Δ=1﹣4(1﹣m)=0,求出,进而结合图象即可求出当直线y=x+m与图象G只有四个交点时,m的取值范围.
【解答】解:如图所示,
将抛物线y=x2先向左平移1个单位长度,得到抛物线为y=(x+1)2
令y=4,则4=(x+1)2,
解得x=﹣3或1,
∴A(1,4),
直线位于l1和l2时,它与新图象有三个不同的公共点.
①当直线位于l1时,此时l1过点A(1,4),
∴4=1+m,即m=3;
②当直线位于l2时,此时l2与抛物线的图象有一个公共点,
∴方程x+m=x2+2x+1,
即x2+x+1﹣m=0有两个相等实根,
∴Δ=1﹣4(1﹣m)=0,
即;
由以上分析可知若直线y=x+m与新图象只有四个交点,m的取值范围为.
故选:C.
【点评】本题主要考查了二次函数图象与几何变换、一次函数的性质、函数图象交点,解题的关键是正确分析图象.
6.(2025 济南模拟)定义平面内任意两点P(x1,y1),Q(x2,y2)之间的距离dPQ=|x2﹣x1|+|y2﹣y1|,称为这两点间的曼哈顿距离(简称为曼距).例如,在平面直角坐标系中,点P(﹣3,﹣2)与点Q(2,2)之间的曼距dPQ=|﹣3﹣2|+|﹣2﹣2|=5+4=9,若点A在直线上,点B为抛物线y=x2+2x上一点,则曼距dAB的最小值( )
A. B. C. D.
【考点】二次函数的最值;一次函数的性质;一次函数图象上点的坐标特征;二次函数图象上点的坐标特征.
【专题】新定义;二次函数图象及其性质;推理能力.
【答案】C
【分析】根据定义表示出曼距dAB,当A、B两点横坐标相等时,dAB取得最小值,求解即可.
【解答】解:由题意得:设,B(b,b2+2b),
∴,
当A、B两点横坐标相等时,dAB取得最小值,
∴,
∴曼距dAB的最小值为;
故选:C.
【点评】本题考查了二次函数与一次函数的综合应用,二次函数的最值,弄清题中的新定义是解本题的关键.
7.(2025 雁塔区校级一模)若二次函数y=ax2+2ax+3a的图象过不同的三个点A(t,y1),B(1﹣t,y2),C(﹣1,y3),且y1>y2>y3,则t的取值范围是( )
A. B. C.t>且t≠2 D.
【考点】二次函数图象上点的坐标特征.
【专题】二次函数图象及其性质;推理能力.
【答案】C
【分析】根据二次函数的解析式可得出二次函数的对称轴为直线x=﹣1,由题意推出二次项系数大于0,可找出函数的单调区间,再结合A、B点坐标的特点即可得出关于t的一元一次不等式,解不等式即可得出结论.
【解答】解:二次函数y=ax2+2ax+3a的对称轴为直线x=﹣=﹣1,
∵点A(t,y1),B(1﹣t,y2),C(﹣1,y3)在二次函数y=ax2+2ax+3a的图象上,且y1>y2>y3,
∴a>0,1﹣t≠﹣1,
∴二次函数图象在x<﹣1上单调递减,在x≥﹣1上单调递增.
∵点A(t,y1),B(1﹣t,y2)都在二次函数y=ax2+2ax+3a(a>0)的图象上,且y1>y2,
∴|﹣1﹣t|>|﹣1﹣1+t|,
解得:t且t≠2.
故选:C.
【点评】本题考查了二次函数图象上点的坐标特征,二次函数的性质.本题属于基础题,难度不大,解决该题型题目时,根据二次函数的性质结合二次函数的对称轴找出关于点的横坐标的不等式是关键.
8.(2025 江北区模拟)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
A. B.4ac﹣b2>0 C.9a+3b+c<0 D.2a﹣b=0
【考点】二次函数图象与系数的关系.
【专题】二次函数图象及其性质;推理能力.
【答案】C
【分析】根据所给二次函数图象,可得出a,b,c的正负,再结合抛物线的对称性及抛物线上点的坐标特征,依次对所给选项进行判断即可.
【解答】解:由函数图象可知,
a>0,b<0,c<0,
所以.
故A选项不符合题意.
因为抛物线与x轴有两个不同的交点,
所以方程ax2+bx+c=0有两个不相等的实数根,
则b2﹣4ac>0,
所以4ac﹣b2<0.
故B选项不符合题意.
因为抛物线的对称轴为直线x=1,
所以x=3时的函数值与x=﹣1时的函数值相等.
由函数图象可知,x=﹣1时函数值小于零,
所以x=3时函数值也小于零,
即9a+3b+c<0.
故C选项符合题意.
因为抛物线的对称轴为直线x=1,
所以,
即2a+b=0.
故D选项不符合题意.
故选:C.
【点评】本题主要考查了二次函数图象与系数的关系,熟知二次函数的图象与性质是解题的关键.
9.(2025 永寿县校级一模)已知二次函数y=﹣x2+4ax+5(a>0),则下列说法正确的是( )
A.该函数的最大值为5
B.该函数的图象开口向上
C.该函数的图象一定经过点(2a,5)
D.该函数的图象对称轴在y轴右侧
【考点】二次函数图象与系数的关系;二次函数图象上点的坐标特征;二次函数的最值.
【专题】二次函数图象及其性质;运算能力.
【答案】D
【分析】先把二次函数解析式化为顶点式,得到二次函数开口向下,顶点坐标为(2a,4a2+5),对称轴为直线x=2a,可判断B错误;结合a>0可判断A错误;把x=2a代入解析式可判断C错误;根据对称轴为直线x=2a,a>0可判断D正确.
【解答】解:将二次函数解析式配方得为y=﹣x2+4ax+5=﹣(x﹣2a)2+4a2+5,
∴二次函数开口向下,顶点坐标为(2a,4a2+5),对称轴为直线x=2a,故B错误,
∵a>0,
∴4a2+5>5,
∴该函数的最大值大于5,故A错误;
∵当x=2a时,y=4a2+5≠5,
∴该函数的图象不经过点(2a,5),故C错误;
∵a>0,
∴2a>0,
∴该函数的图象对称轴在y轴右侧,故D正确.
故选:D.
【点评】本题考查了二次函数图象的性质,熟练掌握该知识点是关键.
10.(2025 佛山一模)在平面直角坐标系xOy中,点A的坐标为(3,4),点M是抛物线y=ax2+bx+2(a≠0)对称轴上的一个动点.小明经过探究发现:当的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定.若抛物线y=ax2+bx+2(a≠0)的对称轴上存在3个不同的点M,使△AOM为直角三角形,则的值是( )
A.﹣8 B.或﹣8 C.2 D.2或﹣8
【考点】二次函数的应用;切线的判定与性质.
【专题】二次函数的应用;运算能力.
【答案】D
【分析】如图(见解析),分三种情况:①当∠AOM=90°时,则点M在与OA垂直的直线l1上运动(不含点O),②当∠OAM=90°时,则点M在与OA垂直的直线l2上运动(不含点A),③当∠OMA=90°时,则点M在以OA为直径的圆上运动,圆心为OA的中点P,判断出这个抛物线的对称轴(图中的l3和l4)与⊙P相切,由此计算即可得.
【解答】解:由题意可知,有以下三种情况:
①如图,当∠AOM=90°时,OA⊥OM,△AOM为直角三角形,
则点M在与OA垂直的直线l1上运动(不含点O),且M点是l1与抛物线对称轴的交点;
②当∠OAM=90°时,OA⊥AM,△AOM为直角三角形,
则点M在与OA垂直的直线l2上运动(不含点A),且M点是l2与抛物线对称轴的交点;
③当∠OMA=90°时,OM⊥AM,△AOM为直角三角形,
则点M在以OA为直径的圆上运动,圆心为OA的中点P;
∵O(0,0),A(3,4),
∴,⊙P的半径为,
抛物线的对称轴为直线,
∵抛物线的对称轴上存在3个不同的点M,使△AOM为直角三角形,
∴这个抛物线的对称轴(图中的l3和l4)与⊙P相切时,只有一个点M,使△AOM为直角三角形;
∴,
解得或,
∴或,
故选:D.
【点评】本题考查了二次函数的应用、圆的切线的性质等知识,综合性较强,有一定难度.正确分情况讨论,找出抛物线的对称轴的位置是解题关键.
二.填空题(共5小题)
11.(2025 福建模拟)把抛物线y=x2+1向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 y=(x+1)2+4 .
【考点】二次函数图象与几何变换.
【专题】二次函数图象及其性质;运算能力.
【答案】y=(x+1)2+4.
【分析】依据题意,根据抛物线平移的规律:左加右减,上加下减,即可判断得解.
【解答】解:由题意,抛物线y=x2+1向左平移1个单位,然后向上平移3个单位,
∴平移后抛物线的解析式为y=(x+1)2+1+3=(x+1)2+4.
故答案为:y=(x+1)2+4.
【点评】本题主要考查了二次函数图象与几何变换,解题时要熟练掌握并能灵活运用是关键.
12.(2025 旺苍县一模)已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=﹣(x﹣2)2+k的图象上,则y1,y2,y3的大小关系是 y3<y1<y2 .
【考点】二次函数图象上点的坐标特征.
【专题】计算题.
【答案】见试题解答内容
【分析】先利用顶点式得到抛物线对称轴为直线x=2,再比较点A、B、C到直线x=2的距离,然后根据二次函数的性质判断函数值的大小.
【解答】解:二次函数y=﹣(x﹣2)2+k的图象的对称轴为直线x=2,
因为点B(,y2)到直线x=2的距离最小,点C(﹣2,y3)到直线x=2的距离最大,
而抛物线的开口向下,
所以y3<y1<y2.
故答案为y3<y1<y2.
【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.熟练掌握二次函数的性质是解决本题的关键.
13.(2025 晋安区校级模拟)二次函数y=2x2﹣4x+1的顶点坐标为 (1,﹣1) .
【考点】二次函数的性质.
【专题】二次函数图象及其性质;运算能力.
【答案】(1,﹣1).
【分析】先,然后利用二次函数的性质解决问题.
【解答】解:把一般式配成顶点式得y=2(x﹣1)2﹣1,
∴抛物线的顶点坐标为(1,﹣1).
故答案为:(1,﹣1).
【点评】本题考查了二次函数的性质.熟练掌握该知识点是关键.
14.(2025 登封市一模)在平面直角坐标系中,若将二次函数y=(x+1)(x﹣2023)﹣4的图象向上平移4个单位长度,则所得新函数的图象与x轴两交点之间的距离是 2024 .
【考点】抛物线与x轴的交点;二次函数图象与几何变换.
【专题】二次函数图象及其性质;应用意识.
【答案】2024.
【分析】由题意得,所得新函数的解析式为y=(x+1)(x﹣2023),令(x+1)(x﹣2023)=0,解得x1=﹣1,x2=2023,则可得新函数的图象与x轴两交点之间的距离是2023﹣(﹣1)=2024.
【解答】解:将二次函数y=(x+1)(x﹣2023)﹣4的图象向上平移4个单位长度,所得新函数的解析式为y=(x+1)(x﹣2023),
令(x+1)(x﹣2023)=0,
解得x1=﹣1,x2=2023,
∴所得新函数的图象与x轴两交点之间的距离是2023﹣(﹣1)=2024.
故答案为:2024.
【点评】本题考查抛物线与x轴的交点、二次函数图象与几何变换,解题的关键是理解题意,灵活运用所学知识解决问题.
15.(2025 潍坊模拟)一种玻璃水杯的截面如图1所示,其左右轮廓线AC,BD为某一抛物线的一部分,杯口AB=8cm,杯底CD=4cm,且AB∥CD,杯深12cm,如图2若盛有部分水的水杯倾斜45°(即∠ABP=45°),水面正好经过点B,则此时点P到杯口AB的距离为 7 .
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】7.
【分析】建立合适的坐标系,求出抛物线的解析式,求P点坐标,就可求出点P到杯口AB的距离.
【解答】解:建立如图所示坐标系,作PE⊥x轴于点E,
各点坐标为:A(﹣4,0),B(4,0),C(﹣2,﹣12),D(2,﹣12).
设y=a(x+4)(x﹣4),
把点C坐标代入解析式得:﹣12=a(﹣2+4)(﹣2﹣4),
解得a=1,
∴y=(x+4)(x﹣4)=x2﹣16,
∵∠ABP=45°,∠PEB=90°,
∴∠BPE=45°,
∴∠EPB=∠EBP,
∴EP=EB,
设P(x,y),
∴BE=4﹣x,EP=﹣y,
∴﹣y=4﹣x,
即﹣(x2﹣16)=4﹣x,
解得x1=4(舍去),x2=﹣3,
∴y=9﹣16=﹣7,
∴PE=﹣y=7.
故答案为:7.
【点评】本题考查了二次函数的应用,关键是建立合适的坐标系,求出抛物线的解析式.
三.解答题(共5小题)
16.(2024 五莲县二模)如图(1),二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(3,0),C(0,3).把过A,C两点的直线绕点A旋转,旋转过程中记作直线l,l与抛物线的交于点P.
(1)①求这个二次函数的解析式;②若直线l始终与线段BC有交点,点B,C到直线l的距离分别为d1,d2,求d1+d2的最大值,并说明理由;
(2)如图(2),当点P是抛物线的顶点时,过P作PH⊥AB于H.若点Q在对称轴右侧的抛物线上,过点Q作QM⊥AP于M,△PQM与△APH相似,求点Q的坐标.
(3)直线l与AC的夹角为α(α为锐角),若tanα=,直接写出点P的坐标.
【考点】二次函数综合题.
【专题】压轴题.
【答案】见试题解答内容
【分析】(1)①利用待定系数法即可解决问题;
②如图1中,作BM⊥直线l于M,CN⊥直线l于N.则d1=BM≤BD,d2=CN≤CD,可得d1+d2≤CD+BD,推出d1+d2≤BC,即可解决问题;
(2)如图2中,延长PQ交x轴于N.首先证明AN=NP,设AN=NP=m,在Rt△PHN中,利用勾股定理求出m的值,再求出直线AN的解析式,构建方程组确定点P坐标即可;
(3)如图3中,设直线PA交y轴与D,作DE⊥AC于E.设DE=k.首先求出直线AP的解析式,利用方程组确定解得P坐标,再根据对称性,求出直线AP关于直线AC 的对称的直线AD′的解析式,利用方程组确定交点坐标即可;
【解答】解:(1)①把点A(﹣1,0),B(3,0),C(0,3)代入二次函数y=ax2+bx+c得到
,
解得,
∴二次函数的解析式为y=﹣x2+2x+3.
②如图1中,作BM⊥直线l于M,CN⊥直线l于N.
则d1=BM≤BD,d2=CN≤CD,
∴d1+d2≤CD+BD,
∴d1+d2≤BC,
∵OC=OB=3,
∴BC=3,
∴d1+d2的最大值为3.
(2)如图2中,延长PQ交x轴于N.由题意P(1,4).
∵△PQM与△APH相似,
观察图象可知,只有∠QPM=∠PAH,
∴NA=PN,设NA=PN=m,
在Rt△PNH中,∵PH2+NH2=PN2,
∴m2=42+(m﹣2)2,
解得m=5,
∴ON=4,
∴N(4,0),
∴直线PN的解析式为y=﹣x+,
由,解得或,
∴Q(,).
(3)如图3中,设直线PA交y轴与D,作DE⊥AC于E.设DE=k.
∵tan∠EAD=,tan∠DCE=,
∴AE=2k,EC=3k,
∴AC=5k,
∵AC==,
∴k=,
∴DE=,EC=,
∴CD==2,
∴D(0,1),
∴直线AP的解析式为y=x+1,
由,解得或,
∴P(2,3).
作点D关于直线AC的对称点D′,
∵E(﹣,),
∴D′(﹣,),
∴直线AD′的解析式为y=﹣7x﹣7,
由解得或,
∴P(10,﹣77),
综上所述,满足条件的点P坐标为(2,3)或(10,﹣77).
【点评】本题考查二次函数综合题、垂线段最短、一次函数的应用等知识,解题的关键是学会添加常用辅助线,学会利用参数构建方程解决问题,学会构建一次函数,利用方程组确定两个函数的交点坐标解决问题,属于中考压轴题.
17.(2025 安阳模拟)在如图所示的平面直角坐标系中,抛物线y=ax2+bx+c的对称轴为直线x=1,且与y轴交于点B(0,﹣3),与x轴交于点C(﹣1,0).
(1)求此抛物线的函数表达式,并直接写出抛物线与x轴的另一个交点A的坐标;
(2)点P是直线AB下方,直线x=1左侧的抛物线上一点,过点P作PE⊥x轴,交AB于点E,作PF⊥y轴,交直线x=1右侧的抛物线于点F,若4PE+PF=6,求点F的坐标.
【考点】二次函数综合题.
【专题】二次函数图象及其性质.
【答案】(1)y=x2﹣2x﹣3;A(3,0);
(2)点F坐标为.
【分析】(1)用待定系数法可得抛物线的函数表达式;令y=0,得x2﹣2x﹣3=0,解方程即可求解;
(2)先用待定系数法求出直线AB的解析式,再设P(m,m2﹣2m﹣3),则E(m,m﹣3),F(2﹣m,m2﹣2m﹣3),求出PE=﹣m2+3m,PF=2(1﹣m),再解方程求出m的值,并得出点F坐标.
【解答】解:(1)∵抛物线y=ax2+bx+c的对称轴为直线x=1,
∴,
把B(0,﹣3),C(﹣1,0)代入y=ax2+bx+c得:
,
解得,
∴抛物线的函数表达式为y=x2﹣2x﹣3;
令y=0,则x2﹣2x﹣3=0,
∴x1=3,x2=﹣1,
∴A(3,0);
(2)设直线AB解析式为y=kx+t,
把A(3,0),B(0,﹣3)代入y=kx+t得:
,
解得,
∴直线AB解析式为y=x﹣3,
设P(m,m2﹣2m﹣3),则E(m,m﹣3),F(2﹣m,m2﹣2m﹣3),
∴PE=﹣m2+3m,PF=2(1﹣m),
∵点P是直线AB下方,直线x=1左侧的抛物线上一点,
∴0<m<1,
∵4PE+PF=6,
∴4(﹣m2+3m)+2(1﹣m)=6,
整理得2m2﹣5m+2=0,
解得(舍),
∴当时,,
此时点F坐标为.
【点评】本题考查待定系数法求二次函数的解析式,抛物线与x轴的交点,二次函数与几何图形的综合等问题,关键是利用二次函数的性质求解.
18.(2025 十堰校级模拟)在平面直角坐标系xOy中,点(1,m),(3,n)在抛物线y=ax2+bx+c(a>0)上,设抛物线的对称轴为直线x=t.
(1)当c=2,m=n时,求抛物线与y轴交点的坐标及t的值;
(2)点(x0,m)(x0≠1)在抛物线上,若m<n<c,求t的取值范围及x0的取值范围.
【考点】二次函数的性质;二次函数图象上点的坐标特征.
【专题】二次函数图象及其性质;推理能力.
【答案】(1)抛物线与y轴交点的坐标为(0,2),t=2;(2)2<x0<3.
【分析】(1)将点(1,m),(3,n)代入抛物线解析式,再根据m=n得出b=﹣4a,再求对称轴即可;
(2)再根据m<n<c,可确定出对称轴的取值范围,进而可确定x0的取值范围.
【解答】解:(1)法一、将点(1,m),(3,n)代入抛物线解析式,
∴,
∵m=n,
∴a+b+c=9a+3b+c,整理得,b=﹣4a,
∴抛物线的对称轴为直线x=﹣=﹣=2;
∴t=2,
∵c=2,
∴抛物线与y轴交点的坐标为(0,2).
法二、当m=n时,点A(1,m),B(3,n)的纵坐标相等,
由抛物线的对称性可得,抛物线的对称轴为直线x=,
∴t=2,
∵c=2,
∴抛物线与y轴交点的坐标为(0,2).
(2)∵m<n<c,
∴a+b+c<9a+3b+c<c,
解得﹣4a<b<﹣3a,
∴3a<﹣b<4a,
∴<﹣<,即<t<2.
由题意可知,点(x0,m)与点(1,m)关于x=t对称;
∴t=;
当t=时,x0=2;
当t=2时,x0=3.
∴x0的取值范围2<x0<3.
综上,t的取值范围为:<t<2;x0的取值范围2<x0<3.
【点评】本题考查二次函数的性质,解题关键是根据数形结合求解.
19.(2025 永寿县校级一模)近年来,露营成为广受人们欢迎的假日休闲方式,从家边绿地到旷野山林,各具特色的露营地吸引着大家前去体验,各式帐篷已成为户外活动的必要装备,其中抛物线型帐篷支架简单,携带方便,适合休闲旅行使用.如图1,这款帐篷搭建时张开的宽度AB=4m,顶部高度h=2m,在图1中以AB所在直线为x轴,AB的中点为原点,建立平面直角坐标系.
(1)求帐篷支架对应的抛物线的函数表达式;
(2)每款帐篷张开时的宽度和顶部高度都会影响其容纳椅子的数量,图2为一张椅子摆入这款帐篷后的简易视图,椅子高度CE=0.72m,宽度CD=0.5m,若在帐篷内沿AB所在的水平方向摆放一排这种椅子(椅子间的间隔忽略不计),求最多可摆放的椅子数量.
【考点】二次函数的应用.
【专题】二次函数的应用;运算能力.
【答案】(1);
(2)6把.
【分析】(1)先求出A(﹣2,0),B(2,0),顶点坐标为(0,2),设抛物线的函数表达式为y=ax2+2,然后用待定系数法求解即可;
(2)将y=0.72代入,解出x1,x2的值,然后用两根之差除以椅子的宽度即可作答.
【解答】解:(1)由题意可得:A(﹣2,0),B(2,0),顶点坐标为(0,2).
设抛物线的函数表达式为y=ax2+2,
将A(﹣2,0)代入,得0=4a+2,
解得,
∴;
(2)∵椅子的高度CE=0.72m,宽度CD=0.5m,
∴将y=0.72代入,
得,
解得x1=1.6,x2=﹣1.6,
1.6﹣(﹣1.6)=3.2(m),
3.2÷0.5=6.4(把),
∴最多可撰放6把椅子.
【点评】本题考查了二次函数的应用,正确进行计算是解题关键.
20.(2025 旺苍县一模)文旅发展促进经济增长的同时,也带动了电器销售.一电器商城销售某品牌空调,该空调每台进货价为2500元,已知该商店6月份售出75台空调,8月份售出108台空调.求该商城7、8两个月售出空调数的月平均增长率;调查发现,当该空调售价为3000元时,平均每天能售出8台;售价每降低50元,平均每天能多售出4台,该商城如何定价能使每天的利润最大?最大利润是多少?
【考点】二次函数的应用;一元二次方程的应用.
【专题】二次函数的应用;运算能力.
【答案】(1)该商城7、8两个月售出空调数的月平均增长率为20%;
(2)该商城将空调定价为2800元时,每天的利润最大,最大利润是7200元.
【分析】(1)设该商城7、8两个月售出空调数的月平均增长率为x,根据题意列方程求解即可;
(2)设该商城每台空调降价m元,则每天可多售台,每天的利润为w元.
根据题意列出,然后根据二次函数的性质即可求解.
【解答】解(1)设月平均增长率为x,根据题意得:75(1+x)2=108,
解得:x1=0.2=20%,x2=﹣2.2(舍去).
答:该商城7、8两个月售出空调数的月平均增长率为20%;
(2)设该商城每台空调降价m元,则每天可多售台,每天的利润为w元,
根据题意得出:
=
=,
当m=200时,w最大=5000,
则3000﹣m=2800,
答:该商城将空调定价为2800元时,每天的利润最大,最大利润是7200元.
【点评】本题考查了一元二次方程的应用,二次函数的应用,解题的关键是理解题意,正确建立方程模型与函数模型解决问题.
21世纪教育网(www.21cnjy.com)
同课章节目录
