【中考押题卷】2025年中考数学二轮复习考前预测:图形的对称(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学二轮复习考前预测:图形的对称(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 12:23:07 | ||
图片预览


文档简介
2025年中考数学二轮复习考前预测:图形的对称
一.选择题(共10小题)
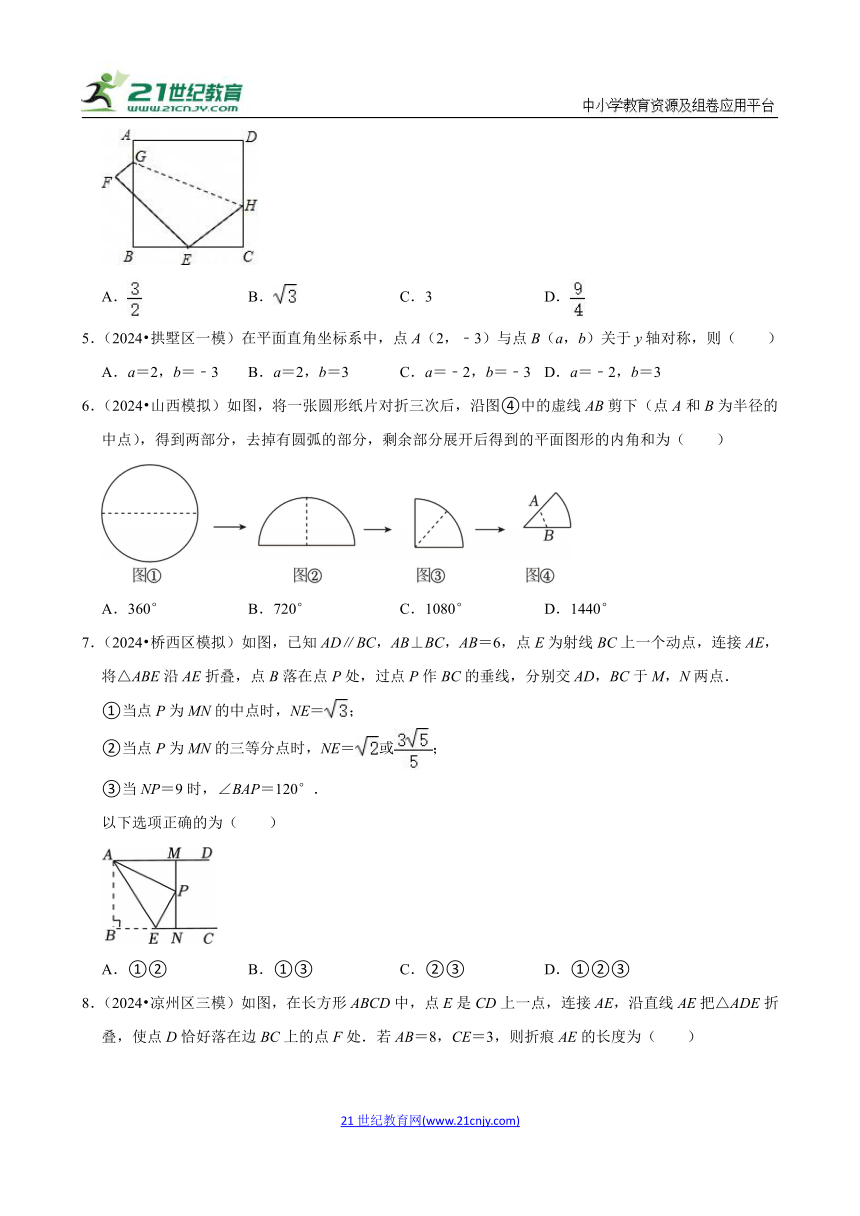
1.(2025 雁塔区校级模拟)在刚刚过去的第33届夏季奥运会中,中国健儿创造了新的境外参加奥运会的最佳成绩.在以下给出的运动图标中,属于轴对称图形的是( )
A. B.
C. D.
2.(2025 安阳模拟)如图,将一个正方形纸片沿图中虚线剪成四部分,恰能拼成一个没有缝隙且不重叠的等腰三角形,则这个正方形的边长与等腰三角形的底边长的比为( )
A. B. C. D.
3.(2025 河北模拟)如图, ABCD中,AB=5,AD=8,将 ABCD沿对角线BD折叠,使点A落在平面上A′处.若A'C=5,则BD长为( )
A.8 B. C.7.8 D.
4.(2025 碑林区校级一模)如图,正方形ABCD的边长为6,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若点E恰好是BC的中点,则线段CH的长为( )
A. B. C.3 D.
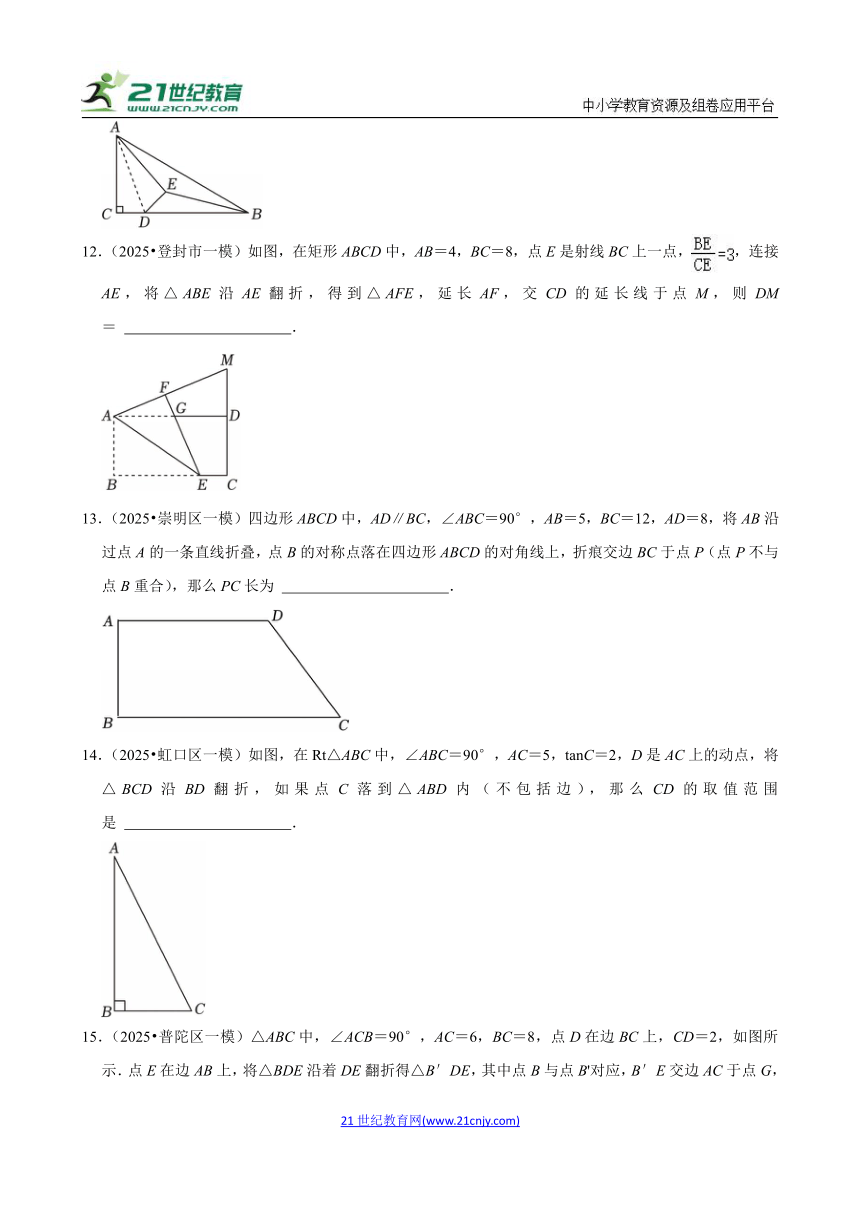
5.(2024 拱墅区一模)在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则( )
A.a=2,b=﹣3 B.a=2,b=3 C.a=﹣2,b=﹣3 D.a=﹣2,b=3
6.(2024 山西模拟)如图,将一张圆形纸片对折三次后,沿图④中的虚线AB剪下(点A和B为半径的中点),得到两部分,去掉有圆弧的部分,剩余部分展开后得到的平面图形的内角和为( )
A.360° B.720° C.1080° D.1440°
7.(2024 桥西区模拟)如图,已知AD∥BC,AB⊥BC,AB=6,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点P处,过点P作BC的垂线,分别交AD,BC于M,N两点.
①当点P为MN的中点时,NE=;
②当点P为MN的三等分点时,NE=或;
③当NP=9时,∠BAP=120°.
以下选项正确的为( )
A.①② B.①③ C.②③ D.①②③
8.(2024 凉州区三模)如图,在长方形ABCD中,点E是CD上一点,连接AE,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.若AB=8,CE=3,则折痕AE的长度为( )
A. B.10 C. D.15
9.(2024 武汉模拟)对于平面直角坐标系xOy中的任意线段MN,给出如下定义:线段MN上各点到x轴距离的最大值,叫做线段MN的“轴距”,记作dMN.例如,如图,点M(﹣2,﹣3),N(4,1),则线段MN的“轴距”为3,记作dMN=3.已知点E(﹣1,m),F(2,m+2),线段EF关于直线y=2的对称线段为GH.若dGH=3,则m的值为( )
A.1或7 B.5或﹣1 C.7或﹣1 D.1或5
10.(2024 邯山区校级三模)①~⑥是三个三角形的碎片,若组合其中的两个,恰能拼成一个轴对称图形,则应选择( )
A.①⑥ B.②④ C.③⑤ D.④⑥
二.填空题(共5小题)
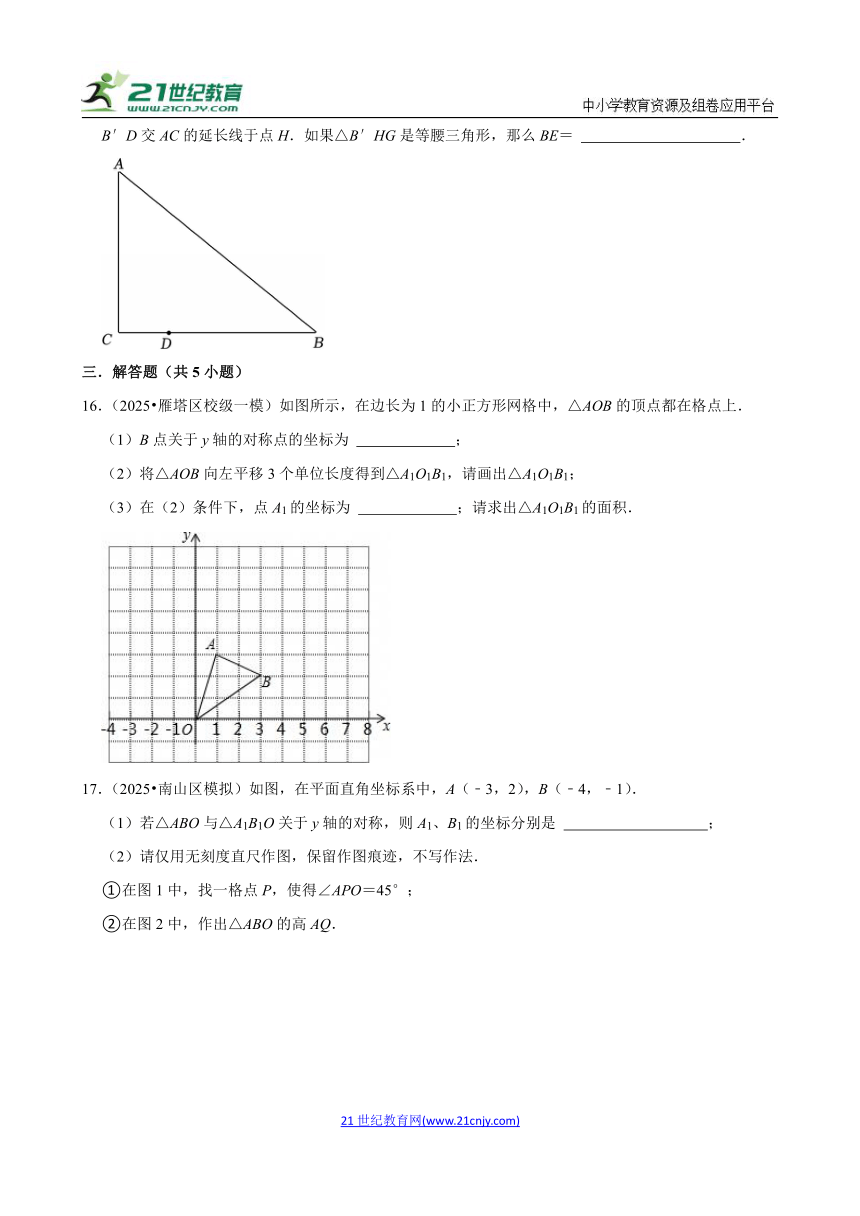
11.(2025 汕头模拟)如图,在直角三角形ABC中,∠C=90°,∠BAC=60°,AC=6,点D是BC边上的一点(不与B、C重合),连接AD,将△ACD沿AD折叠,使点C落在点E处,当△BDE是直角三角形时,CD的长为 .
12.(2025 登封市一模)如图,在矩形ABCD中,AB=4,BC=8,点E是射线BC上一点,,连接AE,将△ABE沿AE翻折,得到△AFE,延长AF,交CD的延长线于点M,则DM= .
13.(2025 崇明区一模)四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=12,AD=8,将AB沿过点A的一条直线折叠,点B的对称点落在四边形ABCD的对角线上,折痕交边BC于点P(点P不与点B重合),那么PC长为 .
14.(2025 虹口区一模)如图,在Rt△ABC中,∠ABC=90°,AC=5,tanC=2,D是AC上的动点,将△BCD沿BD翻折,如果点C落到△ABD内(不包括边),那么CD的取值范围是 .
15.(2025 普陀区一模)△ABC中,∠ACB=90°,AC=6,BC=8,点D在边BC上,CD=2,如图所示.点E在边AB上,将△BDE沿着DE翻折得△B′DE,其中点B与点B'对应,B′E交边AC于点G,B′D交AC的延长线于点H.如果△B′HG是等腰三角形,那么BE= .
三.解答题(共5小题)
16.(2025 雁塔区校级一模)如图所示,在边长为1的小正方形网格中,△AOB的顶点都在格点上.
(1)B点关于y轴的对称点的坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)条件下,点A1的坐标为 ;请求出△A1O1B1的面积.
17.(2025 南山区模拟)如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣1).
(1)若△ABO与△A1B1O关于y轴的对称,则A1、B1的坐标分别是 ;
(2)请仅用无刻度直尺作图,保留作图痕迹,不写作法.
①在图1中,找一格点P,使得∠APO=45°;
②在图2中,作出△ABO的高AQ.
18.(2024 南宁一模)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,1),B(3,4),C(4,2).
(1)在图中画出△ABC关于x轴对称的△A1B1C1;
(2)通过平移,使C1移动到原点O的位置,画出平移后的△A2B2C2.
(3)在△ABC中有一点P(m,n),则经过以上两次变换后点P的对应点P2的坐标为 .
19.(2024 香坊区校级四模)如图是4×4的正方形网格,请仅用无刻度尺的直尺按要求完成以下作图.
(1)在图1中作四边形ABCD,使点C,D在格点上,并且四边形ABCD为轴对称图形.(画出一种即可)
(2)在图2中的线段AB上作点Q,使PQ最短.(用实线保留作图痕迹)
20.(2024 丰台区二模)如图,在等边△ABC中,过点A在AB的右侧作射线AP,设∠BAP=α(60°<α<90°),点B与点E关于直线AP对称,连接AE,BE,CE,且BE,CE分别交射线AP于点D,F.
(1)依题意补全图形;
(2)求∠AFE的大小;
(3)用等式表示线段AF,CF,DF之间的数量关系,并证明.
2025年中考数学二轮复习考前预测:图形的对称
参考答案与试题解析
一.选择题(共10小题)
1.(2025 雁塔区校级模拟)在刚刚过去的第33届夏季奥运会中,中国健儿创造了新的境外参加奥运会的最佳成绩.在以下给出的运动图标中,属于轴对称图形的是( )
A. B.
C. D.
【考点】轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】B
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:选项A、C、D的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项B的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.(2025 安阳模拟)如图,将一个正方形纸片沿图中虚线剪成四部分,恰能拼成一个没有缝隙且不重叠的等腰三角形,则这个正方形的边长与等腰三角形的底边长的比为( )
A. B. C. D.
【考点】图形的剪拼;等腰三角形的判定与性质;正方形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;推理能力.
【答案】C
【分析】如图,等腰三角形纸片沿图中虚线剪成四块图形,能拼成一个没有缝隙的正方形和矩形,根据题意得(a+b)2=b(b+a+b),设a=1,求出,进而求出正方形的边长与等腰三角形的底边长的比.
【解答】解:如图,等腰三角形纸片沿图中虚线剪成四块图形,能拼成一个没有缝隙的正方形和矩形,
设a=1,
根据题意,得(a+b)2=b(b+a+b),
解得,(负值舍去),
∴正方形的边长与等腰三角形的底边长的比为:
.
故选:C.
【点评】本题主要考查一元二次方程与图形有关的应用,解此题的关键在于将等腰三角形拆解拼成另一个没有缝隙的矩形,再利用面积相等得到相关边的长度关系.
3.(2025 河北模拟)如图, ABCD中,AB=5,AD=8,将 ABCD沿对角线BD折叠,使点A落在平面上A′处.若A'C=5,则BD长为( )
A.8 B. C.7.8 D.
【考点】翻折变换(折叠问题);勾股定理;平行四边形的性质;矩形的判定与性质.
【答案】C
【分析】由平行四边形和折叠得到AB=A′B=CD=5,AD=A′D=BC=8,∠ADB=∠A′DB=∠CBD,过C作CF⊥BD于F,过A′作A′E⊥BD于E,再证明△BCF≌△DA′E(AAS),得到A′E=CF,DE=BF,即可得到DF=BE,四边形A′EFC是矩形,A′C=EF=5,设DF=BE=x,则BF=EF+BE=5+x,BD=DF+BF=5+2x,再在Rt△BCF和Rt△DCF中,利用勾股定理得到CF2=BC2﹣BF2=DC2﹣DF2,代入列方程求解即可.
【解答】解:过C作CF⊥BD于F,过A′作A′E⊥BD于E,则∠A′EB=∠A′ED=∠CFB=∠CFD=90°,
由题意可得:AB=CD=5,AD=BC=8,AD∥BC,
∴∠ADB=∠CBD,
∵由折叠的性质可得:
∴AB=A′B=5,AD=A′D=8,∠ADB=∠A′DB,
∴AB=A′B=CD=5,AD=A′D=BC=8,∠ADB=∠A′DB=∠CBD,
∵∠A′ED=∠CFB=90°,A′D=BC=8,∠A′DB=∠CBD,
∴△BCF≌△DA′E(AAS),
∴A′E=CF,DE=BF,
∴DE﹣EF=BF﹣EF,
即DF=BE,
∵∠A′ED=∠CFB=90°,
∴A′E∥CF,
∵A′E=CF,
∴四边形A′EFC是矩形,
∴A′C=EF=5,
设DF=BE=x,则BF=EF+BE=5+x,BD=DF+BF=5+2x,
∴CF2=BC2﹣BF2=82﹣(5+x)2,
∴CF2=DC2﹣DF2=52﹣x2,
∴82﹣(5+x)2=52﹣x2,
∴x=1.4,
∴BD=5+2x=7.8.
故选:C.
【点评】本题考查平行四边形的性质,矩形的判定与性质,折叠的性质,勾股定理,根据题意,作出辅助线,综合运用这些知识点是解题关键.
4.(2025 碑林区校级一模)如图,正方形ABCD的边长为6,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若点E恰好是BC的中点,则线段CH的长为( )
A. B. C.3 D.
【考点】翻折变换(折叠问题);正方形的性质.
【专题】平移、旋转与对称.
【答案】D
【分析】根据折叠可得DH=EH,在直角△CEH中,设CH=x,则DH=EH=6﹣x,根据E是BC的中点,可得CE=3,可以根据勾股定理列出方程,从而解出CH的长.
【解答】解:设CH=x,则DH=EH=6﹣x,
∵点E恰好是BC的中点,BC=6,
∴CE=BC=3,
∵在Rt△ECH中,EH2=EC2+CH2,
∴(6﹣x)2=32+x2,
解得:x=,
即CH=.
故选:D.
【点评】本题主要考查正方形的性质以及翻折变换,折叠问题其实质是轴对称变换.在直角三角形中,利用勾股定理列出方程进行求解是解决本题的关键.
5.(2024 拱墅区一模)在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则( )
A.a=2,b=﹣3 B.a=2,b=3 C.a=﹣2,b=﹣3 D.a=﹣2,b=3
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】C
【分析】根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”即可求出a、b的值.
【解答】解:在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则a=﹣2,b=﹣3.
故选:C.
【点评】本题考查了关于y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于y轴对称的点,纵坐标相同,横坐标互为相反数.
6.(2024 山西模拟)如图,将一张圆形纸片对折三次后,沿图④中的虚线AB剪下(点A和B为半径的中点),得到两部分,去掉有圆弧的部分,剩余部分展开后得到的平面图形的内角和为( )
A.360° B.720° C.1080° D.1440°
【考点】剪纸问题.
【专题】多边形与平行四边形;运算能力.
【答案】C
【分析】由题意得出剩余部分展开后得到的平面图形是正八边形,再根据多边形的内角和公式计算即可得出答案.
【解答】解:将一张圆形纸片对折三次后,沿图④中的虚线AB剪下(点A和B为半径的中点),得到两部分,去掉有圆弧的部分,剩余部分展开后得到的平面图形是正八边形,
∴剩余部分展开后得到的平面图形的内角和为(8﹣2)×180°=1080°,
故选:C.
【点评】本题考查了多边形的内角和,解题的关键是掌握相关知识的灵活运用.
7.(2024 桥西区模拟)如图,已知AD∥BC,AB⊥BC,AB=6,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点P处,过点P作BC的垂线,分别交AD,BC于M,N两点.
①当点P为MN的中点时,NE=;
②当点P为MN的三等分点时,NE=或;
③当NP=9时,∠BAP=120°.
以下选项正确的为( )
A.①② B.①③ C.②③ D.①②③
【考点】翻折变换(折叠问题);平行线的性质.
【专题】线段、角、相交线与平行线;平移、旋转与对称;运算能力;推理能力.
【答案】B
【分析】由AD∥BC,AB⊥BC,证明∠B=∠DAB=90°,而MN⊥BC于点N,则∠MNB=90°,可证明四边形ABNM是矩形,所以∠AMN=90°,MN=AB=6,可证明∠EPN=∠PAM,则=tan∠EPN=tan∠PAM=,由折叠得AP=AB=6,当点P为MN的中点时,则PM=PN=3,所以AM=3,求得NE==,可判断①正确;当点P为MN的三等分点,且PM=MN=2,则PN=4,所以AM=4,求得NE==;当点P为MN的三等分点,且PM=MN=4,则PN=2,所以AM=2,求得NE==,可判断②错误;若PN=9,则PM=PN﹣MN=3,所以sin∠PAM==,则∠PAM=30°,求得∠BAP=120°,可判断③正确,于是得到问题的答案.
【解答】解:∵AD∥BC,AB⊥BC,
∴∠B=90°,
∴∠DAB=180°﹣∠B=90°,
∵MN⊥BC于点N,交AD于点M,
∴∠MNB=90°,
∴四边形ABNM是矩形,
∴∠AMN=90°,MN=AB=6,
∴∠EPN=∠PAM=90°﹣∠APM,
∴=tan∠EPN=tan∠PAM=,
由折叠得AP=AB=6,
如图1,点P为MN的中点,则PM=PN=MN=3,
∴AM===3,
∴NE===,
故①正确;
如图2,点P为MN的三等分点,且PM=MN=2,则PN=MN=4,
∴AM===4,
∴NE===;
如图3,点P为MN的三等分点,且PM=MN=4,则PN=MN=2,
∴AM===2,
∴NE===,
∴NE=或,
故②错误;
如图4,PN=9,则PM=PN﹣MN=9﹣6=3,
∵∠AMP=∠MNB=90°,
∴sin∠PAM===,
∴∠PAM=30°,
∴∠BAP=∠DAB+∠PAM=90°+30°=120°,
故③正确,
故选:B.
【点评】此题重点考查平行线的性质、轴对称的性质、矩形的判定与性质、同角的余角相等、勾股定理、锐角三角函数与解直角三角形等知识,证明∠EPN=∠PAM并且推导出=是解题的关键.
8.(2024 凉州区三模)如图,在长方形ABCD中,点E是CD上一点,连接AE,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.若AB=8,CE=3,则折痕AE的长度为( )
A. B.10 C. D.15
【考点】翻折变换(折叠问题);矩形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;几何直观.
【答案】C
【分析】由矩形的性质得出CD=AB=8,AD=BC,由折叠的性质得AF=AD,EF=DE=CD﹣CE=5,在Rt△CEF中,由勾股定理得CF==4,设BC=AD=AF=x,则BF=x﹣4,在Rt△ABF中,由勾股定理解出方程,即可求出AE得到答案.
【解答】解:∵四边形ABCD是矩形,
∴CD=AB=8,AD=BC,∠C=∠B=90°,
由折叠的性质得:AF=AD,EF=DE=CD﹣CE=8﹣3=5,
在Rt△CEF中,由勾股定理得:CF==4,
设BC=AD=AF=x,则BF=x﹣4,
在Rt△ABF中,由勾股定理得:82+(x﹣4)2=x2,
解得:x=10,
∴AD=10,
在Rt△ADE中,
AE===5,
故选:C.
【点评】本题考查了翻折变换的性质、矩形的性质、直角三角形的性质、勾股定理等知识;熟练掌握翻折变换和矩形的性质,由勾股定理得出方程是解题的关键.
9.(2024 武汉模拟)对于平面直角坐标系xOy中的任意线段MN,给出如下定义:线段MN上各点到x轴距离的最大值,叫做线段MN的“轴距”,记作dMN.例如,如图,点M(﹣2,﹣3),N(4,1),则线段MN的“轴距”为3,记作dMN=3.已知点E(﹣1,m),F(2,m+2),线段EF关于直线y=2的对称线段为GH.若dGH=3,则m的值为( )
A.1或7 B.5或﹣1 C.7或﹣1 D.1或5
【考点】坐标与图形变化﹣对称.
【专题】平面直角坐标系;推理能力.
【答案】D
【分析】先求出G、H的坐标,然后根据轴距的定义,构建方程.
【解答】解:∵点E(﹣1,m),F(2,m+2),
∴E,F关于直线y=2的对称点G(﹣1,﹣m+4),H(2,﹣m+2),
当|4﹣m|≥|2﹣m|时,dGH=3,
∴|4﹣m|=3,
∴m=1或=7,
当|4﹣m|<2﹣m|时,dGH=3,
∴|2﹣m|=3,
∴m=﹣1或=5,
综上所述m=1或=5,
故选:D.
【点评】考查了轴坐标与图形变化﹣对称,线段PQ的“轴距”的定义等知识,解题的关键是理解新定义,属于中考常考题型.
10.(2024 邯山区校级三模)①~⑥是三个三角形的碎片,若组合其中的两个,恰能拼成一个轴对称图形,则应选择( )
A.①⑥ B.②④ C.③⑤ D.④⑥
【考点】利用轴对称设计图案.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】根据三角形内角和是180°且利用图形已知的两个角的度数分别求出另一个角的度数,然后利用等腰三角形定义及等腰三角形是轴对称图形判断即可
【解答】解:∵②180°﹣(30°+75°)=75°,④图形一个角是75°,
∴②和④可以组成一个三角形,且这个三角形是等腰三角形,是轴对称图形,
∵⑤180°﹣(30°+35°)=115°,③图形一个角是115°,
∴③和⑤可以组成一个三角形,这个三角形三个角都不相等,故不是轴对称图形,
∵180°﹣(90°+63°)=27°,①图形一个角是27°,
∴①和⑥可以组成一个三角形,这个三角形三个角都不相等,故不是轴对称图形.
故选:B.
【点评】本题考查了三角形内角和和轴对称图形,熟练掌握三角形内角和定理和轴对称图形的定义是解题的关键;
二.填空题(共5小题)
11.(2025 汕头模拟)如图,在直角三角形ABC中,∠C=90°,∠BAC=60°,AC=6,点D是BC边上的一点(不与B、C重合),连接AD,将△ACD沿AD折叠,使点C落在点E处,当△BDE是直角三角形时,CD的长为 6或2 .
【考点】翻折变换(折叠问题);含30度角的直角三角形;勾股定理.
【专题】平移、旋转与对称;运算能力;推理能力.
【答案】见试题解答内容
【分析】根据勾股定理得到BC==6,根据已知条件得到当△BDE是直角三角形时,∠BDE=90°或∠BED=90°,①当∠BDE=90°时,则∠CDE=90°,根据折叠的性质得到∠ADC=∠ADE=45°,于是得到CD=AC=6,②当∠BED=90°时,根据折叠的性质得到∠AED=∠C=90°,∠CAD=∠EAD,AC=AE,推出点E在AB上,根据勾股定理即可得到结论.
【解答】解:在Rt△ABC中,∠BAC=60°,AC=6,
∴∠ABC=30°,
∴AB=2AC=12,
∴BC==6,
∵点D是BC边上的一点,
∴∠DBE≠90°,
∴当△BDE是直角三角形时,∠BDE=90°或∠BED=90°,
①当∠BDE=90°时,则∠CDE=90°,
∵将△ACD沿AD折叠,使点C落在点E处,
∴∠ADC=∠ADE=45°,
∴CD=AC=6,
②当∠BED=90°时,
∵将△ACD沿AD折叠,使点C落在点E处,
∴∠AED=∠C=90°,∠CAD=∠EAD,AC=AE,
∴∠AED+∠BED=180°,
∴点E在AB上,如图,
∴AE=AC=6,BE=AB﹣AE=6,∠CAD=∠BAD,
∴CD=DE,
∵DE2+BE2=BD2,
∴CD2+62=(6﹣CD)2,
∴CD=2,
综上所述,CD的长为 6或2,
故答案为:6或2.
【点评】本题考查了翻折变换(折叠问题),勾股定理,直角三角形的性质,熟练掌握折叠的性质是解题的关键.
12.(2025 登封市一模)如图,在矩形ABCD中,AB=4,BC=8,点E是射线BC上一点,,连接AE,将△ABE沿AE翻折,得到△AFE,延长AF,交CD的延长线于点M,则DM= 或 .
【考点】翻折变换(折叠问题);矩形的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】或.
【分析】情形①如图当点E在线段BC上时,情形②如图当点E在线段BC的延长线上时分别求解即可解决问题;
【解答】解:情形①如图当点E在线段BC上时,
∵BC=8,BE=3EC,
∴EC=2,EB=EF=6,∵四边形ABCD是矩形,
∴∠ADC=∠ADM=90°,AD∥BC,
∴∠DAE=∠AEB=∠AEG,
∴AG=EG,设AG=EG=x,
在Rt△AFG中,∠AFG=90°,AF=AB=4,FG=6﹣x,
∴x2=42+(6﹣x)2,
∴x=,
∴FG=EF﹣EG=,
∵tan∠DAM==,
∴=,
∴DM=,
情形②如图当点E在线段BC的延长线上时,
∵BC=8,BE=3EC,
∴EC=4,EB=EF=12,
∵四边形ABCD是矩形,
∴∠ADC=∠ADG=90°,AD∥BC,
∴∠DAE=∠AEB=∠AEG,
∴AG=EG,设AG=EG=x,
在Rt△AFG中,∠AFG=90°,AF=AB=4,FG=12﹣x,
∴x2=42+(12﹣x)2,
∴x=,
∴FG=EF﹣EG=,
∵tan∠DAM==,
∴=,
∴DM=,
故答案为:或.
【点评】本题考查翻折变换(折叠问题)、矩形的性质、相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考填空题中的压轴题.
13.(2025 崇明区一模)四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=12,AD=8,将AB沿过点A的一条直线折叠,点B的对称点落在四边形ABCD的对角线上,折痕交边BC于点P(点P不与点B重合),那么PC长为 或 .
【考点】翻折变换(折叠问题);平行线的性质.
【专题】平移、旋转与对称;推理能力.
【答案】或.
【分析】分点B的对称点B'落在对角线AC上和落在对角线BD上两种情况,分别画出图形解答即可求解.
【解答】解:如图,当点B的对称点B'落在对角线AC上时,
由折叠可得,AB'=AB=5,PB'=PB,∠AB'P=∠ABP=90°,
∴∠CB'P=90°,
∵∠ABC=90°,AB=5,BC=12,
∴,
∴B'C=AC﹣AB=13﹣5=8,
设P'B=PB=x,则PC=12﹣x,
∵PB'2+B'C2=PC2,
∴x2+82=(12﹣x)2,
解得=,
∴,
∴;
如图,当点B的对称点B'落在对角线BD上时,设AP与BD相交于点G,
由折叠可得,AP⊥BD,
∴∠AGB=∠BGP=90°,
∵AD∥BC,∠ABC=90°,
∴∠BAD=180°﹣∠ABC=180°﹣90°=90°,
∴,
∵,
∴,
∴,
∴,
∵∠BAG+∠ABG=90°,∠PBG+∠ABG=90°,
∴∠PBG=∠BAG,
∵∠BGP=∠AGB=90°,
∴△BGP∽△AGB,
∴即,
∴,
∴;
综上,PC长为或,
故答案为:或.
【点评】本题考查的折叠的性质,勾股定理,相似三角形的判定和性质,运用分类讨论思想解答是解题的关键.
14.(2025 虹口区一模)如图,在Rt△ABC中,∠ABC=90°,AC=5,tanC=2,D是AC上的动点,将△BCD沿BD翻折,如果点C落到△ABD内(不包括边),那么CD的取值范围是 1<CD< .
【考点】翻折变换(折叠问题);解直角三角形.
【专题】等腰三角形与直角三角形;平移、旋转与对称;运算能力.
【答案】1<CD<.
【分析】由∠ABC=90°,tanC=2,AC=5,求出AB=2,BC=,设C的对应点为C',当C'在AC上时,求出CD=1;当C'在AB上时,过D作DH⊥AB于H,求出CD=,即可得1<CD<.
【解答】解:∵∠ABC=90°,tanC=2,
∴AB=2BC,
∵AC=5,
∴AB2+BC2=5,
∴AB=2,BC=,
设C的对应点为C',
当C'在AC上时,如图:
∵将△BCD沿BD翻折,
∴∠BDC=∠BDC'=90°,
∴tanC==2,即BD=2CD,
∵BD2+CD2=BC2,
∴(2CD)2+CD2=5,
∴CD=1;
当C'在AB上时,过D作DH⊥AB于H,如图:
∵将△BCD沿BD翻折,
∴BC=BC'=,∠CBD=∠C'BD=∠ABC=45°,CD=C'D,∠C=∠BC'D,
∴△BDH是等腰直角三角形,tan∠BC'D=2,
∴BH=DH,DH=2C'H,
设C'H=x,则DH=BH=2x,
∵C'H+BH=BC'=,
∴x+2x=,
解得x=,
∴C'H=,DH=,
∴C'D==,
∴CD=;
∵C'落到△ABD内(不包括边),
∴1<CD<;
故答案为:1<CD<.
【点评】本题考查直角三角形中的翻折问题,涉及解直角三角形,勾股定理等知识,解题的关键是求出临界点时CD的值.
15.(2025 普陀区一模)△ABC中,∠ACB=90°,AC=6,BC=8,点D在边BC上,CD=2,如图所示.点E在边AB上,将△BDE沿着DE翻折得△B′DE,其中点B与点B'对应,B′E交边AC于点G,B′D交AC的延长线于点H.如果△B′HG是等腰三角形,那么BE= .
【考点】翻折变换(折叠问题);等腰三角形的性质;勾股定理.
【专题】平移、旋转与对称;推理能力.
【答案】.
【分析】先画出图形,过点H作HF⊥B′E于点F,确定如果ΔB'HG是等腰三角形,则只能是B′H=GH,设B′E=BE=x(0<x<10),则AE=10﹣x,再证出△AEG∽△ACB,根据相似三角形的性质可得,,然后证出△HFG∽△AEG,根据相似三角形的性质可得,从而可得CH,HD的长,最后在Rt△CDH中,利用勾股定理求解即可得.
【解答】解:由题意,画出图形如下:过点H作HF⊥BE于点F,
∵∠ACB=90°,
∴∠DCH=90°,
∵B'E交边AC于点G,B'D交AC的延长线于点H,
∴∠B'HG=∠DCH+∠CDH=90°+∠CDH>90°,
∴如果△B′HG是等腰三角形,则只能是∠B'HG为顶角,B'H=GH,
∴∠B'=∠B'GH,
由对顶角相等得:∠AGE=∠B'GH,
∴∠AGE=∠B',
由折叠的性质得:∠B=∠B',
∴∠AGE=∠B,
∵在△ABC中,∠ACB=90°,AC=6,BC=8,CD=2,
∴∠A+∠B=90°,,BD=BC﹣CD=6,
∴∠A+∠AGE=90°,
∴∠AEG=90°,即B'E⊥AB,
由折叠的性质得:B'E=BE,B'D=BD=6,
设B'E=BE=x(0<x<10),则AE=AB﹣BE=10﹣x,
在△AEG 和△ACB中,
,
∴△AEG∽△ACB,
∴,即,
解得:,EG=,
∴,,
∵B'H=GH,HF⊥B'E,
∴,
又∵B'E⊥AB,HF⊥B'E,
∴AB∥HF,
∴△HFG∽△AEG,
∴,即,
解得,
∴,CH=HG﹣CG=,
在Rt△CDH中,CH2+CD2=HD2,即,
解得(不符合题意,舍去),
即,
故答案为:.
【点评】本题考查了折叠的性质、相似三角形的判定与性质、勾股定理、一元二次方程的应用、等腰三角形的性质等知识,熟练掌握相似三角形的判定与性质是解题关键.
三.解答题(共5小题)
16.(2025 雁塔区校级一模)如图所示,在边长为1的小正方形网格中,△AOB的顶点都在格点上.
(1)B点关于y轴的对称点的坐标为 (﹣3,2) ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)条件下,点A1的坐标为 (﹣2,3) ;请求出△A1O1B1的面积.
【考点】作图﹣轴对称变换;作图﹣平移变换.
【答案】见试题解答内容
【分析】(1)首先根据坐标系确定B点坐标,再根据关于y轴的对称点的坐标横坐标相反,纵坐标不变可得答案;
(2)首先确定A、B、O三点向左平移3个单位长度后的对应点位置,再连接即可;
(3)根据坐标系写出点A1的坐标,再利用正方形的面积减去周围多余三角形的面积可得答案.
【解答】解:(1)B点关于y轴的对称点的坐标为(﹣3,2),
故答案为:(﹣3,2);
(2)如图所示:
(3)点A1的坐标为(﹣2,3),
△A1O1B1的面积:3×3﹣×3×1﹣×1×2﹣×2×3=3.5.
故答案为:(﹣2,3).
【点评】此题主要考查了作图﹣﹣平移变换,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
17.(2025 南山区模拟)如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣1).
(1)若△ABO与△A1B1O关于y轴的对称,则A1、B1的坐标分别是 (3,2),(4,﹣1) ;
(2)请仅用无刻度直尺作图,保留作图痕迹,不写作法.
①在图1中,找一格点P,使得∠APO=45°;
②在图2中,作出△ABO的高AQ.
【考点】作图﹣轴对称变换.
【专题】作图题;几何直观.
【答案】(1)(2)作图见解析部分.
【分析】(1)利用轴对称的性质分别作出A,B的对应点A1,B1即可;
(2)①构造等腰直角三角形解决问题即可;
②取格点M,N,连接MN交网格线于J,连接AJ延长AJ交OB于点Q,线段AQ即为所求.
【解答】解:(1)如图,△A1B1O即为所求,则A1、B1的坐标分别(3,2),(4,﹣1);
(2)①如图1在,点P即为所求(答案不唯一,(2,2),(0,﹣1)也满足条件);
②如图2中,线段AQ即为所求.
【点评】本题考查作图﹣轴对称变换,等腰直角三角形的性质等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型
18.(2024 南宁一模)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,1),B(3,4),C(4,2).
(1)在图中画出△ABC关于x轴对称的△A1B1C1;
(2)通过平移,使C1移动到原点O的位置,画出平移后的△A2B2C2.
(3)在△ABC中有一点P(m,n),则经过以上两次变换后点P的对应点P2的坐标为 (m﹣4,﹣n+2) .
【考点】作图﹣轴对称变换;作图﹣平移变换.
【专题】作图题;几何直观.
【答案】见试题解答内容
【分析】(1)依据轴对称的性质,即可得到△ABC关于x轴对称的△A1B1C1;
(2)依据C1移动到原点O的位置,即可得到平移的方向和距离,进而得到平移后的△A2B2C2.
(3)依据轴对称的性质以及平移的性质,即可得到两次变换后点P的对应点P2的坐标.
【解答】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)点P(m,n)经过第一次变换后的点P1的坐标为(m,﹣n),经过第二次变换后的对应点P2的坐标为(m﹣4,﹣n+2).
故答案为:(m﹣4,﹣n+2).
【点评】本题考查了利用平移变换和轴对称变换作图,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.
19.(2024 香坊区校级四模)如图是4×4的正方形网格,请仅用无刻度尺的直尺按要求完成以下作图.
(1)在图1中作四边形ABCD,使点C,D在格点上,并且四边形ABCD为轴对称图形.(画出一种即可)
(2)在图2中的线段AB上作点Q,使PQ最短.(用实线保留作图痕迹)
【考点】作图﹣轴对称变换.
【专题】作图题;平移、旋转与对称;几何直观;应用意识.
【答案】(1)见解答.
(2)见解答.
【分析】(1)根据轴对称图形的定义画图即可.
(2)结合垂线段最短,过点P作AB的垂线,交AB于点Q,则点Q即为所求.
【解答】解:(1)如图1,四边形ABCD即为所求.
(2)如图2,过点P作AB的垂线,交AB于点Q,
则点Q即为所求.
【点评】本题考查作图﹣轴对称变换、垂线段最短,熟练掌握轴对称图形的定义、垂线段最短是解答本题的关键.
20.(2024 丰台区二模)如图,在等边△ABC中,过点A在AB的右侧作射线AP,设∠BAP=α(60°<α<90°),点B与点E关于直线AP对称,连接AE,BE,CE,且BE,CE分别交射线AP于点D,F.
(1)依题意补全图形;
(2)求∠AFE的大小;
(3)用等式表示线段AF,CF,DF之间的数量关系,并证明.
【考点】作图﹣轴对称变换;等边三角形的性质.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2)60°;
(3)AF+FC=2DF.证明见解析.
【分析】(1)根据要求画出图形;
(2)利用圆周角定理求解;
(3)结论:AF+CF=2DF.连接BF,在N=BF上截取一点T,使得FC=FT.证明△BCT≌△ACF,推出BT=AF,再证明BF=2DF,可得结论.
【解答】解:(1)图形如图所示:
(2)由题意点A是△BEC的外接圆的圆心,
∴∠BEC=∠BAC,
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠BEC=30°,
∵B,E关于AP对称,
∴∠EDF=90°,
∴∠AFE=90°﹣30°=60°;
(3)结论:AF+CF=2DF.
理由:连接BF,在N=BF上截取一点T,使得FC=FT.
∵∠AFE=60°,
∴∠AFC=120°,
∵△ABC是等边三角形,
∴∠ABC=60°,AC=BC,
∴∠ABC+∠AFC=180°,
∴A,B,C,F四点共圆,
∴∠BFC=∠BAC=60°,
∴△FCT是等边三角形,
∴CT=CF,∠ECT=60°,
∵∠ACB=∠FCE=60°,
∴∠BCT=∠ACF,
∵CB=CA,CT=CF,
∴△BCT≌△ACF(SAS),
∴BT=AF,
∴AF+CF=BT+FT=BF,
∵B,E关于AP对称,
∴BF=EF,
∴∠FBD=∠FED=30°,
∵∠BDF=90°,
∴BF=2DF,
∴AF+FC=2DF.
【点评】本题考查作图﹣轴对称变换,等边三角形的性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2025 雁塔区校级模拟)在刚刚过去的第33届夏季奥运会中,中国健儿创造了新的境外参加奥运会的最佳成绩.在以下给出的运动图标中,属于轴对称图形的是( )
A. B.
C. D.
2.(2025 安阳模拟)如图,将一个正方形纸片沿图中虚线剪成四部分,恰能拼成一个没有缝隙且不重叠的等腰三角形,则这个正方形的边长与等腰三角形的底边长的比为( )
A. B. C. D.
3.(2025 河北模拟)如图, ABCD中,AB=5,AD=8,将 ABCD沿对角线BD折叠,使点A落在平面上A′处.若A'C=5,则BD长为( )
A.8 B. C.7.8 D.
4.(2025 碑林区校级一模)如图,正方形ABCD的边长为6,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若点E恰好是BC的中点,则线段CH的长为( )
A. B. C.3 D.
5.(2024 拱墅区一模)在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则( )
A.a=2,b=﹣3 B.a=2,b=3 C.a=﹣2,b=﹣3 D.a=﹣2,b=3
6.(2024 山西模拟)如图,将一张圆形纸片对折三次后,沿图④中的虚线AB剪下(点A和B为半径的中点),得到两部分,去掉有圆弧的部分,剩余部分展开后得到的平面图形的内角和为( )
A.360° B.720° C.1080° D.1440°
7.(2024 桥西区模拟)如图,已知AD∥BC,AB⊥BC,AB=6,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点P处,过点P作BC的垂线,分别交AD,BC于M,N两点.
①当点P为MN的中点时,NE=;
②当点P为MN的三等分点时,NE=或;
③当NP=9时,∠BAP=120°.
以下选项正确的为( )
A.①② B.①③ C.②③ D.①②③
8.(2024 凉州区三模)如图,在长方形ABCD中,点E是CD上一点,连接AE,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.若AB=8,CE=3,则折痕AE的长度为( )
A. B.10 C. D.15
9.(2024 武汉模拟)对于平面直角坐标系xOy中的任意线段MN,给出如下定义:线段MN上各点到x轴距离的最大值,叫做线段MN的“轴距”,记作dMN.例如,如图,点M(﹣2,﹣3),N(4,1),则线段MN的“轴距”为3,记作dMN=3.已知点E(﹣1,m),F(2,m+2),线段EF关于直线y=2的对称线段为GH.若dGH=3,则m的值为( )
A.1或7 B.5或﹣1 C.7或﹣1 D.1或5
10.(2024 邯山区校级三模)①~⑥是三个三角形的碎片,若组合其中的两个,恰能拼成一个轴对称图形,则应选择( )
A.①⑥ B.②④ C.③⑤ D.④⑥
二.填空题(共5小题)
11.(2025 汕头模拟)如图,在直角三角形ABC中,∠C=90°,∠BAC=60°,AC=6,点D是BC边上的一点(不与B、C重合),连接AD,将△ACD沿AD折叠,使点C落在点E处,当△BDE是直角三角形时,CD的长为 .
12.(2025 登封市一模)如图,在矩形ABCD中,AB=4,BC=8,点E是射线BC上一点,,连接AE,将△ABE沿AE翻折,得到△AFE,延长AF,交CD的延长线于点M,则DM= .
13.(2025 崇明区一模)四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=12,AD=8,将AB沿过点A的一条直线折叠,点B的对称点落在四边形ABCD的对角线上,折痕交边BC于点P(点P不与点B重合),那么PC长为 .
14.(2025 虹口区一模)如图,在Rt△ABC中,∠ABC=90°,AC=5,tanC=2,D是AC上的动点,将△BCD沿BD翻折,如果点C落到△ABD内(不包括边),那么CD的取值范围是 .
15.(2025 普陀区一模)△ABC中,∠ACB=90°,AC=6,BC=8,点D在边BC上,CD=2,如图所示.点E在边AB上,将△BDE沿着DE翻折得△B′DE,其中点B与点B'对应,B′E交边AC于点G,B′D交AC的延长线于点H.如果△B′HG是等腰三角形,那么BE= .
三.解答题(共5小题)
16.(2025 雁塔区校级一模)如图所示,在边长为1的小正方形网格中,△AOB的顶点都在格点上.
(1)B点关于y轴的对称点的坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)条件下,点A1的坐标为 ;请求出△A1O1B1的面积.
17.(2025 南山区模拟)如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣1).
(1)若△ABO与△A1B1O关于y轴的对称,则A1、B1的坐标分别是 ;
(2)请仅用无刻度直尺作图,保留作图痕迹,不写作法.
①在图1中,找一格点P,使得∠APO=45°;
②在图2中,作出△ABO的高AQ.
18.(2024 南宁一模)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,1),B(3,4),C(4,2).
(1)在图中画出△ABC关于x轴对称的△A1B1C1;
(2)通过平移,使C1移动到原点O的位置,画出平移后的△A2B2C2.
(3)在△ABC中有一点P(m,n),则经过以上两次变换后点P的对应点P2的坐标为 .
19.(2024 香坊区校级四模)如图是4×4的正方形网格,请仅用无刻度尺的直尺按要求完成以下作图.
(1)在图1中作四边形ABCD,使点C,D在格点上,并且四边形ABCD为轴对称图形.(画出一种即可)
(2)在图2中的线段AB上作点Q,使PQ最短.(用实线保留作图痕迹)
20.(2024 丰台区二模)如图,在等边△ABC中,过点A在AB的右侧作射线AP,设∠BAP=α(60°<α<90°),点B与点E关于直线AP对称,连接AE,BE,CE,且BE,CE分别交射线AP于点D,F.
(1)依题意补全图形;
(2)求∠AFE的大小;
(3)用等式表示线段AF,CF,DF之间的数量关系,并证明.
2025年中考数学二轮复习考前预测:图形的对称
参考答案与试题解析
一.选择题(共10小题)
1.(2025 雁塔区校级模拟)在刚刚过去的第33届夏季奥运会中,中国健儿创造了新的境外参加奥运会的最佳成绩.在以下给出的运动图标中,属于轴对称图形的是( )
A. B.
C. D.
【考点】轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】B
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:选项A、C、D的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项B的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.(2025 安阳模拟)如图,将一个正方形纸片沿图中虚线剪成四部分,恰能拼成一个没有缝隙且不重叠的等腰三角形,则这个正方形的边长与等腰三角形的底边长的比为( )
A. B. C. D.
【考点】图形的剪拼;等腰三角形的判定与性质;正方形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;推理能力.
【答案】C
【分析】如图,等腰三角形纸片沿图中虚线剪成四块图形,能拼成一个没有缝隙的正方形和矩形,根据题意得(a+b)2=b(b+a+b),设a=1,求出,进而求出正方形的边长与等腰三角形的底边长的比.
【解答】解:如图,等腰三角形纸片沿图中虚线剪成四块图形,能拼成一个没有缝隙的正方形和矩形,
设a=1,
根据题意,得(a+b)2=b(b+a+b),
解得,(负值舍去),
∴正方形的边长与等腰三角形的底边长的比为:
.
故选:C.
【点评】本题主要考查一元二次方程与图形有关的应用,解此题的关键在于将等腰三角形拆解拼成另一个没有缝隙的矩形,再利用面积相等得到相关边的长度关系.
3.(2025 河北模拟)如图, ABCD中,AB=5,AD=8,将 ABCD沿对角线BD折叠,使点A落在平面上A′处.若A'C=5,则BD长为( )
A.8 B. C.7.8 D.
【考点】翻折变换(折叠问题);勾股定理;平行四边形的性质;矩形的判定与性质.
【答案】C
【分析】由平行四边形和折叠得到AB=A′B=CD=5,AD=A′D=BC=8,∠ADB=∠A′DB=∠CBD,过C作CF⊥BD于F,过A′作A′E⊥BD于E,再证明△BCF≌△DA′E(AAS),得到A′E=CF,DE=BF,即可得到DF=BE,四边形A′EFC是矩形,A′C=EF=5,设DF=BE=x,则BF=EF+BE=5+x,BD=DF+BF=5+2x,再在Rt△BCF和Rt△DCF中,利用勾股定理得到CF2=BC2﹣BF2=DC2﹣DF2,代入列方程求解即可.
【解答】解:过C作CF⊥BD于F,过A′作A′E⊥BD于E,则∠A′EB=∠A′ED=∠CFB=∠CFD=90°,
由题意可得:AB=CD=5,AD=BC=8,AD∥BC,
∴∠ADB=∠CBD,
∵由折叠的性质可得:
∴AB=A′B=5,AD=A′D=8,∠ADB=∠A′DB,
∴AB=A′B=CD=5,AD=A′D=BC=8,∠ADB=∠A′DB=∠CBD,
∵∠A′ED=∠CFB=90°,A′D=BC=8,∠A′DB=∠CBD,
∴△BCF≌△DA′E(AAS),
∴A′E=CF,DE=BF,
∴DE﹣EF=BF﹣EF,
即DF=BE,
∵∠A′ED=∠CFB=90°,
∴A′E∥CF,
∵A′E=CF,
∴四边形A′EFC是矩形,
∴A′C=EF=5,
设DF=BE=x,则BF=EF+BE=5+x,BD=DF+BF=5+2x,
∴CF2=BC2﹣BF2=82﹣(5+x)2,
∴CF2=DC2﹣DF2=52﹣x2,
∴82﹣(5+x)2=52﹣x2,
∴x=1.4,
∴BD=5+2x=7.8.
故选:C.
【点评】本题考查平行四边形的性质,矩形的判定与性质,折叠的性质,勾股定理,根据题意,作出辅助线,综合运用这些知识点是解题关键.
4.(2025 碑林区校级一模)如图,正方形ABCD的边长为6,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若点E恰好是BC的中点,则线段CH的长为( )
A. B. C.3 D.
【考点】翻折变换(折叠问题);正方形的性质.
【专题】平移、旋转与对称.
【答案】D
【分析】根据折叠可得DH=EH,在直角△CEH中,设CH=x,则DH=EH=6﹣x,根据E是BC的中点,可得CE=3,可以根据勾股定理列出方程,从而解出CH的长.
【解答】解:设CH=x,则DH=EH=6﹣x,
∵点E恰好是BC的中点,BC=6,
∴CE=BC=3,
∵在Rt△ECH中,EH2=EC2+CH2,
∴(6﹣x)2=32+x2,
解得:x=,
即CH=.
故选:D.
【点评】本题主要考查正方形的性质以及翻折变换,折叠问题其实质是轴对称变换.在直角三角形中,利用勾股定理列出方程进行求解是解决本题的关键.
5.(2024 拱墅区一模)在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则( )
A.a=2,b=﹣3 B.a=2,b=3 C.a=﹣2,b=﹣3 D.a=﹣2,b=3
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】C
【分析】根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”即可求出a、b的值.
【解答】解:在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则a=﹣2,b=﹣3.
故选:C.
【点评】本题考查了关于y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于y轴对称的点,纵坐标相同,横坐标互为相反数.
6.(2024 山西模拟)如图,将一张圆形纸片对折三次后,沿图④中的虚线AB剪下(点A和B为半径的中点),得到两部分,去掉有圆弧的部分,剩余部分展开后得到的平面图形的内角和为( )
A.360° B.720° C.1080° D.1440°
【考点】剪纸问题.
【专题】多边形与平行四边形;运算能力.
【答案】C
【分析】由题意得出剩余部分展开后得到的平面图形是正八边形,再根据多边形的内角和公式计算即可得出答案.
【解答】解:将一张圆形纸片对折三次后,沿图④中的虚线AB剪下(点A和B为半径的中点),得到两部分,去掉有圆弧的部分,剩余部分展开后得到的平面图形是正八边形,
∴剩余部分展开后得到的平面图形的内角和为(8﹣2)×180°=1080°,
故选:C.
【点评】本题考查了多边形的内角和,解题的关键是掌握相关知识的灵活运用.
7.(2024 桥西区模拟)如图,已知AD∥BC,AB⊥BC,AB=6,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点P处,过点P作BC的垂线,分别交AD,BC于M,N两点.
①当点P为MN的中点时,NE=;
②当点P为MN的三等分点时,NE=或;
③当NP=9时,∠BAP=120°.
以下选项正确的为( )
A.①② B.①③ C.②③ D.①②③
【考点】翻折变换(折叠问题);平行线的性质.
【专题】线段、角、相交线与平行线;平移、旋转与对称;运算能力;推理能力.
【答案】B
【分析】由AD∥BC,AB⊥BC,证明∠B=∠DAB=90°,而MN⊥BC于点N,则∠MNB=90°,可证明四边形ABNM是矩形,所以∠AMN=90°,MN=AB=6,可证明∠EPN=∠PAM,则=tan∠EPN=tan∠PAM=,由折叠得AP=AB=6,当点P为MN的中点时,则PM=PN=3,所以AM=3,求得NE==,可判断①正确;当点P为MN的三等分点,且PM=MN=2,则PN=4,所以AM=4,求得NE==;当点P为MN的三等分点,且PM=MN=4,则PN=2,所以AM=2,求得NE==,可判断②错误;若PN=9,则PM=PN﹣MN=3,所以sin∠PAM==,则∠PAM=30°,求得∠BAP=120°,可判断③正确,于是得到问题的答案.
【解答】解:∵AD∥BC,AB⊥BC,
∴∠B=90°,
∴∠DAB=180°﹣∠B=90°,
∵MN⊥BC于点N,交AD于点M,
∴∠MNB=90°,
∴四边形ABNM是矩形,
∴∠AMN=90°,MN=AB=6,
∴∠EPN=∠PAM=90°﹣∠APM,
∴=tan∠EPN=tan∠PAM=,
由折叠得AP=AB=6,
如图1,点P为MN的中点,则PM=PN=MN=3,
∴AM===3,
∴NE===,
故①正确;
如图2,点P为MN的三等分点,且PM=MN=2,则PN=MN=4,
∴AM===4,
∴NE===;
如图3,点P为MN的三等分点,且PM=MN=4,则PN=MN=2,
∴AM===2,
∴NE===,
∴NE=或,
故②错误;
如图4,PN=9,则PM=PN﹣MN=9﹣6=3,
∵∠AMP=∠MNB=90°,
∴sin∠PAM===,
∴∠PAM=30°,
∴∠BAP=∠DAB+∠PAM=90°+30°=120°,
故③正确,
故选:B.
【点评】此题重点考查平行线的性质、轴对称的性质、矩形的判定与性质、同角的余角相等、勾股定理、锐角三角函数与解直角三角形等知识,证明∠EPN=∠PAM并且推导出=是解题的关键.
8.(2024 凉州区三模)如图,在长方形ABCD中,点E是CD上一点,连接AE,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.若AB=8,CE=3,则折痕AE的长度为( )
A. B.10 C. D.15
【考点】翻折变换(折叠问题);矩形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;几何直观.
【答案】C
【分析】由矩形的性质得出CD=AB=8,AD=BC,由折叠的性质得AF=AD,EF=DE=CD﹣CE=5,在Rt△CEF中,由勾股定理得CF==4,设BC=AD=AF=x,则BF=x﹣4,在Rt△ABF中,由勾股定理解出方程,即可求出AE得到答案.
【解答】解:∵四边形ABCD是矩形,
∴CD=AB=8,AD=BC,∠C=∠B=90°,
由折叠的性质得:AF=AD,EF=DE=CD﹣CE=8﹣3=5,
在Rt△CEF中,由勾股定理得:CF==4,
设BC=AD=AF=x,则BF=x﹣4,
在Rt△ABF中,由勾股定理得:82+(x﹣4)2=x2,
解得:x=10,
∴AD=10,
在Rt△ADE中,
AE===5,
故选:C.
【点评】本题考查了翻折变换的性质、矩形的性质、直角三角形的性质、勾股定理等知识;熟练掌握翻折变换和矩形的性质,由勾股定理得出方程是解题的关键.
9.(2024 武汉模拟)对于平面直角坐标系xOy中的任意线段MN,给出如下定义:线段MN上各点到x轴距离的最大值,叫做线段MN的“轴距”,记作dMN.例如,如图,点M(﹣2,﹣3),N(4,1),则线段MN的“轴距”为3,记作dMN=3.已知点E(﹣1,m),F(2,m+2),线段EF关于直线y=2的对称线段为GH.若dGH=3,则m的值为( )
A.1或7 B.5或﹣1 C.7或﹣1 D.1或5
【考点】坐标与图形变化﹣对称.
【专题】平面直角坐标系;推理能力.
【答案】D
【分析】先求出G、H的坐标,然后根据轴距的定义,构建方程.
【解答】解:∵点E(﹣1,m),F(2,m+2),
∴E,F关于直线y=2的对称点G(﹣1,﹣m+4),H(2,﹣m+2),
当|4﹣m|≥|2﹣m|时,dGH=3,
∴|4﹣m|=3,
∴m=1或=7,
当|4﹣m|<2﹣m|时,dGH=3,
∴|2﹣m|=3,
∴m=﹣1或=5,
综上所述m=1或=5,
故选:D.
【点评】考查了轴坐标与图形变化﹣对称,线段PQ的“轴距”的定义等知识,解题的关键是理解新定义,属于中考常考题型.
10.(2024 邯山区校级三模)①~⑥是三个三角形的碎片,若组合其中的两个,恰能拼成一个轴对称图形,则应选择( )
A.①⑥ B.②④ C.③⑤ D.④⑥
【考点】利用轴对称设计图案.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】根据三角形内角和是180°且利用图形已知的两个角的度数分别求出另一个角的度数,然后利用等腰三角形定义及等腰三角形是轴对称图形判断即可
【解答】解:∵②180°﹣(30°+75°)=75°,④图形一个角是75°,
∴②和④可以组成一个三角形,且这个三角形是等腰三角形,是轴对称图形,
∵⑤180°﹣(30°+35°)=115°,③图形一个角是115°,
∴③和⑤可以组成一个三角形,这个三角形三个角都不相等,故不是轴对称图形,
∵180°﹣(90°+63°)=27°,①图形一个角是27°,
∴①和⑥可以组成一个三角形,这个三角形三个角都不相等,故不是轴对称图形.
故选:B.
【点评】本题考查了三角形内角和和轴对称图形,熟练掌握三角形内角和定理和轴对称图形的定义是解题的关键;
二.填空题(共5小题)
11.(2025 汕头模拟)如图,在直角三角形ABC中,∠C=90°,∠BAC=60°,AC=6,点D是BC边上的一点(不与B、C重合),连接AD,将△ACD沿AD折叠,使点C落在点E处,当△BDE是直角三角形时,CD的长为 6或2 .
【考点】翻折变换(折叠问题);含30度角的直角三角形;勾股定理.
【专题】平移、旋转与对称;运算能力;推理能力.
【答案】见试题解答内容
【分析】根据勾股定理得到BC==6,根据已知条件得到当△BDE是直角三角形时,∠BDE=90°或∠BED=90°,①当∠BDE=90°时,则∠CDE=90°,根据折叠的性质得到∠ADC=∠ADE=45°,于是得到CD=AC=6,②当∠BED=90°时,根据折叠的性质得到∠AED=∠C=90°,∠CAD=∠EAD,AC=AE,推出点E在AB上,根据勾股定理即可得到结论.
【解答】解:在Rt△ABC中,∠BAC=60°,AC=6,
∴∠ABC=30°,
∴AB=2AC=12,
∴BC==6,
∵点D是BC边上的一点,
∴∠DBE≠90°,
∴当△BDE是直角三角形时,∠BDE=90°或∠BED=90°,
①当∠BDE=90°时,则∠CDE=90°,
∵将△ACD沿AD折叠,使点C落在点E处,
∴∠ADC=∠ADE=45°,
∴CD=AC=6,
②当∠BED=90°时,
∵将△ACD沿AD折叠,使点C落在点E处,
∴∠AED=∠C=90°,∠CAD=∠EAD,AC=AE,
∴∠AED+∠BED=180°,
∴点E在AB上,如图,
∴AE=AC=6,BE=AB﹣AE=6,∠CAD=∠BAD,
∴CD=DE,
∵DE2+BE2=BD2,
∴CD2+62=(6﹣CD)2,
∴CD=2,
综上所述,CD的长为 6或2,
故答案为:6或2.
【点评】本题考查了翻折变换(折叠问题),勾股定理,直角三角形的性质,熟练掌握折叠的性质是解题的关键.
12.(2025 登封市一模)如图,在矩形ABCD中,AB=4,BC=8,点E是射线BC上一点,,连接AE,将△ABE沿AE翻折,得到△AFE,延长AF,交CD的延长线于点M,则DM= 或 .
【考点】翻折变换(折叠问题);矩形的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】或.
【分析】情形①如图当点E在线段BC上时,情形②如图当点E在线段BC的延长线上时分别求解即可解决问题;
【解答】解:情形①如图当点E在线段BC上时,
∵BC=8,BE=3EC,
∴EC=2,EB=EF=6,∵四边形ABCD是矩形,
∴∠ADC=∠ADM=90°,AD∥BC,
∴∠DAE=∠AEB=∠AEG,
∴AG=EG,设AG=EG=x,
在Rt△AFG中,∠AFG=90°,AF=AB=4,FG=6﹣x,
∴x2=42+(6﹣x)2,
∴x=,
∴FG=EF﹣EG=,
∵tan∠DAM==,
∴=,
∴DM=,
情形②如图当点E在线段BC的延长线上时,
∵BC=8,BE=3EC,
∴EC=4,EB=EF=12,
∵四边形ABCD是矩形,
∴∠ADC=∠ADG=90°,AD∥BC,
∴∠DAE=∠AEB=∠AEG,
∴AG=EG,设AG=EG=x,
在Rt△AFG中,∠AFG=90°,AF=AB=4,FG=12﹣x,
∴x2=42+(12﹣x)2,
∴x=,
∴FG=EF﹣EG=,
∵tan∠DAM==,
∴=,
∴DM=,
故答案为:或.
【点评】本题考查翻折变换(折叠问题)、矩形的性质、相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考填空题中的压轴题.
13.(2025 崇明区一模)四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=12,AD=8,将AB沿过点A的一条直线折叠,点B的对称点落在四边形ABCD的对角线上,折痕交边BC于点P(点P不与点B重合),那么PC长为 或 .
【考点】翻折变换(折叠问题);平行线的性质.
【专题】平移、旋转与对称;推理能力.
【答案】或.
【分析】分点B的对称点B'落在对角线AC上和落在对角线BD上两种情况,分别画出图形解答即可求解.
【解答】解:如图,当点B的对称点B'落在对角线AC上时,
由折叠可得,AB'=AB=5,PB'=PB,∠AB'P=∠ABP=90°,
∴∠CB'P=90°,
∵∠ABC=90°,AB=5,BC=12,
∴,
∴B'C=AC﹣AB=13﹣5=8,
设P'B=PB=x,则PC=12﹣x,
∵PB'2+B'C2=PC2,
∴x2+82=(12﹣x)2,
解得=,
∴,
∴;
如图,当点B的对称点B'落在对角线BD上时,设AP与BD相交于点G,
由折叠可得,AP⊥BD,
∴∠AGB=∠BGP=90°,
∵AD∥BC,∠ABC=90°,
∴∠BAD=180°﹣∠ABC=180°﹣90°=90°,
∴,
∵,
∴,
∴,
∴,
∵∠BAG+∠ABG=90°,∠PBG+∠ABG=90°,
∴∠PBG=∠BAG,
∵∠BGP=∠AGB=90°,
∴△BGP∽△AGB,
∴即,
∴,
∴;
综上,PC长为或,
故答案为:或.
【点评】本题考查的折叠的性质,勾股定理,相似三角形的判定和性质,运用分类讨论思想解答是解题的关键.
14.(2025 虹口区一模)如图,在Rt△ABC中,∠ABC=90°,AC=5,tanC=2,D是AC上的动点,将△BCD沿BD翻折,如果点C落到△ABD内(不包括边),那么CD的取值范围是 1<CD< .
【考点】翻折变换(折叠问题);解直角三角形.
【专题】等腰三角形与直角三角形;平移、旋转与对称;运算能力.
【答案】1<CD<.
【分析】由∠ABC=90°,tanC=2,AC=5,求出AB=2,BC=,设C的对应点为C',当C'在AC上时,求出CD=1;当C'在AB上时,过D作DH⊥AB于H,求出CD=,即可得1<CD<.
【解答】解:∵∠ABC=90°,tanC=2,
∴AB=2BC,
∵AC=5,
∴AB2+BC2=5,
∴AB=2,BC=,
设C的对应点为C',
当C'在AC上时,如图:
∵将△BCD沿BD翻折,
∴∠BDC=∠BDC'=90°,
∴tanC==2,即BD=2CD,
∵BD2+CD2=BC2,
∴(2CD)2+CD2=5,
∴CD=1;
当C'在AB上时,过D作DH⊥AB于H,如图:
∵将△BCD沿BD翻折,
∴BC=BC'=,∠CBD=∠C'BD=∠ABC=45°,CD=C'D,∠C=∠BC'D,
∴△BDH是等腰直角三角形,tan∠BC'D=2,
∴BH=DH,DH=2C'H,
设C'H=x,则DH=BH=2x,
∵C'H+BH=BC'=,
∴x+2x=,
解得x=,
∴C'H=,DH=,
∴C'D==,
∴CD=;
∵C'落到△ABD内(不包括边),
∴1<CD<;
故答案为:1<CD<.
【点评】本题考查直角三角形中的翻折问题,涉及解直角三角形,勾股定理等知识,解题的关键是求出临界点时CD的值.
15.(2025 普陀区一模)△ABC中,∠ACB=90°,AC=6,BC=8,点D在边BC上,CD=2,如图所示.点E在边AB上,将△BDE沿着DE翻折得△B′DE,其中点B与点B'对应,B′E交边AC于点G,B′D交AC的延长线于点H.如果△B′HG是等腰三角形,那么BE= .
【考点】翻折变换(折叠问题);等腰三角形的性质;勾股定理.
【专题】平移、旋转与对称;推理能力.
【答案】.
【分析】先画出图形,过点H作HF⊥B′E于点F,确定如果ΔB'HG是等腰三角形,则只能是B′H=GH,设B′E=BE=x(0<x<10),则AE=10﹣x,再证出△AEG∽△ACB,根据相似三角形的性质可得,,然后证出△HFG∽△AEG,根据相似三角形的性质可得,从而可得CH,HD的长,最后在Rt△CDH中,利用勾股定理求解即可得.
【解答】解:由题意,画出图形如下:过点H作HF⊥BE于点F,
∵∠ACB=90°,
∴∠DCH=90°,
∵B'E交边AC于点G,B'D交AC的延长线于点H,
∴∠B'HG=∠DCH+∠CDH=90°+∠CDH>90°,
∴如果△B′HG是等腰三角形,则只能是∠B'HG为顶角,B'H=GH,
∴∠B'=∠B'GH,
由对顶角相等得:∠AGE=∠B'GH,
∴∠AGE=∠B',
由折叠的性质得:∠B=∠B',
∴∠AGE=∠B,
∵在△ABC中,∠ACB=90°,AC=6,BC=8,CD=2,
∴∠A+∠B=90°,,BD=BC﹣CD=6,
∴∠A+∠AGE=90°,
∴∠AEG=90°,即B'E⊥AB,
由折叠的性质得:B'E=BE,B'D=BD=6,
设B'E=BE=x(0<x<10),则AE=AB﹣BE=10﹣x,
在△AEG 和△ACB中,
,
∴△AEG∽△ACB,
∴,即,
解得:,EG=,
∴,,
∵B'H=GH,HF⊥B'E,
∴,
又∵B'E⊥AB,HF⊥B'E,
∴AB∥HF,
∴△HFG∽△AEG,
∴,即,
解得,
∴,CH=HG﹣CG=,
在Rt△CDH中,CH2+CD2=HD2,即,
解得(不符合题意,舍去),
即,
故答案为:.
【点评】本题考查了折叠的性质、相似三角形的判定与性质、勾股定理、一元二次方程的应用、等腰三角形的性质等知识,熟练掌握相似三角形的判定与性质是解题关键.
三.解答题(共5小题)
16.(2025 雁塔区校级一模)如图所示,在边长为1的小正方形网格中,△AOB的顶点都在格点上.
(1)B点关于y轴的对称点的坐标为 (﹣3,2) ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)条件下,点A1的坐标为 (﹣2,3) ;请求出△A1O1B1的面积.
【考点】作图﹣轴对称变换;作图﹣平移变换.
【答案】见试题解答内容
【分析】(1)首先根据坐标系确定B点坐标,再根据关于y轴的对称点的坐标横坐标相反,纵坐标不变可得答案;
(2)首先确定A、B、O三点向左平移3个单位长度后的对应点位置,再连接即可;
(3)根据坐标系写出点A1的坐标,再利用正方形的面积减去周围多余三角形的面积可得答案.
【解答】解:(1)B点关于y轴的对称点的坐标为(﹣3,2),
故答案为:(﹣3,2);
(2)如图所示:
(3)点A1的坐标为(﹣2,3),
△A1O1B1的面积:3×3﹣×3×1﹣×1×2﹣×2×3=3.5.
故答案为:(﹣2,3).
【点评】此题主要考查了作图﹣﹣平移变换,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
17.(2025 南山区模拟)如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣1).
(1)若△ABO与△A1B1O关于y轴的对称,则A1、B1的坐标分别是 (3,2),(4,﹣1) ;
(2)请仅用无刻度直尺作图,保留作图痕迹,不写作法.
①在图1中,找一格点P,使得∠APO=45°;
②在图2中,作出△ABO的高AQ.
【考点】作图﹣轴对称变换.
【专题】作图题;几何直观.
【答案】(1)(2)作图见解析部分.
【分析】(1)利用轴对称的性质分别作出A,B的对应点A1,B1即可;
(2)①构造等腰直角三角形解决问题即可;
②取格点M,N,连接MN交网格线于J,连接AJ延长AJ交OB于点Q,线段AQ即为所求.
【解答】解:(1)如图,△A1B1O即为所求,则A1、B1的坐标分别(3,2),(4,﹣1);
(2)①如图1在,点P即为所求(答案不唯一,(2,2),(0,﹣1)也满足条件);
②如图2中,线段AQ即为所求.
【点评】本题考查作图﹣轴对称变换,等腰直角三角形的性质等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型
18.(2024 南宁一模)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,1),B(3,4),C(4,2).
(1)在图中画出△ABC关于x轴对称的△A1B1C1;
(2)通过平移,使C1移动到原点O的位置,画出平移后的△A2B2C2.
(3)在△ABC中有一点P(m,n),则经过以上两次变换后点P的对应点P2的坐标为 (m﹣4,﹣n+2) .
【考点】作图﹣轴对称变换;作图﹣平移变换.
【专题】作图题;几何直观.
【答案】见试题解答内容
【分析】(1)依据轴对称的性质,即可得到△ABC关于x轴对称的△A1B1C1;
(2)依据C1移动到原点O的位置,即可得到平移的方向和距离,进而得到平移后的△A2B2C2.
(3)依据轴对称的性质以及平移的性质,即可得到两次变换后点P的对应点P2的坐标.
【解答】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)点P(m,n)经过第一次变换后的点P1的坐标为(m,﹣n),经过第二次变换后的对应点P2的坐标为(m﹣4,﹣n+2).
故答案为:(m﹣4,﹣n+2).
【点评】本题考查了利用平移变换和轴对称变换作图,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.
19.(2024 香坊区校级四模)如图是4×4的正方形网格,请仅用无刻度尺的直尺按要求完成以下作图.
(1)在图1中作四边形ABCD,使点C,D在格点上,并且四边形ABCD为轴对称图形.(画出一种即可)
(2)在图2中的线段AB上作点Q,使PQ最短.(用实线保留作图痕迹)
【考点】作图﹣轴对称变换.
【专题】作图题;平移、旋转与对称;几何直观;应用意识.
【答案】(1)见解答.
(2)见解答.
【分析】(1)根据轴对称图形的定义画图即可.
(2)结合垂线段最短,过点P作AB的垂线,交AB于点Q,则点Q即为所求.
【解答】解:(1)如图1,四边形ABCD即为所求.
(2)如图2,过点P作AB的垂线,交AB于点Q,
则点Q即为所求.
【点评】本题考查作图﹣轴对称变换、垂线段最短,熟练掌握轴对称图形的定义、垂线段最短是解答本题的关键.
20.(2024 丰台区二模)如图,在等边△ABC中,过点A在AB的右侧作射线AP,设∠BAP=α(60°<α<90°),点B与点E关于直线AP对称,连接AE,BE,CE,且BE,CE分别交射线AP于点D,F.
(1)依题意补全图形;
(2)求∠AFE的大小;
(3)用等式表示线段AF,CF,DF之间的数量关系,并证明.
【考点】作图﹣轴对称变换;等边三角形的性质.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2)60°;
(3)AF+FC=2DF.证明见解析.
【分析】(1)根据要求画出图形;
(2)利用圆周角定理求解;
(3)结论:AF+CF=2DF.连接BF,在N=BF上截取一点T,使得FC=FT.证明△BCT≌△ACF,推出BT=AF,再证明BF=2DF,可得结论.
【解答】解:(1)图形如图所示:
(2)由题意点A是△BEC的外接圆的圆心,
∴∠BEC=∠BAC,
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠BEC=30°,
∵B,E关于AP对称,
∴∠EDF=90°,
∴∠AFE=90°﹣30°=60°;
(3)结论:AF+CF=2DF.
理由:连接BF,在N=BF上截取一点T,使得FC=FT.
∵∠AFE=60°,
∴∠AFC=120°,
∵△ABC是等边三角形,
∴∠ABC=60°,AC=BC,
∴∠ABC+∠AFC=180°,
∴A,B,C,F四点共圆,
∴∠BFC=∠BAC=60°,
∴△FCT是等边三角形,
∴CT=CF,∠ECT=60°,
∵∠ACB=∠FCE=60°,
∴∠BCT=∠ACF,
∵CB=CA,CT=CF,
∴△BCT≌△ACF(SAS),
∴BT=AF,
∴AF+CF=BT+FT=BF,
∵B,E关于AP对称,
∴BF=EF,
∴∠FBD=∠FED=30°,
∵∠BDF=90°,
∴BF=2DF,
∴AF+FC=2DF.
【点评】本题考查作图﹣轴对称变换,等边三角形的性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
21世纪教育网(www.21cnjy.com)
同课章节目录
