【中考押题卷】2025年中考数学二轮复习考前预测:图形的相似(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学二轮复习考前预测:图形的相似(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 12:18:39 | ||
图片预览


文档简介
2025年中考数学二轮复习考前预测:图形的相似
一.选择题(共10小题)
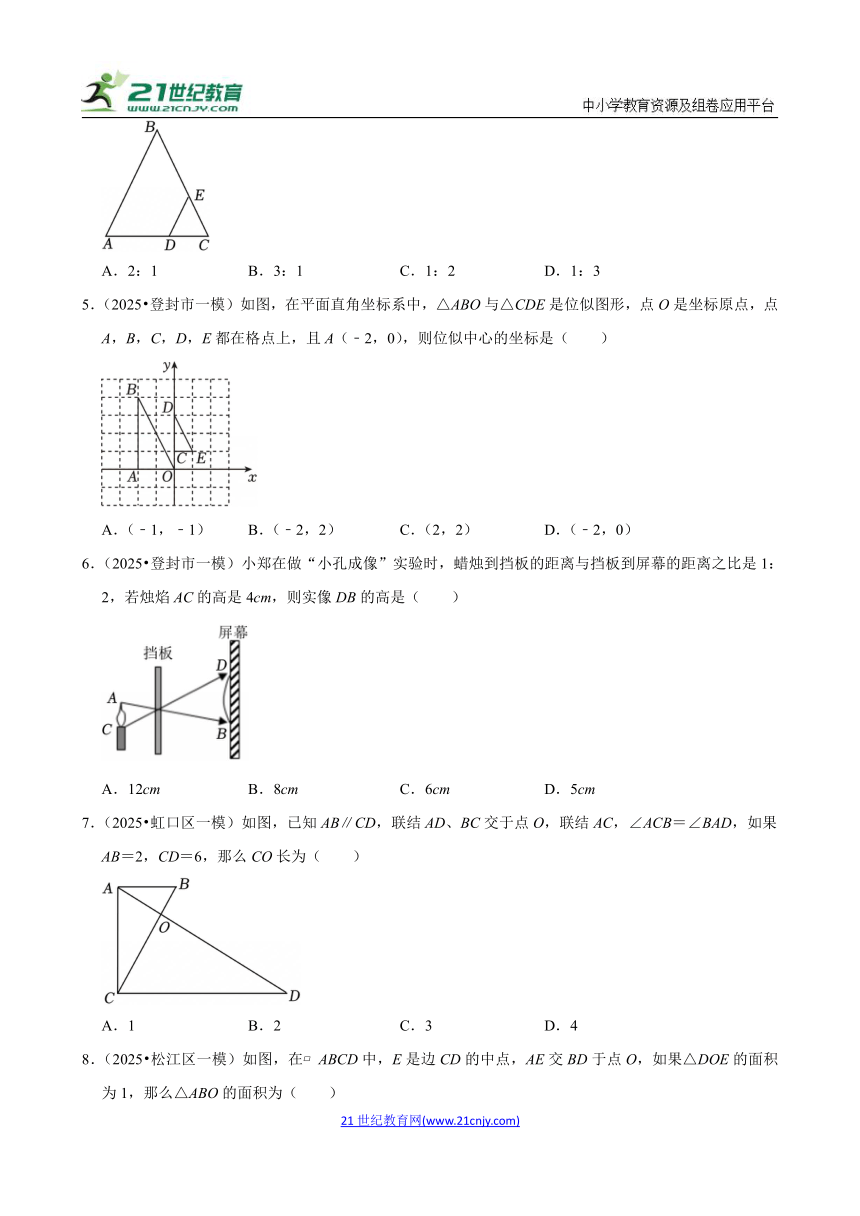
1.(2025 崇明区一模)如图,在三角形纸片ABC中,AB=6,AC=4,BC=8,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A. B.
C. D.
2.(2025 柳州模拟)如图,网格中每个小正方形的边长均为1,点A,B,C,D均在格点上,连接AD,BC交于点E,则S△ABE:S△DCE=( )
A.1:3 B.1:9 C.3:1 D.9:1
3.(2025 大渡口区模拟)如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA:AE=1:2,且四边形ABCD的周长为3,则四边形EFGH的周长为( )
A.6 B.9 C.12 D.27
4.(2025 江北区模拟)如图,点D、点E在△ABC的边上,且DE∥AB,AD:DC=2:1,则△ABC与△DEC的相似比为( )
A.2:1 B.3:1 C.1:2 D.1:3
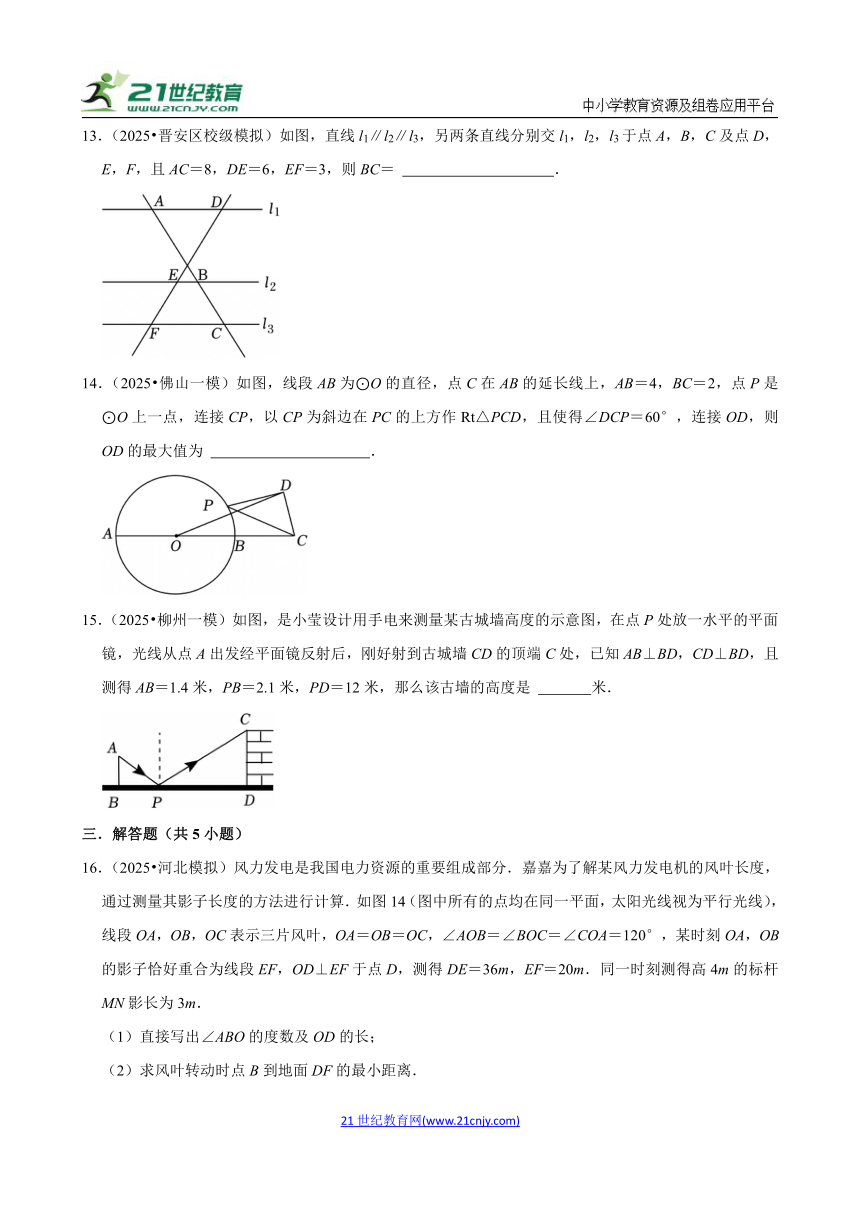
5.(2025 登封市一模)如图,在平面直角坐标系中,△ABO与△CDE是位似图形,点O是坐标原点,点A,B,C,D,E都在格点上,且A(﹣2,0),则位似中心的坐标是( )
A.(﹣1,﹣1) B.(﹣2,2) C.(2,2) D.(﹣2,0)
6.(2025 登封市一模)小郑在做“小孔成像”实验时,蜡烛到挡板的距离与挡板到屏幕的距离之比是1:2,若烛焰AC的高是4cm,则实像DB的高是( )
A.12cm B.8cm C.6cm D.5cm
7.(2025 虹口区一模)如图,已知AB∥CD,联结AD、BC交于点O,联结AC,∠ACB=∠BAD,如果AB=2,CD=6,那么CO长为( )
A.1 B.2 C.3 D.4
8.(2025 松江区一模)如图,在 ABCD中,E是边CD的中点,AE交BD于点O,如果△DOE的面积为1,那么△ABO的面积为( )
A.2 B.4 C.6 D.9
9.(2025 青浦区一模)如图,在△ABC中,AC=BC,∠C=36°,AD是△ABC的角平分线.是( )
A. B. C. D.
10.(2025 黄浦区一模)某学习小组研究问题“如图,已知D、E、F分别是△ABC的边BC、CA、AB的中点,求证:△DEF∽△ABC.”经过小组讨论得到以下方法,其中存在错误的是( )
A.可证,进而证得△DEF∽△ABC
B.可证∠B=∠FED,∠C=∠EFD,进而证得△DEF∽△ABC
C.可证∠B=∠FED,,进而证得△DEF∽△ABC
D.可证△FBD∽△DEF,△FBD∽△ABC,进而证得△DEF∽△ABC
二.填空题(共5小题)
11.(2025 永寿县校级一模)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD=1,AD=2,则BC的长为 .
12.(2025 安阳模拟)已知a,b,c使等式成立,则代数式的值是 .
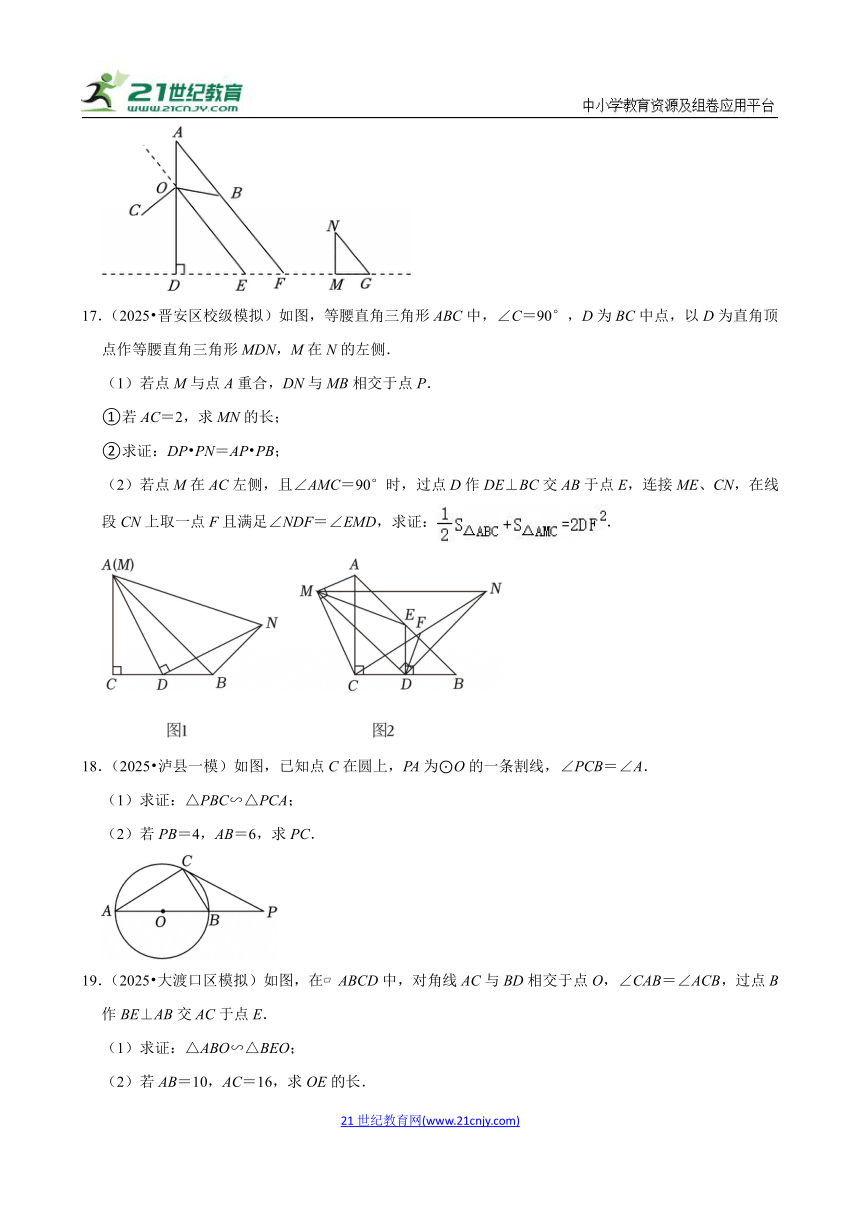
13.(2025 晋安区校级模拟)如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AC=8,DE=6,EF=3,则BC= .
14.(2025 佛山一模)如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使得∠DCP=60°,连接OD,则OD的最大值为 .
15.(2025 柳州一模)如图,是小莹设计用手电来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.4米,PB=2.1米,PD=12米,那么该古墙的高度是 米.
三.解答题(共5小题)
16.(2025 河北模拟)风力发电是我国电力资源的重要组成部分.嘉嘉为了解某风力发电机的风叶长度,通过测量其影子长度的方法进行计算.如图14(图中所有的点均在同一平面,太阳光线视为平行光线),线段OA,OB,OC表示三片风叶,OA=OB=OC,∠AOB=∠BOC=∠COA=120°,某时刻OA,OB的影子恰好重合为线段EF,OD⊥EF于点D,测得DE=36m,EF=20m.同一时刻测得高4m的标杆MN影长为3m.
(1)直接写出∠ABO的度数及OD的长;
(2)求风叶转动时点B到地面DF的最小距离.
17.(2025 晋安区校级模拟)如图,等腰直角三角形ABC中,∠C=90°,D为BC中点,以D为直角顶点作等腰直角三角形MDN,M在N的左侧.
(1)若点M与点A重合,DN与MB相交于点P.
①若AC=2,求MN的长;
②求证:DP PN=AP PB;
(2)若点M在AC左侧,且∠AMC=90°时,过点D作DE⊥BC交AB于点E,连接ME、CN,在线段CN上取一点F且满足∠NDF=∠EMD,求证:.
18.(2025 泸县一模)如图,已知点C在圆上,PA为⊙O的一条割线,∠PCB=∠A.
(1)求证:△PBC∽△PCA;
(2)若PB=4,AB=6,求PC.
19.(2025 大渡口区模拟)如图,在 ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:△ABO∽△BEO;
(2)若AB=10,AC=16,求OE的长.
20.(2025 茅箭区校级模拟)在Rt△ABC中,AC=1,∠C=90°,D为BC边上一动点,且(n为正整数),在直线BC上方作△ADE,使得△ADE∽△ACB.
(1)如图1,在点D运动过程中,△ACD与△ABE始终保持相似关系,请说明理由;
(2)如图2,若n=2,M为AB中点,当点E在射线CM上时,求CD的长;
(3)如图3,设AE的中点为P,求点D从点C运动到点B的过程中,点P运动的路径长(用含n的代数式表示).
2025年中考数学二轮复习考前预测:图形的相似
参考答案与试题解析
一.选择题(共10小题)
1.(2025 崇明区一模)如图,在三角形纸片ABC中,AB=6,AC=4,BC=8,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A. B.
C. D.
【考点】相似三角形的判定.
【专题】图形的相似;推理能力.
【答案】A
【分析】根据相似三角形的判定分别进行判断即可得出答案即可.
【解答】解:在三角形纸片ABC中,AB=6,BC=8,AC=4.
A、∵=,∠C=∠C,
故沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项符合题意;
B、∵≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项不符合题意;
C、∵≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项不符合题意;
D、∵≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项不符合题意;
故选:A.
【点评】本题考查了相似三角形的判定,掌握相似三角形的判定方法是解题的关键.
2.(2025 柳州模拟)如图,网格中每个小正方形的边长均为1,点A,B,C,D均在格点上,连接AD,BC交于点E,则S△ABE:S△DCE=( )
A.1:3 B.1:9 C.3:1 D.9:1
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】D
【分析】判定△ABE∽△DCE,由相似三角形面积的比等于相似比的平方,即可求解.
【解答】解:∵CD∥AB,
∴△ABE∽△DCE,
∴S△ABE:S△DCE=AB2:CD2,
∵AB=6,CD=2,
∴S△ABE:S△DCE=9:1.
故选:D.
【点评】本题考查相似三角形的判定与性质,关键是由△ABE∽△DCE,推出S△ABE:S△DCE=AB2:CD2.
3.(2025 大渡口区模拟)如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA:AE=1:2,且四边形ABCD的周长为3,则四边形EFGH的周长为( )
A.6 B.9 C.12 D.27
【考点】位似变换.
【专题】图形的相似;运算能力;推理能力.
【答案】B
【分析】根据位似图形的概念得到AD∥EH,根据相似三角形的性质解答即可.
【解答】解:∵四边形ABCD与四边形EFGH位似,
∴AD∥EH,
∴△OAD∽△OEH,
∴===,即四边形ABCD与四边形EFGH的相似比为,
∵四边形ABCD的周长为3,
∴四边形EFGH的周长为9,
故选:B.
【点评】本题考查的是位似图形的概念、相似三角形的判定和性质、相似多边形的性质,熟记相似多边形的周长比等于相似比是解题的关键.
4.(2025 江北区模拟)如图,点D、点E在△ABC的边上,且DE∥AB,AD:DC=2:1,则△ABC与△DEC的相似比为( )
A.2:1 B.3:1 C.1:2 D.1:3
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据相似三角形的判定与性质求解即可.
【解答】解:∵AD:DC=2:1,
∴AC:DC=3:1,
∵DE∥AB,
∴△CDE∽△CAB,
∴△ABC与△DEC的相似比==3:1,
故选:B.
【点评】本题考查了相似三角形的性质和判定的应用,熟记相似三角形的判定与性质是解题的关键.
5.(2025 登封市一模)如图,在平面直角坐标系中,△ABO与△CDE是位似图形,点O是坐标原点,点A,B,C,D,E都在格点上,且A(﹣2,0),则位似中心的坐标是( )
A.(﹣1,﹣1) B.(﹣2,2) C.(2,2) D.(﹣2,0)
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;几何直观.
【答案】C
【分析】连接AC,BD,OE,并分别延长,相交于点P,则△ABO与△CDE是以点P为位似中心的位似图形,即可得出答案.
【解答】解:如图,连接AC,BD,OE,并分别延长,相交于点P,
则△ABO与△CDE是以点P为位似中心的位似图形,
∴位似中心的坐标是(2,2).
故选:C.
【点评】本题考查位似变换、坐标与图形性质,熟练掌握位似的性质是解答本题的关键.
6.(2025 登封市一模)小郑在做“小孔成像”实验时,蜡烛到挡板的距离与挡板到屏幕的距离之比是1:2,若烛焰AC的高是4cm,则实像DB的高是( )
A.12cm B.8cm C.6cm D.5cm
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】B
【分析】根据AC∥DB证明△AOC∽△BOD,利用相似三角形的性质求解即可.
【解答】解:如图所示:AB、CD相交于点O,
∵AC是烛焰的高,DB是实像的高,
∴AC∥DB,
∴△AOC∽△BOD,
∵蜡烛到挡板距离与挡板到屏幕距离之比是1:2,AC=4cm,
∴=,
∴BD=8cm.
故选:B.
【点评】本题考查了相似三角形的应用,熟练掌握相似三角形的性质是解答本题的关键.
7.(2025 虹口区一模)如图,已知AB∥CD,联结AD、BC交于点O,联结AC,∠ACB=∠BAD,如果AB=2,CD=6,那么CO长为( )
A.1 B.2 C.3 D.4
【考点】相似三角形的判定与性质.
【专题】图形的相似;运算能力;推理能力.
【答案】C
【分析】由AB∥CD,证明△AOB∽△DOC,得==,则CO=3BO,所以CB=4BO,由∠ACB=∠BAD,∠B=∠B,证明△ACB∽△OAB,所以=,则CB BO=AB2=22=4,所以4BO2=4,求得BO=1,则CO=3,于是得到问题的答案.
【解答】解:∵AB∥CD,AB=2,CD=6,
∴△AOB∽△DOC,
∴===,
∴CO=3BO,
∴CB=BO+3BO=4BO,
∵∠ACB=∠BAD,∠B=∠B,
∴△ACB∽△OAB,
∴=,
∴CB BO=AB2=22=4,
∴4BO2=4,
解得BO=1或BO=﹣1(不符合题意,舍去),
∴CO=3,
故选:C.
【点评】此题重点考查相似三角形的判定与性质,证明△AOB∽△DOC及△ACB∽△OAB是解题的关键.
8.(2025 松江区一模)如图,在 ABCD中,E是边CD的中点,AE交BD于点O,如果△DOE的面积为1,那么△ABO的面积为( )
A.2 B.4 C.6 D.9
【考点】相似三角形的判定与性质;平行四边形的性质.
【专题】多边形与平行四边形;图形的相似;几何直观;推理能力.
【答案】B
【分析】根据平行四边形的性质求得△AOB~△EOD,根据相似三角形的面积比等于相似比的平方来求出S△AOB=4.
【解答】解:∵ ABCD中,E为CD边上的中点,
∴DE=CD=AB,AB∥CD,
∵AB∥CD,
∴∠ABO=∠EDO,∠OAB=∠OED,
∴△AOB∽△EOD,
∴===2,
∴==22=4,
∴S△AOB=4S△DOE=4,
故选:B.
【点评】本题考查了平行边形的性质,相似三角形的判定和性质,理解相似三角形的面积比等于相似比的平方是解答关键.
9.(2025 青浦区一模)如图,在△ABC中,AC=BC,∠C=36°,AD是△ABC的角平分线.是( )
A. B. C. D.
【考点】相似三角形的判定与性质.
【专题】等腰三角形与直角三角形;图形的相似;推理能力.
【答案】C
【分析】根据AC=BC,∠C=36°,求出∠B=∠BAC=72°,根据AD平分∠BAC可得∠BAD=∠CAD=36°,进而证得△ABD∽△CBA,根据相似三角形的性质证得结论.
【解答】解:∵AC=BC,∠C=36°,
∴∠B=∠BAC=72°,
∵AD平分∠BAC,
∠BAD=∠CAD=36°,
∴∠BAD=∠C=∠CAD=36°,
∴AD=CD,∠ADB=72°,
∴AB=AD,
∴AB=AD=CD,
∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴,
设BC=AC=a,BD=x,
则AD=CD=AB=a﹣x,
∴,
解得x=a(不符合题意,舍去)或x=a,
∴AB=a﹣x=a,
∴.
故选:C.
【点评】本题考查了相似三角形的性质,解题的关键掌握相似三角形的判定方法.
10.(2025 黄浦区一模)某学习小组研究问题“如图,已知D、E、F分别是△ABC的边BC、CA、AB的中点,求证:△DEF∽△ABC.”经过小组讨论得到以下方法,其中存在错误的是( )
A.可证,进而证得△DEF∽△ABC
B.可证∠B=∠FED,∠C=∠EFD,进而证得△DEF∽△ABC
C.可证∠B=∠FED,,进而证得△DEF∽△ABC
D.可证△FBD∽△DEF,△FBD∽△ABC,进而证得△DEF∽△ABC
【考点】相似三角形的判定;三角形中位线定理;相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】由D、E、F分别是△ABC的边BC、CA、AB的中点,得DE=AB,EF=BC,FD=AC,则===,所以△DEF∽△ABC,可判断A不符合题意;由DE∥BF,EF∥BD,证明四边形BDEF是平行四边形,则∠B=∠FED,同理∠C=∠EFD,则△DEF∽△ABC,可判断B不符合题意;由AB∥ED,证明△ABC∽△EDC,得=,而DC=EF,所以=,可知=不成立,所以由∠B=∠FED,=,不能证得△DEF∽△ABC,可判断C符合题意;由∠BFD=∠EDF,∠BDF=∠EFD,证明△FBD∽△DEF,由FD∥AC,证明△FBD∽△ABC,则△DEF∽△ABC,可判断D不符合题意,于是得到问题的答案.
【解答】解:∵D、E、F分别是△ABC的边BC、CA、AB的中点,
∴DE∥AB,且DE=AB,EF∥BC,且EF=BC,FD∥AC,且FD=AC,
∴===,
∴△DEF∽△ABC,
故A不符合题意;
∵DE∥BF,EF∥BD,
∴四边形BDEF是平行四边形,
∴∠B=∠FED,
同理四边形CDFE是平行四边形,
∴∠C=∠EFD,
∴△DEF∽△ABC,
故B不符合题意;
∵AB∥ED,
∴△ABC∽△EDC,
∴=,
∵DC=EF,
∴=,
∴=不成立,
∴由∠B=∠FED,=,不能证得△DEF∽△ABC,
故C符合题意;
∵DE∥AB,EF∥BC,
∴∠BFD=∠EDF,∠BDF=∠EFD,
∴△FBD∽△DEF,
∵FD∥AC,
∴△FBD∽△ABC,
∴△DEF∽△ABC,
故D不符合题意,
故选:C.
【点评】此题重点考查三角形中位线定理、平行四边形的判定与性质、相似三角形的判定与性质等知识,适当选择相似三角形的判定定理证明△DEF∽△ABC是解题的关键.
二.填空题(共5小题)
11.(2025 永寿县校级一模)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD=1,AD=2,则BC的长为 5 .
【考点】射影定理;直角三角形的性质;相似三角形的判定与性质.
【专题】三角形.
【答案】5.
【分析】根据题意,得∠BAD=90°﹣∠DAC=∠C,结合∠BDA=90°=∠ADC,证明△BAD∽△ACD,列比例式解答即可.
【解答】解:∵∠BAC=90°,AD⊥BC,
∴∠BAD=90°﹣∠DAC=∠C,∠BDA=90°=∠ADC,
∴△BAD∽△ACD,
∴,
∵BD=1,AD=2,
∴,
解得DC=4,
∴BC=BD+DC=5,
故答案为:5.
【点评】本题考查了三角形相似的判定和性质,直角三角形的性质,熟练掌握判定是解题的关键.
12.(2025 安阳模拟)已知a,b,c使等式成立,则代数式的值是 ﹣1 .
【考点】比例的性质.
【专题】计算题.
【答案】﹣1.
【分析】设,求得k=1,得到a=b=c,然后代入代数式化简解题即可.
【解答】解:设,
∴a=bk,b=ck,c=ak,
∴a=ck k=ak k k=ak3,
∴k3=1,解得k=1,
∴a=b=c,
∴,
故答案为:﹣1.
【点评】本题考查比例的性质,注意正确计算.
13.(2025 晋安区校级模拟)如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AC=8,DE=6,EF=3,则BC= .
【考点】平行线分线段成比例.
【专题】线段、角、相交线与平行线;运算能力.
【答案】.
【分析】根据平行线分线段成比例定理列式计算即可得解.
【解答】解:∵l1∥l2∥l3,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,
∴,
∵AC=8,DE=6,EF=3,
∴,
解得.
故答案为:.
【点评】本题主要考查了平行线分线段成比例定理,正确进行计算是解题关键.
14.(2025 佛山一模)如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使得∠DCP=60°,连接OD,则OD的最大值为 2 +1 .
【考点】相似三角形的判定与性质;三角形三边关系;勾股定理;点与圆的位置关系.
【专题】图形的相似;推理能力.
【答案】2+1.
【分析】如图,作△COE,使得∠CEO=90°,∠ECO=60°,连接OP,则CO=2CE,OE=2 ,∠OCP=∠ECD,由△COP∽△CED,得比例式,从而求得ED=1(定长),由点E是定点,DE是定长,推出点D在半径为1的⊙E上,由此即可解决问题.
【解答】解:如图,作△COE,使得∠CEO=90°,∠ECO=60°,连接OP,则 CO=2CE,OE=2 ,∠OCP=∠ECD,
∵∠CDP=90°,∠DCP=60°,
∴CP=2CD,
∴=2
∴△COP∽△CED,
∴=2,
即ED=OP=1(定长),
∵点E是定点,DE是定长,
∴点D在半径为的⊙E上,
∵OD OE+DE,
∴OD≤2+1,
∴OD的最大值为2+1,
故答案为:2+1.
【点评】本题考查了相似三角形的判定与性质及圆的有关概念及性质,熟练掌握相关性质及定理是解题的关键.
15.(2025 柳州一模)如图,是小莹设计用手电来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.4米,PB=2.1米,PD=12米,那么该古墙的高度是 8 米.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】8.
【分析】由光学知识反射角等于入射角不难分析得出∠APB=∠CPD,再由∠ABP=∠CDP=90°得到△ABP∽△CDP,得到=代入数值求的CD=8.
【解答】解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴=,
即=,
解得:CD=8.
故答案为:8.
【点评】本题考查了直角三角形的有关知识,同时渗透光学中反射原理,注意到相似三角形,解决本题关键.
三.解答题(共5小题)
16.(2025 河北模拟)风力发电是我国电力资源的重要组成部分.嘉嘉为了解某风力发电机的风叶长度,通过测量其影子长度的方法进行计算.如图14(图中所有的点均在同一平面,太阳光线视为平行光线),线段OA,OB,OC表示三片风叶,OA=OB=OC,∠AOB=∠BOC=∠COA=120°,某时刻OA,OB的影子恰好重合为线段EF,OD⊥EF于点D,测得DE=36m,EF=20m.同一时刻测得高4m的标杆MN影长为3m.
(1)直接写出∠ABO的度数及OD的长;
(2)求风叶转动时点B到地面DF的最小距离.
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】(1)∠ABO=30°,OD=48m;
(2)16m.
【分析】(1)通过△ODE∽△NMG,即可求得DO=48m,再根据等腰三角形的性质结合三角形的内角和定理即可求解∠ABO的度数;
(2)过点O作OH⊥AB于点H,过点E作EI⊥AF于点I,由△EIF∽△NMG,求得EI=16m,则OH=EI=16m,根据直角三角形的性质得到BO=2OH=32m,故当OB⊥DF时,风叶转动时点B到地面DF的最小距离为48﹣32=16(m);
【解答】解:(1)如图,
由题意得OE∥NG,∠ODE=∠NMG=90°,
∴∠OED=∠G,
∴△ODE∽△NMG,
根据三角形相似性质可得:
,
∴,
∴DO=48m,
∵OA=OB,∠AOB=120°,
∴;
(2)过点O作OH⊥AB于点H,过点E作EI⊥AF于点I,
在Rt△NMG中,由勾股定理得NG=5m;
同理可证明:△EIF∽△NMG,
∴,
∴,
∴EI=16m,
由题意得,OE∥AF,而OH⊥AF,EI⊥AF,
∴OH=EI=16m,
∵在Rt△OBH中,∠ABO=30°,
∴BO=2OH=32m,
∴当OB⊥DF时,48﹣32=16(m),
答:风叶转动时点B到地面DF的最小距离为16m.
【点评】本题考查了相似三角形的实际应用,勾股定理,含30度直角三角形的性质,等腰三角形的性质,三角形的内角和定理等知识点,正确运用相似三角形的性质是解题的关键.
17.(2025 晋安区校级模拟)如图,等腰直角三角形ABC中,∠C=90°,D为BC中点,以D为直角顶点作等腰直角三角形MDN,M在N的左侧.
(1)若点M与点A重合,DN与MB相交于点P.
①若AC=2,求MN的长;
②求证:DP PN=AP PB;
(2)若点M在AC左侧,且∠AMC=90°时,过点D作DE⊥BC交AB于点E,连接ME、CN,在线段CN上取一点F且满足∠NDF=∠EMD,求证:.
【考点】相似形综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)①;
②见解析;
(2)见解析.
【分析】(1)①如图,过点N作NK⊥CB交CB延长线于点K,则∠K=90°,证明△ACD≌△DKN,则DK=AC=2,NK=CD=1,故BK=DK﹣DB=1,对Rt△BKN中运用勾股定理得,在Rt△MDN中,由勾股定理即可求得MN;
②证明△APD∽△NPB,即可得到DP PN=AP PB;
(2)过点E作AE的垂线与MC的延长线交于点J,连接CE,BN,由平行线分线段成比例得点E为AB中点,可证明A,M,C,E四点共圆,则∠EMC=∠CAB=45°,故△MEJ为等腰直角三角形,∠AME=∠AMC﹣∠EMC=45°,△CEA为等腰直角三角形,可证明△EAM≌△ECJ,同理可得△EDB为等腰直角三角形,△MDN为等腰直角三角形,同理可证明:△MDE≌△NDB,导角∠3=∠4,得DF∥BN,则有△CDF∽△CBN,得BN=2DF,在等腰Rt△MEJ中,由勾股定理得,故,由,得,即,再利用三角形面积公式即可得证.
【解答】(1)①解:如图1,过点N作NK⊥CB交CB延长线于点K,则∠K=90°;
∵∠ACB=90°,CB=CA,
∴AC=BC=2,
∴由勾股定理得,
∵点D为BC中点,
∴CD=BD=1,
∵△MDN是等腰直角三角形,
∴MD=ND,∠MDN=90°,
∴∠NDK+∠ADC=∠DAC+∠ADC=90°,
∴∠NDK=∠DAC,
∵∠C=∠K=90°,
∴△ACD≌△DKN,
∴DK=AC=2,NK=CD=1,
在Rt△DKN中,由勾股定理得:,
在Rt△MDN中,由勾股定理得:;
②证明:由①得△ACD≌△DKN,
∴DK=AC=BC,NK=CD=BD,
∴CD=BK,
∴NK=BK,
∴△BKN是等腰直角三角形,
∴∠NBK=45°,
∴∠ABN=180°﹣45°﹣45°=90°=∠ADN,
∵∠APD=∠NPB,
∴△APD∽△NPB,
∴,
∴DP PN=AP PB;
(2)解:过点E作ME的垂线与MC的延长线交于点J,连接CE,BN,
∵∠ACB=90°,
∴AC⊥BC,
∵DE⊥BC,
∴DE∥AC,
∴,
∴点E为AB中点,
∵CA=CB,
∴CE⊥AB,
∴∠5+∠6=∠6+∠7=90°,
∴∠5=∠7,
∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵∠AMC=90°,∠AEC=90°,
∴∠AMC+∠AEC=180°,
∴A,M,C,E四点共圆,
∴∠EMC=∠CAB=45°,
∴△MEJ为等腰直角三角形,∠AME=∠AMC﹣∠EMC=45°,
∴EM=EJ,∠J=45°,
∴∠J=∠AME,
∵CE⊥AB,∠CAB=45°,
∴△CEA为等腰直角三角形,
∴CE=AE,
在△EAM和△ECJ中,
,
∴△EAM≌△ECJ(ASA),
∴AM=CJ,
∵同理可得△EDB为等腰直角三角形,
∴DE=DB,
∵△MDN为等腰直角三角形,
同理可证明:△MDE≌△NDB,
∴EM=BN,∠2=∠4,
∵∠2=∠3,
∴∠3=∠4,
∴DF∥BN,
∴△CDF∽△CBN,
∴,则BN=2DF,
在等腰Rt△MEJ中,由勾股定理得,
∴,
∵,
∴,
∴,
∴(AM+CM)2=8DF2,即AM2+CM2+2AM×CM=8DF2,
∴AC2+2AM×CM=8DF2,
∵,,
∴AC2=2S△ABC,AM×CM=2S△AMC,
∴,
∴.
【点评】本题属于相似形综合题,主要考查了全等三角形的判定与性质,相似三角形的判定与性质,圆周角定理,勾股定理,等腰直角三角形的判定与性质,熟练构造基本全等模型是解决本题的关键.
18.(2025 泸县一模)如图,已知点C在圆上,PA为⊙O的一条割线,∠PCB=∠A.
(1)求证:△PBC∽△PCA;
(2)若PB=4,AB=6,求PC.
【考点】相似三角形的判定与性质.
【专题】与圆有关的位置关系;推理能力.
【答案】(1)见解答;
(2)2.
【分析】(1)根据有2组角对应相等的两三角形相似可判定△PBC∽△PCA;
(2)根据相似三角形的性质得到PB:PC=PC:PA,即4:PC=PC:(4+6),然后利用比例的性质求出PC.
【解答】(1)证明:∵∠CPB=∠APC,∠PCB=∠A,
∴△PBC∽△PCA;
(2)解:∵△PBC∽△PCA,
∴PB:PC=PC:PA,
即4:PC=PC:(4+6),
解得PC=2或PC=﹣2(舍去),
即PC的长为2.
【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用;灵活运用相似三角形的性质表示线段之间的关系.
19.(2025 大渡口区模拟)如图,在 ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:△ABO∽△BEO;
(2)若AB=10,AC=16,求OE的长.
【考点】相似三角形的判定与性质;勾股定理;平行四边形的性质;菱形的判定与性质.
【专题】图形的相似;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)证AB=CB,得 ABCD是菱形,再由菱形的性质得AC⊥BD,可得∠AOB=∠BOE=90°,再由BE⊥AB,可得∠EBA=90°,从而得出∠BEO=∠ABO,
然后证△ABO∽△BEO即可;
(2)由勾股定理得OB=6,由△ABO∽△BEO,得,即可得出结论.
【解答】(1)证明:∵∠CAB=∠ACB,
∴AB=CB,
∴ ABCD是菱形,
∴AC⊥BD,
∴∠AOB=∠BOE=90°,
∵BE⊥AB,
∴∠EBA=90°,
∴∠BEO+∠BAO=∠ABO+∠BAO=90°,
∴∠BEO=∠ABO,
∴△ABO∽△BEO;
(2)解:∵ ABCD是菱形,
∴,AC⊥BD,
∴∠AOB=∠BOE=90°,
∴,
∵△BOE∽△AOB,
∴,
即,
解得:,
即OE的长为.
【点评】本题考查了平行四边形的性质、菱形的判定与性质、等腰三角形的判定、勾股定理以及相似三角形的判定与性质等知识,熟练掌握平行四边形的性质和菱形的判定与性质是解题的关键.
20.(2025 茅箭区校级模拟)在Rt△ABC中,AC=1,∠C=90°,D为BC边上一动点,且(n为正整数),在直线BC上方作△ADE,使得△ADE∽△ACB.
(1)如图1,在点D运动过程中,△ACD与△ABE始终保持相似关系,请说明理由;
(2)如图2,若n=2,M为AB中点,当点E在射线CM上时,求CD的长;
(3)如图3,设AE的中点为P,求点D从点C运动到点B的过程中,点P运动的路径长(用含n的代数式表示).
【考点】相似形综合题.
【专题】几何综合题;运算能力;推理能力.
【答案】(1)理由见解答;
(2)CD的长是;
(3)点P运动的路径长是.
【分析】(1)由△ADE∽△ACB,得=,∠EAD=∠BAC,可推导出=,∠DAC=∠EAB,即可根据“两边成比例且夹角相等的两个三角形相似”证明△ACD∽△ABE;
(2)作CG⊥AB于点G,则∠ACG=∠ABC=90°﹣∠BAC,由AC=1,=,n=2,得BC=nAC=n=2,则AB==,求得AM=BM=,进而求得AG=AC=,CG=AC=,所以MG=AM﹣AG=,由相似三角形的性质得∠ACD=∠ABE=∠MGC=90°,∠BME=∠GMC,=,则=tan∠BME=tan∠GMC==,所以==,则CD=AC=;
(3)取AB的中点L,连接PL,则PL∥EB,PL=EB,所以∠ALP=∠ABE=90°,可知点P在经过AB中点且与AB垂直的直线PL上运动,根据勾股定理求得AB==,当点D与点B重合时,PL的值最大,线段PL的长即为点P运动的路径长,由△ABE∽△ACB,得=,求得EB=,则PL=,所以点P运动的路径长是.
【解答】解:(1)理由:如图1,∵△ADE∽△ACB,
∴=,∠EAD=∠BAC,
∴=,∠BAC﹣∠BAD=∠EAD﹣∠BAD,
∴∠DAC=∠EAB,
∴△ACD∽△ABE.
(2)如图2,作CG⊥AB于点G,则∠AGC=90°,
∵∠ACB=90°,
∴∠ACG=∠ABC=90°﹣∠BAC,
∵AC=1,=,
∴BC=nAC=n,
∵n=2,
∴BC=2,
∴AB===,
∵M为AB中点,
∴AM=BM=AB=,
∵=sin∠ACG=sin∠ABC===,=cos∠ACG=cos∠ABC===,
∴AG=AC=×1=,CG=AC=×1=,
∴MG=AM﹣AG=﹣=,
∵△ACD∽△ABE,
∴∠ACD=∠ABE=∠MGC=90°,∠BME=∠GMC,=,
∴=tan∠BME=tan∠GMC===,
∴===,
∴==,
∴CD=AC=×1=,
∴CD的长是.
(3)如图3,取AB的中点L,连接PL,
∵AE的中点为P,
∴PL∥EB,PL=EB,
∴∠ALP=∠ABE=90°,
∴点P在经过AB中点且与AB垂直的直线PL上运动,
∵∠ACB=90°,AC=1,BC=n,
∴AB===,
当点D与点C重合时,则点P与点L重合;
当点D与点B重合时,如图4,此时PL的值最大,
∴线段PL的长即为点P运动的路径长,
∵△ABE∽△ACB,
∴=,
∴EB===,
∴PL=EB=,
∴点P运动的路径长是.
【点评】此题重点考查相似三角形的判定与性质、勾股定理、锐角三角函数与解直角三角形、三角形的中位线定理等知识,此题综合性强,难度较大,正确地作出所需要的辅助线是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2025 崇明区一模)如图,在三角形纸片ABC中,AB=6,AC=4,BC=8,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A. B.
C. D.
2.(2025 柳州模拟)如图,网格中每个小正方形的边长均为1,点A,B,C,D均在格点上,连接AD,BC交于点E,则S△ABE:S△DCE=( )
A.1:3 B.1:9 C.3:1 D.9:1
3.(2025 大渡口区模拟)如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA:AE=1:2,且四边形ABCD的周长为3,则四边形EFGH的周长为( )
A.6 B.9 C.12 D.27
4.(2025 江北区模拟)如图,点D、点E在△ABC的边上,且DE∥AB,AD:DC=2:1,则△ABC与△DEC的相似比为( )
A.2:1 B.3:1 C.1:2 D.1:3
5.(2025 登封市一模)如图,在平面直角坐标系中,△ABO与△CDE是位似图形,点O是坐标原点,点A,B,C,D,E都在格点上,且A(﹣2,0),则位似中心的坐标是( )
A.(﹣1,﹣1) B.(﹣2,2) C.(2,2) D.(﹣2,0)
6.(2025 登封市一模)小郑在做“小孔成像”实验时,蜡烛到挡板的距离与挡板到屏幕的距离之比是1:2,若烛焰AC的高是4cm,则实像DB的高是( )
A.12cm B.8cm C.6cm D.5cm
7.(2025 虹口区一模)如图,已知AB∥CD,联结AD、BC交于点O,联结AC,∠ACB=∠BAD,如果AB=2,CD=6,那么CO长为( )
A.1 B.2 C.3 D.4
8.(2025 松江区一模)如图,在 ABCD中,E是边CD的中点,AE交BD于点O,如果△DOE的面积为1,那么△ABO的面积为( )
A.2 B.4 C.6 D.9
9.(2025 青浦区一模)如图,在△ABC中,AC=BC,∠C=36°,AD是△ABC的角平分线.是( )
A. B. C. D.
10.(2025 黄浦区一模)某学习小组研究问题“如图,已知D、E、F分别是△ABC的边BC、CA、AB的中点,求证:△DEF∽△ABC.”经过小组讨论得到以下方法,其中存在错误的是( )
A.可证,进而证得△DEF∽△ABC
B.可证∠B=∠FED,∠C=∠EFD,进而证得△DEF∽△ABC
C.可证∠B=∠FED,,进而证得△DEF∽△ABC
D.可证△FBD∽△DEF,△FBD∽△ABC,进而证得△DEF∽△ABC
二.填空题(共5小题)
11.(2025 永寿县校级一模)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD=1,AD=2,则BC的长为 .
12.(2025 安阳模拟)已知a,b,c使等式成立,则代数式的值是 .
13.(2025 晋安区校级模拟)如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AC=8,DE=6,EF=3,则BC= .
14.(2025 佛山一模)如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使得∠DCP=60°,连接OD,则OD的最大值为 .
15.(2025 柳州一模)如图,是小莹设计用手电来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.4米,PB=2.1米,PD=12米,那么该古墙的高度是 米.
三.解答题(共5小题)
16.(2025 河北模拟)风力发电是我国电力资源的重要组成部分.嘉嘉为了解某风力发电机的风叶长度,通过测量其影子长度的方法进行计算.如图14(图中所有的点均在同一平面,太阳光线视为平行光线),线段OA,OB,OC表示三片风叶,OA=OB=OC,∠AOB=∠BOC=∠COA=120°,某时刻OA,OB的影子恰好重合为线段EF,OD⊥EF于点D,测得DE=36m,EF=20m.同一时刻测得高4m的标杆MN影长为3m.
(1)直接写出∠ABO的度数及OD的长;
(2)求风叶转动时点B到地面DF的最小距离.
17.(2025 晋安区校级模拟)如图,等腰直角三角形ABC中,∠C=90°,D为BC中点,以D为直角顶点作等腰直角三角形MDN,M在N的左侧.
(1)若点M与点A重合,DN与MB相交于点P.
①若AC=2,求MN的长;
②求证:DP PN=AP PB;
(2)若点M在AC左侧,且∠AMC=90°时,过点D作DE⊥BC交AB于点E,连接ME、CN,在线段CN上取一点F且满足∠NDF=∠EMD,求证:.
18.(2025 泸县一模)如图,已知点C在圆上,PA为⊙O的一条割线,∠PCB=∠A.
(1)求证:△PBC∽△PCA;
(2)若PB=4,AB=6,求PC.
19.(2025 大渡口区模拟)如图,在 ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:△ABO∽△BEO;
(2)若AB=10,AC=16,求OE的长.
20.(2025 茅箭区校级模拟)在Rt△ABC中,AC=1,∠C=90°,D为BC边上一动点,且(n为正整数),在直线BC上方作△ADE,使得△ADE∽△ACB.
(1)如图1,在点D运动过程中,△ACD与△ABE始终保持相似关系,请说明理由;
(2)如图2,若n=2,M为AB中点,当点E在射线CM上时,求CD的长;
(3)如图3,设AE的中点为P,求点D从点C运动到点B的过程中,点P运动的路径长(用含n的代数式表示).
2025年中考数学二轮复习考前预测:图形的相似
参考答案与试题解析
一.选择题(共10小题)
1.(2025 崇明区一模)如图,在三角形纸片ABC中,AB=6,AC=4,BC=8,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A. B.
C. D.
【考点】相似三角形的判定.
【专题】图形的相似;推理能力.
【答案】A
【分析】根据相似三角形的判定分别进行判断即可得出答案即可.
【解答】解:在三角形纸片ABC中,AB=6,BC=8,AC=4.
A、∵=,∠C=∠C,
故沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项符合题意;
B、∵≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项不符合题意;
C、∵≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项不符合题意;
D、∵≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项不符合题意;
故选:A.
【点评】本题考查了相似三角形的判定,掌握相似三角形的判定方法是解题的关键.
2.(2025 柳州模拟)如图,网格中每个小正方形的边长均为1,点A,B,C,D均在格点上,连接AD,BC交于点E,则S△ABE:S△DCE=( )
A.1:3 B.1:9 C.3:1 D.9:1
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】D
【分析】判定△ABE∽△DCE,由相似三角形面积的比等于相似比的平方,即可求解.
【解答】解:∵CD∥AB,
∴△ABE∽△DCE,
∴S△ABE:S△DCE=AB2:CD2,
∵AB=6,CD=2,
∴S△ABE:S△DCE=9:1.
故选:D.
【点评】本题考查相似三角形的判定与性质,关键是由△ABE∽△DCE,推出S△ABE:S△DCE=AB2:CD2.
3.(2025 大渡口区模拟)如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA:AE=1:2,且四边形ABCD的周长为3,则四边形EFGH的周长为( )
A.6 B.9 C.12 D.27
【考点】位似变换.
【专题】图形的相似;运算能力;推理能力.
【答案】B
【分析】根据位似图形的概念得到AD∥EH,根据相似三角形的性质解答即可.
【解答】解:∵四边形ABCD与四边形EFGH位似,
∴AD∥EH,
∴△OAD∽△OEH,
∴===,即四边形ABCD与四边形EFGH的相似比为,
∵四边形ABCD的周长为3,
∴四边形EFGH的周长为9,
故选:B.
【点评】本题考查的是位似图形的概念、相似三角形的判定和性质、相似多边形的性质,熟记相似多边形的周长比等于相似比是解题的关键.
4.(2025 江北区模拟)如图,点D、点E在△ABC的边上,且DE∥AB,AD:DC=2:1,则△ABC与△DEC的相似比为( )
A.2:1 B.3:1 C.1:2 D.1:3
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据相似三角形的判定与性质求解即可.
【解答】解:∵AD:DC=2:1,
∴AC:DC=3:1,
∵DE∥AB,
∴△CDE∽△CAB,
∴△ABC与△DEC的相似比==3:1,
故选:B.
【点评】本题考查了相似三角形的性质和判定的应用,熟记相似三角形的判定与性质是解题的关键.
5.(2025 登封市一模)如图,在平面直角坐标系中,△ABO与△CDE是位似图形,点O是坐标原点,点A,B,C,D,E都在格点上,且A(﹣2,0),则位似中心的坐标是( )
A.(﹣1,﹣1) B.(﹣2,2) C.(2,2) D.(﹣2,0)
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;几何直观.
【答案】C
【分析】连接AC,BD,OE,并分别延长,相交于点P,则△ABO与△CDE是以点P为位似中心的位似图形,即可得出答案.
【解答】解:如图,连接AC,BD,OE,并分别延长,相交于点P,
则△ABO与△CDE是以点P为位似中心的位似图形,
∴位似中心的坐标是(2,2).
故选:C.
【点评】本题考查位似变换、坐标与图形性质,熟练掌握位似的性质是解答本题的关键.
6.(2025 登封市一模)小郑在做“小孔成像”实验时,蜡烛到挡板的距离与挡板到屏幕的距离之比是1:2,若烛焰AC的高是4cm,则实像DB的高是( )
A.12cm B.8cm C.6cm D.5cm
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】B
【分析】根据AC∥DB证明△AOC∽△BOD,利用相似三角形的性质求解即可.
【解答】解:如图所示:AB、CD相交于点O,
∵AC是烛焰的高,DB是实像的高,
∴AC∥DB,
∴△AOC∽△BOD,
∵蜡烛到挡板距离与挡板到屏幕距离之比是1:2,AC=4cm,
∴=,
∴BD=8cm.
故选:B.
【点评】本题考查了相似三角形的应用,熟练掌握相似三角形的性质是解答本题的关键.
7.(2025 虹口区一模)如图,已知AB∥CD,联结AD、BC交于点O,联结AC,∠ACB=∠BAD,如果AB=2,CD=6,那么CO长为( )
A.1 B.2 C.3 D.4
【考点】相似三角形的判定与性质.
【专题】图形的相似;运算能力;推理能力.
【答案】C
【分析】由AB∥CD,证明△AOB∽△DOC,得==,则CO=3BO,所以CB=4BO,由∠ACB=∠BAD,∠B=∠B,证明△ACB∽△OAB,所以=,则CB BO=AB2=22=4,所以4BO2=4,求得BO=1,则CO=3,于是得到问题的答案.
【解答】解:∵AB∥CD,AB=2,CD=6,
∴△AOB∽△DOC,
∴===,
∴CO=3BO,
∴CB=BO+3BO=4BO,
∵∠ACB=∠BAD,∠B=∠B,
∴△ACB∽△OAB,
∴=,
∴CB BO=AB2=22=4,
∴4BO2=4,
解得BO=1或BO=﹣1(不符合题意,舍去),
∴CO=3,
故选:C.
【点评】此题重点考查相似三角形的判定与性质,证明△AOB∽△DOC及△ACB∽△OAB是解题的关键.
8.(2025 松江区一模)如图,在 ABCD中,E是边CD的中点,AE交BD于点O,如果△DOE的面积为1,那么△ABO的面积为( )
A.2 B.4 C.6 D.9
【考点】相似三角形的判定与性质;平行四边形的性质.
【专题】多边形与平行四边形;图形的相似;几何直观;推理能力.
【答案】B
【分析】根据平行四边形的性质求得△AOB~△EOD,根据相似三角形的面积比等于相似比的平方来求出S△AOB=4.
【解答】解:∵ ABCD中,E为CD边上的中点,
∴DE=CD=AB,AB∥CD,
∵AB∥CD,
∴∠ABO=∠EDO,∠OAB=∠OED,
∴△AOB∽△EOD,
∴===2,
∴==22=4,
∴S△AOB=4S△DOE=4,
故选:B.
【点评】本题考查了平行边形的性质,相似三角形的判定和性质,理解相似三角形的面积比等于相似比的平方是解答关键.
9.(2025 青浦区一模)如图,在△ABC中,AC=BC,∠C=36°,AD是△ABC的角平分线.是( )
A. B. C. D.
【考点】相似三角形的判定与性质.
【专题】等腰三角形与直角三角形;图形的相似;推理能力.
【答案】C
【分析】根据AC=BC,∠C=36°,求出∠B=∠BAC=72°,根据AD平分∠BAC可得∠BAD=∠CAD=36°,进而证得△ABD∽△CBA,根据相似三角形的性质证得结论.
【解答】解:∵AC=BC,∠C=36°,
∴∠B=∠BAC=72°,
∵AD平分∠BAC,
∠BAD=∠CAD=36°,
∴∠BAD=∠C=∠CAD=36°,
∴AD=CD,∠ADB=72°,
∴AB=AD,
∴AB=AD=CD,
∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴,
设BC=AC=a,BD=x,
则AD=CD=AB=a﹣x,
∴,
解得x=a(不符合题意,舍去)或x=a,
∴AB=a﹣x=a,
∴.
故选:C.
【点评】本题考查了相似三角形的性质,解题的关键掌握相似三角形的判定方法.
10.(2025 黄浦区一模)某学习小组研究问题“如图,已知D、E、F分别是△ABC的边BC、CA、AB的中点,求证:△DEF∽△ABC.”经过小组讨论得到以下方法,其中存在错误的是( )
A.可证,进而证得△DEF∽△ABC
B.可证∠B=∠FED,∠C=∠EFD,进而证得△DEF∽△ABC
C.可证∠B=∠FED,,进而证得△DEF∽△ABC
D.可证△FBD∽△DEF,△FBD∽△ABC,进而证得△DEF∽△ABC
【考点】相似三角形的判定;三角形中位线定理;相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】由D、E、F分别是△ABC的边BC、CA、AB的中点,得DE=AB,EF=BC,FD=AC,则===,所以△DEF∽△ABC,可判断A不符合题意;由DE∥BF,EF∥BD,证明四边形BDEF是平行四边形,则∠B=∠FED,同理∠C=∠EFD,则△DEF∽△ABC,可判断B不符合题意;由AB∥ED,证明△ABC∽△EDC,得=,而DC=EF,所以=,可知=不成立,所以由∠B=∠FED,=,不能证得△DEF∽△ABC,可判断C符合题意;由∠BFD=∠EDF,∠BDF=∠EFD,证明△FBD∽△DEF,由FD∥AC,证明△FBD∽△ABC,则△DEF∽△ABC,可判断D不符合题意,于是得到问题的答案.
【解答】解:∵D、E、F分别是△ABC的边BC、CA、AB的中点,
∴DE∥AB,且DE=AB,EF∥BC,且EF=BC,FD∥AC,且FD=AC,
∴===,
∴△DEF∽△ABC,
故A不符合题意;
∵DE∥BF,EF∥BD,
∴四边形BDEF是平行四边形,
∴∠B=∠FED,
同理四边形CDFE是平行四边形,
∴∠C=∠EFD,
∴△DEF∽△ABC,
故B不符合题意;
∵AB∥ED,
∴△ABC∽△EDC,
∴=,
∵DC=EF,
∴=,
∴=不成立,
∴由∠B=∠FED,=,不能证得△DEF∽△ABC,
故C符合题意;
∵DE∥AB,EF∥BC,
∴∠BFD=∠EDF,∠BDF=∠EFD,
∴△FBD∽△DEF,
∵FD∥AC,
∴△FBD∽△ABC,
∴△DEF∽△ABC,
故D不符合题意,
故选:C.
【点评】此题重点考查三角形中位线定理、平行四边形的判定与性质、相似三角形的判定与性质等知识,适当选择相似三角形的判定定理证明△DEF∽△ABC是解题的关键.
二.填空题(共5小题)
11.(2025 永寿县校级一模)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD=1,AD=2,则BC的长为 5 .
【考点】射影定理;直角三角形的性质;相似三角形的判定与性质.
【专题】三角形.
【答案】5.
【分析】根据题意,得∠BAD=90°﹣∠DAC=∠C,结合∠BDA=90°=∠ADC,证明△BAD∽△ACD,列比例式解答即可.
【解答】解:∵∠BAC=90°,AD⊥BC,
∴∠BAD=90°﹣∠DAC=∠C,∠BDA=90°=∠ADC,
∴△BAD∽△ACD,
∴,
∵BD=1,AD=2,
∴,
解得DC=4,
∴BC=BD+DC=5,
故答案为:5.
【点评】本题考查了三角形相似的判定和性质,直角三角形的性质,熟练掌握判定是解题的关键.
12.(2025 安阳模拟)已知a,b,c使等式成立,则代数式的值是 ﹣1 .
【考点】比例的性质.
【专题】计算题.
【答案】﹣1.
【分析】设,求得k=1,得到a=b=c,然后代入代数式化简解题即可.
【解答】解:设,
∴a=bk,b=ck,c=ak,
∴a=ck k=ak k k=ak3,
∴k3=1,解得k=1,
∴a=b=c,
∴,
故答案为:﹣1.
【点评】本题考查比例的性质,注意正确计算.
13.(2025 晋安区校级模拟)如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AC=8,DE=6,EF=3,则BC= .
【考点】平行线分线段成比例.
【专题】线段、角、相交线与平行线;运算能力.
【答案】.
【分析】根据平行线分线段成比例定理列式计算即可得解.
【解答】解:∵l1∥l2∥l3,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,
∴,
∵AC=8,DE=6,EF=3,
∴,
解得.
故答案为:.
【点评】本题主要考查了平行线分线段成比例定理,正确进行计算是解题关键.
14.(2025 佛山一模)如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使得∠DCP=60°,连接OD,则OD的最大值为 2 +1 .
【考点】相似三角形的判定与性质;三角形三边关系;勾股定理;点与圆的位置关系.
【专题】图形的相似;推理能力.
【答案】2+1.
【分析】如图,作△COE,使得∠CEO=90°,∠ECO=60°,连接OP,则CO=2CE,OE=2 ,∠OCP=∠ECD,由△COP∽△CED,得比例式,从而求得ED=1(定长),由点E是定点,DE是定长,推出点D在半径为1的⊙E上,由此即可解决问题.
【解答】解:如图,作△COE,使得∠CEO=90°,∠ECO=60°,连接OP,则 CO=2CE,OE=2 ,∠OCP=∠ECD,
∵∠CDP=90°,∠DCP=60°,
∴CP=2CD,
∴=2
∴△COP∽△CED,
∴=2,
即ED=OP=1(定长),
∵点E是定点,DE是定长,
∴点D在半径为的⊙E上,
∵OD OE+DE,
∴OD≤2+1,
∴OD的最大值为2+1,
故答案为:2+1.
【点评】本题考查了相似三角形的判定与性质及圆的有关概念及性质,熟练掌握相关性质及定理是解题的关键.
15.(2025 柳州一模)如图,是小莹设计用手电来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.4米,PB=2.1米,PD=12米,那么该古墙的高度是 8 米.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】8.
【分析】由光学知识反射角等于入射角不难分析得出∠APB=∠CPD,再由∠ABP=∠CDP=90°得到△ABP∽△CDP,得到=代入数值求的CD=8.
【解答】解:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴=,
即=,
解得:CD=8.
故答案为:8.
【点评】本题考查了直角三角形的有关知识,同时渗透光学中反射原理,注意到相似三角形,解决本题关键.
三.解答题(共5小题)
16.(2025 河北模拟)风力发电是我国电力资源的重要组成部分.嘉嘉为了解某风力发电机的风叶长度,通过测量其影子长度的方法进行计算.如图14(图中所有的点均在同一平面,太阳光线视为平行光线),线段OA,OB,OC表示三片风叶,OA=OB=OC,∠AOB=∠BOC=∠COA=120°,某时刻OA,OB的影子恰好重合为线段EF,OD⊥EF于点D,测得DE=36m,EF=20m.同一时刻测得高4m的标杆MN影长为3m.
(1)直接写出∠ABO的度数及OD的长;
(2)求风叶转动时点B到地面DF的最小距离.
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】(1)∠ABO=30°,OD=48m;
(2)16m.
【分析】(1)通过△ODE∽△NMG,即可求得DO=48m,再根据等腰三角形的性质结合三角形的内角和定理即可求解∠ABO的度数;
(2)过点O作OH⊥AB于点H,过点E作EI⊥AF于点I,由△EIF∽△NMG,求得EI=16m,则OH=EI=16m,根据直角三角形的性质得到BO=2OH=32m,故当OB⊥DF时,风叶转动时点B到地面DF的最小距离为48﹣32=16(m);
【解答】解:(1)如图,
由题意得OE∥NG,∠ODE=∠NMG=90°,
∴∠OED=∠G,
∴△ODE∽△NMG,
根据三角形相似性质可得:
,
∴,
∴DO=48m,
∵OA=OB,∠AOB=120°,
∴;
(2)过点O作OH⊥AB于点H,过点E作EI⊥AF于点I,
在Rt△NMG中,由勾股定理得NG=5m;
同理可证明:△EIF∽△NMG,
∴,
∴,
∴EI=16m,
由题意得,OE∥AF,而OH⊥AF,EI⊥AF,
∴OH=EI=16m,
∵在Rt△OBH中,∠ABO=30°,
∴BO=2OH=32m,
∴当OB⊥DF时,48﹣32=16(m),
答:风叶转动时点B到地面DF的最小距离为16m.
【点评】本题考查了相似三角形的实际应用,勾股定理,含30度直角三角形的性质,等腰三角形的性质,三角形的内角和定理等知识点,正确运用相似三角形的性质是解题的关键.
17.(2025 晋安区校级模拟)如图,等腰直角三角形ABC中,∠C=90°,D为BC中点,以D为直角顶点作等腰直角三角形MDN,M在N的左侧.
(1)若点M与点A重合,DN与MB相交于点P.
①若AC=2,求MN的长;
②求证:DP PN=AP PB;
(2)若点M在AC左侧,且∠AMC=90°时,过点D作DE⊥BC交AB于点E,连接ME、CN,在线段CN上取一点F且满足∠NDF=∠EMD,求证:.
【考点】相似形综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)①;
②见解析;
(2)见解析.
【分析】(1)①如图,过点N作NK⊥CB交CB延长线于点K,则∠K=90°,证明△ACD≌△DKN,则DK=AC=2,NK=CD=1,故BK=DK﹣DB=1,对Rt△BKN中运用勾股定理得,在Rt△MDN中,由勾股定理即可求得MN;
②证明△APD∽△NPB,即可得到DP PN=AP PB;
(2)过点E作AE的垂线与MC的延长线交于点J,连接CE,BN,由平行线分线段成比例得点E为AB中点,可证明A,M,C,E四点共圆,则∠EMC=∠CAB=45°,故△MEJ为等腰直角三角形,∠AME=∠AMC﹣∠EMC=45°,△CEA为等腰直角三角形,可证明△EAM≌△ECJ,同理可得△EDB为等腰直角三角形,△MDN为等腰直角三角形,同理可证明:△MDE≌△NDB,导角∠3=∠4,得DF∥BN,则有△CDF∽△CBN,得BN=2DF,在等腰Rt△MEJ中,由勾股定理得,故,由,得,即,再利用三角形面积公式即可得证.
【解答】(1)①解:如图1,过点N作NK⊥CB交CB延长线于点K,则∠K=90°;
∵∠ACB=90°,CB=CA,
∴AC=BC=2,
∴由勾股定理得,
∵点D为BC中点,
∴CD=BD=1,
∵△MDN是等腰直角三角形,
∴MD=ND,∠MDN=90°,
∴∠NDK+∠ADC=∠DAC+∠ADC=90°,
∴∠NDK=∠DAC,
∵∠C=∠K=90°,
∴△ACD≌△DKN,
∴DK=AC=2,NK=CD=1,
在Rt△DKN中,由勾股定理得:,
在Rt△MDN中,由勾股定理得:;
②证明:由①得△ACD≌△DKN,
∴DK=AC=BC,NK=CD=BD,
∴CD=BK,
∴NK=BK,
∴△BKN是等腰直角三角形,
∴∠NBK=45°,
∴∠ABN=180°﹣45°﹣45°=90°=∠ADN,
∵∠APD=∠NPB,
∴△APD∽△NPB,
∴,
∴DP PN=AP PB;
(2)解:过点E作ME的垂线与MC的延长线交于点J,连接CE,BN,
∵∠ACB=90°,
∴AC⊥BC,
∵DE⊥BC,
∴DE∥AC,
∴,
∴点E为AB中点,
∵CA=CB,
∴CE⊥AB,
∴∠5+∠6=∠6+∠7=90°,
∴∠5=∠7,
∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵∠AMC=90°,∠AEC=90°,
∴∠AMC+∠AEC=180°,
∴A,M,C,E四点共圆,
∴∠EMC=∠CAB=45°,
∴△MEJ为等腰直角三角形,∠AME=∠AMC﹣∠EMC=45°,
∴EM=EJ,∠J=45°,
∴∠J=∠AME,
∵CE⊥AB,∠CAB=45°,
∴△CEA为等腰直角三角形,
∴CE=AE,
在△EAM和△ECJ中,
,
∴△EAM≌△ECJ(ASA),
∴AM=CJ,
∵同理可得△EDB为等腰直角三角形,
∴DE=DB,
∵△MDN为等腰直角三角形,
同理可证明:△MDE≌△NDB,
∴EM=BN,∠2=∠4,
∵∠2=∠3,
∴∠3=∠4,
∴DF∥BN,
∴△CDF∽△CBN,
∴,则BN=2DF,
在等腰Rt△MEJ中,由勾股定理得,
∴,
∵,
∴,
∴,
∴(AM+CM)2=8DF2,即AM2+CM2+2AM×CM=8DF2,
∴AC2+2AM×CM=8DF2,
∵,,
∴AC2=2S△ABC,AM×CM=2S△AMC,
∴,
∴.
【点评】本题属于相似形综合题,主要考查了全等三角形的判定与性质,相似三角形的判定与性质,圆周角定理,勾股定理,等腰直角三角形的判定与性质,熟练构造基本全等模型是解决本题的关键.
18.(2025 泸县一模)如图,已知点C在圆上,PA为⊙O的一条割线,∠PCB=∠A.
(1)求证:△PBC∽△PCA;
(2)若PB=4,AB=6,求PC.
【考点】相似三角形的判定与性质.
【专题】与圆有关的位置关系;推理能力.
【答案】(1)见解答;
(2)2.
【分析】(1)根据有2组角对应相等的两三角形相似可判定△PBC∽△PCA;
(2)根据相似三角形的性质得到PB:PC=PC:PA,即4:PC=PC:(4+6),然后利用比例的性质求出PC.
【解答】(1)证明:∵∠CPB=∠APC,∠PCB=∠A,
∴△PBC∽△PCA;
(2)解:∵△PBC∽△PCA,
∴PB:PC=PC:PA,
即4:PC=PC:(4+6),
解得PC=2或PC=﹣2(舍去),
即PC的长为2.
【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用;灵活运用相似三角形的性质表示线段之间的关系.
19.(2025 大渡口区模拟)如图,在 ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:△ABO∽△BEO;
(2)若AB=10,AC=16,求OE的长.
【考点】相似三角形的判定与性质;勾股定理;平行四边形的性质;菱形的判定与性质.
【专题】图形的相似;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)证AB=CB,得 ABCD是菱形,再由菱形的性质得AC⊥BD,可得∠AOB=∠BOE=90°,再由BE⊥AB,可得∠EBA=90°,从而得出∠BEO=∠ABO,
然后证△ABO∽△BEO即可;
(2)由勾股定理得OB=6,由△ABO∽△BEO,得,即可得出结论.
【解答】(1)证明:∵∠CAB=∠ACB,
∴AB=CB,
∴ ABCD是菱形,
∴AC⊥BD,
∴∠AOB=∠BOE=90°,
∵BE⊥AB,
∴∠EBA=90°,
∴∠BEO+∠BAO=∠ABO+∠BAO=90°,
∴∠BEO=∠ABO,
∴△ABO∽△BEO;
(2)解:∵ ABCD是菱形,
∴,AC⊥BD,
∴∠AOB=∠BOE=90°,
∴,
∵△BOE∽△AOB,
∴,
即,
解得:,
即OE的长为.
【点评】本题考查了平行四边形的性质、菱形的判定与性质、等腰三角形的判定、勾股定理以及相似三角形的判定与性质等知识,熟练掌握平行四边形的性质和菱形的判定与性质是解题的关键.
20.(2025 茅箭区校级模拟)在Rt△ABC中,AC=1,∠C=90°,D为BC边上一动点,且(n为正整数),在直线BC上方作△ADE,使得△ADE∽△ACB.
(1)如图1,在点D运动过程中,△ACD与△ABE始终保持相似关系,请说明理由;
(2)如图2,若n=2,M为AB中点,当点E在射线CM上时,求CD的长;
(3)如图3,设AE的中点为P,求点D从点C运动到点B的过程中,点P运动的路径长(用含n的代数式表示).
【考点】相似形综合题.
【专题】几何综合题;运算能力;推理能力.
【答案】(1)理由见解答;
(2)CD的长是;
(3)点P运动的路径长是.
【分析】(1)由△ADE∽△ACB,得=,∠EAD=∠BAC,可推导出=,∠DAC=∠EAB,即可根据“两边成比例且夹角相等的两个三角形相似”证明△ACD∽△ABE;
(2)作CG⊥AB于点G,则∠ACG=∠ABC=90°﹣∠BAC,由AC=1,=,n=2,得BC=nAC=n=2,则AB==,求得AM=BM=,进而求得AG=AC=,CG=AC=,所以MG=AM﹣AG=,由相似三角形的性质得∠ACD=∠ABE=∠MGC=90°,∠BME=∠GMC,=,则=tan∠BME=tan∠GMC==,所以==,则CD=AC=;
(3)取AB的中点L,连接PL,则PL∥EB,PL=EB,所以∠ALP=∠ABE=90°,可知点P在经过AB中点且与AB垂直的直线PL上运动,根据勾股定理求得AB==,当点D与点B重合时,PL的值最大,线段PL的长即为点P运动的路径长,由△ABE∽△ACB,得=,求得EB=,则PL=,所以点P运动的路径长是.
【解答】解:(1)理由:如图1,∵△ADE∽△ACB,
∴=,∠EAD=∠BAC,
∴=,∠BAC﹣∠BAD=∠EAD﹣∠BAD,
∴∠DAC=∠EAB,
∴△ACD∽△ABE.
(2)如图2,作CG⊥AB于点G,则∠AGC=90°,
∵∠ACB=90°,
∴∠ACG=∠ABC=90°﹣∠BAC,
∵AC=1,=,
∴BC=nAC=n,
∵n=2,
∴BC=2,
∴AB===,
∵M为AB中点,
∴AM=BM=AB=,
∵=sin∠ACG=sin∠ABC===,=cos∠ACG=cos∠ABC===,
∴AG=AC=×1=,CG=AC=×1=,
∴MG=AM﹣AG=﹣=,
∵△ACD∽△ABE,
∴∠ACD=∠ABE=∠MGC=90°,∠BME=∠GMC,=,
∴=tan∠BME=tan∠GMC===,
∴===,
∴==,
∴CD=AC=×1=,
∴CD的长是.
(3)如图3,取AB的中点L,连接PL,
∵AE的中点为P,
∴PL∥EB,PL=EB,
∴∠ALP=∠ABE=90°,
∴点P在经过AB中点且与AB垂直的直线PL上运动,
∵∠ACB=90°,AC=1,BC=n,
∴AB===,
当点D与点C重合时,则点P与点L重合;
当点D与点B重合时,如图4,此时PL的值最大,
∴线段PL的长即为点P运动的路径长,
∵△ABE∽△ACB,
∴=,
∴EB===,
∴PL=EB=,
∴点P运动的路径长是.
【点评】此题重点考查相似三角形的判定与性质、勾股定理、锐角三角函数与解直角三角形、三角形的中位线定理等知识,此题综合性强,难度较大,正确地作出所需要的辅助线是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
