【中考押题卷】2025年中考数学二轮复习考前预测:一元一次方程(含解析)
文档属性
| 名称 | 【中考押题卷】2025年中考数学二轮复习考前预测:一元一次方程(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 284.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 12:20:02 | ||
图片预览




文档简介
2025年中考数学二轮复习考前预测:一元一次方程
一.选择题(共10小题)
1.(2025 佛山一模)方程﹣(|x+3|﹣|x﹣2|)=7满足x+3>0的解的个数为( )
A.5 B.3 C.6 D.0
2.(2025 河北模拟)我国古代数学著作《九章算术》中有一道“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,井深几何?这道题大致意思是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺;如果将绳子折成四等份,那么每等份井外余绳一尺.问井深多少尺?下列说法正确的是( )
A.设井深为x尺,所列方程为3(x+4)=4(x﹣1)
B.设绳子的长为x尺,所列方程为
C.绳子的长是32尺
D.井深8尺
3.(2025 泗洪县一模)我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗,今持粟三斛,得酒五斗,问清,醑酒各几何?”大意是:现有一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒,醑酒各几斗?如果设清酒x斗,那么可列方程为( )
A.10x+3(5﹣x)=30 B.3x+10(5﹣x)=30
C. D.
4.(2025 山东一模)如图,线段AB=20cm,O是线段AB上的中点,P、Q是线段AB上的动点,点P沿A→B→A以4cm/s的速度运动,点Q沿B→A以2cm/s的速度运动.若P、Q点同时运动,当OP=OQ时,运动时间为( )
A.0s、10s或 B.0s、5s或
C.0s、、或10s D.0s、5s、或
5.(2025 茅箭区校级模拟)小明参加了一场2000米的跑步比赛,他以4米/秒的速度跑了一段路程后,又以3米/秒的速度跑完了剩下的路程,一共花了10分钟,设小明以4米/秒的速度跑了x米,则列方程为( )
A.4x=3(x+10) B.
C. D.
6.(2024秋 兴隆县期末)解方程时,去分母正确的是( )
A.2x+1﹣(10x+1)=1 B.4x+1﹣10x+1=6
C.4x+2﹣10x﹣1=6 D.2(2x+1)﹣(10x+1)=1
7.(2024 祁阳市二模)《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )
A. B. C. D.
8.(2024 荷塘区校级模拟)若“△”是新规定的某种运算符号,设x△y=xy+x+y,则2△m=﹣16中,m的值为( )
A.8 B.﹣8 C.6 D.﹣6
9.(2024 凉州区三模)小明在做题时不小心用墨水把方程污染了,污染后的方程:,答案显示此方程的解是x=﹣8,被墨水遮盖的是一个常数,则这个常数是( )
A.1 B.﹣1 C.﹣2 D.2
10.(2024 滦南县校级模拟)下列运用等式的性质变形正确的是( )
A.若x=y,则x+5=y﹣5 B.若a2=b2,则a=b
C.若,则a=b D.若ax=ay,则x=y
二.填空题(共5小题)
11.(2025 碑林区校级一模)某环保队有甲、乙、丙三支队伍,现计划在A地植树1000棵,在B地植树1250棵,甲、乙、丙每天分别能植树28、32、30棵.甲在A地,乙在B地,丙在A与B两地之间来回帮忙,同时开始,同时结束,丙在A地植树 棵.
12.(2025 碑林区校级一模)父亲对儿子说:“我像你这么大时,你才4岁.当你像我这么大时,我就79岁了.”现在父亲 岁.
13.(2024 凉州区二模)已知(a﹣1)x|a|+2024=0是关于x的一元一次方程,则a= .
14.(2024 凉州区二模)已知关于x的一元一次方程x+3=2x+b的解为x=2,那么关于y的一元一次方程(y+1)+3=2(y+1)+b的解为y= .
15.(2024 湘阴县二模)已知关于x的方程2x+m﹣8=0的解是x=5,则m的值为 .
三.解答题(共5小题)
16.(2025 雁塔区校级模拟)某班手工兴趣小组的同学们计划制作一批中国结送给敬老院作为新年礼物.如果每人制作9个,那么就比计划少做17个;如果每人制作12个,那么就比计划多做4个.这个手工兴趣小组共有多少人?计划要做的这批中国结有多少个?
17.(2025 福田区一模)实验表明,物体在做匀加速直线运动时,速度V(m/s)随着运动时间t(s)的改变而改变,它的速度可用公式V=V0+at计算,已测得当t=1(s)时,速度 V=5.5(m/s);当t=6(s)时,速度 V=18(m/s),求:
(1)V0,a的值.
(2)当速度V=21(m/s) 时该物体的运动时间t.
18.(2025 雁塔区校级一模)袁隆平,“共和国勋章”获得者,中国工程院院士,“中国杂交水稻之父”,一生致力于对水稻的研究.现有A、B两块试验田各30亩,A块试验田种植普通水稻,B块试验田种植杂交水稻,杂交水稻的亩产量是普通水稻的1.2倍,两块试验田单次共收获水稻56100千克,求杂交水稻的亩产量是多少千克?
19.(2024 天山区校级三模)(1)先化简,再求值:(a+b)2+(a+b)(a﹣b)﹣2a(a﹣b),其中.
(2)“绿水青山就是金山银山”,希望中学每年都会组织学生进行植树活动.今年该校又买了一批树苗,并组建了植树小组.如果每组植5棵,就会多出6棵树苗;如果每组植6棵,就会缺少9棵树苗.求学校这次共买了多少棵树苗?
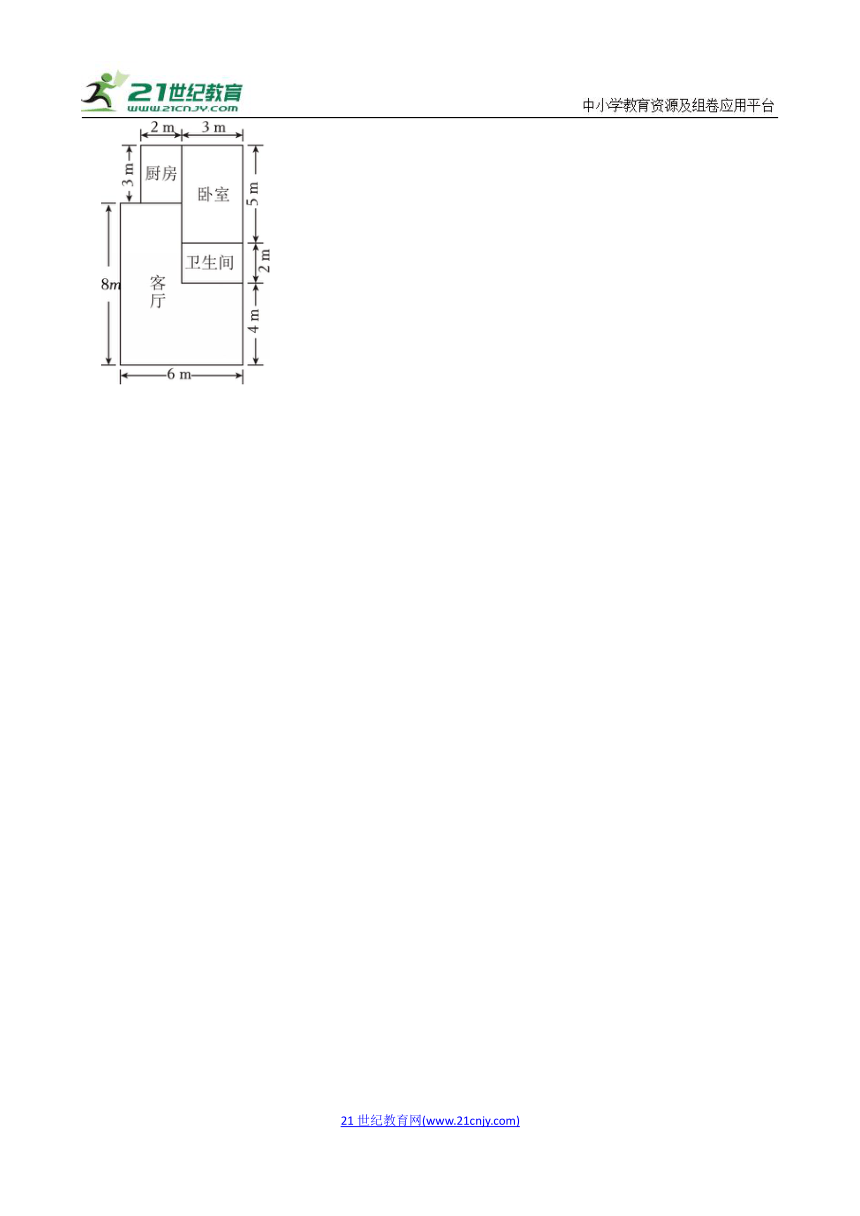
20.(2024 大兴区校级模拟)如图是某房屋的平面示意图.房主准备将客厅和卧室地面铺设木地板,厨房和卫生间地面铺设瓷砖.将房间地面全部铺设完预计需要花费10000元,其中包含安装费1270元.若每平方米木地板和瓷砖的价格之比是5:3,求每平方米木地板和瓷砖的价格.
2025年中考数学二轮复习考前预测:一元一次方程
参考答案与试题解析
一.选择题(共10小题)
1.(2025 佛山一模)方程﹣(|x+3|﹣|x﹣2|)=7满足x+3>0的解的个数为( )
A.5 B.3 C.6 D.0
【考点】含绝对值符号的一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】D
【分析】先求出x>﹣3,当x>﹣3时,|x+3|﹣|x﹣2|=﹣7,求解得出x=﹣4,可得出答案.
【解答】解:由条件可知x>﹣3,
当x>﹣3时,方程变形为:|x+3|﹣|x﹣2|=﹣7,
∴x+3﹣(2﹣x)=﹣7,
解得:x=﹣4,
∴方程﹣(|x+3|﹣|x﹣2|)=7满足x+3>0的解的个数为0,
故选:D.
【点评】本题考查一元一次不等式,绝对值方程,熟练掌握以上知识点是关键.
2.(2025 河北模拟)我国古代数学著作《九章算术》中有一道“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,井深几何?这道题大致意思是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺;如果将绳子折成四等份,那么每等份井外余绳一尺.问井深多少尺?下列说法正确的是( )
A.设井深为x尺,所列方程为3(x+4)=4(x﹣1)
B.设绳子的长为x尺,所列方程为
C.绳子的长是32尺
D.井深8尺
【考点】由实际问题抽象出一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】D
【分析】用代数式表示井深即可得方程.此题中的等量关系有:①将绳三折测之,绳多四尺;②绳四折测之,绳多一尺.据此解答即可.
【解答】解:设井深为x尺,故3(x+4)=4(x+1),故选项A错误,不符合题意;
设绳子的长为x尺,根据井深度一定,可得,故选项B错误,不符合题意;
解方程3(x+4)=4(x+1)得,x=8,
∴井深为8尺,绳长为3×(8+4)=36尺,故选项C错误,不符合题意;选项D正确,符合题意.
故选:D.
【点评】此题主要考查了由实际问题抽象出一元一次方程,理解题意是关键.
3.(2025 泗洪县一模)我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗,今持粟三斛,得酒五斗,问清,醑酒各几何?”大意是:现有一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒,醑酒各几斗?如果设清酒x斗,那么可列方程为( )
A.10x+3(5﹣x)=30 B.3x+10(5﹣x)=30
C. D.
【考点】由实际问题抽象出一元一次方程;数学常识.
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】根据共换了5斗酒,其中清酒x斗,则可得到醑酒(5﹣x)斗,再根据拿30斗谷子,共换了5斗酒,即可列出相应的方程.
【解答】解:设清酒x斗,则醑酒(5﹣x)斗,
由题意可得:10x+3(5﹣x)=30,
故选:A.
【点评】本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程.
4.(2025 山东一模)如图,线段AB=20cm,O是线段AB上的中点,P、Q是线段AB上的动点,点P沿A→B→A以4cm/s的速度运动,点Q沿B→A以2cm/s的速度运动.若P、Q点同时运动,当OP=OQ时,运动时间为( )
A.0s、10s或 B.0s、5s或
C.0s、、或10s D.0s、5s、或
【考点】一元一次方程的应用;两点间的距离;线段的和差.
【专题】一次方程(组)及应用;运算能力.
【答案】C
【分析】设运动时间为t s,分别表示出OP和OQ的长,再结合OP=OQ列出方程,求出t的值即可解答.
【解答】解:由条件可知,
设运动时间为t s,则BQ=2tcm,
∴AQ=AB﹣BQ=(20﹣2t)cm,
∴OQ=|AQ﹣AO|=|20﹣2t﹣10|=|10﹣2t|cm,
∴分两种情况讨论:
①当点P沿A→B运动时,点P到达点B需要时间20÷4=5s,
当0≤t≤5时,AP=4tcm,
∴OP=|AO﹣AP|=|10﹣4t|cm,
∵OP=OQ,
∴|10﹣4t|=|10﹣2t|,
∴10﹣4t=10﹣2t或10﹣4t=2t﹣10,
解得:t=0或,
②当点P沿B→A运动时,此时5≤t≤10,BP=4t﹣20,
∴AP=AB﹣BP=20﹣(4t﹣20)=(40﹣4t)cm,
∴OP=|AP﹣AO|=|40﹣4t﹣10|=|30﹣4t|cm,
∵OP=OQ,
∴|30﹣4t|=|10﹣2t|,
∴30﹣4t=10﹣2t或30﹣4t=2t﹣10,
解得:t=10或,
∴综上所述,当OP=OQ时,运动时间为0s、、或10s.
故选:C.
【点评】本题考查了动点问题、一元一次方程的应用,学会根据两点间的距离列出方程是解题的关键.
5.(2025 茅箭区校级模拟)小明参加了一场2000米的跑步比赛,他以4米/秒的速度跑了一段路程后,又以3米/秒的速度跑完了剩下的路程,一共花了10分钟,设小明以4米/秒的速度跑了x米,则列方程为( )
A.4x=3(x+10) B.
C. D.
【考点】由实际问题抽象出一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】D
【分析】根据“以4米/秒的速度跑了x米的时间+以3米/秒的速度跑了(2000﹣x)米的时间=60×10秒”建立方程即可得.
【解答】解:以4米/秒的速度跑了x米的时间+以3米/秒的速度跑了(2000﹣x)米的时间=60×10秒可列方程:
.
故选:D.
【点评】本题考查了列一元一次方程,找准等量关系,正确建立方程是解题关键.
6.(2024秋 兴隆县期末)解方程时,去分母正确的是( )
A.2x+1﹣(10x+1)=1 B.4x+1﹣10x+1=6
C.4x+2﹣10x﹣1=6 D.2(2x+1)﹣(10x+1)=1
【考点】解一元一次方程.
【专题】计算题;运算能力.
【答案】C
【分析】去分母的方法是方程两边同时乘以各分母的最小公倍数6,在去分母的过程中注意分数线右括号的作用,以及去分母时不能漏乘没有分母的项.
【解答】解:方程两边同时乘以6得:4x+2﹣(10x+1)=6,
去括号得:4x+2﹣10x﹣1=6.
故选:C.
【点评】在去分母的过程中注意分数线起到括号的作用,并注意不能漏乘没有分母的项.
7.(2024 祁阳市二模)《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )
A. B. C. D.
【考点】由实际问题抽象出一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】根据车的辆数不变,即可得出关于x的一元一次方程,此题得解.
【解答】解:依题意,得:+2=.
故选:A.
【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.
8.(2024 荷塘区校级模拟)若“△”是新规定的某种运算符号,设x△y=xy+x+y,则2△m=﹣16中,m的值为( )
A.8 B.﹣8 C.6 D.﹣6
【考点】解一元一次方程.
【专题】新定义.
【答案】D
【分析】利用题中的新定义化简所求方程,求出方程的解即可得到m的值.
【解答】解:根据题中的新定义得:2△m=2m+2+m=﹣16,
移项合并得:3m=﹣18,
解得:m=﹣6.
故选:D.
【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.
9.(2024 凉州区三模)小明在做题时不小心用墨水把方程污染了,污染后的方程:,答案显示此方程的解是x=﹣8,被墨水遮盖的是一个常数,则这个常数是( )
A.1 B.﹣1 C.﹣2 D.2
【考点】一元一次方程的解.
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】用a表示污染的数.把x=﹣8代入方程,即可得到一个关于a的方程,从而求解.
【解答】解:用a表示污染的数,把x=﹣8代入方程得:,
解得:a=1.
故选:A.
【点评】本题考查了方程的解的意义,解一元一次方程,弄懂方程的解就是能够使方程左右两边相等的未知数的值是关键.
10.(2024 滦南县校级模拟)下列运用等式的性质变形正确的是( )
A.若x=y,则x+5=y﹣5 B.若a2=b2,则a=b
C.若,则a=b D.若ax=ay,则x=y
【考点】等式的性质.
【专题】整式;推理能力.
【答案】C
【分析】根据等式的基本性质进而判断即可.
【解答】解:A:若x=y,则x+5=y+5,故A不正确,不合题意;
B:若a2=b2,则a=±b,故B不正确,不合题意;
C:若,则a=b,故C正确,符合题意;
D:若ax=ay,则a≠0时x=y,故D不正确,不合题意;
故选:C.
【点评】本题考查等式的基本性质,正确把握相关性质是解题的关键.
二.填空题(共5小题)
11.(2025 碑林区校级一模)某环保队有甲、乙、丙三支队伍,现计划在A地植树1000棵,在B地植树1250棵,甲、乙、丙每天分别能植树28、32、30棵.甲在A地,乙在B地,丙在A与B两地之间来回帮忙,同时开始,同时结束,丙在A地植树 300 棵.
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】300.
【分析】先设丙在A地植树x棵,则甲在A地植树(100﹣x)棵,然后根据甲在A地,乙在B地,丙在A与B两地之间来回帮忙,同时开始,同时结束,可以列出方程32×+30(﹣)=1250,然后求解即可.
【解答】解:设丙在A地植树x棵,
由题意可得:32×+30(﹣)=1250,
解得x=300,
答:丙在A地植树300棵,
故答案为:300.
【点评】本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的方程.
12.(2025 碑林区校级一模)父亲对儿子说:“我像你这么大时,你才4岁.当你像我这么大时,我就79岁了.”现在父亲 54 岁.
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】见试题解答内容
【分析】设现在父亲x岁,然后根据题意可知:他们的年龄差为(79﹣x)岁,再根据题意可以列出方程x﹣(79﹣x)=4+(79﹣x),然后求解即可.
【解答】解:设现在父亲x岁,
由题意可得:x﹣(79﹣x)=4+(79﹣x),
解得x=54,
答:现在父亲54岁,
故答案为:54.
【点评】本题考查一元一次方程的应用,解答本题的关键是明确题意,写出年龄差,列出相应的方程.
13.(2024 凉州区二模)已知(a﹣1)x|a|+2024=0是关于x的一元一次方程,则a= ﹣1 .
【考点】一元一次方程的定义;绝对值.
【专题】一次方程(组)及应用;运算能力.
【答案】﹣1.
【分析】根据一元一次方程的定义解答即可.
【解答】解:由题意得:|a|=1且a﹣1≠0,
∴a=﹣1,
故答案为:﹣1.
【点评】本题考查了一元一次方程的定义,熟知只含有一个未知数(元),且未知数的次数是1,这样的方程叫一元一次方程是解题的关键.
14.(2024 凉州区二模)已知关于x的一元一次方程x+3=2x+b的解为x=2,那么关于y的一元一次方程(y+1)+3=2(y+1)+b的解为y= 1 .
【考点】一元一次方程的解.
【专题】一次方程(组)及应用;运算能力.
【答案】见试题解答内容
【分析】根据已知条件得出方程y+1=2,求出方程的解即可.
【解答】解:∵关于x的一元一次方程x+3=2x+b的解为x=2,
∴关于y的一元一次方程(y+1)+3=2(y+1)+b中y+1=2,
解得:y=1,
故答案为:1.
【点评】本题考查了解一元一次方程和一元一次方程的解,掌握一元一次方程的解的定义是解此题的关键.
15.(2024 湘阴县二模)已知关于x的方程2x+m﹣8=0的解是x=5,则m的值为 ﹣2 .
【考点】一元一次方程的解;解一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】﹣2.
【分析】根据一元一次方程的解的定义把x=5代入关于x的方程2x+m﹣8=0中,得到关于m的一元一次方程,然后求解即可.
【解答】解:把x=5代入关于x的方程2x+m﹣8=0中,得2×5+m﹣8=0,
解得m=﹣2,
故答案为:﹣2.
【点评】本题考查了一元一次方程的解,解一元一次方程,熟知方程的解的定义是解题的关键.
三.解答题(共5小题)
16.(2025 雁塔区校级模拟)某班手工兴趣小组的同学们计划制作一批中国结送给敬老院作为新年礼物.如果每人制作9个,那么就比计划少做17个;如果每人制作12个,那么就比计划多做4个.这个手工兴趣小组共有多少人?计划要做的这批中国结有多少个?
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】这个手工兴趣小组共有7人,计划要做的这批中国结有80个.
【分析】设这个手工兴趣小组共有x人,由题意表示出计划做的个数为(9x+17)或(12x﹣4),由此列出方程求得人数,进一步求得计划做的个数即可.
【解答】解:设这个手工兴趣小组共有x人,
由题意可得:9x+17=12x﹣4,
解得:x=7,
∴9x+17=80,
答:这个手工兴趣小组共有7人,计划要做的这批中国结有80个.
【点评】本题考查了一元一次方程的应用,根据题意列出方程是解题的关键.
17.(2025 福田区一模)实验表明,物体在做匀加速直线运动时,速度V(m/s)随着运动时间t(s)的改变而改变,它的速度可用公式V=V0+at计算,已测得当t=1(s)时,速度 V=5.5(m/s);当t=6(s)时,速度 V=18(m/s),求:
(1)V0,a的值.
(2)当速度V=21(m/s) 时该物体的运动时间t.
【考点】解一元一次方程;解二元一次方程组.
【专题】一次方程(组)及应用;运算能力.
【答案】见试题解答内容
【分析】(1)由题意列得关于V0,a的二元一次方程组,解方程组即可;
(2)将V=21(m/s)代入公式,解方程即可.
【解答】解:(1)由题意可得,
解得:;
(2)由(1)可得V=3+2.5t,
当V=21(m/s)时,
即3+2.5t=21,
解得:t=7.2.
【点评】本题考查一元一次方程及二元一次方程组的应用,结合已知条件列得正确的方程组及方程是解题的关键.
18.(2025 雁塔区校级一模)袁隆平,“共和国勋章”获得者,中国工程院院士,“中国杂交水稻之父”,一生致力于对水稻的研究.现有A、B两块试验田各30亩,A块试验田种植普通水稻,B块试验田种植杂交水稻,杂交水稻的亩产量是普通水稻的1.2倍,两块试验田单次共收获水稻56100千克,求杂交水稻的亩产量是多少千克?
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】杂交水稻的亩产量是1020千克.
【分析】设普通水稻的亩产量是a千克,则杂交水稻的亩产量是1.2a千克,根据两块试验田单次共收获水稻56100千克,可得出关于a的一元一次方程,解之即可得出a的值,再将其代入1.2a中,即可求出结论.
【解答】解:设普通水稻的亩产量是a千克,根据题意得:30a+30×1.2a=56100,
解得:a=850,
∴1.2a=850×1.2=1020.
答:杂交水稻的亩产量是1020千克.
【点评】本题考查了一元一次方程的应用,理解题意,找到等量关系是关键.
19.(2024 天山区校级三模)(1)先化简,再求值:(a+b)2+(a+b)(a﹣b)﹣2a(a﹣b),其中.
(2)“绿水青山就是金山银山”,希望中学每年都会组织学生进行植树活动.今年该校又买了一批树苗,并组建了植树小组.如果每组植5棵,就会多出6棵树苗;如果每组植6棵,就会缺少9棵树苗.求学校这次共买了多少棵树苗?
【考点】一元一次方程的应用;整式的混合运算—化简求值.
【专题】一次方程(组)及应用;运算能力.
【答案】(1)4ab,﹣4;
(2)81棵树苗.
【分析】(1)先利用完全平方公式和平方差公式展开,再进行整式的加减计算,最后再代入求值;
(2)设学校这次共买了x棵树苗,根据组植5棵,就会多出6棵树苗;如果每组植6棵,就会缺少9棵树苗列出方程求解即可.
【解答】解:(1)原式=a2+2ab+b2+a2﹣b2﹣2a2+2ab
=4ab,
当,;
(2)设学校这次共买了x棵树苗,
,
∴x=81,
答:学校这次共买了81棵树苗.
【点评】本题考查了整式的混合运算,化简求值,一元一次方程的应用,熟练掌握知识点是解题的关键.
20.(2024 大兴区校级模拟)如图是某房屋的平面示意图.房主准备将客厅和卧室地面铺设木地板,厨房和卫生间地面铺设瓷砖.将房间地面全部铺设完预计需要花费10000元,其中包含安装费1270元.若每平方米木地板和瓷砖的价格之比是5:3,求每平方米木地板和瓷砖的价格.
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】150元,90元.
【分析】设每平方米木地板的价格为5x元,则每平方米瓷砖的价格为3x元,根据总费用为10000元列方程解答即可.
【解答】解:设每平方米木地板的价格为5x元,则每平方米瓷砖的价格为3x元,根据题意得:
[6×4+(6﹣3)×(5+2﹣3)+5×3] 5x+3×2×2×3x+1270=10000,
解得x=30,
∴每平方米木地板的价格为:5×30=150(元),每平方米瓷砖的价格为:3×30=90(元),
答:每平方米木地板和瓷砖的价格分别为150元,90元.
【点评】本题考查了一元一次方程的应用,根据题意列出方程是解题的关键.
21世纪教育网(www.21cnjy.com)
一.选择题(共10小题)
1.(2025 佛山一模)方程﹣(|x+3|﹣|x﹣2|)=7满足x+3>0的解的个数为( )
A.5 B.3 C.6 D.0
2.(2025 河北模拟)我国古代数学著作《九章算术》中有一道“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,井深几何?这道题大致意思是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺;如果将绳子折成四等份,那么每等份井外余绳一尺.问井深多少尺?下列说法正确的是( )
A.设井深为x尺,所列方程为3(x+4)=4(x﹣1)
B.设绳子的长为x尺,所列方程为
C.绳子的长是32尺
D.井深8尺
3.(2025 泗洪县一模)我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗,今持粟三斛,得酒五斗,问清,醑酒各几何?”大意是:现有一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒,醑酒各几斗?如果设清酒x斗,那么可列方程为( )
A.10x+3(5﹣x)=30 B.3x+10(5﹣x)=30
C. D.
4.(2025 山东一模)如图,线段AB=20cm,O是线段AB上的中点,P、Q是线段AB上的动点,点P沿A→B→A以4cm/s的速度运动,点Q沿B→A以2cm/s的速度运动.若P、Q点同时运动,当OP=OQ时,运动时间为( )
A.0s、10s或 B.0s、5s或
C.0s、、或10s D.0s、5s、或
5.(2025 茅箭区校级模拟)小明参加了一场2000米的跑步比赛,他以4米/秒的速度跑了一段路程后,又以3米/秒的速度跑完了剩下的路程,一共花了10分钟,设小明以4米/秒的速度跑了x米,则列方程为( )
A.4x=3(x+10) B.
C. D.
6.(2024秋 兴隆县期末)解方程时,去分母正确的是( )
A.2x+1﹣(10x+1)=1 B.4x+1﹣10x+1=6
C.4x+2﹣10x﹣1=6 D.2(2x+1)﹣(10x+1)=1
7.(2024 祁阳市二模)《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )
A. B. C. D.
8.(2024 荷塘区校级模拟)若“△”是新规定的某种运算符号,设x△y=xy+x+y,则2△m=﹣16中,m的值为( )
A.8 B.﹣8 C.6 D.﹣6
9.(2024 凉州区三模)小明在做题时不小心用墨水把方程污染了,污染后的方程:,答案显示此方程的解是x=﹣8,被墨水遮盖的是一个常数,则这个常数是( )
A.1 B.﹣1 C.﹣2 D.2
10.(2024 滦南县校级模拟)下列运用等式的性质变形正确的是( )
A.若x=y,则x+5=y﹣5 B.若a2=b2,则a=b
C.若,则a=b D.若ax=ay,则x=y
二.填空题(共5小题)
11.(2025 碑林区校级一模)某环保队有甲、乙、丙三支队伍,现计划在A地植树1000棵,在B地植树1250棵,甲、乙、丙每天分别能植树28、32、30棵.甲在A地,乙在B地,丙在A与B两地之间来回帮忙,同时开始,同时结束,丙在A地植树 棵.
12.(2025 碑林区校级一模)父亲对儿子说:“我像你这么大时,你才4岁.当你像我这么大时,我就79岁了.”现在父亲 岁.
13.(2024 凉州区二模)已知(a﹣1)x|a|+2024=0是关于x的一元一次方程,则a= .
14.(2024 凉州区二模)已知关于x的一元一次方程x+3=2x+b的解为x=2,那么关于y的一元一次方程(y+1)+3=2(y+1)+b的解为y= .
15.(2024 湘阴县二模)已知关于x的方程2x+m﹣8=0的解是x=5,则m的值为 .
三.解答题(共5小题)
16.(2025 雁塔区校级模拟)某班手工兴趣小组的同学们计划制作一批中国结送给敬老院作为新年礼物.如果每人制作9个,那么就比计划少做17个;如果每人制作12个,那么就比计划多做4个.这个手工兴趣小组共有多少人?计划要做的这批中国结有多少个?
17.(2025 福田区一模)实验表明,物体在做匀加速直线运动时,速度V(m/s)随着运动时间t(s)的改变而改变,它的速度可用公式V=V0+at计算,已测得当t=1(s)时,速度 V=5.5(m/s);当t=6(s)时,速度 V=18(m/s),求:
(1)V0,a的值.
(2)当速度V=21(m/s) 时该物体的运动时间t.
18.(2025 雁塔区校级一模)袁隆平,“共和国勋章”获得者,中国工程院院士,“中国杂交水稻之父”,一生致力于对水稻的研究.现有A、B两块试验田各30亩,A块试验田种植普通水稻,B块试验田种植杂交水稻,杂交水稻的亩产量是普通水稻的1.2倍,两块试验田单次共收获水稻56100千克,求杂交水稻的亩产量是多少千克?
19.(2024 天山区校级三模)(1)先化简,再求值:(a+b)2+(a+b)(a﹣b)﹣2a(a﹣b),其中.
(2)“绿水青山就是金山银山”,希望中学每年都会组织学生进行植树活动.今年该校又买了一批树苗,并组建了植树小组.如果每组植5棵,就会多出6棵树苗;如果每组植6棵,就会缺少9棵树苗.求学校这次共买了多少棵树苗?
20.(2024 大兴区校级模拟)如图是某房屋的平面示意图.房主准备将客厅和卧室地面铺设木地板,厨房和卫生间地面铺设瓷砖.将房间地面全部铺设完预计需要花费10000元,其中包含安装费1270元.若每平方米木地板和瓷砖的价格之比是5:3,求每平方米木地板和瓷砖的价格.
2025年中考数学二轮复习考前预测:一元一次方程
参考答案与试题解析
一.选择题(共10小题)
1.(2025 佛山一模)方程﹣(|x+3|﹣|x﹣2|)=7满足x+3>0的解的个数为( )
A.5 B.3 C.6 D.0
【考点】含绝对值符号的一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】D
【分析】先求出x>﹣3,当x>﹣3时,|x+3|﹣|x﹣2|=﹣7,求解得出x=﹣4,可得出答案.
【解答】解:由条件可知x>﹣3,
当x>﹣3时,方程变形为:|x+3|﹣|x﹣2|=﹣7,
∴x+3﹣(2﹣x)=﹣7,
解得:x=﹣4,
∴方程﹣(|x+3|﹣|x﹣2|)=7满足x+3>0的解的个数为0,
故选:D.
【点评】本题考查一元一次不等式,绝对值方程,熟练掌握以上知识点是关键.
2.(2025 河北模拟)我国古代数学著作《九章算术》中有一道“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,井深几何?这道题大致意思是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺;如果将绳子折成四等份,那么每等份井外余绳一尺.问井深多少尺?下列说法正确的是( )
A.设井深为x尺,所列方程为3(x+4)=4(x﹣1)
B.设绳子的长为x尺,所列方程为
C.绳子的长是32尺
D.井深8尺
【考点】由实际问题抽象出一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】D
【分析】用代数式表示井深即可得方程.此题中的等量关系有:①将绳三折测之,绳多四尺;②绳四折测之,绳多一尺.据此解答即可.
【解答】解:设井深为x尺,故3(x+4)=4(x+1),故选项A错误,不符合题意;
设绳子的长为x尺,根据井深度一定,可得,故选项B错误,不符合题意;
解方程3(x+4)=4(x+1)得,x=8,
∴井深为8尺,绳长为3×(8+4)=36尺,故选项C错误,不符合题意;选项D正确,符合题意.
故选:D.
【点评】此题主要考查了由实际问题抽象出一元一次方程,理解题意是关键.
3.(2025 泗洪县一模)我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗,今持粟三斛,得酒五斗,问清,醑酒各几何?”大意是:现有一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒,醑酒各几斗?如果设清酒x斗,那么可列方程为( )
A.10x+3(5﹣x)=30 B.3x+10(5﹣x)=30
C. D.
【考点】由实际问题抽象出一元一次方程;数学常识.
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】根据共换了5斗酒,其中清酒x斗,则可得到醑酒(5﹣x)斗,再根据拿30斗谷子,共换了5斗酒,即可列出相应的方程.
【解答】解:设清酒x斗,则醑酒(5﹣x)斗,
由题意可得:10x+3(5﹣x)=30,
故选:A.
【点评】本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程.
4.(2025 山东一模)如图,线段AB=20cm,O是线段AB上的中点,P、Q是线段AB上的动点,点P沿A→B→A以4cm/s的速度运动,点Q沿B→A以2cm/s的速度运动.若P、Q点同时运动,当OP=OQ时,运动时间为( )
A.0s、10s或 B.0s、5s或
C.0s、、或10s D.0s、5s、或
【考点】一元一次方程的应用;两点间的距离;线段的和差.
【专题】一次方程(组)及应用;运算能力.
【答案】C
【分析】设运动时间为t s,分别表示出OP和OQ的长,再结合OP=OQ列出方程,求出t的值即可解答.
【解答】解:由条件可知,
设运动时间为t s,则BQ=2tcm,
∴AQ=AB﹣BQ=(20﹣2t)cm,
∴OQ=|AQ﹣AO|=|20﹣2t﹣10|=|10﹣2t|cm,
∴分两种情况讨论:
①当点P沿A→B运动时,点P到达点B需要时间20÷4=5s,
当0≤t≤5时,AP=4tcm,
∴OP=|AO﹣AP|=|10﹣4t|cm,
∵OP=OQ,
∴|10﹣4t|=|10﹣2t|,
∴10﹣4t=10﹣2t或10﹣4t=2t﹣10,
解得:t=0或,
②当点P沿B→A运动时,此时5≤t≤10,BP=4t﹣20,
∴AP=AB﹣BP=20﹣(4t﹣20)=(40﹣4t)cm,
∴OP=|AP﹣AO|=|40﹣4t﹣10|=|30﹣4t|cm,
∵OP=OQ,
∴|30﹣4t|=|10﹣2t|,
∴30﹣4t=10﹣2t或30﹣4t=2t﹣10,
解得:t=10或,
∴综上所述,当OP=OQ时,运动时间为0s、、或10s.
故选:C.
【点评】本题考查了动点问题、一元一次方程的应用,学会根据两点间的距离列出方程是解题的关键.
5.(2025 茅箭区校级模拟)小明参加了一场2000米的跑步比赛,他以4米/秒的速度跑了一段路程后,又以3米/秒的速度跑完了剩下的路程,一共花了10分钟,设小明以4米/秒的速度跑了x米,则列方程为( )
A.4x=3(x+10) B.
C. D.
【考点】由实际问题抽象出一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】D
【分析】根据“以4米/秒的速度跑了x米的时间+以3米/秒的速度跑了(2000﹣x)米的时间=60×10秒”建立方程即可得.
【解答】解:以4米/秒的速度跑了x米的时间+以3米/秒的速度跑了(2000﹣x)米的时间=60×10秒可列方程:
.
故选:D.
【点评】本题考查了列一元一次方程,找准等量关系,正确建立方程是解题关键.
6.(2024秋 兴隆县期末)解方程时,去分母正确的是( )
A.2x+1﹣(10x+1)=1 B.4x+1﹣10x+1=6
C.4x+2﹣10x﹣1=6 D.2(2x+1)﹣(10x+1)=1
【考点】解一元一次方程.
【专题】计算题;运算能力.
【答案】C
【分析】去分母的方法是方程两边同时乘以各分母的最小公倍数6,在去分母的过程中注意分数线右括号的作用,以及去分母时不能漏乘没有分母的项.
【解答】解:方程两边同时乘以6得:4x+2﹣(10x+1)=6,
去括号得:4x+2﹣10x﹣1=6.
故选:C.
【点评】在去分母的过程中注意分数线起到括号的作用,并注意不能漏乘没有分母的项.
7.(2024 祁阳市二模)《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )
A. B. C. D.
【考点】由实际问题抽象出一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】根据车的辆数不变,即可得出关于x的一元一次方程,此题得解.
【解答】解:依题意,得:+2=.
故选:A.
【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.
8.(2024 荷塘区校级模拟)若“△”是新规定的某种运算符号,设x△y=xy+x+y,则2△m=﹣16中,m的值为( )
A.8 B.﹣8 C.6 D.﹣6
【考点】解一元一次方程.
【专题】新定义.
【答案】D
【分析】利用题中的新定义化简所求方程,求出方程的解即可得到m的值.
【解答】解:根据题中的新定义得:2△m=2m+2+m=﹣16,
移项合并得:3m=﹣18,
解得:m=﹣6.
故选:D.
【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.
9.(2024 凉州区三模)小明在做题时不小心用墨水把方程污染了,污染后的方程:,答案显示此方程的解是x=﹣8,被墨水遮盖的是一个常数,则这个常数是( )
A.1 B.﹣1 C.﹣2 D.2
【考点】一元一次方程的解.
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】用a表示污染的数.把x=﹣8代入方程,即可得到一个关于a的方程,从而求解.
【解答】解:用a表示污染的数,把x=﹣8代入方程得:,
解得:a=1.
故选:A.
【点评】本题考查了方程的解的意义,解一元一次方程,弄懂方程的解就是能够使方程左右两边相等的未知数的值是关键.
10.(2024 滦南县校级模拟)下列运用等式的性质变形正确的是( )
A.若x=y,则x+5=y﹣5 B.若a2=b2,则a=b
C.若,则a=b D.若ax=ay,则x=y
【考点】等式的性质.
【专题】整式;推理能力.
【答案】C
【分析】根据等式的基本性质进而判断即可.
【解答】解:A:若x=y,则x+5=y+5,故A不正确,不合题意;
B:若a2=b2,则a=±b,故B不正确,不合题意;
C:若,则a=b,故C正确,符合题意;
D:若ax=ay,则a≠0时x=y,故D不正确,不合题意;
故选:C.
【点评】本题考查等式的基本性质,正确把握相关性质是解题的关键.
二.填空题(共5小题)
11.(2025 碑林区校级一模)某环保队有甲、乙、丙三支队伍,现计划在A地植树1000棵,在B地植树1250棵,甲、乙、丙每天分别能植树28、32、30棵.甲在A地,乙在B地,丙在A与B两地之间来回帮忙,同时开始,同时结束,丙在A地植树 300 棵.
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】300.
【分析】先设丙在A地植树x棵,则甲在A地植树(100﹣x)棵,然后根据甲在A地,乙在B地,丙在A与B两地之间来回帮忙,同时开始,同时结束,可以列出方程32×+30(﹣)=1250,然后求解即可.
【解答】解:设丙在A地植树x棵,
由题意可得:32×+30(﹣)=1250,
解得x=300,
答:丙在A地植树300棵,
故答案为:300.
【点评】本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的方程.
12.(2025 碑林区校级一模)父亲对儿子说:“我像你这么大时,你才4岁.当你像我这么大时,我就79岁了.”现在父亲 54 岁.
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】见试题解答内容
【分析】设现在父亲x岁,然后根据题意可知:他们的年龄差为(79﹣x)岁,再根据题意可以列出方程x﹣(79﹣x)=4+(79﹣x),然后求解即可.
【解答】解:设现在父亲x岁,
由题意可得:x﹣(79﹣x)=4+(79﹣x),
解得x=54,
答:现在父亲54岁,
故答案为:54.
【点评】本题考查一元一次方程的应用,解答本题的关键是明确题意,写出年龄差,列出相应的方程.
13.(2024 凉州区二模)已知(a﹣1)x|a|+2024=0是关于x的一元一次方程,则a= ﹣1 .
【考点】一元一次方程的定义;绝对值.
【专题】一次方程(组)及应用;运算能力.
【答案】﹣1.
【分析】根据一元一次方程的定义解答即可.
【解答】解:由题意得:|a|=1且a﹣1≠0,
∴a=﹣1,
故答案为:﹣1.
【点评】本题考查了一元一次方程的定义,熟知只含有一个未知数(元),且未知数的次数是1,这样的方程叫一元一次方程是解题的关键.
14.(2024 凉州区二模)已知关于x的一元一次方程x+3=2x+b的解为x=2,那么关于y的一元一次方程(y+1)+3=2(y+1)+b的解为y= 1 .
【考点】一元一次方程的解.
【专题】一次方程(组)及应用;运算能力.
【答案】见试题解答内容
【分析】根据已知条件得出方程y+1=2,求出方程的解即可.
【解答】解:∵关于x的一元一次方程x+3=2x+b的解为x=2,
∴关于y的一元一次方程(y+1)+3=2(y+1)+b中y+1=2,
解得:y=1,
故答案为:1.
【点评】本题考查了解一元一次方程和一元一次方程的解,掌握一元一次方程的解的定义是解此题的关键.
15.(2024 湘阴县二模)已知关于x的方程2x+m﹣8=0的解是x=5,则m的值为 ﹣2 .
【考点】一元一次方程的解;解一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】﹣2.
【分析】根据一元一次方程的解的定义把x=5代入关于x的方程2x+m﹣8=0中,得到关于m的一元一次方程,然后求解即可.
【解答】解:把x=5代入关于x的方程2x+m﹣8=0中,得2×5+m﹣8=0,
解得m=﹣2,
故答案为:﹣2.
【点评】本题考查了一元一次方程的解,解一元一次方程,熟知方程的解的定义是解题的关键.
三.解答题(共5小题)
16.(2025 雁塔区校级模拟)某班手工兴趣小组的同学们计划制作一批中国结送给敬老院作为新年礼物.如果每人制作9个,那么就比计划少做17个;如果每人制作12个,那么就比计划多做4个.这个手工兴趣小组共有多少人?计划要做的这批中国结有多少个?
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】这个手工兴趣小组共有7人,计划要做的这批中国结有80个.
【分析】设这个手工兴趣小组共有x人,由题意表示出计划做的个数为(9x+17)或(12x﹣4),由此列出方程求得人数,进一步求得计划做的个数即可.
【解答】解:设这个手工兴趣小组共有x人,
由题意可得:9x+17=12x﹣4,
解得:x=7,
∴9x+17=80,
答:这个手工兴趣小组共有7人,计划要做的这批中国结有80个.
【点评】本题考查了一元一次方程的应用,根据题意列出方程是解题的关键.
17.(2025 福田区一模)实验表明,物体在做匀加速直线运动时,速度V(m/s)随着运动时间t(s)的改变而改变,它的速度可用公式V=V0+at计算,已测得当t=1(s)时,速度 V=5.5(m/s);当t=6(s)时,速度 V=18(m/s),求:
(1)V0,a的值.
(2)当速度V=21(m/s) 时该物体的运动时间t.
【考点】解一元一次方程;解二元一次方程组.
【专题】一次方程(组)及应用;运算能力.
【答案】见试题解答内容
【分析】(1)由题意列得关于V0,a的二元一次方程组,解方程组即可;
(2)将V=21(m/s)代入公式,解方程即可.
【解答】解:(1)由题意可得,
解得:;
(2)由(1)可得V=3+2.5t,
当V=21(m/s)时,
即3+2.5t=21,
解得:t=7.2.
【点评】本题考查一元一次方程及二元一次方程组的应用,结合已知条件列得正确的方程组及方程是解题的关键.
18.(2025 雁塔区校级一模)袁隆平,“共和国勋章”获得者,中国工程院院士,“中国杂交水稻之父”,一生致力于对水稻的研究.现有A、B两块试验田各30亩,A块试验田种植普通水稻,B块试验田种植杂交水稻,杂交水稻的亩产量是普通水稻的1.2倍,两块试验田单次共收获水稻56100千克,求杂交水稻的亩产量是多少千克?
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】杂交水稻的亩产量是1020千克.
【分析】设普通水稻的亩产量是a千克,则杂交水稻的亩产量是1.2a千克,根据两块试验田单次共收获水稻56100千克,可得出关于a的一元一次方程,解之即可得出a的值,再将其代入1.2a中,即可求出结论.
【解答】解:设普通水稻的亩产量是a千克,根据题意得:30a+30×1.2a=56100,
解得:a=850,
∴1.2a=850×1.2=1020.
答:杂交水稻的亩产量是1020千克.
【点评】本题考查了一元一次方程的应用,理解题意,找到等量关系是关键.
19.(2024 天山区校级三模)(1)先化简,再求值:(a+b)2+(a+b)(a﹣b)﹣2a(a﹣b),其中.
(2)“绿水青山就是金山银山”,希望中学每年都会组织学生进行植树活动.今年该校又买了一批树苗,并组建了植树小组.如果每组植5棵,就会多出6棵树苗;如果每组植6棵,就会缺少9棵树苗.求学校这次共买了多少棵树苗?
【考点】一元一次方程的应用;整式的混合运算—化简求值.
【专题】一次方程(组)及应用;运算能力.
【答案】(1)4ab,﹣4;
(2)81棵树苗.
【分析】(1)先利用完全平方公式和平方差公式展开,再进行整式的加减计算,最后再代入求值;
(2)设学校这次共买了x棵树苗,根据组植5棵,就会多出6棵树苗;如果每组植6棵,就会缺少9棵树苗列出方程求解即可.
【解答】解:(1)原式=a2+2ab+b2+a2﹣b2﹣2a2+2ab
=4ab,
当,;
(2)设学校这次共买了x棵树苗,
,
∴x=81,
答:学校这次共买了81棵树苗.
【点评】本题考查了整式的混合运算,化简求值,一元一次方程的应用,熟练掌握知识点是解题的关键.
20.(2024 大兴区校级模拟)如图是某房屋的平面示意图.房主准备将客厅和卧室地面铺设木地板,厨房和卫生间地面铺设瓷砖.将房间地面全部铺设完预计需要花费10000元,其中包含安装费1270元.若每平方米木地板和瓷砖的价格之比是5:3,求每平方米木地板和瓷砖的价格.
【考点】一元一次方程的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】150元,90元.
【分析】设每平方米木地板的价格为5x元,则每平方米瓷砖的价格为3x元,根据总费用为10000元列方程解答即可.
【解答】解:设每平方米木地板的价格为5x元,则每平方米瓷砖的价格为3x元,根据题意得:
[6×4+(6﹣3)×(5+2﹣3)+5×3] 5x+3×2×2×3x+1270=10000,
解得x=30,
∴每平方米木地板的价格为:5×30=150(元),每平方米瓷砖的价格为:3×30=90(元),
答:每平方米木地板和瓷砖的价格分别为150元,90元.
【点评】本题考查了一元一次方程的应用,根据题意列出方程是解题的关键.
21世纪教育网(www.21cnjy.com)
同课章节目录
