高考二轮复习微专题 球的切接问题 课件(共34张PPT)
文档属性
| 名称 | 高考二轮复习微专题 球的切接问题 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-13 07:03:30 | ||
图片预览








文档简介
(共34张PPT)
微专题 球的切接问题
一、多面体与球的切接问题
(一)正方体与球
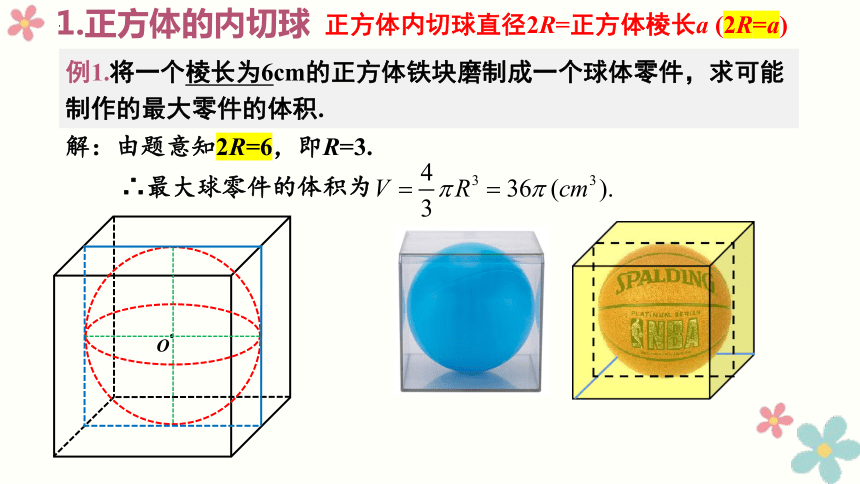
例1.将一个棱长为6cm的正方体铁块磨制成一个球体零件,求可能制作的最大零件的体积.
O
解:由题意知2R=6,即R=3.
∴最大球零件的体积为
正方体内切球直径2R=正方体棱长a (2R=a)
1.正方体的内切球
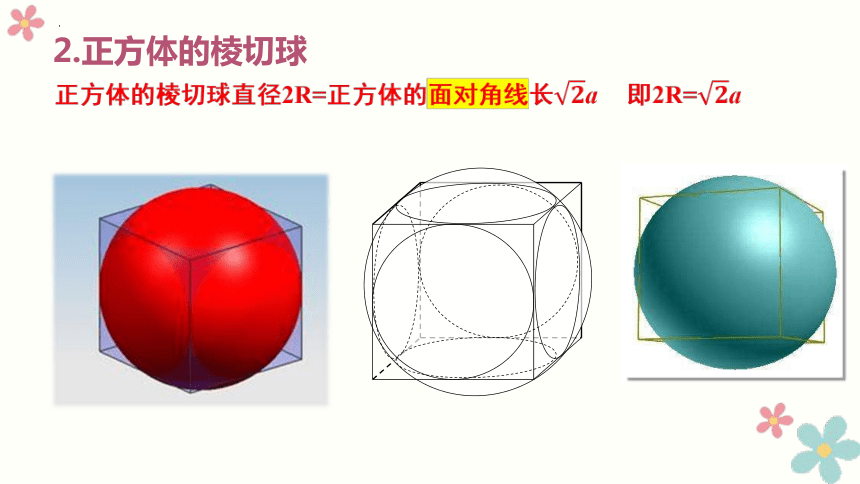
2.正方体的棱切球
正方体的棱切球直径2R=正方体的面对角线长a
即2R=a
例2.棱长为a cm的正方体的顶点都在球面上,
求球的体积.
3.正方体的外接球
③正方体的外接球直径=正方体体对角线长.
正方体的中心与其外接球球心重合.
[变式1]一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为____.
一、多面体与球的切接问题
(二)长方体与球
思考:一般的长方体有内切球吗?
如果一个长方体有内切球,那么它一定是
正方体
1.长方体的内切球
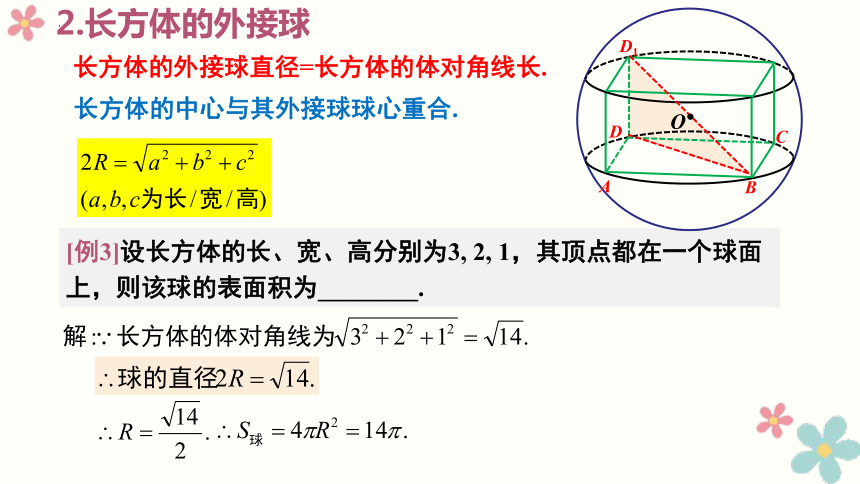
[例3]设长方体的长、宽、高分别为3, 2, 1,其顶点都在一个球面上,则该球的表面积为________.
2.长方体的外接球
O
长方体的外接球直径=长方体的体对角线长.
长方体的中心与其外接球球心重合.
A
B
C
D
D1
2.长方体的外接球
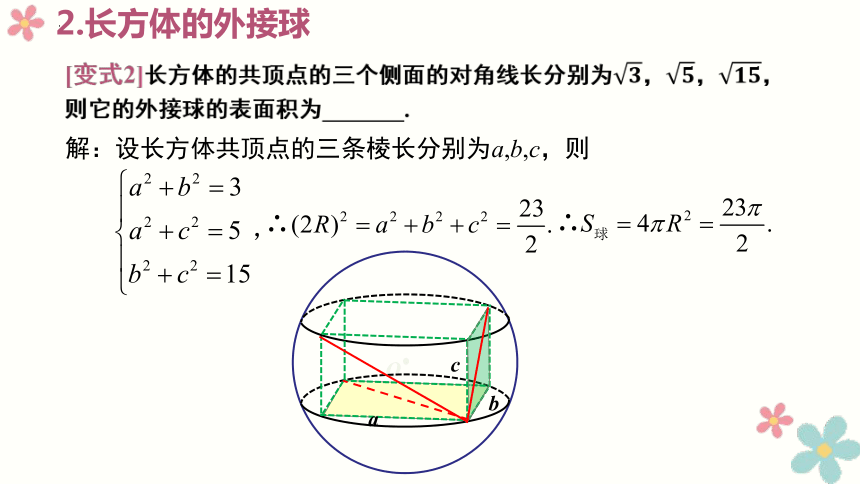
解:设长方体共顶点的三条棱长分别为a,b,c,则
O
a
b
c
[变式2]长方体的共顶点的三个侧面的对角线长分别为,,,则它的外接球的表面积为_______.
一、多面体与球的切接问题
(三)正棱锥与球
法1:等体积法
1.正棱锥的内切球
1.正棱锥的内切球
练习:已知正四棱锥的侧棱长为 ,底面边长为2,则该四棱锥的内切球的体积为_________.
1.正棱锥的内切球
法2:利用相似三角形求内切球的半径
1.正棱锥的内切球
2.正棱锥的外接球
正棱锥的外接球球心在其高上.
底面正多边形的外接圆圆心为Q,半径为r,
正棱锥外接球半径为R,高为h
[例5]已知正三棱锥的四个顶点都在同一个球面上,若该棱锥的高为4,底面边长为2,则此球的半径为____.
一、多面体与球的切接问题
(四)正四面体与球
O
D
R
O′
P
C
B
A
a
R
O
A
D
O′
P
R
a
R
若正四面体的棱长为a,高为h,正四面体的外接球半径为R,内切球半径为r,则h=a,R=a,r=a,R:r=3:1.
r
8.正四面体的外接球、内切球
O
D
R
O′
P
C
B
A
a
(法1)如图构造直角三角形.
R
O
A
D
O′
P
R
a
R
8.正四面体的外接球
若棱长为a的正四面体的各个顶点都在半径为R的球面上,求球的表面积.
(法2:补形法)把正四面体放在正方体中,
则正方体的外接球就是正四面体的外接球,
设正方体棱长为x,
O
P
C
B
A
8.正四面体的外接球
若棱长为a的正四面体的各个顶点都在半径为R的球面上,求球的表面积.
正四面体内切球与外接球
一、多面体与球的切接问题
(五)正三棱柱与球
[例7]设直三棱柱的所有棱长都为2,且顶点都在一个球面上,则该球的表面积为______.
5.正三棱柱的外接球
球心到正三棱柱两底面的距离相等。
O
O2
C
B
A
2
O1
2
正三棱柱两底面中心连线的中点为其外接球球心.
D
二、旋转体与球的切接问题
1.圆柱的外接球
1.圆柱的外接球
2.圆锥的外接球
[例9]球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该圆锥的体积和此球体积的比值为_______.
O
2.圆锥的外接球
解:①当圆锥顶点与底面在球心两侧时,设球的半径为r,
②当圆锥顶点与底面在球心同侧时,设球的半径为r,
三、补形法
(一)补形为长方体
1.底面是直角三角形的直三棱柱
A
B
C
A
B
C
例10
2.三条侧棱两两垂直的三棱锥
例11.在球面上有四个点P,A,B,C,若PA,PB,PC两两垂直
且PA=PB=PC=2,则该球的体积为_____.
END
微专题 球的切接问题
一、多面体与球的切接问题
(一)正方体与球
例1.将一个棱长为6cm的正方体铁块磨制成一个球体零件,求可能制作的最大零件的体积.
O
解:由题意知2R=6,即R=3.
∴最大球零件的体积为
正方体内切球直径2R=正方体棱长a (2R=a)
1.正方体的内切球
2.正方体的棱切球
正方体的棱切球直径2R=正方体的面对角线长a
即2R=a
例2.棱长为a cm的正方体的顶点都在球面上,
求球的体积.
3.正方体的外接球
③正方体的外接球直径=正方体体对角线长.
正方体的中心与其外接球球心重合.
[变式1]一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为____.
一、多面体与球的切接问题
(二)长方体与球
思考:一般的长方体有内切球吗?
如果一个长方体有内切球,那么它一定是
正方体
1.长方体的内切球
[例3]设长方体的长、宽、高分别为3, 2, 1,其顶点都在一个球面上,则该球的表面积为________.
2.长方体的外接球
O
长方体的外接球直径=长方体的体对角线长.
长方体的中心与其外接球球心重合.
A
B
C
D
D1
2.长方体的外接球
解:设长方体共顶点的三条棱长分别为a,b,c,则
O
a
b
c
[变式2]长方体的共顶点的三个侧面的对角线长分别为,,,则它的外接球的表面积为_______.
一、多面体与球的切接问题
(三)正棱锥与球
法1:等体积法
1.正棱锥的内切球
1.正棱锥的内切球
练习:已知正四棱锥的侧棱长为 ,底面边长为2,则该四棱锥的内切球的体积为_________.
1.正棱锥的内切球
法2:利用相似三角形求内切球的半径
1.正棱锥的内切球
2.正棱锥的外接球
正棱锥的外接球球心在其高上.
底面正多边形的外接圆圆心为Q,半径为r,
正棱锥外接球半径为R,高为h
[例5]已知正三棱锥的四个顶点都在同一个球面上,若该棱锥的高为4,底面边长为2,则此球的半径为____.
一、多面体与球的切接问题
(四)正四面体与球
O
D
R
O′
P
C
B
A
a
R
O
A
D
O′
P
R
a
R
若正四面体的棱长为a,高为h,正四面体的外接球半径为R,内切球半径为r,则h=a,R=a,r=a,R:r=3:1.
r
8.正四面体的外接球、内切球
O
D
R
O′
P
C
B
A
a
(法1)如图构造直角三角形.
R
O
A
D
O′
P
R
a
R
8.正四面体的外接球
若棱长为a的正四面体的各个顶点都在半径为R的球面上,求球的表面积.
(法2:补形法)把正四面体放在正方体中,
则正方体的外接球就是正四面体的外接球,
设正方体棱长为x,
O
P
C
B
A
8.正四面体的外接球
若棱长为a的正四面体的各个顶点都在半径为R的球面上,求球的表面积.
正四面体内切球与外接球
一、多面体与球的切接问题
(五)正三棱柱与球
[例7]设直三棱柱的所有棱长都为2,且顶点都在一个球面上,则该球的表面积为______.
5.正三棱柱的外接球
球心到正三棱柱两底面的距离相等。
O
O2
C
B
A
2
O1
2
正三棱柱两底面中心连线的中点为其外接球球心.
D
二、旋转体与球的切接问题
1.圆柱的外接球
1.圆柱的外接球
2.圆锥的外接球
[例9]球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该圆锥的体积和此球体积的比值为_______.
O
2.圆锥的外接球
解:①当圆锥顶点与底面在球心两侧时,设球的半径为r,
②当圆锥顶点与底面在球心同侧时,设球的半径为r,
三、补形法
(一)补形为长方体
1.底面是直角三角形的直三棱柱
A
B
C
A
B
C
例10
2.三条侧棱两两垂直的三棱锥
例11.在球面上有四个点P,A,B,C,若PA,PB,PC两两垂直
且PA=PB=PC=2,则该球的体积为_____.
END
同课章节目录
