2025年九年级中考数学三轮冲刺练习反比例函数综合训练(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习反比例函数综合训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 912.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 14:35:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习反比例函数综合训练
1.如图,一次函数y=kx+2(k≠0)的图象与反比例函数的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(﹣4,0).
(1)求k与m的值;
(2)P为x轴上的一动点,当△APC的面积为9时,求点P的坐标;
(3)在y轴上是否存在点Q使得△ACQ为等腰三角形,若存在,请直接写出点Q的坐标.
2.已知:一次函数yx+m与反比例函数y的图象在第一象限的交点为A(1,n).
(1)求m与n的值;
(2)设一次函数的图象与x轴交于点B,C为x轴上一点,连接AC,若△ABC为等腰三角形,求C的坐标.
3.如图,矩形ABCO的顶点C,A分别在x轴、y轴的正半轴上,点B的坐标为(4,2),反比例函数的图象经过AB的中点D,与BC交于点E,连接OD,OE,DE.
(1)直接写出结果:k= ,点E的坐标为 ;
(2)点M是y轴正半轴上一点,若S△MBO=S△ODE,求点M的坐标;
(3)点P为x轴上一点,点Q为反比例函数图象上一点,是否存在点P,Q,使得以点P,Q,D,E为顶点的四边形为平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由.
4.如图,一次函数y=ax+b(a≠0)的图象与反比例函数(k≠0)的图象交于点A(﹣1,4),B(n,﹣1).
(1)求反比例函数和一次函数的表达式;
(2)利用图象,直接写出不等式的解集;
(3)已知点D在x轴上,点C在反比例函数图象上.若以A、B、C、D为顶点的四边形是平行四边形,求点C的坐标.
5.平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
6.已知:一次函数y=﹣2x+10的图象与反比例函数y(k>0)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若,求△ABC的面积.
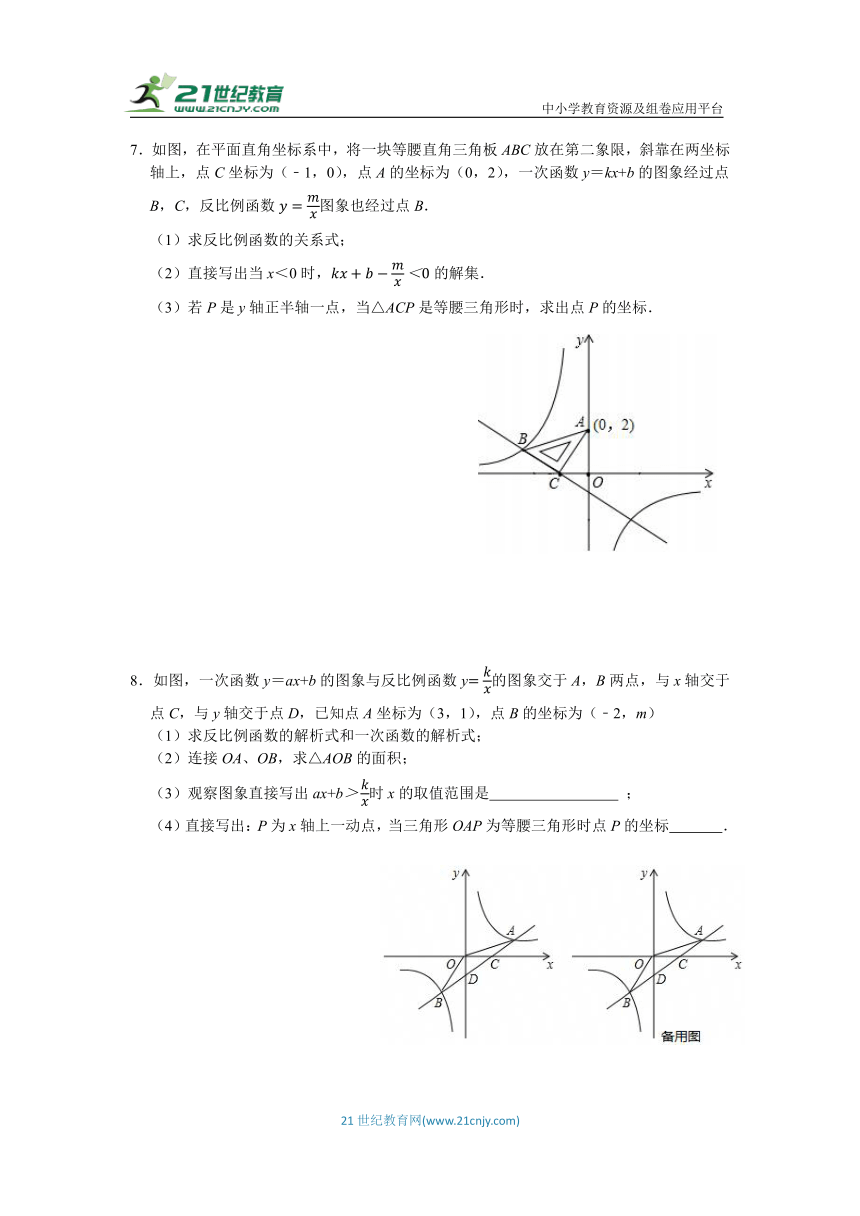
7.如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(﹣1,0),点A的坐标为(0,2),一次函数y=kx+b的图象经过点B,C,反比例函数图象也经过点B.
(1)求反比例函数的关系式;
(2)直接写出当x<0时,的解集.
(3)若P是y轴正半轴一点,当△ACP是等腰三角形时,求出点P的坐标.
8.如图,一次函数y=ax+b的图象与反比例函数y的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知点A坐标为(3,1),点B的坐标为(﹣2,m)
(1)求反比例函数的解析式和一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)观察图象直接写出ax+b时x的取值范围是 ;
(4)直接写出:P为x轴上一动点,当三角形OAP为等腰三角形时点P的坐标 .
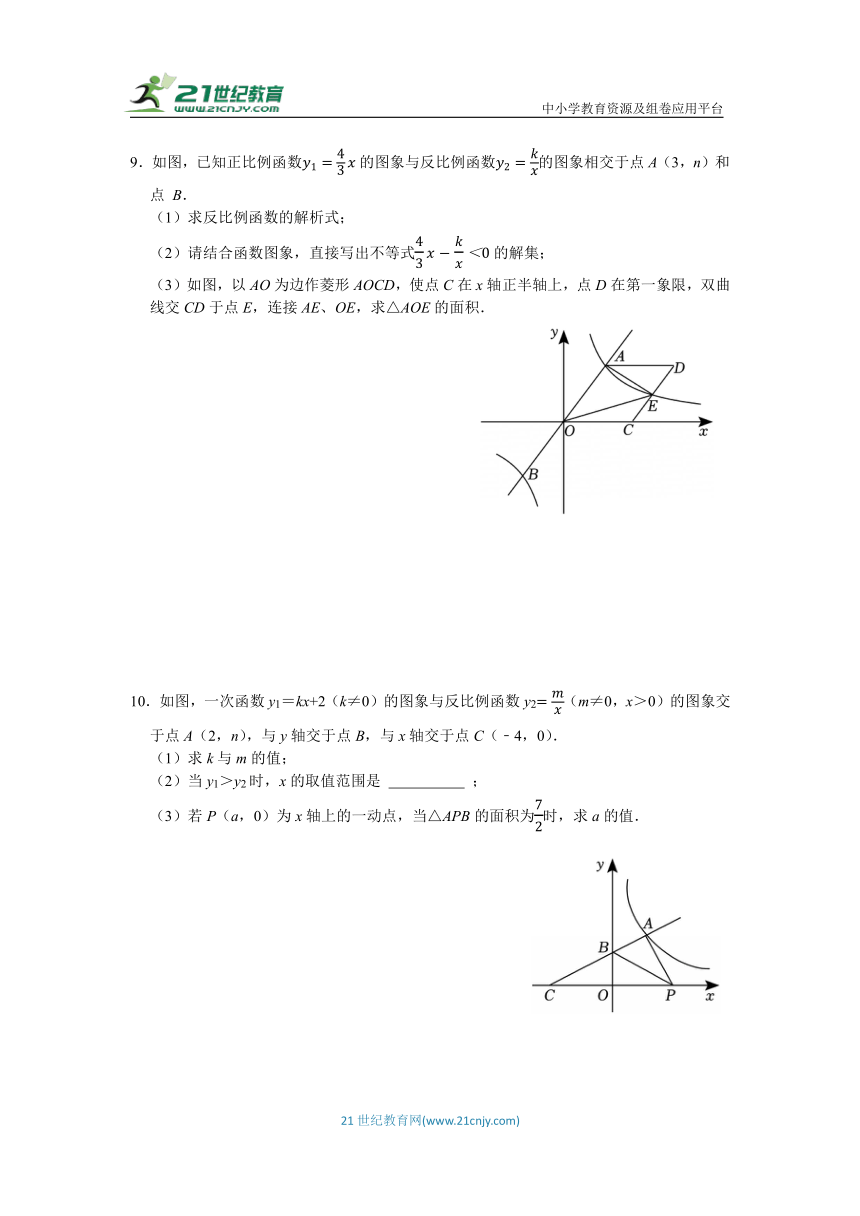
9.如图,已知正比例函数的图象与反比例函数的图象相交于点A(3,n)和点 B.
(1)求反比例函数的解析式;
(2)请结合函数图象,直接写出不等式的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
10.如图,一次函数y1=kx+2(k≠0)的图象与反比例函数y2(m≠0,x>0)的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(﹣4,0).
(1)求k与m的值;
(2)当y1>y2时,x的取值范围是 ;
(3)若P(a,0)为x轴上的一动点,当△APB的面积为时,求a的值.
11.如图(1),菱形ABCD顶点A在y轴上,顶点D在反比例函数上,边BC交y轴于点E,AD∥x轴,AE=2EC,AD=5.
(1)求k.
(2)如图(2),延长BA交x轴于点F,问是否在该反比例函数上存在点P,坐标轴上的点Q,使得以A、F、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点Q的坐标,若不存在,请说明理由.
12.如图1,已知A(﹣1,0),B(0,﹣2),平行四边形ABCD的边AD、BC分别与y轴、x轴交于点E、F,且点E为AD中点,双曲线y(k为常数,k≠0)经过C、D两点.
(1)求k的值;
(2)如图2,点G是y轴正半轴上的一个动点,过点G作y轴的垂线,分别交反比例函数y(k为常数,k≠0)图象于点M,交反比例函数y(x<0)的图象于点N,当FM=FN时,求G点坐标;
(3)点P在双曲线y上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求出满足要求的所有点Q的坐标.
13.如图1,正方形ABCD中,C(﹣2,0),D(0,3).过A点作AF⊥y轴于F点,过B点作x轴的垂线交过A点的反比例函数的图象于E点,交x轴于G点.
(1)求证:△CDO≌△DAF;
(2)求反比例函数的表达式及点E的坐标;
(3)如图2,过点C作直线l∥AE,点P是直线l上的一点,在平面内是否存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形,若存在,请直接写出点Q的横坐标,若不存在,请说明理由.
14.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数(k>0,x>0)的图象上,点D的坐标为(4,3).设AB所在直线解析式为y=ax+b(a≠0).
(1)求反比例和一次函数解析式;
(2)若将菱形ABCD沿x轴正方向平移m个单位,在平移中若反比例函数图象与菱形的边AD始终有交点,求m的取值范围;
(3)在直线AB上是否存在M、N两点,使以MNOD四点的四边形构成矩形?若不存在,请说明理由,若存在直接求出M、N(点M在点N的上方)两点的坐标.
15.如图,矩形OABC的顶点A,C分别在x轴,y轴上,点O为坐标原点,点B的坐标为(2,3),反比例函数的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求反比例函数的解析式;
(2)求△BDE的面积;
(3)若点F是y轴上一点,且△FBC与△DEB相似,求点F的坐标.
16.如图,一次函数y1=mx+n与反比例函数y2(x>0)的图象分别交于点A(a,4)和点B(8,1),与坐标轴分别交于点C和点D.
(1)求一次函数与反比例函数的表达式.
(2)直接写出不等式mx+n(x>0)的解集.
(3)在x轴上是否存在点P,使△COD与△ADP相似,若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
1.【解答】解:(1)把C(﹣4,0)代入y=kx+2得:0=﹣4k+2,
解得:k.把A(2,n)代入y=kx+2得:n=3.
∴A(2,3).
把A(2,3)代入得:m=2×3=6.
∴k的值为,m的值为6;
(2)设点P(x,0),
则△APC的面积CP×yA|x+4|×3=9,
解得:x=2或﹣10,
即点P(2,0)或(﹣10,0);
(3)存在,理由:
设点Q(0,y),
由点A、C、Q的坐标得,AC2=45,CQ2=16+y2,AQ2=4+(y﹣3)2,
当CA=CQ时,
则45=16+y2,则y=±,
则点P(0,)或(0,);
当AC=AQ或CQ=AQ时,
同理可得:16+y2=4+(y﹣3)2或45=4+(y﹣3)2,
解得:y或3±,
则点P(0,)或(0,3)或(0,3).
综上,P(0,)或(0,)或(0,)或(0,3)或(0,3).
2.【解答】解:(1)∵A(1,n)在反比例数的图象上,
∴,
∴n=2,
∴A(1,2),
将A(1,2)代入得:
,
解得:;
(2)由(1)得,
当y=0时,x=﹣5,
∵一次函数的图象与x轴交于点B,
∴B(﹣5,0),
∴,
如图所示,设C(x,0),
当BC=BA时,点C的坐标为或;
当CB=CA时,得:CB2=CA2,
∴(x+5)2=(1﹣x)2+22,
解得:;
当AB=AC时,
∵A(1,2),xA﹣xB=6,
∴C(7,0),
综上所述满足条件的点C坐标为或或或C(7,0).
3.【解答】解:(1)∵矩形ABCO的顶点C,A分别在x轴、y轴的正半轴上,点B的坐标为(4,2),
∴BA⊥y轴,BC⊥x轴,A(0,2),
∵D是AB的中点,
∴D(2,2),
∵,反比例函数的图象经过AB的中点D,与BC交于点E,将点D的坐标代入得:
,
解得:k=4,
∴反比例函数解析式为,
在中,当x=4时,,
∴E(4,1),
故答案为:4;(4,1);
(2)设点M(0,m),
∵B(4,2),D(2,2),E(4,1),
∴,,
当△MBO的面积等于△ODE的面积时,3=2m,
解得:,
∴;
(3)存在点P,Q,使得以点P,Q,D,E为顶点的四边形为平行四边形;理由如下:
设点P(p,0),
∵点P,Q,D,E为顶点的四边形为平行四边形,
∴当以DE为对角线时,
,
∴Q(6﹣p,3),
∵点Q在反比例的图象上,
∴,
解得:,
∴;
当以PE为对角线时,
,
∴Q(2+p,﹣1),
∵点Q在反比例的图象上,
∴,
解得:p=﹣6,
∴Q2(﹣4,﹣1);
当以PD为对角线时,
,
即Q(p﹣2,1),
∵点Q在反比例的图象上,
∴,
解得:p=6,
∴Q3(4,1),与点E重合,不符合题意舍去;
综上所述:存在Q使得以点P,Q,D,E为顶点的四边形为平行四边形;点Q的坐标为或(﹣4,﹣1).
4.【解答】解:(1)一次函数y=ax+b(a≠0)的图象与反比例函数(k≠0)的图象交于点A(﹣1,4),B(n,﹣1),把点A,点B的坐标代入得:
,
解得:k=﹣4,
∴反比例函数的表达式为;
将点B(n,﹣1)代入得:
∴,
解得:n=4,
∴点B(4,﹣1),
把点A,点B的坐标代入一次函数y=ax+b(a≠0)得:
,
解得:,
∴y=﹣x+3,
∴一次函数的表达式为:y=﹣x+3;
(2)∵A(﹣1,4),B(4,﹣1),
当一次函数y=ax+b的图象在反比例函数的图象上时,,
∴当x<﹣1或0<x<4时,.
(3)∵点D在x轴上,点C在反比例函数图象,
∴设点D(a,0),,
∵四边形ABCD是平行四边形,分三种情况讨论:
∴①当AC,BD是对角线,
依题意得:,
解得:,
∴点C的坐标为;
②当BC,AD是对角线时,
依题意得:,
解得:,
∴点C的坐标为;
③当AB,CD是对角线时,
依题意得:,
解得:,
∴点C的坐标为;
综上所述,点C的坐标为或或时,以A、B、C、D为顶点的四边形是平行四边形.
5.【解答】解:(1)①由已知,点B(4,2)在y1(x>0)的图象上
∴k=8
∴y1
∵a=2
∴点A坐标为(2,4),A′坐标为(﹣2,﹣4)
把B(4,2),A(﹣2,﹣4)代入y2=mx+n
解得
∴y2=x﹣2
②当y1>y2>0时,y1图象在y2=x﹣2图象上方,且两函数图象在x轴上方
∴由图象得:2<x<4
(2)分别过点A、B作AC⊥x轴于点C,BD⊥x轴于点D,连BO
∵O为AA′中点
S△AOBS△ABA′=8
∵点A、B在双曲线上
∴S△AOC=S△BOD
∴S△AOB=S四边形ACDB=8
由已知点A、B坐标都表示为(a,)(3a,)
∴
解得k=6
(3)由已知A(a,),则A′为(﹣a,)
把A′代入到y
∴n
∴A′D解析式为y
当x=a时,点D纵坐标为
∴AD
∵AD=AF,
∴点F和点P横坐标为
∴点P纵坐标为
∴点P在y1(x>0)的图象上
6.【解答】解:(1)把A(4,2)代入y,得k=4×2=8.
∴反比例函数的解析式为y.
解方程组,得
或,
∴点B的坐标为(1,8);
(2)①若∠BAP=90°,
过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,
对于y=﹣2x+10,
当y=0时,﹣2x+10=0,解得x=5,
∴点E(5,0),OE=5.
∵A(4,2),∴OH=4,AH=2,
∴HE=5﹣4=1.
∵AH⊥OE,∴∠AHM=∠AHE=90°.
又∵∠BAP=90°,
∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,
∴∠MAH=∠AEM,
∴△AHM∽△EHA,
∴,
∴,
∴MH=4,
∴M(0,0),
可设直线AP的解析式为y=mx
则有4m=2,解得m,
∴直线AP的解析式为yx,
解方程组,得
或,
∴点P的坐标为(﹣4,﹣2).
②若∠ABP=90°,
同理可得:点P的坐标为(﹣16,).
综上所述:符合条件的点P的坐标为(﹣4,﹣2)、(﹣16,);
(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,
则有BS∥CT,
∴△CTD∽△BSD,
∴.
∵,
∴.
∵A(a,﹣2a+10),B(b,﹣2b+10),
∴C(﹣a,2a﹣10),CT=a,BS=b,
∴,即ba.
∵A(a,﹣2a+10),B(b,﹣2b+10)都在反比例函数y的图象上,
∴a(﹣2a+10)=b(﹣2b+10),
∴a(﹣2a+10)a(﹣2a+10).
∵a≠0,
∴﹣2a+10(﹣2a+10),
解得:a=3.
∴A(3,4),B(2,6),C(﹣3,﹣4).
设直线BC的解析式为y=px+q,
则有,
解得:,
∴直线BC的解析式为y=2x+2.
当x=0时,y=2,则点D(0,2),OD=2,
∴S△COB=S△ODC+S△ODB
OD CTOD BS
2×32×2=5.
∵OA=OC,
∴S△AOB=S△COB,
∴S△ABC=2S△COB=10.
7.【解答】解:(1)过点B作BF⊥x轴于点F,
∵∠BCA=90°,
∴∠BCF+∠ACO=90°.
又∵∠CAO+∠ACO=90°,
∴∠BCF=∠CAO,
∵∠BFC=∠COA=90°,BC=AC.
∴△BFC≌△COA(AAS),
∴CF=OA=2,BF=OC=1,
∴点B的坐标为(﹣3,1),
将点B的坐标代入反比例函数解析式可得:,解得:k=﹣3,
故可得反比例函数解析式为;
(2)结合点B的坐标及图象,可得:
当x<0时,的解集为:﹣3<x<0;
(3)分三种情况求解:如图,
①当AP=AC时,
∵点P在y轴正半轴,
∴P1符合要求,P2不符合要求,
∵A(0,2),C(﹣1,0),
∴,
∴,
∴,
∴;
②当AC=CP时,P3在y轴负半轴,不符合题意,在正半轴上点P与点A重合,不符合题意,故AC=CP时,不存在;
③当AP=CP时,设P4(0,m),
∴P4C=P4A=2﹣m,
在Rt△OCP4中,由勾股定理,得
12+m2=(2﹣m)2,
解得,,
∴,
综上所述,点P坐标为或.
8.【解答】解:(1)∵点A坐标为(3,1)
把点A的坐标代入y中得:k=3
∴反比例函数的解析式是:y
把点B的坐标为(﹣2,m)代入y中,得:﹣2m=3,m
∴B(﹣2,)
把A、B两点的坐标代入y=ax+b中得:,解得:
∴一次函数的解析式为:yx;
(2)如图1,当y=0时,x0,x=1,
∴C(1,0),
∴S△AOB=S△AOC+S△BOC;
(3)由图象得:ax+b时x的取值范围是:x>3或﹣2<x<0;
故答案为:x>3或﹣2<x<0;
(4)当△AOP是等腰三角形时,存在以下三种情况:
①当OA=OP时,如图2,
∵A(3,1),
∴OA,
∴P1(,0)或P2(,0);
②当OA=AP时,如图3,
∴P(6,0);
③当OP=AP时,如图4,过A作AE⊥x轴于E,
设OP=x,则AP=x,PE=3﹣x,
∴AP2=AE2+PE2,
∴12+(3﹣x)2=x2,
x,
∴P(,0);
综上,P的坐标为(,0)或(,0)或(6,0)或(,0).
故答案为:(,0)或(,0)或(6,0)或(,0).
9.【解答】解:(1)把点A(3,n)代入正比例函数可得:n=4,
∴点A(3,4),
把点A(3,4)代入反比例函数,
可得:k=3×4=12,
∴反比例函数的解析式为;
(2)∵点A与点B是关于原点对称的,
∴点B(﹣3,﹣4),
∴根据图象可得,不等式的解集为:x<﹣3或0<x<3;
(3)如图所示,过点A作AG⊥x轴,垂足为G,
∵A(3,4),
∴OG=3,AG=4,
在Rt△AOG中,,
∵四边形AOCD是菱形,
∴OC=OA=5,,
∴.
10.【解答】解:(1)把C(﹣4,0)代入y=kx+2得:0=﹣4k+2,
解得:k,
把A(2,n)代入y=kx+2得:n=3.
∴A(2,3).
把A(2,3)代入y=得:m=6.
∴k的值为,m的值为6.
(2)由图象可知:当 x>2时,yx+2的图象在y的上方,
∴当y1>y2时,x的取值范围是:x>2.
故答案为:x>2.
(3)当x=0时,yx+2=2.
∴B(0,2),
∵P(a,0)为x轴上的一动点,
∴PC=|a+4|.
∴S△CBPPC OB|a+4|×2=|a+4|,
S△CAPPC yA|a+4|×3|a+4|,
∵S△CAP=S△ABP+S△CBP,
∴|a+4||a+4|,
∴a=3或a=﹣11.
11.【解答】解:(1)设EC=x,则AE=2EC=2x,
在菱形ABCD中,AD∥BC,AB=BC=AD=5,
∵AD∥x轴,
∴BC∥x轴,
∴AE⊥BC,
则BE=5﹣x,
在△ABE中,根据勾股定理,
得(5﹣x)2+4x2=25,
解得x=2,
∴EC=2,AE=4,
∴C(2,),
D(5,),
∴4,
解得k.
(2)∵D(5,),C(2,),
∴A(0,),B(﹣3,),
设AB的解析式:y=kx+b,
代入A,B点坐标,得,
解得,
∴AB的解析式:.
当0时,x=2,
∴F(2,0),
设P(m,),存在以A、F、P、Q为顶点的四边形是平行四边形,
∵Q在坐标轴上,
①Q在x轴上,设Q(n,0),
当AF,PQ为对角线时,,
解得,
∴Q(﹣3,0),
当AP,FQ为对角线时,得,
解得(舍),
当AQ,FP为对角线,得,
解得,
∴Q(7,0).
②当Q在y轴上,设Q(0,n),
当AF,PQ为对角线时,,
解得,
∴Q(0,4),
当AP,FQ为对角线时,得,
解得,
∴Q(0,),
当AQ,FP为对角线,得,
解得(舍),
综上,Q点坐标(﹣3,0),(7,0),(0,4)或(0,).
12.【解答】解:(1)∵A(﹣1,0),B(0,﹣2),E为AD中点,
∴xD=1,
设D(1,t),
又∵DC∥AB,
∴C(2,t﹣2),
∴t=2t﹣4,
∴t=4,
∴k=4;
(2)由(1)得C(2,2),
∵B(0,﹣2),
∴直线BC的解析式为y=2x﹣2,
当y=0时,x=1,
∴F(1,0),
∴OF=1,
设点G的坐标为(0,m),
∵MN∥x轴,
∴M(,m),N(,m),
∵FM=FN,
∴1﹣()1,
解得:m或m=0(不合题意舍去),
∴点G的坐标为(0,);
(3)∵由(1)知k=4,
∴反比例函数的解析式为y,
∵点P在双曲线上,点Q在y轴上,
∴设Q(0,y),P(x,),
①当AB为边时:
如图1,若ABPQ为平行四边形,
则0,
解得x=1,
此时P1(1,4),Q1(0,6);
如图2,若ABQP为平行四边形,
则,
解得x=﹣1,
此时P2(﹣1,﹣4),Q2(0,﹣6);
②如图3,当AB为对角线时,
AP=BQ,且AP∥BQ;
∴,
解得x=﹣1,
∴P3(﹣1,﹣4),Q3(0,2);
故点Q的坐标为(0,6)或(0,﹣6)或(0,2).
13.【解答】(1)证明:如图1,∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADF+∠CDO=90°,
∵AF⊥y轴,
∴∠AFD=∠DOC=90°,
∴∠CDO+∠DCO=90°,
∴∠ADF=∠DCO,
在△CDO和△DAF中,
,
∴△CDO≌△DAF(AAS);
(2)解:∵C(﹣2,0),D(0,3),
∴OC=2,OD=3,
∵△CDO≌△DAF,
∴DF=OC,AF=OD,
∴OG=OF=OD+DF=3+2=5,
∴A(﹣3,5),
设反比例函数的表达式为y(k≠0),把A(﹣3,5)代入,得k=﹣15,
∴y,
当x=﹣5时,y3,
∴点E的坐标为(﹣5,3);
(3)在平面内存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形.理由如下:
设直线AE的解析式为y=k′x+b,把A(﹣3,5),E(﹣5,3)代入,
得,
解得:,
∴直线AE的解析式为y=x+8,
∵直线l∥AE,
∴设直线l的解析式为y=x+b′,把C(﹣2,0)代入得﹣2+b′=0,
解得:b′=2,
∴直线l的解析式为y=x+2,
∵点P是直线l上的一点,点Q是平面内一点,
∴设P(m,m+2),Q(t,s),
又A(﹣3,5),C(﹣2,0),
当AC、PQ为对角线时,
,
解得:,
∴Q(,);
当CP、AQ为对角线时,
,
解得:或(舍去),
∴Q(3,﹣1);
当AP、CQ为对角线时,
,
解得:或,
∴Q(﹣3,5)或(﹣3,5);
综上所述,在平面内存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形,点Q的横坐标为或3或﹣3或﹣3.
14.【解答】解:(1)如图,延长AD交x轴于F,由题意得AF⊥x轴,
∵点D的坐标为(4,3),
∴OF=4,DF=3,
∴OD=5,
∴AD=5,
∴点A坐标为(4,8),
∴k=xy=4×8=32,
由菱形的性质得到B(0,5),
设直线AB的方程为:y=ax+b(a≠0),则
,
解得,
故反比例解析式为y;直线AB的方程为:yx+5;
(2)将菱形ABCD沿x轴正方向平移m个单位,
使得点D落在函数y(x>0)的图象D'点处,
∴点D'的坐标为(4+m,3),
∵点D'在y的图象上,
∴3,
解得m,
∴0≤m;
(3)如图,存在,
理由:
∵四边形ABCD是菱形,
∴OB=OD=5,
过D作DE⊥x轴于E,过N作NF⊥y轴于F,过M作MH⊥y轴于H,
∴∠DEO=∠ONB=∠NOD=90°,
∴∠BON+∠BOD=∠BOD+∠DOE=90°,
∴△BON≌△DOE(AAS),
∴BN=DE=3,ON=OE=4,
∴S△OBNOB NFBN ON,
∴NF,
∵点N在直线AB上,
∴N(,),
设M(n,n+5),
∴MH=n,OHn+5,
∵BM2=BH2+MH2,
∴22=(n+5﹣5)2+n2,
∴n=±,
∵n>0,
∴M(,).
15.【解答】解:(1)矩形OABC的顶点A,C分别在x轴,y轴上,点O为坐标原点,点B的坐标为(2,3),反比例函数的图象经过BC的中点D,
∴D(1,3),
将点D的坐标代入反比例函数得:
,
解得:k=3,
∴反比例函数的解析式为;
(2)反比例函数的图象与AB交于点E,
又∵点B与点E的横坐标相等,
∴把x=2代入得:
,
∴,
∴,
∵,
∴△BDE的面积;
(3)设点F的坐标为(0,m),则CF=|m﹣3|,
∵∠BCF=∠B=90°,
∴△FBC与△DEB相似,需满足或,
当时,,
解得或;
当时,,
解得m=0或m=6;
综上,点F的坐标为或或(0,0)或(0,6).
16.【解答】解:(1)把B(8,1)代入反比例函数 ,得k=8,
∴反比例函数的表达式为,
∵点A(a,4)在 图象上,
∴a=2,即A(2,4),
把A(2,4),B(8,1)两点代入y1=mx+n,
解得 ,n=5,
所以一次函数的表达式为;
(2)由图象可得,当x>0时,不等式mx+n(x>0)的解集2<x<8;
(3)由(1)得一次函数的表达式为 ,
当x=0时,y=5,
∴C(0,5),
即OC=5,
当y=0时,x=10,
∴D点坐标为(10,0),
即OD=10,
∴,
∵A(2,4),
∴,
设P点坐标为(b,0),当点P在点D左侧,则PD=10﹣b,
由∠CDO=∠ADP 可得:
①当△COD∽△APD时,,
∴,
解得b=2,故点P坐标为(2,0);
②当△COD∽△PAD时,,
∴,
解得b=0,
即点P的坐标为(0,0),
因此,点P的坐标为(2,0)或(0,0)时,△COD与△ADP相似.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习反比例函数综合训练
1.如图,一次函数y=kx+2(k≠0)的图象与反比例函数的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(﹣4,0).
(1)求k与m的值;
(2)P为x轴上的一动点,当△APC的面积为9时,求点P的坐标;
(3)在y轴上是否存在点Q使得△ACQ为等腰三角形,若存在,请直接写出点Q的坐标.
2.已知:一次函数yx+m与反比例函数y的图象在第一象限的交点为A(1,n).
(1)求m与n的值;
(2)设一次函数的图象与x轴交于点B,C为x轴上一点,连接AC,若△ABC为等腰三角形,求C的坐标.
3.如图,矩形ABCO的顶点C,A分别在x轴、y轴的正半轴上,点B的坐标为(4,2),反比例函数的图象经过AB的中点D,与BC交于点E,连接OD,OE,DE.
(1)直接写出结果:k= ,点E的坐标为 ;
(2)点M是y轴正半轴上一点,若S△MBO=S△ODE,求点M的坐标;
(3)点P为x轴上一点,点Q为反比例函数图象上一点,是否存在点P,Q,使得以点P,Q,D,E为顶点的四边形为平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由.
4.如图,一次函数y=ax+b(a≠0)的图象与反比例函数(k≠0)的图象交于点A(﹣1,4),B(n,﹣1).
(1)求反比例函数和一次函数的表达式;
(2)利用图象,直接写出不等式的解集;
(3)已知点D在x轴上,点C在反比例函数图象上.若以A、B、C、D为顶点的四边形是平行四边形,求点C的坐标.
5.平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
6.已知:一次函数y=﹣2x+10的图象与反比例函数y(k>0)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若,求△ABC的面积.
7.如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(﹣1,0),点A的坐标为(0,2),一次函数y=kx+b的图象经过点B,C,反比例函数图象也经过点B.
(1)求反比例函数的关系式;
(2)直接写出当x<0时,的解集.
(3)若P是y轴正半轴一点,当△ACP是等腰三角形时,求出点P的坐标.
8.如图,一次函数y=ax+b的图象与反比例函数y的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知点A坐标为(3,1),点B的坐标为(﹣2,m)
(1)求反比例函数的解析式和一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)观察图象直接写出ax+b时x的取值范围是 ;
(4)直接写出:P为x轴上一动点,当三角形OAP为等腰三角形时点P的坐标 .
9.如图,已知正比例函数的图象与反比例函数的图象相交于点A(3,n)和点 B.
(1)求反比例函数的解析式;
(2)请结合函数图象,直接写出不等式的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
10.如图,一次函数y1=kx+2(k≠0)的图象与反比例函数y2(m≠0,x>0)的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(﹣4,0).
(1)求k与m的值;
(2)当y1>y2时,x的取值范围是 ;
(3)若P(a,0)为x轴上的一动点,当△APB的面积为时,求a的值.
11.如图(1),菱形ABCD顶点A在y轴上,顶点D在反比例函数上,边BC交y轴于点E,AD∥x轴,AE=2EC,AD=5.
(1)求k.
(2)如图(2),延长BA交x轴于点F,问是否在该反比例函数上存在点P,坐标轴上的点Q,使得以A、F、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点Q的坐标,若不存在,请说明理由.
12.如图1,已知A(﹣1,0),B(0,﹣2),平行四边形ABCD的边AD、BC分别与y轴、x轴交于点E、F,且点E为AD中点,双曲线y(k为常数,k≠0)经过C、D两点.
(1)求k的值;
(2)如图2,点G是y轴正半轴上的一个动点,过点G作y轴的垂线,分别交反比例函数y(k为常数,k≠0)图象于点M,交反比例函数y(x<0)的图象于点N,当FM=FN时,求G点坐标;
(3)点P在双曲线y上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求出满足要求的所有点Q的坐标.
13.如图1,正方形ABCD中,C(﹣2,0),D(0,3).过A点作AF⊥y轴于F点,过B点作x轴的垂线交过A点的反比例函数的图象于E点,交x轴于G点.
(1)求证:△CDO≌△DAF;
(2)求反比例函数的表达式及点E的坐标;
(3)如图2,过点C作直线l∥AE,点P是直线l上的一点,在平面内是否存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形,若存在,请直接写出点Q的横坐标,若不存在,请说明理由.
14.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数(k>0,x>0)的图象上,点D的坐标为(4,3).设AB所在直线解析式为y=ax+b(a≠0).
(1)求反比例和一次函数解析式;
(2)若将菱形ABCD沿x轴正方向平移m个单位,在平移中若反比例函数图象与菱形的边AD始终有交点,求m的取值范围;
(3)在直线AB上是否存在M、N两点,使以MNOD四点的四边形构成矩形?若不存在,请说明理由,若存在直接求出M、N(点M在点N的上方)两点的坐标.
15.如图,矩形OABC的顶点A,C分别在x轴,y轴上,点O为坐标原点,点B的坐标为(2,3),反比例函数的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求反比例函数的解析式;
(2)求△BDE的面积;
(3)若点F是y轴上一点,且△FBC与△DEB相似,求点F的坐标.
16.如图,一次函数y1=mx+n与反比例函数y2(x>0)的图象分别交于点A(a,4)和点B(8,1),与坐标轴分别交于点C和点D.
(1)求一次函数与反比例函数的表达式.
(2)直接写出不等式mx+n(x>0)的解集.
(3)在x轴上是否存在点P,使△COD与△ADP相似,若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
1.【解答】解:(1)把C(﹣4,0)代入y=kx+2得:0=﹣4k+2,
解得:k.把A(2,n)代入y=kx+2得:n=3.
∴A(2,3).
把A(2,3)代入得:m=2×3=6.
∴k的值为,m的值为6;
(2)设点P(x,0),
则△APC的面积CP×yA|x+4|×3=9,
解得:x=2或﹣10,
即点P(2,0)或(﹣10,0);
(3)存在,理由:
设点Q(0,y),
由点A、C、Q的坐标得,AC2=45,CQ2=16+y2,AQ2=4+(y﹣3)2,
当CA=CQ时,
则45=16+y2,则y=±,
则点P(0,)或(0,);
当AC=AQ或CQ=AQ时,
同理可得:16+y2=4+(y﹣3)2或45=4+(y﹣3)2,
解得:y或3±,
则点P(0,)或(0,3)或(0,3).
综上,P(0,)或(0,)或(0,)或(0,3)或(0,3).
2.【解答】解:(1)∵A(1,n)在反比例数的图象上,
∴,
∴n=2,
∴A(1,2),
将A(1,2)代入得:
,
解得:;
(2)由(1)得,
当y=0时,x=﹣5,
∵一次函数的图象与x轴交于点B,
∴B(﹣5,0),
∴,
如图所示,设C(x,0),
当BC=BA时,点C的坐标为或;
当CB=CA时,得:CB2=CA2,
∴(x+5)2=(1﹣x)2+22,
解得:;
当AB=AC时,
∵A(1,2),xA﹣xB=6,
∴C(7,0),
综上所述满足条件的点C坐标为或或或C(7,0).
3.【解答】解:(1)∵矩形ABCO的顶点C,A分别在x轴、y轴的正半轴上,点B的坐标为(4,2),
∴BA⊥y轴,BC⊥x轴,A(0,2),
∵D是AB的中点,
∴D(2,2),
∵,反比例函数的图象经过AB的中点D,与BC交于点E,将点D的坐标代入得:
,
解得:k=4,
∴反比例函数解析式为,
在中,当x=4时,,
∴E(4,1),
故答案为:4;(4,1);
(2)设点M(0,m),
∵B(4,2),D(2,2),E(4,1),
∴,,
当△MBO的面积等于△ODE的面积时,3=2m,
解得:,
∴;
(3)存在点P,Q,使得以点P,Q,D,E为顶点的四边形为平行四边形;理由如下:
设点P(p,0),
∵点P,Q,D,E为顶点的四边形为平行四边形,
∴当以DE为对角线时,
,
∴Q(6﹣p,3),
∵点Q在反比例的图象上,
∴,
解得:,
∴;
当以PE为对角线时,
,
∴Q(2+p,﹣1),
∵点Q在反比例的图象上,
∴,
解得:p=﹣6,
∴Q2(﹣4,﹣1);
当以PD为对角线时,
,
即Q(p﹣2,1),
∵点Q在反比例的图象上,
∴,
解得:p=6,
∴Q3(4,1),与点E重合,不符合题意舍去;
综上所述:存在Q使得以点P,Q,D,E为顶点的四边形为平行四边形;点Q的坐标为或(﹣4,﹣1).
4.【解答】解:(1)一次函数y=ax+b(a≠0)的图象与反比例函数(k≠0)的图象交于点A(﹣1,4),B(n,﹣1),把点A,点B的坐标代入得:
,
解得:k=﹣4,
∴反比例函数的表达式为;
将点B(n,﹣1)代入得:
∴,
解得:n=4,
∴点B(4,﹣1),
把点A,点B的坐标代入一次函数y=ax+b(a≠0)得:
,
解得:,
∴y=﹣x+3,
∴一次函数的表达式为:y=﹣x+3;
(2)∵A(﹣1,4),B(4,﹣1),
当一次函数y=ax+b的图象在反比例函数的图象上时,,
∴当x<﹣1或0<x<4时,.
(3)∵点D在x轴上,点C在反比例函数图象,
∴设点D(a,0),,
∵四边形ABCD是平行四边形,分三种情况讨论:
∴①当AC,BD是对角线,
依题意得:,
解得:,
∴点C的坐标为;
②当BC,AD是对角线时,
依题意得:,
解得:,
∴点C的坐标为;
③当AB,CD是对角线时,
依题意得:,
解得:,
∴点C的坐标为;
综上所述,点C的坐标为或或时,以A、B、C、D为顶点的四边形是平行四边形.
5.【解答】解:(1)①由已知,点B(4,2)在y1(x>0)的图象上
∴k=8
∴y1
∵a=2
∴点A坐标为(2,4),A′坐标为(﹣2,﹣4)
把B(4,2),A(﹣2,﹣4)代入y2=mx+n
解得
∴y2=x﹣2
②当y1>y2>0时,y1图象在y2=x﹣2图象上方,且两函数图象在x轴上方
∴由图象得:2<x<4
(2)分别过点A、B作AC⊥x轴于点C,BD⊥x轴于点D,连BO
∵O为AA′中点
S△AOBS△ABA′=8
∵点A、B在双曲线上
∴S△AOC=S△BOD
∴S△AOB=S四边形ACDB=8
由已知点A、B坐标都表示为(a,)(3a,)
∴
解得k=6
(3)由已知A(a,),则A′为(﹣a,)
把A′代入到y
∴n
∴A′D解析式为y
当x=a时,点D纵坐标为
∴AD
∵AD=AF,
∴点F和点P横坐标为
∴点P纵坐标为
∴点P在y1(x>0)的图象上
6.【解答】解:(1)把A(4,2)代入y,得k=4×2=8.
∴反比例函数的解析式为y.
解方程组,得
或,
∴点B的坐标为(1,8);
(2)①若∠BAP=90°,
过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,
对于y=﹣2x+10,
当y=0时,﹣2x+10=0,解得x=5,
∴点E(5,0),OE=5.
∵A(4,2),∴OH=4,AH=2,
∴HE=5﹣4=1.
∵AH⊥OE,∴∠AHM=∠AHE=90°.
又∵∠BAP=90°,
∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,
∴∠MAH=∠AEM,
∴△AHM∽△EHA,
∴,
∴,
∴MH=4,
∴M(0,0),
可设直线AP的解析式为y=mx
则有4m=2,解得m,
∴直线AP的解析式为yx,
解方程组,得
或,
∴点P的坐标为(﹣4,﹣2).
②若∠ABP=90°,
同理可得:点P的坐标为(﹣16,).
综上所述:符合条件的点P的坐标为(﹣4,﹣2)、(﹣16,);
(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,
则有BS∥CT,
∴△CTD∽△BSD,
∴.
∵,
∴.
∵A(a,﹣2a+10),B(b,﹣2b+10),
∴C(﹣a,2a﹣10),CT=a,BS=b,
∴,即ba.
∵A(a,﹣2a+10),B(b,﹣2b+10)都在反比例函数y的图象上,
∴a(﹣2a+10)=b(﹣2b+10),
∴a(﹣2a+10)a(﹣2a+10).
∵a≠0,
∴﹣2a+10(﹣2a+10),
解得:a=3.
∴A(3,4),B(2,6),C(﹣3,﹣4).
设直线BC的解析式为y=px+q,
则有,
解得:,
∴直线BC的解析式为y=2x+2.
当x=0时,y=2,则点D(0,2),OD=2,
∴S△COB=S△ODC+S△ODB
OD CTOD BS
2×32×2=5.
∵OA=OC,
∴S△AOB=S△COB,
∴S△ABC=2S△COB=10.
7.【解答】解:(1)过点B作BF⊥x轴于点F,
∵∠BCA=90°,
∴∠BCF+∠ACO=90°.
又∵∠CAO+∠ACO=90°,
∴∠BCF=∠CAO,
∵∠BFC=∠COA=90°,BC=AC.
∴△BFC≌△COA(AAS),
∴CF=OA=2,BF=OC=1,
∴点B的坐标为(﹣3,1),
将点B的坐标代入反比例函数解析式可得:,解得:k=﹣3,
故可得反比例函数解析式为;
(2)结合点B的坐标及图象,可得:
当x<0时,的解集为:﹣3<x<0;
(3)分三种情况求解:如图,
①当AP=AC时,
∵点P在y轴正半轴,
∴P1符合要求,P2不符合要求,
∵A(0,2),C(﹣1,0),
∴,
∴,
∴,
∴;
②当AC=CP时,P3在y轴负半轴,不符合题意,在正半轴上点P与点A重合,不符合题意,故AC=CP时,不存在;
③当AP=CP时,设P4(0,m),
∴P4C=P4A=2﹣m,
在Rt△OCP4中,由勾股定理,得
12+m2=(2﹣m)2,
解得,,
∴,
综上所述,点P坐标为或.
8.【解答】解:(1)∵点A坐标为(3,1)
把点A的坐标代入y中得:k=3
∴反比例函数的解析式是:y
把点B的坐标为(﹣2,m)代入y中,得:﹣2m=3,m
∴B(﹣2,)
把A、B两点的坐标代入y=ax+b中得:,解得:
∴一次函数的解析式为:yx;
(2)如图1,当y=0时,x0,x=1,
∴C(1,0),
∴S△AOB=S△AOC+S△BOC;
(3)由图象得:ax+b时x的取值范围是:x>3或﹣2<x<0;
故答案为:x>3或﹣2<x<0;
(4)当△AOP是等腰三角形时,存在以下三种情况:
①当OA=OP时,如图2,
∵A(3,1),
∴OA,
∴P1(,0)或P2(,0);
②当OA=AP时,如图3,
∴P(6,0);
③当OP=AP时,如图4,过A作AE⊥x轴于E,
设OP=x,则AP=x,PE=3﹣x,
∴AP2=AE2+PE2,
∴12+(3﹣x)2=x2,
x,
∴P(,0);
综上,P的坐标为(,0)或(,0)或(6,0)或(,0).
故答案为:(,0)或(,0)或(6,0)或(,0).
9.【解答】解:(1)把点A(3,n)代入正比例函数可得:n=4,
∴点A(3,4),
把点A(3,4)代入反比例函数,
可得:k=3×4=12,
∴反比例函数的解析式为;
(2)∵点A与点B是关于原点对称的,
∴点B(﹣3,﹣4),
∴根据图象可得,不等式的解集为:x<﹣3或0<x<3;
(3)如图所示,过点A作AG⊥x轴,垂足为G,
∵A(3,4),
∴OG=3,AG=4,
在Rt△AOG中,,
∵四边形AOCD是菱形,
∴OC=OA=5,,
∴.
10.【解答】解:(1)把C(﹣4,0)代入y=kx+2得:0=﹣4k+2,
解得:k,
把A(2,n)代入y=kx+2得:n=3.
∴A(2,3).
把A(2,3)代入y=得:m=6.
∴k的值为,m的值为6.
(2)由图象可知:当 x>2时,yx+2的图象在y的上方,
∴当y1>y2时,x的取值范围是:x>2.
故答案为:x>2.
(3)当x=0时,yx+2=2.
∴B(0,2),
∵P(a,0)为x轴上的一动点,
∴PC=|a+4|.
∴S△CBPPC OB|a+4|×2=|a+4|,
S△CAPPC yA|a+4|×3|a+4|,
∵S△CAP=S△ABP+S△CBP,
∴|a+4||a+4|,
∴a=3或a=﹣11.
11.【解答】解:(1)设EC=x,则AE=2EC=2x,
在菱形ABCD中,AD∥BC,AB=BC=AD=5,
∵AD∥x轴,
∴BC∥x轴,
∴AE⊥BC,
则BE=5﹣x,
在△ABE中,根据勾股定理,
得(5﹣x)2+4x2=25,
解得x=2,
∴EC=2,AE=4,
∴C(2,),
D(5,),
∴4,
解得k.
(2)∵D(5,),C(2,),
∴A(0,),B(﹣3,),
设AB的解析式:y=kx+b,
代入A,B点坐标,得,
解得,
∴AB的解析式:.
当0时,x=2,
∴F(2,0),
设P(m,),存在以A、F、P、Q为顶点的四边形是平行四边形,
∵Q在坐标轴上,
①Q在x轴上,设Q(n,0),
当AF,PQ为对角线时,,
解得,
∴Q(﹣3,0),
当AP,FQ为对角线时,得,
解得(舍),
当AQ,FP为对角线,得,
解得,
∴Q(7,0).
②当Q在y轴上,设Q(0,n),
当AF,PQ为对角线时,,
解得,
∴Q(0,4),
当AP,FQ为对角线时,得,
解得,
∴Q(0,),
当AQ,FP为对角线,得,
解得(舍),
综上,Q点坐标(﹣3,0),(7,0),(0,4)或(0,).
12.【解答】解:(1)∵A(﹣1,0),B(0,﹣2),E为AD中点,
∴xD=1,
设D(1,t),
又∵DC∥AB,
∴C(2,t﹣2),
∴t=2t﹣4,
∴t=4,
∴k=4;
(2)由(1)得C(2,2),
∵B(0,﹣2),
∴直线BC的解析式为y=2x﹣2,
当y=0时,x=1,
∴F(1,0),
∴OF=1,
设点G的坐标为(0,m),
∵MN∥x轴,
∴M(,m),N(,m),
∵FM=FN,
∴1﹣()1,
解得:m或m=0(不合题意舍去),
∴点G的坐标为(0,);
(3)∵由(1)知k=4,
∴反比例函数的解析式为y,
∵点P在双曲线上,点Q在y轴上,
∴设Q(0,y),P(x,),
①当AB为边时:
如图1,若ABPQ为平行四边形,
则0,
解得x=1,
此时P1(1,4),Q1(0,6);
如图2,若ABQP为平行四边形,
则,
解得x=﹣1,
此时P2(﹣1,﹣4),Q2(0,﹣6);
②如图3,当AB为对角线时,
AP=BQ,且AP∥BQ;
∴,
解得x=﹣1,
∴P3(﹣1,﹣4),Q3(0,2);
故点Q的坐标为(0,6)或(0,﹣6)或(0,2).
13.【解答】(1)证明:如图1,∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADF+∠CDO=90°,
∵AF⊥y轴,
∴∠AFD=∠DOC=90°,
∴∠CDO+∠DCO=90°,
∴∠ADF=∠DCO,
在△CDO和△DAF中,
,
∴△CDO≌△DAF(AAS);
(2)解:∵C(﹣2,0),D(0,3),
∴OC=2,OD=3,
∵△CDO≌△DAF,
∴DF=OC,AF=OD,
∴OG=OF=OD+DF=3+2=5,
∴A(﹣3,5),
设反比例函数的表达式为y(k≠0),把A(﹣3,5)代入,得k=﹣15,
∴y,
当x=﹣5时,y3,
∴点E的坐标为(﹣5,3);
(3)在平面内存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形.理由如下:
设直线AE的解析式为y=k′x+b,把A(﹣3,5),E(﹣5,3)代入,
得,
解得:,
∴直线AE的解析式为y=x+8,
∵直线l∥AE,
∴设直线l的解析式为y=x+b′,把C(﹣2,0)代入得﹣2+b′=0,
解得:b′=2,
∴直线l的解析式为y=x+2,
∵点P是直线l上的一点,点Q是平面内一点,
∴设P(m,m+2),Q(t,s),
又A(﹣3,5),C(﹣2,0),
当AC、PQ为对角线时,
,
解得:,
∴Q(,);
当CP、AQ为对角线时,
,
解得:或(舍去),
∴Q(3,﹣1);
当AP、CQ为对角线时,
,
解得:或,
∴Q(﹣3,5)或(﹣3,5);
综上所述,在平面内存在点Q,使得点A、C、P、Q四个点依次连接构成的四边形是菱形,点Q的横坐标为或3或﹣3或﹣3.
14.【解答】解:(1)如图,延长AD交x轴于F,由题意得AF⊥x轴,
∵点D的坐标为(4,3),
∴OF=4,DF=3,
∴OD=5,
∴AD=5,
∴点A坐标为(4,8),
∴k=xy=4×8=32,
由菱形的性质得到B(0,5),
设直线AB的方程为:y=ax+b(a≠0),则
,
解得,
故反比例解析式为y;直线AB的方程为:yx+5;
(2)将菱形ABCD沿x轴正方向平移m个单位,
使得点D落在函数y(x>0)的图象D'点处,
∴点D'的坐标为(4+m,3),
∵点D'在y的图象上,
∴3,
解得m,
∴0≤m;
(3)如图,存在,
理由:
∵四边形ABCD是菱形,
∴OB=OD=5,
过D作DE⊥x轴于E,过N作NF⊥y轴于F,过M作MH⊥y轴于H,
∴∠DEO=∠ONB=∠NOD=90°,
∴∠BON+∠BOD=∠BOD+∠DOE=90°,
∴△BON≌△DOE(AAS),
∴BN=DE=3,ON=OE=4,
∴S△OBNOB NFBN ON,
∴NF,
∵点N在直线AB上,
∴N(,),
设M(n,n+5),
∴MH=n,OHn+5,
∵BM2=BH2+MH2,
∴22=(n+5﹣5)2+n2,
∴n=±,
∵n>0,
∴M(,).
15.【解答】解:(1)矩形OABC的顶点A,C分别在x轴,y轴上,点O为坐标原点,点B的坐标为(2,3),反比例函数的图象经过BC的中点D,
∴D(1,3),
将点D的坐标代入反比例函数得:
,
解得:k=3,
∴反比例函数的解析式为;
(2)反比例函数的图象与AB交于点E,
又∵点B与点E的横坐标相等,
∴把x=2代入得:
,
∴,
∴,
∵,
∴△BDE的面积;
(3)设点F的坐标为(0,m),则CF=|m﹣3|,
∵∠BCF=∠B=90°,
∴△FBC与△DEB相似,需满足或,
当时,,
解得或;
当时,,
解得m=0或m=6;
综上,点F的坐标为或或(0,0)或(0,6).
16.【解答】解:(1)把B(8,1)代入反比例函数 ,得k=8,
∴反比例函数的表达式为,
∵点A(a,4)在 图象上,
∴a=2,即A(2,4),
把A(2,4),B(8,1)两点代入y1=mx+n,
解得 ,n=5,
所以一次函数的表达式为;
(2)由图象可得,当x>0时,不等式mx+n(x>0)的解集2<x<8;
(3)由(1)得一次函数的表达式为 ,
当x=0时,y=5,
∴C(0,5),
即OC=5,
当y=0时,x=10,
∴D点坐标为(10,0),
即OD=10,
∴,
∵A(2,4),
∴,
设P点坐标为(b,0),当点P在点D左侧,则PD=10﹣b,
由∠CDO=∠ADP 可得:
①当△COD∽△APD时,,
∴,
解得b=2,故点P坐标为(2,0);
②当△COD∽△PAD时,,
∴,
解得b=0,
即点P的坐标为(0,0),
因此,点P的坐标为(2,0)或(0,0)时,△COD与△ADP相似.
21世纪教育网(www.21cnjy.com)
同课章节目录
