2025年九年级中考数学三轮冲刺练习反比例函数压轴题练习(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺练习反比例函数压轴题练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 14:38:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺练习反比例函数压轴题练习
1.如图所示,反比例函数y(m≠0)的图象与一次函数y=kx+b(k≠0)的图象交于A(2,a+2)、B(a﹣10,﹣1)两点,直线AB分别与x轴、y轴交于点C、D.
(1)分别求反比例函数和一次函数的解析式;
(2)若P(t,0)(t≠2)是x轴的正半轴上一动点,过P作x轴的垂线,分别与一次函数的图象和反比例函数的图象交于点M、N,设MN的长为d,求出d与t之间的函数关系式;
(3)在第二象限内是否存在点Q,使得△CDQ是等腰直角三角形.若存在,请直接写出点Q的坐标;若不存在,请说明理由.
2.如图,在直角坐标平面内,一个正比例函数y=kx的图象与反比例函数图象在第一象限内的交点为点A,过点A作AB⊥x轴,垂足为点B,AB=3.
(1)求正比例函数的解析式;
(2)在直线AB上是否存在点C,使点C到直线OA的距离等于它到点B的距离?若存在,求点C的坐标;若不存在,请说明理由;
(3)已知点P在直线AB上,如果△AOP是等腰三角形,请直接写出点P的坐标.
3.如图,在平面直角坐标系xOy中,一次函数yx+b的图象与反比例函数y的图象交于A,B两点,与y轴交于点C.已知点B的坐标为(5,1).
(1)求m,b的值;
(2)设P是线段BC上一点,过点P作PD∥y轴交反比例函数的图象于点D,连接AD,若DP=6,求△ADP的面积;
(3)在(2)的条件下,将直线AB向下平移a(a>0)个单位长度后,与射线OP交于点F,与反比例函数在第一象限内的图象交于点E,若四边形ABEF是平行四边形,求a的值.
4.如图,一次函数的图象与反比例函数的图象交于点A(a,3),与y轴交于点B.
(1)求a,k的值;
(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.
①求△ABC的面积;
②利用图象信息,直接写出不等式的解集.
③点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.
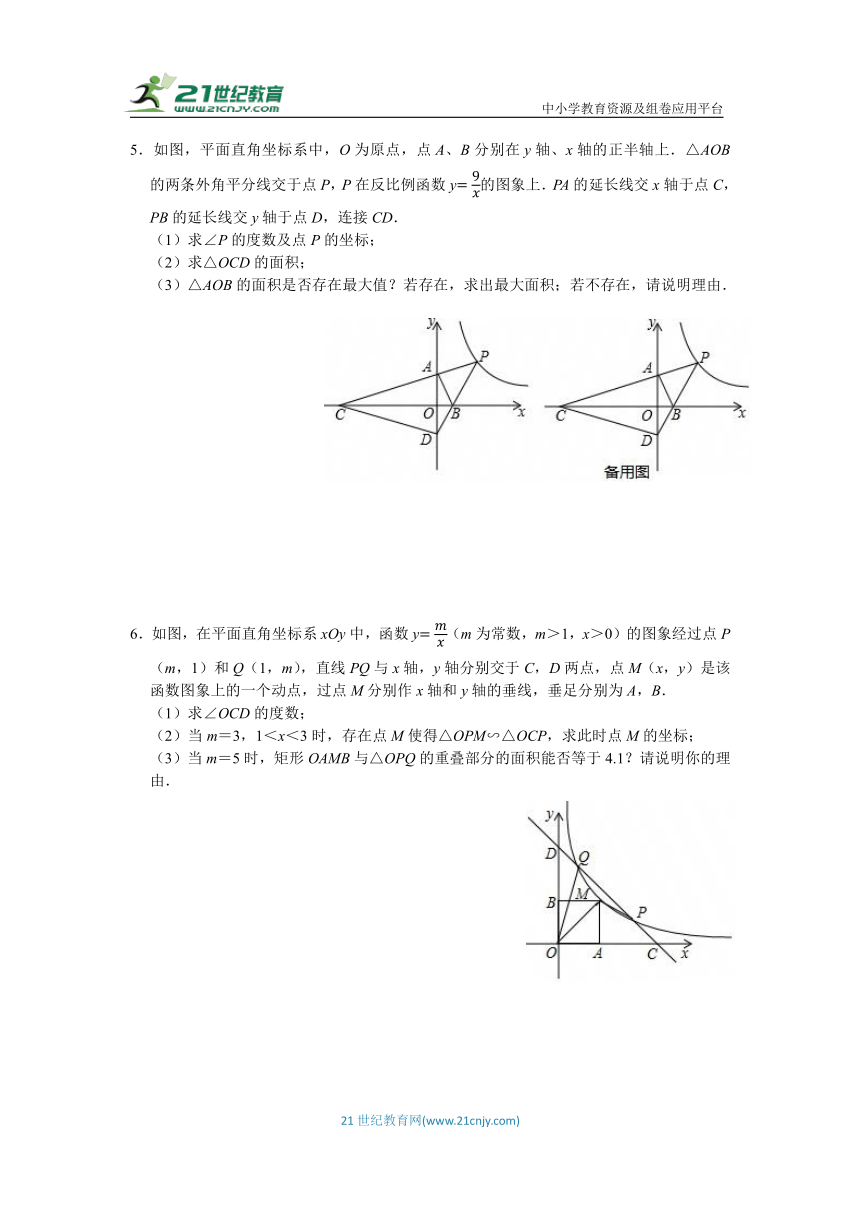
5.如图,平面直角坐标系中,O为原点,点A、B分别在y轴、x轴的正半轴上.△AOB的两条外角平分线交于点P,P在反比例函数y的图象上.PA的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD.
(1)求∠P的度数及点P的坐标;
(2)求△OCD的面积;
(3)△AOB的面积是否存在最大值?若存在,求出最大面积;若不存在,请说明理由.
6.如图,在平面直角坐标系xOy中,函数y(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(1)求∠OCD的度数;
(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;
(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.
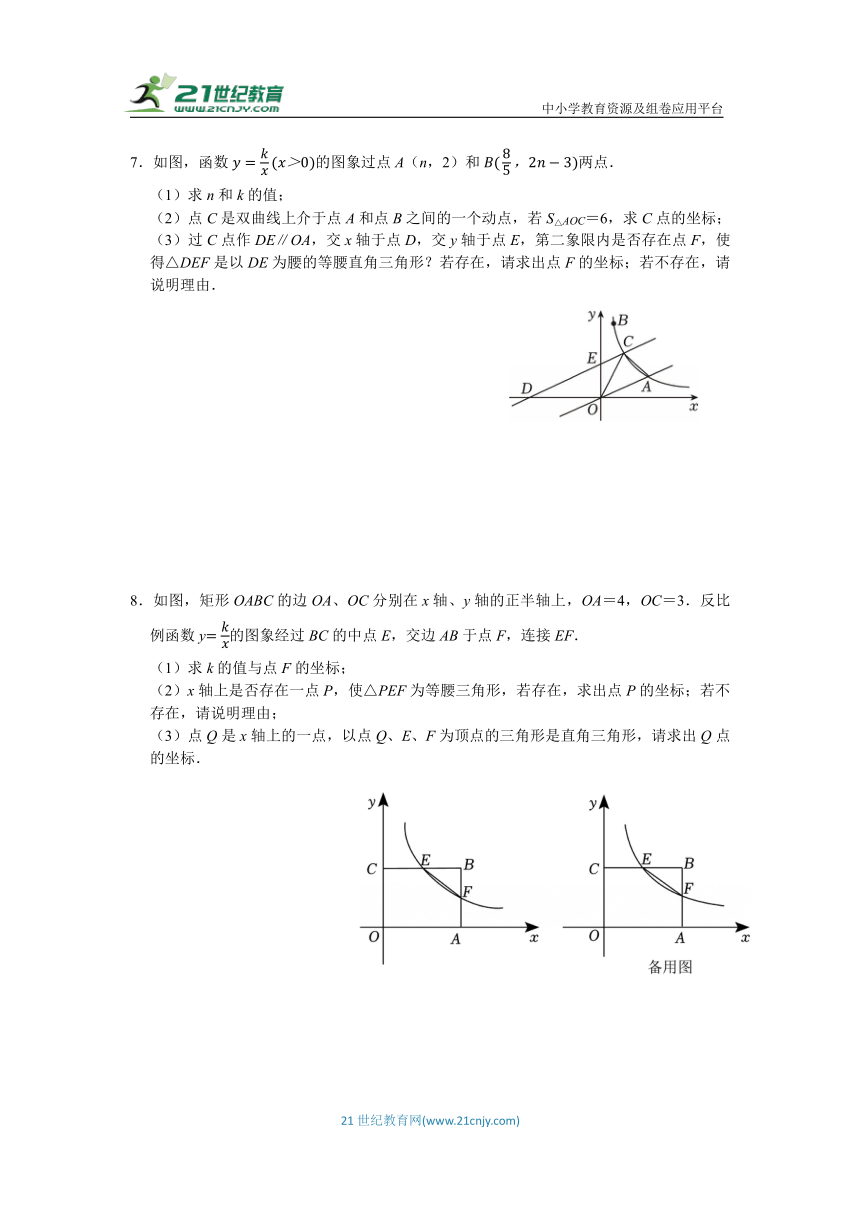
7.如图,函数的图象过点A(n,2)和两点.
(1)求n和k的值;
(2)点C是双曲线上介于点A和点B之间的一个动点,若S△AOC=6,求C点的坐标;
(3)过C点作DE∥OA,交x轴于点D,交y轴于点E,第二象限内是否存在点F,使得△DEF是以DE为腰的等腰直角三角形?若存在,请求出点F的坐标;若不存在,请说明理由.
8.如图,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=3.反比例函数y的图象经过BC的中点E,交边AB于点F,连接EF.
(1)求k的值与点F的坐标;
(2)x轴上是否存在一点P,使△PEF为等腰三角形,若存在,求出点P的坐标;若不存在,请说明理由;
(3)点Q是x轴上的一点,以点Q、E、F为顶点的三角形是直角三角形,请求出Q点的坐标.
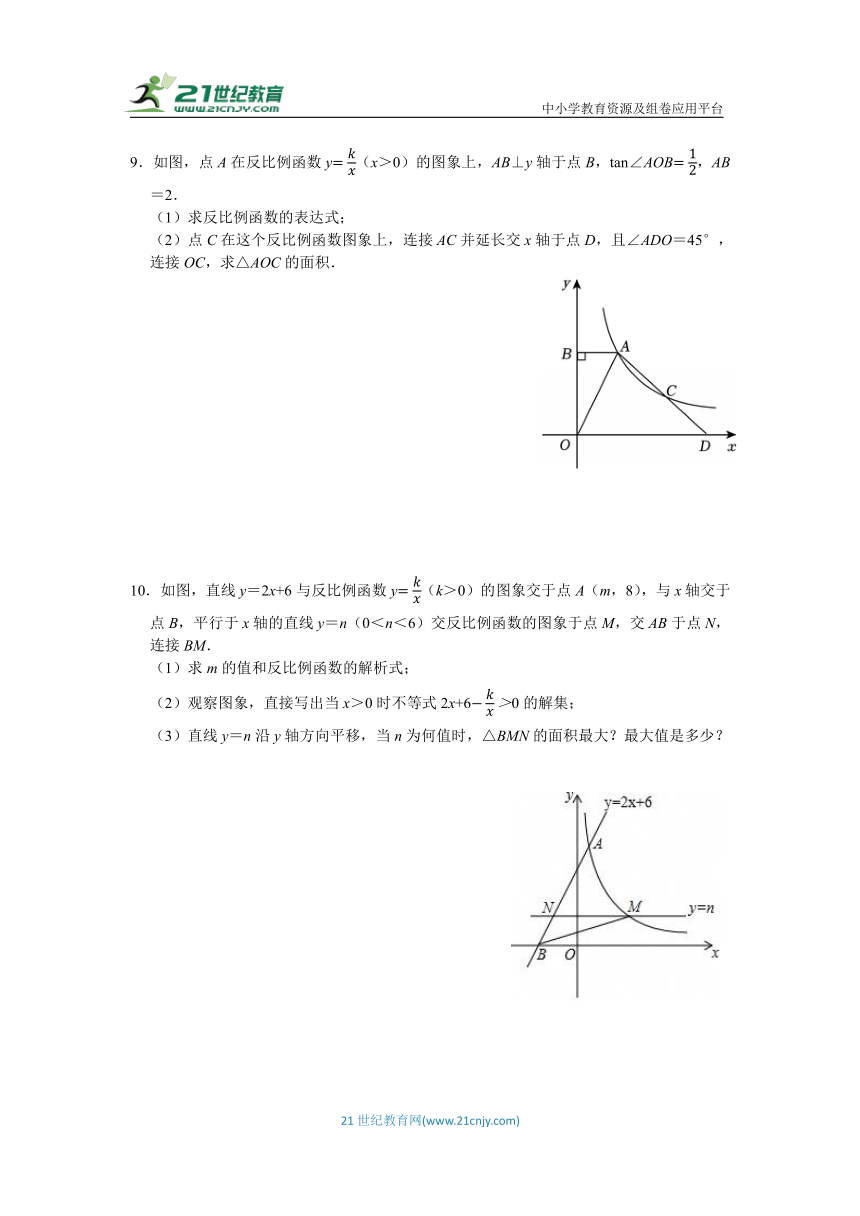
9.如图,点A在反比例函数y(x>0)的图象上,AB⊥y轴于点B,tan∠AOB,AB=2.
(1)求反比例函数的表达式;
(2)点C在这个反比例函数图象上,连接AC并延长交x轴于点D,且∠ADO=45°,连接OC,求△AOC的面积.
10.如图,直线y=2x+6与反比例函数y(k>0)的图象交于点A(m,8),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的解析式;
(2)观察图象,直接写出当x>0时不等式2x+60的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
11.如图1,在平面直角坐标系中,反比例函数(k为常数,x>0)的图象经过点A(2,m),B(6,n)两点.
(1)m与n的数量关系是 .
A.m=3n
B.n=3m
C.m+n=8
D.m﹣n=4
(2)如图2,若点A绕x轴上的点P顺时针旋转90°,恰好与点B重合.
①求点P的坐标及反比例函数的表达式;
②连接OA、OB,则△AOB的面积为 ;
(3)若点M在反比例函数的图象上,点N在y轴上,在(2)的条件下,是否存在以A、B、M、N为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标,若不存在,请说明理由.
12.如图1,已知点A(a,0),B(0,b),且a、b满足(a+b+3)2=0,平行四边形ABCD的边AD与y轴交于点E,且E为AD中点,双曲线y经过C、D两点.
(1)a= ,b= ;
(2)求反比例函数表达式;
(3)点P在双曲线y上,点Q在x轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,求满足要求的所有点Q的坐标.
13.如图,反比例函数y(k≠0)的图象与正比例函数y=2x的图象相交于A(1,a)、B两点,点C在第四象限,BC∥x轴.
(1)求k的值;
(2)以AB、BC为边作菱形ABCD,求D点坐标.
14.如图,平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y在第二象限内的图象相交于点A,与x轴的负半轴交于点B,与y轴的负半轴交于点C.
(1)求∠BCO的度数;
(2)若y轴上一点M的纵坐标是4,且AM=BM,求点A的坐标;
(3)在(2)的条件下,若点P在y轴上,点Q是平面直角坐标系中的一点,当以点A、M、P、Q为顶点的四边形是菱形时,请直接写出点Q的坐标.
15.如图,直线y=ax+2与x轴、y轴分别相交于A、B两点,与双曲线y(x>0)相交于点P,PC⊥x轴于点C,且PC=4,点A的坐标为(﹣4,0).
(1)求一次函数的解析式;
(2)求双曲线的解析式;
(3)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
16.如图,一次函数y=ax+1的图象与x轴、y轴分别相交于A、B两点,与反比例函数y(k>0)的图象交于P,G两点,过点P作PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求反比例函数的表达式;
(2)观察图象,直接写出不等式的解集:
(3)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于点H,当△QCH∽△BAO时,求点Q的坐标.
参考答案
1.【解答】解:(1)∵反比例函数y(m≠0)的图象经过A(2,a+2)、B(a﹣10,﹣1)两点,
∴,
解得:,
∴A(2,4)、B(﹣8,﹣1),反比例函数的解析式是y,
把A(2,4)、B(﹣8,﹣1)分别代入y=kx+b得,,
解得,,
∴一次函数的解析式为yx+3;
(2)由题意得,M(t,t+3),N(t,),
∴PMt+3,PN,
当t>2时,d=PM﹣PNt+3;
当0<t≤2时,d=PN﹣PM(t+3);
(3)由(1)知,直线AB的解析式为yx+3,
令x=0,则yx+3=3,
令y=0,则0x+3,
∴x=﹣6,
∴C(﹣6,0),D(0,3),
∴OC=6,OD=3,如图,
∵△CDQ是等腰直角三角形,
∴①当∠CDQ=90°时,CD=QD,
过点Q作QH⊥y轴于H,
∴∠QDH+∠DQH=90°,
∵∠CDQ=90°,
∴∠QDH+∠CDO=90°,
∴∠CDO=∠DQH,
∴△COD≌△HDQ(AAS),
∴QH=OD=3,DH=OC=6,
∴OH=OD+DH=9,
∴Q(﹣3,9);
②当∠DCQ=90°时,同①的方法得,Q'(﹣9,6);
③当∠CQD=90°时,
同①的方法得,△CLQ''≌△DKQ'',
∴Q''L=Q''K,CL=DK,
∴设Q''(﹣a,a),
∴Q''K=Q''K=a,
∴CL=6﹣a,DK=a﹣3,
∴6﹣a=3﹣a,
∴a,∴Q''(,),
即满足条件的点Q的坐标为(﹣3,9)或(﹣9,6)或(,).
2.【解答】解:(1)∵AB=3,
∴点A的纵坐标为3,∵反比例函数y的图象经过点A,
当y=3时,x,
∴A(,3),
将点A(,3)代入y=kx得k,
∴正比例函数的解析式为yx;
(2)∵AB⊥x轴于点B,设点C的坐标为(,y),
在Rt△ABO中,OB,AB=3,
由勾股定理可得OA=2,
∵OB,
∴∠OAB=30°,
过点C作CG⊥OA于G,
由题意得CB=CG,
当点C在AB上时,
则OC平分∠AOB,
∴∠BOC=30°,
∴BCOB=1,
∴C(,1);
当点C在AB延长线上时,
同理可得C'(,﹣3);
综上所述:C(,1)或(,﹣3);
(3)①当AO=AP=2时,
则P(,3﹣2)或(,3+2);
②当OA=OP时,
由OB⊥AP得,AB=BP,
∴P(,﹣3);
③当PA=PO时,
∴∠OAP=∠POA=30°,
则OP平分∠AOB,
∴P(,1);
综上所述:P(,3﹣2)或(,3+2)或(,1)或(,﹣3).
3.【解答】解:(1)∵一次函数的图象与反比例函数的图象交于A,B两点,且点B的坐标为(5,1),将点B的坐标代入得:
,
解得:,
∴,m=5;
(2)由(1)可知反比例函数解析式为,一次函数解析式为,
设,
∵PD∥y轴交反比例函数的图象于点D,
∴.
∵DP=6,
∴,
解得:t1=1,t2=﹣10(不合题意,舍去),
∴D(1,5).
联立得,
解得:或,
∴,
∴S△ADPDP (xD﹣xA)6×[1﹣(﹣2)]=9;
(3)如图,
∵将直线AB向下平移a(a>0)个单位长度,
∴平移后的直线解析式为,
由(2)可知P(1,﹣1),
∴直线OP的解析式为y=﹣x.
联立得:,
解得:,
∴.
∵平移后的直线与射线OP交于点F,与反比例函数在第一象限内的图象交于点E,
∴AB∥EF.
∵四边形ABEF是平行四边形,,B(5,1),
∴,
∴.
∵点E在反比例函数图象上,
∴,
解得:(不合题意,舍去),a2=3,
∴a的值为3.
4.【解答】解:(1)一次函数的图象与反比例函数的图象交于点A(a,3),与y轴交于点B.把x=a,y=3代入得:
,
解得:a=4,
把x=4,y=3代入得:
,
解得:k=12;
(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,点A(4,3),D点的纵坐标是0,
∴点C的纵坐标是3×2﹣0=6,把y=6代入,得x=2,
∴C(2,6),
①如图,作CF⊥x轴于F,交AB于E,作AM⊥y轴于M,
当x=2时,,
∴E(2,2),
∵C(2,6),A(4,3),
∴CE=6﹣2=4,AM=4,
∴;
②由图象可得,当x≥4时,一次函数的图象在反比例函数的图象上或上方,
∴当x≥4时,;
③设,Q(n,0),
∵A(4,3),B(0,1).
当AB为对角线时,,
∴,
∴P(3,4);
当AP为对角线时,
解得,
∴P(﹣6,﹣2),
∵﹣6<0,
∴不合题意,舍去;
当AQ为对角线时,
解得:,
∴P(6,2),
综上P点坐标为(3,4)或(6,2).
5.【解答】解:(1)如图,作PM⊥OA于M,PN⊥OB于N,PH⊥AB于H.
∴∠PMA=∠PHA=90°,
∵∠PAM=∠PAH,PA=PA,
∴△PAM≌△PAH(AAS),
∴PM=PH,∠APM=∠APH,
同理可证:△BPN≌△BPH,
∴PH=PN,∠BPN=∠BPH,
∴PM=PN,
∵∠PMO=∠MON=∠PNO=90°,
∴四边形PMON是矩形,
∴∠MPN=90°,
∴∠APB=∠APH+∠BPH(∠MPH+∠NPH)=45°,
∵PM=PN,
∴可以假设P(m,m),
∵P(m,m)在y上,
∴m2=9,
∵m>0,
∴m=3,
∴P(3,3).
(2)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∵AB2=OA2+OB2,
∴a2+b2=(6﹣a﹣b)2,
可得ab=6a+6b﹣18,
∴3a+3b﹣9ab,
∵PM∥OC,
∴,
∴,
∴OC,同法可得OD,
∴S△COD OC DO 9.
解法二:连接OP.
∵∠POA=∠POB=∠CPD=45°,
∴∠COP=∠POD=135°,
∵∠POB=∠PCO+∠OPC=45°,∠APO+∠OPD=45°,
∴∠PCO=∠OPD,
∴△COP∽△POD,
∴OC OD=OP2=18,可求△COD的面积等于9.
(3)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∴OA+OB+AB=6,
∴a+b6,
∴26,
∴(2)6,
∴3(2),
∴ab≤54﹣36,
∴S△AOBab≤27﹣18,
∴△AOB的面积的最大值为27﹣18.
6.【解答】解:(1)设直线PQ的解析式为y=kx+b,则有,
解得,
∴y=﹣x+m+1,
令x=0,得到y=m+1,∴D(0,m+1),
令y=0,得到x=m+1,∴C(m+1,0),
∴OC=OD,
∵∠COD=90°,
∴∠OCD=45°.
(2)设M(a,),
∵△OPM∽△OCP,
∴,
∴OP2=OC OM,
当m=3时,P(3,1),C(4,0),
OP2=32+12=10,OC=4,OM,
∴,
∴10=4,
∴4a4﹣25a2+36=0,
(4a2﹣9)(a2﹣4)=0,
∴a=±,a=±2,
∵1<a<3,
∴a或2,
当a时,M(,2),
PM,CP,
(舍弃),
当a=2时,M(2,),PM,CP,
∴,成立,
∴M(2,).
解法二:∵△OPM∽△OCP,
∴()2,
∵S△OCP=2,
∴S△OPM,
∴3×(),
解得,x=2或(舍弃),
∴M(2,).
(3)不存在.理由如下:
当m=5时,P(5,1),Q(1,5),设M(x,),
OP的解析式为:yx,OQ的解析式为y=5x,
①当1<x<5时,如图1中,
∴E(,),F(x,x),
S=S矩形OAMB﹣S△OAF﹣S△OBE
=5 x x 4.1,
化简得到:x4﹣9x2+25=0,
Δ<0,
∴没有实数根.
②当x≤1时,如图2中,
S=S△OGH<S△OAM=2.5,
∴不存在,
③当x≥5时,如图3中,
S=S△OTS<S△OBM=2.5,
∴不存在,
综上所述,不存在.
7.【解答】解:(1)∵函数的图象过点A(n,2)和两点,代入得:
,
解得,
故n和k的值分别为4,8;
(2)∵n=4,k=8,
∴,
设直线OA的解析式为:y=mx,
把A(4,2)代入y=mx,得2=4m,
解得m,
∴直线OA的解析式为:,
过点C作CG⊥x轴于点G,交直线OA于点H,如图1,
设,
∴,
∴,
∴,
∴m=2或m=8(不符合题意舍去),
∴C(2,4),
(3)第二象限内存在点F,使得△DEF是以DE为腰的等腰直角三角形,理由如下:
∵DE∥OA,直线OA的解析式为:,
∴设直线DE的解析式为:,
∵点C(2,4)在直线DE上,,
∴,即b=3,
∴直线DE的解析式为:;
当x=0时,y=3,
∴E(0,3),OE=3
当y=0时,x=﹣6,
∴D(﹣6,0),OD=6,
根据题意,分两种情况进行讨论:
①以DE为直角边,D为直角顶点;
如图2,过F1做F1K⊥x轴于点K,可知:∠F1KD=∠DOE=90°,
∵∠F1DE=90°,
∴∠F1DK+∠EDO=90°,
又∵∠DEO+∠EDO=90°,
∴∠F1DK=∠DEO,
又∵DF1=DE,
∴△F1KD≌△DOE(AAS),
∴F1K=DO=6,KD=OE=3,
故点D到点F1的平移规律是:D向左移3个单位,向上移6个单位得点F1坐标,
∵D(﹣6,0),且F在第二象限,
∴F1(﹣6﹣3,0+6)即F1(﹣9,6);
②以DE为直角边,E为直角顶点;同①理得,将E点向左移3个单位,向上移6个单位得点F坐标,得F2(﹣3,9).
综上所述:点F(﹣9,6)或(﹣3,9).
8.【解答】解:(1)∵OA=4,OC=3,四边形OABC是矩形,
∴AB=OC=3,BC=AO=4,
∴B(4,3),
∵E是BC的中点,
∴E(2,3),
∵反比例函数的图象经过点E,
∴k=2×3=6,
∴反比例数解析式为,
∵反比例函数的图象经过点F,F的横坐标为4,
∴,
∴;
(2)解:存在,设P(m,0),
∵E(2,3),,
∴PE2=(m﹣2)2+32=m2﹣4m+13,,,
设直线EF的解析式为y=kx+b,
则,
解得:,
∴,
①当PE=PF时,m2﹣4m+13,
解得:,
∴;
②当EP=EF时,m2﹣4m+13,,
此方程无解;
③当FP=FE时,,
解得m=2或m=6;
∵线段EF的解析式为,当x=6时,,
∴P(6,0)在直线EF上,
综上所述,P(2,0)或;
(3)Q是x轴上的一点,设Q(n,0),则QE2=(n﹣2)2+32=n2﹣4n+13,QF2=(n﹣4)2+()2=n2﹣8n,,
①当E为直角顶点时,EQ2+EF2=FQ2,即,
解得:,
则;
②当F为直角顶点时,EF2+FQ2=EQ2,即,
解得:,
则Q;
③当Q为直角顶点时,EQ2+FQ2=EF2,即,
此方程无解,
综上所述,或.
9.【解答】解:(1)∵AB⊥y轴于点B,
∴∠OBA=90°,
在Rt△OBA中,AB=2,tan∠AOB,
∴OB=4,
∴A(2,4),
∵点A在反比例函数y(x>0)的图象上,
∴k=4×2=8;
∴反比例函数的解析式为y;
(2)如图,过A作AF⊥x轴于F,过C作CE⊥x轴于E,
∴∠AFD=90°,
∵∠ADO=45°,
∴∠FAD=90°﹣∠CDE=45°,
∴AF=DF=OB=4,
∵OF=AB=2,
∴OD=6,
∴D(6,0),
设直线AC的解析式为y=ax+b,
∵点A(2,4),D(6,0)在直线AC上,
∴,
解得,
∴直线AC的解析式为y=﹣x+6①,
由(1)知,反比例函数的解析式为y②,
联立①②解得,或,
∴C(4,2),
∵△AOF的面积OF AF2×4=4,△OCE的面积OE CE2×4=4,
∴△AOF的面积=△OCE的面积,
∴△AOF的面积﹣△OFH的面积=△OCE的面积﹣△OFH的面积,
∴△AOF的面积=梯形CEFH的面积,
∴△AOC的面积=梯形CEFH的面积(AF+CE) EF(4+2)(4﹣2)=6.
10.【解答】解:(1)∵直线y=2x+6经过点A(m,8),
∴2×m+6=8,
解得m=1,
∴A(1,8),
∴k=2×1+6=8,
∴反比例函数的解析式为y.
(2)不等式2x+60的解集为x>1.
(3)由题意,点M,N的坐标为M(,n),N(,n),
∵0<n<6,
∴0,
∴0
∴S△BMN|MN|×|yM|()×n(n﹣3)2,
∴n=3时,△BMN的面积最大,最大值为.
11.【解答】解:(1)将点A(2,m),B(6,n)分别代入y,得:
k=2m,k=6n,
∴m=3n,
故选:A;
(2)①由(1)得:A(2,3n),B(6,n),设P(t,0),
过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
∴∠ACP=∠PDB=90°,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
∵AP=PB,
∴△ACP≌△PDB(AAS),
∴AC=PD,PC=BD,
即,
∴n=1,t=3,
∴P(3,0),B(6,1),
∴反比例函数的表达式为:y;
②如图,作AF⊥x轴于F,BG⊥x轴于G,
由①知,A(2,3),B(6,1),
∴AF=3,BG=1,FG=4,
∵S△AOF=S△BOG,
∴S△AOB=S梯形AFGB8,
故答案为:8;
(3)①AB为边,
则xB﹣xA=xM﹣xN,
即6﹣2=xM﹣0,
∴xM=4,
∴M(4,);
②AB为对角线,
则xA﹣xN=xM﹣xB,
即2﹣0=xM﹣6,
∴xM=8,
∴M(8,),
综上:M(4,)或(8,).
12.【解答】解:(1)∵(a+b+3)2=0,,且0,(a+b+3)2≥0,
,
解得,
故答案为:﹣1,﹣2;
(2)设反比例函数表达式为y,
由(1)知,a=﹣1,b=﹣2,
∴A(﹣1,0),B(0,﹣2),
∵E为AD中点,
∴xD=1,
设D(1,t),
又∵四边形ABCD是平行四边形,
∴C(2,t﹣2),
∴t=2t﹣4,
∴t=4,
∴D(1,4),
∵D点在反比例函数y的图象上,
∴4,
∴k=4,
∴反比例函数表达式为y;
(3)由(2)知,反比例函数的解析式为y,
∵点P在双曲线y上,点Q在y轴上,
∴设Q(x,0),P(x,),
①当AB为边时:
如图2①所示:若ABPQ为平行四边形,则2,解得x=﹣2,此时P1(﹣2,﹣2),Q1(﹣3,0);
如图2②所示;若ABQP为平行四边形,则2,解得x=2,此时P2(2,2),Q2(3,0);
②如图2③所示;当AB为对角线时:AQ=BP,且AQ∥BP;
则2,解得x=﹣2,此时P3(﹣2,﹣2),AQ=2,,
∴OQ=AQ﹣AO=1,
∴Q3(1,0);
∴P3(﹣2,﹣2),Q3(1,0);
故Q1(﹣3,0);Q2(3,0);Q3(1,0).
13.【解答】解:(1)∵点A(1,a)在直线y=2x上,
∴a=2×1=2,
即点A的坐标为(1,2),
∵点A(1,2)是反比例函数y(k≠0)的图象与正比例函数y=2x图象的交点,
∴k=1×2=2,
即k的值是2;
(2)由题意得:2x,
解得:x=1或﹣1,
经检验x=1或﹣1是原方程的解,
∴B(﹣1,﹣2),
∵点A(1,2),
∴AB2,
∵菱形ABCD是以AB、BC为边,且BC∥x轴,
∴AD=AB=2,
∴D(1+2,2).
14.【解答】解:(1)∵一次函数y=﹣x+b的图象交x轴于B,交y轴于C,则B(b,0),C(0,b),
∴OB=OC=﹣b,
∵∠BOC=90°
∴△OBC是等腰直角三角形,
∴∠BCO=45°.
(2)如图1中,作MN⊥AB于N.
∵M(0,4),MN⊥AC,直线AC的解析式为y=﹣x+b,
∴直线MN的解析式为y=x+4,
由,解得,
∴N(,),
∵MA=MB,MN⊥AB,
∴NA=BN,设A(m,n),
则有,解得,
∴A(﹣4,b+4),
∵点A在y上,
∴﹣4(b+4)=﹣4,
∴b=﹣3,
∴A(﹣4,1).
(3)如图2中,
由(2)可知A(﹣4,1),M(0,4),
∴AM5,
当菱形以AM为边时,AQ=AQ′=5,AQ∥OM,可得Q(﹣4,﹣4),Q′(﹣4,6),
当A,Q关于y轴对称时,也满足条件,此时Q(4,1)
当AM为菱形的对角线时,设P″(0,b),
则有(4﹣b)2=42+(b﹣1)2,
∴b.
∴AQ″=MP″,
∴Q″(﹣4,),
综上所述,满足条件的点Q坐标为(﹣4,﹣4)或(﹣4,6)或(﹣4,)或(4,1).
15.【解答】解:(1)∵PC⊥x轴于点C,BO⊥x轴,
∴OB∥PC,
∴△ABO∽△APC,
∵直线y=ax+2与y轴交于B点,
∴B(0,2),即BO=2,
∵PC=4,A的坐标为(﹣4,0),
∴,
∵OA=4,
∴AC=4×2=8,
∴OC=4,即P(4,4),
将P(4,4)代入y=ax+2,
∴4=4a+2,解得,
∴,
(2)由(1)可知P(4,4),直接代入,
∴,解得 k=16,
∴;
(3)如图,
当△ABO∽△CQH时,
∴,
设HQ为x,则CH=2x,
∴Q(4+2x,x),直接代入,
∴,解得x=﹣4或2,
∵x>0,
∴x=2,
∴Q(8,2),
当△ABO∽△QCH时,
∴,
设CH为x,则HQ=2x,
∴Q(4+x,2x),直接代入,
∴,解得或,
∵x>0,
∴,
∴,
综上所述,或Q(8,2).
16.【解答】解:(1)把A(﹣2,0)代入y=ax+1中,求得a,
∴yx+1①,
由PC=2,把y=2代入yx+1中,得x=2,
即P(2,2),
把P代入y得:k=4,
则双曲线解析式为y②;
(2)联立①②并整理得:x2+2x﹣8=0,
解得x=2或﹣4,
观察图象得,不等式ax+1的解集为x≥2或﹣4≤x<0;
(3)设Q(m,n)(m>0),
∵Q(m,n)在y上,
∴n,
当△QCH∽△BAO时,可得,即,
∴m﹣2=2n,即m﹣2,
整理得:m2﹣2m﹣8=0,
解得:m=4或m=﹣2(舍去),
∴点Q的坐标为(4,1).
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺练习反比例函数压轴题练习
1.如图所示,反比例函数y(m≠0)的图象与一次函数y=kx+b(k≠0)的图象交于A(2,a+2)、B(a﹣10,﹣1)两点,直线AB分别与x轴、y轴交于点C、D.
(1)分别求反比例函数和一次函数的解析式;
(2)若P(t,0)(t≠2)是x轴的正半轴上一动点,过P作x轴的垂线,分别与一次函数的图象和反比例函数的图象交于点M、N,设MN的长为d,求出d与t之间的函数关系式;
(3)在第二象限内是否存在点Q,使得△CDQ是等腰直角三角形.若存在,请直接写出点Q的坐标;若不存在,请说明理由.
2.如图,在直角坐标平面内,一个正比例函数y=kx的图象与反比例函数图象在第一象限内的交点为点A,过点A作AB⊥x轴,垂足为点B,AB=3.
(1)求正比例函数的解析式;
(2)在直线AB上是否存在点C,使点C到直线OA的距离等于它到点B的距离?若存在,求点C的坐标;若不存在,请说明理由;
(3)已知点P在直线AB上,如果△AOP是等腰三角形,请直接写出点P的坐标.
3.如图,在平面直角坐标系xOy中,一次函数yx+b的图象与反比例函数y的图象交于A,B两点,与y轴交于点C.已知点B的坐标为(5,1).
(1)求m,b的值;
(2)设P是线段BC上一点,过点P作PD∥y轴交反比例函数的图象于点D,连接AD,若DP=6,求△ADP的面积;
(3)在(2)的条件下,将直线AB向下平移a(a>0)个单位长度后,与射线OP交于点F,与反比例函数在第一象限内的图象交于点E,若四边形ABEF是平行四边形,求a的值.
4.如图,一次函数的图象与反比例函数的图象交于点A(a,3),与y轴交于点B.
(1)求a,k的值;
(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.
①求△ABC的面积;
②利用图象信息,直接写出不等式的解集.
③点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.
5.如图,平面直角坐标系中,O为原点,点A、B分别在y轴、x轴的正半轴上.△AOB的两条外角平分线交于点P,P在反比例函数y的图象上.PA的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD.
(1)求∠P的度数及点P的坐标;
(2)求△OCD的面积;
(3)△AOB的面积是否存在最大值?若存在,求出最大面积;若不存在,请说明理由.
6.如图,在平面直角坐标系xOy中,函数y(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(1)求∠OCD的度数;
(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;
(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.
7.如图,函数的图象过点A(n,2)和两点.
(1)求n和k的值;
(2)点C是双曲线上介于点A和点B之间的一个动点,若S△AOC=6,求C点的坐标;
(3)过C点作DE∥OA,交x轴于点D,交y轴于点E,第二象限内是否存在点F,使得△DEF是以DE为腰的等腰直角三角形?若存在,请求出点F的坐标;若不存在,请说明理由.
8.如图,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=3.反比例函数y的图象经过BC的中点E,交边AB于点F,连接EF.
(1)求k的值与点F的坐标;
(2)x轴上是否存在一点P,使△PEF为等腰三角形,若存在,求出点P的坐标;若不存在,请说明理由;
(3)点Q是x轴上的一点,以点Q、E、F为顶点的三角形是直角三角形,请求出Q点的坐标.
9.如图,点A在反比例函数y(x>0)的图象上,AB⊥y轴于点B,tan∠AOB,AB=2.
(1)求反比例函数的表达式;
(2)点C在这个反比例函数图象上,连接AC并延长交x轴于点D,且∠ADO=45°,连接OC,求△AOC的面积.
10.如图,直线y=2x+6与反比例函数y(k>0)的图象交于点A(m,8),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的解析式;
(2)观察图象,直接写出当x>0时不等式2x+60的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
11.如图1,在平面直角坐标系中,反比例函数(k为常数,x>0)的图象经过点A(2,m),B(6,n)两点.
(1)m与n的数量关系是 .
A.m=3n
B.n=3m
C.m+n=8
D.m﹣n=4
(2)如图2,若点A绕x轴上的点P顺时针旋转90°,恰好与点B重合.
①求点P的坐标及反比例函数的表达式;
②连接OA、OB,则△AOB的面积为 ;
(3)若点M在反比例函数的图象上,点N在y轴上,在(2)的条件下,是否存在以A、B、M、N为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标,若不存在,请说明理由.
12.如图1,已知点A(a,0),B(0,b),且a、b满足(a+b+3)2=0,平行四边形ABCD的边AD与y轴交于点E,且E为AD中点,双曲线y经过C、D两点.
(1)a= ,b= ;
(2)求反比例函数表达式;
(3)点P在双曲线y上,点Q在x轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,求满足要求的所有点Q的坐标.
13.如图,反比例函数y(k≠0)的图象与正比例函数y=2x的图象相交于A(1,a)、B两点,点C在第四象限,BC∥x轴.
(1)求k的值;
(2)以AB、BC为边作菱形ABCD,求D点坐标.
14.如图,平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y在第二象限内的图象相交于点A,与x轴的负半轴交于点B,与y轴的负半轴交于点C.
(1)求∠BCO的度数;
(2)若y轴上一点M的纵坐标是4,且AM=BM,求点A的坐标;
(3)在(2)的条件下,若点P在y轴上,点Q是平面直角坐标系中的一点,当以点A、M、P、Q为顶点的四边形是菱形时,请直接写出点Q的坐标.
15.如图,直线y=ax+2与x轴、y轴分别相交于A、B两点,与双曲线y(x>0)相交于点P,PC⊥x轴于点C,且PC=4,点A的坐标为(﹣4,0).
(1)求一次函数的解析式;
(2)求双曲线的解析式;
(3)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
16.如图,一次函数y=ax+1的图象与x轴、y轴分别相交于A、B两点,与反比例函数y(k>0)的图象交于P,G两点,过点P作PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求反比例函数的表达式;
(2)观察图象,直接写出不等式的解集:
(3)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于点H,当△QCH∽△BAO时,求点Q的坐标.
参考答案
1.【解答】解:(1)∵反比例函数y(m≠0)的图象经过A(2,a+2)、B(a﹣10,﹣1)两点,
∴,
解得:,
∴A(2,4)、B(﹣8,﹣1),反比例函数的解析式是y,
把A(2,4)、B(﹣8,﹣1)分别代入y=kx+b得,,
解得,,
∴一次函数的解析式为yx+3;
(2)由题意得,M(t,t+3),N(t,),
∴PMt+3,PN,
当t>2时,d=PM﹣PNt+3;
当0<t≤2时,d=PN﹣PM(t+3);
(3)由(1)知,直线AB的解析式为yx+3,
令x=0,则yx+3=3,
令y=0,则0x+3,
∴x=﹣6,
∴C(﹣6,0),D(0,3),
∴OC=6,OD=3,如图,
∵△CDQ是等腰直角三角形,
∴①当∠CDQ=90°时,CD=QD,
过点Q作QH⊥y轴于H,
∴∠QDH+∠DQH=90°,
∵∠CDQ=90°,
∴∠QDH+∠CDO=90°,
∴∠CDO=∠DQH,
∴△COD≌△HDQ(AAS),
∴QH=OD=3,DH=OC=6,
∴OH=OD+DH=9,
∴Q(﹣3,9);
②当∠DCQ=90°时,同①的方法得,Q'(﹣9,6);
③当∠CQD=90°时,
同①的方法得,△CLQ''≌△DKQ'',
∴Q''L=Q''K,CL=DK,
∴设Q''(﹣a,a),
∴Q''K=Q''K=a,
∴CL=6﹣a,DK=a﹣3,
∴6﹣a=3﹣a,
∴a,∴Q''(,),
即满足条件的点Q的坐标为(﹣3,9)或(﹣9,6)或(,).
2.【解答】解:(1)∵AB=3,
∴点A的纵坐标为3,∵反比例函数y的图象经过点A,
当y=3时,x,
∴A(,3),
将点A(,3)代入y=kx得k,
∴正比例函数的解析式为yx;
(2)∵AB⊥x轴于点B,设点C的坐标为(,y),
在Rt△ABO中,OB,AB=3,
由勾股定理可得OA=2,
∵OB,
∴∠OAB=30°,
过点C作CG⊥OA于G,
由题意得CB=CG,
当点C在AB上时,
则OC平分∠AOB,
∴∠BOC=30°,
∴BCOB=1,
∴C(,1);
当点C在AB延长线上时,
同理可得C'(,﹣3);
综上所述:C(,1)或(,﹣3);
(3)①当AO=AP=2时,
则P(,3﹣2)或(,3+2);
②当OA=OP时,
由OB⊥AP得,AB=BP,
∴P(,﹣3);
③当PA=PO时,
∴∠OAP=∠POA=30°,
则OP平分∠AOB,
∴P(,1);
综上所述:P(,3﹣2)或(,3+2)或(,1)或(,﹣3).
3.【解答】解:(1)∵一次函数的图象与反比例函数的图象交于A,B两点,且点B的坐标为(5,1),将点B的坐标代入得:
,
解得:,
∴,m=5;
(2)由(1)可知反比例函数解析式为,一次函数解析式为,
设,
∵PD∥y轴交反比例函数的图象于点D,
∴.
∵DP=6,
∴,
解得:t1=1,t2=﹣10(不合题意,舍去),
∴D(1,5).
联立得,
解得:或,
∴,
∴S△ADPDP (xD﹣xA)6×[1﹣(﹣2)]=9;
(3)如图,
∵将直线AB向下平移a(a>0)个单位长度,
∴平移后的直线解析式为,
由(2)可知P(1,﹣1),
∴直线OP的解析式为y=﹣x.
联立得:,
解得:,
∴.
∵平移后的直线与射线OP交于点F,与反比例函数在第一象限内的图象交于点E,
∴AB∥EF.
∵四边形ABEF是平行四边形,,B(5,1),
∴,
∴.
∵点E在反比例函数图象上,
∴,
解得:(不合题意,舍去),a2=3,
∴a的值为3.
4.【解答】解:(1)一次函数的图象与反比例函数的图象交于点A(a,3),与y轴交于点B.把x=a,y=3代入得:
,
解得:a=4,
把x=4,y=3代入得:
,
解得:k=12;
(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,点A(4,3),D点的纵坐标是0,
∴点C的纵坐标是3×2﹣0=6,把y=6代入,得x=2,
∴C(2,6),
①如图,作CF⊥x轴于F,交AB于E,作AM⊥y轴于M,
当x=2时,,
∴E(2,2),
∵C(2,6),A(4,3),
∴CE=6﹣2=4,AM=4,
∴;
②由图象可得,当x≥4时,一次函数的图象在反比例函数的图象上或上方,
∴当x≥4时,;
③设,Q(n,0),
∵A(4,3),B(0,1).
当AB为对角线时,,
∴,
∴P(3,4);
当AP为对角线时,
解得,
∴P(﹣6,﹣2),
∵﹣6<0,
∴不合题意,舍去;
当AQ为对角线时,
解得:,
∴P(6,2),
综上P点坐标为(3,4)或(6,2).
5.【解答】解:(1)如图,作PM⊥OA于M,PN⊥OB于N,PH⊥AB于H.
∴∠PMA=∠PHA=90°,
∵∠PAM=∠PAH,PA=PA,
∴△PAM≌△PAH(AAS),
∴PM=PH,∠APM=∠APH,
同理可证:△BPN≌△BPH,
∴PH=PN,∠BPN=∠BPH,
∴PM=PN,
∵∠PMO=∠MON=∠PNO=90°,
∴四边形PMON是矩形,
∴∠MPN=90°,
∴∠APB=∠APH+∠BPH(∠MPH+∠NPH)=45°,
∵PM=PN,
∴可以假设P(m,m),
∵P(m,m)在y上,
∴m2=9,
∵m>0,
∴m=3,
∴P(3,3).
(2)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∵AB2=OA2+OB2,
∴a2+b2=(6﹣a﹣b)2,
可得ab=6a+6b﹣18,
∴3a+3b﹣9ab,
∵PM∥OC,
∴,
∴,
∴OC,同法可得OD,
∴S△COD OC DO 9.
解法二:连接OP.
∵∠POA=∠POB=∠CPD=45°,
∴∠COP=∠POD=135°,
∵∠POB=∠PCO+∠OPC=45°,∠APO+∠OPD=45°,
∴∠PCO=∠OPD,
∴△COP∽△POD,
∴OC OD=OP2=18,可求△COD的面积等于9.
(3)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∴OA+OB+AB=6,
∴a+b6,
∴26,
∴(2)6,
∴3(2),
∴ab≤54﹣36,
∴S△AOBab≤27﹣18,
∴△AOB的面积的最大值为27﹣18.
6.【解答】解:(1)设直线PQ的解析式为y=kx+b,则有,
解得,
∴y=﹣x+m+1,
令x=0,得到y=m+1,∴D(0,m+1),
令y=0,得到x=m+1,∴C(m+1,0),
∴OC=OD,
∵∠COD=90°,
∴∠OCD=45°.
(2)设M(a,),
∵△OPM∽△OCP,
∴,
∴OP2=OC OM,
当m=3时,P(3,1),C(4,0),
OP2=32+12=10,OC=4,OM,
∴,
∴10=4,
∴4a4﹣25a2+36=0,
(4a2﹣9)(a2﹣4)=0,
∴a=±,a=±2,
∵1<a<3,
∴a或2,
当a时,M(,2),
PM,CP,
(舍弃),
当a=2时,M(2,),PM,CP,
∴,成立,
∴M(2,).
解法二:∵△OPM∽△OCP,
∴()2,
∵S△OCP=2,
∴S△OPM,
∴3×(),
解得,x=2或(舍弃),
∴M(2,).
(3)不存在.理由如下:
当m=5时,P(5,1),Q(1,5),设M(x,),
OP的解析式为:yx,OQ的解析式为y=5x,
①当1<x<5时,如图1中,
∴E(,),F(x,x),
S=S矩形OAMB﹣S△OAF﹣S△OBE
=5 x x 4.1,
化简得到:x4﹣9x2+25=0,
Δ<0,
∴没有实数根.
②当x≤1时,如图2中,
S=S△OGH<S△OAM=2.5,
∴不存在,
③当x≥5时,如图3中,
S=S△OTS<S△OBM=2.5,
∴不存在,
综上所述,不存在.
7.【解答】解:(1)∵函数的图象过点A(n,2)和两点,代入得:
,
解得,
故n和k的值分别为4,8;
(2)∵n=4,k=8,
∴,
设直线OA的解析式为:y=mx,
把A(4,2)代入y=mx,得2=4m,
解得m,
∴直线OA的解析式为:,
过点C作CG⊥x轴于点G,交直线OA于点H,如图1,
设,
∴,
∴,
∴,
∴m=2或m=8(不符合题意舍去),
∴C(2,4),
(3)第二象限内存在点F,使得△DEF是以DE为腰的等腰直角三角形,理由如下:
∵DE∥OA,直线OA的解析式为:,
∴设直线DE的解析式为:,
∵点C(2,4)在直线DE上,,
∴,即b=3,
∴直线DE的解析式为:;
当x=0时,y=3,
∴E(0,3),OE=3
当y=0时,x=﹣6,
∴D(﹣6,0),OD=6,
根据题意,分两种情况进行讨论:
①以DE为直角边,D为直角顶点;
如图2,过F1做F1K⊥x轴于点K,可知:∠F1KD=∠DOE=90°,
∵∠F1DE=90°,
∴∠F1DK+∠EDO=90°,
又∵∠DEO+∠EDO=90°,
∴∠F1DK=∠DEO,
又∵DF1=DE,
∴△F1KD≌△DOE(AAS),
∴F1K=DO=6,KD=OE=3,
故点D到点F1的平移规律是:D向左移3个单位,向上移6个单位得点F1坐标,
∵D(﹣6,0),且F在第二象限,
∴F1(﹣6﹣3,0+6)即F1(﹣9,6);
②以DE为直角边,E为直角顶点;同①理得,将E点向左移3个单位,向上移6个单位得点F坐标,得F2(﹣3,9).
综上所述:点F(﹣9,6)或(﹣3,9).
8.【解答】解:(1)∵OA=4,OC=3,四边形OABC是矩形,
∴AB=OC=3,BC=AO=4,
∴B(4,3),
∵E是BC的中点,
∴E(2,3),
∵反比例函数的图象经过点E,
∴k=2×3=6,
∴反比例数解析式为,
∵反比例函数的图象经过点F,F的横坐标为4,
∴,
∴;
(2)解:存在,设P(m,0),
∵E(2,3),,
∴PE2=(m﹣2)2+32=m2﹣4m+13,,,
设直线EF的解析式为y=kx+b,
则,
解得:,
∴,
①当PE=PF时,m2﹣4m+13,
解得:,
∴;
②当EP=EF时,m2﹣4m+13,,
此方程无解;
③当FP=FE时,,
解得m=2或m=6;
∵线段EF的解析式为,当x=6时,,
∴P(6,0)在直线EF上,
综上所述,P(2,0)或;
(3)Q是x轴上的一点,设Q(n,0),则QE2=(n﹣2)2+32=n2﹣4n+13,QF2=(n﹣4)2+()2=n2﹣8n,,
①当E为直角顶点时,EQ2+EF2=FQ2,即,
解得:,
则;
②当F为直角顶点时,EF2+FQ2=EQ2,即,
解得:,
则Q;
③当Q为直角顶点时,EQ2+FQ2=EF2,即,
此方程无解,
综上所述,或.
9.【解答】解:(1)∵AB⊥y轴于点B,
∴∠OBA=90°,
在Rt△OBA中,AB=2,tan∠AOB,
∴OB=4,
∴A(2,4),
∵点A在反比例函数y(x>0)的图象上,
∴k=4×2=8;
∴反比例函数的解析式为y;
(2)如图,过A作AF⊥x轴于F,过C作CE⊥x轴于E,
∴∠AFD=90°,
∵∠ADO=45°,
∴∠FAD=90°﹣∠CDE=45°,
∴AF=DF=OB=4,
∵OF=AB=2,
∴OD=6,
∴D(6,0),
设直线AC的解析式为y=ax+b,
∵点A(2,4),D(6,0)在直线AC上,
∴,
解得,
∴直线AC的解析式为y=﹣x+6①,
由(1)知,反比例函数的解析式为y②,
联立①②解得,或,
∴C(4,2),
∵△AOF的面积OF AF2×4=4,△OCE的面积OE CE2×4=4,
∴△AOF的面积=△OCE的面积,
∴△AOF的面积﹣△OFH的面积=△OCE的面积﹣△OFH的面积,
∴△AOF的面积=梯形CEFH的面积,
∴△AOC的面积=梯形CEFH的面积(AF+CE) EF(4+2)(4﹣2)=6.
10.【解答】解:(1)∵直线y=2x+6经过点A(m,8),
∴2×m+6=8,
解得m=1,
∴A(1,8),
∴k=2×1+6=8,
∴反比例函数的解析式为y.
(2)不等式2x+60的解集为x>1.
(3)由题意,点M,N的坐标为M(,n),N(,n),
∵0<n<6,
∴0,
∴0
∴S△BMN|MN|×|yM|()×n(n﹣3)2,
∴n=3时,△BMN的面积最大,最大值为.
11.【解答】解:(1)将点A(2,m),B(6,n)分别代入y,得:
k=2m,k=6n,
∴m=3n,
故选:A;
(2)①由(1)得:A(2,3n),B(6,n),设P(t,0),
过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
∴∠ACP=∠PDB=90°,
∴∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
∵AP=PB,
∴△ACP≌△PDB(AAS),
∴AC=PD,PC=BD,
即,
∴n=1,t=3,
∴P(3,0),B(6,1),
∴反比例函数的表达式为:y;
②如图,作AF⊥x轴于F,BG⊥x轴于G,
由①知,A(2,3),B(6,1),
∴AF=3,BG=1,FG=4,
∵S△AOF=S△BOG,
∴S△AOB=S梯形AFGB8,
故答案为:8;
(3)①AB为边,
则xB﹣xA=xM﹣xN,
即6﹣2=xM﹣0,
∴xM=4,
∴M(4,);
②AB为对角线,
则xA﹣xN=xM﹣xB,
即2﹣0=xM﹣6,
∴xM=8,
∴M(8,),
综上:M(4,)或(8,).
12.【解答】解:(1)∵(a+b+3)2=0,,且0,(a+b+3)2≥0,
,
解得,
故答案为:﹣1,﹣2;
(2)设反比例函数表达式为y,
由(1)知,a=﹣1,b=﹣2,
∴A(﹣1,0),B(0,﹣2),
∵E为AD中点,
∴xD=1,
设D(1,t),
又∵四边形ABCD是平行四边形,
∴C(2,t﹣2),
∴t=2t﹣4,
∴t=4,
∴D(1,4),
∵D点在反比例函数y的图象上,
∴4,
∴k=4,
∴反比例函数表达式为y;
(3)由(2)知,反比例函数的解析式为y,
∵点P在双曲线y上,点Q在y轴上,
∴设Q(x,0),P(x,),
①当AB为边时:
如图2①所示:若ABPQ为平行四边形,则2,解得x=﹣2,此时P1(﹣2,﹣2),Q1(﹣3,0);
如图2②所示;若ABQP为平行四边形,则2,解得x=2,此时P2(2,2),Q2(3,0);
②如图2③所示;当AB为对角线时:AQ=BP,且AQ∥BP;
则2,解得x=﹣2,此时P3(﹣2,﹣2),AQ=2,,
∴OQ=AQ﹣AO=1,
∴Q3(1,0);
∴P3(﹣2,﹣2),Q3(1,0);
故Q1(﹣3,0);Q2(3,0);Q3(1,0).
13.【解答】解:(1)∵点A(1,a)在直线y=2x上,
∴a=2×1=2,
即点A的坐标为(1,2),
∵点A(1,2)是反比例函数y(k≠0)的图象与正比例函数y=2x图象的交点,
∴k=1×2=2,
即k的值是2;
(2)由题意得:2x,
解得:x=1或﹣1,
经检验x=1或﹣1是原方程的解,
∴B(﹣1,﹣2),
∵点A(1,2),
∴AB2,
∵菱形ABCD是以AB、BC为边,且BC∥x轴,
∴AD=AB=2,
∴D(1+2,2).
14.【解答】解:(1)∵一次函数y=﹣x+b的图象交x轴于B,交y轴于C,则B(b,0),C(0,b),
∴OB=OC=﹣b,
∵∠BOC=90°
∴△OBC是等腰直角三角形,
∴∠BCO=45°.
(2)如图1中,作MN⊥AB于N.
∵M(0,4),MN⊥AC,直线AC的解析式为y=﹣x+b,
∴直线MN的解析式为y=x+4,
由,解得,
∴N(,),
∵MA=MB,MN⊥AB,
∴NA=BN,设A(m,n),
则有,解得,
∴A(﹣4,b+4),
∵点A在y上,
∴﹣4(b+4)=﹣4,
∴b=﹣3,
∴A(﹣4,1).
(3)如图2中,
由(2)可知A(﹣4,1),M(0,4),
∴AM5,
当菱形以AM为边时,AQ=AQ′=5,AQ∥OM,可得Q(﹣4,﹣4),Q′(﹣4,6),
当A,Q关于y轴对称时,也满足条件,此时Q(4,1)
当AM为菱形的对角线时,设P″(0,b),
则有(4﹣b)2=42+(b﹣1)2,
∴b.
∴AQ″=MP″,
∴Q″(﹣4,),
综上所述,满足条件的点Q坐标为(﹣4,﹣4)或(﹣4,6)或(﹣4,)或(4,1).
15.【解答】解:(1)∵PC⊥x轴于点C,BO⊥x轴,
∴OB∥PC,
∴△ABO∽△APC,
∵直线y=ax+2与y轴交于B点,
∴B(0,2),即BO=2,
∵PC=4,A的坐标为(﹣4,0),
∴,
∵OA=4,
∴AC=4×2=8,
∴OC=4,即P(4,4),
将P(4,4)代入y=ax+2,
∴4=4a+2,解得,
∴,
(2)由(1)可知P(4,4),直接代入,
∴,解得 k=16,
∴;
(3)如图,
当△ABO∽△CQH时,
∴,
设HQ为x,则CH=2x,
∴Q(4+2x,x),直接代入,
∴,解得x=﹣4或2,
∵x>0,
∴x=2,
∴Q(8,2),
当△ABO∽△QCH时,
∴,
设CH为x,则HQ=2x,
∴Q(4+x,2x),直接代入,
∴,解得或,
∵x>0,
∴,
∴,
综上所述,或Q(8,2).
16.【解答】解:(1)把A(﹣2,0)代入y=ax+1中,求得a,
∴yx+1①,
由PC=2,把y=2代入yx+1中,得x=2,
即P(2,2),
把P代入y得:k=4,
则双曲线解析式为y②;
(2)联立①②并整理得:x2+2x﹣8=0,
解得x=2或﹣4,
观察图象得,不等式ax+1的解集为x≥2或﹣4≤x<0;
(3)设Q(m,n)(m>0),
∵Q(m,n)在y上,
∴n,
当△QCH∽△BAO时,可得,即,
∴m﹣2=2n,即m﹣2,
整理得:m2﹣2m﹣8=0,
解得:m=4或m=﹣2(舍去),
∴点Q的坐标为(4,1).
21世纪教育网(www.21cnjy.com)
同课章节目录
