湖南省祁阳市浯溪二中2025年中考二轮数学有关二次函数的应用存在性问题专题训练(含答案)
文档属性
| 名称 | 湖南省祁阳市浯溪二中2025年中考二轮数学有关二次函数的应用存在性问题专题训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 17:14:26 | ||
图片预览




文档简介
湖南省祁阳市浯溪二中2025年中考二轮数学有关二次函数的应用存在性问题专题训练
1.直播购物已经逐渐走进了人们的生活,某电商直播销售一款水杯,每个水杯的成本为30元.当每个水杯的售价为40元时,平均每月售出600个.通过市场调查发现,若售价每上涨1元,其月销售量就减少10个.
(1)当每个水杯的售价为45元时,平均每月售出 个水杯,月销售利润是 元.
(2)若每个水杯售价上涨x元(x>0),每月能售出 个水杯(用含x的代数式表示).
(3)若月销售利润恰好为10000元,且尽量减少库存,求每个水杯的售价.
(4)在涨价的前提下,利润是否存在最大值?若能,求出最大值及售价;若不能,请说明理由.
2.如图,学校计划建一个矩形花圃,其中一边靠墙,已知墙长为42米,篱笆长为60米,若设垂直于墙的边AB的长为x米,平行于墙的边BC长为y米,围成的矩形花圃的面积为S平方米.
(1)当x=10米时,y= 米,S= 平方米;
(2)求S与x之间的函数表达式;
(3)围成的矩形花圃是否存在最大面积?若存在,求出这个最大面积,并求出此时x的值,若不存在,说明理由.
3.某网店销售一种小商品,成本为每件20元,销售大数据分析表明:当每件商品的售价为30元时,平均月销售量240件:若每件商品的售价上涨1元,则月销售量就减少10件.设每件商品的售价为x元,月销售数量为y件,月销售利润为w元.
(1)求y与x、w与x的函数关系式;
(2)若月销售利润2640元,求x的值;
(3)月销售利润是否存在最大值?若存在,求出这个最大值,并求出此时x的值.
4.某网店专门销售江西特色产品——赣南脐橙,已知每千克脐橙的成本为8元.根据销售大数据分析得出:当每千克脐橙的售价为10元时,平均月销售量为600千克;若每千克脐橙的售价每上涨1元,月销售量就会减少100千克.设每千克脐橙的售价为x元,月销售量为y千克,月销售利润为w元.
(1)求y与x的函数解析式;
(2)月销售利润w是否存在最大值?若存在,求出这个最大值,并求出此时x的值.
5.把一个足球垂直于地面向上踢,t秒后该足球的高度h米满足关系式h=﹣5t2+at.已知该足球被踢出4秒后回到地面.
(1)a的值为 .
(2)若t秒后和(t+2)秒后,足球的高度相同,求t的值.
(3)是否存在这样的情况:(t+1)秒后足球的高度比t秒后足球的高度高18米?若存在,请通过计算进行说明;若不存在,请说明理由.
6.【课题学习】
学习主题:探究电流最值
课题背景:数学在电工电子中有着广泛的应用,可以帮助工程师进行电路设计和分析,控制系统设计,信号处理等工作,这些工作需要遵循物理学的规律,我们知道函数是描述变化规律的一种数学模型,欧潭数学探究小组受电流和电压间关系式的启发,以探究“探究电流最值”为主题展开项目式学习.
学习素材:
名称 内容 备注
素材1 用总长60m的篱笆围成一个矩形场地,矩形面积S随矩形一边长l的变化而变化. 课本例题
素材2 观察下列两个数的乘积,说明其中哪个积最大. 1×100,2×99,3×98,4×97,…,99×2,100×1 课本数学活动
素材3 串联电路的总电阻等于各串联电阻之和: 并联电路总电阻的倒数等于各并联电阻的倒数之和; 电压一定的情况下,电流与电阻成反比关系. 物理学知识
研究步骤:
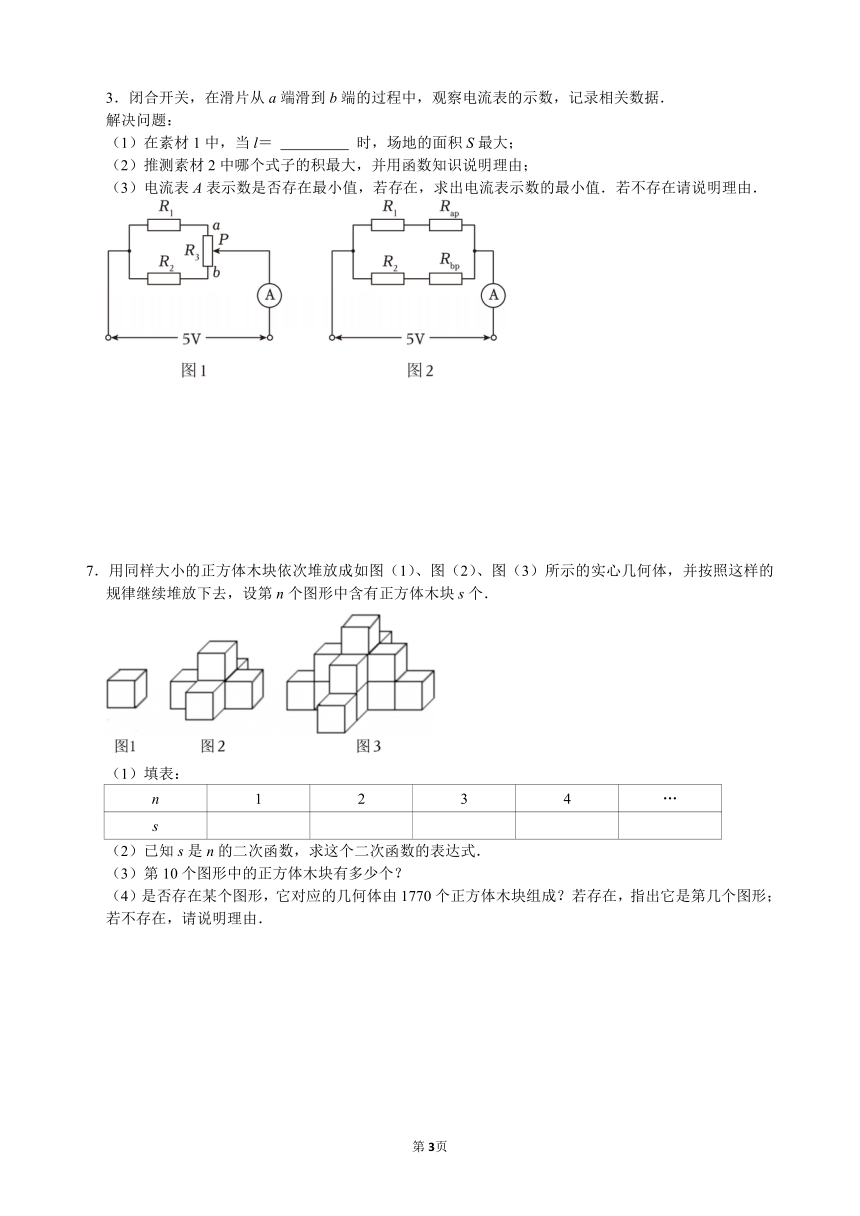
1.画出电路图.在如图1所示的电路中,R1=2Ω,R2=3Ω,滑动变阻器的最大电阻R3=5Ω,其等效电路图如图2所示,其中Rap+Rbp=R3.
2.根据电路图连结实验器材,图略.
3.闭合开关,在滑片从a端滑到b端的过程中,观察电流表的示数,记录相关数据.
解决问题:
(1)在素材1中,当l= 时,场地的面积S最大;
(2)推测素材2中哪个式子的积最大,并用函数知识说明理由;
(3)电流表A表示数是否存在最小值,若存在,求出电流表示数的最小值.若不存在请说明理由.
7.用同样大小的正方体木块依次堆放成如图(1)、图(2)、图(3)所示的实心几何体,并按照这样的规律继续堆放下去,设第n个图形中含有正方体木块s个.
(1)填表:
n 1 2 3 4 …
s
(2)已知s是n的二次函数,求这个二次函数的表达式.
(3)第10个图形中的正方体木块有多少个?
(4)是否存在某个图形,它对应的几何体由1770个正方体木块组成?若存在,指出它是第几个图形;若不存在,请说明理由.
8.2024年9月10日是我国第40个教师节,今年教师节的主题是“大力弘扬教育家精神,加快建设教育强国”,我市某学校为教师定制了水杯,如图是定制的水杯包装盒的表面展开图,设包装盒的高为x cm.
(1)若此包装盒的容积为1500cm3,请列出关于x的方程,并求出x的值.
(2)是否存在这样的x的值,使得此包装盒的容积为1560cm3?若存在,请求出相应的x的值;若不存在,请说明理由.
9.如图,用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,若在铁片的四个角截去四个相同的小正方形,设小正方形的边长为x cm.
(1)底面的长AB= cm,宽BC= cm(用含x的代数式表示)
(2)当做成盒子的底面积为300cm2时,求该盒子的容积.
(3)该盒子的侧面积S是否存在最大的情况?若存在,求出x的值及最大值是多少?若不存在,说明理由.
10.如图,利用一面墙(墙长28米),用总长度49米的栅栏(图中实线部分)围成一个矩形围栏ABCD,且中间共留两个1米的小门,设栅栏BC长为x米.
(1)若矩形围栏ABCD面积为210平方米,求栅栏BC的长;
(2)矩形围栏ABCD面积是否有可能达到240平方米?若有可能,求出相应x的值,若不可能,请说明理由;
(3)矩形围栏ABCD面积是否存在最大面积?若存在,求出矩形围栏BC的长;不存在请说明理由.
11.如图,正方形纸片ABCD的边长为4,将它剪去四个全等的直角三角形,得到四边形EFGH.设AE的长为x,四边形EFGH的面积为y.
(1)求y关于x的函数表达式;
(2)四边形EFGH的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
12.问题探究
(1)如图1,在菱形ABCD中,∠A=120°,AB=4,点P为边CD的中点,Q为边AD上一点,且DP+DQ=5,连接BP、PQ、BQ,求△BPQ的面积;
问题解决
(2)为响应市政府“建设美丽城市,改善生活环境”的号召,某小区欲建造如图2所示的四边形ABCD休闲广场,∠A=∠ABC=∠C=90°,AB=40米,BC=60米.按照规划要求,点P、Q分别在边CD、AD上,满足DP+DQ=40米,连接BP、PQ、BQ,其中△PBQ为健身休闲区,其他区域为景观绿化区,为了使绿化面积尽可能大,希望健身休闲区的面积尽可能小,那么按此要求修建的这个健身休闲区(△PBQ)是否存在最小面积?若存在,求出最小面积及此时DP的长;若不存在,请说明理由.
13.甲、乙、丙三同学玩跳绳,绳被甩到最高处时的形状是如图所示的抛物线.已知拿绳的甲、乙两同学甩绳时手间距AB为6米,手到地面的距离AD和BC都为1.3米,身高为1.6米的丙同学站在距点D的水平距离为1米的E点处,绳子甩到最高处时刚好擦过丙同学头顶F.以点D为原点建立如图所示的平面直角坐标系.
(1)求此抛物线解析式,并注明x的取值范围;
(2)如果绳子甩到最高处时刚好擦过丙同学头顶F,丙同学在CD之间是否存在除E外的另一站点,若存在,求该站点到点D的距离;若不存在,说明理由.
14.某市进行河滩治理,优化美化人居生态环境.如图所示,现规划在河畔的一处滩地上规划一个五边形河畔公园ABCDE.按设计要求,使点O,P,M,N分别在边BC,CD,AE,AB上,且满足BO=2AN=2CP,AM=OC,∠A=∠B=∠C=90°,AB=800米,BC=1200米,CD=600米,AE=900米.为满足人工湖周边各功能场所及绿化用地需要,是否存在符合设计要求的面积最小的四边形人工湖OPMN?若存在,求四边形OPMN面积的最小值及这时点N到点A的距离,请说明理由.
15.为进一步激发学生的劳动热情和创新创造活力,盐城市鹿鸣路初级中学李老师在“空翠圃”劳动实践基地开展劳动节田间管理专题实践活动.如图,正方形菜圃ABCD的边长为8米,现将它阴影部分4个全等的直角三角形种植青菜,剩余的四边形EFGH种植南瓜.设AE的长为x,四边形EFGH的面积为y.
(1)求y关于x的函数表达式;
(2)当四边形EFGH的面积为40平方米时,求AE的值;
(3)四边形EFGH的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
16.我国著名数学家华罗庚曾说过:“数与形,本是相倚依,焉能分作两边飞.数缺形时少直观,形少数时难入微;数形结合百般好,割裂分家万事非.切莫忘,几何代数统一体,永远联系,切莫分离!”数形结合是解决数学问题的重要思想方法.请结合所学的数学解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.
设函数y=(k+2)x2﹣(3k﹣2)x+2k﹣4(实数k为常数)的图象为图象T.
(1)求证:无论k取什么实数,图象T与x轴总有公共点;
(2)是否存在非负整数k,使图象T与x轴的公共点都是整点?若存在,求所有非负整数k的值;若不存在,请说明理由.
17.数和形是数学研究客观物体的两个方面,数(代数)侧重研究物体数量方面,具有精确性、形(几何)侧重研究物体形的方面,具有直观性.数和形相互联系,可用数来反映空间形式,也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题,充分利用代数、几何各自的优势,数形互化,共同解决问题.
同学们,请你结合所学的数学解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.
设函数y=(a﹣1)x2+(3﹣a)x﹣2a﹣2(实数a为常数)的图象为图象T.
(1)求证:无论a取什么实数,图象T与x轴总有公共点;
(2)是否存在整数a,使图象T与x轴的正半轴的公共点都是整点?若存在,求所有整数a的值;若不存在,请说明理由.
18.现有一个三角形广场ABC,如图所示,经测量,AC的长度为100米,点B到线段AC的距离为50米,∠A,∠C均为锐角.点E为AB边上的一动点(点E不与点A,B重合),点F为BC边上一动点(点F不与点B,C重合),且EF∥AC.
(1)当EF的长为50米时,△BEF的面积为 平方米;
(2)设点B关于EF的对称点为B',△B'EF与四边形EFCA的重叠部分的面积记为S平方米,现准备在该重叠部分内种花.请问重叠部分的面积S是否存在最大值?若存在,请求出S的最大值及此时EF的长;若不存在,请说明理由.
19.郑州市彩虹桥新桥将于2023年9月底建成通车,新桥采用三跨连续单拱肋钢箱系杆拱桥,既保留了历史记忆,又展示出郑州的开放与创新,新桥的中跨大拱的拱肋ACB可视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋的跨度AB为120米,与AB中点O相距30米处有一高度为27米的系杆EF,以AB所在直线为x轴,抛物线的对称轴为y轴建立如图②所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)正中间系杆OC的长度是多少米?若相邻系杆之间的间距均为3米(不考虑系杆的粗细),是否存在一根系杆的长度恰好是OC长度的?请说明理由.
20.问题探究
(1)如图1,在菱形ABCD中,AB=BD=8,对角线AC、BD相交于点O,点P在AB上,PE⊥AC于点E,PF⊥BD于点F,若AP=2,求四边形PEOF的面积;
问题解决
(2)如图2,菱形ABCD是某生态农庄的规划缩略图,管理人员计划在该农庄规划一个四边形PEFD的垂钓中心,使点P、E分别在AD、AC上,且PE⊥AC,∠PEF=∠ADF,DF平分∠ADC,,AC=8cm.为了让更多的游客能够同时进行垂钓,要求垂钓中心(四边形PEFD)的面积尽可能的大,请问垂钓中心的面积是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
参考答案
1.解:(1)每上涨1元,其月销售量就减少10个.当每个水杯的售价为45元时,依题意得:
600﹣10×(45﹣40)=600﹣10×5=600﹣50=550(个),
(45﹣30)×550=15×550=8250(元),
故答案为:550;8250;
(2)依题意得:若每个水杯售价上涨x元(x>0),每月能售出(600﹣10x)个水杯,
故答案为:(600﹣10x);
(3)依题意得:(40+x﹣30)(600﹣10x)=10000,
整理得:x2﹣50x+400=0,
解得:x1=10,x2=40,
当x1=10时,600﹣10x=600﹣10×10=500,
当x2=40时,600﹣10x=600﹣10×40=200,
又∵要尽量减少库存,
∴x=10,
∴40+x=40+10=50,
答:每个水杯的售价为50元;
(4)在涨价的前提下,利润存在最大值;理由如下:
设月销售利润为y元,依题意得:
∴y=(40+x﹣30)(600﹣10x)=﹣10x2+500x+6000=﹣10(x﹣25)2+12250,
∵a=﹣10<0,
∴每个书包涨价25元时,利润最大,此时书包的售价为25+40=65元,
∴书包的售价为65元时,最大利润为12250元.
2.解:(1)根据题意得:当x=10米时,y=60﹣2x=60﹣2×10=40(米),S=xy=10×40=400(平方米).
故答案为:40,400;
(2)根据题意得:S=xy=x(60﹣2x),
∴S=﹣2x2+60x.
∵,
∴9≤x<30,
∴S与x之间的函数表达式为S=﹣2x2+60x(9≤x<30);
(3)S=﹣2x2+60x=﹣2(x﹣15)2+450,
∵﹣2<0,
∴当x=15时,S取得最大值,最大值为450,
∴围成的矩形花圃存在最大面积,这个最大面积是450平方米,此时x的值为15.
3.解:(1)根据题意得:y=240﹣10(x﹣30),
∴y=﹣10x+540;
w=(x﹣20)(﹣10x+540),
∴w=﹣10x2+740x﹣10800;
(2)当w=2640时,﹣10x2+740x﹣10800=2640,
整理得:x2﹣74x+1344=0,
解得:x1=32,x2=42.
答:x的值为32或42;
(3)w=﹣10x2+740x﹣10800=﹣10(x﹣37)2+2890,
∵﹣10<0,
∴当x=37时,w取得最大值,最大值为2890.
答:月销售利润存在最大值,这个最大值为2890,此时x的值为37.
4.解:(1)设每千克脐橙的售价为x元,那么相比10元上涨了(x﹣10)元,则月销售量减少100(x﹣10)千克,
∴y=600﹣100(x﹣10)=﹣100x+1600;
(2)由每千克脐橙的成本为8元,售价为x元,月销售量为y=﹣100x+1600件,
月销售利润w为w=(x﹣8)(﹣100x+1600)=﹣100x2+2400x﹣12800,
∵a=﹣100<0,
∴该函数图象开口向下,存在最大值,
当,可得最大利润,最大利润为w=﹣100×122+2400×12﹣12800=1600(元),
答:月销售利润w存在最大值,最大值为1600元,此时x的值为12.
5.解:(1)由题意,∵足球被踢出4秒后回到地面,
∴﹣5×42+4a=0.
∴a=20.
故答案为:20.
(2)由题意,抛物线h=﹣5t2+20t的对称轴为直线t=2.
∵t秒后和(t+2)秒后,足球的高度相同,
∴t+t+2=2×2.
∴t=1.
(3)不存在.理由:由题意得,﹣5(t+1)2+20(t+1)﹣(﹣5t2+20t)=18,
∴(不合题意,舍去),故不存在这样的情况.
6.解:(1)根据题意,矩形一边长l,则另一边长为60÷2﹣l=30﹣l,
所以,S=l(30﹣l)=﹣(l﹣15)2+225,
所以,当l=15,场地的面积S最大,最大为225平方米;
故答案为:15;
(2)50×51和51×50的积最大,理由如下:
设其中一个因数为x,则另一个因数为101﹣x,
则y=x(101﹣x)=﹣x2+101x(1≤x≤100,且为正整数),
对称轴为,因为x是正整数,且1≤x≤100,
所以x取50或51时,y最大为2550;
(3)设Rap=xΩ,则Rbp=(5﹣x)Ω,0≤x≤5,设总电流为I,
则,
由分式的性质可知,若分子为不变的正数,则分母最大时,分式最小,
设W=(2+x)(8﹣x)=﹣(x﹣3)2+25,
∵﹣1<0,则抛物线W开口向下,且0≤x≤5,
∴当x=3时,W取最大值为25,
此时I取最小值为,两支路电阻分别为2+3=5Ω和8﹣3=5Ω,两支路电阻相等,
∴当两支路的电阻相等时,电流表示数最小,最小值为2A.
7.解:(1)∵第1叠放的图形中,小正方体木块个数有1个;
第2个叠放的图形中,小正方体木块个数有1+1+4=6个;
第3个叠放的图形中,小正方体木块个数应有1+1+4+1+2×4=15个;
第4个叠放的图形中,小正方体木块个数应是2×42﹣4=28个;
…
∴第n个叠放的图形中,小正方体木块个数应有1+1+1×4+1+2×4+1+3×4+…+1+4(n﹣1)=n+4n(n﹣1)=2n2﹣n个,
故答案为:1;6;19;28,2n2﹣n;
(2)二次函数的表达式为s=2n2﹣n;
(3)当n=10时,s=2×102﹣10=190,
答:第10个图形中的正方体木块有190个;
(4)当s=1770时,即2n2﹣n=1770,
解得:n=119(负值舍去),
∴存在,它是第30个图形.
8.解:(1)设包装盒的高为x cm,由图得宽为,高为x cm,包装盒的长为15cm,
∵此包装盒的容积为1500cm3,
∴(20﹣x)×15x=1500,
解得:x1=x2=10,
∴x的值为10;
(2)设该包装盒的容积为y cm3,依题意得:
∴y=(20﹣x)×15x=﹣15(x﹣10)2+1500.
∵﹣15<0,
∴当x=10时,此包装盒的容积最大,最大容积为1500cm3,
∴不存在这样的x的值,使得此包装盒的容积为1560cm3.
9.解:(1)∵用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,在铁片的四个角截去四个相同的小正方形,
设小正方形的边长为xcm,
∴底面的长AB=(50﹣2x)cm,宽BC=(30﹣2x)cm,
故答案为:50﹣2x,30﹣2x;
(2)依题意,得:
(50﹣2x)(30﹣2x)=300
整理,得:x2﹣40x+300=0
解得:x1=10,x2=30(不符合题意,舍去)
当x1=10时,盒子容积=(50﹣20)(30﹣20)×10=3000(cm3);
(3)盒子的侧面积为:
S=2x(50﹣2x)+2x(30﹣2x)
=100x﹣4x2+60x﹣4x2
=﹣8x2+160x=﹣8(x2﹣20x)
=﹣8[(x﹣10)2﹣100]
=﹣8(x﹣10)2+800
∵﹣8(x﹣10)2≤0,
∴﹣8(x﹣10)2+800≤800,
∴当x=10时,S有最大值,最大值为800.
10.解:(1)∵设栅栏BC长为x米,
∴DC=49+2﹣3x=(51﹣3x)米,
依题意,得:(51﹣3x)x=210,
整理,得:x2﹣17x+70=0,
解得:x1=7,x2=10.
当x=7时,AB=51﹣3x=30>28,不合题意,舍去,
当x=10时,AB=51﹣3x=21,符合题意,
答:栅栏BC的长为10米;
(2)矩形围栏ABCD面积不可能达到240平方米;理由如下:
依题意,得:(51﹣3x)x=240,
整理得:x2﹣17x+80=0,
∵Δ=(﹣17)2﹣4×1×80=﹣31<0,
∴方程没有实数根,
∴矩形围栏ABCD面积不可能达到240平方米;
(3)矩形围栏ABCD面积存在最大面积;理由如下:
设矩形围栏ABCD面积为S,
根据题意得,51﹣3x>0,
∴x<17,
∴,
∵﹣3<0,
∴当时,即米时,S有最大值.
11.解:(1)∵在正方形纸片ABCD上剪去4个全等的直角三角形,
在△AEH中,AE=x,AH=BE=AB﹣AE=4﹣x,∠A=90°,
∴y=S正方形ABCD﹣4S△AEH
=2x2﹣8x+16;
(2)正方形EFGH的面积为:y=2x2﹣8x+16=2(x﹣2)2+8(0<x<4),
∴当x=2时,y有最小值8,即四边形EFGH的面积最小为8.
12.解:(1)如图,过点B作BE⊥AD交DA的延长线于点E,过点P作PM⊥AD于点M,延长MP交BC的延长线于点N,
∴∠BAE=∠ABC=∠DCN=∠D=60°,
在菱形ABCD中,AB=4,点P为边CD的中点,
∴DP=CP=2,
∵DP+DQ=5,
∴DQ=3,
∴AQ=1,
在Rt△ABE中,BE=AB sin60°=2,
在Rt△CPN中,PN=CP sin60°,
在Rt△DPM中,PM=DP sin60°,
∴S△BPQ=S菱形ABCD﹣S△ABQ﹣S△BCP﹣S△DPQ
=4×21×243
.
(2)∵∠A=∠ABC=∠C=90°,
∴四边形ABCD是矩形,
∴AB=CD=40米,BC=AD=60米,
设DP=x米,则CP=(40﹣x)米,DQ=(40﹣x)米,AQ=(20+x)米,
∴S△BPQ=S矩形ABCD﹣S△ABQ﹣S△BCP﹣S△DPQ
=40×6040(20+x)60×(40﹣x)x(40﹣x)
x2﹣10x+800
(x﹣10)2+750.
∴当x=10时,S△BPQ的最小值为750.
∴按此要求修建的这个健身休闲区(△PBQ)存在最小面积,最小面积为750平方米,此时DP的长为10米.
13.解:(1)设此抛物线的解析式为 y=ax2+bx+c,
由题意得点A(0,1.3),F(1,1.6),B(6,1.3),
代入 y=ax2+bx+c 得,
解得,
∴抛物线的解析式为y=﹣0.06x2+0.36x+1.3(0≤x≤6);
(2)存在,理由:
设站点到点D的距离为x,
则﹣0.06x2+0.36x+1.3=1.6,
解得x=1或5,
∵x=1即为站点E,
∴存在另一站点到点D的距离为5米.
14.解:存在,如图延长AE、CD相交于点F,
∵∠A=∠B=∠C=90°,
∴四边形ABCF是矩形,
∴AF=BC=1200,AB=FC=800,
∵AM=OC,BO=2AN=2CP,
∴MF=BO,BN=FP,
设AN=x,则CP=x,BO=MF=2x,AM=OC=1200﹣2x,BN=FP=800﹣x,
此时 S四边形OPMN=S ABCF﹣S△BNO﹣S△ANM﹣S△FMP﹣S△CPO
=960000﹣(1600x﹣2x2)﹣(1200x﹣2x2)
=960000﹣2800x+4x2
=4(x﹣350)2+470000,
∵4>0,
∴当x=350时,S四边形OPMN有最小值470000平方米,
当x=350时,AN=350米,AM=1200﹣2x=500米<AE=900米,
CP=x=350米<CD=600米,
∴存在符合设计要求的面积最小值为470000平方米的四边形人工湖OPMN,
此时点N到点A的距离为350米.
15.解:(1)∵正方形纸片ABCD的边长为8,4个直角三角形全等,
∴AB=AD=BC=CD=8,AE=DH=x,BE=AH=8﹣x,∠A=∠D=90°,EH=HG=FG=EF,∠AEH=∠GHD.
∵∠AEH+∠AHE=90°,
∴∠AHE+∠DHG=90°,
∴∠EHG=90°,
∴四边形EFGH是正方形.
∴y=AE2+AH2=x2+(8﹣x)2=2x2﹣16x+64;
(2)当y=40时,即2x2﹣16x+64=40,
∴x2﹣8x+12=0.
解得x=2或x=6,
答:当AE取2或6时,四边形EFGH的面积为40;
(3)∵y=2x2﹣16x+64=2(x﹣4)2+32,
∵2>0,
∴y有最小值,最小值为32.
即四边形EFGH的面积有最小值,最小值为32.
16.(1)证明:当k+2=0时,
函数y=8x﹣8,该函数和x轴有交点(1,0);
当k+2≠0时,
∵Δ=(2﹣3k)2﹣4(k+2)(2k﹣4)=(k﹣6)2≥0,
故该函数和x轴有交点,
故图象T与x轴总有公共点;
(2)解:存在,理由:
∵k为非负整数,
则k+2≠0,
令y=(k+2)x2﹣(3k﹣2)x+2k﹣4=0,
解得:x=1或,
而x2,
当k=0,2,6时,x=﹣2,0,1,符合题意,
故k=0或2或6.
17.(1)证明:当a=1时,函数表达式为y=2x﹣4,
令y=0得:x=2,
∴此时函数y=(a﹣1)x2+(3﹣a)x﹣2a﹣2(实数a为常数)的图象与x轴有交点;
当a≠1时,
y=(a﹣1)x2+(3﹣a)x﹣2a﹣2为二次函数,
∴Δ=(3﹣a)2﹣4(4a﹣1)(﹣2a﹣2)=9a2﹣6a+1=(3a﹣1)2≥0,
∴函数y=(a﹣1)x2+(3﹣a)x﹣2a﹣2(实数a为常数)的图象与x轴有交点;
综上所述,无论a取什么实数,图象T与x轴总有公共点;
(2)解:存在整数a,使图象T与x轴的公共点中有整点,理由如下:
当a=1时,图象与x轴交于(2,0),符合题意;
当a≠1时,令y=0得:
0=(a﹣1)x2+(3﹣a)x﹣2a﹣2,
[(a﹣1)x+(a+1)](x﹣2)=0,
解得x=2或x,
∵x1,a是整数,
∴当a﹣1是2的因数时,x是整数,
∵图象T与x轴的正半轴的公共点都是整点,
∴2,
解得:a=2,
∴a=1或a=2.
18.解:(1)不妨设点B到线段EF,AC的距离分别为h小,h大,
∵EF∥AC,
∴△BEF∽△BAC,
∴,
∴,
解得h小=25,
∴S△BEF50×25=625,
故答案为:625;
(2)存在.由题意得,
设EF的长度为x米,
∵EF∥AC,
∴∠BEF=∠A,∠BFE=∠C,
∴△BEF∽△BAC,
∴,即,
∴,
分两种情况讨论:
①当点B'落在四边形EFCA内或AC边上时,0<x≤50
如图1,此时S=S△BEFx2,
所以当0<x≤50时,S的最大值为625m2;
②当B'落在四边形EFCA外时,50<x<100,
如图2,连接BB',与EF交于点M,与AC交于点N,
连接EB',与AC交于点G,连接FB′,与AC交于点H,
∵EF∥AC,
∴即,
∴,
∴,
∴B'N=BB'﹣BN=x﹣50,
∴()2,
即()2,
∴S△B′GH=x2﹣100x+2500,
∴S=S四边形EFHG=SΔG'EF﹣S△B'GH,
当时,S最大,最大值为.
综上所述,当m时,S最大,最大值为.
19.解:(1)结合图象由题意可知:B(60,0),E(30,27),设该抛物线解析式为:y=ax2+c,则:
,解得:,∴y36.
(2)当x=0时,y=36,∴正中间系杆OC的长度是36米.
设存在一根系杆的长度是OC的,即这根系杆的长度是12米,则1236,
解得:x=±20.∵相邻系杆之间的间距均为3米,最中间系标OC在y轴上,
∴每根系杆上的点的横坐标均为整数.
∴x=±20与实际不符.∴不存在一根系杆的长度恰好是OC长度的.
20.解:(1)∵PE⊥AC,PF⊥BD,∴∠PEA=∠BOA,∴PE∥BO,∴△PEA∽△BOA,∠PAE=∠BPF,又∵∠PEA=∠BFP=90°,∴△PEA∽△BFP,∴,,∵菱形ABCD中AB=BD=8,∴AC⊥DB,DO=BO=4,∴Rt△ABO中,,∴,∴,∴,即四边形PEOF的面积为;
(2)连接DB,
∵菱形ABCD,
∴DB⊥AC,AO=CO,DO=BO,DB平分∠ADC,
又∵DF平分∠ADC,∴F在DB上,∵,AC=8cm,∴AO=CO=4cm,
∴Rt△ABO中,,∵PE⊥AC,DF⊥AC,∴∠PEO=∠DOC=90°,∴PE∥DF,∴∠PEF=∠EFO,又∵∠PEF=∠ADF,∴∠ADF=∠EFO,∴PD∥EF,同理可得△PEA∽△DOA,△PEA∽△FOE,设AE=a cm,
∴,,
∵,∴,,
∴,
当时,S四边形PEFD有最大值为2cm2.
第18页
1.直播购物已经逐渐走进了人们的生活,某电商直播销售一款水杯,每个水杯的成本为30元.当每个水杯的售价为40元时,平均每月售出600个.通过市场调查发现,若售价每上涨1元,其月销售量就减少10个.
(1)当每个水杯的售价为45元时,平均每月售出 个水杯,月销售利润是 元.
(2)若每个水杯售价上涨x元(x>0),每月能售出 个水杯(用含x的代数式表示).
(3)若月销售利润恰好为10000元,且尽量减少库存,求每个水杯的售价.
(4)在涨价的前提下,利润是否存在最大值?若能,求出最大值及售价;若不能,请说明理由.
2.如图,学校计划建一个矩形花圃,其中一边靠墙,已知墙长为42米,篱笆长为60米,若设垂直于墙的边AB的长为x米,平行于墙的边BC长为y米,围成的矩形花圃的面积为S平方米.
(1)当x=10米时,y= 米,S= 平方米;
(2)求S与x之间的函数表达式;
(3)围成的矩形花圃是否存在最大面积?若存在,求出这个最大面积,并求出此时x的值,若不存在,说明理由.
3.某网店销售一种小商品,成本为每件20元,销售大数据分析表明:当每件商品的售价为30元时,平均月销售量240件:若每件商品的售价上涨1元,则月销售量就减少10件.设每件商品的售价为x元,月销售数量为y件,月销售利润为w元.
(1)求y与x、w与x的函数关系式;
(2)若月销售利润2640元,求x的值;
(3)月销售利润是否存在最大值?若存在,求出这个最大值,并求出此时x的值.
4.某网店专门销售江西特色产品——赣南脐橙,已知每千克脐橙的成本为8元.根据销售大数据分析得出:当每千克脐橙的售价为10元时,平均月销售量为600千克;若每千克脐橙的售价每上涨1元,月销售量就会减少100千克.设每千克脐橙的售价为x元,月销售量为y千克,月销售利润为w元.
(1)求y与x的函数解析式;
(2)月销售利润w是否存在最大值?若存在,求出这个最大值,并求出此时x的值.
5.把一个足球垂直于地面向上踢,t秒后该足球的高度h米满足关系式h=﹣5t2+at.已知该足球被踢出4秒后回到地面.
(1)a的值为 .
(2)若t秒后和(t+2)秒后,足球的高度相同,求t的值.
(3)是否存在这样的情况:(t+1)秒后足球的高度比t秒后足球的高度高18米?若存在,请通过计算进行说明;若不存在,请说明理由.
6.【课题学习】
学习主题:探究电流最值
课题背景:数学在电工电子中有着广泛的应用,可以帮助工程师进行电路设计和分析,控制系统设计,信号处理等工作,这些工作需要遵循物理学的规律,我们知道函数是描述变化规律的一种数学模型,欧潭数学探究小组受电流和电压间关系式的启发,以探究“探究电流最值”为主题展开项目式学习.
学习素材:
名称 内容 备注
素材1 用总长60m的篱笆围成一个矩形场地,矩形面积S随矩形一边长l的变化而变化. 课本例题
素材2 观察下列两个数的乘积,说明其中哪个积最大. 1×100,2×99,3×98,4×97,…,99×2,100×1 课本数学活动
素材3 串联电路的总电阻等于各串联电阻之和: 并联电路总电阻的倒数等于各并联电阻的倒数之和; 电压一定的情况下,电流与电阻成反比关系. 物理学知识
研究步骤:
1.画出电路图.在如图1所示的电路中,R1=2Ω,R2=3Ω,滑动变阻器的最大电阻R3=5Ω,其等效电路图如图2所示,其中Rap+Rbp=R3.
2.根据电路图连结实验器材,图略.
3.闭合开关,在滑片从a端滑到b端的过程中,观察电流表的示数,记录相关数据.
解决问题:
(1)在素材1中,当l= 时,场地的面积S最大;
(2)推测素材2中哪个式子的积最大,并用函数知识说明理由;
(3)电流表A表示数是否存在最小值,若存在,求出电流表示数的最小值.若不存在请说明理由.
7.用同样大小的正方体木块依次堆放成如图(1)、图(2)、图(3)所示的实心几何体,并按照这样的规律继续堆放下去,设第n个图形中含有正方体木块s个.
(1)填表:
n 1 2 3 4 …
s
(2)已知s是n的二次函数,求这个二次函数的表达式.
(3)第10个图形中的正方体木块有多少个?
(4)是否存在某个图形,它对应的几何体由1770个正方体木块组成?若存在,指出它是第几个图形;若不存在,请说明理由.
8.2024年9月10日是我国第40个教师节,今年教师节的主题是“大力弘扬教育家精神,加快建设教育强国”,我市某学校为教师定制了水杯,如图是定制的水杯包装盒的表面展开图,设包装盒的高为x cm.
(1)若此包装盒的容积为1500cm3,请列出关于x的方程,并求出x的值.
(2)是否存在这样的x的值,使得此包装盒的容积为1560cm3?若存在,请求出相应的x的值;若不存在,请说明理由.
9.如图,用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,若在铁片的四个角截去四个相同的小正方形,设小正方形的边长为x cm.
(1)底面的长AB= cm,宽BC= cm(用含x的代数式表示)
(2)当做成盒子的底面积为300cm2时,求该盒子的容积.
(3)该盒子的侧面积S是否存在最大的情况?若存在,求出x的值及最大值是多少?若不存在,说明理由.
10.如图,利用一面墙(墙长28米),用总长度49米的栅栏(图中实线部分)围成一个矩形围栏ABCD,且中间共留两个1米的小门,设栅栏BC长为x米.
(1)若矩形围栏ABCD面积为210平方米,求栅栏BC的长;
(2)矩形围栏ABCD面积是否有可能达到240平方米?若有可能,求出相应x的值,若不可能,请说明理由;
(3)矩形围栏ABCD面积是否存在最大面积?若存在,求出矩形围栏BC的长;不存在请说明理由.
11.如图,正方形纸片ABCD的边长为4,将它剪去四个全等的直角三角形,得到四边形EFGH.设AE的长为x,四边形EFGH的面积为y.
(1)求y关于x的函数表达式;
(2)四边形EFGH的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
12.问题探究
(1)如图1,在菱形ABCD中,∠A=120°,AB=4,点P为边CD的中点,Q为边AD上一点,且DP+DQ=5,连接BP、PQ、BQ,求△BPQ的面积;
问题解决
(2)为响应市政府“建设美丽城市,改善生活环境”的号召,某小区欲建造如图2所示的四边形ABCD休闲广场,∠A=∠ABC=∠C=90°,AB=40米,BC=60米.按照规划要求,点P、Q分别在边CD、AD上,满足DP+DQ=40米,连接BP、PQ、BQ,其中△PBQ为健身休闲区,其他区域为景观绿化区,为了使绿化面积尽可能大,希望健身休闲区的面积尽可能小,那么按此要求修建的这个健身休闲区(△PBQ)是否存在最小面积?若存在,求出最小面积及此时DP的长;若不存在,请说明理由.
13.甲、乙、丙三同学玩跳绳,绳被甩到最高处时的形状是如图所示的抛物线.已知拿绳的甲、乙两同学甩绳时手间距AB为6米,手到地面的距离AD和BC都为1.3米,身高为1.6米的丙同学站在距点D的水平距离为1米的E点处,绳子甩到最高处时刚好擦过丙同学头顶F.以点D为原点建立如图所示的平面直角坐标系.
(1)求此抛物线解析式,并注明x的取值范围;
(2)如果绳子甩到最高处时刚好擦过丙同学头顶F,丙同学在CD之间是否存在除E外的另一站点,若存在,求该站点到点D的距离;若不存在,说明理由.
14.某市进行河滩治理,优化美化人居生态环境.如图所示,现规划在河畔的一处滩地上规划一个五边形河畔公园ABCDE.按设计要求,使点O,P,M,N分别在边BC,CD,AE,AB上,且满足BO=2AN=2CP,AM=OC,∠A=∠B=∠C=90°,AB=800米,BC=1200米,CD=600米,AE=900米.为满足人工湖周边各功能场所及绿化用地需要,是否存在符合设计要求的面积最小的四边形人工湖OPMN?若存在,求四边形OPMN面积的最小值及这时点N到点A的距离,请说明理由.
15.为进一步激发学生的劳动热情和创新创造活力,盐城市鹿鸣路初级中学李老师在“空翠圃”劳动实践基地开展劳动节田间管理专题实践活动.如图,正方形菜圃ABCD的边长为8米,现将它阴影部分4个全等的直角三角形种植青菜,剩余的四边形EFGH种植南瓜.设AE的长为x,四边形EFGH的面积为y.
(1)求y关于x的函数表达式;
(2)当四边形EFGH的面积为40平方米时,求AE的值;
(3)四边形EFGH的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
16.我国著名数学家华罗庚曾说过:“数与形,本是相倚依,焉能分作两边飞.数缺形时少直观,形少数时难入微;数形结合百般好,割裂分家万事非.切莫忘,几何代数统一体,永远联系,切莫分离!”数形结合是解决数学问题的重要思想方法.请结合所学的数学解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.
设函数y=(k+2)x2﹣(3k﹣2)x+2k﹣4(实数k为常数)的图象为图象T.
(1)求证:无论k取什么实数,图象T与x轴总有公共点;
(2)是否存在非负整数k,使图象T与x轴的公共点都是整点?若存在,求所有非负整数k的值;若不存在,请说明理由.
17.数和形是数学研究客观物体的两个方面,数(代数)侧重研究物体数量方面,具有精确性、形(几何)侧重研究物体形的方面,具有直观性.数和形相互联系,可用数来反映空间形式,也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题,充分利用代数、几何各自的优势,数形互化,共同解决问题.
同学们,请你结合所学的数学解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.
设函数y=(a﹣1)x2+(3﹣a)x﹣2a﹣2(实数a为常数)的图象为图象T.
(1)求证:无论a取什么实数,图象T与x轴总有公共点;
(2)是否存在整数a,使图象T与x轴的正半轴的公共点都是整点?若存在,求所有整数a的值;若不存在,请说明理由.
18.现有一个三角形广场ABC,如图所示,经测量,AC的长度为100米,点B到线段AC的距离为50米,∠A,∠C均为锐角.点E为AB边上的一动点(点E不与点A,B重合),点F为BC边上一动点(点F不与点B,C重合),且EF∥AC.
(1)当EF的长为50米时,△BEF的面积为 平方米;
(2)设点B关于EF的对称点为B',△B'EF与四边形EFCA的重叠部分的面积记为S平方米,现准备在该重叠部分内种花.请问重叠部分的面积S是否存在最大值?若存在,请求出S的最大值及此时EF的长;若不存在,请说明理由.
19.郑州市彩虹桥新桥将于2023年9月底建成通车,新桥采用三跨连续单拱肋钢箱系杆拱桥,既保留了历史记忆,又展示出郑州的开放与创新,新桥的中跨大拱的拱肋ACB可视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋的跨度AB为120米,与AB中点O相距30米处有一高度为27米的系杆EF,以AB所在直线为x轴,抛物线的对称轴为y轴建立如图②所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)正中间系杆OC的长度是多少米?若相邻系杆之间的间距均为3米(不考虑系杆的粗细),是否存在一根系杆的长度恰好是OC长度的?请说明理由.
20.问题探究
(1)如图1,在菱形ABCD中,AB=BD=8,对角线AC、BD相交于点O,点P在AB上,PE⊥AC于点E,PF⊥BD于点F,若AP=2,求四边形PEOF的面积;
问题解决
(2)如图2,菱形ABCD是某生态农庄的规划缩略图,管理人员计划在该农庄规划一个四边形PEFD的垂钓中心,使点P、E分别在AD、AC上,且PE⊥AC,∠PEF=∠ADF,DF平分∠ADC,,AC=8cm.为了让更多的游客能够同时进行垂钓,要求垂钓中心(四边形PEFD)的面积尽可能的大,请问垂钓中心的面积是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
参考答案
1.解:(1)每上涨1元,其月销售量就减少10个.当每个水杯的售价为45元时,依题意得:
600﹣10×(45﹣40)=600﹣10×5=600﹣50=550(个),
(45﹣30)×550=15×550=8250(元),
故答案为:550;8250;
(2)依题意得:若每个水杯售价上涨x元(x>0),每月能售出(600﹣10x)个水杯,
故答案为:(600﹣10x);
(3)依题意得:(40+x﹣30)(600﹣10x)=10000,
整理得:x2﹣50x+400=0,
解得:x1=10,x2=40,
当x1=10时,600﹣10x=600﹣10×10=500,
当x2=40时,600﹣10x=600﹣10×40=200,
又∵要尽量减少库存,
∴x=10,
∴40+x=40+10=50,
答:每个水杯的售价为50元;
(4)在涨价的前提下,利润存在最大值;理由如下:
设月销售利润为y元,依题意得:
∴y=(40+x﹣30)(600﹣10x)=﹣10x2+500x+6000=﹣10(x﹣25)2+12250,
∵a=﹣10<0,
∴每个书包涨价25元时,利润最大,此时书包的售价为25+40=65元,
∴书包的售价为65元时,最大利润为12250元.
2.解:(1)根据题意得:当x=10米时,y=60﹣2x=60﹣2×10=40(米),S=xy=10×40=400(平方米).
故答案为:40,400;
(2)根据题意得:S=xy=x(60﹣2x),
∴S=﹣2x2+60x.
∵,
∴9≤x<30,
∴S与x之间的函数表达式为S=﹣2x2+60x(9≤x<30);
(3)S=﹣2x2+60x=﹣2(x﹣15)2+450,
∵﹣2<0,
∴当x=15时,S取得最大值,最大值为450,
∴围成的矩形花圃存在最大面积,这个最大面积是450平方米,此时x的值为15.
3.解:(1)根据题意得:y=240﹣10(x﹣30),
∴y=﹣10x+540;
w=(x﹣20)(﹣10x+540),
∴w=﹣10x2+740x﹣10800;
(2)当w=2640时,﹣10x2+740x﹣10800=2640,
整理得:x2﹣74x+1344=0,
解得:x1=32,x2=42.
答:x的值为32或42;
(3)w=﹣10x2+740x﹣10800=﹣10(x﹣37)2+2890,
∵﹣10<0,
∴当x=37时,w取得最大值,最大值为2890.
答:月销售利润存在最大值,这个最大值为2890,此时x的值为37.
4.解:(1)设每千克脐橙的售价为x元,那么相比10元上涨了(x﹣10)元,则月销售量减少100(x﹣10)千克,
∴y=600﹣100(x﹣10)=﹣100x+1600;
(2)由每千克脐橙的成本为8元,售价为x元,月销售量为y=﹣100x+1600件,
月销售利润w为w=(x﹣8)(﹣100x+1600)=﹣100x2+2400x﹣12800,
∵a=﹣100<0,
∴该函数图象开口向下,存在最大值,
当,可得最大利润,最大利润为w=﹣100×122+2400×12﹣12800=1600(元),
答:月销售利润w存在最大值,最大值为1600元,此时x的值为12.
5.解:(1)由题意,∵足球被踢出4秒后回到地面,
∴﹣5×42+4a=0.
∴a=20.
故答案为:20.
(2)由题意,抛物线h=﹣5t2+20t的对称轴为直线t=2.
∵t秒后和(t+2)秒后,足球的高度相同,
∴t+t+2=2×2.
∴t=1.
(3)不存在.理由:由题意得,﹣5(t+1)2+20(t+1)﹣(﹣5t2+20t)=18,
∴(不合题意,舍去),故不存在这样的情况.
6.解:(1)根据题意,矩形一边长l,则另一边长为60÷2﹣l=30﹣l,
所以,S=l(30﹣l)=﹣(l﹣15)2+225,
所以,当l=15,场地的面积S最大,最大为225平方米;
故答案为:15;
(2)50×51和51×50的积最大,理由如下:
设其中一个因数为x,则另一个因数为101﹣x,
则y=x(101﹣x)=﹣x2+101x(1≤x≤100,且为正整数),
对称轴为,因为x是正整数,且1≤x≤100,
所以x取50或51时,y最大为2550;
(3)设Rap=xΩ,则Rbp=(5﹣x)Ω,0≤x≤5,设总电流为I,
则,
由分式的性质可知,若分子为不变的正数,则分母最大时,分式最小,
设W=(2+x)(8﹣x)=﹣(x﹣3)2+25,
∵﹣1<0,则抛物线W开口向下,且0≤x≤5,
∴当x=3时,W取最大值为25,
此时I取最小值为,两支路电阻分别为2+3=5Ω和8﹣3=5Ω,两支路电阻相等,
∴当两支路的电阻相等时,电流表示数最小,最小值为2A.
7.解:(1)∵第1叠放的图形中,小正方体木块个数有1个;
第2个叠放的图形中,小正方体木块个数有1+1+4=6个;
第3个叠放的图形中,小正方体木块个数应有1+1+4+1+2×4=15个;
第4个叠放的图形中,小正方体木块个数应是2×42﹣4=28个;
…
∴第n个叠放的图形中,小正方体木块个数应有1+1+1×4+1+2×4+1+3×4+…+1+4(n﹣1)=n+4n(n﹣1)=2n2﹣n个,
故答案为:1;6;19;28,2n2﹣n;
(2)二次函数的表达式为s=2n2﹣n;
(3)当n=10时,s=2×102﹣10=190,
答:第10个图形中的正方体木块有190个;
(4)当s=1770时,即2n2﹣n=1770,
解得:n=119(负值舍去),
∴存在,它是第30个图形.
8.解:(1)设包装盒的高为x cm,由图得宽为,高为x cm,包装盒的长为15cm,
∵此包装盒的容积为1500cm3,
∴(20﹣x)×15x=1500,
解得:x1=x2=10,
∴x的值为10;
(2)设该包装盒的容积为y cm3,依题意得:
∴y=(20﹣x)×15x=﹣15(x﹣10)2+1500.
∵﹣15<0,
∴当x=10时,此包装盒的容积最大,最大容积为1500cm3,
∴不存在这样的x的值,使得此包装盒的容积为1560cm3.
9.解:(1)∵用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,在铁片的四个角截去四个相同的小正方形,
设小正方形的边长为xcm,
∴底面的长AB=(50﹣2x)cm,宽BC=(30﹣2x)cm,
故答案为:50﹣2x,30﹣2x;
(2)依题意,得:
(50﹣2x)(30﹣2x)=300
整理,得:x2﹣40x+300=0
解得:x1=10,x2=30(不符合题意,舍去)
当x1=10时,盒子容积=(50﹣20)(30﹣20)×10=3000(cm3);
(3)盒子的侧面积为:
S=2x(50﹣2x)+2x(30﹣2x)
=100x﹣4x2+60x﹣4x2
=﹣8x2+160x=﹣8(x2﹣20x)
=﹣8[(x﹣10)2﹣100]
=﹣8(x﹣10)2+800
∵﹣8(x﹣10)2≤0,
∴﹣8(x﹣10)2+800≤800,
∴当x=10时,S有最大值,最大值为800.
10.解:(1)∵设栅栏BC长为x米,
∴DC=49+2﹣3x=(51﹣3x)米,
依题意,得:(51﹣3x)x=210,
整理,得:x2﹣17x+70=0,
解得:x1=7,x2=10.
当x=7时,AB=51﹣3x=30>28,不合题意,舍去,
当x=10时,AB=51﹣3x=21,符合题意,
答:栅栏BC的长为10米;
(2)矩形围栏ABCD面积不可能达到240平方米;理由如下:
依题意,得:(51﹣3x)x=240,
整理得:x2﹣17x+80=0,
∵Δ=(﹣17)2﹣4×1×80=﹣31<0,
∴方程没有实数根,
∴矩形围栏ABCD面积不可能达到240平方米;
(3)矩形围栏ABCD面积存在最大面积;理由如下:
设矩形围栏ABCD面积为S,
根据题意得,51﹣3x>0,
∴x<17,
∴,
∵﹣3<0,
∴当时,即米时,S有最大值.
11.解:(1)∵在正方形纸片ABCD上剪去4个全等的直角三角形,
在△AEH中,AE=x,AH=BE=AB﹣AE=4﹣x,∠A=90°,
∴y=S正方形ABCD﹣4S△AEH
=2x2﹣8x+16;
(2)正方形EFGH的面积为:y=2x2﹣8x+16=2(x﹣2)2+8(0<x<4),
∴当x=2时,y有最小值8,即四边形EFGH的面积最小为8.
12.解:(1)如图,过点B作BE⊥AD交DA的延长线于点E,过点P作PM⊥AD于点M,延长MP交BC的延长线于点N,
∴∠BAE=∠ABC=∠DCN=∠D=60°,
在菱形ABCD中,AB=4,点P为边CD的中点,
∴DP=CP=2,
∵DP+DQ=5,
∴DQ=3,
∴AQ=1,
在Rt△ABE中,BE=AB sin60°=2,
在Rt△CPN中,PN=CP sin60°,
在Rt△DPM中,PM=DP sin60°,
∴S△BPQ=S菱形ABCD﹣S△ABQ﹣S△BCP﹣S△DPQ
=4×21×243
.
(2)∵∠A=∠ABC=∠C=90°,
∴四边形ABCD是矩形,
∴AB=CD=40米,BC=AD=60米,
设DP=x米,则CP=(40﹣x)米,DQ=(40﹣x)米,AQ=(20+x)米,
∴S△BPQ=S矩形ABCD﹣S△ABQ﹣S△BCP﹣S△DPQ
=40×6040(20+x)60×(40﹣x)x(40﹣x)
x2﹣10x+800
(x﹣10)2+750.
∴当x=10时,S△BPQ的最小值为750.
∴按此要求修建的这个健身休闲区(△PBQ)存在最小面积,最小面积为750平方米,此时DP的长为10米.
13.解:(1)设此抛物线的解析式为 y=ax2+bx+c,
由题意得点A(0,1.3),F(1,1.6),B(6,1.3),
代入 y=ax2+bx+c 得,
解得,
∴抛物线的解析式为y=﹣0.06x2+0.36x+1.3(0≤x≤6);
(2)存在,理由:
设站点到点D的距离为x,
则﹣0.06x2+0.36x+1.3=1.6,
解得x=1或5,
∵x=1即为站点E,
∴存在另一站点到点D的距离为5米.
14.解:存在,如图延长AE、CD相交于点F,
∵∠A=∠B=∠C=90°,
∴四边形ABCF是矩形,
∴AF=BC=1200,AB=FC=800,
∵AM=OC,BO=2AN=2CP,
∴MF=BO,BN=FP,
设AN=x,则CP=x,BO=MF=2x,AM=OC=1200﹣2x,BN=FP=800﹣x,
此时 S四边形OPMN=S ABCF﹣S△BNO﹣S△ANM﹣S△FMP﹣S△CPO
=960000﹣(1600x﹣2x2)﹣(1200x﹣2x2)
=960000﹣2800x+4x2
=4(x﹣350)2+470000,
∵4>0,
∴当x=350时,S四边形OPMN有最小值470000平方米,
当x=350时,AN=350米,AM=1200﹣2x=500米<AE=900米,
CP=x=350米<CD=600米,
∴存在符合设计要求的面积最小值为470000平方米的四边形人工湖OPMN,
此时点N到点A的距离为350米.
15.解:(1)∵正方形纸片ABCD的边长为8,4个直角三角形全等,
∴AB=AD=BC=CD=8,AE=DH=x,BE=AH=8﹣x,∠A=∠D=90°,EH=HG=FG=EF,∠AEH=∠GHD.
∵∠AEH+∠AHE=90°,
∴∠AHE+∠DHG=90°,
∴∠EHG=90°,
∴四边形EFGH是正方形.
∴y=AE2+AH2=x2+(8﹣x)2=2x2﹣16x+64;
(2)当y=40时,即2x2﹣16x+64=40,
∴x2﹣8x+12=0.
解得x=2或x=6,
答:当AE取2或6时,四边形EFGH的面积为40;
(3)∵y=2x2﹣16x+64=2(x﹣4)2+32,
∵2>0,
∴y有最小值,最小值为32.
即四边形EFGH的面积有最小值,最小值为32.
16.(1)证明:当k+2=0时,
函数y=8x﹣8,该函数和x轴有交点(1,0);
当k+2≠0时,
∵Δ=(2﹣3k)2﹣4(k+2)(2k﹣4)=(k﹣6)2≥0,
故该函数和x轴有交点,
故图象T与x轴总有公共点;
(2)解:存在,理由:
∵k为非负整数,
则k+2≠0,
令y=(k+2)x2﹣(3k﹣2)x+2k﹣4=0,
解得:x=1或,
而x2,
当k=0,2,6时,x=﹣2,0,1,符合题意,
故k=0或2或6.
17.(1)证明:当a=1时,函数表达式为y=2x﹣4,
令y=0得:x=2,
∴此时函数y=(a﹣1)x2+(3﹣a)x﹣2a﹣2(实数a为常数)的图象与x轴有交点;
当a≠1时,
y=(a﹣1)x2+(3﹣a)x﹣2a﹣2为二次函数,
∴Δ=(3﹣a)2﹣4(4a﹣1)(﹣2a﹣2)=9a2﹣6a+1=(3a﹣1)2≥0,
∴函数y=(a﹣1)x2+(3﹣a)x﹣2a﹣2(实数a为常数)的图象与x轴有交点;
综上所述,无论a取什么实数,图象T与x轴总有公共点;
(2)解:存在整数a,使图象T与x轴的公共点中有整点,理由如下:
当a=1时,图象与x轴交于(2,0),符合题意;
当a≠1时,令y=0得:
0=(a﹣1)x2+(3﹣a)x﹣2a﹣2,
[(a﹣1)x+(a+1)](x﹣2)=0,
解得x=2或x,
∵x1,a是整数,
∴当a﹣1是2的因数时,x是整数,
∵图象T与x轴的正半轴的公共点都是整点,
∴2,
解得:a=2,
∴a=1或a=2.
18.解:(1)不妨设点B到线段EF,AC的距离分别为h小,h大,
∵EF∥AC,
∴△BEF∽△BAC,
∴,
∴,
解得h小=25,
∴S△BEF50×25=625,
故答案为:625;
(2)存在.由题意得,
设EF的长度为x米,
∵EF∥AC,
∴∠BEF=∠A,∠BFE=∠C,
∴△BEF∽△BAC,
∴,即,
∴,
分两种情况讨论:
①当点B'落在四边形EFCA内或AC边上时,0<x≤50
如图1,此时S=S△BEFx2,
所以当0<x≤50时,S的最大值为625m2;
②当B'落在四边形EFCA外时,50<x<100,
如图2,连接BB',与EF交于点M,与AC交于点N,
连接EB',与AC交于点G,连接FB′,与AC交于点H,
∵EF∥AC,
∴即,
∴,
∴,
∴B'N=BB'﹣BN=x﹣50,
∴()2,
即()2,
∴S△B′GH=x2﹣100x+2500,
∴S=S四边形EFHG=SΔG'EF﹣S△B'GH,
当时,S最大,最大值为.
综上所述,当m时,S最大,最大值为.
19.解:(1)结合图象由题意可知:B(60,0),E(30,27),设该抛物线解析式为:y=ax2+c,则:
,解得:,∴y36.
(2)当x=0时,y=36,∴正中间系杆OC的长度是36米.
设存在一根系杆的长度是OC的,即这根系杆的长度是12米,则1236,
解得:x=±20.∵相邻系杆之间的间距均为3米,最中间系标OC在y轴上,
∴每根系杆上的点的横坐标均为整数.
∴x=±20与实际不符.∴不存在一根系杆的长度恰好是OC长度的.
20.解:(1)∵PE⊥AC,PF⊥BD,∴∠PEA=∠BOA,∴PE∥BO,∴△PEA∽△BOA,∠PAE=∠BPF,又∵∠PEA=∠BFP=90°,∴△PEA∽△BFP,∴,,∵菱形ABCD中AB=BD=8,∴AC⊥DB,DO=BO=4,∴Rt△ABO中,,∴,∴,∴,即四边形PEOF的面积为;
(2)连接DB,
∵菱形ABCD,
∴DB⊥AC,AO=CO,DO=BO,DB平分∠ADC,
又∵DF平分∠ADC,∴F在DB上,∵,AC=8cm,∴AO=CO=4cm,
∴Rt△ABO中,,∵PE⊥AC,DF⊥AC,∴∠PEO=∠DOC=90°,∴PE∥DF,∴∠PEF=∠EFO,又∵∠PEF=∠ADF,∴∠ADF=∠EFO,∴PD∥EF,同理可得△PEA∽△DOA,△PEA∽△FOE,设AE=a cm,
∴,,
∵,∴,,
∴,
当时,S四边形PEFD有最大值为2cm2.
第18页
同课章节目录
