2024-2025学年人教版八年级数学下册 第17章勾股定理 单元测试(含答案)
文档属性
| 名称 | 2024-2025学年人教版八年级数学下册 第17章勾股定理 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 957.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-12 14:38:45 | ||
图片预览

文档简介
第17章勾股定理
(满分120分)
一、单选题(共10小题每题4分;共40分)
1. 如图,公路 , 互相垂直,点 为公路 的中点,要测量湖泊两侧 , 两点间的距离,若测得 的长为 ,则 , 两点间的距离为
A. B. C. D.
2. 下列命题中,其逆命题为假命题的是
A. 角平分线所在直线上的点到这个角的两边的距离相等
B. 全等三角形的对应角相等
C. 若 ,则
D. 若 是钝角三角形,则
3. 【课后测试 】如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形 ,,, 的面积分别是 ,,,,则最大正方形 的边长是
A. B. C. D. 无法确定
4. 如图,三个村庄 ,, 之间的距离分别为 千米, 千米, 千米.要从 村庄修一条公路直达 .已知公路的造价为 元/千米,则修这条公路的最低造价为
A. 元 B. 元 C. 元 D. 元
5. 的三边 ,, 满足 ,则 为
A. 直角三角形 B. 等腰三角形
C. 等边三角形 D. 等腰直角三角形
6. 小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多 ,当他把绳子的下端拉开 后,发现绳子拉直且下端刚好接触地面,则旗杆的高度是
A. B. C. D.
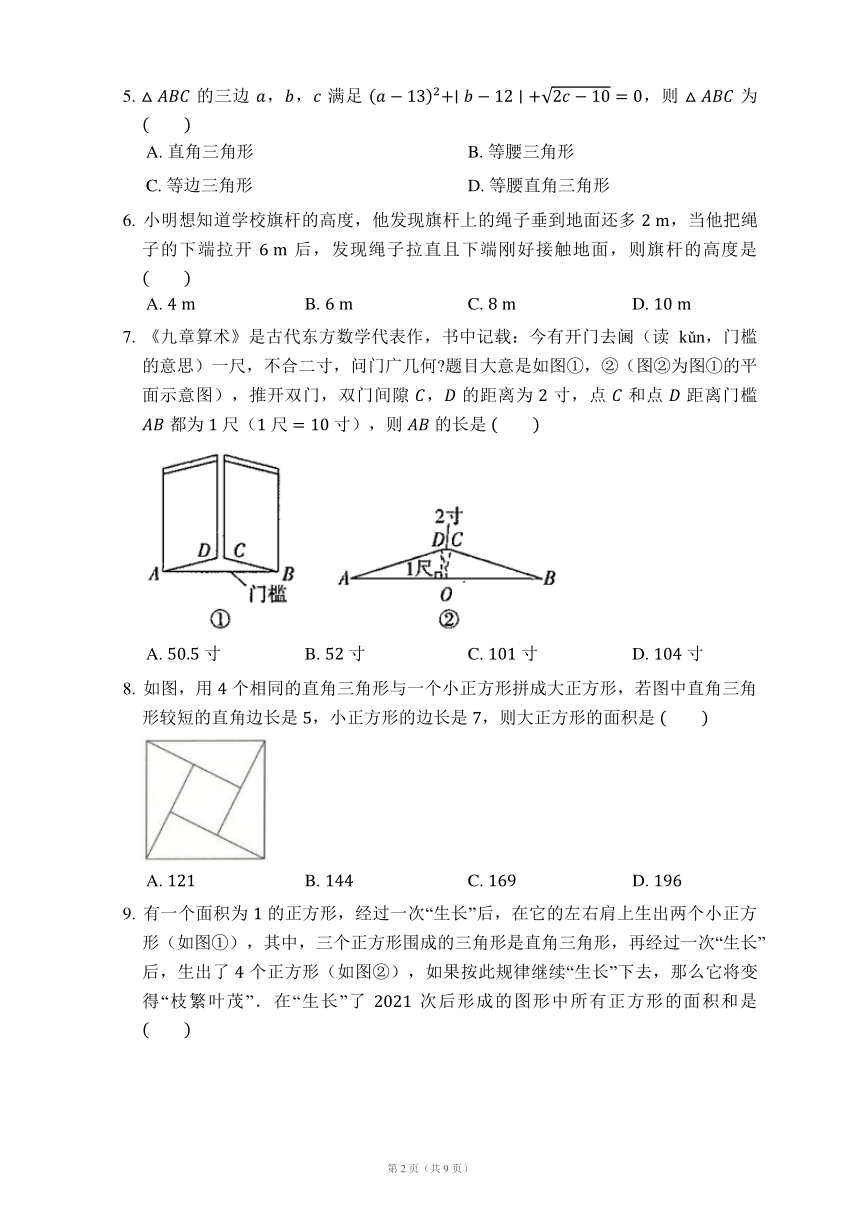
7. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是如图①,②(图②为图①的平面示意图),推开双门,双门间隙 , 的距离为 寸,点 和点 距离门槛 都为 尺( 尺 寸),则 的长是
A. 寸 B. 寸 C. 寸 D. 寸
8. 如图,用 个相同的直角三角形与一个小正方形拼成大正方形,若图中直角三角形较短的直角边长是 ,小正方形的边长是 ,则大正方形的面积是
A. B. C. D.
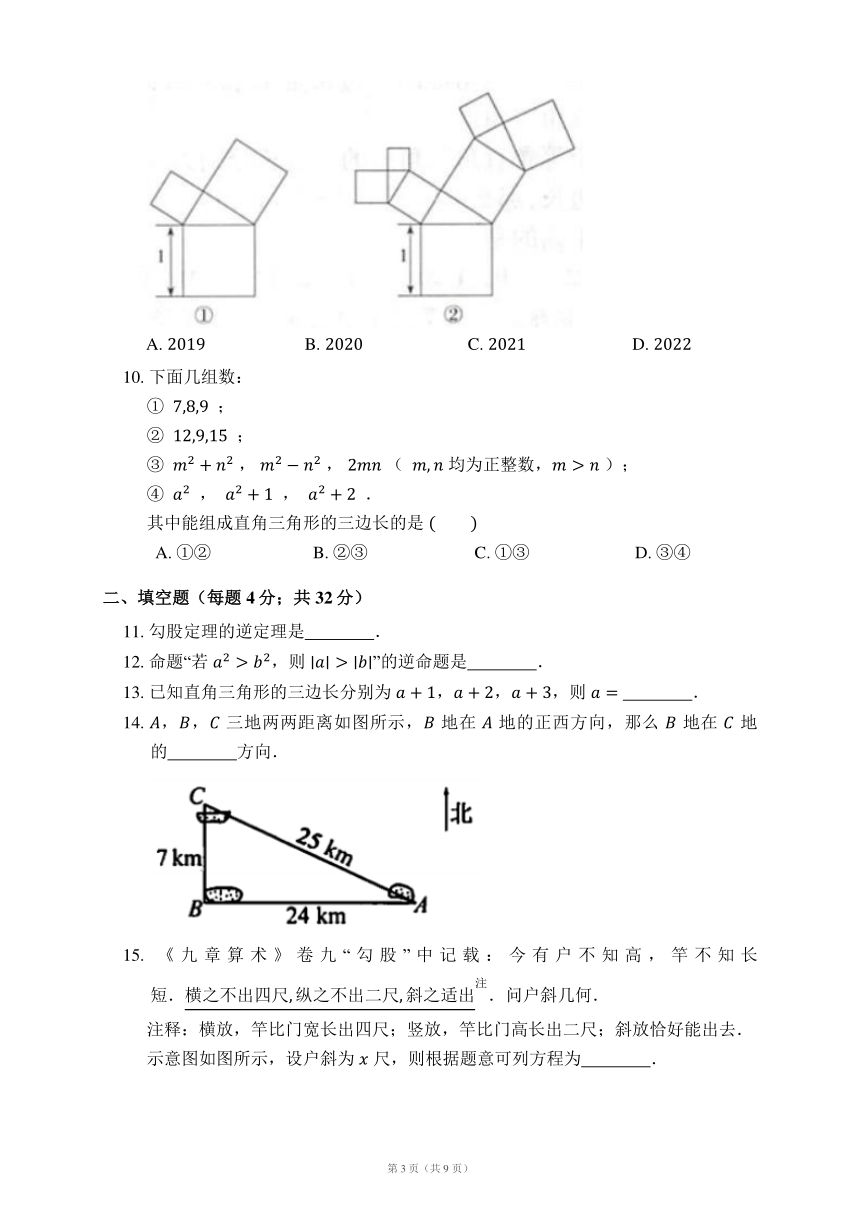
9. 有一个面积为 的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图①),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了 个正方形(如图②),如果按此规律继续“生长”下去,那么它将变得“枝繁叶茂”.在“生长”了 次后形成的图形中所有正方形的面积和是
A. B. C. D.
10. 下面几组数:
① ;
② ;
③ , , ( 均为正整数, );
④ , , .
其中能组成直角三角形的三边长的是
A. ①② B. ②③ C. ①③ D. ③④
二、填空题(每题4分;共32分)
11. 勾股定理的逆定理是 .
12. 命题“若 ,则 ”的逆命题是 .
13. 已知直角三角形的三边长分别为 ,,,则 .
14. ,, 三地两两距离如图所示, 地在 地的正西方向,那么 地在 地的 方向.
15. 《九章算术》卷九“勾股”中记载:今有户不知高,竿不知长短..问户斜几何.
注释:横放,竿比门宽长出四尺;竖放,竿比门高长出二尺;斜放恰好能出去.
示意图如图所示,设户斜为 尺,则根据题意可列方程为 .
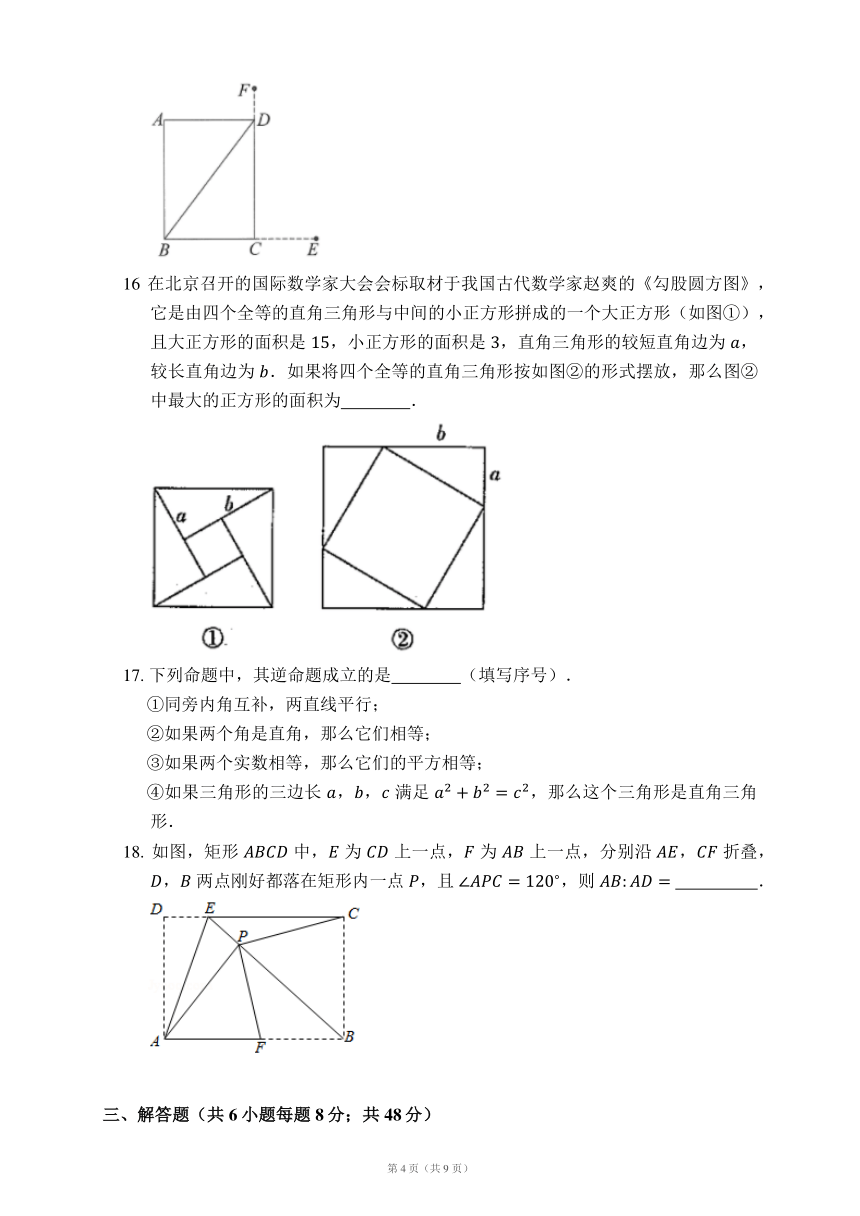
16在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图①),且大正方形的面积是 ,小正方形的面积是 ,直角三角形的较短直角边为 ,较长直角边为 .如果将四个全等的直角三角形按如图②的形式摆放,那么图②中最大的正方形的面积为 .
17. 下列命题中,其逆命题成立的是 (填写序号).
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长 ,, 满足 ,那么这个三角形是直角三角形.
18. 如图,矩形 中, 为 上一点, 为 上一点,分别沿 , 折叠,, 两点刚好都落在矩形内一点 ,且 ,则 .
三、解答题(共6小题每题8分;共48分)
19. 如图,车高 ,货车卸货时后面挡板 折落在地面 处,经过测量 ,求 的长.
20. 下列定理有逆定理吗 如果有逆定理,说出其逆定理.
(1)等边三角形的三个内角都相等.
(2)全等三角形的对应角相等.
21. 如图, 是 的高,,,.
求证: 是等腰三角形.
22. 在寻找马航 航班过程中,两艘搜救舰艇接到消息,在海面上有疑似漂浮目标 ,.接到消息后,一艘舰艇以 海里/时的速度离开港口 (如图所示)向北偏东 方向航行,另一艘舰艇在同时以 海里/时的速度向北偏西一定角度的航向行驶,已知它们离港口一个半小时后相距 海里,问另一艘舰艇的航行方向是北偏西多少度
23. 如图,在正方形 中, 为 边的中点, 为 边上一点,.求证:.
24. 如图,已知等腰 的底边 , 是腰 上一点,且 ,.
(1)求证: 是直角三角形;
(2)求 的长.
答案
一 单选题
1. A
2. B
3. C
【解析】正方形 ,,, 的面积分别是 ,,,,
由勾股定理得,正方形 的面积为:,
正方形 的面积为:,
则正方形 的面积为:,
最大正方形 的边长是 ;
故选:C.
4. C
5. A
6. C
7. C
8. C
9. D
【解析】设正方形 ,, 围成的直角三角形的三条边长分别是 ,,.
如图,
根据勾股定理,得 ,
一次“生长”后,.
第二次“生长”后,,
推而广之,“生长”了 次后形成的图形中所有的正方形的面积和是 .
10. B
二 填空题
11. 如果三角形的三边长 ,,,满足 ,那么这个三角形是直角三角形
12. 若 ,则
【解析】“若 ,则 ”的逆命题是:若 ,则 .
13.
14. 正南
15.
16.
17. ①④
18.
【解析】如图,设 .过点 作 于 .
由翻折的性质可知,,
,,
,,
,
四边形 是矩形,
,
,
,
故答案为 .
三 解答题
19. 由题意得,,,
设 ,
则 ,
在 中,,
即 ,
解得 .
的长为 .
20. (1) 有逆定理,三个内角都相等的三角形是等边三角形.
(2) 没有逆定理.
21. 略
22. 由题意得,(海里),
(海里),
又 海里,
,即 ,
.
,
,
则另一艘舰艇的航行方向是北偏西 .
23. 连接 ,设正方形的边长为 .利用勾股定理先求出 三边的长,再判断 是直角三角形.
24. (1) ,,,
,
为直角三角形.
(2) 设 的长为 ,
是等腰三角形,
.
,
.
解得 ,
.
第1页(共9 页)
(满分120分)
一、单选题(共10小题每题4分;共40分)
1. 如图,公路 , 互相垂直,点 为公路 的中点,要测量湖泊两侧 , 两点间的距离,若测得 的长为 ,则 , 两点间的距离为
A. B. C. D.
2. 下列命题中,其逆命题为假命题的是
A. 角平分线所在直线上的点到这个角的两边的距离相等
B. 全等三角形的对应角相等
C. 若 ,则
D. 若 是钝角三角形,则
3. 【课后测试 】如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形 ,,, 的面积分别是 ,,,,则最大正方形 的边长是
A. B. C. D. 无法确定
4. 如图,三个村庄 ,, 之间的距离分别为 千米, 千米, 千米.要从 村庄修一条公路直达 .已知公路的造价为 元/千米,则修这条公路的最低造价为
A. 元 B. 元 C. 元 D. 元
5. 的三边 ,, 满足 ,则 为
A. 直角三角形 B. 等腰三角形
C. 等边三角形 D. 等腰直角三角形
6. 小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多 ,当他把绳子的下端拉开 后,发现绳子拉直且下端刚好接触地面,则旗杆的高度是
A. B. C. D.
7. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是如图①,②(图②为图①的平面示意图),推开双门,双门间隙 , 的距离为 寸,点 和点 距离门槛 都为 尺( 尺 寸),则 的长是
A. 寸 B. 寸 C. 寸 D. 寸
8. 如图,用 个相同的直角三角形与一个小正方形拼成大正方形,若图中直角三角形较短的直角边长是 ,小正方形的边长是 ,则大正方形的面积是
A. B. C. D.
9. 有一个面积为 的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图①),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了 个正方形(如图②),如果按此规律继续“生长”下去,那么它将变得“枝繁叶茂”.在“生长”了 次后形成的图形中所有正方形的面积和是
A. B. C. D.
10. 下面几组数:
① ;
② ;
③ , , ( 均为正整数, );
④ , , .
其中能组成直角三角形的三边长的是
A. ①② B. ②③ C. ①③ D. ③④
二、填空题(每题4分;共32分)
11. 勾股定理的逆定理是 .
12. 命题“若 ,则 ”的逆命题是 .
13. 已知直角三角形的三边长分别为 ,,,则 .
14. ,, 三地两两距离如图所示, 地在 地的正西方向,那么 地在 地的 方向.
15. 《九章算术》卷九“勾股”中记载:今有户不知高,竿不知长短..问户斜几何.
注释:横放,竿比门宽长出四尺;竖放,竿比门高长出二尺;斜放恰好能出去.
示意图如图所示,设户斜为 尺,则根据题意可列方程为 .
16在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图①),且大正方形的面积是 ,小正方形的面积是 ,直角三角形的较短直角边为 ,较长直角边为 .如果将四个全等的直角三角形按如图②的形式摆放,那么图②中最大的正方形的面积为 .
17. 下列命题中,其逆命题成立的是 (填写序号).
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长 ,, 满足 ,那么这个三角形是直角三角形.
18. 如图,矩形 中, 为 上一点, 为 上一点,分别沿 , 折叠,, 两点刚好都落在矩形内一点 ,且 ,则 .
三、解答题(共6小题每题8分;共48分)
19. 如图,车高 ,货车卸货时后面挡板 折落在地面 处,经过测量 ,求 的长.
20. 下列定理有逆定理吗 如果有逆定理,说出其逆定理.
(1)等边三角形的三个内角都相等.
(2)全等三角形的对应角相等.
21. 如图, 是 的高,,,.
求证: 是等腰三角形.
22. 在寻找马航 航班过程中,两艘搜救舰艇接到消息,在海面上有疑似漂浮目标 ,.接到消息后,一艘舰艇以 海里/时的速度离开港口 (如图所示)向北偏东 方向航行,另一艘舰艇在同时以 海里/时的速度向北偏西一定角度的航向行驶,已知它们离港口一个半小时后相距 海里,问另一艘舰艇的航行方向是北偏西多少度
23. 如图,在正方形 中, 为 边的中点, 为 边上一点,.求证:.
24. 如图,已知等腰 的底边 , 是腰 上一点,且 ,.
(1)求证: 是直角三角形;
(2)求 的长.
答案
一 单选题
1. A
2. B
3. C
【解析】正方形 ,,, 的面积分别是 ,,,,
由勾股定理得,正方形 的面积为:,
正方形 的面积为:,
则正方形 的面积为:,
最大正方形 的边长是 ;
故选:C.
4. C
5. A
6. C
7. C
8. C
9. D
【解析】设正方形 ,, 围成的直角三角形的三条边长分别是 ,,.
如图,
根据勾股定理,得 ,
一次“生长”后,.
第二次“生长”后,,
推而广之,“生长”了 次后形成的图形中所有的正方形的面积和是 .
10. B
二 填空题
11. 如果三角形的三边长 ,,,满足 ,那么这个三角形是直角三角形
12. 若 ,则
【解析】“若 ,则 ”的逆命题是:若 ,则 .
13.
14. 正南
15.
16.
17. ①④
18.
【解析】如图,设 .过点 作 于 .
由翻折的性质可知,,
,,
,,
,
四边形 是矩形,
,
,
,
故答案为 .
三 解答题
19. 由题意得,,,
设 ,
则 ,
在 中,,
即 ,
解得 .
的长为 .
20. (1) 有逆定理,三个内角都相等的三角形是等边三角形.
(2) 没有逆定理.
21. 略
22. 由题意得,(海里),
(海里),
又 海里,
,即 ,
.
,
,
则另一艘舰艇的航行方向是北偏西 .
23. 连接 ,设正方形的边长为 .利用勾股定理先求出 三边的长,再判断 是直角三角形.
24. (1) ,,,
,
为直角三角形.
(2) 设 的长为 ,
是等腰三角形,
.
,
.
解得 ,
.
第1页(共9 页)
