粤教版高中物理必修第二册学业水平考试常考点6-常考点10课件(52页PPT)
文档属性
| 名称 | 粤教版高中物理必修第二册学业水平考试常考点6-常考点10课件(52页PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-12 14:36:42 | ||
图片预览











文档简介
(共52张PPT)
1.向心加速度
向心力产生的加速度
2.向心加速度的方向
总是指向圆心
3.向心加速度的几种表达式
[特别提醒]
(1)向心加速度方向指向圆心,表示速度方向变化的快慢。
(2)切向加速度方向沿切线方向,表示速度大小变化的快慢。
(3)做匀速圆周运动物体的加速度即为向心加速度,方向总是指向圆心;做非匀速圆周运动物体的加速度一般不等于向心加速度,方向一般不指向圆心。
[全悉考法]
1.关于向心加速度,下列说法正确的是 ( )
A.向心加速度越大,线速度也越大
B.向心加速度越大,角速度也越大
C.向心加速度越大,圆周运动半径越小
D.向心加速度越大,线速度和角速度的乘积也越大
2.某学校开设了糕点制作的选修课,小明同学在体验糕点制作“裱花”环节时,他在绕中心匀速转动的圆盘上放了一块直径8英寸(20 cm)的蛋糕,在蛋糕上每隔4 s均匀“点”一次奶油, 蛋糕一周均匀“点”上15个奶油花,则下列说法正确的是 ( )
3.如图所示,一偏心轮绕O点做匀速转动,则偏心轮边缘上A、B两点的 ( )
A.线速度大小相同
B.角速度大小相同
C.向心加速度大小相等
D.向心加速度方向相同
解析:偏心轮上各点的角速度相等,故B正确;由v=ωr可知做圆周运动半径不同的点,线速度不同,故A错误;根据公式a=ω2r,向心加速度与各点到转动轴O的距离成正比,半径不同的点,向心加速度大小不相等,故C错误;向心加速度的方向始终指向圆心,所以A、B两点向心加速度的方向不同,故D错误。
答案:B
4.如图所示,正在匀速转动的水平转盘上固定有三个可视为质点
的小物块A、B、C,它们的质量关系为mA=2mB=2mC,到轴O
的距离关系为rC=2rA=2rB。下列说法中正确的是 ( )
A.B的线速度比C大 B.A的角速度比C大
C.B的向心加速度比C小 D.A的向心加速度比B大
解析:因为A、B、C共轴转动,角速度相同,根据v=rω可知半径越大,线速度越大,所以C的线速度最大,所以A、B错误;根据a=rω2,A的半径等于B的半径,所以A、B的向心加速度大小相等且小于C的向心加速度,故C正确,D错误。
答案:C
5.如图所示,“共享单车”极大地方便了老百姓的出行,某高档“共享单车”通过变速器调整链条在轮盘和飞轮的挂入位置,改变行驶速度。轮盘和飞轮的齿数如下表所示:
名称 轮盘 飞轮
A轮 B轮 C轮 D轮 E轮
齿数N/个 48 39 24 18 13
则下列说法正确的是 ( )
A.当A轮与C轮组合时,两轮的转速之比为1∶1
B.当A轮与C轮组合时,两轮边缘上的点的线速度大小之比为1∶2
C.当B轮与E轮组合时,两轮角速度之比为1∶3
D.当B轮与E轮组合时,两轮边缘上的点的向心加速度大小之比为3∶1
解析:A轮与C轮通过链条连接,轮边缘上的点的线速度大小相等,齿数之比为2∶1,齿数之比等于轮的半径之比,转速之比为1∶2,选项A、B错误;B轮与E轮通过链条连接,轮边缘上的点的线速度大小相等,齿数之比为3∶1,转速之比为1∶3,角速度之比为1∶3,轮边缘上的点的向心加速度之比为1∶3,选项C正确,D错误。
答案:C
[主干回扣]
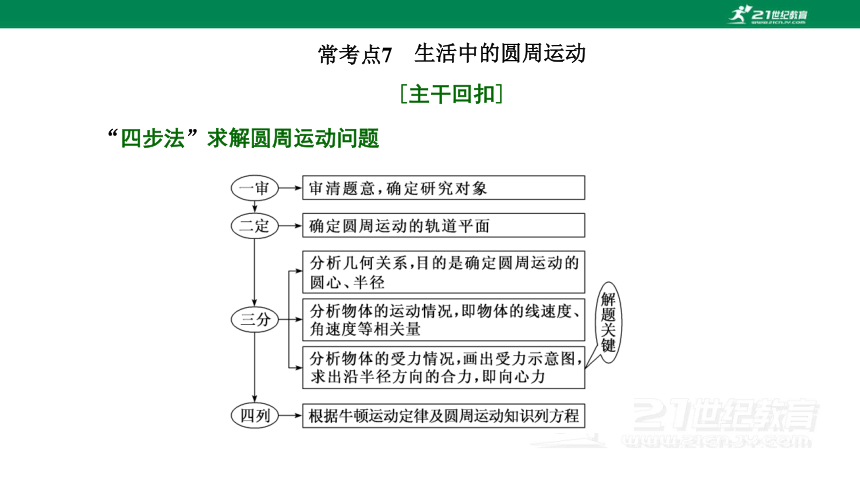
“四步法”求解圆周运动问题
[特别提醒]
(1)做匀速圆周运动的物体所受合外力恰好全部提供向心力。
(2)做非匀速圆周运动的物体所受合外力一般不等于向心力,但在某些位置合外力可能等于向心力。
[全悉考法]
1.火车转弯时,如果铁路弯道内外轨一样高,外轨对轮缘(如图甲所示)挤压的弹力F提供了火车转弯的向心力(如图乙所示),但是靠这种办法得到向心力极易使铁轨和车轮受损。在修筑铁路时,弯道处的外轨会略高于内轨(如图丙所示),当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时的速度大小为v,以下说法中正确的是 ( )
2.如图所示是浙江沿海的风力发电机,A、B是同一台发电机
叶片上的两点。发电机工作时A、B两点的角速度大小分别
为ωA、ωB,线速度大小分别为vA、vB,则 ( )
A.ωA>ωB B.ωA<ωB
C.vA>vB D.vA<vB
解析:A、B两点的角速度相同,A点的半径大于B点的半径,根据v=ωr可得,A点的线速度大于B点的线速度,选项A、B、D错误,选项C正确。
答案:C
3.城市中为了解决交通问题,修建了许多立交桥。如图所
示,桥面半径为R的圆弧形的立交桥AB横跨在水平路面
上,一辆质量为m的小汽车,从A端冲上该立交桥,小汽车到达桥顶时的速度大小为v1,若小汽车在上桥过程中保持速率不变,则 ( )
A.小汽车通过桥顶时处于失重状态
B.小汽车通过桥顶时处于超重状态
4.如图所示,过山车的轨道可视为竖直平面内半径为R的圆轨道。质量为m的游客随过山车一起运动,当游客以速度v经过圆轨道的最高点时 ( )
A.处于超重状态
B.向心加速度方向竖直向下
5.暑假里,小明去游乐场游玩,坐了一次旋转飞椅,如图1所示,该旋转飞椅顶上有一个半径为4.5 m的伞盖,伞盖在转动过程中带动下面的悬绳转动,其示意图如图2所示。旋转飞椅高O1O2=5.8 m,绳长为5 m。小明挑选了一个悬挂在伞盖边缘的最外侧的椅子坐下,他与座椅的总质量为40 kg。小明和椅子的转动可简化为如图2所示的圆周运动。在某段时间内,伞盖保持在水平面内稳定旋转,绳与竖直方向夹角为37°。g取10 m/s2,sin 37°=0.6, cos 37°=0.8,在此过程中,求:
(1)座椅受到绳子的拉力大小;
(2)小明运动的线速度大小;
(3)小明随身带的玻璃球从座椅上不慎滑落,求落地点与中心转轴(即图2中O1点)的距离(结果可用根号表示)。
解析:(1)对小明和椅子整体受力分析,如图所示,受到重力和绳子的拉力作用,其合力提供向心力,在竖直方向受力平衡,有FTcos 37°=mg,
解得拉力FT=500 N。
[主干回扣]
对开普勒定律的理解
定律 内容 研究角度 理解
开普勒第一定律 所有行星围绕太阳运行的轨道都是椭圆,太阳处在椭圆的一个焦点上 轨道的空间分布 (1)各行星的椭圆轨道尽管大小不同,但太阳位于所有椭圆轨道的一个共同焦点处
(2)不同行星的轨道是不同的,可能相差很大
[全悉考法]
1.物理学发展历程中,在前人研究基础上经过多年的尝试性计算,首先发表行星运动的三个定律的科学家是 ( )
A.哥白尼 B.第谷 C.伽利略 D.开普勒
解析:开普勒首先发表了开普勒行星运动三定律,故D正确。
答案:D
2. 如图所示,O表示地球,P表示一个绕地球沿椭圆轨道做逆时针方向运动的人造卫星,AB为长轴,CD为短轴。在卫星绕地球运动一周的时间内,从A到B的时间为tAB,同理从B到A、从C到D、从D到C的时间分别为tBA、tCD、tDC。下列关系式正确的是 ( )
A.tAB>tBA B.tAB<tBA
C.tCD>tDC D.tCD<tDC
解析:由卫星做椭圆运动的对称性得tAB=tBA,选项A、B错误;由开普勒第二定律,卫星在近地点时运动快,在远地点时运动慢,所以tCD<tDC,选项C错误,D正确。
答案:D
3.某行星绕恒星运行的椭圆轨道如图所示,E和F是椭圆的两个焦点,O是椭圆的中心,行星在A点的线速度比在B点的线速度大。则恒星位于 ( )
A.A点 B.E点 C.F点 D.O点
解析:根据开普勒第二定律,对任意一个行星来说,它与太阳的连线在相等时间内扫过的面积相等。则行星在距离恒星较近的位置速度较大,因行星在A点的线速度比在B点的线速度大,则恒星位于E点,故选项B正确。
答案:B
4.如图所示,一颗卫星绕地球做椭圆运动,运动周期为T,图中虚线为卫星的运行轨迹,A、B、C、D是轨迹上的四个位置,其中A距离地球最近,C距离地球最远。B和D点是弧线ABC和ADC的中点,下列说法正确的是 ( )
A.卫星在C点的速度最大
B.卫星在C点的加速度最大
[主干回扣]
1.内容
宇宙间的一切物体都是互相吸引的。两个物体间引力的方向在它们的连线上,引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r的二次方成反比。
3.引力常量G
①数值:G=6.67×10-11 N·m2/kg2;适用于任何问题。
②物理意义:引力常量在数值上等于两个质量都是1 kg的质点相距1 m时的相互吸引力。
③G的测定:由英国科学家卡文迪什(又称卡文迪许)在实验室里首先通过卡文迪什扭秤装置测出的。
④测定G的意义:证实了万有引力的存在及万有引力定律的正确性。
4.适用条件
适用于计算两个质点间的万有引力。
[特别提醒]
(1)距离r的理解:
①对于两个质量均匀分布的球体,r应是两球心间的距离。
②对于一个均匀球体与球外一个质点,r应是球体球心到质点的距离。
③对于两个物体间的距离比物体本身大得多时,物体可以看成质点,r应是两个物体间的距离。
(2)地球周围物体间的万有引力很小,受力分析时可以忽略;但是天体间的万有引力是巨大的,对于天体的运动起决定作用。
[全悉考法]
1.符合发现和完善万有引力定律历史事实的是 ( )
A.哥白尼提出三大行星定律
B.卡文迪什提出地心说
C.牛顿接受了胡克等科学家关于吸引力与两物体中心距离的平方成反比的猜想
D.开普勒根据大量实验数据得出了比例系数G的大小
解析:开普勒提出三大行星定律,故A错误;托勒密提出地心说,故B错误;万有引力定律是由牛顿发现的,故C正确;卡文迪什根据大量实验数据得出了比例系数G的大小,故D错误。
答案:C
2.关于万有引力和万有引力定律的理解正确的是 ( )
A.m1与m2受到的引力总是大小相等、方向相反,是一对平衡力
B.m1与m2受到的引力总是大小相等的,而与m1、m2是否相等无关
C.不能看作质点的两物体间不存在相互作用的引力
解析:m1与m2之间的万有引力总是大小相等,方向相反,是一对相互作用力,不是一对平衡力,而与m1、m2是否相等无关,故选项B正确,A错误;万有引力存在于一切物体之间,故选项C错误;r为两物体之间的距离,就是重心到重心的距离,所以如果知道两个物体间重心之间的距离,就算不能看成质点也能用万有引力公式进行计算,例如两个靠得很近的铅球之间的万有引力,故选项D错误。
答案:B
4.我国航天员在空间站内多次开设了“天宫课堂”。已知地球质量为M,半径为R,引力常量为G。若我国空间站质量为m,在离地面高度为h的轨道上做匀速圆周运动,则下列说法正确的是( )
5.因为地球的自转,同一物体在地球上不同的纬度处重力不同,一质量为m的物体在北极时的重力与其在赤道时的重力的差为F。将地球看成质量分布均匀的球体,半径为R。则地球的自转周期是 ( )
[主干回扣]
1.计算天体质量和密度的方法
(1)自力更生(g-R)法。
2.天体运动问题的分析与计算
(1)基本思路。
行星绕恒星(或卫星绕行星)的运动可看作匀速圆周运动,向心力由中心天体的万有引力提供。
(2)两个重要关系。
[特别提醒] 计算天体质量和密度的两点注意:
(1)卫星的轨道半径与中心天体的半径不要混淆,只有近地卫星的轨道半径才近似等于天体半径。
(2)搞清“以谁为研究对象,谁是中心天体”“受力特点”“谁做圆周运动”等,明确一般只能求解中心天体的质量和密度,不能求解环绕天体的质量和密度。
[全悉考法]
1.设太阳质量为M,某行星绕太阳公转周期为T,轨道可视为半径为r的圆。已知引力常量为G,则描述该行星运动的上述物理量满足 ( )
3.据报道,科学家在距离地球20万光年外发现了首颗系外“宜居”行星。假设该行星质量约为地球质量的6.4倍,半径约为地球半径的2倍。那么,一个在地球表面能举起64 kg物体的人在这个行星表面能举起的物体的质量约为(地球表面重力加速度g=10 m/s2) ( )
A.40 kg B.50 kg
C.60 kg D.30 kg
4.“嫦娥五号”任务将是我国首次月球表面采样返回任务,这次任务的完成将标志着我国探月工程“三步走”顺利收官。若已知引力常量G,那么在下列给出的各种情景中,能根据测量的数据求出月球密度的是 ( )
A.在月球表面使一个小球做自由落体运动,测出落下的高度H和时间t
B.嫦娥五号贴近月球表面做匀速圆周运动,测出运行周期T
C.嫦娥五号在高空绕月球做匀速圆周运动,测出距月球表面的高度H和运行周期T
D.观察月球绕地球的匀速圆周运动,测出月球的直径D和运行周期T
5.[多选]有消息称,英国曼彻斯特大学的天文学家,已经在银河系里发现一颗由曾经的庞大恒星转变而成的体积较小的行星,这颗行星完全由钻石构成。若已知引力常量G,还需知道哪些信息可以计算该行星的质量 ( )
A.该行星表面的重力加速度及绕行星运行的卫星的轨道半径
B.该行星的自转周期与星体的半径
C.围绕该行星做圆周运动的卫星公转周期及运行半径
D.围绕该行星做圆周运动的卫星公转周期及公转线速度
1.向心加速度
向心力产生的加速度
2.向心加速度的方向
总是指向圆心
3.向心加速度的几种表达式
[特别提醒]
(1)向心加速度方向指向圆心,表示速度方向变化的快慢。
(2)切向加速度方向沿切线方向,表示速度大小变化的快慢。
(3)做匀速圆周运动物体的加速度即为向心加速度,方向总是指向圆心;做非匀速圆周运动物体的加速度一般不等于向心加速度,方向一般不指向圆心。
[全悉考法]
1.关于向心加速度,下列说法正确的是 ( )
A.向心加速度越大,线速度也越大
B.向心加速度越大,角速度也越大
C.向心加速度越大,圆周运动半径越小
D.向心加速度越大,线速度和角速度的乘积也越大
2.某学校开设了糕点制作的选修课,小明同学在体验糕点制作“裱花”环节时,他在绕中心匀速转动的圆盘上放了一块直径8英寸(20 cm)的蛋糕,在蛋糕上每隔4 s均匀“点”一次奶油, 蛋糕一周均匀“点”上15个奶油花,则下列说法正确的是 ( )
3.如图所示,一偏心轮绕O点做匀速转动,则偏心轮边缘上A、B两点的 ( )
A.线速度大小相同
B.角速度大小相同
C.向心加速度大小相等
D.向心加速度方向相同
解析:偏心轮上各点的角速度相等,故B正确;由v=ωr可知做圆周运动半径不同的点,线速度不同,故A错误;根据公式a=ω2r,向心加速度与各点到转动轴O的距离成正比,半径不同的点,向心加速度大小不相等,故C错误;向心加速度的方向始终指向圆心,所以A、B两点向心加速度的方向不同,故D错误。
答案:B
4.如图所示,正在匀速转动的水平转盘上固定有三个可视为质点
的小物块A、B、C,它们的质量关系为mA=2mB=2mC,到轴O
的距离关系为rC=2rA=2rB。下列说法中正确的是 ( )
A.B的线速度比C大 B.A的角速度比C大
C.B的向心加速度比C小 D.A的向心加速度比B大
解析:因为A、B、C共轴转动,角速度相同,根据v=rω可知半径越大,线速度越大,所以C的线速度最大,所以A、B错误;根据a=rω2,A的半径等于B的半径,所以A、B的向心加速度大小相等且小于C的向心加速度,故C正确,D错误。
答案:C
5.如图所示,“共享单车”极大地方便了老百姓的出行,某高档“共享单车”通过变速器调整链条在轮盘和飞轮的挂入位置,改变行驶速度。轮盘和飞轮的齿数如下表所示:
名称 轮盘 飞轮
A轮 B轮 C轮 D轮 E轮
齿数N/个 48 39 24 18 13
则下列说法正确的是 ( )
A.当A轮与C轮组合时,两轮的转速之比为1∶1
B.当A轮与C轮组合时,两轮边缘上的点的线速度大小之比为1∶2
C.当B轮与E轮组合时,两轮角速度之比为1∶3
D.当B轮与E轮组合时,两轮边缘上的点的向心加速度大小之比为3∶1
解析:A轮与C轮通过链条连接,轮边缘上的点的线速度大小相等,齿数之比为2∶1,齿数之比等于轮的半径之比,转速之比为1∶2,选项A、B错误;B轮与E轮通过链条连接,轮边缘上的点的线速度大小相等,齿数之比为3∶1,转速之比为1∶3,角速度之比为1∶3,轮边缘上的点的向心加速度之比为1∶3,选项C正确,D错误。
答案:C
[主干回扣]
“四步法”求解圆周运动问题
[特别提醒]
(1)做匀速圆周运动的物体所受合外力恰好全部提供向心力。
(2)做非匀速圆周运动的物体所受合外力一般不等于向心力,但在某些位置合外力可能等于向心力。
[全悉考法]
1.火车转弯时,如果铁路弯道内外轨一样高,外轨对轮缘(如图甲所示)挤压的弹力F提供了火车转弯的向心力(如图乙所示),但是靠这种办法得到向心力极易使铁轨和车轮受损。在修筑铁路时,弯道处的外轨会略高于内轨(如图丙所示),当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时的速度大小为v,以下说法中正确的是 ( )
2.如图所示是浙江沿海的风力发电机,A、B是同一台发电机
叶片上的两点。发电机工作时A、B两点的角速度大小分别
为ωA、ωB,线速度大小分别为vA、vB,则 ( )
A.ωA>ωB B.ωA<ωB
C.vA>vB D.vA<vB
解析:A、B两点的角速度相同,A点的半径大于B点的半径,根据v=ωr可得,A点的线速度大于B点的线速度,选项A、B、D错误,选项C正确。
答案:C
3.城市中为了解决交通问题,修建了许多立交桥。如图所
示,桥面半径为R的圆弧形的立交桥AB横跨在水平路面
上,一辆质量为m的小汽车,从A端冲上该立交桥,小汽车到达桥顶时的速度大小为v1,若小汽车在上桥过程中保持速率不变,则 ( )
A.小汽车通过桥顶时处于失重状态
B.小汽车通过桥顶时处于超重状态
4.如图所示,过山车的轨道可视为竖直平面内半径为R的圆轨道。质量为m的游客随过山车一起运动,当游客以速度v经过圆轨道的最高点时 ( )
A.处于超重状态
B.向心加速度方向竖直向下
5.暑假里,小明去游乐场游玩,坐了一次旋转飞椅,如图1所示,该旋转飞椅顶上有一个半径为4.5 m的伞盖,伞盖在转动过程中带动下面的悬绳转动,其示意图如图2所示。旋转飞椅高O1O2=5.8 m,绳长为5 m。小明挑选了一个悬挂在伞盖边缘的最外侧的椅子坐下,他与座椅的总质量为40 kg。小明和椅子的转动可简化为如图2所示的圆周运动。在某段时间内,伞盖保持在水平面内稳定旋转,绳与竖直方向夹角为37°。g取10 m/s2,sin 37°=0.6, cos 37°=0.8,在此过程中,求:
(1)座椅受到绳子的拉力大小;
(2)小明运动的线速度大小;
(3)小明随身带的玻璃球从座椅上不慎滑落,求落地点与中心转轴(即图2中O1点)的距离(结果可用根号表示)。
解析:(1)对小明和椅子整体受力分析,如图所示,受到重力和绳子的拉力作用,其合力提供向心力,在竖直方向受力平衡,有FTcos 37°=mg,
解得拉力FT=500 N。
[主干回扣]
对开普勒定律的理解
定律 内容 研究角度 理解
开普勒第一定律 所有行星围绕太阳运行的轨道都是椭圆,太阳处在椭圆的一个焦点上 轨道的空间分布 (1)各行星的椭圆轨道尽管大小不同,但太阳位于所有椭圆轨道的一个共同焦点处
(2)不同行星的轨道是不同的,可能相差很大
[全悉考法]
1.物理学发展历程中,在前人研究基础上经过多年的尝试性计算,首先发表行星运动的三个定律的科学家是 ( )
A.哥白尼 B.第谷 C.伽利略 D.开普勒
解析:开普勒首先发表了开普勒行星运动三定律,故D正确。
答案:D
2. 如图所示,O表示地球,P表示一个绕地球沿椭圆轨道做逆时针方向运动的人造卫星,AB为长轴,CD为短轴。在卫星绕地球运动一周的时间内,从A到B的时间为tAB,同理从B到A、从C到D、从D到C的时间分别为tBA、tCD、tDC。下列关系式正确的是 ( )
A.tAB>tBA B.tAB<tBA
C.tCD>tDC D.tCD<tDC
解析:由卫星做椭圆运动的对称性得tAB=tBA,选项A、B错误;由开普勒第二定律,卫星在近地点时运动快,在远地点时运动慢,所以tCD<tDC,选项C错误,D正确。
答案:D
3.某行星绕恒星运行的椭圆轨道如图所示,E和F是椭圆的两个焦点,O是椭圆的中心,行星在A点的线速度比在B点的线速度大。则恒星位于 ( )
A.A点 B.E点 C.F点 D.O点
解析:根据开普勒第二定律,对任意一个行星来说,它与太阳的连线在相等时间内扫过的面积相等。则行星在距离恒星较近的位置速度较大,因行星在A点的线速度比在B点的线速度大,则恒星位于E点,故选项B正确。
答案:B
4.如图所示,一颗卫星绕地球做椭圆运动,运动周期为T,图中虚线为卫星的运行轨迹,A、B、C、D是轨迹上的四个位置,其中A距离地球最近,C距离地球最远。B和D点是弧线ABC和ADC的中点,下列说法正确的是 ( )
A.卫星在C点的速度最大
B.卫星在C点的加速度最大
[主干回扣]
1.内容
宇宙间的一切物体都是互相吸引的。两个物体间引力的方向在它们的连线上,引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r的二次方成反比。
3.引力常量G
①数值:G=6.67×10-11 N·m2/kg2;适用于任何问题。
②物理意义:引力常量在数值上等于两个质量都是1 kg的质点相距1 m时的相互吸引力。
③G的测定:由英国科学家卡文迪什(又称卡文迪许)在实验室里首先通过卡文迪什扭秤装置测出的。
④测定G的意义:证实了万有引力的存在及万有引力定律的正确性。
4.适用条件
适用于计算两个质点间的万有引力。
[特别提醒]
(1)距离r的理解:
①对于两个质量均匀分布的球体,r应是两球心间的距离。
②对于一个均匀球体与球外一个质点,r应是球体球心到质点的距离。
③对于两个物体间的距离比物体本身大得多时,物体可以看成质点,r应是两个物体间的距离。
(2)地球周围物体间的万有引力很小,受力分析时可以忽略;但是天体间的万有引力是巨大的,对于天体的运动起决定作用。
[全悉考法]
1.符合发现和完善万有引力定律历史事实的是 ( )
A.哥白尼提出三大行星定律
B.卡文迪什提出地心说
C.牛顿接受了胡克等科学家关于吸引力与两物体中心距离的平方成反比的猜想
D.开普勒根据大量实验数据得出了比例系数G的大小
解析:开普勒提出三大行星定律,故A错误;托勒密提出地心说,故B错误;万有引力定律是由牛顿发现的,故C正确;卡文迪什根据大量实验数据得出了比例系数G的大小,故D错误。
答案:C
2.关于万有引力和万有引力定律的理解正确的是 ( )
A.m1与m2受到的引力总是大小相等、方向相反,是一对平衡力
B.m1与m2受到的引力总是大小相等的,而与m1、m2是否相等无关
C.不能看作质点的两物体间不存在相互作用的引力
解析:m1与m2之间的万有引力总是大小相等,方向相反,是一对相互作用力,不是一对平衡力,而与m1、m2是否相等无关,故选项B正确,A错误;万有引力存在于一切物体之间,故选项C错误;r为两物体之间的距离,就是重心到重心的距离,所以如果知道两个物体间重心之间的距离,就算不能看成质点也能用万有引力公式进行计算,例如两个靠得很近的铅球之间的万有引力,故选项D错误。
答案:B
4.我国航天员在空间站内多次开设了“天宫课堂”。已知地球质量为M,半径为R,引力常量为G。若我国空间站质量为m,在离地面高度为h的轨道上做匀速圆周运动,则下列说法正确的是( )
5.因为地球的自转,同一物体在地球上不同的纬度处重力不同,一质量为m的物体在北极时的重力与其在赤道时的重力的差为F。将地球看成质量分布均匀的球体,半径为R。则地球的自转周期是 ( )
[主干回扣]
1.计算天体质量和密度的方法
(1)自力更生(g-R)法。
2.天体运动问题的分析与计算
(1)基本思路。
行星绕恒星(或卫星绕行星)的运动可看作匀速圆周运动,向心力由中心天体的万有引力提供。
(2)两个重要关系。
[特别提醒] 计算天体质量和密度的两点注意:
(1)卫星的轨道半径与中心天体的半径不要混淆,只有近地卫星的轨道半径才近似等于天体半径。
(2)搞清“以谁为研究对象,谁是中心天体”“受力特点”“谁做圆周运动”等,明确一般只能求解中心天体的质量和密度,不能求解环绕天体的质量和密度。
[全悉考法]
1.设太阳质量为M,某行星绕太阳公转周期为T,轨道可视为半径为r的圆。已知引力常量为G,则描述该行星运动的上述物理量满足 ( )
3.据报道,科学家在距离地球20万光年外发现了首颗系外“宜居”行星。假设该行星质量约为地球质量的6.4倍,半径约为地球半径的2倍。那么,一个在地球表面能举起64 kg物体的人在这个行星表面能举起的物体的质量约为(地球表面重力加速度g=10 m/s2) ( )
A.40 kg B.50 kg
C.60 kg D.30 kg
4.“嫦娥五号”任务将是我国首次月球表面采样返回任务,这次任务的完成将标志着我国探月工程“三步走”顺利收官。若已知引力常量G,那么在下列给出的各种情景中,能根据测量的数据求出月球密度的是 ( )
A.在月球表面使一个小球做自由落体运动,测出落下的高度H和时间t
B.嫦娥五号贴近月球表面做匀速圆周运动,测出运行周期T
C.嫦娥五号在高空绕月球做匀速圆周运动,测出距月球表面的高度H和运行周期T
D.观察月球绕地球的匀速圆周运动,测出月球的直径D和运行周期T
5.[多选]有消息称,英国曼彻斯特大学的天文学家,已经在银河系里发现一颗由曾经的庞大恒星转变而成的体积较小的行星,这颗行星完全由钻石构成。若已知引力常量G,还需知道哪些信息可以计算该行星的质量 ( )
A.该行星表面的重力加速度及绕行星运行的卫星的轨道半径
B.该行星的自转周期与星体的半径
C.围绕该行星做圆周运动的卫星公转周期及运行半径
D.围绕该行星做圆周运动的卫星公转周期及公转线速度
同课章节目录
