2024-2025学年甘肃省兰州市志成中学九年级(上)期末数学试卷(无答案)
文档属性
| 名称 | 2024-2025学年甘肃省兰州市志成中学九年级(上)期末数学试卷(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 619.0KB | ||
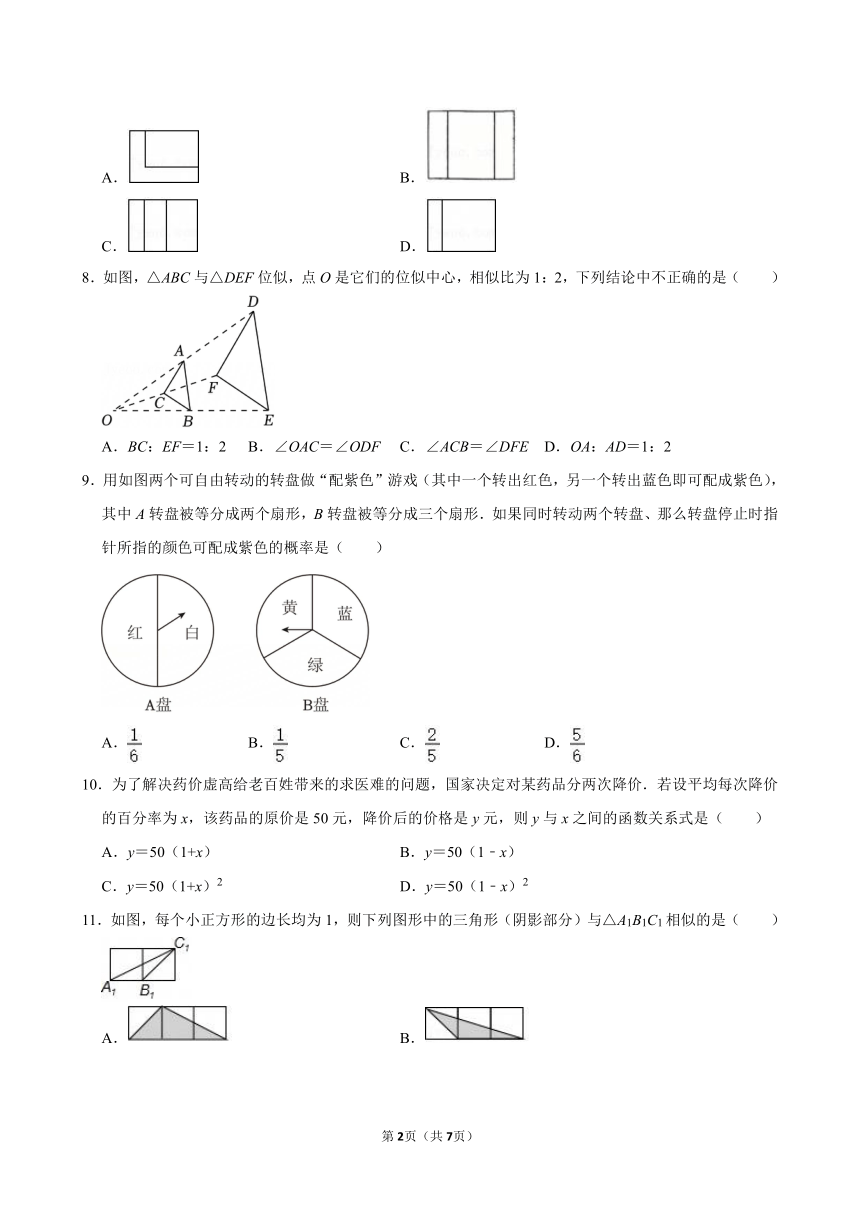
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 16:07:02 | ||
图片预览


文档简介
2024-2025学年甘肃省兰州市志成中学九年级(上)期末数学试卷
一、单选题(本大题共12小题,每题3分,共36分)
1.下列关于x的一元二次方程的是( )
A.2x=3 B.x2+1=0 C.x2+y=5 D.
2.反比例函数的图象一定经过的点是( )
A.(1,10) B.(﹣2,5) C.(2,5) D.(5,2)
3.若∠A为锐角,且,则cosA的值为( )
A. B. C. D.
4.如图,利用标杆DA测量楼高,点C,A,B在同一直线上,DA⊥CB,EB⊥CB,垂足分别为A,B.若测得影长AB=16米,DA=3米,影长CA=4米,则楼高EB为( )
A.10米 B.12米 C.15米 D.20米
5.若函数+mx+1是关于x的二次函数,则m的值是( )
A.0 B.3 C.0或3 D.1或2
6.如图,菱形ABCD对角线AC与BD交于点O,AC=8,BD=6,则菱形的面积为( )
A.48 B.40 C.24 D.10
7.如图,表示一个用于防震的L形的包装用泡沫塑料,它的俯视图是( )
A. B.
C. D.
8.如图,△ABC与△DEF位似,点O是它们的位似中心,相似比为1:2,下列结论中不正确的是( )
A.BC:EF=1:2 B.∠OAC=∠ODF C.∠ACB=∠DFE D.OA:AD=1:2
9.用如图两个可自由转动的转盘做“配紫色”游戏(其中一个转出红色,另一个转出蓝色即可配成紫色),其中A转盘被等分成两个扇形,B转盘被等分成三个扇形.如果同时转动两个转盘、那么转盘停止时指针所指的颜色可配成紫色的概率是( )
A. B. C. D.
10.为了解决药价虚高给老百姓带来的求医难的问题,国家决定对某药品分两次降价.若设平均每次降价的百分率为x,该药品的原价是50元,降价后的价格是y元,则y与x之间的函数关系式是( )
A.y=50(1+x) B.y=50(1﹣x)
C.y=50(1+x)2 D.y=50(1﹣x)2
11.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
A. B.
C. D.
12.如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且DE∥CA,DF∥BA.下列四种说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果AD⊥BC,且AB=AC,那么四边形AEDF是正方形.
其中,正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,每题3分,共12分)
13.如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为 .
14.若反比例函数的图象位于第二、四象限,那么a的取值范围为 .
15.抛物线y=2x2+8x﹣6的顶点坐标是 .
16.通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色,一次化学课上,学生用酚酞溶液检测四瓶标签被污染无法分辨的无色溶液的酸碱性.已知四瓶溶液分别是A:盐酸(呈酸性),B:硝酸钾溶液(呈中性),C:氢氧化钠溶液(呈碱性),D:氢氧化钾溶液(呈碱性).小周同时将任选的两瓶溶液滴入酚酞溶液进行检测,两瓶溶液恰好都变红色的概率是 .
三、解答题(本大题共12小题,共72分,解答时写出必要的文字说明,证明过程或演算步骤)
17.解方程:4(x+1)2﹣8=0.
18.解方程:2x2﹣4x﹣3=0.
19.计算:.
20.如图,CD为 ADEC的对角线,延长AD至点B,使得BD=AD,连接BE,且BE=CE.
(1)求证:四边形CDBE是菱形;
(2)连接BC,若AC=BC,试判断四边形CDBE的形状,并说明理由.
21.如图,直线y1=﹣x+m与双曲线交于A,B两点,点A的坐标为(1,2).
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)当y2>y1时,直接写出x的范围.
22.某商店以每个8元的成本价购进了一批玩具陀螺,如果以每个14元的价格出售,那么每天可销售40个,经市场调查发现,若每个陀螺的售价上涨1元,则每天的销售量就减少2个.
(1)每个陀螺涨价多少元时,才能让顾客得到实惠的同时商店每天获得的利润为320元?
(2)每个陀螺涨价多少元时,商店每天获得的利润最大?最大利润是多少?
23.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)请在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在平面直角坐标系中画出△A2B2C2;
(3)①点B1的坐标为 .
②求△A2B2C2的面积.
24.如图,某中学为培养学生的综合实践能力,准备在学校围建一个矩形苗圃园,其中一边靠墙,另外三边由长度为30m的篱笆围成.如图,墙长为16m,设这个苗圃园垂直于墙的一边长为x m.请列出方程并解答:
(1)若苗圃园的面积为108m2,求x的值;
(2)苗圃园的面积能达到120m2吗?若能,求出x的值;若不能,说明理由.
25.2023年10月5日,杭州亚运会女篮决赛,中国女篮以74比72战胜日本女篮夺得冠军,女篮的夺冠跟队员们平时的刻苦训练是分不开的.如图,这是一位篮球运动员在进行投篮训练,篮球以一定的速度斜向上抛出,不计空气阻力,在空中划过的运动路线可以看作是抛物线y=ax2+x+c的一部分.以O为坐标原点,建立平面直角坐标系.已知投篮处A到地面的距离AO=2.25m,最高点B的坐标为(2.5,3.5),篮筐中心距离地面的竖直高度是3.05m.
(1)求抛物线的函数表达式.
(2)当篮球运动员距篮筐中心的水平距离OC为4m时,这次投篮训练是否成功?请判断并说明理由.
26.如图,点E是矩形ABCD中AD边上一点,△ABE沿BE折叠为△FBE,点F落在CD上.(1)求证:△CFB∽△DEF;
(2)若,,求BF的值.
27.自2024年10月29日起,巴中恩阳机场开通了到无锡的新航线,进一步方便了广大市民.如图,市民甲在C处看见飞机A的仰角为45°,同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°,已知斜坡CF的坡比=1:3,铅垂高度DG=30米(点E、G、C、B在同一水平线上).(结果保留根号)
(1)求此时甲、乙两市民的距离CD;
(2)求飞机此时距离地面的高度AB.
28.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件 .
(2)问题探究
如图2,已知∠ACB=90°,,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
①四边形ACBD (填“是”或“不是”)等邻边四边形;
②求线段DB的长度.
(3)拓展应用
如图3,在等邻边四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC和BD为四边形的对角线,△BCD为等边三角形,试探究AC和AB的数量关系,并说明理由.
第6页(共7页)
一、单选题(本大题共12小题,每题3分,共36分)
1.下列关于x的一元二次方程的是( )
A.2x=3 B.x2+1=0 C.x2+y=5 D.
2.反比例函数的图象一定经过的点是( )
A.(1,10) B.(﹣2,5) C.(2,5) D.(5,2)
3.若∠A为锐角,且,则cosA的值为( )
A. B. C. D.
4.如图,利用标杆DA测量楼高,点C,A,B在同一直线上,DA⊥CB,EB⊥CB,垂足分别为A,B.若测得影长AB=16米,DA=3米,影长CA=4米,则楼高EB为( )
A.10米 B.12米 C.15米 D.20米
5.若函数+mx+1是关于x的二次函数,则m的值是( )
A.0 B.3 C.0或3 D.1或2
6.如图,菱形ABCD对角线AC与BD交于点O,AC=8,BD=6,则菱形的面积为( )
A.48 B.40 C.24 D.10
7.如图,表示一个用于防震的L形的包装用泡沫塑料,它的俯视图是( )
A. B.
C. D.
8.如图,△ABC与△DEF位似,点O是它们的位似中心,相似比为1:2,下列结论中不正确的是( )
A.BC:EF=1:2 B.∠OAC=∠ODF C.∠ACB=∠DFE D.OA:AD=1:2
9.用如图两个可自由转动的转盘做“配紫色”游戏(其中一个转出红色,另一个转出蓝色即可配成紫色),其中A转盘被等分成两个扇形,B转盘被等分成三个扇形.如果同时转动两个转盘、那么转盘停止时指针所指的颜色可配成紫色的概率是( )
A. B. C. D.
10.为了解决药价虚高给老百姓带来的求医难的问题,国家决定对某药品分两次降价.若设平均每次降价的百分率为x,该药品的原价是50元,降价后的价格是y元,则y与x之间的函数关系式是( )
A.y=50(1+x) B.y=50(1﹣x)
C.y=50(1+x)2 D.y=50(1﹣x)2
11.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
A. B.
C. D.
12.如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且DE∥CA,DF∥BA.下列四种说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果AD⊥BC,且AB=AC,那么四边形AEDF是正方形.
其中,正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,每题3分,共12分)
13.如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为 .
14.若反比例函数的图象位于第二、四象限,那么a的取值范围为 .
15.抛物线y=2x2+8x﹣6的顶点坐标是 .
16.通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色,一次化学课上,学生用酚酞溶液检测四瓶标签被污染无法分辨的无色溶液的酸碱性.已知四瓶溶液分别是A:盐酸(呈酸性),B:硝酸钾溶液(呈中性),C:氢氧化钠溶液(呈碱性),D:氢氧化钾溶液(呈碱性).小周同时将任选的两瓶溶液滴入酚酞溶液进行检测,两瓶溶液恰好都变红色的概率是 .
三、解答题(本大题共12小题,共72分,解答时写出必要的文字说明,证明过程或演算步骤)
17.解方程:4(x+1)2﹣8=0.
18.解方程:2x2﹣4x﹣3=0.
19.计算:.
20.如图,CD为 ADEC的对角线,延长AD至点B,使得BD=AD,连接BE,且BE=CE.
(1)求证:四边形CDBE是菱形;
(2)连接BC,若AC=BC,试判断四边形CDBE的形状,并说明理由.
21.如图,直线y1=﹣x+m与双曲线交于A,B两点,点A的坐标为(1,2).
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)当y2>y1时,直接写出x的范围.
22.某商店以每个8元的成本价购进了一批玩具陀螺,如果以每个14元的价格出售,那么每天可销售40个,经市场调查发现,若每个陀螺的售价上涨1元,则每天的销售量就减少2个.
(1)每个陀螺涨价多少元时,才能让顾客得到实惠的同时商店每天获得的利润为320元?
(2)每个陀螺涨价多少元时,商店每天获得的利润最大?最大利润是多少?
23.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)请在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在平面直角坐标系中画出△A2B2C2;
(3)①点B1的坐标为 .
②求△A2B2C2的面积.
24.如图,某中学为培养学生的综合实践能力,准备在学校围建一个矩形苗圃园,其中一边靠墙,另外三边由长度为30m的篱笆围成.如图,墙长为16m,设这个苗圃园垂直于墙的一边长为x m.请列出方程并解答:
(1)若苗圃园的面积为108m2,求x的值;
(2)苗圃园的面积能达到120m2吗?若能,求出x的值;若不能,说明理由.
25.2023年10月5日,杭州亚运会女篮决赛,中国女篮以74比72战胜日本女篮夺得冠军,女篮的夺冠跟队员们平时的刻苦训练是分不开的.如图,这是一位篮球运动员在进行投篮训练,篮球以一定的速度斜向上抛出,不计空气阻力,在空中划过的运动路线可以看作是抛物线y=ax2+x+c的一部分.以O为坐标原点,建立平面直角坐标系.已知投篮处A到地面的距离AO=2.25m,最高点B的坐标为(2.5,3.5),篮筐中心距离地面的竖直高度是3.05m.
(1)求抛物线的函数表达式.
(2)当篮球运动员距篮筐中心的水平距离OC为4m时,这次投篮训练是否成功?请判断并说明理由.
26.如图,点E是矩形ABCD中AD边上一点,△ABE沿BE折叠为△FBE,点F落在CD上.(1)求证:△CFB∽△DEF;
(2)若,,求BF的值.
27.自2024年10月29日起,巴中恩阳机场开通了到无锡的新航线,进一步方便了广大市民.如图,市民甲在C处看见飞机A的仰角为45°,同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°,已知斜坡CF的坡比=1:3,铅垂高度DG=30米(点E、G、C、B在同一水平线上).(结果保留根号)
(1)求此时甲、乙两市民的距离CD;
(2)求飞机此时距离地面的高度AB.
28.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件 .
(2)问题探究
如图2,已知∠ACB=90°,,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
①四边形ACBD (填“是”或“不是”)等邻边四边形;
②求线段DB的长度.
(3)拓展应用
如图3,在等邻边四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC和BD为四边形的对角线,△BCD为等边三角形,试探究AC和AB的数量关系,并说明理由.
第6页(共7页)
同课章节目录
