华师大版(2024)数学七下9.2.2平移的特征 课件(共26张PPT)
文档属性
| 名称 | 华师大版(2024)数学七下9.2.2平移的特征 课件(共26张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 910.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-14 12:07:08 | ||
图片预览





文档简介
(共26张PPT)
(华师大版)七年级
下
9.2.2平移的特征
轴对称、平移与旋转
第9章
“九”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.理解并掌握平移的特征.
2.能根据已知条件画出平移后的图形,并运用图形的平移进行
图案设计.
新知导入
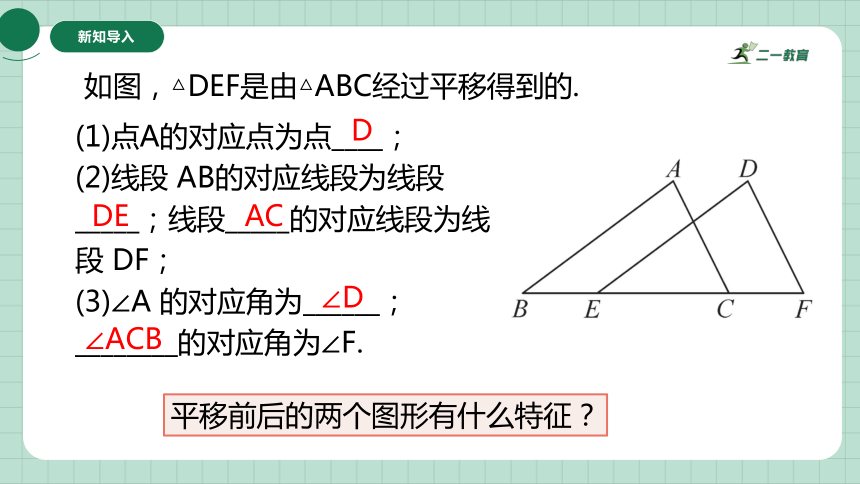
如图,△DEF是由△ABC经过平移得到的.
(1)点A的对应点为点____;
(2)线段 AB的对应线段为线段_____;线段_____的对应线段为线段 DF;
(3)∠A 的对应角为______;________的对应角为∠F.
D
DE
AC
∠D
∠ACB
平移前后的两个图形有什么特征?
新知讲解
如图,在画平行线的时候,有时为了需要,将直尺与三角尺放在倾斜的位置上.
(1)在图中任意选一组对应线段,这两条线段之间有怎样的关系?
AB∥A′B′,AB =A′B′.
新知讲解
如图,在画平行线的时候,有时为了需要,将直尺与三角尺放在倾斜的位置上.
(2)在图中任意选一组对应角,这两个角之间有怎样的关系?
∠B =∠B′
新知讲解
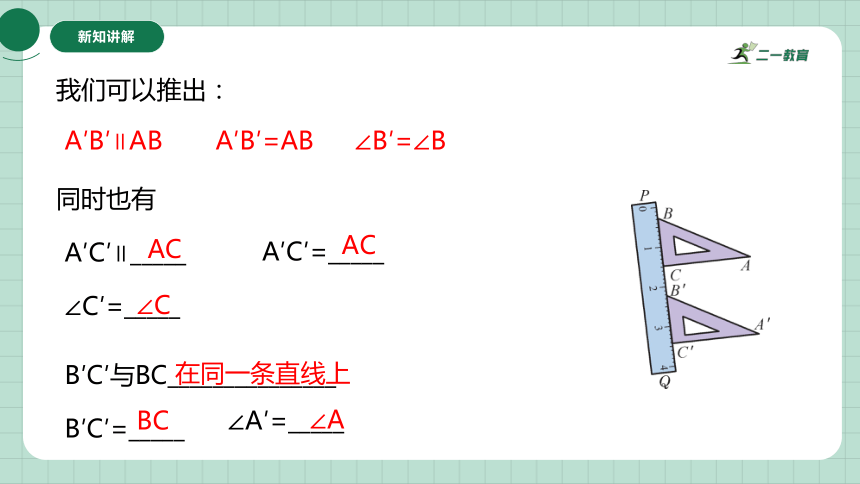
A′B′∥AB
A′B′=AB
∠B′=∠B
我们可以推出:
同时也有
A′C′∥_____
A′C′=_____
∠C′=_____
B′C′与BC_______________
B′C′=_____
∠A′=_____
AC
AC
∠C
在同一条直线上
BC
∠A
新知讲解
图形平移的特征:
平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等,对应角相等,图形的形状与大小不变.
注意
在平移过程中,对应线段也可能在一条直线上.
新知讲解
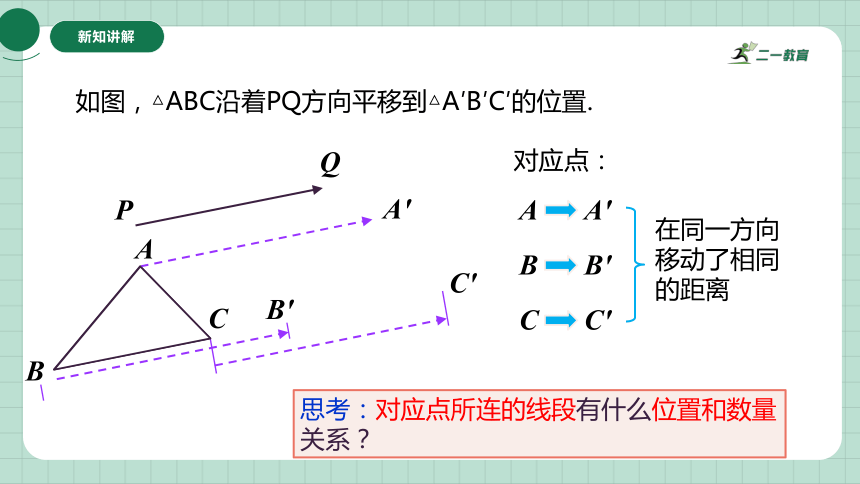
如图,△ABC沿着PQ方向平移到△A′B′C′的位置.
C'
A'
A
C
B
P
Q
思考:对应点所连的线段有什么位置和数量关系?
A
A'
B
B'
C
C'
在同一方向移动了相同的距离
对应点:
B'
新知讲解
C'
A'
A
C
B'
B
P
Q
连接AA′,BB′,CC′,则有
AA′∥BB′
AA′=BB′
AA′∥_____
AA′=_____
CC′
CC′
BB′与CC′______________
在同一条直线上
BB′=_____
CC′
平移后对应点所连的线段平行(或在同一条直线上)且相等.
新知讲解
图形平移的特征:
(1)平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等,对应角相等,图形的形状与大小不变.
(2)平移后对应点所连的线段平行(或在同一条直线上)且相等.
新知讲解
试一试:将下图中的△ABC沿PQ方向平移到△A′B′C′的位置,其平移的距离为线段PQ的长度.
C'
A'
A
C
B'
B
P
Q
观察所得到的对应线段和对应点所连的线段是否符合上述我们所得
到的平移的特征
新知讲解
例 如图,△ABC 经过平移到△A′B′C′ 的位置. 指出平移的方向,并量出平移的距离.(精确到 1 mm)
解:由于点 A 与点 A′ 是一对对应点,因此,如图(2),连结 AA′ ,平移的方向就是点 A 到点 A′ 的方向,平移的距离就是线段 AA′ 的长,经测量约为 25 mm.
新知讲解
试一试:在如图的方格纸中,作出将图中△ABC 向右平移 4 格后的△A′B′C′ ,然后再作出将△A′B′C′ 向上平移 3 格后的△A′′B′′C′′.△A′′B′′C′′ 是否可以看成是△ABC 经过一次平移而得到的?如果是,请指出平移的方向和距离 .
B′
C′
A′
A′′
B′′
C′′
可以看成是经过一次平移得到的
平移的方向是点 A 到 A′ 的方向,平移的距离是线段 AA′ 的长度.
新知讲解
平移作图是平移性质的应用.在具体作图时,应抓住作图的“四部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺序连接对应点.
新知讲解
做一做:如图,在纸上作△ABC 和平行直线 m、n . 作出△ABC 关于直线 m 对称的△A′B′C′,再作出△A′B′C′ 关于直线 n 对称的△A′′B′′C′′.
观察△ABC 和△A′′B′′C′′,你能发现这两个三角形有什么关系吗?
A
B
C
m
n
A′
C′
B′
A′′
C′′
B′′
经过两次翻折(对称轴互相平行)后得到的图形,可以看成是原图形经过平移得到的.
【知识技能类作业】必做题:
课堂练习
1.如图,把向右平移得到 ,下列结论错误的是( )
A. B.
C. D.
D
【知识技能类作业】必做题:
课堂练习
2.如图,将沿射线 方向平移得到,连结,, ,则 的长为( )
A. B. C. D.
C
【知识技能类作业】必做题:
课堂练习
3. 如图,△ABC、△CEF都是由△BDE平移得到,A、C、F三点在同一条直线上.已知∠D=70°,∠BED=45°,BE=2.求:
(1) AF的长;(2) ∠ECF的度数.
解:(1) ∵ △ABC、△CEF都是由△BDE平移得到,
∴ AC=BE=2,CF=BE=2.∴ AF=AC+CF=4
(2) ∵ ∠D=70°,∠BED=45°,
∴ ∠DBE=180°-∠D-∠BED=65°.
∵ △CEF是由△BDE平移得到,∴ ∠ECF=∠DBE=65°
【知识技能类作业】选做题:
课堂练习
4.如图,△ABC是直角三角形,∠ABC=90°,将其沿直角边BC所在的直线向右平移得到△DEF.下列结论中,不一定成立的是( )
A. △ABC与△DEF的形状、大小完全相同
B. ∠A+∠DFE=90°
C. AC∥DF,且AC=DF
D. EC=CF
D
【知识技能类作业】选做题:
课堂练习
5.如图,将△ABC沿BC方向平移8cm得到△DEF,若BF=7CE,则BC的长为
cm.
6
【综合拓展类作业】
课堂练习
6. 如图,将面积为5的△ABC沿射线BC的方向平移到△DEF的位置,平移的距离是边BC长的2倍,求四边形ACED的面积.
解:设点A到边BC的距离为h,则S△ABC=BC·h=5.由平移的
特征,得EF=BC,AD=CF=BE,AD∥BF.∴ AD与CE间的
距离为h,且四边形ACED是梯形.又∵ 平移的距离是边BC长的2倍,
∴ AD=CF=BE=2BC.∴ CE=BC.∴ 四边形ACED的面积为(AD+CE)·h=(2BC+BC)·h=3×BC·h=3×5=15
课堂总结
1.图形平移的特征:
(1)平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等,对应角相等,图形的形状与大小不变.
(2)平移后对应点所连的线段平行(或在同一条直线上)且相等.
2.平移作图步骤:应抓住作图的“四部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺序连接对应点.
板书设计
1.图形平移的特征:
2.平移作图步骤:
课题:9.2.2平移的特征
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
9.2.2平移的特征
轴对称、平移与旋转
第9章
“九”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.理解并掌握平移的特征.
2.能根据已知条件画出平移后的图形,并运用图形的平移进行
图案设计.
新知导入
如图,△DEF是由△ABC经过平移得到的.
(1)点A的对应点为点____;
(2)线段 AB的对应线段为线段_____;线段_____的对应线段为线段 DF;
(3)∠A 的对应角为______;________的对应角为∠F.
D
DE
AC
∠D
∠ACB
平移前后的两个图形有什么特征?
新知讲解
如图,在画平行线的时候,有时为了需要,将直尺与三角尺放在倾斜的位置上.
(1)在图中任意选一组对应线段,这两条线段之间有怎样的关系?
AB∥A′B′,AB =A′B′.
新知讲解
如图,在画平行线的时候,有时为了需要,将直尺与三角尺放在倾斜的位置上.
(2)在图中任意选一组对应角,这两个角之间有怎样的关系?
∠B =∠B′
新知讲解
A′B′∥AB
A′B′=AB
∠B′=∠B
我们可以推出:
同时也有
A′C′∥_____
A′C′=_____
∠C′=_____
B′C′与BC_______________
B′C′=_____
∠A′=_____
AC
AC
∠C
在同一条直线上
BC
∠A
新知讲解
图形平移的特征:
平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等,对应角相等,图形的形状与大小不变.
注意
在平移过程中,对应线段也可能在一条直线上.
新知讲解
如图,△ABC沿着PQ方向平移到△A′B′C′的位置.
C'
A'
A
C
B
P
Q
思考:对应点所连的线段有什么位置和数量关系?
A
A'
B
B'
C
C'
在同一方向移动了相同的距离
对应点:
B'
新知讲解
C'
A'
A
C
B'
B
P
Q
连接AA′,BB′,CC′,则有
AA′∥BB′
AA′=BB′
AA′∥_____
AA′=_____
CC′
CC′
BB′与CC′______________
在同一条直线上
BB′=_____
CC′
平移后对应点所连的线段平行(或在同一条直线上)且相等.
新知讲解
图形平移的特征:
(1)平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等,对应角相等,图形的形状与大小不变.
(2)平移后对应点所连的线段平行(或在同一条直线上)且相等.
新知讲解
试一试:将下图中的△ABC沿PQ方向平移到△A′B′C′的位置,其平移的距离为线段PQ的长度.
C'
A'
A
C
B'
B
P
Q
观察所得到的对应线段和对应点所连的线段是否符合上述我们所得
到的平移的特征
新知讲解
例 如图,△ABC 经过平移到△A′B′C′ 的位置. 指出平移的方向,并量出平移的距离.(精确到 1 mm)
解:由于点 A 与点 A′ 是一对对应点,因此,如图(2),连结 AA′ ,平移的方向就是点 A 到点 A′ 的方向,平移的距离就是线段 AA′ 的长,经测量约为 25 mm.
新知讲解
试一试:在如图的方格纸中,作出将图中△ABC 向右平移 4 格后的△A′B′C′ ,然后再作出将△A′B′C′ 向上平移 3 格后的△A′′B′′C′′.△A′′B′′C′′ 是否可以看成是△ABC 经过一次平移而得到的?如果是,请指出平移的方向和距离 .
B′
C′
A′
A′′
B′′
C′′
可以看成是经过一次平移得到的
平移的方向是点 A 到 A′ 的方向,平移的距离是线段 AA′ 的长度.
新知讲解
平移作图是平移性质的应用.在具体作图时,应抓住作图的“四部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺序连接对应点.
新知讲解
做一做:如图,在纸上作△ABC 和平行直线 m、n . 作出△ABC 关于直线 m 对称的△A′B′C′,再作出△A′B′C′ 关于直线 n 对称的△A′′B′′C′′.
观察△ABC 和△A′′B′′C′′,你能发现这两个三角形有什么关系吗?
A
B
C
m
n
A′
C′
B′
A′′
C′′
B′′
经过两次翻折(对称轴互相平行)后得到的图形,可以看成是原图形经过平移得到的.
【知识技能类作业】必做题:
课堂练习
1.如图,把向右平移得到 ,下列结论错误的是( )
A. B.
C. D.
D
【知识技能类作业】必做题:
课堂练习
2.如图,将沿射线 方向平移得到,连结,, ,则 的长为( )
A. B. C. D.
C
【知识技能类作业】必做题:
课堂练习
3. 如图,△ABC、△CEF都是由△BDE平移得到,A、C、F三点在同一条直线上.已知∠D=70°,∠BED=45°,BE=2.求:
(1) AF的长;(2) ∠ECF的度数.
解:(1) ∵ △ABC、△CEF都是由△BDE平移得到,
∴ AC=BE=2,CF=BE=2.∴ AF=AC+CF=4
(2) ∵ ∠D=70°,∠BED=45°,
∴ ∠DBE=180°-∠D-∠BED=65°.
∵ △CEF是由△BDE平移得到,∴ ∠ECF=∠DBE=65°
【知识技能类作业】选做题:
课堂练习
4.如图,△ABC是直角三角形,∠ABC=90°,将其沿直角边BC所在的直线向右平移得到△DEF.下列结论中,不一定成立的是( )
A. △ABC与△DEF的形状、大小完全相同
B. ∠A+∠DFE=90°
C. AC∥DF,且AC=DF
D. EC=CF
D
【知识技能类作业】选做题:
课堂练习
5.如图,将△ABC沿BC方向平移8cm得到△DEF,若BF=7CE,则BC的长为
cm.
6
【综合拓展类作业】
课堂练习
6. 如图,将面积为5的△ABC沿射线BC的方向平移到△DEF的位置,平移的距离是边BC长的2倍,求四边形ACED的面积.
解:设点A到边BC的距离为h,则S△ABC=BC·h=5.由平移的
特征,得EF=BC,AD=CF=BE,AD∥BF.∴ AD与CE间的
距离为h,且四边形ACED是梯形.又∵ 平移的距离是边BC长的2倍,
∴ AD=CF=BE=2BC.∴ CE=BC.∴ 四边形ACED的面积为(AD+CE)·h=(2BC+BC)·h=3×BC·h=3×5=15
课堂总结
1.图形平移的特征:
(1)平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等,对应角相等,图形的形状与大小不变.
(2)平移后对应点所连的线段平行(或在同一条直线上)且相等.
2.平移作图步骤:应抓住作图的“四部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺序连接对应点.
板书设计
1.图形平移的特征:
2.平移作图步骤:
课题:9.2.2平移的特征
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
