圆的对称性
图片预览


文档简介
课件15张PPT。金水四中第三章 圆的对称性
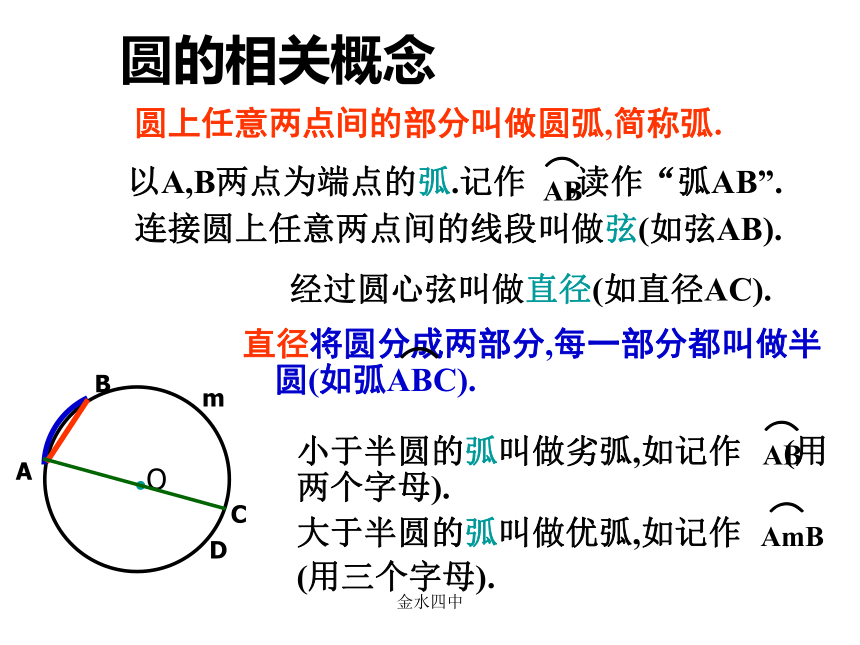
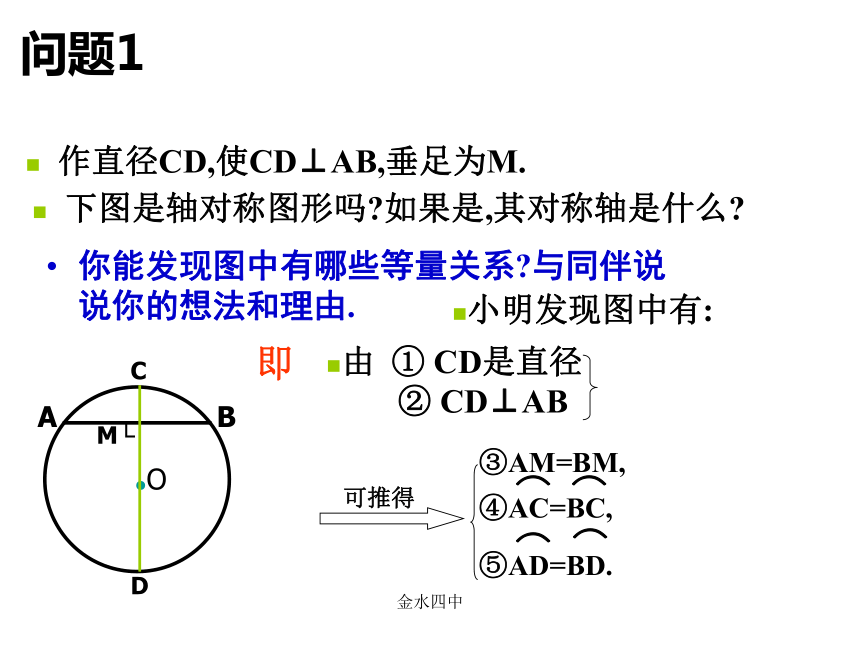
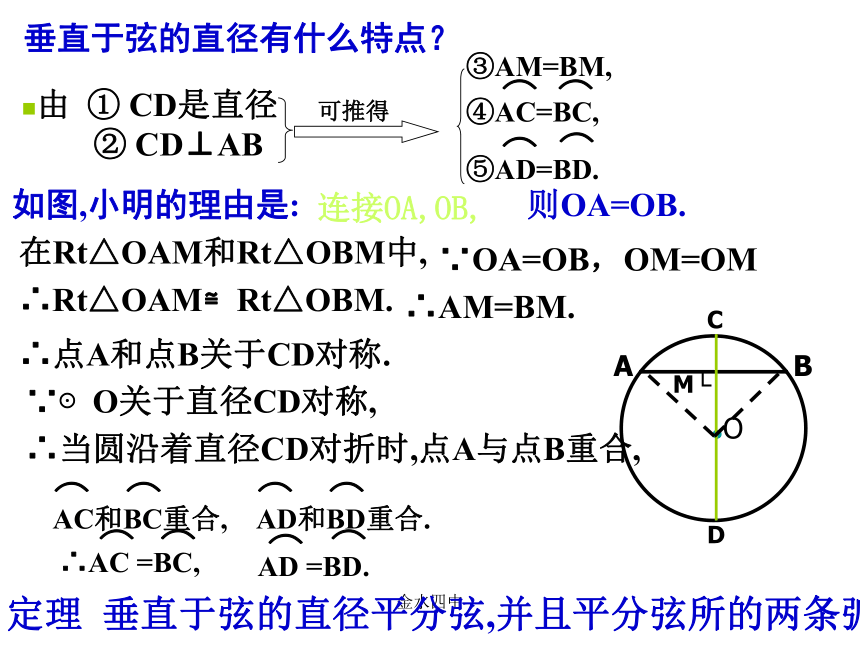
金水四中圆的对称性圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?你是用什么方法解决上述问题的?圆是轴对称图形.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.可利用折叠的方法即可解决上述问题.金水四中圆的相关概念圆上任意两点间的部分叫做圆弧,简称弧.直径将圆分成两部分,每一部分都叫做半圆(如弧ABC).连接圆上任意两点间的线段叫做弦(如弦AB).经过圆心弦叫做直径(如直径AC).⌒金水四中③AM=BM,问题1 垂直于弦的直径有什么特点? AB是⊙O的一条弦.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.作直径CD,使CD⊥AB,垂足为M.下图是轴对称图形吗?如果是,其对称轴是什么?小明发现图中有:由 ① CD是直径② CD⊥AB即金水四中垂直于弦的直径有什么特点?如图,小明的理由是:连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,由 ① CD是直径② CD⊥AB③AM=BM,定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
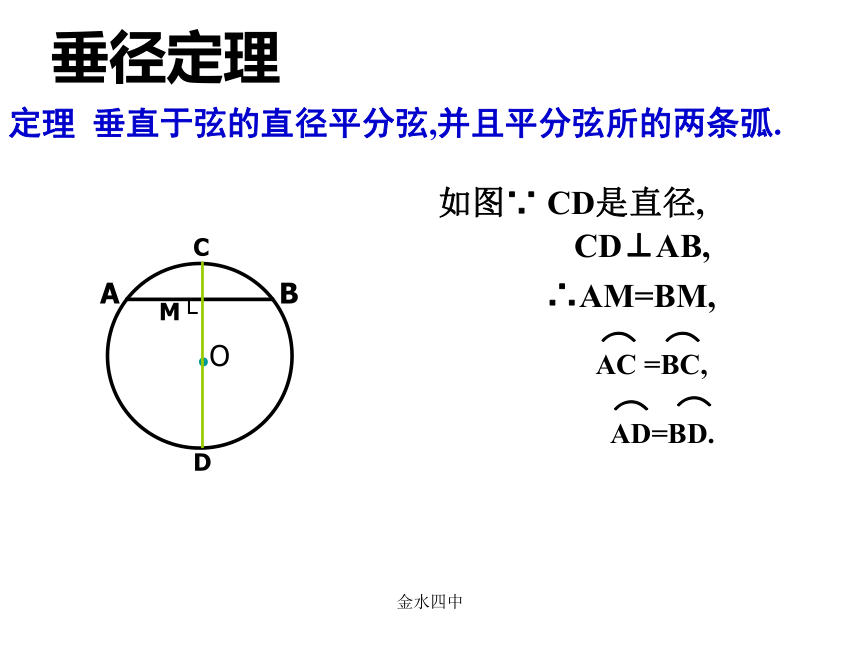
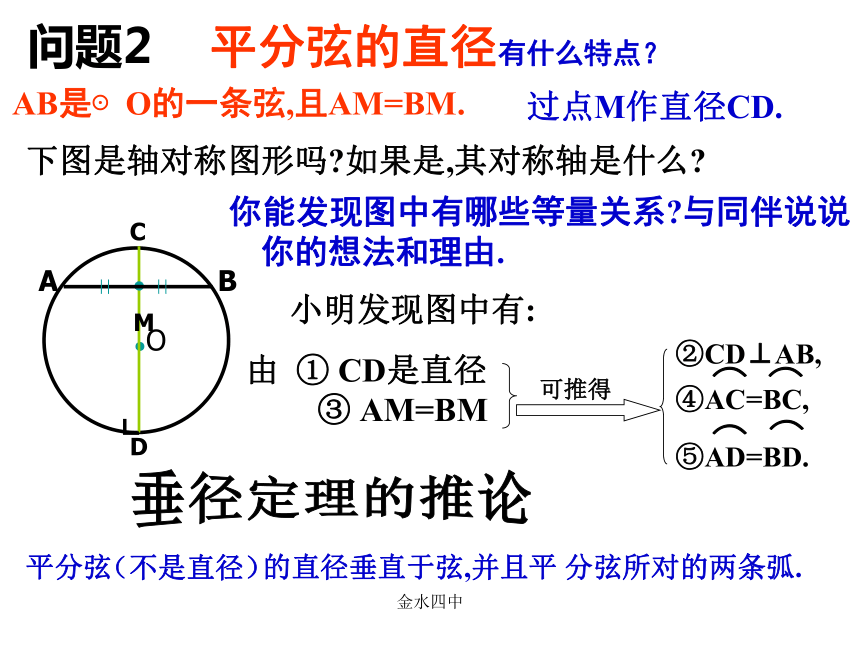
金水四中垂径定理定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.CD⊥AB,如图∵ CD是直径,∴AM=BM,金水四中②CD⊥AB,问题2 平分弦的直径有什么特点?AB是⊙O的一条弦,且AM=BM.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.过点M作直径CD.下图是轴对称图形吗?如果是,其对称轴是什么?小明发现图中有:由 ① CD是直径③ AM=BM┗平分弦 的直径垂直于弦,并且平 分弦所对的两条弧.垂径定理的推论 (不是直径)金水四中挑战自我垂径定理的推论 如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?老师提示: 这两条弦在圆中位置有两种情况:垂径定理的推论 圆的两条平行弦所夹的弧相等.MN金水四中解这个方程,得R=545.例1。如图,一条公路的转弯处是一段圆弧(即图中弧CD,点0是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE垂直于CD,垂足为F,EF=90m.求这段弯路的半径。解:连接OC,设弯路的半径为Rm,则OF=(R-90)m。 ∵ OE ┴ CD∴CF= CD= x600=300(m).根据勾股定理,得
OC2=CF2 +OF2即 R2=3002+(R-90)2.所以,这段弯路的半径为545m金水四中挑战自我画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.金水四中挑战自我填一填1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )对错错对金水四中挑战自我画一画3、已知:如图,⊙O 中, AB为 弦,C 为
AB 的中点,OC交AB 于D ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.·ABOCD金水四中挑战自我 P94:习题3.2 2题祝你成功!金水四中挑战自我画一画4.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.金水四中谢谢大家
金水四中圆的对称性圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?你是用什么方法解决上述问题的?圆是轴对称图形.圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.可利用折叠的方法即可解决上述问题.金水四中圆的相关概念圆上任意两点间的部分叫做圆弧,简称弧.直径将圆分成两部分,每一部分都叫做半圆(如弧ABC).连接圆上任意两点间的线段叫做弦(如弦AB).经过圆心弦叫做直径(如直径AC).⌒金水四中③AM=BM,问题1 垂直于弦的直径有什么特点? AB是⊙O的一条弦.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.作直径CD,使CD⊥AB,垂足为M.下图是轴对称图形吗?如果是,其对称轴是什么?小明发现图中有:由 ① CD是直径② CD⊥AB即金水四中垂直于弦的直径有什么特点?如图,小明的理由是:连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,由 ① CD是直径② CD⊥AB③AM=BM,定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
金水四中垂径定理定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.CD⊥AB,如图∵ CD是直径,∴AM=BM,金水四中②CD⊥AB,问题2 平分弦的直径有什么特点?AB是⊙O的一条弦,且AM=BM.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.过点M作直径CD.下图是轴对称图形吗?如果是,其对称轴是什么?小明发现图中有:由 ① CD是直径③ AM=BM┗平分弦 的直径垂直于弦,并且平 分弦所对的两条弧.垂径定理的推论 (不是直径)金水四中挑战自我垂径定理的推论 如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?老师提示: 这两条弦在圆中位置有两种情况:垂径定理的推论 圆的两条平行弦所夹的弧相等.MN金水四中解这个方程,得R=545.例1。如图,一条公路的转弯处是一段圆弧(即图中弧CD,点0是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE垂直于CD,垂足为F,EF=90m.求这段弯路的半径。解:连接OC,设弯路的半径为Rm,则OF=(R-90)m。 ∵ OE ┴ CD∴CF= CD= x600=300(m).根据勾股定理,得
OC2=CF2 +OF2即 R2=3002+(R-90)2.所以,这段弯路的半径为545m金水四中挑战自我画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.金水四中挑战自我填一填1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )对错错对金水四中挑战自我画一画3、已知:如图,⊙O 中, AB为 弦,C 为
AB 的中点,OC交AB 于D ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.·ABOCD金水四中挑战自我 P94:习题3.2 2题祝你成功!金水四中挑战自我画一画4.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.金水四中谢谢大家
