平均数

课件16张PPT。 第八章 数据的代表平均数（一）学习目标：
1.掌握算术平均数、加权平均数的概念，会求一组数据的平均数和加权平均数。
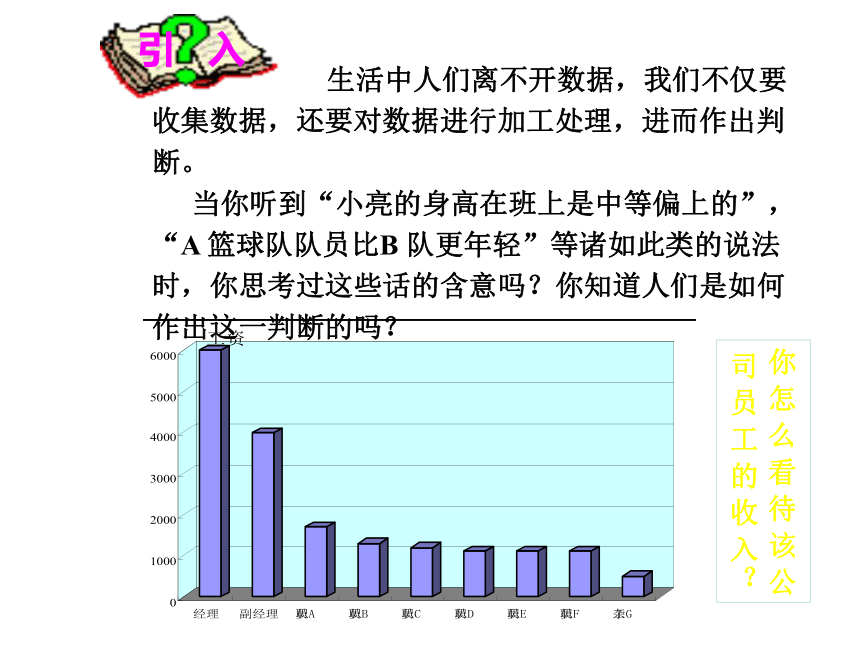
2.体会算术平均数和加权平均数的联系和区别。引 入 你 怎 么 看 待 该 公司 员 工 的 收 入？ 生活中人们离不开数据，我们不仅要收集数据，还要对数据进行加工处理，进而作出判断。
当你听到“小亮的身高在班上是中等偏上的”，“A 篮球队队员比B 队更年轻”等诸如此类的说法时，你思考过这些话的含意吗？你知道人们是如何作出这一判断的吗？ 请欣赏 ：CBA（中国篮球协会）2005—2006赛季“广东宏远队”和
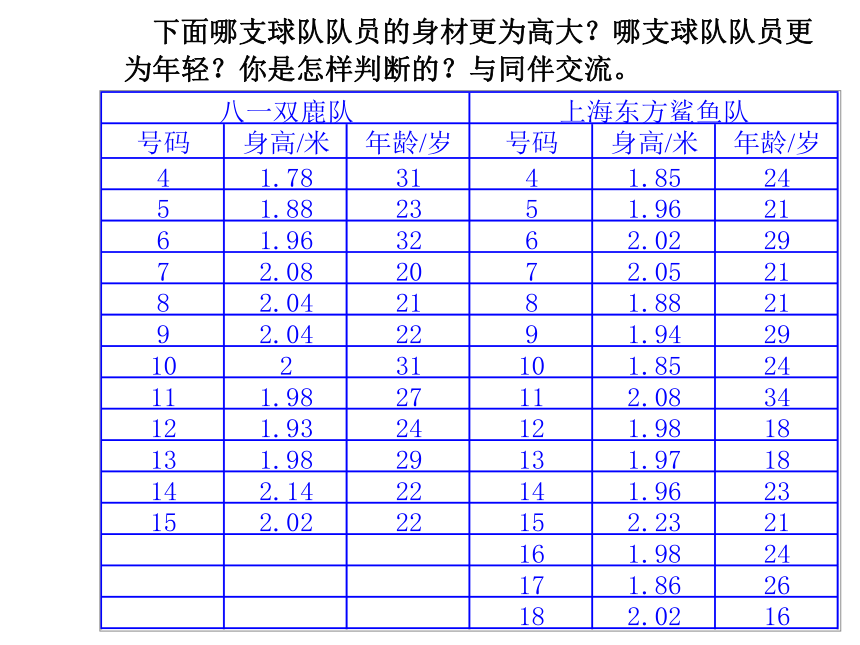
“八一双鹿队”的一场比赛片段 。 思 考 影响比赛的成绩有哪些因素？
如何衡量两个球队队员的身高？
怎样理解“甲队队员的身高比乙队更高”？
要比较两个球队队员的身高，需要收集哪些数据呢？ 下面哪支球队队员的身材更为高大？哪支球队队员更为年轻？你是怎样判断的？与同伴交流。 日常生活中，我们常用平均数 表示一组数据的“平均水平”。
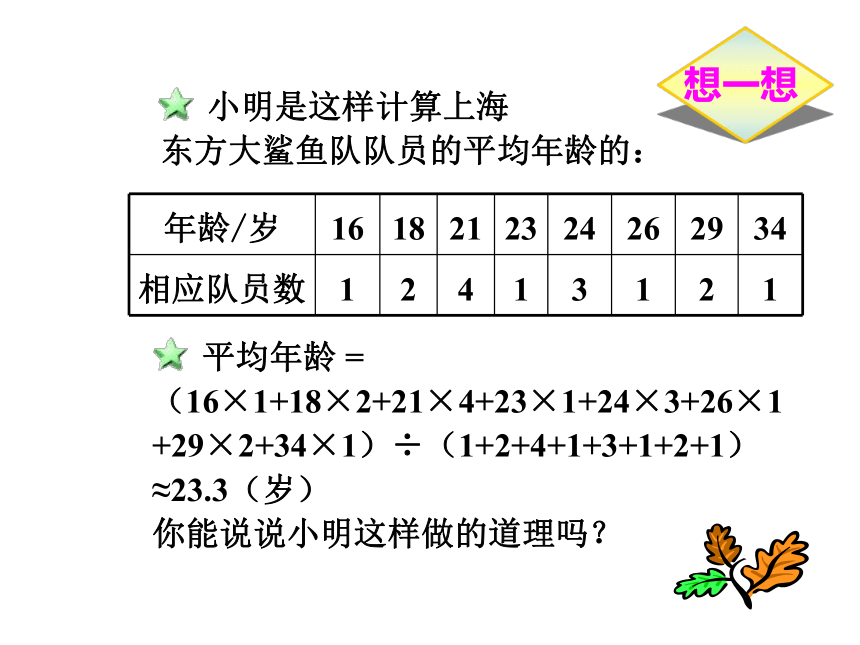
一般地，对于 n 个数 x1，x2，…，xn，我们把 ( x1+x2+…+xn ) /n 叫做这 n 个数的算术平均数，简称平均数。记为 x 。 小明是这样计算上海 东方大鲨鱼队队员的平均年龄的： 平均年龄 =（16×1+18×2+21×4+23×1+24×3+26×1 +29×2+34×1）÷（1+2+4+1+3+1+2+1） ≈23.3（岁） 你能说说小明这样做的道理吗？（1） 如果根据三项测试的平均成绩决定录用人选，那么谁将被录用？ （2）根据实际需要，公司将创新、综合知识和语言三项测试得分按 4∶3∶1 的比例确定各人的测试 成绩，此时谁将被录用？例1 某广告公司欲招聘广告策划人员一名，对A ，B，C 三名候选人进行了三项素质测试，他们的各项测试成绩如下表所示：解: ( 1 ) A 的平均成绩为( 72+50+88) /3 = 70（分）
B 的平均成绩为( 85+74+45 ) /3 = 68（分）
C 的平均成绩为( 67+70+67 ) /3 = 68（分）
因此候选人 A 将被录用。 ( 2 ) 根据题意，3 人的测试成绩如下：
A 的测试成绩为（72×4+50×3+88×1）
/（4+3+1）= 65.75（分）
B 的测试成绩为（85×4+74×3+45×1）
/（4+3+1）= 75. 875（分）
C 的测试成绩为（67×4+70×3+67×1）
/（4+3+1） = 68. 125（分）
因此候选人B 将被录用。
在实际问题中，一组数据里的各个数据的“重要程度” 未必相同。因而，在计算这组数据的平均数时，往往给每个数据一个“权 ”。　 如例1中 4，3，1 分别是创新、综合知识、语言三项测试成绩的权，而称（72×4+50×3+88×1）/（4+3+1） 为A的三项测试成绩的 加权平均数。1. 某班 10 名学生为支援希望工程，
将平时积攒的零花钱捐献给贫困地区的失学儿童。
每人捐款金额如下（单位：元）：
10，12，13. 5，21，40. 8，19. 5，20.8，25，16，30
这10 名同学平均捐款多少元？解：这10名同学平均捐款为
（10+12+13.5+21+40.8+19.5+20.8+25+16+30）
/10 = 20. 86元
答：这10名同学平均捐款20. 86元。
解：小颖这学期的体育成绩是
92×20%+80×30%+84×50% = 84.4（分）
答：小颖这学期的体育成绩是84.4分。2. 某校规定学生的体育成绩由三部 分组成：早锻炼及体育课外活动占成绩 的20%，体育理论测试占30%，体育技能测试占50%。小颖的上述三项成绩依次为 92分、80 分、84 分，则小颖这学期的体育成绩是多少分？ 3. 从一批机器零件毛坯中取出 10 件， 称得它们的质量如下：（单位：千克）
　2001 2007 2002 2006 2005
　2006 2001 2009 2008 2010
( 1 ) 求这批零件质量的平均数。
( 2 ) 你能用新的简便方法计算它们的平均数吗？本节课“我知道了…”，
“我发现了…”，
“我学会了…”，
“我想我以后将…” 作 业1. 课本习题 8. 1 的第1，2 题。
2. 为了反映你们的家乡近几年的变化,请各小组自己命题，并设计方案，利用双休日展开调查,汇总，用平均数的有关知识进行分析，并写出调查报告。 再见！谢谢合作