2.6 用尺规作三角形课件 (1)

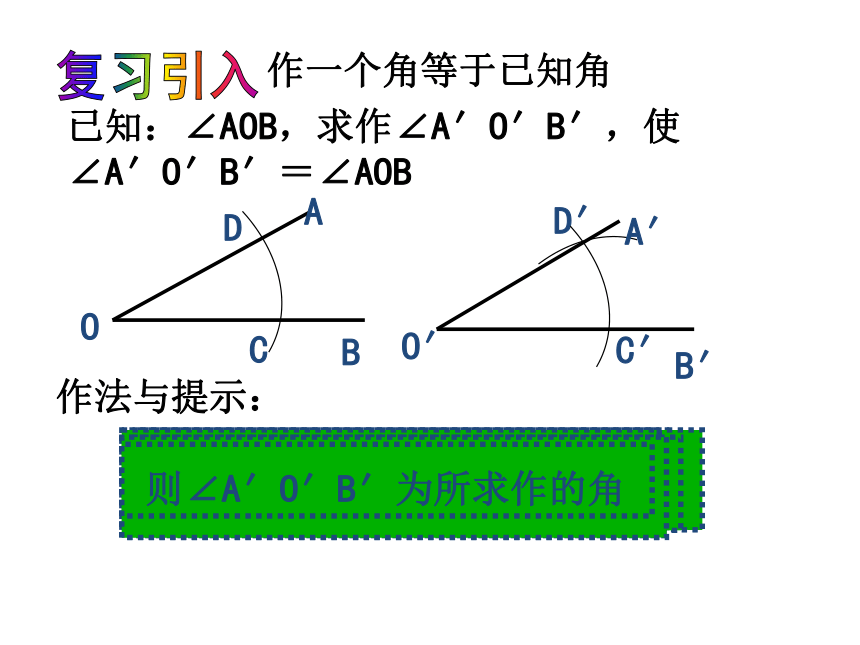
课件30张PPT。2.6用尺规作三角形1、尺规作图的工具是直尺和圆规2、我们已经会用尺规作一条线段等于已知线段、作一个角等于已知角复习引入已知：∠AOB，求作∠A′O′B′，使 ∠A′O′B′＝∠AOBCDO′B′A′D′C′作法与提示：作一个角等于已知角复习引入如何利用尺规作出一个三角形与已知三角
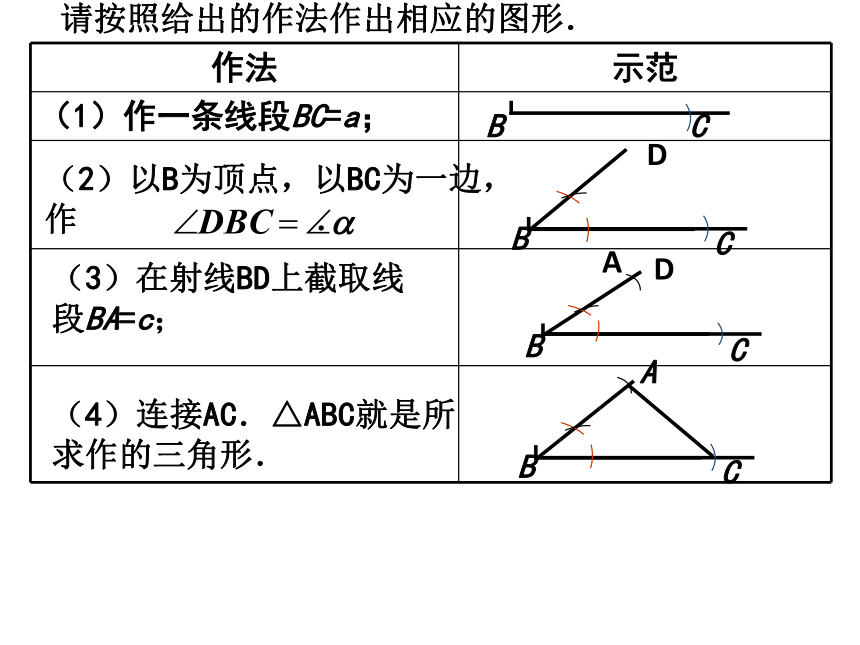
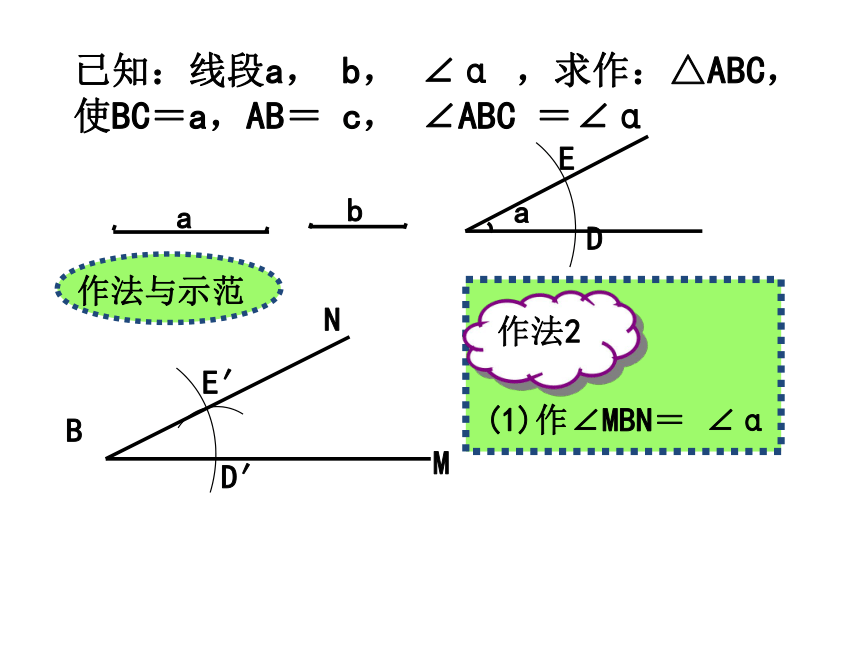
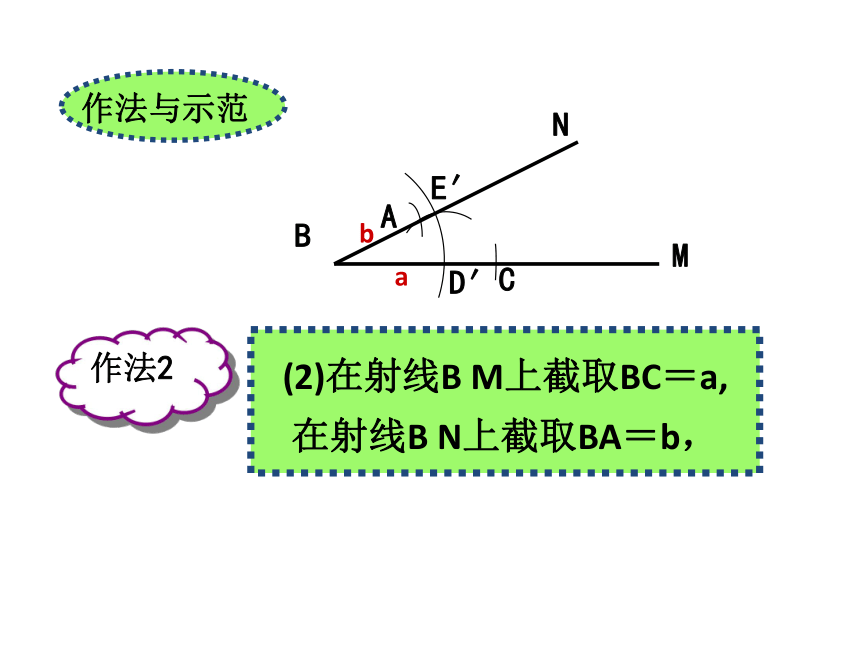
全等？问题1．已知三角形的两边及其夹角，求作这个三角形．已知：线段a, c, .求作：△ABC，使BC=a AB=c, ∠ABC= .做一做（2）以B为顶点，以BC为一边，作 ．BC（3）在射线BD上截取线段BA=c；（4）连接AC．△ABC就是所求作的三角形．ADDA请按照给出的作法作出相应的图形． 将你所作的三角形与同伴作出的三角形进行比较，它们全等吗？为什么？ 两边及它们的夹角对应相等的两个三角形全等(SAS)1. 已知三角形的两边及夹角，求作这个三角形。回顾刚才作三角形的顺序边边夹角夹角边边还有没有其他的作法？已知：线段a， b， ∠α ，求作：△ABC，使BC＝a，AB＝ c， ∠ABC ＝∠αBMDED′E′N (1)作∠MBN＝ ∠α作法2BMD′E′NCA(2)在射线B M上截取BC＝a,
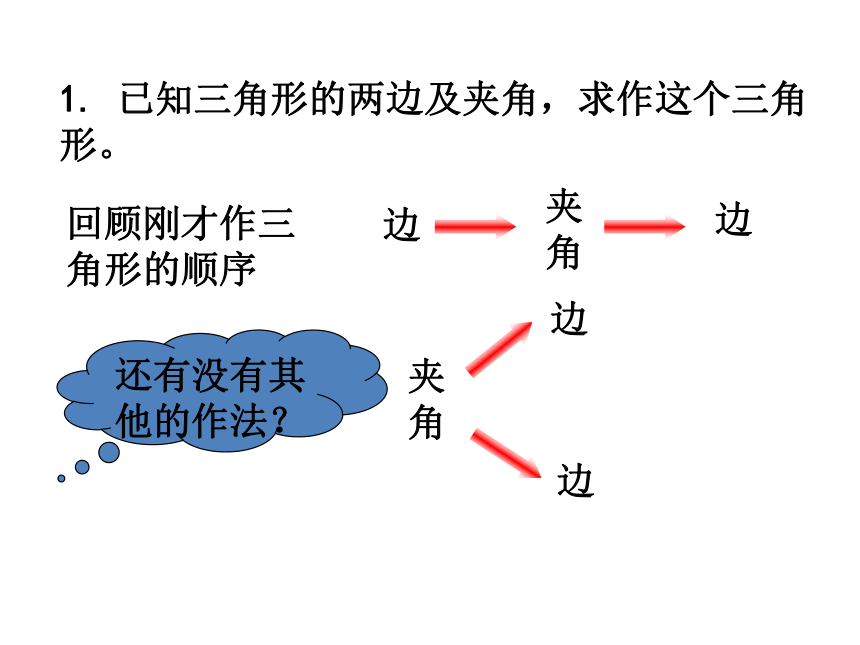
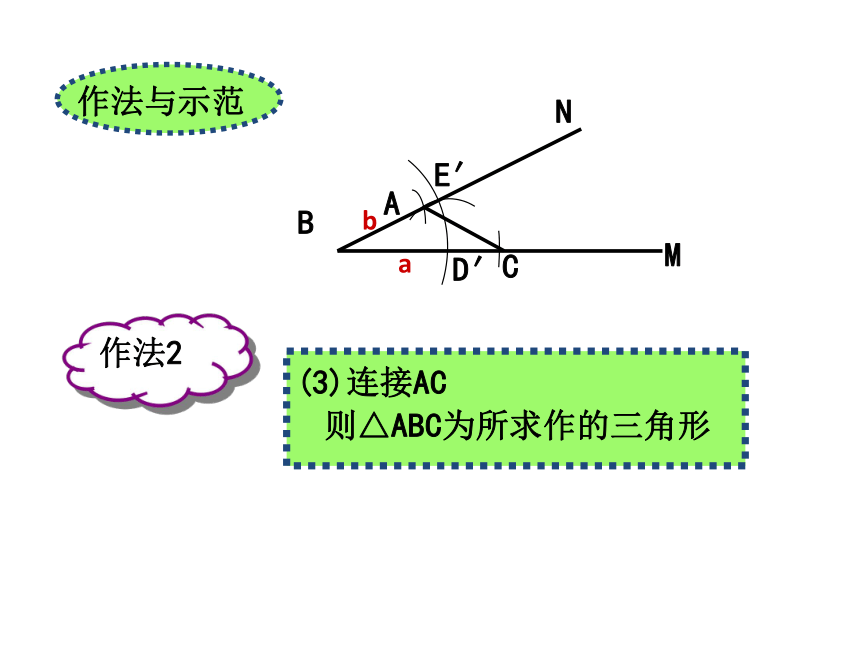
在射线B N上截取BA＝b，作法2abBMD′E′NCA(3)连接AC则△ABC为所求作的三角形作法2ab2．已知三角形的两角及其夹边，求作这个三角形．已知： ， ，线段c．求作：△ABC，使∠A= ，∠B= ，AB=c.做一做已知： ， ，线段c．求作：△ABC，使∠A= ，∠B= ，AB=c.做一做c请按照给出的作法作出相应的图形．（1）作 ．AF（2）在射线AF上截取线段AB=c；CDB（3）以B为顶点，以BA为一边，作 ，BE交AD于点C．则△ABC就是所求作的三角形． 将你所作的三角形与同伴作出的三角形进行比较，它们全等吗？为什么？ 两角及它们的夹边对应相等的两个三角形全等(ASA)2. 已知三角形的两角及其夹边，求作这个三角形。回顾刚才作三角形的顺序角角夹边夹边角角还有没有其他的作法？已知:∠α, ∠β, 线段c，求作：△ＡＢＣ,使∠A＝∠α,∠Ｂ＝∠β，ＡＢ＝ cBNKC经过前面的实践，我们如何来分析作图题呢？1. 假设所求作的图形已经作出，并在草稿纸上作出草图；2. 在草图上标出已给的边、角的对应位置；3. 从草图中首先找出基本图形，由此确定作图的起始步骤；4. 在3的基础上逐步向所求图形扩展。(1)作∠······=∠ ······ ；(2)在······上截取，使······ = ······ ；(3)以···为顶点，以······为一边，作∠ ······ =∠ ······ ；(4)作一条线段······ = ······ ；(5)连接······ ，或连接······交······于点······ ；(6)分别以··· ， ···为圆心，以··· ， ···为半径画弧，两弧交于···点；······ ······ ······ ······ 你知道的常用作图语言有哪些呢？
3．已知三角形的三边，求作这个三角形．已知：线段a，b，c．求作：△ABC，使AB=c，AC=b，BC=a．（1）请写出作法并作出相应的图形．（2）将你所作的三角形与同伴作出的三角形进行比较，它们全等吗？为什么？做一做3.已知三角形的三条边，求作这个三角形。已知：线段 a，b，c。求作：△ABC，使AB=c，AC=b，BC=a。（1）作一条线段BC=a；（2）分别以B，C为圆心，以c，b为半径画弧，两弧交于A点；（3）连接AB,AC。△ABC就是所求作的三角形。abc作法：1. 你能用尺规作一个直角三角形，使其两条直角边分别等于已知线段a，b吗？并写出作法。ab分析：先在草纸上画出一个假设的“已作出的三角形”，会发现是“已知两边及夹角求作三角形”，所以按照此方法作图。我们一起做2. 已知∠α和∠β，线段a，用尺规作一个三角形，使其一个内角等于∠α，另一个内角等于∠β ，且∠α的对边等于a。αa提示：先作出一个角等于∠α+∠β，通过反向延长角的一边得到它的补角，即三角形中的第三个内角∠γ 。由此转换成已知∠β 和∠γ及其这两角的夹边a，求作这个三角形。β我们一起做αβγ βγ aαBCAEFG作法：1. 作∠α+∠β的补角∠γ 2. 作∠GBE=∠β3. 在射线BE上截取BC=a4. 以C为顶点，CB为一边作∠FCB=∠γ 5. 射线BG与射线CF相交于点A△ABC就是所求作的三角形。你所作的三角形与同伴所作的三角形比较，它们全等吗？为什么？已知线段a，b和∠α，求作△ABC，使其有一个内角等于∠α，且∠α的对边等于a，另有一边等于b。abα分析：先在草纸上画出一个假设的“已作出的三角形”；然后在草图上标出已给的边、角的对应位置；再找出边与角，确定作图的顺序。拓展提高αbaaABMNCC'1. 作∠MAN=∠α2. 在射线AM上截取AB=b3. 以B为圆心，以a为半径画弧，交AN于点C， C'4. 连接BC，BC'△ABC和△ABC'就是所求作的三角形。同样是已知两边及一角，为什么会出现两个三角形呢？你从中可以感悟到什么？作法：感悟：已知三角形的两边及一角并不都能只确定一个三角形。当已知两边及夹角时可以确定一个三角形，因此可以用来判定两个三角形全等；而当已知两边及一边的对角时，会画出两个不同的三角形，因此不能用来作为判别两个三角形全等的条件。acα两边及夹角两边及一边的对角 1．利用尺规不能唯一作出的三角形是（ ）
A．已知三边
B．已知两边及夹角
C．已知两角及夹边
D．已知两边及其中一边的对角2．利用尺规不可作的直角三角形是（ ）
A．已知斜边及一条直角边
B．已知两条直角边
C．已知两锐角
D．已知一锐角及一直角边DC练习3．以下列线段为边能作三角形的是（ ）
A．2厘米、3厘米、5厘米
B．4厘米、4厘米、9厘米
C．1厘米、2厘米、 3厘米
D．2厘米、3厘米、4厘米D练习小结1.学会了用尺规作三角形
2.进一步验证了全等三角形的条件．