5.1二次根式 课件 (3)

课件30张PPT。二次根式第5章二次根式5.1 因为速度一定大于0，
所以第一宇宙速度
由于在实数范围内，负实数没有平方根，因此只有当
被开方数是非负实数时，二次根式才在实数范围内有意义． 我们把形如 的式子叫作二次根式，根号下的数
叫作被开方数.
我们已经知道：每一个正实数a有且只有两个平方根，
一个记作 ，称为a的算术平方根；另一个是举
例例1 当x是怎样的实数时，二次根式
在实数范围内有意义？ 解 由 x-1≥0，解得 x ≥ 1.因此，当x≥1时， 在实数范围内有意义. 在本套教材中，我们都是在实数范围内讨论二次根式有没有意义，今后不再每次写出“在实数范围内”这几个字. 对于非负实数a，由于 是a的一个平方根，
因此举
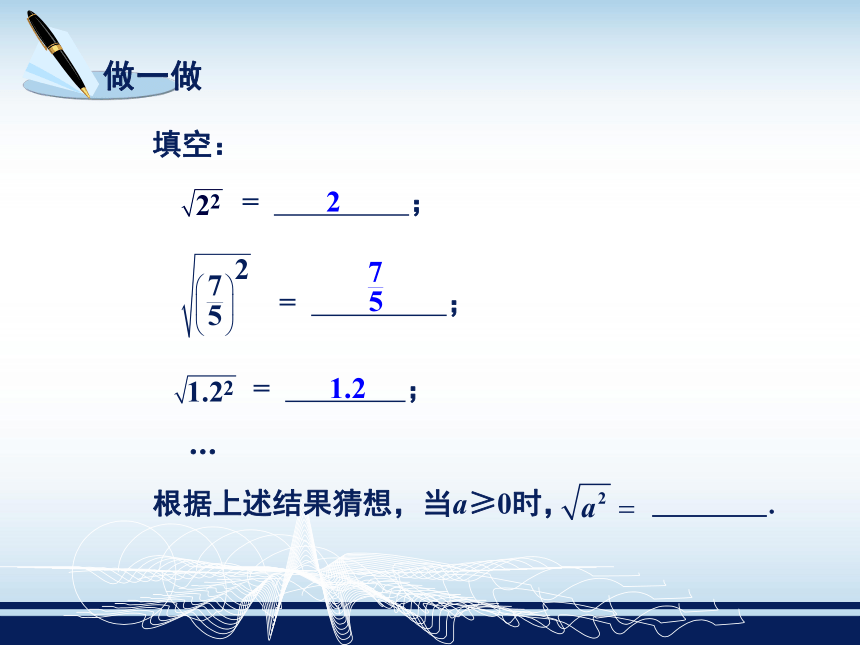
例例2 计算： 解填空：… = 　 　 ； = ； = 　 ；21.2举
例例3 计算： 解一般地，当a<0时， 因此，我们可以得到： 当a<0时， 是否仍然成立？为什么？
1. 当x是怎样的实数时，下列二次根式有意义？ 答案：x≤1答案：x≥ 2. 计算： 答案：3答案： 3. 计算： 答案：7答案：3答案：0.01 计算下列各式，观察计算结果，你发现了什么？
一般地，当a≥0，b≥0时，由于由此得出：例4 化简下列二次根式．举
例解 化简二次根式
时，最后结果要求被开方数中不含开得尽方的因数. 今后在化简二次根式时，可以直接把根号下的每一个平方因子去掉平方号以后移到根号外（注意：从根号下直接移到根号外的数必须是非负数）.举
例例5 化简下列二次根式．解 化简二次根式时，
最后结果要求被开方
数不含分母.解 从例4、 例5可以看出，这些式子的最后结果，
具有以下特点：
（1） 被开方数中不含开得尽方的因数（或因式）；
（2） 被开方数不含分母.
在二次根式的运算中，一般要把最后结果化为
最简二次根式. 我们把满足上述两个条件的二次根式，叫作最简二次根式.解解 化简下列二次根式．解结 束