5.1二次根式课件 (11张ppt)

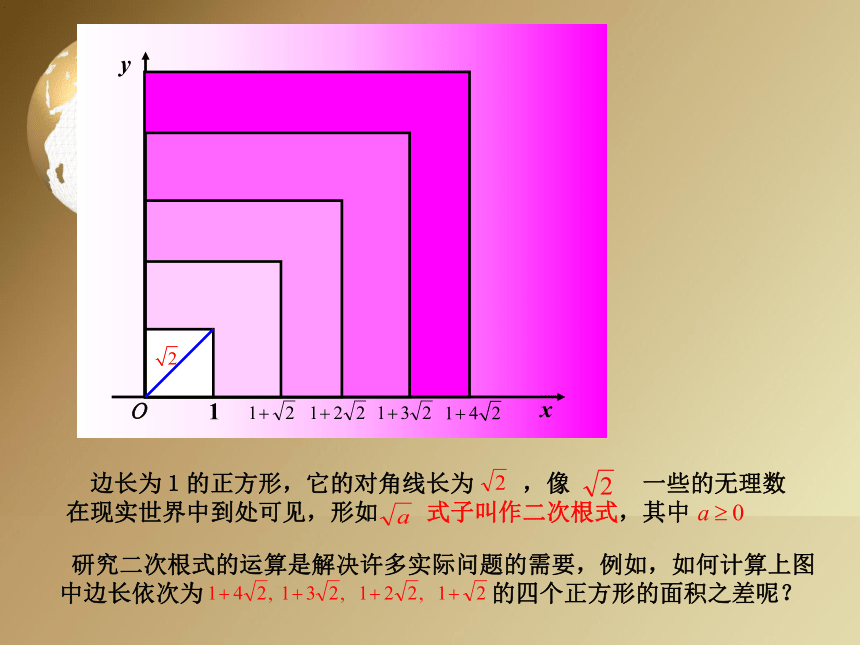
课件11张PPT。 二次根式 边长为１的正方形，它的对角线长为　　，像　　　一些的无理数在现实世界中到处可见，形如　　式子叫作二次根式，其中　　　 研究二次根式的运算是解决许多实际问题的需要，例如，如何计算上图中边长依次为　　　　　　　　　　　　的四个正方形的面积之差呢？
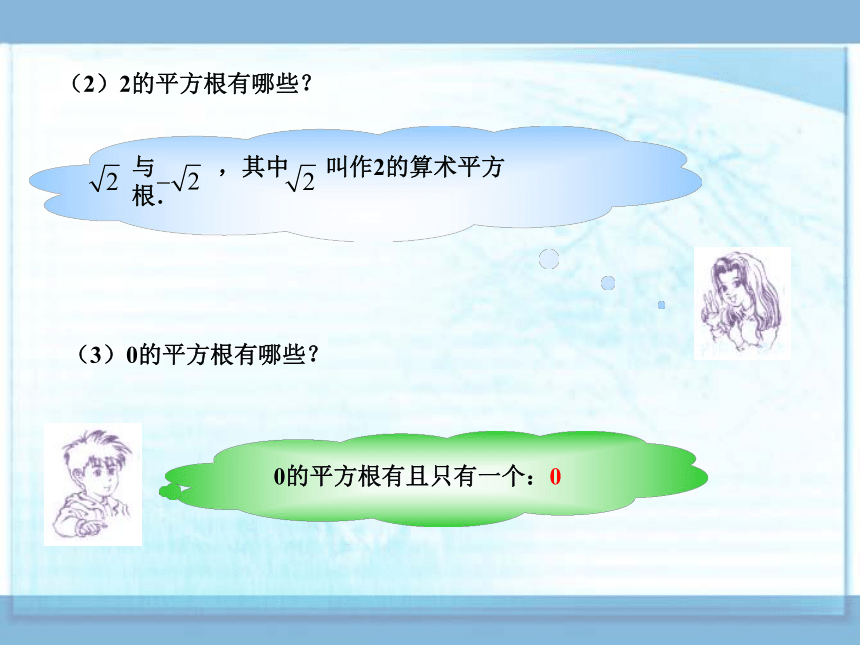
4.1.1 二次根式（1）4的平方根是什么意思？4的平方根有哪些？如果一个数的平方等于4，那么把这个数叫作4的一个平方根．
由于 ，而其他数的平方不会等于4，因此4的平方根有且只有两个：2与－2（2）2的平方根有哪些？与 ，其中 叫作2的算术平方根．（3）0的平方根有哪些？ 0的平方根有且只有一个：0由于任何实数的平方都等于正数或 0，且此负实数没有平方根．（4）负实数有没有平方根？ 每一个正实数 a 有且只有两个平方根，其中一个平方根是正实数，记作 称它为 a 的算术平方根；另一个平方根是0 的平方根记作 把形如 的式子叫作二次根式，符号“ ”叫作二次根号，简称为根号，根号下的数叫作被开方数，由于在实数范围内，负实数没有平方根，因此只有当被开方数是非负实数时，二次根式才在实数范围内有意义．解 由 ，解得 x≥1当x是怎样的实数时，二次根式 在实数范围内有意义？因此，当x≥1时， 在实数范围内有意义．在本套教材中，我们都是在实数范围内讨论二次根式有没有意义，今后不再每次写出“在实数范围内”这几个字．对于非负实数a，由于 是a的一个平方根，因此 计算：解在下面横线上填写适当的数：
由于22＝4，因此 ，即
由于32＝9，因此 ，即
由于42＝16，因此 ，即
由于52＝25，因此 ，即
由于1.52＝2.25，因此 ，即
……根据上述结果，当a≥0时，你猜测
由于a的平方等于a2，因此a是a2的一个平方根，又由于已知a≥0，因此 ，由此得出：23451.5a这个猜测正确吗？所以x≤1时， 有意义1.当x是怎样的实数时，下列二次根式有意义？解(1) 欲使 有意义须x－2≥0所以x≥2时， 有意义(2) 欲使 有意义须x+5≥0所以x≥－5时， 有意义(3) 欲使 有意义须1－ x ≥ 0(4) 欲使 有意义须3－x≥0所以x≤3时， 有意义2.计算：解3.计算：＝8＝0.01解