1.3 直角三角形全等的判定 课件 (2)(25PPT)
文档属性
| 名称 | 1.3 直角三角形全等的判定 课件 (2)(25PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 936.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-08 21:08:07 | ||
图片预览








文档简介
课件25张PPT。湘教版·八年级下册1.3 直角三角形全等判定回
顾
与
思
考1、判定两个三角形全等方法, , , , 。SSSASAAASSAS2、如图,AB⊥BE于B,DE ⊥BE于E,(1)若 ∠A= ∠D,AB=DE,则 △ABC与 △DEF ______, (填“全等”或“不全等”)根据___________. 全等ASA或AAS(2)若AB=DE,BC=EF,则 △ABC与△DEF (填“全等”或“不全等”)根据__________全等SAS或SSS(3)若AB=DE,BC=EF,AC=DF则△ABC与△DEF (填“全等”或“不全等”),
根据___________SSS或SAS或_全等∟∟ 如图,在Rt△ABC和Rt△A′B′C′中, 已知∠C=∠C′=90° AC=A’C’ , AB=A’B’。 那么Rt△ABC和Rt△A′B′C′全等吗?探究思考:通过上述探究,你能发现判定直角三角形全等需要一些什么条件?1有斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”定理或“HL”前提条件1条件2直角三角形全等的条件斜边、直角边公理 (HL):符号语言证明步骤 1.说明所证的两个三角形是直角三角形,
2.再在这两个直角三角形中求出条件1与条件2,
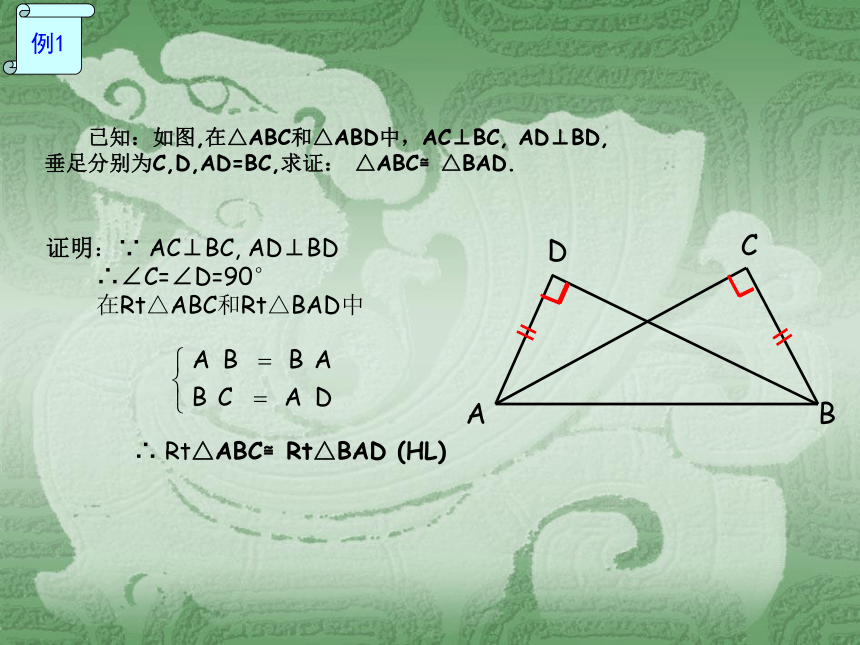
3.写出结论。 已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证: △ABC≌△BAD.BDC证明:∵ AC⊥BC, AD⊥BD
∴∠C=∠D=90°
在Rt△ABC和Rt△BAD中
∴ Rt△ABC≌Rt△BAD (HL)A例1已知线段a、c,利用尺规作一个Rt△ABC,使∠C=900 ,CB=a,AB=c.动手做一做例2作法:⑴ 作∠MCN=90°;⑵ 在射线CM上截取线段CB=a;⑶ 以B为圆心,C为半径画弧,交射线CN于点A;⑷ 连接AB.△ABC就是所求作的三角形.∟∟∟∟思考:通过作图你发现了什么?一、判断:满足下列条件的两个三角形是否全等?为什么?1.一个锐角及这个锐角的对边对应相等的两个直角三角形.全等(AAS)2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.全等( ASA)一、判断:满足下列条件的两个三角形是否全等?为什么?3.两直角边对应相等的两个直角三角形.全等( SAS)一、判断:满足下列条件的两个三角形是否全等?为什么?4.有两边对应相等的两个直角三角形.不一定全等情况1:全等
情况2:全等(SAS)( HL)一、判断:满足下列条件的两个三角形是否全等?为什么?情况3:不全等
一、判断:满足下列条件的两个三角形是否全等?为什么?5.一个锐角及一边对应相等的两个直角三角形.不一定全等1.如图,在 △ABC 中,BD=CD, DE⊥AB, DF⊥AC,E、F为垂足,DE=DF,求证: (1)△BED≌△CFD.二。解答或证明 2.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。 ∴Rt△ADB ≌Rt△ADC (HL)
∴ BD=CD3、已知,如图AB⊥BD,CD⊥BD,AB=DC
求证:AD//BC.证明:∵ AB⊥BD,CD⊥BD ∴∠ABD=∠CDB=900
在RtABD和RtCDB中,
∵AB=CD,(已知)
∠ABD=∠CDB=900
BD=DB(公共边)
∴RtABC≌RtBAD(S.A.S.)4、已知:如图, △ABC中,AB=AC,AD是高
求证:BD=CD ;∠BAD=∠CADABCD (选作题)已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF, 求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。小结(选作题) 已知:如图,在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF, 求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。小结 (选作题) 已知:如图,在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF, 求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。变式3:请你把例题中的∠BAC=∠EDF改为另一个适当条件,使△ABC与△DEF仍能全等。试证明。小结“SAS”“ ASA ”“ AAS ”“ SSS ”“ SAS ”“ ASA ”“ AAS ”“ HL ”灵活运用各种方法证明直角三角形全等应用“ SSS ” (1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ ( HL )
(5) ∠A=∠D, BC=EF ( )
(6) ________,AC=DF ( AAS )
BCAEFD把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.AC=DFBC=EFHLAB=DEAAS∠B=∠E课堂作业:随堂练习
课后作业:练习册同步内容。
再见
顾
与
思
考1、判定两个三角形全等方法, , , , 。SSSASAAASSAS2、如图,AB⊥BE于B,DE ⊥BE于E,(1)若 ∠A= ∠D,AB=DE,则 △ABC与 △DEF ______, (填“全等”或“不全等”)根据___________. 全等ASA或AAS(2)若AB=DE,BC=EF,则 △ABC与△DEF (填“全等”或“不全等”)根据__________全等SAS或SSS(3)若AB=DE,BC=EF,AC=DF则△ABC与△DEF (填“全等”或“不全等”),
根据___________SSS或SAS或_全等∟∟ 如图,在Rt△ABC和Rt△A′B′C′中, 已知∠C=∠C′=90° AC=A’C’ , AB=A’B’。 那么Rt△ABC和Rt△A′B′C′全等吗?探究思考:通过上述探究,你能发现判定直角三角形全等需要一些什么条件?1有斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”定理或“HL”前提条件1条件2直角三角形全等的条件斜边、直角边公理 (HL):符号语言证明步骤 1.说明所证的两个三角形是直角三角形,
2.再在这两个直角三角形中求出条件1与条件2,
3.写出结论。 已知:如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证: △ABC≌△BAD.BDC证明:∵ AC⊥BC, AD⊥BD
∴∠C=∠D=90°
在Rt△ABC和Rt△BAD中
∴ Rt△ABC≌Rt△BAD (HL)A例1已知线段a、c,利用尺规作一个Rt△ABC,使∠C=900 ,CB=a,AB=c.动手做一做例2作法:⑴ 作∠MCN=90°;⑵ 在射线CM上截取线段CB=a;⑶ 以B为圆心,C为半径画弧,交射线CN于点A;⑷ 连接AB.△ABC就是所求作的三角形.∟∟∟∟思考:通过作图你发现了什么?一、判断:满足下列条件的两个三角形是否全等?为什么?1.一个锐角及这个锐角的对边对应相等的两个直角三角形.全等(AAS)2.一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.全等( ASA)一、判断:满足下列条件的两个三角形是否全等?为什么?3.两直角边对应相等的两个直角三角形.全等( SAS)一、判断:满足下列条件的两个三角形是否全等?为什么?4.有两边对应相等的两个直角三角形.不一定全等情况1:全等
情况2:全等(SAS)( HL)一、判断:满足下列条件的两个三角形是否全等?为什么?情况3:不全等
一、判断:满足下列条件的两个三角形是否全等?为什么?5.一个锐角及一边对应相等的两个直角三角形.不一定全等1.如图,在 △ABC 中,BD=CD, DE⊥AB, DF⊥AC,E、F为垂足,DE=DF,求证: (1)△BED≌△CFD.二。解答或证明 2.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。 ∴Rt△ADB ≌Rt△ADC (HL)
∴ BD=CD3、已知,如图AB⊥BD,CD⊥BD,AB=DC
求证:AD//BC.证明:∵ AB⊥BD,CD⊥BD ∴∠ABD=∠CDB=900
在RtABD和RtCDB中,
∵AB=CD,(已知)
∠ABD=∠CDB=900
BD=DB(公共边)
∴RtABC≌RtBAD(S.A.S.)4、已知:如图, △ABC中,AB=AC,AD是高
求证:BD=CD ;∠BAD=∠CADABCD (选作题)已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF, 求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。小结(选作题) 已知:如图,在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF, 求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。小结 (选作题) 已知:如图,在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF, 求证:△ABC≌△DEFABCPDEFQ变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。变式3:请你把例题中的∠BAC=∠EDF改为另一个适当条件,使△ABC与△DEF仍能全等。试证明。小结“SAS”“ ASA ”“ AAS ”“ SSS ”“ SAS ”“ ASA ”“ AAS ”“ HL ”灵活运用各种方法证明直角三角形全等应用“ SSS ” (1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ ( HL )
(5) ∠A=∠D, BC=EF ( )
(6) ________,AC=DF ( AAS )
BCAEFD把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.AC=DFBC=EFHLAB=DEAAS∠B=∠E课堂作业:随堂练习
课后作业:练习册同步内容。
再见
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
