1.3 直角三角形全等的判定 课件 (5)(15PPT)
文档属性
| 名称 | 1.3 直角三角形全等的判定 课件 (5)(15PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 450.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-08 00:00:00 | ||
图片预览

文档简介
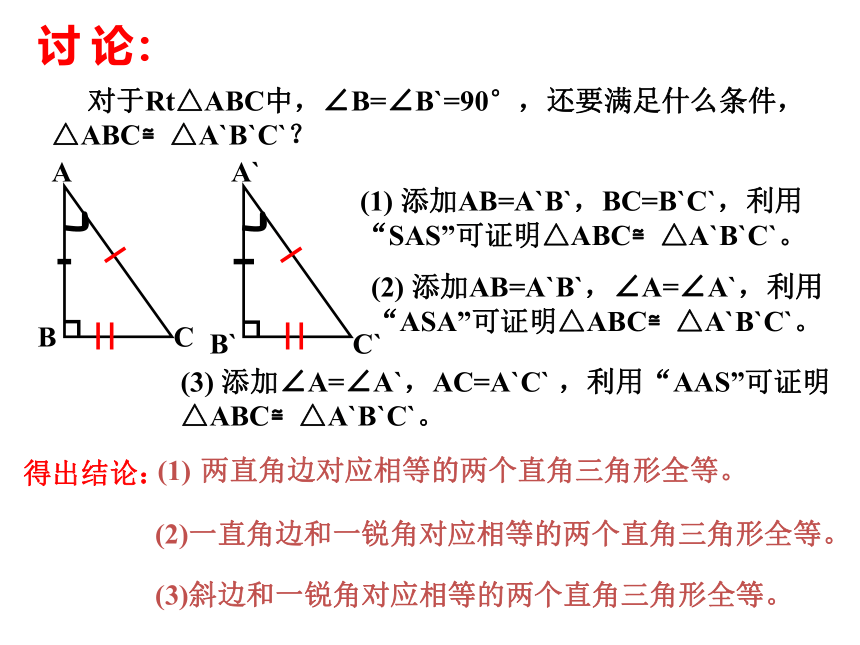
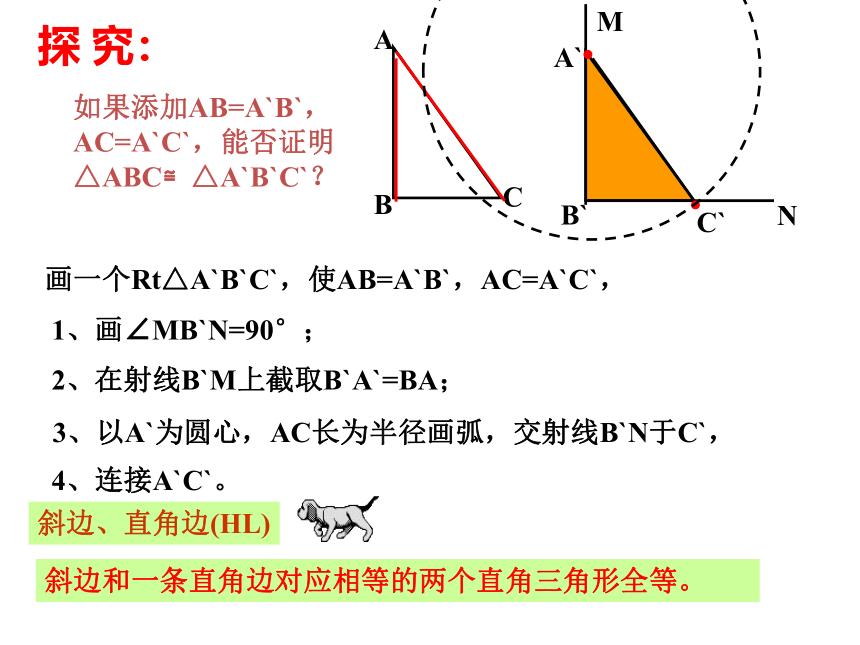
课件15张PPT。 三边对应相等的两个三角形全等。(简写成边 边 边“边边边”或“SSS”)边 角 边“边角边”或“SAS”) 两边和它们夹角对应相等的两个三角形全等。(简写成角 边 角“角边角”或“ASA”) 两角和它们的夹边对应相等的两个三角形全等。(简写成角 角 边 两个角和其中一个角的对边对应相等的两个三角形全等.(简写成“角角边”或“AAS”)讨 论: 对于Rt△ABC中,∠B=∠B`=90°,还要满足什么条件,△ABC≌△A`B`C`?(1) 添加AB=A`B`,BC=B`C`,利用“SAS”可证明△ABC≌△A`B`C`。(2) 添加AB=A`B`,∠A=∠A`,利用“ASA”可证明△ABC≌△A`B`C`。(3) 添加∠A=∠A`,AC=A`C` ,利用“AAS”可证明△ABC≌△A`B`C`。得出结论:两直角边对应相等的两个直角三角形全等。(2)一直角边和一锐角对应相等的两个直角三角形全等。(3)斜边和一锐角对应相等的两个直角三角形全等。┓┓如果添加AB=A`B`,AC=A`C`,能否证明 △ABC≌△A`B`C`?A`B`C`探 究:MN●●画一个Rt△A`B`C`,使AB=A`B`,AC=A`C`,1、画∠MB`N=90°;2、在射线B`M上截取B`A`=BA;3、以A`为圆心,AC长为半径画弧,交射线B`N于C`,4、连接A`C`。斜边、直角边(HL)斜边和一条直角边对应相等的两个直角三角形全等。判定公理: 有斜边和一条直角边对应相等的
两个直角三角形全等.条件1条件2前提斜边和一条直角边对应相等的两个直角三角形全等。斜边、直角边(HL)在Rt△ABC和Rt△A`B`C`中∴ Rt△ABC≌Rt△A`B`C(HL)数学表达式: 如图, ∠ACB =∠ADB=90,要证明△ABC≌ △BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由。
(1) ( )
(2) ( )
(3) ( )
(4) ( )
练一练AD=BC∠ DAB= ∠ CBABD=AC∠ DBA= ∠ CABHL HLAASAAS例1、如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.证明: ∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角。在Rt△ABC和Rt△BAD中,∴Rt△ABC≌ Rt △BAD∴BC=AD新知应用:(HL)(全等三角形对应边相等)例2、如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.课本103页练习证明:∵ AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。又∵CE=BF ∴CE-EF=BF-EF
即CF=BE。 在Rt△ABE和Rt△DCF中∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF1.如图,在 △ABC 中,BD=CD, DE⊥AB, DF⊥AC,E、F为垂足,DE=DF,求证: △BED≌△CFD.练 习2、已知:如图, △ABC中,AB=AC,AD是高
求证:BD=CD ;∠BAD=∠CADABCD等腰三角形三线合一“SAS”“ ASA ”“ AAS ”“ SSS ”“ SAS ”“ ASA ”“ AAS ”“ HL ”灵活运用各种方法证明直角三角形全等“ SSS ”
两个直角三角形全等.条件1条件2前提斜边和一条直角边对应相等的两个直角三角形全等。斜边、直角边(HL)在Rt△ABC和Rt△A`B`C`中∴ Rt△ABC≌Rt△A`B`C(HL)数学表达式: 如图, ∠ACB =∠ADB=90,要证明△ABC≌ △BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由。
(1) ( )
(2) ( )
(3) ( )
(4) ( )
练一练AD=BC∠ DAB= ∠ CBABD=AC∠ DBA= ∠ CABHL HLAASAAS例1、如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.证明: ∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角。在Rt△ABC和Rt△BAD中,∴Rt△ABC≌ Rt △BAD∴BC=AD新知应用:(HL)(全等三角形对应边相等)例2、如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.课本103页练习证明:∵ AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。又∵CE=BF ∴CE-EF=BF-EF
即CF=BE。 在Rt△ABE和Rt△DCF中∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF1.如图,在 △ABC 中,BD=CD, DE⊥AB, DF⊥AC,E、F为垂足,DE=DF,求证: △BED≌△CFD.练 习2、已知:如图, △ABC中,AB=AC,AD是高
求证:BD=CD ;∠BAD=∠CADABCD等腰三角形三线合一“SAS”“ ASA ”“ AAS ”“ SSS ”“ SAS ”“ ASA ”“ AAS ”“ HL ”灵活运用各种方法证明直角三角形全等“ SSS ”
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
