1.4 角平分线的性质 课件 (4)(23PPT)
文档属性
| 名称 | 1.4 角平分线的性质 课件 (4)(23PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 322.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-08 00:00:00 | ||
图片预览





文档简介
课件23张PPT。
《角平分线的性质》复习提问1、角平分线的概念 2、点到直线距离的意义。角平分线是以一个角的顶点为端点的一条射线,它把这个角分成两个相等的角.
下列两图中,能表示角的平分线上的一点P到角的边上的距离的是( )
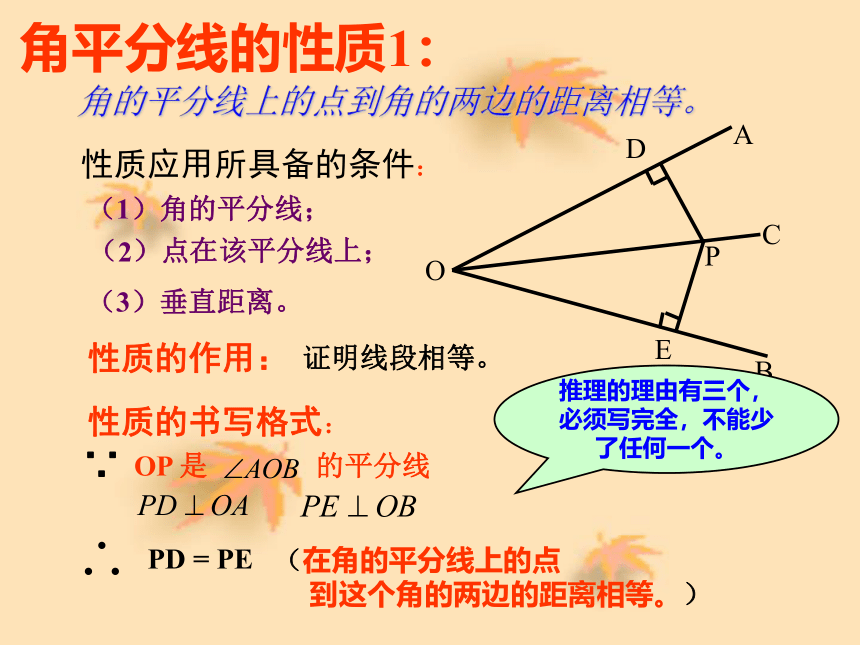
PM 将∠AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论? 可以看一看,第一条折痕是∠AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到∠AOB两边的距离,这两个距离相等.折一折探究1:已知:如图,在∠AOB的平分线 OC上任取一点P,PD⊥OA,PE⊥OB,垂足分别是D,E。试问:PD=PE吗?证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90°(垂直的定义)在△PDO和△PEO中∴ PD=PE(全等三角形的对应边相等)∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP∴ △ PDO≌ △ PEO(AAS)问题探究ABODEPC角平分线的性质1: 角的平分线上的点到角的两边的距离相等。性质应用所具备的条件:性质的作用: 证明线段相等。性质的书写格式:OP 是 的平分线PD = PE(在角的平分线上的点
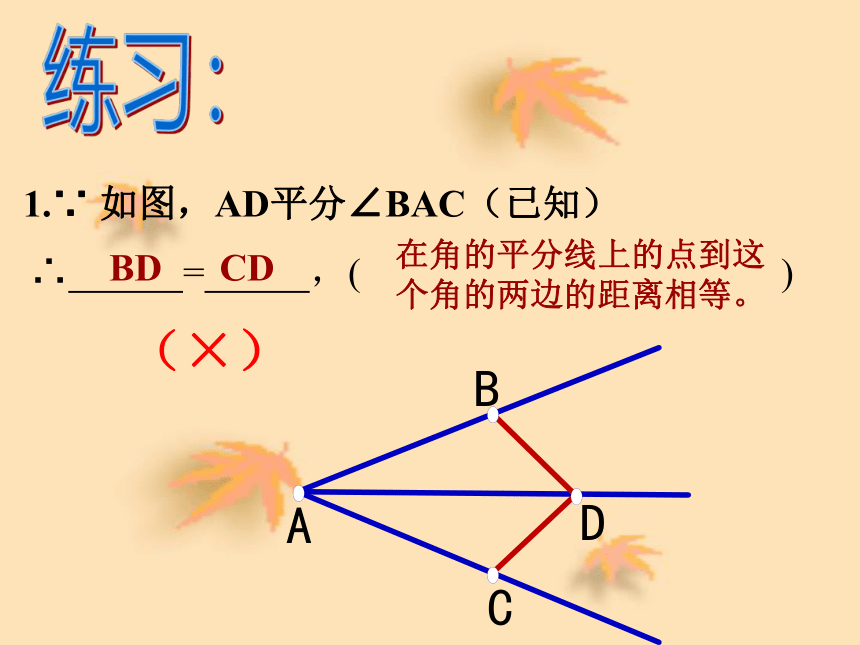
到这个角的两边的距离相等。)∵推理的理由有三个,必须写完全,不能少了任何一个。1.∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
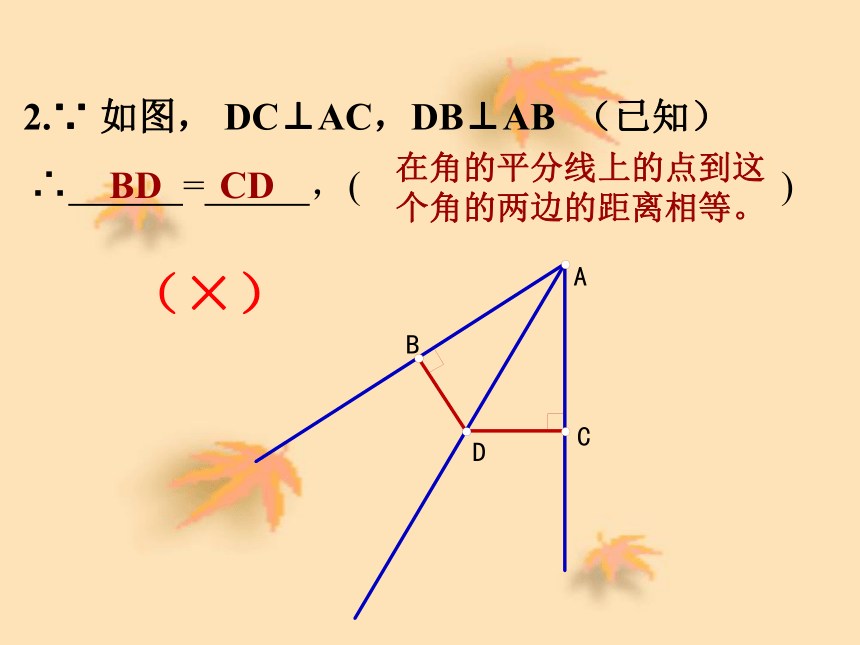
BD CD(×)练习:2.∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
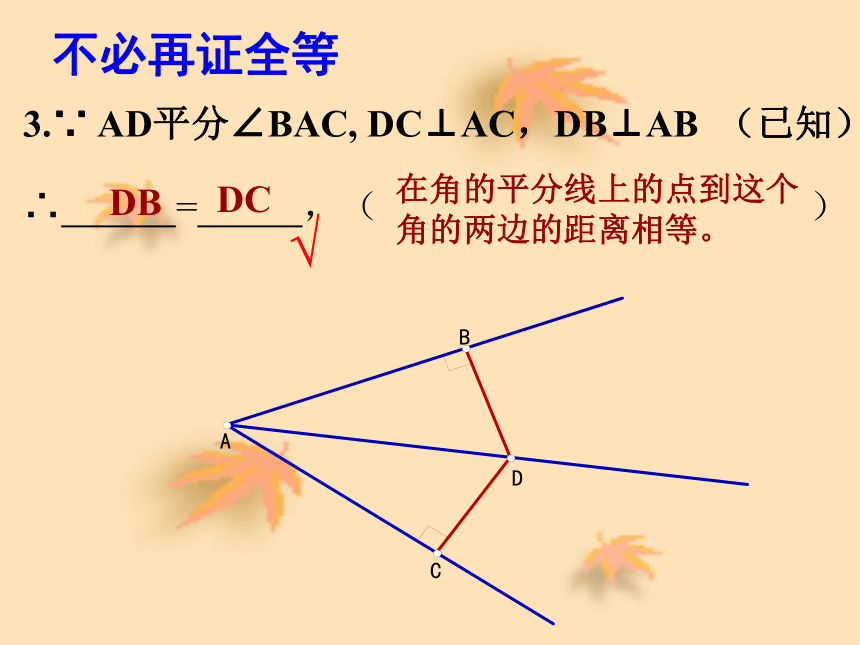
BD CD(×)3.∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等在Rt△PDO和Rt△PEO中,
∵ OP = OP,PD = PE,
∴ Rt△PDO≌Rt△PEO.∵ PD⊥OA, PE⊥OB,
∴ ∠PDO =∠PEO = 90°.如图1-27,过点O,P作射线OC.∴ ∠AOC =∠BOC.∴ OC是∠AOB的平分线,即点P在∠AOB的平分线OC上.图1-27角的内部到角的两边距离相等的点在角的平分线上.
由此得到角平分线的性质定理的逆定理:性质 2的应用书写格式:OP 是 的平分线PD= PE (角的内部到角的两边距离相等的点在角的平分线上.)
∵又 BA⊥AD, BC⊥CD,∴ 点B在∠ADC的平分线上.图1-28(1)求证:点B在∠ADC的平分线上;图1-28证明: 在Rt△BAD和Rt△BCD中,
∵ BA = BC, BD = BD,∴ Rt△BAD≌Rt△BCD.∴ ∠ABD =∠CBD.∴ BD是∠ABC的平分线.(2)求证:BD是∠ABC的平分线.
解 作∠AOB的角平分线,交MN于一点,则这点即为所
求作的点P.(提示:用尺规作图)如图,在直线MN上求作一点P ,使点P到∠AOB两边
的距离相等.P2. 如图,在△ABC 中,AD 平分∠BAC, DE⊥AB
于点E,DF⊥AC 于点F,BD=CD.
求证:AB=AC.回头看一看,我想说......能说出你这节课的收获和体验,
让大家与你分享吗?学而不思则罔性质 1 角的平分线上的点到角的两边距离相等。性质 2 角的内部到角的两边距离相等的点 在角的平分线上。∵PD = PE用途:证线段相等用途:判定一条射线是角平分线
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(2). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)∠1= ∠2DC=DE到角的两边的距离相等的点,在角平分线上。角平分线上的点到角的两边的距离相等2..直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有: ( )
A.一处 B. 两处
C.三处 D.四处课堂作业:
必做 P26 A组 2. 3
选做 P26 4
家庭作业:
练习册
预习下节课内容
下列两图中,能表示角的平分线上的一点P到角的边上的距离的是( )
PM 将∠AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论? 可以看一看,第一条折痕是∠AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到∠AOB两边的距离,这两个距离相等.折一折探究1:已知:如图,在∠AOB的平分线 OC上任取一点P,PD⊥OA,PE⊥OB,垂足分别是D,E。试问:PD=PE吗?证明:∵ PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90°(垂直的定义)在△PDO和△PEO中∴ PD=PE(全等三角形的对应边相等)∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP∴ △ PDO≌ △ PEO(AAS)问题探究ABODEPC角平分线的性质1: 角的平分线上的点到角的两边的距离相等。性质应用所具备的条件:性质的作用: 证明线段相等。性质的书写格式:OP 是 的平分线PD = PE(在角的平分线上的点
到这个角的两边的距离相等。)∵推理的理由有三个,必须写完全,不能少了任何一个。1.∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)练习:2.∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)3.∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等在Rt△PDO和Rt△PEO中,
∵ OP = OP,PD = PE,
∴ Rt△PDO≌Rt△PEO.∵ PD⊥OA, PE⊥OB,
∴ ∠PDO =∠PEO = 90°.如图1-27,过点O,P作射线OC.∴ ∠AOC =∠BOC.∴ OC是∠AOB的平分线,即点P在∠AOB的平分线OC上.图1-27角的内部到角的两边距离相等的点在角的平分线上.
由此得到角平分线的性质定理的逆定理:性质 2的应用书写格式:OP 是 的平分线PD= PE (角的内部到角的两边距离相等的点在角的平分线上.)
∵又 BA⊥AD, BC⊥CD,∴ 点B在∠ADC的平分线上.图1-28(1)求证:点B在∠ADC的平分线上;图1-28证明: 在Rt△BAD和Rt△BCD中,
∵ BA = BC, BD = BD,∴ Rt△BAD≌Rt△BCD.∴ ∠ABD =∠CBD.∴ BD是∠ABC的平分线.(2)求证:BD是∠ABC的平分线.
解 作∠AOB的角平分线,交MN于一点,则这点即为所
求作的点P.(提示:用尺规作图)如图,在直线MN上求作一点P ,使点P到∠AOB两边
的距离相等.P2. 如图,在△ABC 中,AD 平分∠BAC, DE⊥AB
于点E,DF⊥AC 于点F,BD=CD.
求证:AB=AC.回头看一看,我想说......能说出你这节课的收获和体验,
让大家与你分享吗?学而不思则罔性质 1 角的平分线上的点到角的两边距离相等。性质 2 角的内部到角的两边距离相等的点 在角的平分线上。∵PD = PE用途:证线段相等用途:判定一条射线是角平分线
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(2). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)∠1= ∠2DC=DE到角的两边的距离相等的点,在角平分线上。角平分线上的点到角的两边的距离相等2..直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有: ( )
A.一处 B. 两处
C.三处 D.四处课堂作业:
必做 P26 A组 2. 3
选做 P26 4
家庭作业:
练习册
预习下节课内容
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
