1.4 角平分线的性质 课件 (7)(30PPT)
文档属性
| 名称 | 1.4 角平分线的性质 课件 (7)(30PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 532.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-08 00:00:00 | ||
图片预览




文档简介
课件30张PPT。角平分线的性质一、教学目标:
1.经历角的平分线性质的发现过程,初步掌握角的平分线的性质定理及其逆定理.
2.通过测量操作,发现角的平分线的性质定理
3.能用文字语言、符号语言阐述角的平分线的性质定理及其逆定理,提高不同数学语言间的转化能力.
4.能运用角的平分线性质定理及其逆定理解决简单的几何问题.
5.通过合作交流、自主评价,促进良好的学习态度的形成,养成永无止境的科学探索精神.
二、教学重点、难点: 1.教学重点:掌握角的平分线的性质定理及其逆定理.
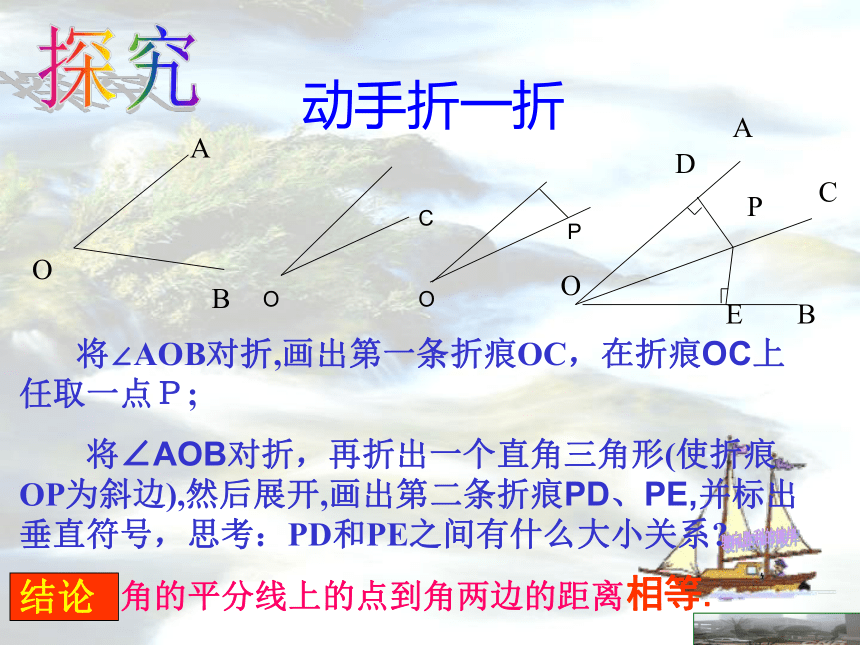
2.教学难点:角平分线定理和逆定理的应用 将∠AOB对折,画出第一条折痕OC,在折痕OC上任取一点P;
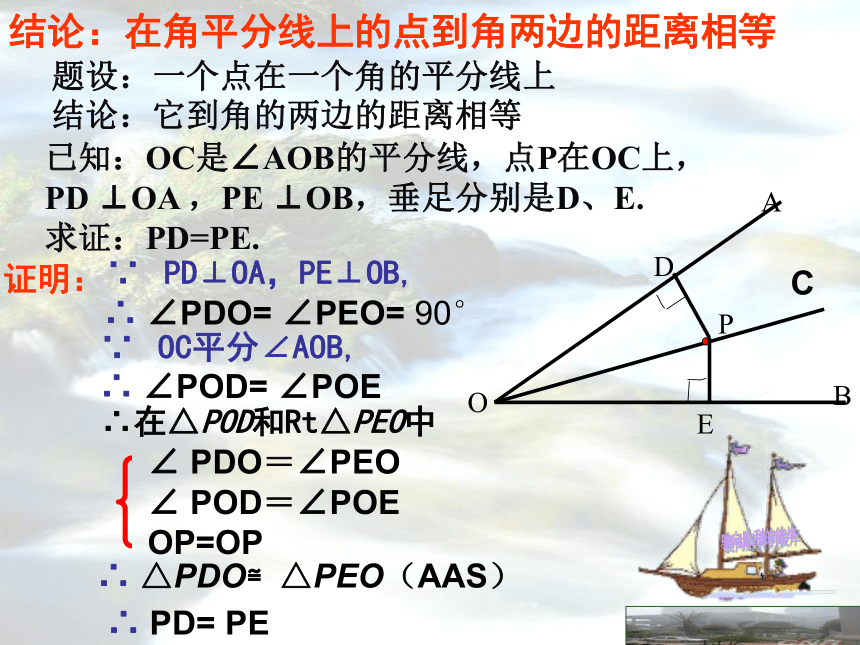
将∠AOB对折,再折出一个直角三角形(使折痕OP为斜边),然后展开,画出第二条折痕PD、PE,并标出垂直符号,思考:PD和PE之间有什么大小关系? 动手折一折探究结论角的平分线上的点到角两边的距离相等.结论:在角平分线上的点到角两边的距离相等题设:一个点在一个角的平分线上结论:它到角的两边的距离相等已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.∵ PD⊥OA,PE⊥OB,证明:∴ ∠PDO= ∠PEO= 90°∴在△POD和Rt△PEO中
∴ △PDO≌△PEO(AAS) ∠ PDO=∠PEO
∠ POD=∠POE
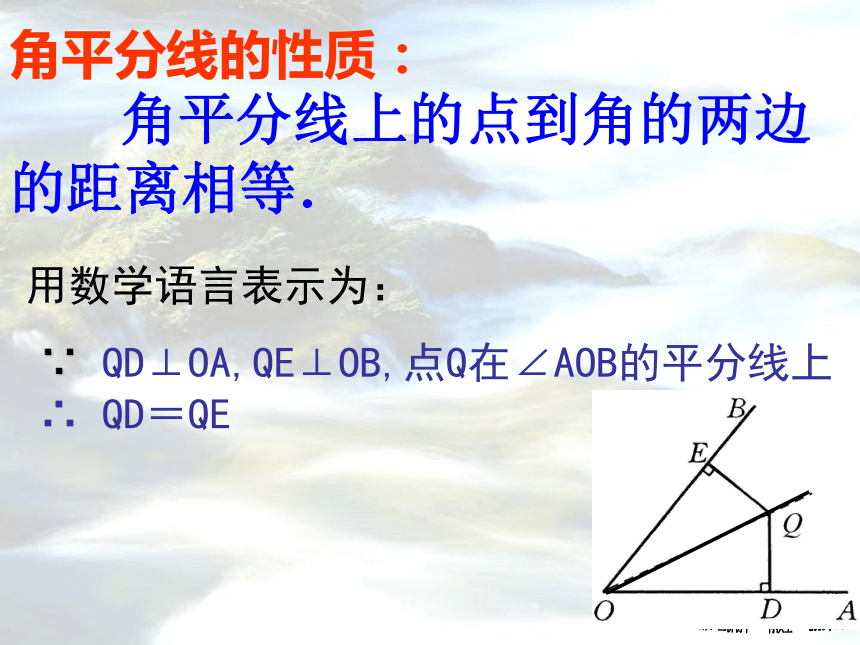
OP=OPC∵ OC平分∠AOB,∴ ∠POD= ∠POE∴ PD= PE角平分线的性质:
角平分线上的点到角的两边的距离相等.∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
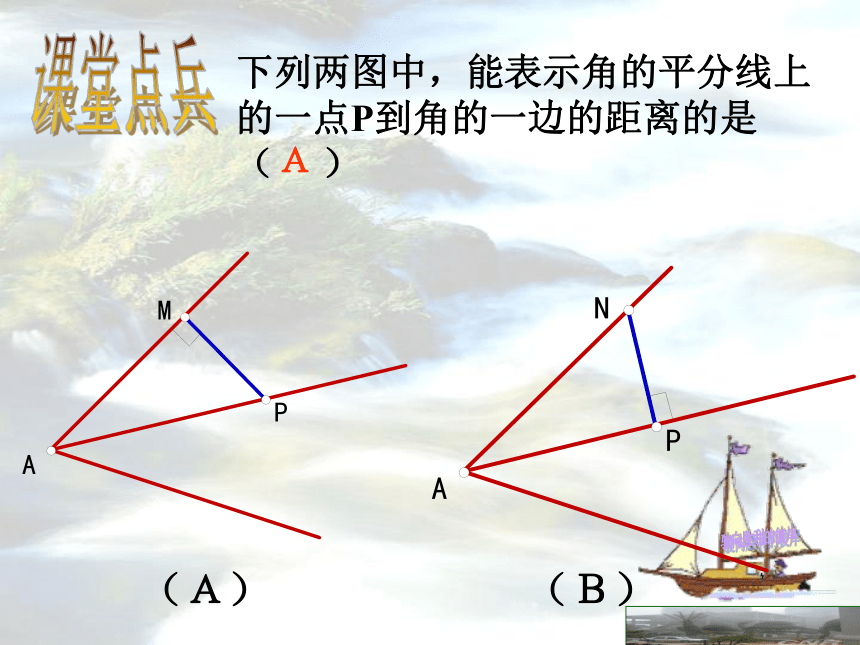
∴ QD=QE用数学语言表示为:下列两图中,能表示角的平分线上的一点P到角的一边的距离的是( )
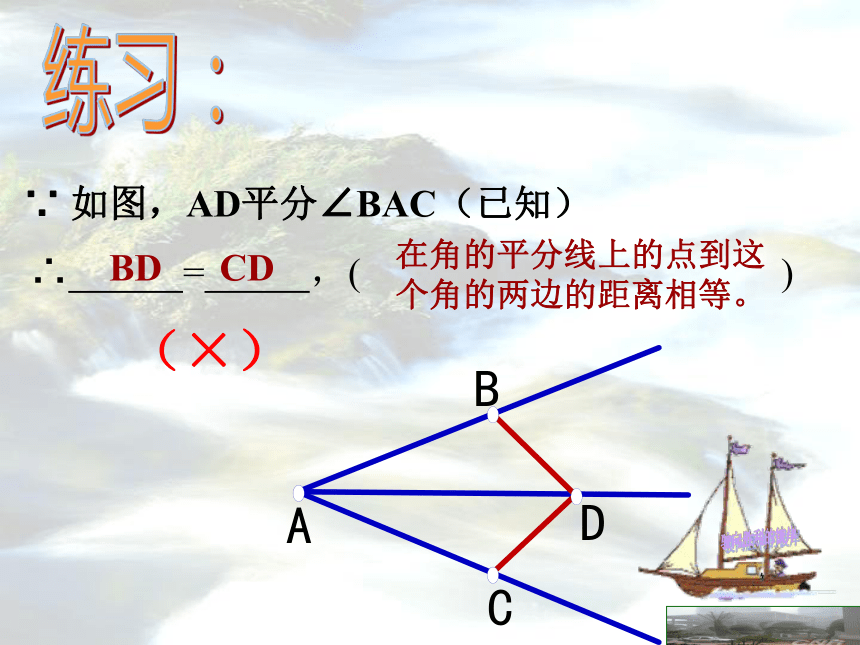
课堂点兵(A)(B)A∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
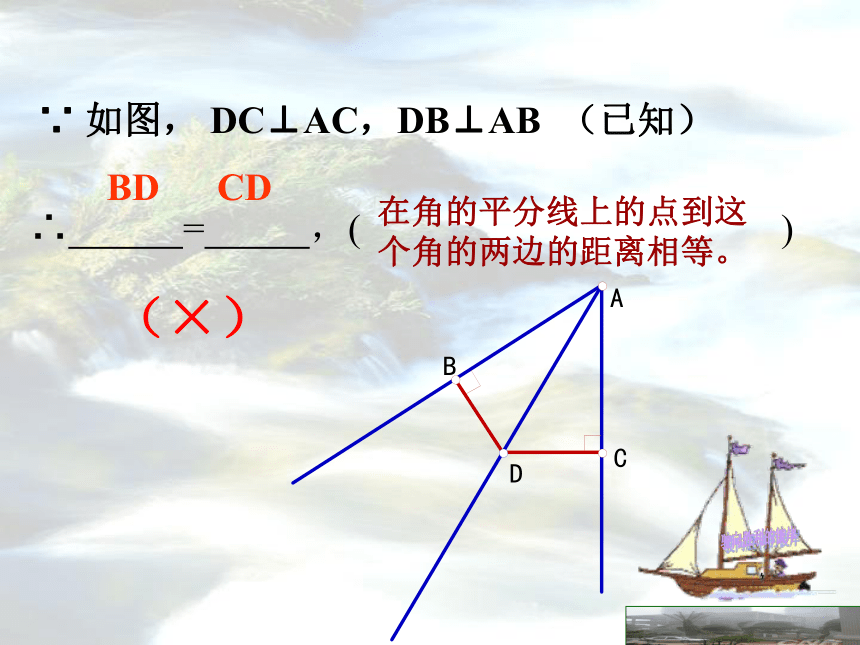
BD CD(×)练习:∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
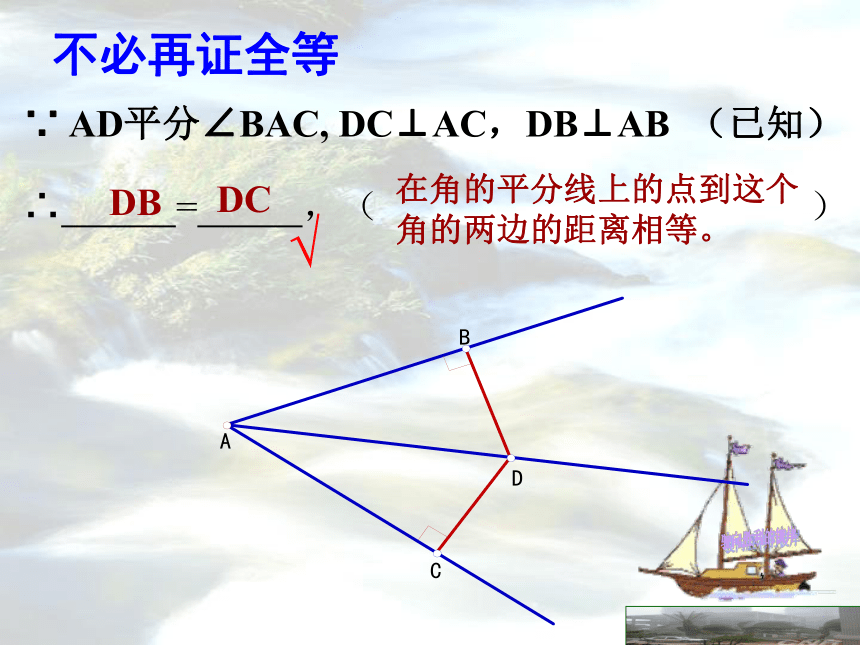
BD CD(×)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
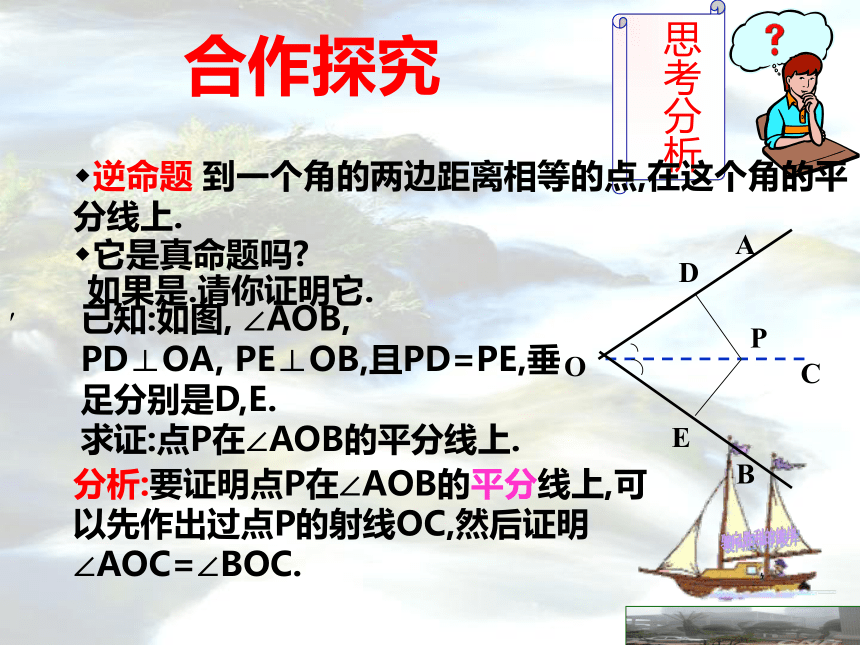
√不必再证全等合作探究′逆命题 到一个角的两边距离相等的点,在这个角的平分线上.它是真命题吗?如果是.请你证明它.已知:如图, ∠AOB,
PD⊥OA, PE⊥OB,且PD=PE,垂足分别是D,E.
求证:点P在∠AOB的平分线上.分析:要证明点P在∠AOB的平分线上,可以先作出过点P的射线OC,然后证明∠AOC=∠BOC.OCBAPDE证明:
∵ PD⊥OA,PE⊥OB(已知),
∴ ∠PDO=∠PEO=90°(垂直的定义) 在Rt△PDO和Rt△PEO中
PO=PO(公共边) PD=PE ∴ Rt△PDO≌Rt△PEO(HL)
∴ ∠ POD=∠POE
∴点P在∠AOB的平分线上已知:如图,∠AOB中,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上.P过点O,P做射线OP逆定理: 到一个角的两边距离相等的点,在这个角的平分线上. 用符号语言表示为:
∵PD⊥OA,PE⊥OB,垂足
分别是D,E,且PD=PE
∴点P在∠AOB的平分线上温馨提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.OCBAPDE二.角平分线性质定理的逆定理 1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等 2.角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上。
4.角平分线的性质定理是证明角相等、线段相等的新途径.角平分线的逆定理是证明点在直线上(或直线经过某一点)的根据之一.3.性质定理和逆定理的关系
点在角平分线上 点到角两边的距离相等总结归纳基本应用填空:
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(1). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)∠1=∠2
DC=DE到一个角的两边的距离相等的点,在这个角平分线上。在角平分线上的点到角的两边的距离相等例1.已知:如图,∠C=900,∠B=300,
AD是Rt△ABC的角平分线.
求证:BD=2CD. ABCDE例:已知:如图,∠C= ∠C′=90° ,AC=AC ′ .
求证(1) ∠ABC= ∠ABC ′ ;(2)BC=BC ′ .(要求不用三角形全等的判定)B·OABCP300m┒┓S解:300m=30000cm
30000÷20000=1.5cm已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC. 老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去. 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。 求证:AD是△ABC的角平分线。变一变已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF,
求证:CF=EB。应用与提高证明:
∵ AD平分∠CAB
DE⊥AB,∠C=90°(已知)
∴ CD=DE (角平分线的性质)
在Rt△CDF和Rt△EDB中,
CD=DE (已证)
DF=DB (已知)
∴ Rt△CDF≌Rt△EDB (HL)
∴ CF=EB (全等三角形对应边相等)拓展与延伸3、已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,求证:点F在∠A的平分线上.1.已知:如图,P是∠AOB平分线上的一点,
PC⊥OA,PD⊥OB,垂足分别C,D.
求证:(1)OC=OD;
(2)OP是CD的垂直平分线. 2、若要在△MON内部全部覆盖绿化, 已知△MON的周长为2000米,∠OMN、∠MON的平分线交于点O,PD⊥MN, 垂足为D,且PD=2米
求: △MON的面积到角的两边的距离相等的点在角的平分线上。∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.用数学语言表示为:角的平分线上的点到角的两边的距离相等.∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE课堂小结用数学语言表示为:课堂作业2、如图,在△ABC中,已知AC=BC,
∠C=900,AD是△ABC的角平分线,
DE⊥AB,垂足为E.(1)如果CD=4cm,AC的长(2)求证:AB=AC+CD.1:如图所示,PB⊥AB,PC⊥AC, 且PB=PC,D是AP上一点。 求证: ∠BDP= ∠CDP例 2 如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、
CA的距离相等DEF 如图,已知△ABC的外角∠CBD和 ∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上. 证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于MGHM∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC∴FG=FM又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC∴FM=FH∴FG=FH∴点F在∠DAE的平分线上 练习小结:1:画一个已知角的角平分线;及画一条已知直线的垂线;2:角平分线的性质:角的平分线上的点到角的两边的距离相等.
3:角平分线的判定结论:到角的两边的距离相等的点在角平分线上。1.利用尺规作出三角形三个内角的平分线. 老师期望:
先分别作出不同形状的三角形,再按要求去作图.你发现了什么?
1.经历角的平分线性质的发现过程,初步掌握角的平分线的性质定理及其逆定理.
2.通过测量操作,发现角的平分线的性质定理
3.能用文字语言、符号语言阐述角的平分线的性质定理及其逆定理,提高不同数学语言间的转化能力.
4.能运用角的平分线性质定理及其逆定理解决简单的几何问题.
5.通过合作交流、自主评价,促进良好的学习态度的形成,养成永无止境的科学探索精神.
二、教学重点、难点: 1.教学重点:掌握角的平分线的性质定理及其逆定理.
2.教学难点:角平分线定理和逆定理的应用 将∠AOB对折,画出第一条折痕OC,在折痕OC上任取一点P;
将∠AOB对折,再折出一个直角三角形(使折痕OP为斜边),然后展开,画出第二条折痕PD、PE,并标出垂直符号,思考:PD和PE之间有什么大小关系? 动手折一折探究结论角的平分线上的点到角两边的距离相等.结论:在角平分线上的点到角两边的距离相等题设:一个点在一个角的平分线上结论:它到角的两边的距离相等已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.∵ PD⊥OA,PE⊥OB,证明:∴ ∠PDO= ∠PEO= 90°∴在△POD和Rt△PEO中
∴ △PDO≌△PEO(AAS) ∠ PDO=∠PEO
∠ POD=∠POE
OP=OPC∵ OC平分∠AOB,∴ ∠POD= ∠POE∴ PD= PE角平分线的性质:
角平分线上的点到角的两边的距离相等.∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE用数学语言表示为:下列两图中,能表示角的平分线上的一点P到角的一边的距离的是( )
课堂点兵(A)(B)A∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)练习:∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等合作探究′逆命题 到一个角的两边距离相等的点,在这个角的平分线上.它是真命题吗?如果是.请你证明它.已知:如图, ∠AOB,
PD⊥OA, PE⊥OB,且PD=PE,垂足分别是D,E.
求证:点P在∠AOB的平分线上.分析:要证明点P在∠AOB的平分线上,可以先作出过点P的射线OC,然后证明∠AOC=∠BOC.OCBAPDE证明:
∵ PD⊥OA,PE⊥OB(已知),
∴ ∠PDO=∠PEO=90°(垂直的定义) 在Rt△PDO和Rt△PEO中
PO=PO(公共边) PD=PE ∴ Rt△PDO≌Rt△PEO(HL)
∴ ∠ POD=∠POE
∴点P在∠AOB的平分线上已知:如图,∠AOB中,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上.P过点O,P做射线OP逆定理: 到一个角的两边距离相等的点,在这个角的平分线上. 用符号语言表示为:
∵PD⊥OA,PE⊥OB,垂足
分别是D,E,且PD=PE
∴点P在∠AOB的平分线上温馨提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.OCBAPDE二.角平分线性质定理的逆定理 1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等 2.角平分线的判定定理:
到一个角的两边的距离相等的点,在这个角平分线上。
4.角平分线的性质定理是证明角相等、线段相等的新途径.角平分线的逆定理是证明点在直线上(或直线经过某一点)的根据之一.3.性质定理和逆定理的关系
点在角平分线上 点到角两边的距离相等总结归纳基本应用填空:
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(1). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)∠1=∠2
DC=DE到一个角的两边的距离相等的点,在这个角平分线上。在角平分线上的点到角的两边的距离相等例1.已知:如图,∠C=900,∠B=300,
AD是Rt△ABC的角平分线.
求证:BD=2CD. ABCDE例:已知:如图,∠C= ∠C′=90° ,AC=AC ′ .
求证(1) ∠ABC= ∠ABC ′ ;(2)BC=BC ′ .(要求不用三角形全等的判定)B·OABCP300m┒┓S解:300m=30000cm
30000÷20000=1.5cm已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC. 老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去. 如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。 求证:AD是△ABC的角平分线。变一变已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF,
求证:CF=EB。应用与提高证明:
∵ AD平分∠CAB
DE⊥AB,∠C=90°(已知)
∴ CD=DE (角平分线的性质)
在Rt△CDF和Rt△EDB中,
CD=DE (已证)
DF=DB (已知)
∴ Rt△CDF≌Rt△EDB (HL)
∴ CF=EB (全等三角形对应边相等)拓展与延伸3、已知:BD⊥AM于点D,CE⊥AN于点E,BD,CE交点F,CF=BF,求证:点F在∠A的平分线上.1.已知:如图,P是∠AOB平分线上的一点,
PC⊥OA,PD⊥OB,垂足分别C,D.
求证:(1)OC=OD;
(2)OP是CD的垂直平分线. 2、若要在△MON内部全部覆盖绿化, 已知△MON的周长为2000米,∠OMN、∠MON的平分线交于点O,PD⊥MN, 垂足为D,且PD=2米
求: △MON的面积到角的两边的距离相等的点在角的平分线上。∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.用数学语言表示为:角的平分线上的点到角的两边的距离相等.∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE课堂小结用数学语言表示为:课堂作业2、如图,在△ABC中,已知AC=BC,
∠C=900,AD是△ABC的角平分线,
DE⊥AB,垂足为E.(1)如果CD=4cm,AC的长(2)求证:AB=AC+CD.1:如图所示,PB⊥AB,PC⊥AC, 且PB=PC,D是AP上一点。 求证: ∠BDP= ∠CDP例 2 如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
(在角平分线上的点到角两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、
CA的距离相等DEF 如图,已知△ABC的外角∠CBD和 ∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上. 证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于MGHM∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC∴FG=FM又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC∴FM=FH∴FG=FH∴点F在∠DAE的平分线上 练习小结:1:画一个已知角的角平分线;及画一条已知直线的垂线;2:角平分线的性质:角的平分线上的点到角的两边的距离相等.
3:角平分线的判定结论:到角的两边的距离相等的点在角平分线上。1.利用尺规作出三角形三个内角的平分线. 老师期望:
先分别作出不同形状的三角形,再按要求去作图.你发现了什么?
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
