2.6.2 菱形的判定 课件 (2)(19PPT)
文档属性
| 名称 | 2.6.2 菱形的判定 课件 (2)(19PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-08 21:50:04 | ||
图片预览




文档简介
课件19张PPT。2.6.2菱形的判定1、探究菱形的判定方法
2、掌握菱形的判定方法并运用它们解决问题 学习目标:(1)菱形具有平行四边形的所有性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直。
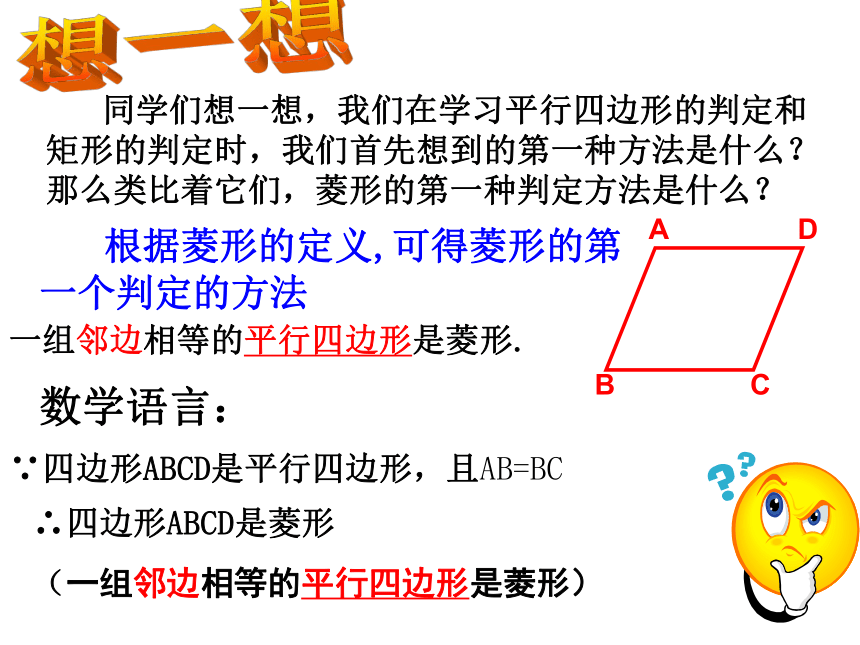
(并且每一条对角线平分一组对角)(4)菱形是轴对称图形,也是中心对称图形。2.菱形有哪些性质?1.菱形的定义:_______________________________有一组邻边相等的平行四边形叫做菱形 同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?一组邻边相等的平行四边形是菱形.想一想 根据菱形的定义,可得菱形的第一个判定的方法数学语言:∵四边形ABCD是平行四边形,且AB=BC∴四边形ABCD是菱形
(一组邻边相等的平行四边形是菱形)
菱形合作与探究(一)已知:在四边形ABCD中,AB=BC=CD=DA.
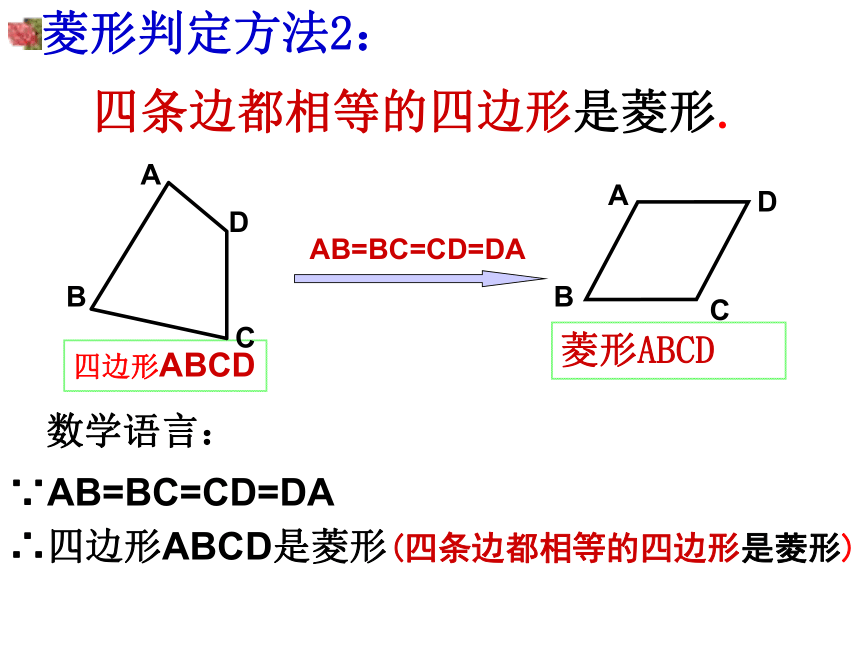
求证:四边形ABCD是菱形证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=BC,∴四边形ABCD是菱形(一组邻边相等的平行四边形是菱形)四条边都相等?四条边都相等的四边形是菱形.菱形判定方法2:∵AB=BC=CD=DA∴四边形ABCD是菱形(四条边都相等的四边形是菱形)
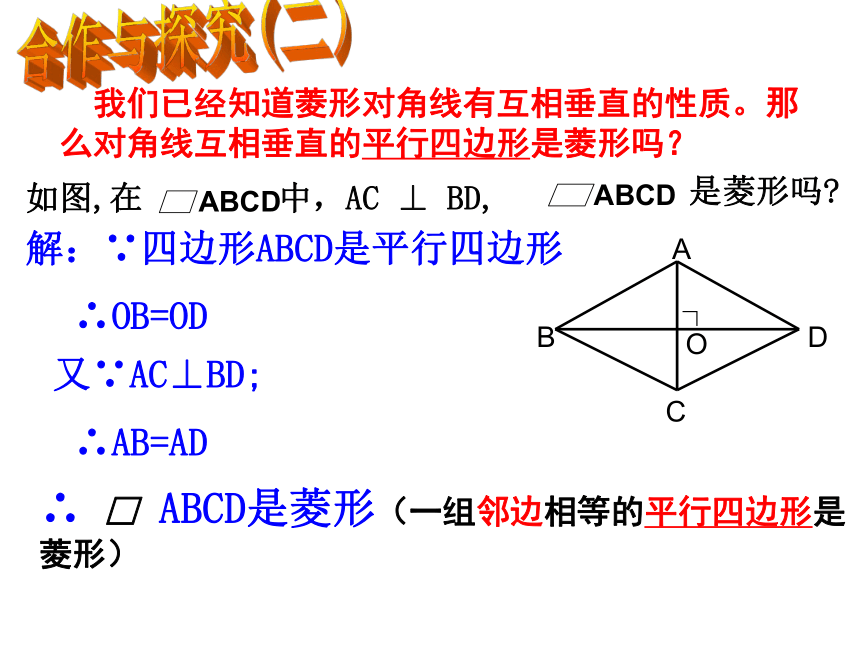
数学语言:解:∵四边形ABCD是平行四边形∴OB=OD又∵AC⊥BD; ∴AB=AD ∴ □ ABCD是菱形(一组邻边相等的平行四边形是菱形)合作与探究(二) 我们已经知道菱形对角线有互相垂直的性质。那么对角线互相垂直的平行四边形是菱形吗? 菱形判定方法3:对角线互相垂直的平行四边形是菱形∵在□ABCD中, AC⊥BD∴四边形ABCD是菱形
(对角线互相垂直的平行四边形是菱形)数学语言:菱形常用的判定方法:
1.有一组邻边相等的平行四边形是菱形.
2.有四条边相等的四边形是菱形.
3.对角线互相垂直的平行四边形是菱形.归纳:判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相平分且有一组邻边相等的四边形是菱形
( )
(4)对角线互相垂直,且有一组邻边相等的四边形是菱形
( )
╳√ ╳ √ 已知:如图,在四边形ABCD 中,线段AC垂直平分BD,且相交于点O,∠1 =∠2.
求证:四边形ABCD是菱形.证明:∵ 线段AC垂直平分BD,∴OB=OD.在△AOB和△COD中,有
∠1 =∠2,OB=OD,∠AOB=∠COD,∴△AOB≌△COD(ASA)又∵ ∠1 =∠2,∴AB∥CD∴AB=CD.∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形)∴四边形ABCD是平行四边形,又∵ AC⊥BD证明 由于线段AC垂直平分BD,因此AB=AD,BC=CD,OB=OD.
在△AOB和△COD中,有
∠1 =∠2,OB=OC,∠AOB=∠COD,所以△AOB≌△COD.从而AB=CD.因此四边形ABCD是菱形.
(四条边都相等的四边形是菱形)所以BA=BC=DA=DC.1.已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形. 练习:自主尝试,巩固新知证明:∵DE ∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE ∥AC
∴∠2= ∠3
∵ AD是△ABC的角平分线
∴ ∠1= ∠2,∴ ∠1= ∠3
∴AE=DE
∴ □ AEDF是菱形(有一组邻边相等的平行四边形是菱形)练习:自主尝试,巩固新知解 ∵ 四边形ABCD为平行四边形,∴又∵ AB=5, ,∴ △AOB是直角三角形.∴ ∠AOB = 90°,即AC⊥BD.∴ 平行四边形ABCD是菱形.(对角线互相垂直
的平行四边形是菱形)∴ 四边形ABCD的周长为4AB=4×5=20 在四边形ABCD中,对角线AC、BD交于点O,从
①AB=CD;②AB∥CD;③OA=OC;④OB=OD;
⑤AC⊥BD; ⑥AC=BD;⑦AC平分∠BAD; ⑧AB=BC
这八个条件中,选取三个推出四边形ABCD是菱形.你选取的三个条件是(至少写三种)
第一种 _____________
第二种______________
第三种______________挑战自我,巩固效果①②⑤③④⑤①②⑧③④⑧①②⑦③④⑦? 今天你学到了什么 ? 菱形识别方法:1、一组邻边相等的平行四边形是菱形3、对角线互相垂直的平行四边形是菱形2、四条边都相等的四边形是菱形BDAC我成长,我快乐,我收获 作业 必做题:教材P70-71习题2.6A组,T3,T5;
选做题:P71,T7谢谢指导!挑战自我,巩固效果C
2、掌握菱形的判定方法并运用它们解决问题 学习目标:(1)菱形具有平行四边形的所有性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直。
(并且每一条对角线平分一组对角)(4)菱形是轴对称图形,也是中心对称图形。2.菱形有哪些性质?1.菱形的定义:_______________________________有一组邻边相等的平行四边形叫做菱形 同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?一组邻边相等的平行四边形是菱形.想一想 根据菱形的定义,可得菱形的第一个判定的方法数学语言:∵四边形ABCD是平行四边形,且AB=BC∴四边形ABCD是菱形
(一组邻边相等的平行四边形是菱形)
菱形合作与探究(一)已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=BC,∴四边形ABCD是菱形(一组邻边相等的平行四边形是菱形)四条边都相等?四条边都相等的四边形是菱形.菱形判定方法2:∵AB=BC=CD=DA∴四边形ABCD是菱形(四条边都相等的四边形是菱形)
数学语言:解:∵四边形ABCD是平行四边形∴OB=OD又∵AC⊥BD; ∴AB=AD ∴ □ ABCD是菱形(一组邻边相等的平行四边形是菱形)合作与探究(二) 我们已经知道菱形对角线有互相垂直的性质。那么对角线互相垂直的平行四边形是菱形吗? 菱形判定方法3:对角线互相垂直的平行四边形是菱形∵在□ABCD中, AC⊥BD∴四边形ABCD是菱形
(对角线互相垂直的平行四边形是菱形)数学语言:菱形常用的判定方法:
1.有一组邻边相等的平行四边形是菱形.
2.有四条边相等的四边形是菱形.
3.对角线互相垂直的平行四边形是菱形.归纳:判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相平分且有一组邻边相等的四边形是菱形
( )
(4)对角线互相垂直,且有一组邻边相等的四边形是菱形
( )
╳√ ╳ √ 已知:如图,在四边形ABCD 中,线段AC垂直平分BD,且相交于点O,∠1 =∠2.
求证:四边形ABCD是菱形.证明:∵ 线段AC垂直平分BD,∴OB=OD.在△AOB和△COD中,有
∠1 =∠2,OB=OD,∠AOB=∠COD,∴△AOB≌△COD(ASA)又∵ ∠1 =∠2,∴AB∥CD∴AB=CD.∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形)∴四边形ABCD是平行四边形,又∵ AC⊥BD证明 由于线段AC垂直平分BD,因此AB=AD,BC=CD,OB=OD.
在△AOB和△COD中,有
∠1 =∠2,OB=OC,∠AOB=∠COD,所以△AOB≌△COD.从而AB=CD.因此四边形ABCD是菱形.
(四条边都相等的四边形是菱形)所以BA=BC=DA=DC.1.已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形. 练习:自主尝试,巩固新知证明:∵DE ∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE ∥AC
∴∠2= ∠3
∵ AD是△ABC的角平分线
∴ ∠1= ∠2,∴ ∠1= ∠3
∴AE=DE
∴ □ AEDF是菱形(有一组邻边相等的平行四边形是菱形)练习:自主尝试,巩固新知解 ∵ 四边形ABCD为平行四边形,∴又∵ AB=5, ,∴ △AOB是直角三角形.∴ ∠AOB = 90°,即AC⊥BD.∴ 平行四边形ABCD是菱形.(对角线互相垂直
的平行四边形是菱形)∴ 四边形ABCD的周长为4AB=4×5=20 在四边形ABCD中,对角线AC、BD交于点O,从
①AB=CD;②AB∥CD;③OA=OC;④OB=OD;
⑤AC⊥BD; ⑥AC=BD;⑦AC平分∠BAD; ⑧AB=BC
这八个条件中,选取三个推出四边形ABCD是菱形.你选取的三个条件是(至少写三种)
第一种 _____________
第二种______________
第三种______________挑战自我,巩固效果①②⑤③④⑤①②⑧③④⑧①②⑦③④⑦? 今天你学到了什么 ? 菱形识别方法:1、一组邻边相等的平行四边形是菱形3、对角线互相垂直的平行四边形是菱形2、四条边都相等的四边形是菱形BDAC我成长,我快乐,我收获 作业 必做题:教材P70-71习题2.6A组,T3,T5;
选做题:P71,T7谢谢指导!挑战自我,巩固效果C
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
