2.6.2 菱形的判定 课件 (3)(14PPT)
文档属性
| 名称 | 2.6.2 菱形的判定 课件 (3)(14PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 211.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-08 00:00:00 | ||
图片预览


文档简介
课件14张PPT。菱形的判定温故而知新,可以为师矣。温习旧的知
识,进而懂
得新的知识,
这样的人可
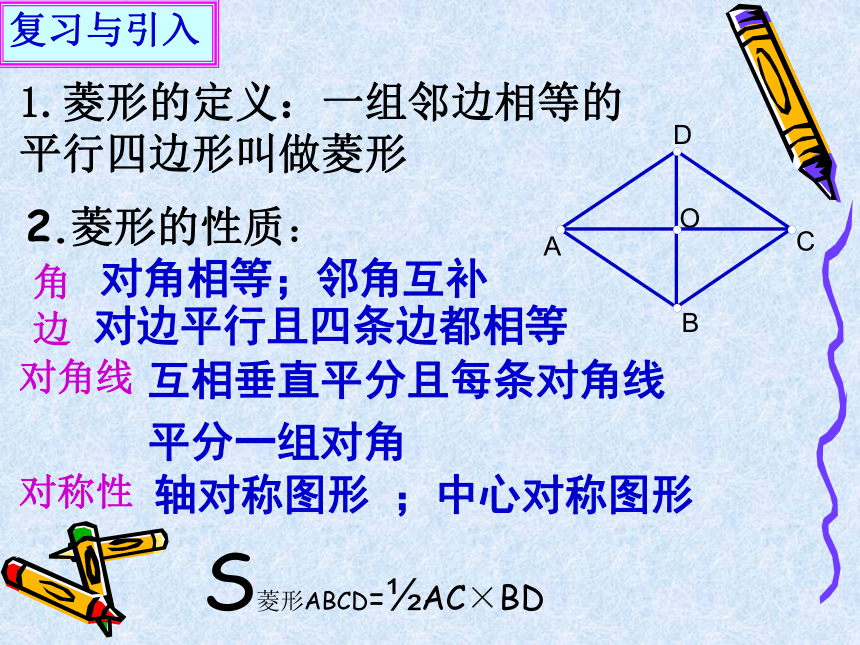
以做老师了。1.菱形的定义:一组邻边相等的平行四边形叫做菱形复习与引入角对角相等;邻角互补边对边平行且四条边都相等对角线互相垂直平分且每条对角线
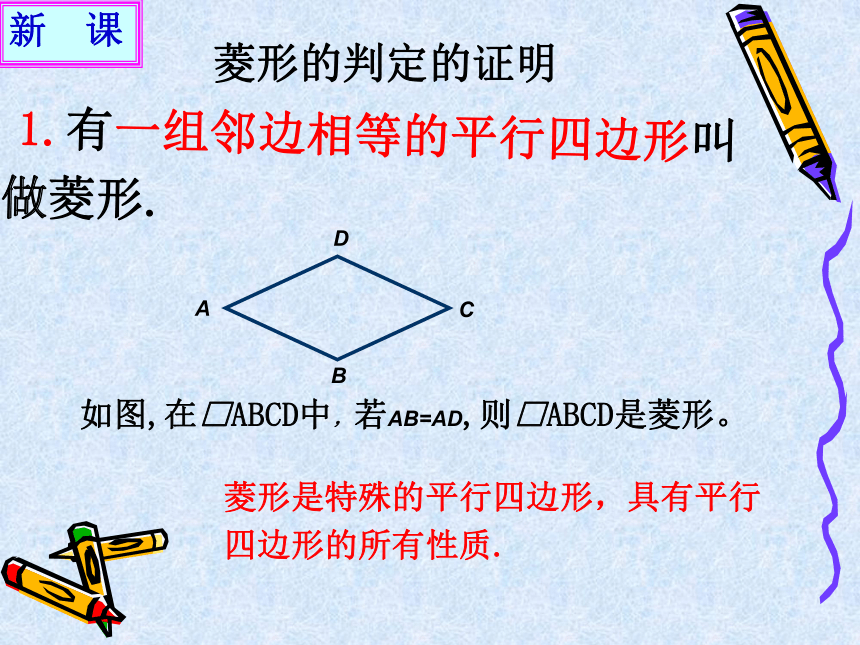
平分一组对角对称性轴对称图形 ;中心对称图形 2.菱形的性质:S菱形ABCD=?AC×BD 菱形的判定的证明 1.有一组邻边相等的平行四边形叫做菱形.菱形是特殊的平行四边形,具有平行四边形的所有性质.
新 课如图,在□ABCD中,若AB=AD,则□ABCD是菱形。
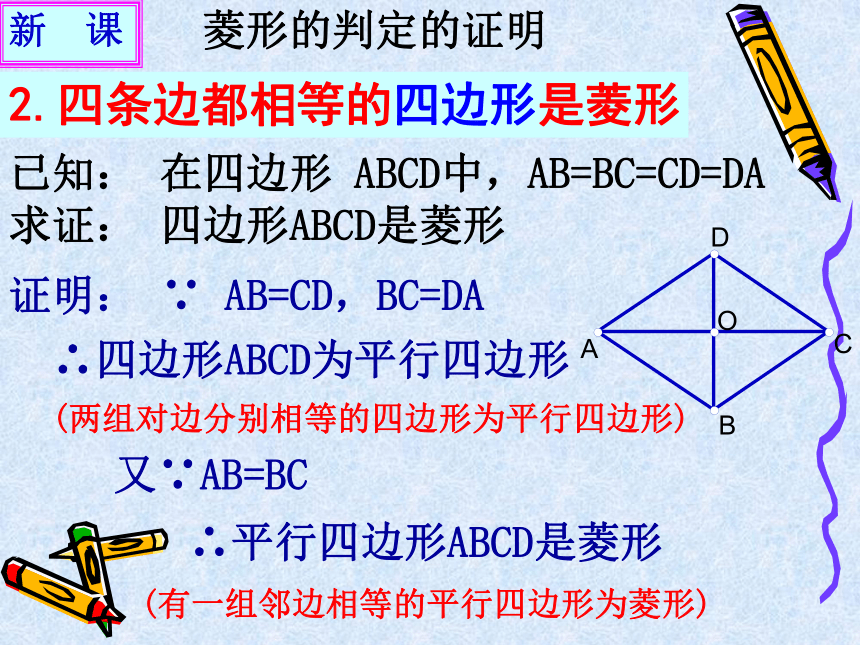
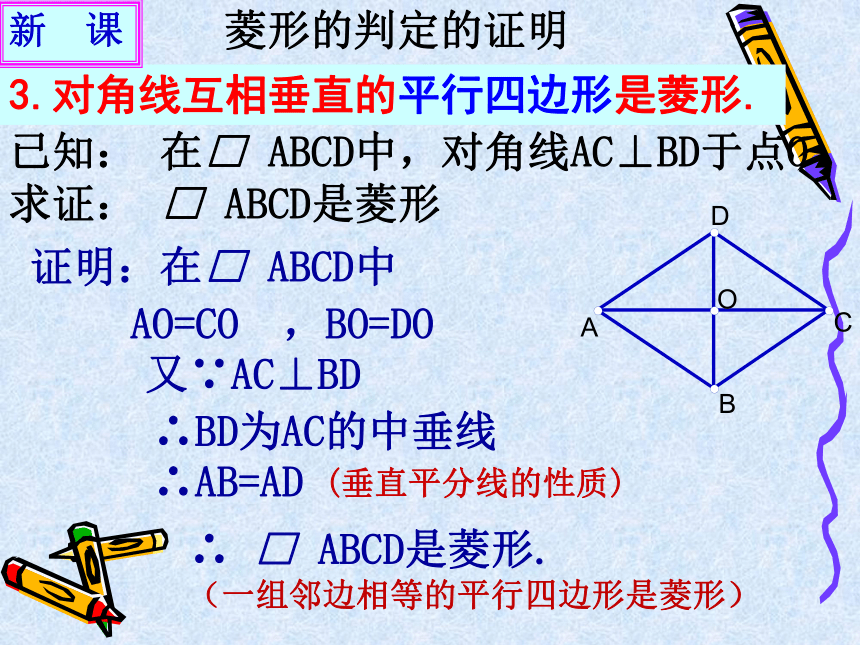
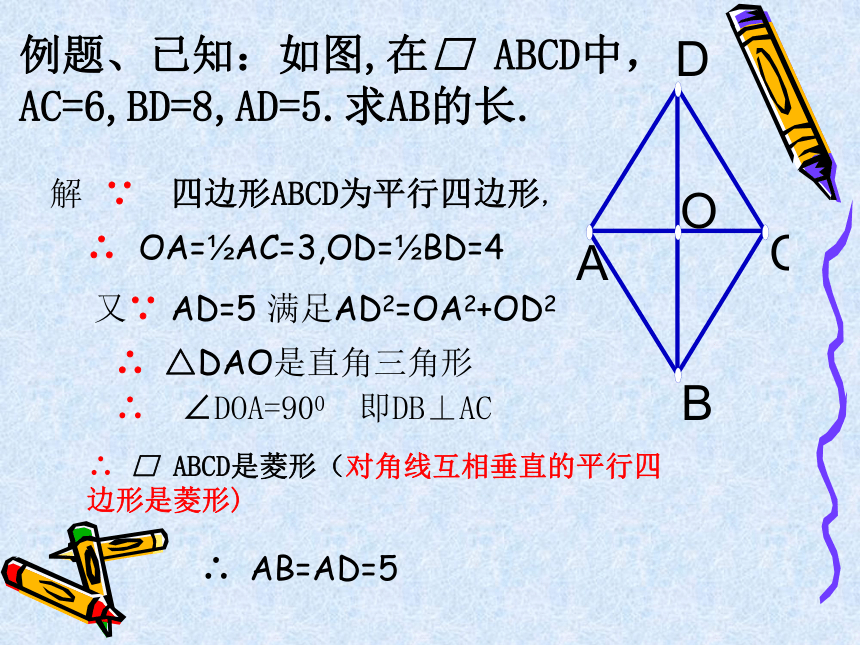
2.四条边都相等的四边形是菱形证明: ∵ AB=CD,BC=DA∴四边形ABCD为平行四边形又∵AB=BC∴平行四边形ABCD是菱形已知: 在四边形 ABCD中,AB=BC=CD=DA 求证: 四边形ABCD是菱形(两组对边分别相等的四边形为平行四边形)(有一组邻边相等的平行四边形为菱形)新 课 菱形的判定的证明∴ □ ABCD是菱形. (一组邻边相等的平行四边形是菱形)3.对角线互相垂直的平行四边形是菱形.证明:在□ ABCD中又∵AC⊥BD∴BD为AC的中垂线∴AB=ADAO=CO ,BO=DO已知: 在□ ABCD中,对角线AC⊥BD于点O 求证: □ ABCD是菱形(垂直平分线的性质)新 课 菱形的判定的证明例题、已知:如图,在□ ABCD中,AC=6,BD=8,AD=5.求AB的长.解 ∵ 四边形ABCD为平行四边形, ∴ OA=?AC=3,OD=?BD=4又∵ AD=5 满足AD2=OA2+OD2∴ △DAO是直角三角形∴ ∠DOA=900 即DB⊥AC∴ □ ABCD是菱形(对角线互相垂直的平行四边形是菱形)∴ AB=AD=5邻边相等对角线互相垂直AD=DC AC⊥BD 四边相等AD=DC=CB=BA对角线互相垂直平分AC⊥BD,AO=CO,BO=DO归纳2、菱形的判定(1)一组邻边相等的平行四边形是菱形(定义).(2)四条边都相等的四边形是菱形;(3)对角线互相垂直的平行四边形是菱形,使用判定定理是要注意基础图形是
四边形还是平行四边形总结尝试练习 1.已知:如图,在□ABCD中,对角线BD平分∠ABC。
求证:四边形ABCD是菱形。证明:平行四边形ABCD中312 AD∥BC ∴∠1=∠3又BD平分∠ABC。∴∠1=∠2
∴∠2=∠3 AB=AD ∴ 四边形ABCD是菱形(一组邻边相等的平行四边形是菱形)证明:在□ABCD中
AD∥BC ∴∠1=∠2 12在△AOE和△COF中
∠1=∠2 AO=CO ∠AOE=∠COF ∴ △AOE≌△COF∴ OE=OF又∵AO=CO AC⊥EF∴四边形AFCE是菱形3.如图,已知AD是△ABC的角平分线,
DE∥AC交AB于E,DF∥AB交AC于F,
求证:AD⊥EF。
1 2
3
证明:∵DE∥AC ,DF∥AB∴四边形AEDF是平行四边形∴ ∠2=∠3∵ AD是△ABC的角平分线∴ ∠1=∠2∴ ∠1=∠3∴ AE=DE∴ □AEDF是菱形∴ AD⊥EF∵DE∥AC 4、已知如图,在△ABC,∠ACB=900,AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF∥BC。
求证:四边形CDEF是菱形O12挑战 你能用直尺和圆规作一个菱形吗?请作图并说明理由。思考与探索
识,进而懂
得新的知识,
这样的人可
以做老师了。1.菱形的定义:一组邻边相等的平行四边形叫做菱形复习与引入角对角相等;邻角互补边对边平行且四条边都相等对角线互相垂直平分且每条对角线
平分一组对角对称性轴对称图形 ;中心对称图形 2.菱形的性质:S菱形ABCD=?AC×BD 菱形的判定的证明 1.有一组邻边相等的平行四边形叫做菱形.菱形是特殊的平行四边形,具有平行四边形的所有性质.
新 课如图,在□ABCD中,若AB=AD,则□ABCD是菱形。
2.四条边都相等的四边形是菱形证明: ∵ AB=CD,BC=DA∴四边形ABCD为平行四边形又∵AB=BC∴平行四边形ABCD是菱形已知: 在四边形 ABCD中,AB=BC=CD=DA 求证: 四边形ABCD是菱形(两组对边分别相等的四边形为平行四边形)(有一组邻边相等的平行四边形为菱形)新 课 菱形的判定的证明∴ □ ABCD是菱形. (一组邻边相等的平行四边形是菱形)3.对角线互相垂直的平行四边形是菱形.证明:在□ ABCD中又∵AC⊥BD∴BD为AC的中垂线∴AB=ADAO=CO ,BO=DO已知: 在□ ABCD中,对角线AC⊥BD于点O 求证: □ ABCD是菱形(垂直平分线的性质)新 课 菱形的判定的证明例题、已知:如图,在□ ABCD中,AC=6,BD=8,AD=5.求AB的长.解 ∵ 四边形ABCD为平行四边形, ∴ OA=?AC=3,OD=?BD=4又∵ AD=5 满足AD2=OA2+OD2∴ △DAO是直角三角形∴ ∠DOA=900 即DB⊥AC∴ □ ABCD是菱形(对角线互相垂直的平行四边形是菱形)∴ AB=AD=5邻边相等对角线互相垂直AD=DC AC⊥BD 四边相等AD=DC=CB=BA对角线互相垂直平分AC⊥BD,AO=CO,BO=DO归纳2、菱形的判定(1)一组邻边相等的平行四边形是菱形(定义).(2)四条边都相等的四边形是菱形;(3)对角线互相垂直的平行四边形是菱形,使用判定定理是要注意基础图形是
四边形还是平行四边形总结尝试练习 1.已知:如图,在□ABCD中,对角线BD平分∠ABC。
求证:四边形ABCD是菱形。证明:平行四边形ABCD中312 AD∥BC ∴∠1=∠3又BD平分∠ABC。∴∠1=∠2
∴∠2=∠3 AB=AD ∴ 四边形ABCD是菱形(一组邻边相等的平行四边形是菱形)证明:在□ABCD中
AD∥BC ∴∠1=∠2 12在△AOE和△COF中
∠1=∠2 AO=CO ∠AOE=∠COF ∴ △AOE≌△COF∴ OE=OF又∵AO=CO AC⊥EF∴四边形AFCE是菱形3.如图,已知AD是△ABC的角平分线,
DE∥AC交AB于E,DF∥AB交AC于F,
求证:AD⊥EF。
1 2
3
证明:∵DE∥AC ,DF∥AB∴四边形AEDF是平行四边形∴ ∠2=∠3∵ AD是△ABC的角平分线∴ ∠1=∠2∴ ∠1=∠3∴ AE=DE∴ □AEDF是菱形∴ AD⊥EF∵DE∥AC 4、已知如图,在△ABC,∠ACB=900,AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF∥BC。
求证:四边形CDEF是菱形O12挑战 你能用直尺和圆规作一个菱形吗?请作图并说明理由。思考与探索
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
