2.6.2 菱形的判定课件 (19张ppt)
文档属性
| 名称 | 2.6.2 菱形的判定课件 (19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 679.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-08 00:00:00 | ||
图片预览






文档简介
课件19张PPT。菱形的判定 复习与回顾:想一想:
1.菱形、矩形的定义?
2.它们分别比平行四边形多了哪些性质?
3.怎样判定一个四边形是矩形? ?
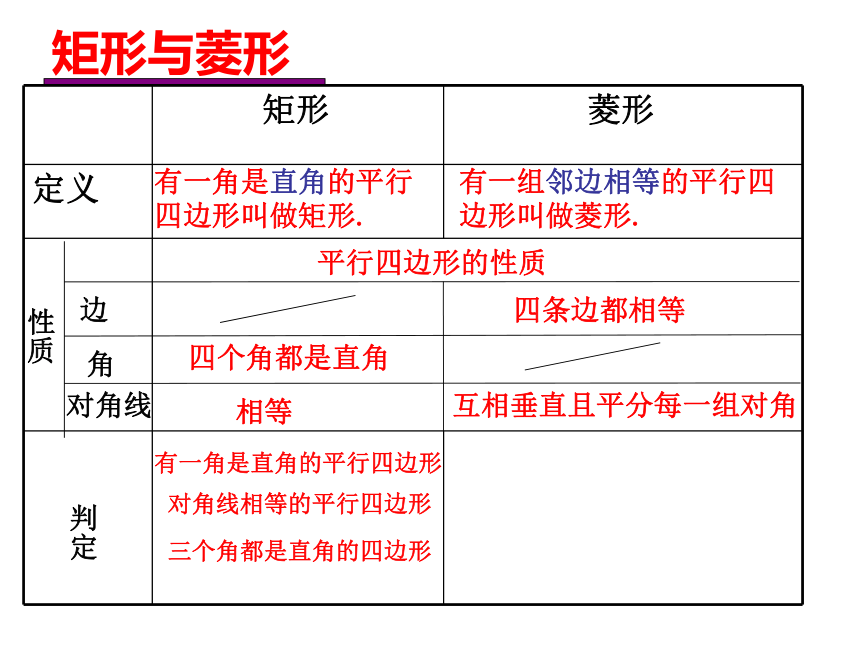
?矩形与菱形有一角是直角的平行四边形叫做矩形.有一组邻边相等的平行四边形叫做菱形.平行四边形的性质性质边角对角线四个角都是直角相等互相垂直且平分每一组对角判定有一角是直角的平行四边形对角线相等的平行四边形三个角都是直角的四边形四条边都相等想一想 同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么? 一组邻边相等的平行四边形是菱形.根据定义得:你能说出菱形性质定理1 :“菱形的四条边都相等”的逆命题吗?它是真命题吗?
逆命题:四条边都相等的四边形是菱形.
探究一命题:有四条边相等的四边形是菱形。已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
证明思路:先证明是平行四边形, 再根据菱形的定义证明是菱形.
证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=AD,∴四边形ABCD是菱形四条边都相等的四边形是菱形.∵在四边形ABCD中AB=BC=CD=DA∴四边形ABCD是菱形判定方法2:数学语言探究二菱形性质定理2:“菱形的两条对角线互相垂直”的逆命题又是什么呢?它是真命题吗?
逆命题:对角线互相垂直的平行四边形是菱形。
命题:对角线互相垂直的平行四边形是菱形.证明: ∵四边形ABCD是 平行四边形
∴OA=OC
又∵ AC ⊥ BD;
∴BA=BC
∴ ABCD是菱形
O证明思路:根据菱形的定义
只要证明平行四边形的两邻
边相等。判定方法3:对角线互相垂直的平行四边形是菱形∵在□ABCD中,AC⊥BD∴ □ABCD是菱形数学语言如图, ABCD的两条对角线AC、BD
相交于点O,AB= 5 ,AC=8,DB=6
求证:四边形ABCD是菱形.∴四边形ABCD是菱形.∴OA=OC=4
OB=OD=3证明:∵ AB=5 ∴AC⊥BD∴ ∠AOB=∵ 四边形ABCD是平行四边形(1)∵ 四边形ABCD是平行四边形(平行四边形的对角线互相平分)(对角线互相垂直的平行四边形是菱形).菱形的判定:∵AB=BC=CD=DA∴四边形ABCD是菱形∵在□ABCD中AC⊥BD∴四边形ABCD是菱形∵在□ABCD中AB=AD∴四边形ABCD是菱形ABCDO 一组邻边相等的平行四边形是菱形 1.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.√ ╳ ╳ ╳ 2.□ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。菱矩矩菱3.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形C4.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对C5.下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BDC1.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.试问四边形AEDF是菱形吗?说明你的理由。习题巩固:四边形AEDF是菱形
理由:∵DE ∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE ∥AC
∴∠2= ∠3
∵ AD是△ABC的角平分线
∴ ∠1= ∠2
∴AE=DE
∴ □ AEDF是菱形2.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.
求证:四边形OCED是菱形一组邻边相等对角线互相垂直四条边相等四种判定方法四边形菱形的判定方法:小结: 谢谢!
再见
1.菱形、矩形的定义?
2.它们分别比平行四边形多了哪些性质?
3.怎样判定一个四边形是矩形? ?
?矩形与菱形有一角是直角的平行四边形叫做矩形.有一组邻边相等的平行四边形叫做菱形.平行四边形的性质性质边角对角线四个角都是直角相等互相垂直且平分每一组对角判定有一角是直角的平行四边形对角线相等的平行四边形三个角都是直角的四边形四条边都相等想一想 同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么? 一组邻边相等的平行四边形是菱形.根据定义得:你能说出菱形性质定理1 :“菱形的四条边都相等”的逆命题吗?它是真命题吗?
逆命题:四条边都相等的四边形是菱形.
探究一命题:有四条边相等的四边形是菱形。已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
证明思路:先证明是平行四边形, 再根据菱形的定义证明是菱形.
证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=AD,∴四边形ABCD是菱形四条边都相等的四边形是菱形.∵在四边形ABCD中AB=BC=CD=DA∴四边形ABCD是菱形判定方法2:数学语言探究二菱形性质定理2:“菱形的两条对角线互相垂直”的逆命题又是什么呢?它是真命题吗?
逆命题:对角线互相垂直的平行四边形是菱形。
命题:对角线互相垂直的平行四边形是菱形.证明: ∵四边形ABCD是 平行四边形
∴OA=OC
又∵ AC ⊥ BD;
∴BA=BC
∴ ABCD是菱形
O证明思路:根据菱形的定义
只要证明平行四边形的两邻
边相等。判定方法3:对角线互相垂直的平行四边形是菱形∵在□ABCD中,AC⊥BD∴ □ABCD是菱形数学语言如图, ABCD的两条对角线AC、BD
相交于点O,AB= 5 ,AC=8,DB=6
求证:四边形ABCD是菱形.∴四边形ABCD是菱形.∴OA=OC=4
OB=OD=3证明:∵ AB=5 ∴AC⊥BD∴ ∠AOB=∵ 四边形ABCD是平行四边形(1)∵ 四边形ABCD是平行四边形(平行四边形的对角线互相平分)(对角线互相垂直的平行四边形是菱形).菱形的判定:∵AB=BC=CD=DA∴四边形ABCD是菱形∵在□ABCD中AC⊥BD∴四边形ABCD是菱形∵在□ABCD中AB=AD∴四边形ABCD是菱形ABCDO 一组邻边相等的平行四边形是菱形 1.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.√ ╳ ╳ ╳ 2.□ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。菱矩矩菱3.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形C4.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对C5.下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BDC1.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.试问四边形AEDF是菱形吗?说明你的理由。习题巩固:四边形AEDF是菱形
理由:∵DE ∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE ∥AC
∴∠2= ∠3
∵ AD是△ABC的角平分线
∴ ∠1= ∠2
∴AE=DE
∴ □ AEDF是菱形2.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.
求证:四边形OCED是菱形一组邻边相等对角线互相垂直四条边相等四种判定方法四边形菱形的判定方法:小结: 谢谢!
再见
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
