4.1.1变量与函数 课件 (1)(16PPT)
文档属性
| 名称 | 4.1.1变量与函数 课件 (1)(16PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 298.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-08 00:00:00 | ||
图片预览






文档简介
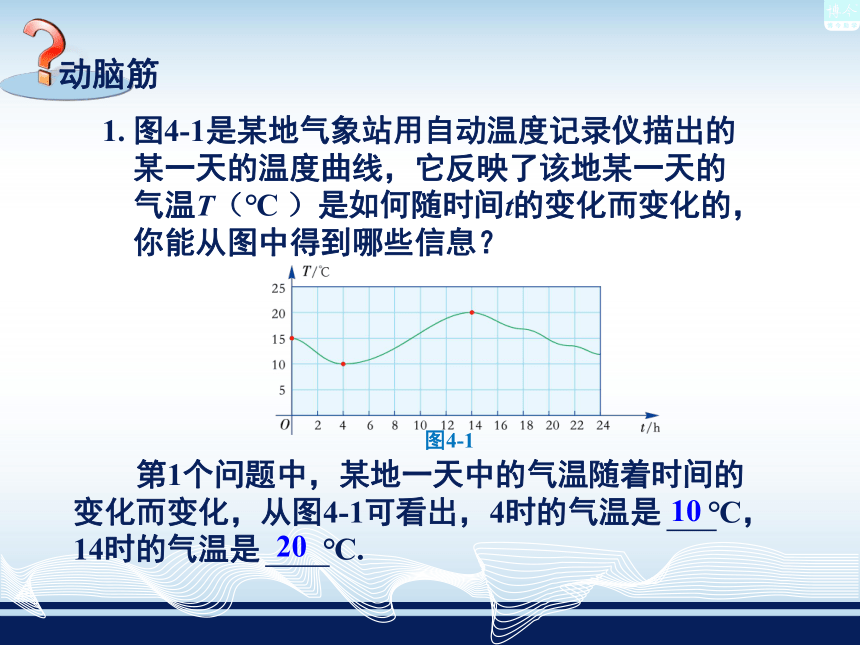
课件16张PPT。一 次 函 数第4章函数和它的表示法4.1——4.1.1 变量与函数
10 202. 当正方形的边长x分别取1,2,3,4,5,… 时,
正方形的面积S分别是多少?试填写下表:第2个问题中,正方形的面积随着它的边长的变化而变化.
14916253649 28.857.6 在讨论问题中,取值会发生变化的量称为变量,
取值固定不变的量称为常量(或常数). 上述问题中,时间t,气温T;正方形的边长x,面积S;使用天然气的体积x,应交纳的费用y等都是变量. 使用每一方米天然气应交纳2.88元,2.88是常量. 一般地,如果变量y随着变量x而变化,并且对于x取的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数,记作y=f(x). 这里的f(x)是英文 a fun_ction of x(x的函数)的简记. 这时把x叫作自变量,把y叫作因变量. 对于自变量x取的每一个值a,因变量y的对应值称为函数值,记作f(a).1. 第一个例子中, 是自变量, 是
的函数.时间t气温T时间t2. 第二个例子中,正方形的边长是 ,
正方形的面积是边长的 .自变量函数3. 第三个例子中, 是自变量,
是 的函数.所用天然气的体积x应交纳费用y所用天然气的体积x 在考虑两个变量间的函数时,还要注意自变量的取值范围. 如上述第1个问题中,自变量t的取值范围是0≤t≤24;而第2、3个问题中,自变量x的取值范围分别是x>0,x≥0.图4-2(2) 当r = 5时, ;
当r = 10 时, .
图4-2(1)用含r 的代数式来表示圆柱的体积V,指出
自变量r 的取值范围.(2)当r = 5 ,10时,V是多少(结果保留π)?答:(1)路程s(km)随行驶时间t(h)的变化而变化;
(2)圆面积S随圆的半径r的变化而变化;
(3)银行的存款利率P随存期t的变化而变化.2. 如图,A港口某天受潮汐的影响,24小时内港 口水深h(m)随时间t(时)的变化而变化.(1) 水深h是时间t的函数吗?
(2) 当t分别取4,10,17时,h是多少?答:是.
答:当t = 4时,h=5;
当t =10时,h=7;
当t = 17时,h=5. 结 束
10 202. 当正方形的边长x分别取1,2,3,4,5,… 时,
正方形的面积S分别是多少?试填写下表:第2个问题中,正方形的面积随着它的边长的变化而变化.
14916253649 28.857.6 在讨论问题中,取值会发生变化的量称为变量,
取值固定不变的量称为常量(或常数). 上述问题中,时间t,气温T;正方形的边长x,面积S;使用天然气的体积x,应交纳的费用y等都是变量. 使用每一方米天然气应交纳2.88元,2.88是常量. 一般地,如果变量y随着变量x而变化,并且对于x取的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数,记作y=f(x). 这里的f(x)是英文 a fun_ction of x(x的函数)的简记. 这时把x叫作自变量,把y叫作因变量. 对于自变量x取的每一个值a,因变量y的对应值称为函数值,记作f(a).1. 第一个例子中, 是自变量, 是
的函数.时间t气温T时间t2. 第二个例子中,正方形的边长是 ,
正方形的面积是边长的 .自变量函数3. 第三个例子中, 是自变量,
是 的函数.所用天然气的体积x应交纳费用y所用天然气的体积x 在考虑两个变量间的函数时,还要注意自变量的取值范围. 如上述第1个问题中,自变量t的取值范围是0≤t≤24;而第2、3个问题中,自变量x的取值范围分别是x>0,x≥0.图4-2(2) 当r = 5时, ;
当r = 10 时, .
图4-2(1)用含r 的代数式来表示圆柱的体积V,指出
自变量r 的取值范围.(2)当r = 5 ,10时,V是多少(结果保留π)?答:(1)路程s(km)随行驶时间t(h)的变化而变化;
(2)圆面积S随圆的半径r的变化而变化;
(3)银行的存款利率P随存期t的变化而变化.2. 如图,A港口某天受潮汐的影响,24小时内港 口水深h(m)随时间t(时)的变化而变化.(1) 水深h是时间t的函数吗?
(2) 当t分别取4,10,17时,h是多少?答:是.
答:当t = 4时,h=5;
当t =10时,h=7;
当t = 17时,h=5. 结 束
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
