4.1.1变量与函数课件 (20张ppt)
文档属性
| 名称 | 4.1.1变量与函数课件 (20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-09 00:00:00 | ||
图片预览


文档简介
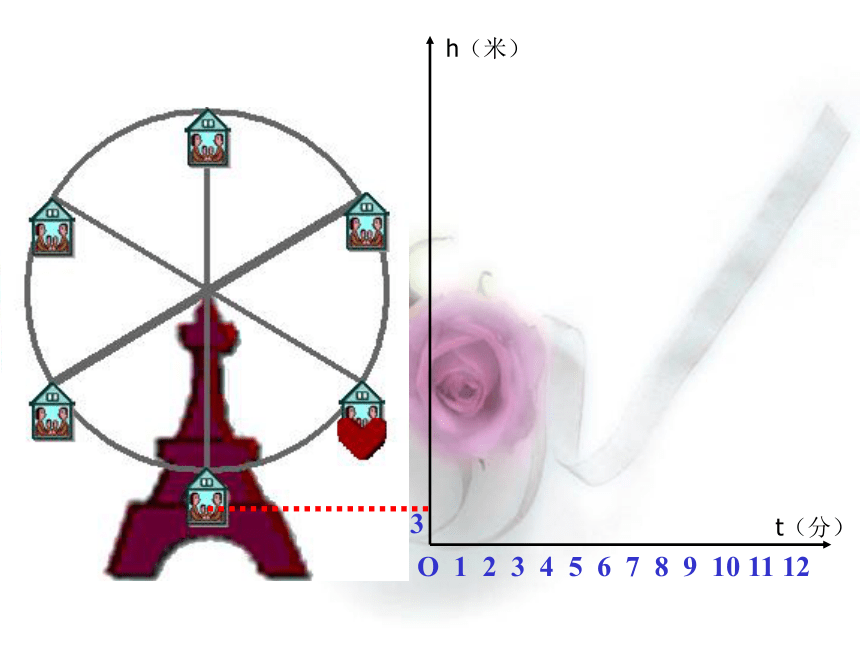
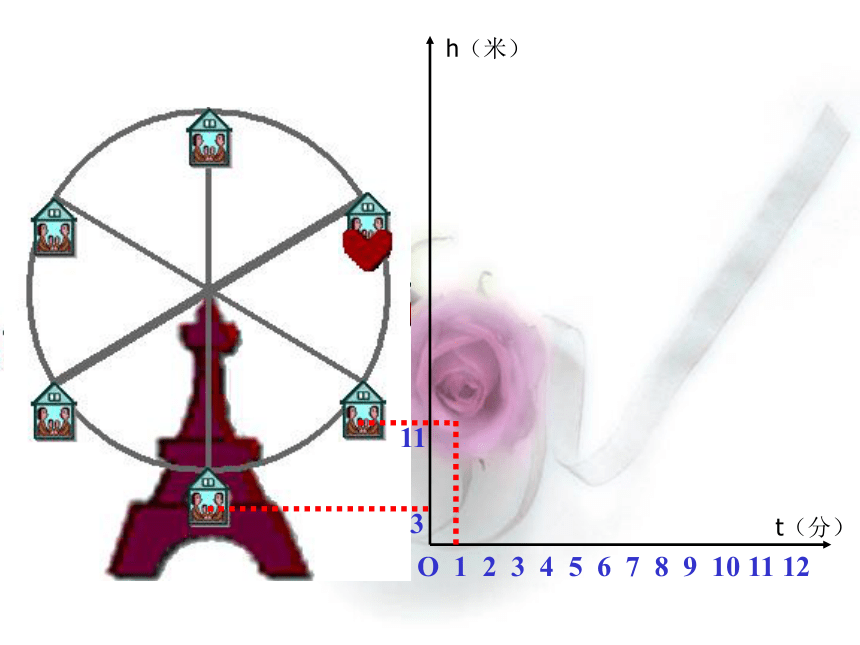
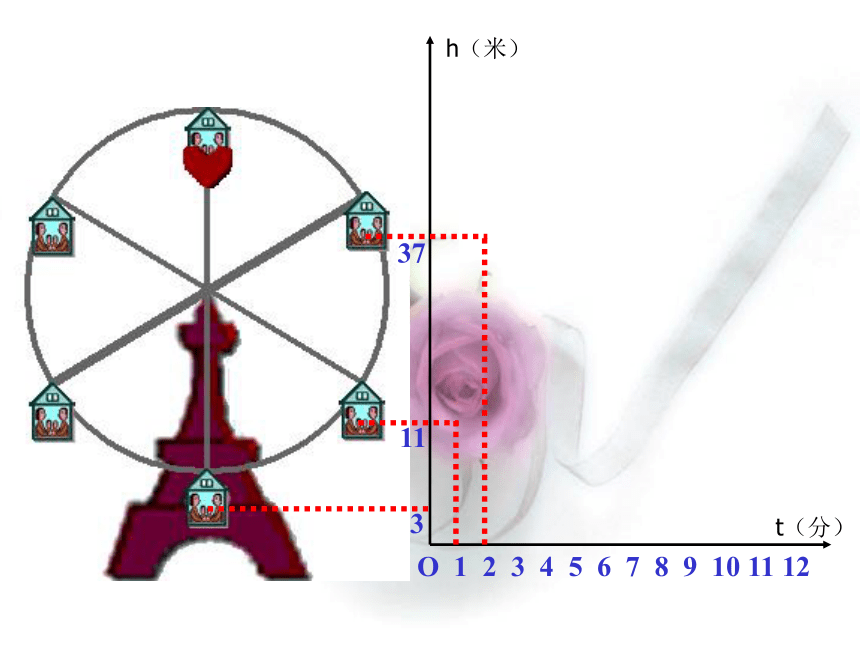
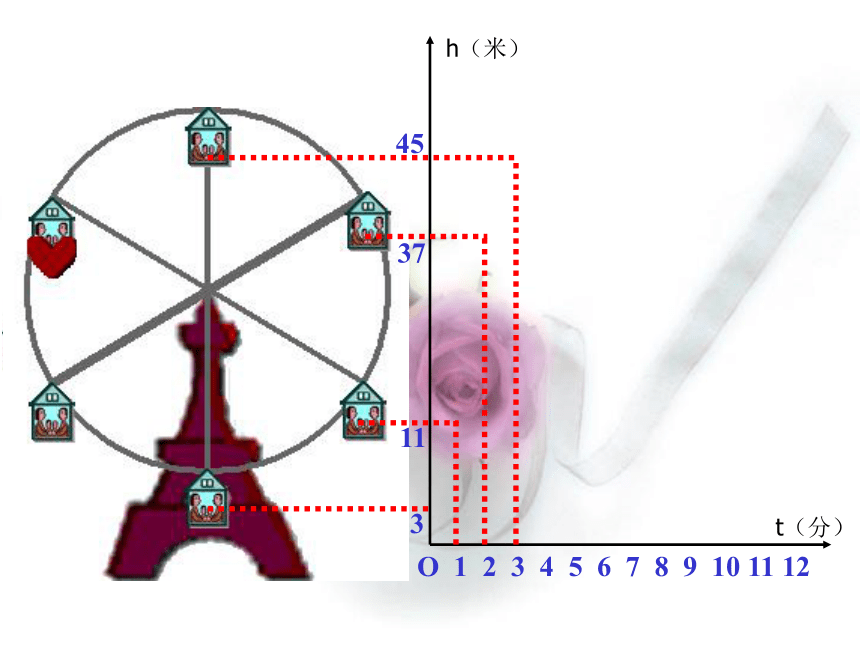
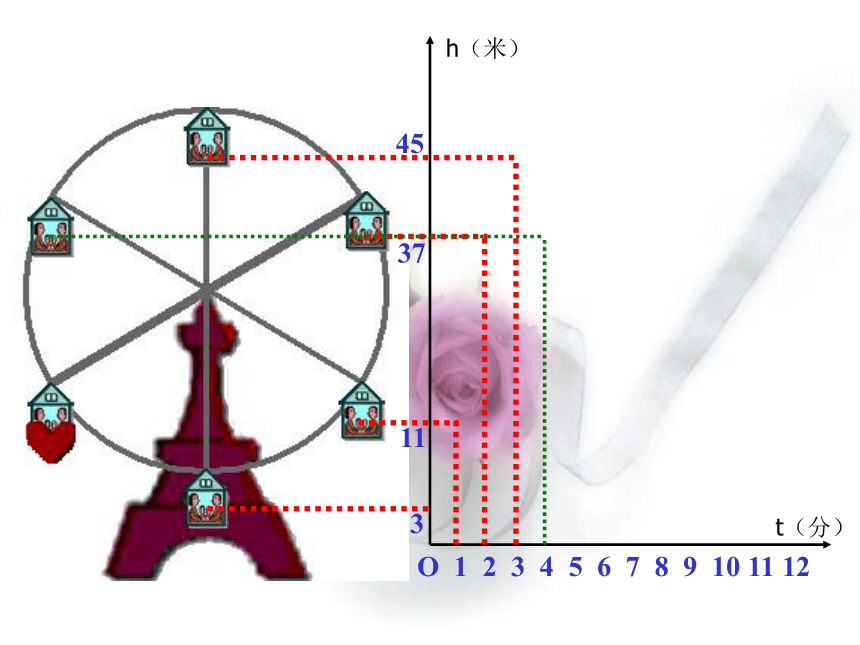
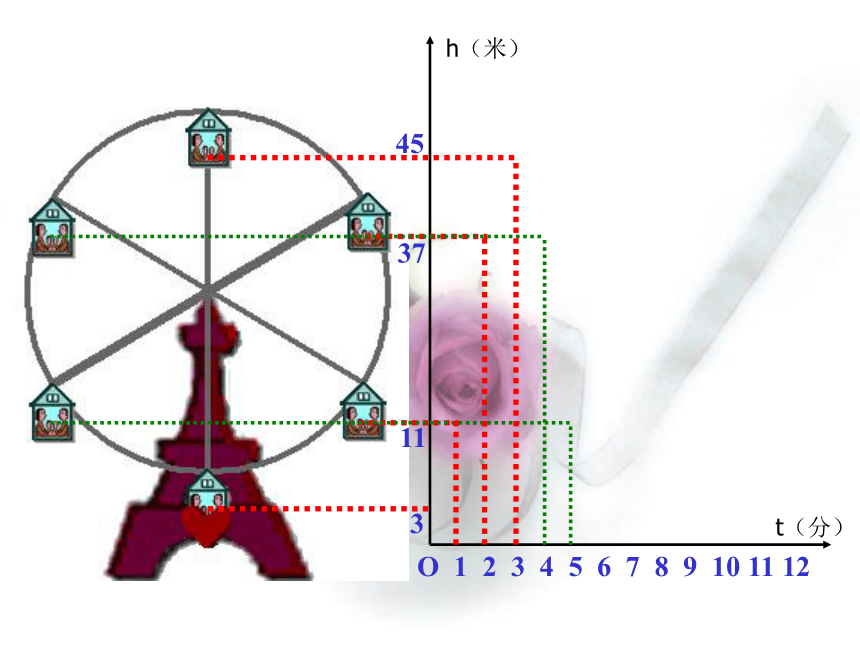
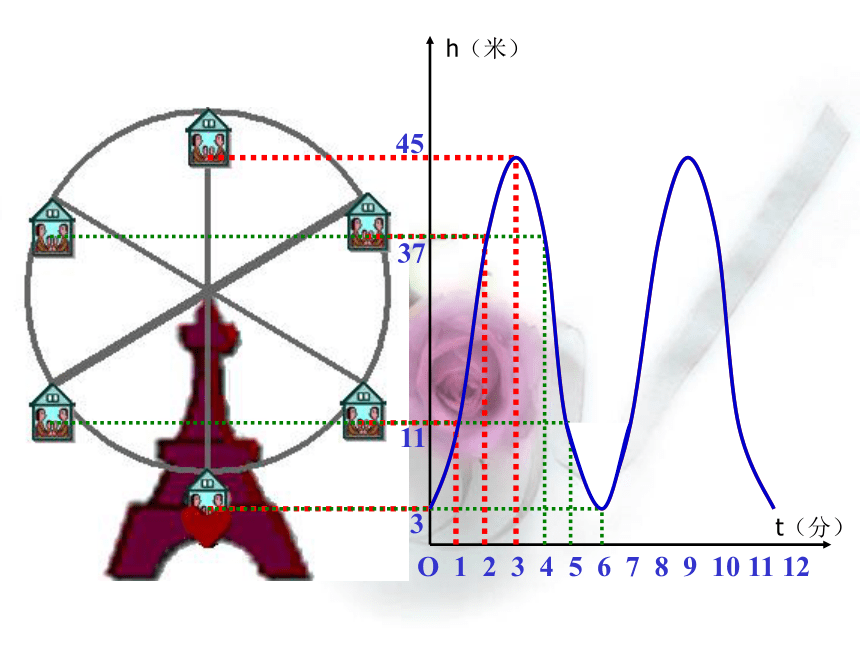
课件20张PPT。变量与 函 数 如果你坐在摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?例1O 1 2 3 4 5 6 7 8 9 10 11 123h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 12311h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 1231137h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)O 1 2 3 4 5 6 7 8 9 10 11 123113745h(米)t(分)下图反映了旋转时间t(分)与摩天轮上一点的高度h(米)之间的关系. 瓶子和罐头盒等圆柱形的物体,常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?1361015例2 圆周长和半径有直接的关系,随着半径的增长,圆周长是怎样变化的呢?123例3 某城市居民用的天然气,1立方米收费1.7元,则使用 x 立方米天然气应交纳的费用 y(元)为 y = 1.7 x例4 大家都知道,路程(s)、速度(v)、时间(t)之间存在关系: s = v t 假设某人开车,速度v为50千米/时,时间 t小时以后 ,此人行驶了多长路程. s = 50 t例5在例1中,摩天轮的高度随着时间的变化而变化.在例2中,物体总数随着层数变化而变化.在例3中,圆的周长随着半径变化而变化.在例4中,交纳的费用随着天然气的体积变化而变化.在例5中,路程随着时间的变化而变化. 仔细观察以上的5个例子,你能总结所给数据之间存在着什么规律吗? 我们可以发现,在以上的5个例子中,有的数会发生变化,有的数不会发生变化.取值会发生变化的量称为变量(variable)取值固定不变的量称为常量(或常数)(constant)聪明的同学们,请结合上面的5个例子,指出哪几个量是常量,哪几个量是常量?关于函数的几个名词 如果变量 y 随着变量 x 而变化,并且对于 x 取得每一个值,y 都有唯一的一个值与它对应,那么称 y是x 的函数(fun_ction),记作y =f (x).
这里的f (x)是英文a fun_ction of x ( x 的函数)的简记.这时把 x 叫作自变量( argument ),
把 y 叫作因变量( dependent variable). 对于自变量 取的每一个值a,因变量y的对应值称为函数值(value of fun_ction),记作f (a).说一说在例1中,____是自变量,____是____的函数.在例2中,____是自变量,____是____的函数.在例3中,____是自变量,____是____的函数.在例4中,____是自变量,____是____的函数.在例5中,____是自变量,____是____的函数.练习 指出下列关系式中的变量与常量1、球的表面积s (cm2)与球半径r(cm)的关系式是s=4лR22、设圆柱的底面半径r(m)不变,圆柱的体积v(m3 )与圆柱的高h(m)的关系式是v=2πr2h3、以固定的速度V0(米/秒)向上抛一个球,小球的高度h(米)与小球运动的时间t(秒)之间的关系式是h=V0t-4.9t2数学是一种艺术,
需要我们用心去研究。
这里的f (x)是英文a fun_ction of x ( x 的函数)的简记.这时把 x 叫作自变量( argument ),
把 y 叫作因变量( dependent variable). 对于自变量 取的每一个值a,因变量y的对应值称为函数值(value of fun_ction),记作f (a).说一说在例1中,____是自变量,____是____的函数.在例2中,____是自变量,____是____的函数.在例3中,____是自变量,____是____的函数.在例4中,____是自变量,____是____的函数.在例5中,____是自变量,____是____的函数.练习 指出下列关系式中的变量与常量1、球的表面积s (cm2)与球半径r(cm)的关系式是s=4лR22、设圆柱的底面半径r(m)不变,圆柱的体积v(m3 )与圆柱的高h(m)的关系式是v=2πr2h3、以固定的速度V0(米/秒)向上抛一个球,小球的高度h(米)与小球运动的时间t(秒)之间的关系式是h=V0t-4.9t2数学是一种艺术,
需要我们用心去研究。
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
