4.1.2函数的表示法 课件 (24张ppt)
文档属性
| 名称 | 4.1.2函数的表示法 课件 (24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 447.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-09 00:00:00 | ||
图片预览








文档简介
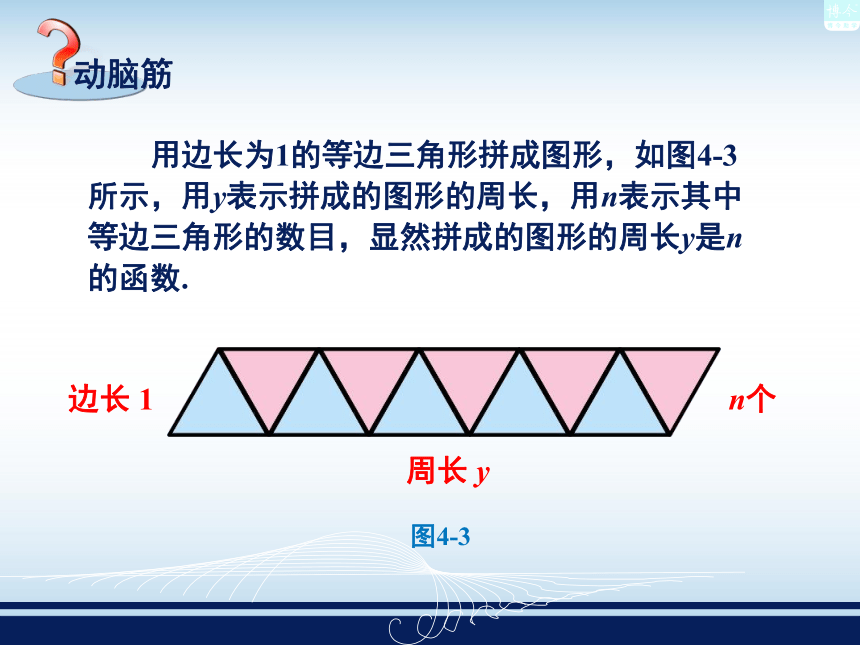
课件24张PPT。 函数和它的表示法——4.1.2 函数的表示法(1)上节问题1是怎样表示气温T与时间t之间的
函数关系的?
(2)上节问题2是怎样表示正方形的面积S与边长x
之间的函数关系的?
(3)上节问题3是怎样表示交纳的费用y与使用天然气
的体积x之间的函数关系的?自学目标: 请同学们预习课本回答下列问题
1、什么是图像法?
2、什么是列表法?
3、什么是公式法?
4、这三种方法各有什么优点? 1、 像上节问题1那样,建立平面直角坐标系,以自变量取的每一个值为横坐标,以相应的值(即因变量的对应值)为纵坐标,描出每一个点,由所有这些点组成的图形称为这个函数的图象. 这种表示函数关系的方法称为图象法.教 第一行表示自变量取的各个值, 2、像上节问题2那样,列一张表, 第二行表示相应的函数值(即因变量的对应值), 这种表示函数关系的方法称为列表法.边长 x 1 2 3 4 5 6 7 …面积 S 1 4 9 16 25 36 49 … 3、像上节问题3那样,用式子表示函数关系的方法称为公式法,这样的式子称为函数的表达式.
用公式法表示函数关系,可以方便地计算函数值.
我们可以看到,用图象法、列表法、公式法均
可以表示两个变量之间的函数关系.
用图象法表示函数关系,可以直观地看出因变量
如何随着自变量而变化; 用列表法表示函数关系,可以很清楚地看出自变量
取的值与因变量的对应值;
(1) 填写下表:边长 1 (2) 试用公式法表示这个函数关系. (3) 试用图象法表示这个函数关系. (1) 当只有1个等边三角形时,图形的周长为3,
每增加1个三角形,周长就增加1,因此填表如下:345678910… (2) n是自变量,y是因变量,周长y与三角形个数n
之间的函数表达式是y = n+2(n为正整数).(3) 因为函数y = n+2中,自变量n的取值范围是正整数集,
因此在平面直角坐标系中可以描出无数个点,这些点
组成了y = n+2的函数图象,如图4-4.(1)自行车发生故障是在什么时间?此时离家有多远?
(2)修车花了多长时间?修好车后又花了多长时间到
达学校?
(3)小明从家到学校的平均速度是多少?图4-5(1)自行车发生故障是在什么时间?此时离家有多远?图4-5(1)自行车发生故障是在什么时间?此时离家有多远?(2)解 从横坐标看出,小明修车花了15 min;
小明修好车后又花了10 min到达学校.(2)修车花了多长时间?修好车后又花了多长时间
到达学校?图4-5图4-5图4-5(3)解 从纵坐标看出,小明家离学校2100 m;
从横坐标看出, 他在路上共花了30 min,
因此, 他从家到学校的平均速度是
2100 ÷ 30 = 70 (m/min).(3)小明从家到学校的平均速度是多少?图4-51. 一个正方形的顶点分别标上号码1,2,3,4,如图2-4所示,直线l经过第2、4号顶点.作关于直线l的轴反射,这个正方形的各个顶点分别变成哪个顶点?填在下表中:3214 这个表给出了y是x的函数.画出它的图象,它的图象由几个点组成?答:图象由4个点组成.答: y = 180°-2x( 0°<x < 90°). 3. 如图是A 市某一天内的气温随时间而变化的函数图象,
结合图象回答下列问题:
(1)这一天中的最高气温是多少?是上午时段,还是
下午时段?
(2)最高气温与最低气温相差多少?
(3)什么时段,气温在逐渐升高?什么时段,气温在
逐渐降低?
答:(1)24℃,下午时段;
(2)16℃;
(3)2:00—14:00时段,气温逐渐升高;
0:00—2:00和14:00—24:00时段,
气温逐渐降低.小结函数的三种表示方法:图像法,列表法,公式法。作业布置第116页T4、T5结 束
函数关系的?
(2)上节问题2是怎样表示正方形的面积S与边长x
之间的函数关系的?
(3)上节问题3是怎样表示交纳的费用y与使用天然气
的体积x之间的函数关系的?自学目标: 请同学们预习课本回答下列问题
1、什么是图像法?
2、什么是列表法?
3、什么是公式法?
4、这三种方法各有什么优点? 1、 像上节问题1那样,建立平面直角坐标系,以自变量取的每一个值为横坐标,以相应的值(即因变量的对应值)为纵坐标,描出每一个点,由所有这些点组成的图形称为这个函数的图象. 这种表示函数关系的方法称为图象法.教 第一行表示自变量取的各个值, 2、像上节问题2那样,列一张表, 第二行表示相应的函数值(即因变量的对应值), 这种表示函数关系的方法称为列表法.边长 x 1 2 3 4 5 6 7 …面积 S 1 4 9 16 25 36 49 … 3、像上节问题3那样,用式子表示函数关系的方法称为公式法,这样的式子称为函数的表达式.
用公式法表示函数关系,可以方便地计算函数值.
我们可以看到,用图象法、列表法、公式法均
可以表示两个变量之间的函数关系.
用图象法表示函数关系,可以直观地看出因变量
如何随着自变量而变化; 用列表法表示函数关系,可以很清楚地看出自变量
取的值与因变量的对应值;
(1) 填写下表:边长 1 (2) 试用公式法表示这个函数关系. (3) 试用图象法表示这个函数关系. (1) 当只有1个等边三角形时,图形的周长为3,
每增加1个三角形,周长就增加1,因此填表如下:345678910… (2) n是自变量,y是因变量,周长y与三角形个数n
之间的函数表达式是y = n+2(n为正整数).(3) 因为函数y = n+2中,自变量n的取值范围是正整数集,
因此在平面直角坐标系中可以描出无数个点,这些点
组成了y = n+2的函数图象,如图4-4.(1)自行车发生故障是在什么时间?此时离家有多远?
(2)修车花了多长时间?修好车后又花了多长时间到
达学校?
(3)小明从家到学校的平均速度是多少?图4-5(1)自行车发生故障是在什么时间?此时离家有多远?图4-5(1)自行车发生故障是在什么时间?此时离家有多远?(2)解 从横坐标看出,小明修车花了15 min;
小明修好车后又花了10 min到达学校.(2)修车花了多长时间?修好车后又花了多长时间
到达学校?图4-5图4-5图4-5(3)解 从纵坐标看出,小明家离学校2100 m;
从横坐标看出, 他在路上共花了30 min,
因此, 他从家到学校的平均速度是
2100 ÷ 30 = 70 (m/min).(3)小明从家到学校的平均速度是多少?图4-51. 一个正方形的顶点分别标上号码1,2,3,4,如图2-4所示,直线l经过第2、4号顶点.作关于直线l的轴反射,这个正方形的各个顶点分别变成哪个顶点?填在下表中:3214 这个表给出了y是x的函数.画出它的图象,它的图象由几个点组成?答:图象由4个点组成.答: y = 180°-2x( 0°<x < 90°). 3. 如图是A 市某一天内的气温随时间而变化的函数图象,
结合图象回答下列问题:
(1)这一天中的最高气温是多少?是上午时段,还是
下午时段?
(2)最高气温与最低气温相差多少?
(3)什么时段,气温在逐渐升高?什么时段,气温在
逐渐降低?
答:(1)24℃,下午时段;
(2)16℃;
(3)2:00—14:00时段,气温逐渐升高;
0:00—2:00和14:00—24:00时段,
气温逐渐降低.小结函数的三种表示方法:图像法,列表法,公式法。作业布置第116页T4、T5结 束
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
