1.3 直角三角形全等的判定 课件 (15张ppt)
文档属性
| 名称 | 1.3 直角三角形全等的判定 课件 (15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 382.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-09 21:20:26 | ||
图片预览






文档简介
课件15张PPT。直角三角形全等的判定执教人:陈良钊 直角三角形全等的判定回
顾
与
思
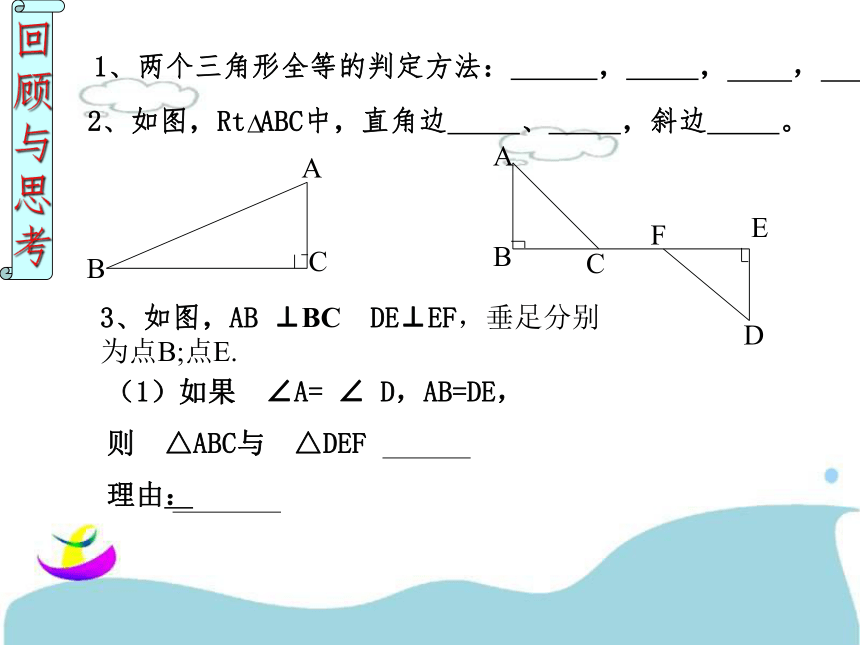
考1、两个三角形全等的判定方法: , , , 。3、如图,AB ⊥BC DE⊥EF,垂足分别为点B;点E. 2、如图,Rt ABC中,直角边 、 ,斜边 。(1)如果 ∠A= ∠ D,AB=DE,
则 △ABC与 △DEF
理由: (2)如果 ∠ A= ∠ D,BC=EF,
则 ABC与 DEF 理由 _ △ △ (3)如果AB=DE,BC=EF,
则 △ ABC与 △DEF 理由 _ (4)如果AB=DE,BC=EF,AC=DF
则 △ABC与 △DEF 理由__ 如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.(1)你能帮他想个办法吗?方法一:测量斜边和一个对应的锐角. (AAS)方法二:测量没遮住的一条直角边和一个对应的锐角. (ASA)或(AAS)⑵ 如果他只带了一把皮尺,能完成这个任务吗? 工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.他的结论对吗?下面让我们一起来验证这个结论。做一做已知线段a、c(a﹤c)和一个直角α,利用尺规作一个Rt△ABC,使∠C= ∠ α ,CB=a,AB=c.你们能作出来吗?按照下面的步骤做一做:⑴ 作∠MCN=∠α=90°;⑵ 在射线CM上截取线段CB=a;⑶ 以点B为圆心,线段C为半径画弧,交射线CN于点A;⑷ 连接AB.⑴ △ABC就是所求作的三角形吗?⑵ 剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗? 斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”或“HL”.直角三角形的判定定理想一想 你能够用几种方法判定两个直角三角形全等? 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.例 如图,BD,CE分别是△ABC的高,且BE=CD. AEDCB求证:Rt△BEC≌Rt△CDB.证明 ∵BC,CE是△ABC的高,∴∠BEC=∠CDB=90° 在Rt△BEC 和Rt△CDB中, ∵ BC=CB (公共边)
BE=CD(已知)
∴ Rt△BEC≌Rt△CDB
提升自我如图:已知AC=AD, ∠C=∠D=90°,能说明BC与BD相等吗?CBDA归纳:在直角三角形全等的证明过程 中,一般可以采用多种方法,但要注意灵活运用,选择最合适的证明方法。 证明: ∵∠C=∠D=90°
∴△ABC和△ABD为Rt△
又∵AC=AD,AB=AB
∴△ABC≌△ABD (HL)
∴BC=BD 课堂训练:教材20页第1、2题课堂训练: 教材20页练习1、2题。课堂小结:本节课我们收获了哪些知识?1、今天所学的直角三角形全等的判定定理是什么?
2、直角三角形全等有几种判定方法?布置作业:
教材第21页习题A组1、2、3、4题。课后作业:
教材21页习题A组1、2、3、4题下 节 课 再 见
顾
与
思
考1、两个三角形全等的判定方法: , , , 。3、如图,AB ⊥BC DE⊥EF,垂足分别为点B;点E. 2、如图,Rt ABC中,直角边 、 ,斜边 。(1)如果 ∠A= ∠ D,AB=DE,
则 △ABC与 △DEF
理由: (2)如果 ∠ A= ∠ D,BC=EF,
则 ABC与 DEF 理由 _ △ △ (3)如果AB=DE,BC=EF,
则 △ ABC与 △DEF 理由 _ (4)如果AB=DE,BC=EF,AC=DF
则 △ABC与 △DEF 理由__ 如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.(1)你能帮他想个办法吗?方法一:测量斜边和一个对应的锐角. (AAS)方法二:测量没遮住的一条直角边和一个对应的锐角. (ASA)或(AAS)⑵ 如果他只带了一把皮尺,能完成这个任务吗? 工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.他的结论对吗?下面让我们一起来验证这个结论。做一做已知线段a、c(a﹤c)和一个直角α,利用尺规作一个Rt△ABC,使∠C= ∠ α ,CB=a,AB=c.你们能作出来吗?按照下面的步骤做一做:⑴ 作∠MCN=∠α=90°;⑵ 在射线CM上截取线段CB=a;⑶ 以点B为圆心,线段C为半径画弧,交射线CN于点A;⑷ 连接AB.⑴ △ABC就是所求作的三角形吗?⑵ 剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗? 斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”或“HL”.直角三角形的判定定理想一想 你能够用几种方法判定两个直角三角形全等? 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.例 如图,BD,CE分别是△ABC的高,且BE=CD. AEDCB求证:Rt△BEC≌Rt△CDB.证明 ∵BC,CE是△ABC的高,∴∠BEC=∠CDB=90° 在Rt△BEC 和Rt△CDB中, ∵ BC=CB (公共边)
BE=CD(已知)
∴ Rt△BEC≌Rt△CDB
提升自我如图:已知AC=AD, ∠C=∠D=90°,能说明BC与BD相等吗?CBDA归纳:在直角三角形全等的证明过程 中,一般可以采用多种方法,但要注意灵活运用,选择最合适的证明方法。 证明: ∵∠C=∠D=90°
∴△ABC和△ABD为Rt△
又∵AC=AD,AB=AB
∴△ABC≌△ABD (HL)
∴BC=BD 课堂训练:教材20页第1、2题课堂训练: 教材20页练习1、2题。课堂小结:本节课我们收获了哪些知识?1、今天所学的直角三角形全等的判定定理是什么?
2、直角三角形全等有几种判定方法?布置作业:
教材第21页习题A组1、2、3、4题。课后作业:
教材21页习题A组1、2、3、4题下 节 课 再 见
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
